Palladium dispersion effects on wet methane oxidation kinetics

Abstract

The catalytic activity for dry and wet methane oxidation over a series of palladium–alumina catalysts with palladium loadings from 0.23 to 3.6 wt% Pd and systematically varied PdO dispersions from 8.1 to 39% was evaluated by flow reactor measurements and compared with multiscale simulations. The catalysts were prepared by industrially relevant incipient wetness impregnation followed by controlled calcination to provide similar active surface area with a realistic contact between active PdO nanoparticles and the alumina support. Kinetic analysis reveals that in wet conditions, the apparent activation energy for methane oxidation decreases as the PdO particle size increases as opposed to dry conditions where it increases. Active sites at the rim of the PdO particles in contact with the alumina support seem to contribute more to the overall activity under dry conditions but are more sensitive to wet conditions than PdO sites farther away from the rim. This sensitivity is likely due to more severe blocking by hydroxyl groups formed by water dissociation and reversed spillover. Simulations support that PdO bound hydroxyls well may form under the present reaction conditions. It is envisaged that the design of palladium–alumina catalysts for high methane turn-over frequency should target high but not too high PdO dispersion, i.e., the PdO particles should not be smaller than about 2 nm, as to balance water tolerance and palladium utilisation.

---

1 Introduction

Combustion of methane rich natural gas and biogas has the advantage of delivering more useful heat per formed carbon dioxide with less formation of toxic emissions, e.g., nitrogen oxides, sulfur oxides and particulates, compared to combustion of coal and diesel/gasoline.¹ Uncontrolled slip of methane from the combustion, however, poses a considerable risk to the environment as methane is a strong greenhouse gas. The preferred method to convert slipped methane is to implement a suitable catalytic after treatment technology that enables its complete oxidation into carbon dioxide and water. The typical catalyst is almost exclusively of the type of a supported noble metal. Common formulations include palladium particles, sometimes with the addition of another noble metal such as platinum,^2–4 on a refractory metal oxide, e.g., alumina (Al₂O₃) or ceria that can have been modified by silica or zirconia.^5–11 When operated in lean conditions, oxygen adsorbs onto the palladium particles that are oxidised into palladium oxide (PdO) particles at operating temperatures. The PdO phase is the catalytic active phase under lean conditions once the oxide is well developed.^12–14 In contrast, for monometallic platinum catalysts, the oxidation of methane over platinum is inhibited by oxygen making palladium the element of choice in applications with oxygen excess.^15–17

The methane oxidation over palladium–alumina formulations is known to be inhibited by water present in the combustion exhaust and/or generated by the complete methane oxidation reaction itself.^18–21 Previous studies report that the inhibition is caused by formation of hydroxyl groups and/or adsorbed water blocking the catalytically active PdO sites.^22–31 Also the formation of an inactive Pd(OH)₂ phase and site blocking by carbonates have been brought forward as additional deactivation mechanisms.^32–34 In the case of water inhibition, infrared spectroscopic measurements evidence that hydroxyl groups build up on the alumina surface both by spill-over of reaction products and direct water dissociation.^35–38 Hydroxyls present in the immediate vicinity of the PdO particles, i.e., on the PdO rim, seem to be of particular importance for the decreased methane oxidation activity. Hence, methane oxidation in wet (lean) conditions should hypothetically depend on the PdO dispersion as highly dispersed catalysts expose a higher fraction of PdO rim sites.

The effects of PdO dispersion on dry methane oxidation have been studied previously,^39–43 but corresponding systematic studies in wet conditions are scarce. Willis et al. elegantly deposited prefabricated, size-controlled, palladium nanocrystals ranging from 2 to 9 nm onto different support materials to obtain a final palladium loading of 0.5 wt%. They report the highest rate for methane oxidation for catalysts with PdO particles of 4–5 nm in diameter in both absence and presence of water vapor.⁴² Here we aim at understanding the role of PdO dispersion on the wet methane oxidation, relevant for lean engine combustion exhausts, over palladium–alumina catalysts prepared by industrially relevant methods that give a realistic interaction between the formed PdO nanoparticles and the γ-Al₂O₃ support. By use of incipient wetness impregnation followed by controlled calcination, a series of PdO/γ-Al₂O₃ powder and monolith catalysts with systematic variation of the PdO dispersion but with similar total active surface area was prepared. The catalytic kinetics was then studied by chemical flow reactor measurements and conceptually by simulations based on a multiscale model developed previously.^44,45

2 Materials and methods

2.1 Catalyst preparation

A parent series of PdO/γ-Al₂O₃ catalysts with target palladium loadings of 0.25, 0.5, 1, 2 and 4 wt% was prepared by incipient wetness impregnation using a palladium nitrate solution, Milli-Q water (18 MΩ cm) and γ-Al₂O₃. The impregnated powder samples were subsequently calcined in stationary air at 500 °C for 2 h. Parts of the parent sample batches with target palladium loadings of 0.5, 1, 2 and 4 wt% were exposed to an additional calcination in stationary air as to obtain catalysts with the same palladium surface area as the 0.25 wt% Pd sample. The calcination temperature and duration are summarised in Table 1 and even the most severe conditions used represent realistic cases. Monolithic catalysts carrying 200 mg of powder catalyst were prepared by dip coating cordierite monolith substrates (l = 20 mm, ∅ = 14 mm, 400 cpsi, Corning®) with a slurry containing catalyst powder, binder (Disperal, Sasol) and 50/50 mix of water and ethanol with intermittent drying under a heating gun until the final weight was achieved. The monolith catalysts were then calcined in static air at 500 °C for 2 h.

Table 1 Summary of catalyst calcination conditions and properties including measured palladium loading, specific surface area (SSA), specific CO uptake, specific number of surface Pd atoms, specific Pd surface area, average Pd dispersion (D_Pd) and hemispherical particle diameter (d_Pd) for fresh (used) powder samples

Sample ID	Calcination conditions	Pd loading (wt%)	SSA (m^2 g^−1)	CO uptake (μmol g^−1)	Surface Pd (μmol g^−1)	Pd area (m^2 g^−1)	D Pd (%)	d Pd (nm)
a Using stoichiometric factors of 2.1. b Using stoichiometric factors of 2.2.
Parent
0.23PdAl	4 h at 500 °C (=STD)	0.23	145 (144)	9.7 (6.3)	20^a (13)	0.96^a (0.63)	93 (62)	1.2 (1.8)
0.47PdAl	STD	0.47	144 (147)	15 (12)	32^a (25)	1.5^a (1.3)	73 (61)	1.5 (1.8)
0.93PdAl	STD	0.93	146 (146)	22 (15)	48^b (33)	2.3^b (1.5)	54 (36)	2.1 (3.1)
1.9PdAl	STD	1.9	140 (134)	28 (24)	62^b (53)	2.9^b (2.5)	34 (29)	3.3 (3.8)
3.6PdAl	STD	3.6	138 (138)	32 (27)	70^b (59)	3.4^b (2.8)	21 (18)	5.3 (6.4)
Modified
0.47PdAl	STD + 7 h at 800 °C	0.47	134 (127)	9.6 (7.9)	21^b (17)	0.99^b (0.82)	47 (39)	2.6 (2.8)
0.93PdAl	STD + 3.5 h at 850 °C	0.93	129 (130)	12 (10)	26^b (22)	1.3^b (1.0)	32 (25)	3.5 (4.5)
1.9PdAl	STD + 4 h at 900 °C	1.9	122 (124)	11 (10)	24^b (22)	1.1^b (1.1)	14 (13)	8.3 (8.8)
3.6PdAl	STD + 6 h at 900 °C	3.6	118 (112)	13 (12)	29^b (26)	1.3^b (1.3)	8.5 (8.1)	13 (13.8)

---

2.2 Physicochemical catalyst characterization

The palladium content of the catalysts was measured with inductively coupled plasma optical emission spectrometry (ICP-OES). For each measurement, about 30 mg of catalyst sample was digested in aqua regia at 180 °C using a microwave oven (Start D, Milestone). The ICP-OES measurements (Optima 8300 instrument, Perkin Elmer) were then performed using the two emission wavelengths 340.458 and 324.270 nm.

The specific surface area (SSA) of each sample was determined by nitrogen physisorption at −196 °C (Micromeritics Tristar 3000) according to the Brunauer–Emmett–Teller (BET) method.⁴⁶ About 200 mg of sample was used for each measurement. The sample was dried for 3 h at 225 °C under nitrogen flow to remove weakly adsorbed species prior to measurement.

The number of surface palladium atoms for reduced samples was determined by combining data from carbon monoxide (CO) uptake measurements using pulsed CO chemisorption and infrared spectroscopic characterisation of adsorbed CO as to determine the stoichiometric factor (F_S) for CO adsorption, i.e., the number of surface palladium atoms probed by one CO molecule. For the pulsed CO chemisorption, about 200 mg sample was loaded between two quartz wool wads in a quartz U-tube enclosed in a high-temperature furnace. The sample was first degassed at 250 °C for 3 h to determine the dry weight of the sample. The pulsed CO chemisorption (ASAP2020 Plus instrument, Micromeritics) procedure was then started by an oxidative treatment in 5 vol% O₂ at 500 °C for 1 h followed by a reductive treatment in 5 vol% H₂ at 500 °C for 1 h. To finalize the pretreatment, the measurement cell was cooled to 35 °C and evacuated for 1 h. The measurement was then carried out at 35 °C by carefully increasing the analysis gas (CO) dosage. The infrared speciation of adsorbed CO was carried out in diffusive reflectance mode with a Fourier transform infrared spectrometer (VERTEX 70, Bruker) equipped with a nitrogen-cooled MCT detector and a high-temperature reaction chamber (Harrick Inc.) with CaF₂ windows all in all mounted in a mirror accessory (Harrick Praying Mantis). The temperature of the sample cup was measured by a thermocouple (type K) and controlled by a PID regulator (Eurotherm 3216) feeding the internal heating element with current. Feed gases were introduced into the reaction chamber via individual mass flow controllers (EL-FLOW® Prestige, Bronkhorst), providing a total flow of 100 ml min⁻¹. In each experiment the sample cup was filled with about 30 mg of powder sample (cf.Table 1). Prior to CO adsorption, each sample was treated with a flow of 5 vol% O₂ with Ar balance (Ar was used as balance throughout the experiments) at a set-point temperature of 550 °C for 30 min and subsequently in a flow of 5 vol% H₂ for 60 min. The temperature was then decreased to 35 °C in hydrogen where an IR reference spectrum composed of an average of 32 scans with a spectral resolution of 1 cm⁻¹ was recorded in Ar. The catalyst samples were then exposed to 0.2 vol% CO while difference spectra were recorded, also with 1 cm⁻¹ spectral resolution, every second minute for 20 minutes. Finally, the CO flow was turned off and spectra were recorded in solely Ar for 20 minutes to remove weakly bound species.

Scanning transmission electron microscopy (STEM) was used to image the size and morphology of the PdO particles for the parent powder catalysts. Prior to the measurements, the samples were mixed with a few drops of ethanol and dispersed onto lacey carbon copper grids. The samples were imaged with a high-angle annular dark-field (HAADF) detector using a microscope (FEI Titan 80-300) operating at 300 kV.

2.3 Catalytic activity tests

The dry and wet methane oxidation kinetics for both powder and monolith catalysts was studied by temperature programmed ignition–extinction experiments using chemical flow reactors. For the powder sample measurements approximately 160 mg catalyst sample was used. Both reactors consist of an insulated quartz tube surrounded with a metal coil for resistive heating. The inlet gas and sample temperatures were measured with thermocouples (type K). A gas-phase FTIR spectrometer (MultiGas 2030, MKS Instruments) was used to measure the effluent composition. Feed gas mixtures with CH₄, O₂, H₂O and Ar as balance were introduced to the reactor via mass flow controllers (Bronkhorst), providing a total flow of 200 and 1200 ml min⁻¹, corresponding to a gas hourly space velocity (GHSV) of 38 000 and 32 000 h⁻¹, for the powder and monolith samples, respectively. The catalytic performance was measured in dry (0.1 vol% CH₄ + 2 vol% O₂) and wet (0.1 vol% CH₄ + 2 vol% O₂ + 10 vol% H₂O) conditions. The temperature was increased with 4 °C min⁻¹ from 200 to 500 °C, kept at 500 °C for 5 min and finally decreased to 200 °C for measurements with powder samples. The lowest temperature reached in the measurements with monolith samples was 300 °C. This temperature cycle was repeated in total five times as to achieve repeatable methane conversion profiles during ignition and extinction.

3 Results and discussion

The focus of this study is to understand the effects of PdO dispersion on the kinetics for catalytic methane oxidation in wet conditions. The aim is to conclude on important design guidelines for industrially relevant palladium–alumina catalysts for catalytic emission control of lean methane combustion exhausts. We study the kinetics of methane oxidation over both powder and monolith catalysts that are operated in the presence of considerable (realistic) water concentrations, and use dry conditions as reference. Complementary to experiments, we conceptually employ multiscale simulations as to predict the methane conversion over the monolith catalysts and analyse the reaction kinetics. The simulations are presented and discussed in the ESI† and just occasionally mentioned herein. In the following section, we first discuss the catalyst characteristics and then the influence of PdO dispersion on the methane oxidation.

3.1 Catalyst characteristics

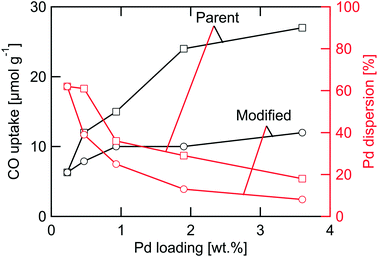
The characteristics of the PdO/γ-Al₂O₃ powder catalysts including target palladium loading, calcination condition and physicochemical properties measured before (fresh) and after (used) kinetic evaluation in flow-reactor are summarized in Table 1. The targeted palladium loading as specified in the Materials and methods section was not fully reached. The ICP-OES measurements reveal actual palladium loadings of 0.23, 0.47, 0.93, 1.9, and 3.6 wt%. The largest deviation is seen for the highest loaded catalyst that contains 90% of the targeted amount of palladium. In all analyses that follows, we use the measured Pd loadings and refer to the samples as 0.23PdAl, 0.47PdAl, 0.93PdAl, 1.9PdAl and 3.6PdAl.

The prepared catalysts can be regarded as two subsets of samples. The first subset is the parent catalysts exposed to 500 °C in air for 4 h referred to as standard (STD) calcination conditions. The SSA of these catalysts is similar, in the range 138–145 m² g⁻¹. The largest difference is between the 0.23PdAl and 3.6PdAl samples, however, not exceeding 5%. For the parent catalysts the palladium surface area increases (non-linearly) with increased Pd loading as is discussed more below. The second subset is the catalysts where the standard calcination procedure was complemented with an individual controlled calcination as to prepare catalysts with the same PdO surface area as that of the parent 0.23PdAl sample irrespective of palladium loading. We refer to these catalysts as modified catalysts and include also the parent 0.23PdAl sample in this subset. For these catalysts, the differences in SSA are larger. Compared to the parent 0.23PdAl sample, the SSA decreases by 8–19% with increasing palladium content for the remaining catalysts due to that increasingly more harsh calcination conditions were used. Still, the SSA is rather high (≥118 m² g⁻¹) and γ-Al₂O₃ is expected to be the dominant phase as measured previously for the same alumina.³⁸ Moreover, comparing the fresh and used samples, the SSA is clearly unaffected by the methane oxidation experiments. Thus it is unlikely that the differences in SSA alone will have major influence on the methane oxidation kinetics. More important, however, is the characteristics of the noble metal phase. The differences in CO uptake, which are highly affected by both the palladium loading and the calcination procedure, are shown in Fig. 1. For the parent catalysts, higher palladium loading clearly results in higher CO uptake. The increase in CO uptake is most pronounced for the low-loaded catalysts, i.e., when the palladium loading is increased from 0.23 to 0.47 and then to 0.93 wt% Pd. Comparing the two extreme samples, 0.23PdAl and 3.6PdAl, a three times higher CO uptake is measured for 3.6PdAl (32 μmol g⁻¹ compared to 9.7 μmol g⁻¹) despite the fact that it contains almost 16 times more palladium. This indicates that a significantly lower PdO dispersion should be expected for the 3.6PdAl sample. The modified catalysts show nearly the same CO uptake (about 10 μmol g⁻¹) irrespective of palladium loading. As can be seen the CO uptake is affected by the methane oxidation experiments. The corresponding numbers decreases with 15–30% for the used samples. However, the desired trends in CO uptake for the parent (increasing) and modified (unaltered) catalyst series remain. In the following, analysis and rate normalisation are based on the CO uptake from the used catalysts. The characteristics of the monolith catalysts are summarised Table S1.† Similar to the powder catalysts, the number of surface Pd atoms was determined by CO chemisorption measurements. The CO uptake is generally lower than targeted. Due to this, the PdO particles on the fresh and used monolith samples were imaged using STEM. From the images (Fig. S3†), the PdO particles appear rather similar although the PdO particle size distribution, obtained from multiple images of different sample regions, may be slightly narrower for the used monolith sample. We conclude, however, that no significant hydrothermal sintering of the PdO particles occurs during the kinetic measurements and that the reason for the low CO uptake is likely due to blocking by/accumulation of binder material during the coating procedure.

Fig. 1 CO uptake (black lines) measured by pulsed CO chemisorption and palladium dispersion (red lines) determined by combined data from CO uptake and infrared spectroscopic characterisation of CO adsorption configurations versus palladium loading for the parent (□) and modified (○) Pd/γ-Al₂O₃ powder catalysts after use in flow-reactor experiments.

The CO uptake is a sensitive indicator for determining the number of surface palladium atoms provided that the CO adsorption stoichiometry is accounted for well. Adsorption of CO on palladium (and noble metals in general) often results in a variety of adsorption configurations including linearly bound and different types of bridge-bonded CO species.⁴⁷ Their relative presence depends on the palladium particle morphology. This is commonly accounted for by inferring a stoichiometric factor (F_S) correlating the number surface palladium atoms probed by one CO molecule. Here, we use infrared spectroscopic characterisation of CO adsorption to achieve the proportions of different CO adsorption configurations and to determine the F_S for each sample (cf.Fig. 2).

Fig. 2 Difference infrared spectra for the parent (panel a) and modified (panel b) Pd/A₂O₃l catalysts recorded in Ar at 35 °C 20 min after exposure to 0.2 vol% CO for 20 min. The deconvolution of the difference spectrum for the parent 3.6PdAl sample into different components representing different CO adsorption configurations is shown as an example (panel c).

Scrutinizing the IR spectra, we first observe that the magnitudes of the IR absorption bands for adsorbed CO on the parent catalysts (panel a) increase with increasing palladium loading whereas for the modified samples, similar band intensities are seen although spectral shapes appear slightly different (panel b). Differences in spectral shape for the modified samples mainly involve the absorption band at 1989 cm⁻¹, which is more intense for catalysts with higher palladium loading. Also, the wider band at 1948 cm⁻¹ tends to be more intense for the modified 1.9PdAl and 3.6PdAl samples compared to the parent 0.23PdAl and modified 0.47PdAl samples. The observations in band intensities for the nine samples are in line with the CO uptake measurements.

To distinguish different CO adsorption configurations in the IR spectra, Voigt profiles,³⁸ were used to deconvolute the vibrational bands for adsorbed CO, see Fig. 2c. By integration of the fitted bands for linearly bound (2084, 2062, and 2047 cm⁻¹), bridge-bonded (1989, 1948 and 1904 cm⁻¹), and three-fold hollow-bonded (1811 cm⁻¹) CO,^48–50 a comparison of the proportions of the different carbonyl species for the different samples can be made to determine F_S, assuming unaltered infrared extinction coefficients.⁵¹ All samples show a predominantly amount of bridge-bonded and three-fold hollow-bonded CO species, giving rise to an F_S of 2.1–2.2 Pd atoms per adsorbed CO molecule. For the high-loaded catalysts calcined at high temperatures, spectral differences are seen in panel b of Fig. 2. The spectra for the thermally treated samples are more similar to the spectrum of the sample with lowest palladium loading, i.e. 0.23PdAl.

By use of the individual F_S, the number of surface palladium atoms can be calculated for each catalyst as well as the palladium area, and average palladium dispersion and particle diameter assuming a Pd cross-section of 7.87 Ų per atom and hemispherical palladium particle shape.⁵² The results are summarised in Table 1. For the parent samples, an increased number of surface palladium atoms as well as palladium area is seen with increased palladium loading. The palladium dispersion, however, is lower for samples with higher palladium loadings, which correlates to a larger average particle diameter. The fraction of palladium atoms located at the rim of the Pd particles is furthermore lower for the higher Pd loadings. For the modified samples, the palladium dispersion decreases significantly compared to the parent samples. This is due to a major loss in surface palladium sites as the average particle diameter becomes significantly larger due to the (deliberate) sintering as a result of the individual calcination. The palladium areas obtained for the modified samples are similar to that of the 0.23PdAl sample for all catalysts, although the number of palladium rim sites is orders of magnitude lower for the 3.6PdAl compared to the 0.23PdAl sample. Further, in Fig. 1, the palladium dispersion is plotted versus the Pd loading (red lines). The dispersion decreases with increased palladium loading for the parent catalysts and even more so for the modified catalysts. Principally, the higher the palladium loading the lower is the fraction of Pd rim sites especially for the thermally treated catalysts having almost the same total palladium area.

3.2 Methane oxidation kinetics

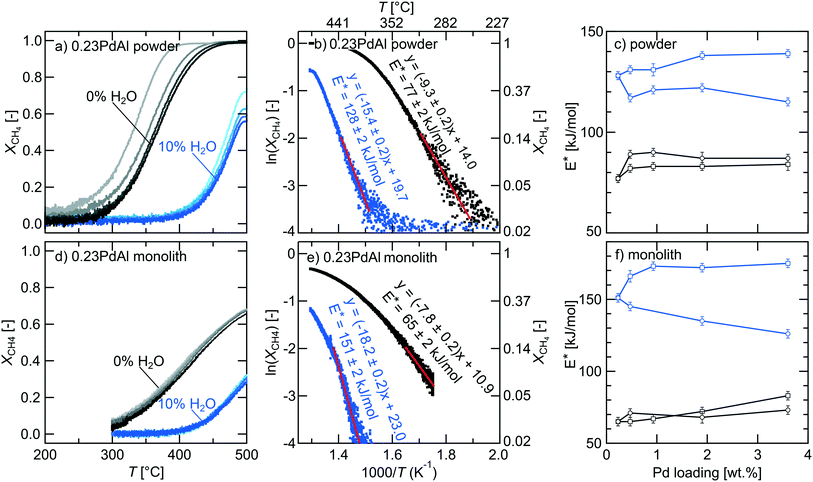
We now turn to the main discussion about wet methane oxidation focusing on the dependence of catalytic activity on the palladium dispersion. By careful analysis of the kinetic behaviour, we aim to establish catalyst design criteria for the palladium–alumina system. Fig. 3a shows the measured methane conversion for the parent 0.23PdAl catalyst during the extinction processes for the five ignition–extinction cycles in dry and wet condition, respectively. To obtain reproducible methane conversion profiles, the ignition–extinction cycle needed to be repeated at least four times in both dry and wet conditions. This procedure can be referred to as “catalyst degreening” and is common when studying supported noble metal catalysts.^53,54 The corresponding final extinction profiles for the remaining catalysts are included in Fig. S3.† In dry conditions, the methane conversion starts at approximately 275 °C for the parent samples and increases with increasing temperature and palladium loading (Fig. S3†). The temperature required to convert methane is significantly higher in the presence of water. For the modified samples, a smaller difference in methane conversion versus temperature is observed. In Table 2, a summary of the temperatures required to achieve 10, 50 and 90% methane conversion are shown for the parent and modified samples. For the parent samples in dry conditions, T₁₀ decreases with increased palladium loading from 299 °C for the 0.23PdAl sample to 248 °C for the 3.6PdAl sample. For the modified samples, no clear change in T₁₀ can be observed with increased palladium loading. Similar trends are observed for T₅₀, and T₉₀ changing from 366 to 300 °C and 423 to 335 °C, respectively. In wet conditions, only the three parent samples with the highest Pd loadings reach 90% conversion. Clearly, water has a negative effect on the methane oxidation activity for all catalysts in line with previous studies referred to in the Introduction. Also the multiscale simulations show that water may poison the PdO surface at the temperatures used here (Fig. S1 and S2†) In Fig. 3d the corresponding extinction profiles for the 0.23PdAl monolith catalyst are shown. The extinction profiles for the remaining catalysts are shown in Fig. S4.† Although the trends are generally the same as for powder catalysts, the extinction curves are notably shifted to higher temperatures and no catalyst reaches full conversion. Also the curves appears closer to each other during the catalyst degreening. As the space velocity is similar in the experiments with powders and monoliths, the difference in methane conversion between the two types is likely due to their principally different physical configurations, i.e., a packed bed versus (multiple) tube reactor, and the different ratio between flow and catalyst mass, which is about five times higher for the monolith experiments.

Fig. 3 Methane conversion over the 0.23 wt% Pd/γ-Al₂O₃ powder (panel a) and monolith (panel d) catalysts during five repeated extinction processes in 2 vol% O₂ + 0.1 vol% CH₄ (black) and 2 vol% O₂ + 0.1 vol% CH₄ + 10 vol% H₂O (blue) conditions, corresponding Arrhenius plots for the last extinction process in dry (black) and wet (blue) conditions where red lines indicate used regression regions (panel b and e), and the apparent activation energies (E*) without explicit consideration of water inhibition for the parent (□) and the modified (○) catalysts versus Pd loading in dry (black) and wet (blue) conditions (panel c and f).

Table 2 Summary of the temperatures (°C) required to convert 10, 50 and 90% methane over the parent (modified) samples in dry (D) and wet (W) conditions using 10%H₂O in the feed

	0.23PdAl	0.47PdAl	0.97PdAl	1.9PdAl	3.6PdAl
T ^D10	299 (299)	275 (313)	251 (329)	249 (315)	248 (309)
T ^D50	366 (366)	334 (388)	313 (396)	301 (375)	300 (367)
T ^D90	423 (423)	386 (466)	360 (451)	343 (428)	335 (409)
T ^W10	429 (429)	402 (432)	368 (428)	364 (430)	364 (424)
T ^W50	486 (486)	456 (—)	425 (—)	412 (499)	411 (484)
T ^W90	— (—)	— (—)	473 (—)	454 (—)	446 (—)

---

For each of the conversion profiles one may construct the corresponding Arrhenius curve by plotting lnX_CH4versus 1/T, where X_CH4 is the methane conversion and T the absolute temperature. Fig. 3b and e show the Arrhenius curves for the final extinction processes in dry and wet conditions for the parent 0.23PdAl powder and monolith catalyst, respectively. The slope of the Arrhenius curve in the low methane conversion region (≤15%), where the overall reaction rate is clearly kinetically controlled (see ESI† for evaluation of external mass transfer and internal mass and heat transport effects), reflects the apparent activation energy (E^app_a), which thus can be obtained by linear regression. However, in contrast to wet conditions, product water of the dry methane oxidation inhibits downstream catalyst sites such that the reactor cannot be considered to operate in differential mode. In this case, the effect of water should be taken into account as to obtain a true value for E^app_a. In our case the reaction order with respect to water is nearly −1 (see Table S2†) and thus E^app_a equals 2E* where E* is the slope of the Arrhenius curve. Despite this, we display E* in Fig. 3b and e, which in the dry case represents E^app_a without taking water into account, as this is the most commonly used approach in experimental studies (see for example Willis et al.⁴²) In this case, the E* for the powder is 77 and 128 kJ mol⁻¹ for dry and wet condition, respectively. These values fall well within the range of reported values and are in good agreement with numerous previous experimental and theoretical studies for similar catalytic systems and reaction conditions.^{24,25,42,55–60}

By making Arrhenius analysis for the final extinction profile for each sample (see Fig. S6†), the obtained E* for both dry and wet conditions can be plotted as a function of palladium loading as in Fig. 3c and f. As can be seen, E* increases with increasing palladium loading for both the parent and modified powder and monolith catalysts in dry condition. For the parent powder catalysts, E* is 77 kJ mol⁻¹ for 0.23PdAl and 84 kJ mol⁻¹ for 3.6PdAl whereas for the modified catalysts, the corresponding increase is 10 kJ mol⁻¹. The corresponding value for the 0.23PdAl and 3.6PdAl monolith catalyst is 65 and 83 kJ mol⁻¹, respectively. For the modified monolith catalysts E* is fairly constant, around 70 kJ mol⁻¹. For wet condition, the E* is generally considerably higher than for dry conditions but its dependence on the palladium loading for the two catalyst subsets is rather different. This is true for both powder and monolith catalysts. For the parent 0.23PdAl powder catalyst, the E* increases from 77 to 128 kJ mol⁻¹ when water is introduced. The E* then becomes higher the higher the palladium loading and reaches 139 kJ mol⁻¹ for the parent 3.6PdAl sample. On the contrary, for the modified catalysts, the E* decreases with increased palladium loading and the corresponding value for the 3.6PdAl catalyst is 115 kJ mol⁻¹. For the monolith catalysts the impact of water is even more pronounced. Although we cannot provide a straightforward explanation for this we suggest that the differences between powder and monolith catalysts is due to the different reactor geometries and the five times larger supply of water per catalyst weight for the monolith catalysts (as space velocity was kept similar for powders and monoliths, see Materials and methods section). Also, we mention that, principally, some caution should be taken when analysing the E* as it depends on the reaction conditions, i.e., temperature. The methane conversion is, of course, much dependent on the available PdO area. Here, that implies that for the parent catalysts with high palladium loading, the onset and kinetically controlled methane conversion is achieved at lower temperatures as compared to the lower loaded catalysts. In contrast, for the modified samples, the corresponding methane conversion occurs in a much narrower temperature interval. Similarly, the methane conversion is achieved at higher temperatures for the monolith catalysts. This behaviour may influence the determination of the E* by, for example, as the relative importance of included steps may differ. However, for the modified catalysts, the calculation of E* is based on data collected in a relatively narrow temperature interval such that artifacts caused by a spread in temperature are considered unlikely.

The observed trends in apparent activation energy as a function of palladium loading for the two catalyst subsets strongly indicate the existence of different active sites, with varying activity for methane oxidation and sensitivity towards water, and their (relative) presence depends on the PdO dispersion. As a qualitative simplification, we may consider the methane oxidation to proceed predominantly on PdO sites without contact with the alumina support for the catalysts with low palladium dispersion whereas for highly dispersed palladium catalysts, the reaction occurs to a significantly higher degree on PdO sites at the particle rim in contact with the alumina support. The latter type of site has in several studies been reported to improve CO oxidation and hydrocarbon activation, and to a high extent contribute to the overall reaction rate for several catalytic systems.^61–68 Further, we have in previous work based on systematic infrared spectroscopic surface speciation reported that active sites at the rim of alumina supported PdO particles are of particular importance for methane oxidation.³⁸ Here, we suggest that the lower activation barrier observed for methane oxidation in dry conditions over catalysts with low palladium loading is due to a higher fraction of PdO rim sites thanks to higher PdO dispersion. At this stage, we cannot unambiguously state whether or not the lower E* is thanks to alumina promoting the activity of small PdO particles or the morphology of the small particles possibly exposing edges and corners with highly active under-coordinated palladium and oxygen sites. It is clear though, that alumina stabilises active PdO particles and that smaller ones are more active than larger ones when the IWI method is used to achieve realistic contact between PdO particles and alumina. This is in line with previous studies that report strong dependency of the reaction rate on the palladium–support interaction when impregnation methods were used.^{36,43,54,69–73} Further, our interpretation is supported by the fact that for prefabricated particles in the range 2 to 9 nm deposited on metal oxides, a method presumably resulting in weaker particle–support interaction, a sole effect of particle size exists but is small.⁴²

Upon adding water to the feed, the methane oxidation clearly becomes inhibited resulting in increased E* for all catalysts. In our previous infrared spectroscopic investigation, we concluded that active sites at the rim of alumina supported PdO particles are highly sensitive to water due to formation of hydroxyl surface species inhibiting the methane oxidation reaction.³⁸ Water adsorption/dissociation is facile on alumina and the PdO rim sites may easily be blocked by reverse spill-over of hydroxyl species. Here, the parent catalysts all have rather highly dispersed PdO particles, the mean Pd particle diameter is below about 5 nm. This means that all parent catalysts have a relatively high fraction of PdO rim sites that contribute significantly to the overall methane conversion but are sensitive to/affected by water inhibition. The higher apparent activation energies for the parent catalysts with higher palladium loading are most likely due to that the relevant (kinetically controlled) data stems from a lower temperature region in which the water inhibition is more severe. Interestingly, however, for the modified catalysts, is that the E* becomes lower as the palladium loading increases or expressed differently when the PdO dispersion decreases. For this catalyst subset, clearly, the fraction of PdO sites not in contact with the alumina support increases at the expense of the fraction of rim sites. These PdO sites are less affected by reverse spill-over of hydroxyls and thus the methane oxidation reaction is less prone to water inhibition.

To further discuss the occurrence of active rim sites and their impact on the overall catalytic activity, reaction rates were extracted from the methane conversion profiles at different temperatures and normalized with, on the one hand, the number of surface palladium atoms, i.e., methane turnover frequency (TOF) and, on the other hand, palladium mass of each catalyst.⁷⁴Fig. 4a and b show the methane TOF for the parent and modified catalysts plotted against the palladium loading. In dry conditions, the methane TOF decreases with increasing palladium loading. This can be expressed as the rate increases with decreasing particle size or increasing proportion of rim sites. The lower rates for modified samples with lower palladium dispersion compared to the 0.23PdAl sample is a strong indication of the importance of the rim sites for the methane oxidation, which corresponds to previous findings.^62–65 In wet conditions, the methane TOF is generally considerably lower for all catalysts and all temperatures (except for the higher loaded parent catalysts at high temperatures) such that most of the activity is lost. The activity drop, however, is higher for the more highly dispersed catalysts. This supports the interpretation that PdO rim sites are highly active in dry conditions but less tolerant to wet conditions due to more severe blocking by, e.g., hydroxyls.³⁸ Scrutinizing Fig. 4a and b in more detail, we propose that the targeted PdO particle size should not be smaller than about 2 nm (here corresponding to the 0.97 wt% Pd sample) as to balance sufficient water tolerance with palladium utilisation. Our results correspond reasonably well with the results reported by Willis et al.⁴² They found an optimal PdO particle size of 4–5 nm. Again, this was found for supported palladium crystals that were prefabricated and size-selected, which is a preparation method that likely results in catalysts with weaker PdO–support interactions as compared to the incipient wetness impregnation used here. The latter method also results in a wider range of particle sizes. However, for industrial catalyst technologies, methane TOF is not the sole parameter for high palladium utilisation. Even though 2 nm Pd particles may balance water tolerance against Pd utilisation in terms of methane TOF and the difference between dry and wet conditions is significant but not huge, the active PdO sites are still part of a particle including also interior palladium atoms that are not utilised for the catalytic reaction. From Fig. 4c and d, which shows the palladium normalised rates versus palladium loading, it is clear that the palladium normalised rate decreases monotonically with increased palladium loading for both the parent and modified series. Thus to utilise the (expensive) palladium for the reaction, a high dispersion including particles also smaller than 2 nm should be targeted. Still, the 2 nm sized particles seem to provide the least variation between dry and wet conditions.

Fig. 4 Methane turn-over frequency and rate normalised with palladium mass for the parent (□) and the modified catalysts (○) plotted against amount of palladium in each catalyst. The rates were acquired in 2 vol% O₂ + 0.1 vol% CH₄ (panel a and c) and 2 vol% O₂ + 0.1 vol% CH₄ + 10 vol% H₂O (panel b and d).

4 Concluding remarks

We show that realistic PdO/γ-Al₂O₃ catalysts with varying PdO dispersion at constant total active surface area can be prepared by incipient wetness impregnation followed by controlled calcination. From flow-reactor measurements of the methane oxidation over these catalysts in dry and wet conditions the apparent activation energy could be extracted as a function of palladium dispersion. With increasing palladium dispersion, the apparent activation energy decreases in dry conditions whereas it increases in wet conditions. We find strong indications of that PdO sites at the rim of the palladium oxide particles in contact with the alumina support play an important role for the oxidation of methane. These sites are more active in dry conditions than sites on the PdO particles not in contact with alumina but are considerably more sensitive to water. The latter is likely caused by surface hydroxyl groups formed by water dissociation and reverse spill-over. Multiscale simulations show that the formation of blocking hydroxyls is possible at the present experimental conditions. In designing palladium–alumina catalysts for high methane TOF in wet feeds we propose that the PdO particle diameter should not be smaller than about 2 nm as to create sufficient water tolerance and utilise the palladium loading, however, we stress that methane TOF is not always the sole parameter for high palladium utilisation.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was financially supported by the Swedish Energy Agency through the FFI program “Fundamental studies on the influence of water on oxidation catalyst for biogas applications” (No. 40274-1) and the Competence Centre for Catalysis, which is hosted by Chalmers University of Technology and financially supported by the Swedish Energy Agency and the member companies AB Volvo, ECAPS AB, Johnson Matthey AB, Preem AB, Scania CV AB, Umicore Denmark ApS and Volvo Car Corporation AB.

References

1. M. Gambino, R. Cericola, P. Corbo and S. Iannaccone, J. Eng. Gas Turbines Power, 1993, 115, 747–749.
2. A. A. Vedyagin, A. M. Volodin, V. O. Stoyanovskii, R. M. Kenzhin, E. M. Slavinskaya, I. V. Mishakov, P. E. Plyusnin and Y. V. Shubin, Catal. Today, 2014, 238, 80–86.
3. N. M. Martin, J. Nilsson, M. Skoglundh, E. C. Adams, X. Wang, G. Smedler, A. Raj, D. Thompsett, G. Agostini, S. Carlson, K. Norén and P.-A. Carlsson, Catal., Struct. React., 2017, 3, 24–32.
4. M. S. Wilburn and W. S. Epling, Appl. Catal., B, 2017, 206, 589–598.
5. P. Gélin and M. Primet, Appl. Catal., B, 2002, 39, 1–37.
6. Z. Li and G. B. Hoflund, J. Nat. Gas Chem., 2003, 12, 153–160.
7. M. Schmal, M. M. V. M. Souza, V. V. Alegre, M. A. P. da Silva, D. V. César and C. A. C. Perez, Catal. Today, 2006, 118, 392–401.
8. J. B. Miller and M. Malatpure, Appl. Catal., A, 2015, 495, 54–62.
9. K. Sekizawa, H. Widjaja, S. Maeda, Y. Ozawa and K. Eguchi, Catal. Today, 2000, 59, 69–74.
10. K. Eguchi and H. Arai, Appl. Catal., A, 2001, 222, 359–367.
11. R. Kikuchi, S. Maeda, K. Sasaki, S. Wennerström, Y. Ozawa and K. Eguchi, Appl. Catal., A, 2003, 239, 169–179.
12. J. Nilsson, P.-A. Carlsson, S. Fouladvand, N. M. Martin, J. Gustafson, M. A. Newton, E. Lundgren, H. Grönbeck and M. Skoglundh, ACS Catal., 2015, 5, 2481–2489.
13. J. Nilsson, P.-A. Carlsson, N. M. Martin, E. C. Adams, G. Agostini, H. Grönbeck and M. Skoglundh, J. Catal., 2017, 356, 237–245.
14. J. Nilsson, P.-A. Carlsson, N. M. Martin, P. Velin, D. M. Meira, H. Grönbeck and M. Skoglundh, Catal. Commun., 2018, 109, 24–27.
15. P.-A. Carlsson, E. Fridell and M. Skoglundh, Catal. Lett., 2007, 115, 1–7.
16. E. Becker, P.-A. Carlsson, H. Grönbeck and M. Skoglundh, J. Catal., 2007, 252, 11–17.
17. E. Becker, P.-A. Carlsson, L. Kylhammar, M. A. Newton and M. Skoglundh, J. Phys. Chem. C, 2010, 115, 944–951.
18. R. Burch, F. Urbano and P. Loader, Appl. Catal., A, 1995, 123, 173–184.
19. N. Sadokhina, G. Smedler, U. Nylén, M. Olofsson and L. Olsson, Appl. Catal., B, 2017, 200, 351–360.
20. O. Mihai, G. Smedler, U. Nylén, M. Olofsson and L. Olsson, Catal. Sci. Technol., 2017, 7, 3084–3096.
21. D. Wang, J. Gong, J. Luo, J. Li, K. Kamasamudram, N. Currier and A. Yezerets, Appl. Catal., A, 2019, 572, 44–50.
22. D. Mowery and M. Graboski, Appl. Catal., A, 1999, 21, 157–169.
23. F. Klingstedt, A. K. Neyestanaki, L. E. Lindfors, M. Lundén, M. Petersson, P. Tengström, T. Ollonqvist and J. Väyrynen, Appl. Catal., A, 2001, 209, 301–316.
24. R. Kikuchi, S. Maeda, K. Sasaki, S. Wennerström and K. Eguchi, Appl. Catal., A, 2002, 232, 23–28.
25. P. Gélin, L. Urfels, M. Primet and E. Tena, Catal. Today, 2003, 83, 45–57.
26. K. Persson, L. D. Pfefferle, W. Schwartz, A. Ersson and S. G. Järås, Appl. Catal., B, 2007, 74, 242–250.
27. R. Gholami, M. Alyani and K. Smith, Catalysts, 2015, 5, 561–594.
28. O. Mihai, G. Smedler, U. Nylén, M. Olofsson and L. Olsson, Catal. Sci. Technol., 2017, 7, 3084–3096.
29. W. Huang, E. D. Goodman, P. Losch and M. Cargnello, Ind. Eng. Chem. Res., 2018, 57, 10261–10268.
30. I. Friberg, N. Sadokhina and L. Olsson, Appl. Catal., B, 2018, 231, 242–250.
31. H. Stotz, L. Maier, A. Boubnov, A. T. Gremminger, J. Grunwaldt and O. Deutschmann, J. Catal., 2019, 370, 152–175.
32. O. Demoulin, M. Navez and P. Ruiz, Appl. Catal., A, 2005, 295, 59–70.
33. H. Na, Z. Liu and T. Zhu, React. Kinet., Mech. Catal., 2014, 111, 137–148.
34. P. J. Jodłowski, R. J. Jȩdrzejczyk, D. Chlebda, M. Gierada and J. Łojewska, J. Catal., 2017, 350, 1–12.
35. D. Ciuparu, E. Perkins and L. Pfefferle, Appl. Catal., A, 2004, 263, 145–153.
36. W. R. Schwartz and L. D. Pfefferle, J. Phys. Chem. C, 2012, 116, 8571–8578.
37. W. R. Schwartz, D. Ciuparu and L. D. Pfefferle, J. Phys. Chem. C, 2012, 116, 8587–8593.
38. P. Velin, M. Ek, M. Skoglundh, A. Schaefer, A. Raj, D. Thompsett, G. Smedler and P.-A. Carlsson, J. Phys. Chem. C, 2019, 123, 25724–25737.
39. C. Muller, M. Maciejewski, R. A. Koeppel, A. Baiker, C. A. Müller, M. Maciejewski, R. A. Koeppel and A. Baiker, Catal. Today, 1999, 47, 245–252.
40. A. M. Batkin, N. S. Teleguina, G. O. Bragina, V. I. Zaikovsky, I. P. Prosvirin, A. K. Khudorozhkov and V. I. Bukhtiyarov, Top. Catal., 2013, 56, 306–310.
41. K. Murata, Y. Mahara, J. Ohyama, Y. Yamamoto, S. Arai and A. Satsuma, Angew. Chem., 2017, 8520, 15993–15997.
42. J. J. Willis, A. Gallo, D. Sokaras, H. Aljama, S. H. Nowak, E. D. Goodman, L. Wu, C. J. Tassone, T. F. Jaramillo, F. Abild-Pedersen and M. Cargnello, ACS Catal., 2017, 7, 7810–7821.
43. K. Murata, D. Kosuge, J. Ohyama, Y. Mahara, Y. Yamamoto, S. Arai and A. Satsuma, ACS Catal., 2020, 10, 1381–1387.
44. C.-R. Florén, M. Van den Bossche, D. Creaser, H. Grönbeck, P.-A. Carlsson, H. Korpi and M. Skoglundh, Catal. Sci. Technol., 2018, 8, 508–520.
45. C.-R. Florén, P.-A. Carlsson, D. Creaser, H. Grönbeck and M. Skoglundh, Catal. Sci. Technol., 2019, 9, 3055–3065.
46. P. H. Emmett, J. Am. Chem. Soc., 1938, 60, 309–319.
47. N. M. Martin, M. Skoglundh, G. Smedler, A. Raj, D. Thompsett, P. Velin, F. J. Martinez-Casado, Z. Matej, O. Balmes and P.-A. Carlsson, J. Phys. Chem. C, 2017, 121, 26321–26329.
48. D. Tessier, A. Rakai and F. Bozon-Verduraz, J. Chem. Soc., Faraday Trans., 1992, 88, 741–749.
49. T. Lear, R. Marshall, J. A. Lopez-Sanchez, S. D. Jackson, T. M. Klapötke, M. Bäumer, G. Rupprechter, H. J. Freund and D. Lennon, J. Chem. Phys., 2005, 123, 174706.
50. S. D. Ebbesen, B. L. Mojet and L. Lefferts, Phys. Chem. Chem. Phys., 2009, 11, 641–649.
51. P. Gelin, A. R. Siedle and J. T. Yates, J. Phys. Chem., 1984, 88, 2978–2985.
52. P. A. Webb and C. Orr, Analytical Methods in Fine Particle Technology, Micromeritics Instrument Corporation, 1997.
53. X. Auvray, A. Lindholm, M. Milh and L. Olsson, Catal. Today, 2018, 299, 212–218.
54. P. Lott, P. Dolcet, M. Casapu, J.-D. Grunwaldt and O. Deutschmann, Ind. Eng. Chem. Res., 2019, 58, 12561–12570.
55. Y.-F. Y. Yao, Ind. Eng. Chem. Prod. Res. Dev., 1980, 19, 293–298.
56. J. Lampert, M. Kazi and R. Farrauto, Appl. Catal., B, 1997, 14, 211–223.
57. J. C. van Giezen, F. R. van den Berg, J. L. Kleinen, A. J. van Dillen and J. W. Geus, Catal. Today, 1999, 47, 287–293.
58. M. R. Lyubovsky and L. D. Pfefferle, Catal. Today, 1999, 47, 29–44.
59. R. E. Hayes, S. T. Kolaczkowski, P. K. C. Li and S. Awdry, Chem. Eng. Sci., 2001, 56, 4815–4835.
60. C. F. Cullis and B. M. Willatt, J. Catal., 1983, 83, 267–285.
61. M. Haruta and M. Daté, Appl. Catal., A, 2001, 222, 427–437.
62. D. Bounechada, S. Fouladvand, L. Kylhammar, T. Pingel, E. Olsson, M. Skoglundh, J. Gustafson, M. Di Michiel, M. A. Newton and P.-A. Carlsson, Phys. Chem. Chem. Phys., 2013, 15, 8648–8661.
63. I. Czekaj, K. A. Kacprzak and J. Mantzaras, Phys. Chem. Chem. Phys., 2013, 15, 11368.
64. S. Fouladvand, M. Skoglundh and P.-A. Carlsson, Catal. Sci. Technol., 2014, 4, 3463–3473.
65. T. P. Senftle, A. C. Van Duin and M. J. Janik, ACS Catal., 2017, 7, 327–332.
66. Y. Suchorski, S. M. Kozlov, I. Bespalov, M. Datler, D. Vogel, Z. Budinska, K. M. Neyman and G. Rupprechter, Nat. Mater., 2018, 17, 519–522.
67. T. K. Slot, D. Eisenberg and G. Rothenberg, ChemCatChem, 2018, 10, 2119–2124.
68. F. Dhainaut and P. Granger, Top. Catal., 2019, 62, 331–335.
69. H. Widjaja, K. Sekizawa, K. Eguchi and H. Arai, Catal. Today, 1997, 35, 197–202.
70. D. Ciuparu and L. Pfefferle, Appl. Catal., A, 2001, 209, 415–428.
71. D. Ciuparu, M. R. Lyubovsky, E. Altman, L. D. Pfefferle and A. Datye, Catal. Rev.: Sci. Eng., 2002, 44, 593–649.
72. L. S. Escandón, S. Ordóñez, A. Vega and F. V. Díez, Chemosphere, 2005, 58, 9–17.
73. S. Nasr, N. Semagina, R. E. Hayes and R. E. Hayes, Emiss. Control Sci. Technol., 2020, 6, 269–278.
74. R. L. Burwell, Manual of Symbols and Terminology for Physicochemical Quantities and Units—Appendix II: Heterogeneous Catalysis, Elsevier, 2013.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy00734j

---