Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular behaviour of methanol and dimethyl ether in H-ZSM-5 catalysts as a function of Si/Al ratio: a quasielastic neutron scattering study†
Toyin
Omojola‡
 a,
Ian P.
Silverwood
a,
Ian P.
Silverwood
 b and
Alexander J.
O'Malley
b and
Alexander J.
O'Malley
 *cd
*cd
aDepartment of Chemical Engineering, University of Bath, Claverton Down, Bath, BA2 7AY, UK
bISIS Pulsed Neutron and Muon Facility, Science and Technology Facilities Council Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Oxon OX11 0QX, UK
cCentre for Sustainable and Circular Technologies, Department of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: a.o'malley@bath.ac.uk
dUK Catalysis Hub, Research Complex at Harwell, Science and Technology Facilities Council Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Oxon, OX11 0QX, UK
First published on 26th May 2020
Abstract
The dynamical behaviour of methanol and dimethyl ether in H-ZSM-5 catalysts of differing Si/Al ratios (36 and 135) was probed using quasielastic neutron scattering to understand the effect of catalyst composition (Brønsted acid site concentration) on the behaviour of species present during the initial stages of the H-ZSM-5 catalysed methanol-to-hydrocarbons process. At room temperature in H-ZSM-5(36) isotropic methanol rotation was observed (rotational diffusional coefficient, DR = 2.6 × 1010 s−1), which contrasted qualitatively with H-ZSM-5(135) in which diffusion confined to a sphere matching the 5.5 Å channel width was observed, suggesting motion is more constrained in the lower Si/Al catalyst. At higher temperatures, confined methanol diffusion is exhibited in both catalysts with self-diffusion coefficients (Ds) measured in the range of 8–9 × 10−10 m2 s−1. However, the population of molecules immobile over the timescale probed by the instrument is significantly larger in H-ZSM-5(36), consistent with the far higher number of Brønsted acid adsorption sites. For dimethyl ether, diffusion confined to a sphere at all temperatures is observed in both catalysts with Ds measured in the range of 9–11 × 10−10 m2 s−1 and a slightly smaller fraction of immobile molecules in H-ZSM-5(135). The larger Ds values obtained for dimethyl ether arise from the sphere of confinement being larger in H-ZSM-5(36) (6.2 Å in diameter) than the 5.5 Å width of the pore channels. This larger width suggests that mobile DME is sited in the channel intersections, in contrast to the mobile methanol which is sited in the channels. An even larger confining sphere of diffusion was derived in H-ZSM-5(135) (∼8 Å in diameter), which we attribute to a lack of Brønsted sites, allowing for a larger free volume for DME diffusion in the channel intersections.
Introduction
Limited gasoline supply in the 1970s led to an increase in oil prices and motivated the search for alternative means of fuel production.1 The conversion of methanol over H-ZSM-5 catalysts was then discovered as a feasible route for gasoline production in 1977.2 The first process plant, constructed in New Zealand in 1985 was under continuous operation for at least 6 years.1 Recently, emphasis on producing value-added chemicals such as olefins have led to a resurgence in the construction of process plant units in China.3 Through gasification of biomass and coal reserves, or steam reforming of natural gas with subsequent syngas liquefaction, methanol conversion is now a viable route for the production of value-added chemicals such as olefins and fuels.2,3 For instance, DICP's MTO technology uses SAPO-34 zeotype catalysts for olefin formation from methanol in a fluidised bed reactor.3 However, a high selectivity to olefins can be obtained over H-ZSM-5 zeolite catalysts when process conditions are tuned towards low pressures4 and high temperatures.5 Although SAPO-34 catalysts are the most carbon efficient in producing light olefins,6 H-ZSM-5 provides the highest propylene yield, the most diverse product distribution and offers the possibility to re-introduce heavier olefins to boost yield of lighter olefins making efficient use of the cracking chemistry.7It is generally accepted that the hydrocarbon pool mechanism regulates product distribution during steady-state methanol-to-hydrocarbon (MTH) conversion in H-ZSM-5.8,9 This is also known as the dual cycle mechanism as it consists of linked reaction cycles involving olefin and aromatic chemistry. However, mechanistic understanding of the early stages of the conversion of methanol, comprising of an induction period and a transition regime are not well defined.10–14 Initially, methanol undergoes an equilibration reaction leading to the formation of dimethyl ether (DME) and water.15 Readily available oxygenates (methanol and DME), water, and aromatics formed from impurities (acetone, ethanol) in the feed16,17 compete for sites and their initial coverages are determined from their competitive adsorption.18 Two of the initial species, that is methanol and DME, are also sources of surface methoxy species19 which are known to proliferate during the direct conversion of oxygenates to olefins20–22 when MTH conversion is tuned towards olefin formation over H-ZSM-5 catalysts. Thus, a detailed understanding of the adsorption/desorption of methanol and DME at the acidic sites would provide insights into their conversion to surface methoxy species and availability for the formation of the first C–C bond.
Optimisation of olefin selectivity is one of the key challenges in MTH chemistry over zeolite and zeotype catalysts. Once the primary olefins are formed, methylation, cracking, hydrogen transfer and cyclisation chemistries regulate olefin selectivity.23 Of these reactions, methylation is one of the most important. Methylation by DME is faster than by methanol due to the abundance of methoxy formed on DME adsorption leading to an additional methylation route.15,24 In the 3D pore architecture of H-ZSM-5, olefin selectivity is governed by the adsorption/desorption/diffusion of oxygenates and surface reaction of active species at the Brønsted sites. Evidently, these processes differ depending on the location of the sites and their intrinsic acidity (which in turn may differ as a function of Si/Al ratio). The concentration of Brønsted acid sites is one of the main descriptors for olefin selectivity.25 These factors are considered in the development of microkinetic models26 which set a conceptual framework where the catalytic cycle can be decoupled, and their interdependencies analysed for selectivity guiding principles. As the hydrocarbon pool ultimately controls the reaction, understanding the processes governing the initial formation provides a mechanistic basis for the modelling of the reaction proceeding afterwards.27
With respect to the initial adsorption of reactant species over zeolite protons, Blaszkowski and van Santen28 observed, using DFT calculations, that DME is formed from methanol through an associative pathway. Omojola et al.19 observed that although methanol adsorbs more easily than DME on H-ZSM-5 catalysts (as shown by higher adsorption constants), the activation energies of desorption of DME are higher than methanol by ca. 10, 4, 6 kJ mol−1 over the highest temperature binding sites of H-ZSM-5 catalysts of Si/Al = 25, 36 and 135 respectively (near vacuum conditions were employed in a temporal analysis of products reactor). In this study, two types of binding sites were observed in H-ZSM-5 catalysts with high Si/Al ratios such as H-ZSM-5(135) and three binding sites were observed in catalysts with lower Si/Al ratios, i.e. H-ZSM-5(25) and (36) using a detailed elementary plug flow reactor model and a Redhead model. The Redhead method29 accounts for desorption alone, while the plug flow reactor model accounts additionally for re-adsorption and bed hydrodynamics. These binding sites are reproduced over working catalysts with a fundamental difference in the number of adsorbing molecules per active site in comparison to fresh catalysts. Molecular adsorption on low temperature binding sites and dissociative adsorption (leading to the reversible formation of surface methoxy groups) on medium and high temperature binding sites were observed for methanol and DME adsorption. Jones and Iglesia30 reached similar conclusions, observing that the mode of adsorption depends on temperature and pressure with the dissociative pathway being dominant at higher temperatures and lower pressures. However, these studies consider adsorption/desorption processes in isolation whereas the influence of diffusion of species could further regulate the availability of oxygenates for primary olefin selectivity, especially in porous materials.
In terms of studying the local, and nanoscale dynamical behaviour of the initial species in H-ZSM-5 catalysts, techniques based on molecular modelling31 and neutron spectroscopy32 can offer particularly insightful qualitative and quantitative observations.
Recent molecular modelling studies of the local dynamical behaviour of the initiation species have employed quantum mechanical molecular dynamics (QMMD) simulations to study framework methoxy formation from both methanol and DME in the presence of water and extra methanol,33 showing that the proton transfer to methanol which initiates the process is accelerated in the presence of excess methanol molecules. However, the reaction with DME is not assisted by the presence of extra methanol. Other studies have probed the above-mentioned methylation reactions, focussing on benzene, where higher methanol loadings encourage methylation from protonated methanol clusters, though this has a higher free energy barrier than methylation from a single methanol molecule in the H-ZSM-5 intersections.34 Furthermore, studies modelling isobutene reactions with methanol/DME compared methylation to the susceptibility of hydrogen transfer to produce isobutane. A particularly interesting observation was that the protonation of isobutene by the zeolite acid site, followed by the hydride shift between the methyl group of the oxygenate and the t-butyl cation occurred simultaneously with methanol, but in two separate steps with DME.35
Examples of neutron spectroscopy contributions include those from O'Malley et al.36 who used a combination of quasielastic neutron scattering (QENS) and vibrational spectroscopy (INS) to show that the immobility of methanol in H-ZSM-5 catalysts at low loadings was due to its complete room temperature conversion to framework methoxy species, in contrast to zeolite HY of the same Si/Al ratio where the methanol hydroxyl stretches were maintained and diffusion coefficients were later quantifiable.37 Later studies into the effect of MTH catalysis, and hydrocarbon pool build-up on active species mobility in H-ZSM-5 were carried out by Matam et al.,38 who further showed that methanol is immobile at room temperature when dosed into fresh, and also working H-ZSM-5 catalysts which had previously been tested at 623 K. However, over working catalysts tested at 673 K, isotropic methanol rotation was observed over the QENS instrumental time scale. The observation of methanol mobility in the catalyst tested at the highest temperature was attributed to development of mesoporosity from framework destruction due to dislodgement of lattice Al at 673 K. Earlier QENS studies by Jobic39 used instruments which probed different timescales, at higher loadings of methanol, to show both ‘local’ diffusion confined to a sphere corresponding to the H-ZSM-5 channel widths, and the longer range jump diffusion mechanisms through the H-ZSM-5 framework structure. Notably, all the aforementioned studies observe a significant immobile fraction of molecules at all temperatures, indicative of the strong adsorption to Brønsted sites in H-ZSM-5.
While nanoscale studies of methanol diffusion in acidic zeolites as a function of framework structure and catalyst use have been revealing, the molecular mobility as a function of Si/Al ratio (and therefore Brønsted acid site density) has not been studied explicitly, and the mobility of DME, to our knowledge, has not been probed experimentally on the nanoscale. The aforementioned differences in binding energies of less than 10 kJ mol−1 between methanol and DME over H-ZSM-5(36) and (135) catalysts suggest that neither species is dominant in terms of competition for sites in H-ZSM-5 at these compositions.27 The mobility of methanol and DME through the catalyst, or indeed their preferred siting in the catalyst framework structure would affect their adsorption to the binding sites and subsequent reaction. This fundamental behaviour of methanol and DME in H-ZSM-5 as a function of Si/Al ratio would therefore be of significant importance in both catalyst design and, in combination with the more macroscale adsorption/desorption studies19 would be crucial in the formulation of microkinetic models of the early stages of the MTH/O process.
We have therefore performed quasielastic neutron scattering experiments studying the dynamical behaviour of methanol and DME in H-ZSM-5 catalysts with Si/Al = 36 and 135. We find significant qualitative differences between the two species, and potentially counterintuitive differences in mobility which may be explained by a difference in preferred siting in the zeolite framework.
Experimental
Materials
The H-ZSM-5 samples used were commercial zeolite catalysts obtained from BP chemicals (Si/Al ratio = 36 and Si/Al ratio = 135) with the bulk crystallinity verified by powder X-ray diffraction in recent studies.19 The H-ZSM-5 samples were originally received in their powdered ammonium form and had to be calcined to achieve their protonated form. This was achieved through heating under vacuum at 5 °C min−1 to 450 °C and holding for 4 h. The calcined samples were dehydrated at 200 °C under vacuum for 8 h. After cooling to room temperature, methanol was then loaded using helium as a carrier gas at a rate of 100 mL min−1 to a loading of ca. 22 molecules per unit cell. H-ZSM-5(36) and (135) were loaded with DME by the gas over the sample at a flow rate of 100 mL min−1, until a loading of ca. 14 molecules per unit cell was reached in both samples. The loadings of all systems were determined gravimetrically as follows: H-ZSM-5(36) and (135) catalysts were loaded with ca. 12 wt% methanol, or DME to match typical conditions studied in kinetic experiments such as those used by Lercher and co-workers.40,41 Specifically, the loading was ∼14 wt% methanol on H-ZSM-5(36), ∼13.5 wt% methanol on H-ZSM-5(135), 12 wt% DME on H-ZSM-5(36), 10 wt% DME on H-ZSM-5(135). We note from previous literature that MTH related processes such as methylation reactions are zero order with respect to methanol when co-fed with olefins42,43 as with DME when co-fed with olefins44 or an order of less than 0.5 with respect to methanol suggesting full surface coverage.45 We therefore aimed to match our loadings with the archived literature for MTH/O kinetics. The samples (ca. 2.5 g of H-ZSM-5(36) loaded with methanol, 4 g of H-ZSM-5(135) loaded with methanol, ca. 3 g of H-ZSM-5(36) loaded with DME, ca. 4 g of H-ZSM-5(135) loaded with DME) were transferred (in a glovebox under argon) to thin walled aluminium cans of annular geometry.Quasielastic neutron scattering
QENS experiments were carried out using the time-of-flight backscattering neutron spectrometer OSIRIS46 at the ISIS Pulsed Neutron and Muon Source. The cells were placed in a top loading closed cycle refrigerator. Each sample was then cooled to a base temperature of 10 K and a resolution measurement was taken. The samples were then heated to 293, 333 and 373 K where the QENS spectra were measured.Pyrolytic graphite 002 analyser crystals were used giving an energy resolution of 24.5 μeV with energy transfers measured in a window of ±0.55 meV; the detector covered measurements over a Q range of 0.2–1.75 Å−1. The measurement was taken of the empty H-ZSM-5 samples and the signal was then subtracted from the signal of the sorbate loaded H-ZSM-5, so that only the signal from the sorbate could be extracted. In this way any scattering from the aluminium container, which is very low in comparison with the zeolite is also subtracted. No further corrections were necessary. All QENS spectra were fitted using the neutron scattering analysis software DAVE47 and MANTID.48
Results and discussion
Methanol
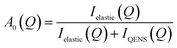
QENS spectra as a function of the momentum transfer vector Q are shown for methanol in H-ZSM-5(36) at 293 and 333 K in Fig. S1 and S2† respectively. The QENS spectra at Q = 1.67 were discounted due to the presence of a Bragg peak in both H-ZSM-5 samples at this Q value, which caused issues upon subtraction of the empty zeolite spectra from those of the loaded zeolite. The spectra were fitted to a delta function convoluted with the resolution measurement taken at 10 K, a single Lorentzian function (which was enough to describe the data satisfactorily) and a flat background function. The figures contain the data points, the total fit (black), and the quasielastic component of the spectra (red) given by the Lorentzian function. It is important to note that the presence of any quasielastic components suggest that full room temperature methoxylation cannot have taken place as in ref. 36. We note that the loadings of methanol are a factor of >5 higher than those in the referenced study, and as such far outnumber the concentration of available Brønsted acid sites per unit cell. As such, there will be a significant amount of intact methanol in the catalyst pores.The presence of a large elastic component in all the spectra suggest that either a large fraction of immobile molecules is present, or a localised motion such as rotation is observed or indeed both. Quantification of the possible localised motions present can be characterised using the elastic incoherent structure factor (EISF), given by eqn (1) is the proportion of the total scattered intensity which is elastic.
 | (1) |
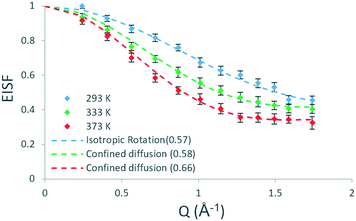 | ||
| Fig. 1 Experimental EISF plots of methanol in H-ZSM-5(36) at 293, 333 and 373 K with the corresponding theoretical models (mobile fractions shown in the legend in brackets). | ||
Several models have been used to characterise the localised motions of methanol, relating to the geometries of motion of the protons in the molecule. The models used to fit the experimental EISF at 293 K are detailed in section S1.1 of the ESI† and are depicted in Fig. 2. They include the isotropic rotation model derived by Sears,49 the model of translation diffusion confined to a sphere as derived by Volino and Dianoux50 and a 3-site jump rotational model around a circle to describe the rotation of protons in a methyl group. The model fittings are shown in Fig. S5,† the use of any of the pure models is not adequate to fit the data, and as such, the incorporation of an immobile fraction, which considers that a population of the loaded molecules are either static, or moving too slowly to be observed in the timescale probed by the instrument (∼1–100 ps), is necessary (detailed in section S1.1†). The models with the optimal immobile fraction are plotted against the experimental EISF in Fig. S6.† The best fit to experimental data at 293 K was the model of isotropic rotation with a fraction of ∼43% immobile molecules. The isotropic rotation model was also validated upon studying the broadenings of the Lorentzian component used to fit the scattering function. The broadenings, plotted in Fig. S7,† show that they are independent of Q, in line with rotational motions being observed. These widths can be used to calculate the rotational diffusion coefficient DR as outlined in ref. 38 and 39 and lead to a DR value of 2.6 × 1010 s−1.38,39
The rotational diffusion coefficient is lower than that obtained at 325 K in previous work studying methanol in H-ZSM-5 (ref. 38) potentially reflecting both the lower temperature in this study and also the presence of mesopores in the above reference generated by framework damage due to the MTH process taking place.
The experimental EISF was then fit at 333 and 373 K. Fig. S8† (section S1.1) shows the experimental EISF of methanol in H-ZSM-5(36) at 333 K. The same models described above are applied to the data. It was clear that none of the models in isolation can fit the data alone. The 3-site model falling above the experimental points at all Q values and also exhibiting a different shape to the experimental data. While the pure isotropic rotation model can fit the data at the lower Q values, it deviates at higher Q values. The pure model of confined diffusion falls well below the experimental data at all Q-values.
When an immobile fraction is incorporated into the models (Fig. S9†), we find that the best fit is given by the confined diffusion model (rconf = 2.75 Å), where 42% of the protons are considered static which fits within the error bars at all Q values. This represents a qualitative change from the behaviour exhibited at 293 K where the motions are localised and limited to rotation and may suggest that between 293 and 333 K a barrier to translational diffusion is overcome. It is notable that the immobile fraction is very similar between 293 and 333 K, potentially suggesting that while a barrier to translational diffusion is overcome for the already non-static molecules, this temperature range is not enough to induce motion in the static molecules, (or at least, enough motion to enter the 1–100 ps time window, which would be the case for non-H-bonded molecules), perhaps through breaking the interactions with the pore walls/acid sites. We find that the same model fits at 373 K, however a smaller immobile fraction of 34% provides the best fit to the data. This suggests that between 333 and 373 K more molecules are able to diffuse on the timescale of the instrument, potentially because some of the interactions with the acidic sites are broken. The experimental EISFs of methanol in H-ZSM-5(36) and their model fits are all shown in Fig. 1.
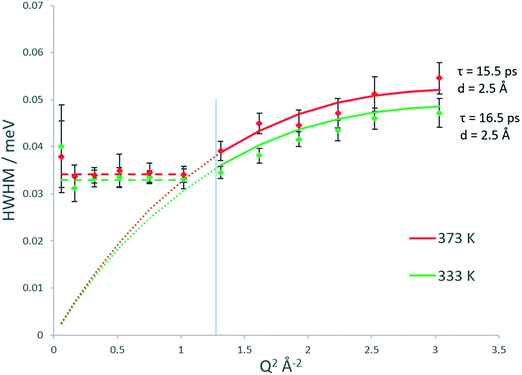
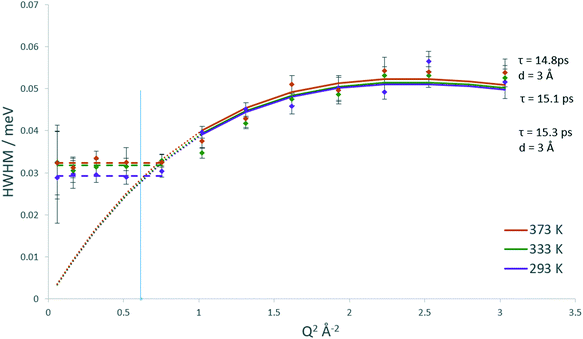
The broadenings of methanol in H-ZSM-5(36) at 333 and 373 K, which give us information about the mechanisms and rates of motion observed are considered next.51,52 The broadenings (Fig. 3) corroborate the model of diffusion confined to a sphere. For groups fitted above Q2 = 1 Å−2, the broadenings of the Lorentzian component fit to the Chudley and Elliot jump diffusion model,53 with a jump distance of 2.5 Å and a residence time of 16.5 ps at 333 K and 15.5 ps at 373 K. There is a plateauing of the broadenings for all data points at, and below Q2 = 1 Å−2. According to the Volino–Dianoux model of diffusion confined to a sphere, the plateauing takes place at a Q value corresponding to the diameter of the sphere of confinement (Q = 2π/dconf) which in this case is between Q = 1.02 and 1.17 Å−1 which corresponds to a sphere of diameter between ∼5.3–6.2 Å. The H-ZSM-5 pore diameter of 5.5 Å fits within this region (as indicated by the blue line in Fig. 3), validating the optimal fitting of the EISF to a spherical radius of 2.75 Å.
With regard to calculating a diffusion coefficient, the most reliable way for confined systems is to take the HWHM values at the low Q plateau point, which is (4.33Ds)/(rconf2).50 Using rconf = 2.75 Å we obtain the self-diffusion coefficient (Ds) values listed in Table 1, in the range of ∼8.6–9 × 10−10 m2 s−1. We note that these values for a confined/localised diffusion coefficient are lower (by a factor of ∼3) than those obtained by Jobic in ref. 39 we consider this may be due to the higher loading used in these experiments, where intermolecular interactions upon confinement can lower the diffusivity of sorbed species.54,55 With translational diffusion only being exhibited at two temperatures of the measured range, an activation energy of confined diffusion cannot be obtained by an Arrhenius plot from these data.
| Methanol | Dimethyl ether | ||||
|---|---|---|---|---|---|
| Si/Al | 36 | 135 | Si/Al | 36 | 135 |
| T (K) | D s | D s | T (K) | D s | D s |
| 293 | n/a | 8.29 × 10−10 | 293 | 9.17 × 10−10 | 9.75 × 10−10 |
| (±0.35 × 10−10) | (±0.34 × 10−10) | (±0.25 × 10−10) | |||
| 333 | 8.64 × 10−10 | 8.39 × 10−10 | 333 | 9.65 × 10−10 | 10.60 × 10−10 |
| (±0.28 × 10−10) | (±0.24 × 10−10) | (±0.31 × 10−10) | (±0.27 × 10−10) | ||
| 373 | 8.98 × 10−10 | 8.87 × 10−10 | 373 | 9.89 × 10−10 | 10.80 × 10−10 |
| (±0.3 × 10−10) | (±0.43 × 10−10) | (±0.36 × 10−10) | (±0.25 × 10−10) | ||
| E a (kJ mol−1) | n/a | 0.58 | E a (kJ mol−1) | 0.96 | 1.33 |
We now consider the behaviour of methanol in the more siliceous H-ZSM-5 sample (Si/Al ratio = 135), with the QENS spectra shown in Fig. S10.† As with H-ZSM-5(36) there is a significant elastic component to all the spectra, suggesting that a localised motion/significant immobile fraction is present.
To understand the geometry of motions present and if there are any qualitative differences between methanol in H-ZSM-5(36) and H-ZSM-5(135), the EISFs at each temperature which are plotted in Fig. 4 are analysed next. After fitting all the models as described for H-ZSM-5(36), the best fitting model at all temperatures is that of diffusion confined to a sphere with a radius of 2.75 Å – as found for H-ZSM-5(36) at 333 and 373 K. There are a number of contrasts with the dynamics observed in H-ZSM-5(36). First, translational diffusion is present in H-ZSM-5(135) at 293 K, which is a qualitative difference from H-ZSM-5(36) at the same temperature where rotational motions are observed. This suggests that the presence of more acidic sites in the H-ZSM-5(36) sample may be responsible for the more localised and constrained nature of the motions present at this temperature, and that in H-ZSM-5(135) translational diffusion is allowed as fewer acidic sites are present.
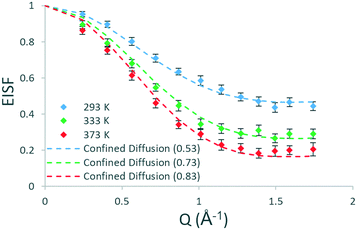 | ||
| Fig. 4 Experimental EISF plots of methanol in H-ZSM-5(135) at 293, 333 and 373 K with the corresponding theoretical models (immobile fractions shown in the legend in brackets). | ||
Another difference is the size of the mobile fractions, which are 0.53, 0.73 and 0.83 in H-ZSM-5(135) at 293, 333 and 373 K respectively, compared to 0.57 (rotation), 0.58 and 0.66 in H-ZSM-5(36). Thus, despite the same mode of motion (confined diffusion) being present at 333 and 373 K in both zeolite samples, the population of molecules able to move in the 1–100 ps timescale is increased by 0.15 and 0.17 in terms of the absolute mobile fraction (a relative increase of ∼25%) at these temperatures when fewer acidic sites are present.
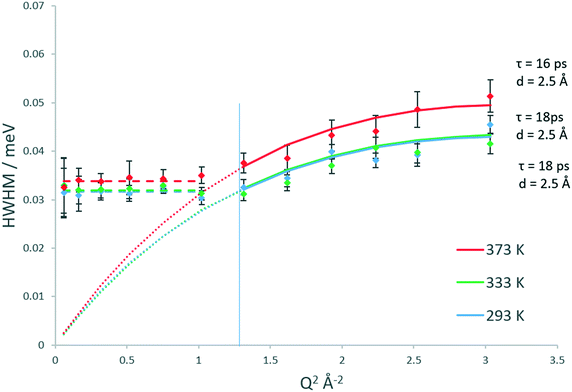
Upon studying the line broadenings for this system (Fig. 5), we find similarly to the H-ZSM-5(36) system that the Chudley–Elliot jump diffusion model is the best fit, with a plateauing of the broadenings at a Q range between Q = 1.02 and 1.17 Å−1 which suggests that the confined diffusion model in a sphere matching the width of the H-ZSM-5 channels is valid. The diffusion coefficients obtained are listed in Table 1. The localised diffusion coefficients are very similar to those obtained in the H-ZSM-5(36) system, certainly within experimental error. Notably, the majority of the data points at 293 and 333 K have overlapping error bars (with the fitted model plots matching almost exactly), suggesting that while the quantity of mobile molecules may differ between catalyst systems, the rate at which the mobile molecules move is not significantly different. It is also important to note that the calculated Ds values have overlapping error bars at all temperatures. For this reason, the Ea of confined/localised diffusion as calculated from an Arrhenius plot must be treated with caution.
To summarise, there are notable consistencies and differences between methanol dynamics in H-ZSM-5 samples on the timescale of the instrument. At 293 K we see a qualitative difference in behaviour between the two samples, with isotropic rotation in H-ZSM-5(36) and diffusion confined to a sphere with a radius corresponding to that of the H-ZSM-5 channels in H-ZSM-5(135). At higher temperatures the confined diffusion model fits the data for both samples (with the radius of confinement also matching the H-ZSM-5 pores), with very similar diffusion coefficients between samples. However, the proportion of mobile molecules is significantly higher in H-ZSM-5(135) compared to H-ZSM-5(36), consistent with the far lower number of adsorption sites in H-ZSM-5(135).
Dimethyl ether
QENS spectra of DME in H-ZSM-5(36) are shown in Fig. S11.† The EISFs are analysed as outlined for methanol with the relevant dimensional values for DME, outlined in section S3.† Due to the C2 symmetry of the DME molecule, the 2-site jump rotation model around a circle may also be employed as detailed in section S3, and shown in Fig. S12.† The fitting of relevant models to the experimental EISF is shown in Fig. S13.† The model of diffusion confined to a sphere (with a mobile fraction of 0.59) is able to fit the data within the error bars at almost all Q values suggesting at this temperature that DME is able to diffuse translationally in H-ZSM-5(36). This contrasts to methanol behaviour in this zeolite sample, which appears to have the more localised motion of isotropic rotation.However, it is clear that a large fraction of the molecules (similar to methanol) are still static, or not exhibiting motion in the 1–100 ps timescale probed by the instrument. It is probable that this fraction is sterically hindered by the constrictive H-ZSM-5 channels, where the population may be located long term, or slowly travelling through the channel system to reach another intersection where they remain locally and observably mobile for longer periods. There is also a high likelihood that a portion of these ‘immobile’ molecules will be interacting strongly with the Brønsted acid sites, as shown to be very favourable in previous QM/MM embedded cluster calculations.56
However, we must note that the radius of the confining sphere calculated to fit the data best was actually 3.2 Å rather than 2.75 Å, suggesting the sphere in which DME was diffusing was ∼6.4 Å in diameter, larger than the H-ZSM-5 channels. We therefore suggest at this point that the DME is more likely diffusing in the spherically shaped channel intersections which are quoted as being up to 8–9 Å in diameter57–60 which will be discussed in more detail later.
The EISFs of DME in H-ZSM-5(36) at all temperatures are plotted in Fig. 6 where the model of diffusion confined to a sphere (r = 3.2 Å) fits the data at all temperatures, but with a mobile fraction which increases with each temperature. Despite the increase in temperature of 40 K at each step, the increase in mobile fraction with temperature is far smaller for DME than that found for methanol in H-ZSM-5(36). This could potentially be an indication of either stronger adsorption to Brønsted sites, or the higher level of steric hindrance to mobility of the larger DME molecules in the H-ZSM-5 channels. Notably, the data points of 333 and 373 K are all within the error bars of each other.
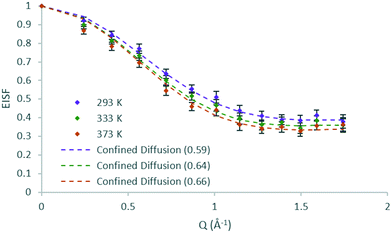 | ||
| Fig. 6 Experimental EISF plots of dimethyl ether in H-ZSM-5(36) at 293, 333 and 373 K with the corresponding confined diffusion model plot (immobile fractions shown in the legend in brackets). | ||
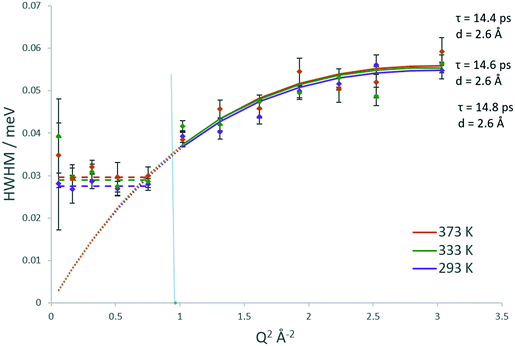
The Lorentzian broadenings are shown in Fig. 7, where the Q dependence validates the choice of confined translational diffusion over rotational motions. The Chudley–Elliot jump diffusion model appears to fit to the broadenings well, until a plateau at Q = 0.87–1.01 Å−1 is reached. This conforms to the Volino–Dianoux model with a sphere of radius 3.1–3.6 Å−1, corroborating the diameter of 6.4 Å as extrapolated from the EISF. The diffusion coefficients were calculated as outlined above and are listed in Table 1. We note that the diffusion coefficients (in the range of ∼9.2–9.9 × 10−10 m2 s−1) are slightly higher than those obtained by methanol in the same system, but this is a reflection of the larger sphere used in the calculation. The increase in diffusivity for dimethyl ether is somewhat counterintuitive given the larger size of the DME molecule. But if one were to consider the possibility that its diffusion over this timescale is located in the larger volume intersection rather than the more constrictive channel system it may be a logical observation. However, the significant error values in the calculated Ds must be taken into consideration. The values of the activation energy in Table 1 must also be treated with caution due to the overlapping error bars of the Ds values.
The QENS spectra for DME in H-ZSM-5(135) are shown in Fig. S14.† The EISF plots for DME in H-ZSM-5(135) are shown in Fig. 8. As with DME in H-ZSM-5(36) the best fitting model at each temperature is that of diffusion confined to a sphere, with a mobile fraction of 0.64, 0.67 and 0.68 respectively. We note that these mobile fractions are slightly higher than those obtained for H-ZSM-5(36) reflecting the fewer adsorption sites present. However, when considering the proportion of DME molecules mobile in the 1–100 ps timescale between H-ZSM-5(36) and H-ZSM-5(135) is significantly less than that observed for methanol between the two samples. This suggests that steric hindrance of the larger DME molecule (particularly if there is a fraction located in the H-ZSM-5 channels rather than the intersections) is the dominant factor in preventing its diffusion, rather than strong interactions with Brønsted sites as suggested for methanol. The most significant observation however, is that the radius of the sphere necessary to fit the EISF to the Volino–Dianoux model is 4 Å (a diameter of 8 Å), as opposed to the 3.2 Å in H-ZSM-5(36), which will be discussed in more detail below. The broadenings as a function of Q for DME in H-ZSM-5(135) are shown in Fig. 9. The broadenings also fit to the Chudley–Elliot jump diffusion model as for H-ZSM-5(36), with very similar residence times. However, we note that the jump distance is larger (3 Å compared to ∼2.5 Å) which may reflect the larger sphere available for diffusion. The plateauing of the broadenings corresponds to a spherical radius range of 3.6–4.3 Å, again corroborating the fitting of the EISF to a sphere of diameter 8 Å.
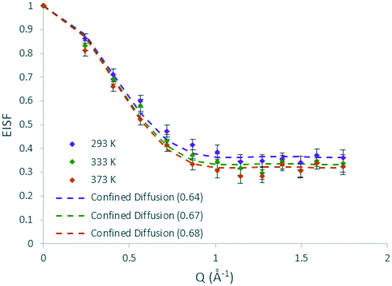 | ||
| Fig. 8 Experimental EISF plots of methanol in H-ZSM-5(135) at 293, 333 and 373 K with the corresponding confined diffusion model (immobile fractions shown in the legend in brackets). | ||
The confined diffusion coefficients calculated from the plateauing of the broadenings at low Q are listed in Table 1. We note that at all temperatures the Ds is slightly higher than that of the H-ZSM-5(36) in the range of 9.75–10.8 × 10−10 m2 s−1. The difference however is very small particularly when the error values associated with each value are considered, and is more a reflection of the larger sphere radius used in the Volino–Dianoux model to calculate Ds. As with the methanol samples, the errors of the Ds at all temperatures overlap, and as such any activation energies of confined diffusion (Table 1) must be treated with caution.
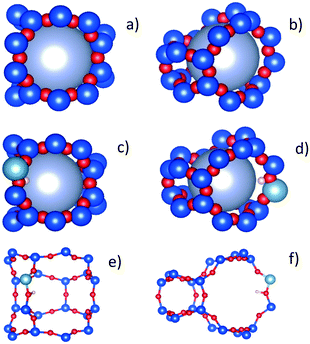
We have tentatively suggested that the DME motions in the H-ZSM-5(36) and (135) require a larger radius of confined diffusion in order to fit the EISF to the Volino–Dianoux diffusion model, because the DME is located in the larger channel intersections. While this appears plausible, we must also account for the observation of a larger confining sphere in H-ZSM-5(135) than H-ZSM-5(36). A potential explanation is considered upon taking the atomic positions of a channel intersection, generated and extracted from the periodic unit cell of silicalite obtained experimentally61 shown in Fig. 10a and b to approximate an intersection found in H-ZSM-5(135). We may then compare this to an intersection containing a single Brønsted acid site generated from a large, geometry optimised QM/MM embedded cluster from previous work62 approximating an intersection found in H-ZSM-5(36) in Fig. 10c and d. Upon accounting for the atomic radii and expanding the largest sphere possible into the intersection, we found that the largest sphere in the H-ZSM-5(36) intersection has a radius of approximately 3.6 Å due to the proton of the Brønsted site protruding into the channel. However, a significantly larger sphere of 4.4 Å radius can fit into the intersection approximation of H-ZSM-5(135). The radii used to model the EISFs of DME diffusion in each sample fit appropriately within these possible spherical voids.
This fitting supports the use of radii larger than that of the H-ZSM-5 channels to fit the confined diffusion models for the EISF, and its attributing to DME location/diffusion in the intersections. It also supports that the use of a larger sphere to fit to the EISF of DME in H-ZSM-5(135) sample is due to the relative absence of Brønsted acid sites in this catalyst, allowing for a larger intersection void space for DME to diffuse in. The observations for DME are significant as they suggest a qualitative difference in DME behaviour compared to methanol, where mobile DME is primarily in the intersections (likely due to the increased molecular dimensions) compared to methanol which appears to remain in the H-ZSM-5 channels, despite both species showing confined diffusion at higher temperatures of similar rates.
Implications of QENS derived dynamical values for kinetic modelling and MTH/MTO catalysis
We now consider the potential implications of the QENS observations from this study on the development of future microkinetic models of the MTH/MTO process. We define microkinetic models in the full sense that molecular events such as adsorption, diffusion, desorption and reaction steps are decoupled without any assumptions on rate-limiting steps. As mentioned in the introduction, formation of the first C–C bond is key to understanding factors governing olefin selectivity over H-ZSM-5 catalysts when MTH conversion is tuned towards olefin formation at relatively high temperatures and low pressures. We provide evidence that fractions of DME and methanol which are mobile over the instrumental timescale of 1–100 ps have different locations of confinement in the H-ZSM-5 catalyst. We can consider that mobile methanol would likely be interacting with the active sites present in the channels, while mobile DME appears to be located in the MFI intersections, able to interact with Brønsted sites located there. We also observe a different mode of motion for methanol in the zeolite catalyst of higher aluminium content at lower temperatures. The differing species, preferential locations, Brønsted acid site concentrations and temperatures have lead to differing qualitative and quantitative dynamical observations illustrating the complexity of the system even when probed only on a local scale in a fresh catalyst.Brønsted acid site concentration, strength and location can influence the deprotonation energies, adsorption energies and methoxylation reactivity of methanol when it is fed over H-ZSM-5 catalysts. The local coordination to the Brønsted acid site and the presence of other polar molecules influence the adsorption energies and methoxylation process.36,62,63 Molecular scale descriptors such as adsorption energies and calculated H-bond lengths give a nuanced description of factors governing adsorption, reaction and desorption. To accurately integrate these molecular scale descriptors into microkinetic models used for microporous catalysts,64,65 descriptors which also define molecular diffusion through the zeolite framework on the nanoscale (i.e. jump diffusion from cage-to-cage or between unit cells), and dynamics restricted to parts of the framework structure, and local to the active site are necessary.
For particles in a fixed bed reactor (mesoscale–macroscale level), the adsorption and desorption of species is affected by sorbate concentration across catalyst particles, bed concentration gradients, carrier gas flow rate, re-adsorption and fluid hydrodynamics.66,67 The ideal or non-ideal plug flow reactor model19 which is used to describe the behaviour of industrial catalysts in fixed bed reactors, is based on material balance for a reaction component, for a differential element of volume, which is later integrated across the whole reactor.68 However, valid material balances for the mesoscale–macroscale level do not take into account the dynamics on a much smaller (molecular) scale which include more localised degrees of freedom such as those associated with the rotational motion considered for methanol at 293 K in H-ZSM-5(36) and the locally confined diffusion at higher temperatures.
Typical multiscale modelling of adsorption and diffusion inside the pores of zeolite catalysts is carried out by separating the length and time scales of the problem, and linking the various levels of modelling retroactively.69,70 First, the change in composition of reactants across the pore system is given by adsorption isotherms obtained either experimentally or modelled by configurational-bias Monte Carlo (CMBC) simulations and ideal adsorbed solution theory (IAST). Compositions and temperatures are then used in classical molecular dynamics simulations which are used to obtain bulk self-diffusivities which may be compared to experimental QENS data (where different timescales may be probed by the simulations, and chosen to match the time window of the instrument). At the continuum (reactor) level, these bulk self-diffusivities are placed in the respective partial differential equations to simulate the temporal behaviour of adsorbing and reacting species in a porous particle/pellet.69,70
On the timescales of this study (1–100 ps), self-diffusion coefficients confined to a spherical region local to the active site (Ds(local)) can be obtained from the QENS broadenings according to eqn (2) adapted from the Volino–Dianoux model50 below.
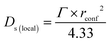 | (2) |
We note that the aforementioned rotational diffusion coefficients (DR) may also provide another descriptor for the interaction strength with the pore wall and steric constriction in the channels, where a higher DR suggests weaker interaction and less steric constriction. Incorporating local dynamics such as DR and Ds(local) into models which also account for the meso–macroscale has, hitherto, not been carried out. These experimentally obtained local descriptors may also be probed using molecular dynamics simulations and crucially may even be used to help tune the force fields on which these simulations are based.
Previous work by Jobic39 has shown how one may use different QENS instruments to differentiate between diffusivity confined to an area local to the active site (or at least a portion of the channel approximated by a sphere) using an instrument probing the ∼1–100 ps timescale, and how one may track jump diffusion throughout the framework using a higher resolution instrument which probes motion over ∼1–10 ns (though at the expense of the wider energy window which allows for faster local motions to be tracked). Indeed, motions over the scale of hundreds of nanoseconds would be necessary for larger species of the hydrocarbon pool, requiring the neutron spin-echo technique to probe motions over this timescale.71 It is therefore not possible for a single QENS instrument to bridge the gap between direct molecule–Brønsted acid interactions studied with adsorption energies and vibrational spectroscopy, and the microscale probed by adsorption/desorption and mass transport studies. However, a range of instruments may provide descriptors for dynamical behaviour at or around the active site (rotation or confined local diffusion), and jump diffusion through cage windows and along the channels of the catalyst framework. Incorporating these descriptors into microkinetic models allows for the more nuanced kinetic modelling of the system across scales previously mentioned, enabling us to more accurately model changes induced by varying the Si/Al ratio of the zeolite catalyst, as demonstrated by this study. There is indeed great potential for these techniques to enable the more detailed modelling of such complex catalytic systems as a function of catalyst composition, which are necessary for understanding factors important to activity and selectivity in MTH/MTO processes over zeolite catalysts.
We now consider the direct incorporation of relevant diffusion coefficients which have been extrapolated from our empirical studies into equations appropriate to kinetic modelling of the MTH/O process. Several studies into the kinetics of the MTH/O process either do not specify the diffusion coefficients used24,72 or rely on an effective diffusivity calculated by accounting for Knudsen and bulk diffusion in the zeolite pores.45 However, QENS measurements such as those carried out in this study provide direct measurements of a self-diffusivity on a given scale which could instead be used in catalytic investigations. The use of Maxwell–Stefan equations as well as continuity equations with accurate self-diffusivity coefficients would allow for a thorough investigation of the effect of diffusion on the kinetics of MTH/O conversion. Ortega et al.45 studied the conversion of methanol to DME and water in an external recycle reactor using calculated effective values of diffusion coefficients based on Knudsen and bulk diffusion coefficients. In their calculation, a derived diffusion coefficient of 3.71 × 10−6 m2 s−1 (taking into account bulk and Knudsen diffusivity) was used in the calculation of criteria for the absence of internal mass transfer limitations given by the Wagner–Weisz–Wheeler modulus73 at 190 °C in the catalyst grain. We may consider that our QENS experiments which provide an effective diffusion coefficient of the order of 10−10 m2 s−1 (which inherently takes into account both the tortuosity/porosity of the catalyst structure) for methanol at 190 °C (upon extrapolated using an activation energy of 0.58 kJ mol−1 for methanol in H-ZSM-5(135) listed in Table 1), may perhaps be a more accurate description of molecular mobility in the micropores in the zeolite catalysts. The difference in four orders of magnitude between the diffusion coefficients at the catalyst grain level and the intracrystalline diffusion coefficients may have implications on whether the experiments conducted by Ortega et al.45 were under intrinsic kinetic conditions (i.e. not influenced by mass transport limitations). We do however emphasise the importance of the lengthscales considered in this study, and the need to properly combine experimental measurements using different instruments across scales as mentioned earlier in this section.
In terms of DME, Pérez et al.24 constructed a kinetic model for the reaction of DME to olefins over a H-ZSM-5 zeolite catalyst in a fixed bed reactor under a pure DME feed, and through co-feeding with helium, methanol, and water. In their reaction scheme, the transformation of DME to olefins and methanol to olefins was decoupled. The kinetic constant of DME conversion to olefins (at 623 K) was found to be 20 times greater than that of methanol conversion. As with Ortega et al.45 the parameters obtained by Perez et al. were stated to have been obtained under intrinsic kinetic conditions.
We may use the Wagner–Weisz–Wheeler modulus (Mw)73 to determine the influence of intracrystalline diffusion on reaction kinetics at the micropore level.
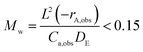 | (3) |
When extrapolating our diffusivities to 623 K using our activation energies in Table 1 we obtain diffusivities of 1.13 × 10−9 m2 s−1 and 1.30 × 10−9 m2 s−1 for DME over H-ZSM-5(36) and (135) respectively. We have incorporated them into calculations which are based on a pure feed at ca. 1 atm (as indicated in the ref. 24) in Table 2 to calculate Mw. We also obtain a diffusion coefficient 9.36 × 10−10 m2 s−1 for methanol in H-ZSM-5(135) using activation the activation energy of diffusion of 0.58 kJ mol−1 (this was not possible for methanol in H-ZSM-5(36) as only two self-diffusion coefficient could be obtained, ruling out an Arrhenius plot). We once again note the need for caution in using these activation energies due to the error bars associated with the each diffusion coefficient, however have confidence in a value on the order of 10−9–10−10 m2 s−1. We assume also that the kinetic parameters are constant with respect to crystal size and Si/Al ratio since they are intrinsic as reported by Perez et al.
| Parameter | DME | Methanol |
|---|---|---|
| Kinetic constant | 4.99 × 10−2 molc gcat−1 h−1 atm−1 | 2.43 × 10−3 molc gcat−1 h−1 atm−1 |
| Kinetic constant | 2.50 × 10−2 molDME gcat−1 h−1 atm−1 | 2.43 × 10−3 molMEOH gcat−1 h−1 atm−1 |
| Rate (pure feed at 1 atm) | 2.50 × 10−2 molDME gcat−1 h−1 | 2.43 × 10−3 molMEOH gcat−1 h−1 |
| Observed rate (−rA,obs) | 7.62 molDME mcat−3 s−1 | 0.74 molMeOH mcat−3 s−1 |
| D E (623 K) | 1.13 × 10−9 m2 s−1 (Si/Al = 35) | n/a (Si/Al = 35) |
| 1.30 × 10−9 m2 s−1 (Si/Al = 136) | 9.36 × 10−10 m2 s−1 (Si/Al = 136) | |
| M w – H-ZSM-5(36) | 1.04 × 10−6 | n/a |
| M w – H-ZSM-5(135) | 5.07 × 10−6 | 6.83 × 10−7 |
Characteristic lengths are based on SEM values of crystallites obtained in Omojola et al.19 Crystallite diameter for these specific industrial samples of H-ZSM-5(36) catalysts is 0.33 μm, and 0.78 μm for H-ZSM-5(135) catalysts. A catalyst density of 1.1 × 106 gcat mcat−3 was used from the referenced study.
The calculations suggest that if these catalysts were used under pure feed at 1 atm under laboratory conditions, they would be suitable for kinetic measurements in the absence of intracrystalline pore diffusion limitations, in crystallites of these measured sizes. Laboratory measurements require the observation of intrinsic rates as reported by Pérez et al.24 However, the industrial MTO process would require process conditions leading to faster rates of methanol conversion. If the observed rates of methanol conversion were increased further, the calculations suggest that pore diffusion becomes rate limiting first for H-ZSM-5(135) due to its larger crystallite sizes which increase with Si/Al ratio with these H-ZSM-5 samples.19 In the simulated industrial MTO process using these particular industrial catalyst samples, and these particular extrapolated Ds values, further design should thus be based on an intermediate crystallite size and Si/Al ratio between these samples of H-ZSM-5(36) and (135).
While a detailed discussion and analysis of the potential activity and product distribution as a function DME and methanol mobility/siting within the catalyst is outside of the scope of this study, there may well be some immediate insights gleaned from these experiments. We note that methanol has been previously shown to adsorb and desorb relatively easily from these catalyst samples19 but according to our QENS measurements moves relatively slowly (or rotates close in proximity to binding sites) in the channel system of H-ZSM-5. DME adsorption on the other hand, has been shown to be slower than methanol, and its desorption requires higher temperatures potentially due to higher activation energies of desorption over all types of binding sites,19 but also potentially due to a higher steric hindrance in the H-ZSM-5 channel system as shown in our QENS experiments (concluded through its only observable mobility occurring in the channel intersections).
One may tentatively consider that despite DME and methanol having similar steric access to all regions of the catalyst framework, DME is more able to remain in all regions of the H-ZSM-5 framework (channels and intersections), leading to an increased interaction with more of the different Brønsted acid sites which vary in strength as a function of location. The formation of the first C–C bond which drives the formation of primary olefins from the equilibrium mixture of methanol, DME and water, may therefore take place in a situation where DME would be bound to a wider range of vacant sites, with a higher abundance and coverage given its differing adsorption and desorption behaviour.
Recent work18 has shown that even during the competitive adsorption of oxygenates and aromatics over H-ZSM-5 catalysts, DME still has a higher surface coverage at typical MTH/O conditions. This higher coverage may suggest a more DME-mediated pathway towards the formation of primary olefins in the absence of diffusion constraints. The higher diffusion coefficients obtained in this study for DME compared to methanol (derived from the differing location of DME allowing more space to be mobile in) suggests that even if a DME-mediated pathway to olefin formation were to occur, its mobility may not limit the establishment of significant surface coverages throughout the pore architecture of H-ZSM-5 catalysts. Previous work24,74,75 as well as the industrial DICP MTO process3 in the archived literature support the use of DME, or a mixture of methanol/DME as feedstock for primary olefin formation over zeolite and zeotype catalysts. Our qualitative and quantitative insights from these QENS measurements may provide a more fundamental understanding of the consequences of using this varied feedstock.
Future contributions of the QENS technique to MTH/MTO catalysis research
With regard to future applications of the QENS technique to MTH catalysis, there are a number of opportunities. One important consideration would be to test a wider range of Si/Al ratios, we anticipate that lower Si/Al ratios would likely encourage more occurrences of hindered rotational motions, potentially at higher temperatures which would give us some insight into how the barrier from rotation to translation changes as a function of zeolite composition. Another important variable would be to vary the loading of methanol and DME in H-ZSM-5. In this study we have chosen this specific loading due to their catalytic relevance to other kinetic investigations in archived literature. Exploring lower loadings would allow us to more reliably gauge the effect of Si/Al ratio decoupled from sorbate–sorbate interactions which are known to cause significant differences in diffusivity. Dosing a matching concentration of molecules into the sample as there are acid sites would allow for the H-bonding strength of each acid site to be the most influential factor in sorbate diffusivity. However, we would need to be careful with our choice of H-ZSM-5 samples. Carrying out such a study with the samples from this work would lead to significantly different sorbate loadings such that the different magnitude of sorbate–sorbate interactions would likely be a significant variable (we also note that the very low concentration needed for the H-ZSM-5(135) sample may approach the limit of instrument sensitivity).Finally, we consider the importance of probing temperatures closer to that of the catalytic reaction (>573 K for the MTH process). Our local self-diffusivities extrapolated to 623 K are listed in Table 2, though we have explained the need for caution with these values, and note that they neglect the inevitable buildup of the hydrocarbon pool which will affect mobility in the real system. The potential for methoxylation reactions to occur even at temperatures close to 373 K would cause issues with the measurement due to the increasing concentration of water in the system, which would be mobile over the same timescales as methanol (though DME measurements may be less problematic). One possible option would be to use the siliceous analogue of H-ZSM-5, silicalite-1, to gauge the effect of the MFI framework on species diffusivity without reaction complications at these higher temperatures. Future, more realistic studies must embrace the complexity of the hydrocarbon pool build-up and its effects on starting species behaviour at catalysis relevant temperatures, building on previous work which attempted this at ambient temperatures.38 We consider that future experimental developments such as reliable flow-through neutron sample environments may allow for the in situ dosing of species to the working catalyst, and that this dosing may be combined with the strategic deuteration of the catalyst and the build-up of a deuterated hydrocarbon pool, such that its scattering cross-section is negligible compared to an incoming hydrogenous reactant stream. At a time where the flux to neutron instruments is ever increasing, allowing for a fast measurement of diffusion coefficients before the reactant stream is consumed, selective measurements of relevant species' mobility under increasingly realistic conditions may well be an achievable goal for neutron scattering experiments in the coming years.
Summary and conclusion
Quasielastic neutron scattering experiments sampling timescales of motion of 1–100 ps have been employed to study the molecular motions of methanol and dimethyl ether in H-ZSM-5 catalysts of Si/Al = 36 and 135. The zeolite composition has significant effects on methanol motion. In H-ZSM-5(36) at room temperature, methanol exhibits isotropic rotation (DR = 2.6 × 1010 s−1) with a fraction of molecules (∼43%) which are ‘immobile’ over the timescale probed by the instrument. At 333 K and 393 K methanol exhibits jump diffusion confined to sphere matching the H-ZSM-5 channel diameter (5.5 Å) with immobile populations of 42 and 34% respectively, with confined Ds values of 8.6–9 × 10−10 m2 s−1. In the H-ZSM-5(135) sample, diffusion confined to a sphere of the same diameter was observed at all temperatures. This showed a qualitative difference in methanol motion observed at 293 K between samples, while the same confined jump diffusion was observed giving very similar diffusion coefficients between samples at higher temperatures. The immobile populations at 333 and 393 K were significantly lower (27 and 17% respectively) in H-ZSM-5(135) than in H-ZSM-5(36), which we consider as reflective of the far lower number of adsorption sites in the H-ZSM-5(135) catalyst sample.Measurements of DME motion showed that in H-ZSM-5(36), diffusion confined to a sphere is observed at all temperatures. This contrasts with methanol in this sample, which showed rotational motion at 293 K, suggesting that DME is freer to diffuse at 293 K despite the increase in molecular dimensions. However, DME showed diffusion confined in a sphere of diameter 6.2 Å, with immobile fractions of 41–34% with increasing temperature (far smaller increases in mobile populations with temperature compared to methanol). The confined radius is larger than that of the H-ZSM-5 channels, suggesting that the DME dynamics are confined to the H-ZSM-5 intersections. Ds values were obtained in the range of 9.2–9.9 × 10−10 m2 s−1, slightly larger than those for methanol in the same sample, however this is more indicative of the larger sphere radius derived for the Volino–Dianoux model used to calculate the Ds. In the H-ZSM-5(135) sample, confined spherical diffusion was also observed, with slightly lower immobile fractions (36–32% with increasing temperature). The Ds values calculated were slightly higher (9.7–10.8 × 10−10 m2 s−1) that those obtained in the H-ZSM-5(36) sample. The sphere to which diffusion was confined in H-ZSM-5(135) was even larger than that of the H-ZSM-5(36) sample, with a diameter of 8 Å (the increase in Ds is again, due primarily to the larger sphere in the Volino–Dianoux calculating model). This suggests that if DME diffusion is confined to the intersection in H-ZSM-5(135) as with H-ZSM-5(36), that the intersection has a larger free volume for diffusion, probably due to the lack of Brønsted acid sites present. This was supported by an investigation of the atomic configuration of the intersection from an experimental silicalite sample, and geometry optimised H-ZSM-5 structure.
The study illustrates the complex nature of sorbate behaviour in the methanol-to-hydrocarbons process even under fresh catalyst conditions. The catalyst composition and concentration of Brønsted sites can have qualitative differences in behaviour of methanol at ambient temperatures, and significant differences in the size of ‘immobile’ fractions at higher temperatures between samples. In contrast, despite the larger molecular dimensions of DME, the diffusion of molecules which are mobile on the instrumental timescale does not appear to be significantly hindered with increasing Brønsted acid site concentration, potentially due to their location in the larger channel intersections of the framework, which may differ in free volume depending on catalyst composition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. J. O. M. acknowledges the Ramsay Memorial Trust for the provision of a Ramsay Memorial Fellowship, and Roger and Sue Whorrod for the funding of the Whorrod Fellowship. The ISIS Neutron and Muon Source at the STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities; the data from our experiment RB1810011 can be found at DOI: 10.5286/ISIS.E.RB1810011. We acknowledge Dmitry Lukyanov (Department of Chemical Engineering, University of Bath) for providing the ZSM-5 catalyst samples and Andre van Veen (School of Engineering, University of Warwick) for preliminary discussions leading to the proposal of neutron experiment.References
- C. D. Chang, The New Zealand Gas-to-Gasoline plant: An engineering tour de force, Catal. Today, 1992, 13(1), 103–111 CrossRef CAS.
- C. D. Chang and A. J. Silvestri, The conversion of methanol and other O-compounds to hydrocarbons over zeolite catalysts, J. Catal., 1977, 47(2), 249–259 CrossRef CAS.
- P. Tian, Y. Wei, M. Ye and Z. Liu, Methanol to olefins (MTO): From fundamentals to commercialization, ACS Catal., 2015, 5(3), 1922–1938 CrossRef CAS.
- C. D. Chang, W. H. Lang and R. L. Smith, The conversion of methanol and other O-compounds to hydrocarbons over zeolite catalysts. II. Pressure effects, J. Catal., 1979, 56(2), 169–173 CrossRef CAS.
- J. Liang, H. Li, S. Zhao, W. Guo, R. Wang and M. Ying, Characteristics and performance of SAPO-34 catalyst for methanol-to-olefin conversion, Appl. Catal., 1990, 64, 31–40 CrossRef CAS.
- B. Vora, J. Q. Chen, A. Bozzano, B. Glover and P. Barger, Various routes to methane utilization—SAPO-34 catalysis offers the best option, Catal. Today, 2009, 141(1), 77–83 CrossRef CAS.
- C. D. Chang and A. J. Silvestri, MTG: Origin, Evoltuion, Operation, Chem. Tech., 1987, 17(10), 624–631 CAS.
- M. Bjørgen, S. Svelle, F. Joensen, J. Nerlov, S. Kolboe, F. Bonino, L. Palumbo, S. Bordiga and U. Olsbye, Conversion of methanol to hydrocarbons over zeolite H-ZSM-5: On the origin of the olefinic species, J. Catal., 2007, 249(2), 195–207 CrossRef.
- M. Bjørgen, F. Joensen, K. P. Lillerud, U. Olsbye and S. Svelle, The mechanisms of ethene and propene formation from methanol over high silica H-ZSM-5 and H-beta, Catal. Today, 2009, 142(1–2), 90–97 CrossRef.
- T. Omojola, D. B. Lukyanov, N. Cherkasov, V. L. Zholobenko and A. C. van Veen, Influence of Precursors on the Induction Period and Transition Regime of Dimethyl Ether Conversion to Hydrocarbons over H-ZSM-5 Catalysts, Ind. Eng. Chem. Res., 2019, 58(36), 16479–16488 CrossRef CAS.
- L. Qi, Y. Wei, L. Xu and Z. Liu, Reaction Behaviors and Kinetics during Induction Period of Methanol Conversion on HZSM-5 Zeolite, ACS Catal., 2015, 5(7), 3973–3982 CrossRef CAS.
- K. Y. Lee, H. J. Chae, S. Y. Jeong and G. Seo, Effect of crystallite size of SAPO-34 catalysts on their induction period and deactivation in methanol-to-olefin reactions, Appl. Catal., A, 2009, 369(1–2), 60–66 CrossRef CAS.
- L. Qi, J. Li, Y. Wei, L. Xu and Z. Liu, Role of naphthalene during the induction period of methanol conversion on HZSM-5 zeolite, Catal. Sci. Technol., 2016, 6(11), 3737–3744 RSC.
- T. Omojola, D. B. Lukyanov and A. C. van Veen, Transient kinetic studies and microkinetic modeling of primary olefin formation from dimethyl ether over H-ZSM-5 catalysts, Int. J. Chem. Kinet., 2019, 51(7), 528–537 CrossRef CAS.
- S. Svelle, S. Kolboe, O. Swang and U. Olsbye, Methylation of Alkenes and Methylbenzenes by Dimethyl Ether or Methanol on Acidic Zeolites, J. Phys. Chem. B, 2005, 109(26), 12874–12878 CrossRef CAS PubMed.
- W. Song, D. M. Marcus, H. Fu, J. O. Ehresmann and J. F. Haw, An oft-studied reaction that may never have been: Direct catalytic conversion of methanol or dimethyl ether to hydrocarbons on the solid acids HZSM-5 or HSAPO-34, J. Am. Chem. Soc., 2002, 124(15), 3844–3845 CrossRef CAS PubMed.
- W. Song, J. B. Nicholas and J. F. Haw, A persistent carbenium ion on the methanol-to-olefin catalyst HSAPO-34: Acetone shows the way, J. Phys. Chem. B, 2001, 105(19), 4317–4323 CrossRef CAS.
- T. Omojola and A. C. Van Veen, Competitive Adsorption of Oxygenates and Aromatics during the Initial Steps of the Formation of Primary Olefins over H-ZSM-5 catalysts, Catal. Commun., 2020, 140, 106010 CrossRef CAS.
- T. Omojola, N. Cherkasov, A. I. McNab, D. B. Lukyanov, J. A. Anderson, E. V. Rebrov and A. C. van Veen, Mechanistic Insights into the Desorption of Methanol and Dimethyl Ether Over H-ZSM-5 Catalysts, Catal. Lett., 2018, 148(1), 474–488 CrossRef CAS.
- H. Yamazaki, H. Shima, H. Imai, T. Yokoi, T. Tatsumi and J. N. Kondo, Direct production of propene from methoxy species and dimethyl ether over H-ZSM-5, J. Phys. Chem. C, 2012, 116(45), 24091–24097 CrossRef CAS.
- Y. Jiang, M. Hunger and W. Wang, On the reactivity of surface methoxy species in acidic zeolites, J. Am. Chem. Soc., 2006, 128(35), 11679–11692 CrossRef CAS PubMed.
- W. Wang and M. Hunger, Reactivity of surface alkoxy species on acidic zeolite catalysts, Acc. Chem. Res., 2008, 41(8), 895–904 CrossRef CAS PubMed.
- S. Ilias and A. Bhan, Mechanism of the catalytic conversion of methanol to hydrocarbons, ACS Catal., 2013, 3, 18–31 CrossRef CAS.
- P. Pérez-Uriarte, A. Ateka, A. T. Aguayo, A. G. Gayubo and J. Bilbao, Kinetic model for the reaction of DME to olefins over a HZSM-5 zeolite catalyst, Chem. Eng. J., 2016, 302, 801–810 CrossRef.
- I. Yarulina, K. De Wispelaere, S. Bailleul, J. Goetze, M. Radersma, E. Abou-Hamad, I. Vollmer, M. Goesten, B. Mezari, E. J. M. Hensen, J. S. Martínez-Espín, M. Morten, S. Mitchell, J. Perez-Ramirez, U. Olsbye, B. M. Weckhuysen, V. Van Speybroeck, F. Kapteijn and J. Gascon, Structure–performance descriptors and the role of Lewis acidity in the methanol-to-propylene process, Nat. Chem., 2018, 10(8), 804–812 CrossRef CAS PubMed.
- J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Trevino, The Microkinetics of Heterogeneous Catalysis, American Chemical Society, Washington D.C, 1993 Search PubMed.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Surface Equilibria, in Fundamental Concepts in Heterogeneous Catalysis, 2014, pp. 26–46 Search PubMed.
- S. R. Blaszkowski and R. A. Van Santen, The mechanism of dimethyl ether formation from methanol catalyzed by zeolitic protons, J. Am. Chem. Soc., 1996, 118(21), 5152–5153 CrossRef CAS.
- P. A. Redhead, Thermal desorption of gases, Vacuum, 1962, 12(4), 203–211 CrossRef CAS.
- A. J. Jones and E. Iglesia, Kinetic, Spectroscopic, and Theoretical Assessment of Associative and Dissociative Methanol Dehydration Routes in Zeolites, Angew. Chem., 2014, 126(45), 12373–12377 CrossRef.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Advances in theory and their application within the field of zeolite chemistry, Chem. Soc. Rev., 2015, 44(20), 7044–7111 RSC.
- A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Neutron spectroscopy as a tool in catalytic science, Chem. Commun., 2017, 53(90), 12164–12176 RSC.
- J. Van der Mynsbrugge, S. L. C. Moors, K. De Wispelaere and V. Van Speybroeck, Insight into the Formation and Reactivity of Framework-Bound Methoxide Species in H-ZSM-5 from Static and Dynamic Molecular Simulations, ChemCatChem, 2014, 6(7), 1906–1918 CrossRef CAS.
- J. Van Der Mynsbrugge, M. Visur, U. Olsbye, P. Beato, M. Bjorgen, V. Van Speybroeck and S. Svelle, Methylation of benzene by methanol: Single-site kinetics over H-ZSM-5 and H-beta zeolite catalysts, J. Catal., 2012, 292, 201–212 CrossRef CAS.
- J. S. Martinez-Espin, K. De Wispelaere, T. V. W. Janssens, S. Svelle, K. P. Lillerud, P. Beato, V. Van Speybroeck and U. Olsbye, Hydrogen Transfer versus Methylation: On the Genesis of Aromatics Formation in the Methanol-To-Hydrocarbons Reaction over H-ZSM-5, ACS Catal., 2017,(7), 5773–5780 CrossRef CAS.
- A. J. O'Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. Garcia-Sakai and C. R. A. Catlow, Room temperature methoxylation in zeolites: insight into a key step of the methanol-to-hydrocarbons process, Chem. Commun., 2016, 52, 2897–2900 RSC.
- A. J. O'Malley, V. García Sakai, I. P. Silverwood, N. Dimitratos, S. F. Parker and C. R. A. Catlow, Methanol diffusion in zeolite HY: A combined quasielastic neutron scattering and molecular dynamics simulation study, Phys. Chem. Chem. Phys., 2016, 18(26), 17294–17302 RSC.
- S. K. Matam, A. J. O'Malley, C. R. A. Catlow, Suwardiyanto, P. Collier, A. P. Hawkins, A. Zachariou, D. Lennon, I. Silverwood, S. F. Parker and R. F. Howe, The effects of MTG catalysis on methanol mobility in H-ZSM-5, Catal. Sci. Technol., 2018, 8(13), 3304–3312 RSC.
- H. Jobic, A. Renouprez, M. Bee and C. Poinsignon, Quasi-elastic neutron scattering study of the molecular motions of methanol adsorbed on H-ZSM-5, J. Phys. Chem., 1986, 90(6), 1059–1065 CrossRef CAS.
- X. Sun, S. Mueller, Y. Liu, H. Shi, G. L. Haller, M. Sanchez-Sanchez, A. C. Van Veen and J. A. Lercher, On reaction pathways in the conversion of methanol to hydrocarbons on HZSM-5, J. Catal., 2014, 317, 185–197 CrossRef CAS.
- X. Sun, S. Mueller, H. Shi, G. L. Haller, M. Sanchez-Sanchez, A. C. Van Veen and J. A. Lercher, On the impact of co-feeding aromatics and olefins for the methanol-to-olefins reaction on HZSM-5, J. Catal., 2014, 314, 21–31 CrossRef CAS.
- S. Svelle, P. O. Rønning and S. Kolboe, Kinetic studies of zeolite-catalyzed methylation reactions: 1. Coreaction of [12C]ethene and [13C]methanol, J. Catal., 2004, 224(1), 115–123 CrossRef CAS.
- S. Svelle, P. O. Rønning, U. Olsbye and S. Kolboe, Kinetic studies of zeolite-catalyzed methylation reactions. Part 2. Co-reaction of [12C]propene or [12C]n-butene and [ 13C]methanol, J. Catal., 2005, 234(2), 385–400 CrossRef CAS.
- I. M. Hill, S. A. Hashimi and A. Bhan, Kinetics and mechanism of olefin methylation reactions on zeolites, J. Catal., 2012, 285(1), 115–123 CrossRef CAS.
- C. Ortega, M. Rezaei, V. Hessel and G. Kolb, Methanol to dimethyl ether conversion over a H-ZSM-5 catalyst: Intrinsic kinetic study on an external recycle reactor, Chem. Eng. J., 2018, 347, 741–753 CrossRef CAS.
- M. T. Telling, S. I. Campbell, D. Engberg, D. M. Marero and K. H. Andersen, Spectroscopic characteristics of the OSIRIS near-backscattering crystal analyser spectrometer on the ISIS pulsed neutron source, Phys. Chem. Chem. Phys., 2005, 7(6), 1255–1261 RSC.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, DAVE: A comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data, J. Res. Natl. Inst. Stand. Technol., 2009, 114(6), 341–358 CrossRef CAS PubMed.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Mantid - Data analysis and visualization package for neutron scattering and μ SR experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- V. F. Sears, Theory of Cold Neutron Scattering by Homonuclear Diatomic Liquids:1. Free Rotation, Can. J. Phys., 1966, 44(6), 1279–1297 CrossRef CAS.
- F. Volino and A. J. Dianoux, Neutron incoherent scattering law for diffusion in a potential of spherical symmetry: General formalism and application to diffusion inside a sphere, Mol. Phys., 1980, 41(2), 271–279 CrossRef CAS.
- H. Jobic and D. N. Theodorou, Quasi-elastic neutron scattering and molecular dynamics simulation as complementary techniques for studying diffusion in zeolites, Microporous Mesoporous Mater., 2007, 102(1–3), 21–50 CrossRef CAS.
- A. J. O'Malley and C. R. A. Catlow, Sorbate Dynamics in Zeolite Catalysts, in Experimental Methods in the Physical Sciences, ed. F. Fernandez-Alonso and D. L.Price, Academic Press, 2017, vol. 49, pp. 349–401 Search PubMed.
- C. T. Chudley and R. J. Elliott, Neutron scattering from a liquid on a jump diffusion model, Proc. Phys. Soc., London, 1961, 77(2), 353–361 CrossRef.
- H. Jobic, M. Bée and G. J. Kearley, Dynamics of ethane and propane in zeolite H-ZSM-5 studied by quasi-elastic neutron scattering, Zeolites, 1992, 12(2), 146–151 CrossRef CAS.
- H. Jobic, A. N. Fitch and J. Combet, Diffusion of benzene in NaX and NaY zeolites studied by quasi-elastic neutron scattering, J. Phys. Chem. B, 2000, 104(35), 8491–8497 CrossRef CAS.
- T. Maihom, B. Boekfa, J. Sirijaraensre, T. Nanok, M. Probst and J. Limtrakul, Reaction mechanisms of the methylation of ethene with methanol and dimethyl ether over h-zsm-5: An ONIOM study, J. Phys. Chem. C, 2009, 113(16), 6654–6662 CrossRef CAS.
- B. Boekfa, P. Pantu, M. Probst and J. Limtrakul, Adsorption and Tautomerization Reaction of Acetone on Acidic Zeolites: The Confinement Effect in Different Types of Zeolites, J. Phys. Chem. C, 2010, 114(35), 15061–15067 CrossRef CAS.
- D. Chen, H. P. Rebo, K. Moljord and A. Holmen, Influence of Coke Deposition on Selectivity in Zeolite Catalysis, Ind. Eng. Chem. Res., 1997, 36(9), 3473–3479 CrossRef CAS.
- N. Y. Chen, T. F. Degnan Jr and M. C. Smith, Molecular Transport and Reaction in Zeolites: Design and Application of Shape Selective Catalysis, Wiley, 1994 Search PubMed.
- M. Conte, B. Xu, T. E. Davies, J. K. Bartley, A. F. Carley, S. H. Taylor, K. Khalid and G. J. Hutchings, Enhanced selectivity to propene in the methanol to hydrocarbons reaction by use of H-ZSM-5/11 intergrowth zeolite, Microporous Mesoporous Mater., 2012, 164, 207–213 CrossRef CAS.
- G. Artioli, C. Lamberti and G. L. Marra, Neutron powder diffraction study of orthorhombic and monoclinic defective silicalite, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56(1), 2–10 CrossRef PubMed.
- A. J. O'Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Modelling metal centres, acid sites and reaction mechanisms in microporous catalysts, Faraday Discuss., 2016, 188, 235–255 RSC.
- S. A. F. Nastase, A. J. O'Malley, C. R. A. Catlow and A. J. Logsdail, Computational QM/MM investigation of the adsorption of MTH active species in H-Y and H-ZSM-5, Phys. Chem. Chem. Phys., 2019, 21(5), 2639–2650 RSC.
- P. Kumar, J. W. Thybaut, S. Svelle, U. Olsbye and G. B. Marin, Single-event microkinetics for methanol to olefins on H-ZSM-5, Ind. Eng. Chem. Res., 2013, 52(4), 1491–1507 CrossRef CAS.
- P. Kumar, J. W. Thybaut, S. Teketel, S. Svelle, P. Beato, U. Olsbye and G. B. Marin, Single-Event MicroKinetics (SEMK) for Methanol to Hydrocarbons (MTH) on H-ZSM-23, Catal. Today, 2013, 215, 224–232 CrossRef CAS.
- R. J. Gorte, Design parameters for temperature programmed desorption from porous catalysts, J. Catal., 1982, 75(1), 164–174 CrossRef CAS.
- R. A. Demmin and R. J. Gorte, Design parameters for temperature-programmed desorption from a packed bed, J. Catal., 1984, 90(1), 32–39 CrossRef CAS.
- B. R. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena Revised, John Wiley & Sons, Inc., 2nd edn, 2007 Search PubMed.
- F. J. Keil, Multiscale modelling in computational heterogeneous catalysis, Top. Curr. Chem., 2012, 307, 69–108 CrossRef CAS PubMed.
- F. J. Keil, Molecular modelling for reactor design, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 201–227 CrossRef PubMed.
- A. J. O'Malley, C. R. A. Catlow, M. Monkenbusch and H. Jobic, Diffusion of Isobutane in Silicalite: A Neutron Spin-Echo and Molecular Dynamics Simulation Study, J. Phys. Chem. C, 2015, 119(48), 26999–27006 CrossRef.
- A. T. Aguayo, D. Mier, A. G. Gayubo, M. Gamero and J. Bilbao, Kinetics of methanol transformation into hydrocarbons on a HZSM-5 zeolite catalyst at high temperature (400-550 °c), Ind. Eng. Chem. Res., 2010, 49(24), 12371–12378 CrossRef CAS.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, 3rd edn, 1999, p. 668 Search PubMed.
- P. Pérez-Uriarte, A. Ateka, A. G. Gayubo, T. Cordero-Lanzac, A. T. Aguayo and J. Bilbao, Deactivation kinetics for the conversion of dimethyl ether to olefins over a HZSM-5 zeolite catalyst, Chem. Eng. J., 2017, 311, 367–377 CrossRef.
- J. Mann, V. Y. Doluda, C. Leonard, Y. B. Losovyj, D. G. Morgan, S. S. Bukalov, Z. Shifrina, B. D. Stein, N. Cherkasov, E. V. Rebrov, Z. D. Harms, M. Pink, E. M. Sulman and L. Bronstein, Metal oxide–zeolite composites in transformation of methanol to hydrocarbons: do iron oxide and nickel oxide matter?, RSC Adv., 2016, 6(79), 75166–75177 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy00670j |
| ‡ Current address: Department of Inorganic Chemistry, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. |
| This journal is © The Royal Society of Chemistry 2020 |