First-principles insight into CO hindered agglomeration of Rh and Pt single atoms on m-ZrO₂

Abstract

In this first-principles study we evaluate the thermodynamic and kinetic stability of Rh and Pt single-atoms (SAs) and subnano clusters on the monoclinic zirconia surface with and without a CO atmosphere. To address the kinetic stability and agglomeration of SAs to clusters and nanoparticles, a non-equilibrium nanothermodynamic approach is developed and parametrised using data computed with density functional theory. The bare subnano clusters are more stable than SA and become more so with increasing size, which means the agglomeration is always favoured. CO binds strongly to the single atoms and clusters, and our atomistic thermodynamics treatment indicates that some CO will be present even at ultra-high vacuum conditions. A CO atmosphere is shown to hinder cluster growth from SA, and is even capable of spontaneous cluster disintegration in the case of Pt clusters. Analysis of the CO stretching frequencies reveals that subnano clusters and single atoms should give peaks in the same region, and that using them to distinguish between surface species requires caution.

---

1 Introduction

Single atom catalysts (SAC) form a class of catalytic materials where the active sites are single atoms (SA) and they have been a hot topic in recent years.^1–3 SACs typically consist of single transition metal atoms,^4,5 deposited on a host material, which is often a reducible^5–8 or irreducible^9,10 oxide, a carbon based material like graphene,^4,11 or another pure metal.¹² SACs can be synthesised from precursor materials, but they can also be formed dynamically in situ as mobile species due to Ostwalt ripening and reactant induced disintegration of larger particles.^13,14

Characterisation of SAC has become easier in the past years due to the development of high-resolution microscopic and spectroscopic techniques, although the techniques are still mainly performed ex situ.¹⁵ Methods like density functional theory (DFT) offer atomic scale resolution, and thus are complementary to experiments for studies involving SAC. DFT calculations further benefit from the fact that building models for SACs is relatively simple. Oxide surfaces are routinely modelled with surface slabs, and adding a single metal atom to the surface is not very costly. However one must consider which morphology, facet, and site of the oxide should be chosen for a given study. The metal single-atom can be added to the model as an adsorbate, or as a substituent to a lattice ion. This choice can be based on stability or experimental characterisation.

SAs are highly dispersed on the support surface, making them desirable for heterogeneous catalysis because they maximise the efficiency of using expensive noble metals. They have also demonstrated high activity towards a variety of reactions such as methane conversion,⁹ CO oxidation,⁷ and selective hydrogenation.¹¹ DFT calculations predict that SA can modify the electronic and structural properties of an oxide support, such as the reducibility,^16,17 and have been suggested to follow different BEP scaling relations than pure metals.^3,12,18,19 Even similar SAs on the same oxide support may exhibit distinct reactivity.^20–22

A major obstacle for the use of SAs in heterogeneous processes is their instability at reaction conditions. SAs have a tendency to agglomerate to form larger particles at the expense of SA and small clusters, change sites,²³ and the catalyst may become deactivated in the process. The stability of SAs or small nanoclusters is often assessed in the framework of Ostwald ripening or coalescence.²⁴ In both models, particle growth takes place via surface diffusion of either SAs or small clusters. The kinetics of these processes is determined by SA or cluster diffusion on the support. Decrease in surface energy is traditionally considered as the thermodynamic driving force for ripening and coalescence. The surface tension is, however, a macroscopic and extensive thermodynamic quantity, which cannot completely characterise SA or small cluster thermodynamics.^25,26 As discussed in the present work, non-extensive nanothermodynamics^25,27,28 provides a well-defined theoretical framework to analyse the kinetic and thermodynamic stability of SAs and to understand the thermodynamic driving force in ripening and sintering.

SAs are generally kinetically stabilised by support defects such as oxygen vacancies and low-coordinated sites.²⁹ Both experiments and calculations also suggest that different surface species such as CO^30,31 could protect SAs against agglomeration or even induce particle disintegration,^32,33 making it possible to recover SA after agglomeration has taken place. In addition to its possible role in SA stability and agglomeration, carbon monoxide is widely used as a probe molecule in experimental^9,15,34–36 as well as theoretical³⁵ studies. Two “geminal” COs bound to a supported Rh SA are thought to give a characteristic doublet peak in the IR spectra, which has been previously used to verify the presence of Rh SAs.^9,36 In the case of Pt, the SA is identified from a single peak, whose exact position depends on the identity of the support.¹⁵ However, given that CO has the ability to disintegrate clusters and small particles, is it fair to use it as a probe molecule for SAC that aren't intended to be used under a CO atmosphere?

Rh^9,32,36 and Pt^5,7,8 are both popular metals for SAC. Zirconia supported Pt SA and sub-nano particles have recently shown superior performance towards conversion of glycerol to lactic acid,³⁷ while Rh/ZrO₂ SAC have demonstrated activity towards direct methane conversion.⁹

In this combined DFT and nanothermodynamic study, we model the SA as well as small sub-nano clusters to get information about the ensemble of metal species that populate the support surface at reaction conditions. The initial stages of agglomeration of SA species into clusters was investigated in the absence and presence of CO. We also report the CO stretching frequencies for the most stable SA and clusters at various CO coverages, and discuss how these coincide with experimental observations. The mobility of SA on the zirconia support was also evaluated by determining their diffusion barriers from one site to the next. To analyse the kinetic and thermodynamic stability, a theoretical method combining nanothermodynamics and non-equilibrium thermodynamics was developed and parametrised using the DFT data. Our results highlight the importance of the CO atmosphere on thermodynamic and kinetic stability of SAs and small clusters and pinpoint issues related to using CO as a probe molecule.

2 Methods

2.1 Computational details

Periodic density functional theory (DFT) calculations were carried out using the Perdew–Burke–Ernzerhof (PBE) functional^38,39 in the grid-based projector augmented wave (PAW) formalism using the GPAW 1.4.0 software.^40–43 For the cation and anion vacancy containing zirconia surfaces the calculations were performed spin-polarized with a Hubbard correction of U = 2 eV applied to the d orbitals of zirconium atoms.⁴⁴ For the ideal zirconia the calculations were performed spin-paired to reduce computational burden. The Hubbard correction was excluded from the spin-paired calculations. Test calculations show that its influence on the adhesion of Rh and Pt single atoms on ideal zirconia is minor being only 0.1 eV and 0.05 eV, respectively. The agglomeration energy per atom (entries in Table S2 of ESI†) changes at most by 0.16 eV when the calculations are performed spin-polarized and with +U. The core electrons of heavy elements were represented with the PAW⁴⁵ setups in the frozen-core approximation. The Brillouin zones for all catalyst models and gas phase species were treated at the Γ-point, with the exception of the zirconia edge, for which a (4 × 4 × 1) Monkhorst–Pack mesh of k-points was used instead. The approach has been validated in our previous work.⁴⁶ The zirconia terrace was modelled with a m-ZrO₂(1̄11) (3 × 3) 2D slab cut from monoclinic zirconia bulk. The slab was two stoichiometric ZrO₂ layers thick with atoms in the bottom layer fixed at their ideal bulk positions. The zirconia edge was modelled with a (1 × 1) (2̄12) surface slab four atomic layers thick with the two bottom layers frozen in the ideal bulk positions. The bulk is described in detail in our previous work.⁴⁶ The bulk Rh and Pt metals were optimised in plane-wave basis with a 800 eV cutoff energy, a (16 × 16 × 16) Monkhorst–Pack mesh of k-points, and maximum residual force of 0.025 eV Å⁻¹. Zirconia supported Rh and Pt cluster models consisting of 13, 19, and 43 metal atoms are globally optimized structures described in detail in our previous work.⁴⁷

The Rh/ZrO₂ and Pt/ZrO₂ single atom catalyst models were constructed by placing the metal on the zirconia slab either as an ad-atom, or substituting (in the case of the (1̄11) surface) the metal atom for one of the Zr atoms. Several initial structures with different placement of the Rh and Pt adatoms on all zirconia sites were considered, and the most stable configurations were selected for further calculations.

Small clusters of two, three, and four metal atoms were constructed from the SA models by atom-wise adding one, two, and three metal atoms in contact with the first one and relaxing the structures. Several starting structures were attempted in each case, and the most stable ones were selected for the subsequent calculations.

Gas phase H₂O, H₂, CO, and CO₂ molecules were optimised in a non-periodic computational cell that was 18 × 18 × 18 Å in size. For the calculation of cluster adhesion energies, the single-point energies of the metal clusters were calculated in the gas-phase constrained to their supported geometries. The calculations were performed spin-polarized and the resulting cluster multiplicities can be found in Table S5.† All structures, with the exception of the bulk metals, were optimised in the grid basis with a 0.2 Å maximum grid spacing, and allowed to relax until the maximum residual force was below 0.05 eV Å⁻¹. The CO stretching modes and the adsorbate modes used to calculate zero-point energies were calculated from the Hessian matrix using the finite difference approach.

Diffusion barriers of Rh and Pt atoms on the ideal m-ZrO₂(1̄11) surface were calculated using the climbing image nudged elastic band method (CI-NEB).^48–51 Formulae used for computing the thermodynamic and kinetic parameters are detailed in the ESI.†

3 Results & discussion

3.1 Single atom stability

The formation energy, E^f_sa, of a SA (see ESI† for full formula) measures how difficult it is to form an SA on the support surface with respect to the bulk metal and gives a convenient way to compare the stabilities of single atoms on different sites of an oxide.¹³ Formation energies and Bader charges were calculated for Rh and Pt atoms on ideal and anion/cation defected ZrO₂ terrace, and on ideal and anion defected ZrO₂ edge (see ESI† for tabulated data). The formation energy is strongly endothermic for both metals at the ideal edge and terrace sites, being 3.44/2.93 and 2.61/1.29 eV for Rh/Pt, respectively. Both metal atoms are nearly neutral on the ideal terrace and edge sites, with Pt having slightly negative and Rh slightly positive Bader charges. The E^f_sa value for Pt is always lower than that for Rh at the same site, which indicates a higher affinity of Pt towards the zirconia surface. This is in agreement with our previous study, where small Pt clusters supported on zirconia were shown to have higher adhesion energies than Rh particles of the same size.⁴⁷ In the case of both Rh and Pt, the formation energy is lower at the edge site, indicating that the metal atom prefers under-coordinated sites, as previously suggested for Pt on alumina.¹⁰

Next, we consider the SA located on the defected zirconia. The maximum concentration of vacancies, and therefore the amount SA they can host, is related to the thermodynamic cost of creating them. On the pure zirconia terrace, the vacancy formation energy is very endothermic being 3.62 and 11.80 eV for the oxygen and zirconium vacancies, respectively (see ESI† for formulas used). In our previous study we reported that adsorbed Rh species lower the formation energy of a nearby oxygen vacancy.¹⁶ The same effect is seen here for Pt SA, which lowers the oxygen vacancy formation energy so much that it becomes exothermic by −0.74 eV. The Bader charges show that Pt is able to accommodate a more negative charge than the Rh atom, accepting more electrons left over from creating the vacancy. The oxygen vacancy formation energy in the presence of Rh is 0.80 eV. Pt and Rh SA also significantly lower the zirconium vacancy formation energies to 5.78 and 4.60 eV, respectively, which is still highly thermodynamically unfavourable.

The SA formation energy of both metals on an oxygen vacancy containing ZrO₂(1̄11) surface is much less endothermic than on the corresponding ideal surface, and is even exothermic in the case of Pt. In the case of the structures with a Zr vacancy, the metal atoms occupy the vacancy as a substitute for the missing surface Zr atom, both having Bader charges of ca. +1.4|e|. The formation energies are strongly exothermic for both metals, the value for Rh being more exothermic than that for Pt by 0.5 eV. The exothermic formation energies are due to the Zr vacancy being very unstable, and that formation of the substituted single atom site is strongly favoured.

3.2 Agglomeration thermodynamics

The agglomeration energy describes the energy gained per atom when N supported SA clump together to form a supported cluster of N atoms. The calculated values and the equations used are tabulated in the ESI.†

As expected, the agglomeration energy on the pristine zirconia terrace becomes more exothermic with increasing cluster size, the largest values being −2.13 and −1.73 eV with respect to 43-atom cluster for Rh and Pt, respectively. The agglomeration energies of the two metals are nearly identical in the 2–4 atom range. Beyond 4 atom clusters the agglomeration energy continues to become more exothermic, but the change is not as rapid as for the smallest clusters. For Pt in particular there is very little change in energy between the Pt₄ and Pt₁₃ clusters.

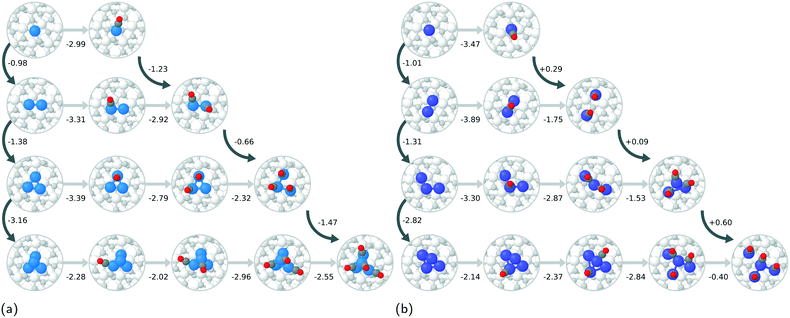
The adhesion energies (see ESI† for tabulated values and for equations used) of the Pt and Rh single atoms are essentially the same, being −2.46 and −2.44 eV, respectively. For Pt clusters, the adhesion energy becomes more exothermic with increasing cluster size, while for Rh, clusters with 1–3 atoms have almost the same adhesion energy. The 3- and 4-atom Rh clusters have much less exothermic adhesion energies than the corresponding Pt clusters, which suggests that the metal–support interaction for Rh is weaker as observed previously for the zirconia supported 13- and 19-atom Rh and Pt clusters.⁴⁷ On the other hand, the Rh–Rh and Pt–Pt cohesive energies are −6.07 and −5.72 eV, respectively, indicating that the metal–metal interactions in the rhodium clusters are stronger. The differences in the cohesive and adhesive energies are reflected in the cluster geometries (see Fig. 2a and b), as the supported Pt clusters prefer more open structures with longer Pt–Pt bonds while Rh prefers more compact cluster geometries, which are quite similar in shape to optimised gas-phase Rh clusters found in literature.⁵² Similar differences in cluster morphologies between Rh and Pt have been observed for the larger clusters.⁴⁷

On the oxygen or zirconium vacancy containing zirconia, the agglomeration energies can be calculated in a few different ways (see ESI† for equations used) that describe slightly different processes. First, the SA atoms could agglomerate in such a way that empty vacancies are left behind, while the cluster forms in the vicinity of just one vacancy. Leaving unfilled oxygen vacancies behind is highly thermodynamically unfavourable and the total energy change of four atoms agglomerating together would be +3.36 and +9.75 eV for Rh and Pt, respectively. For comparison, the corresponding values on the defect free zirconia are −5.51 and −5.14 eV. Agglomeration of SA is even more unfavourable if any Zr vacancies are left behind, being ca. +17 eV for the case of four Rh atoms. This is likely due to the high cost of Zr vacancy formation. Clearly, agglomeration into particles cannot occur on a catalyst that contains Rh or Pt as substituted species unless the vacancies are filled with something else, or if there are free metal SA species on the surface that could fill in the vacancy. The surface could also restructure in a way that is not accounted for in the calculations performed here. Alternatively, one could consider the SA sitting in a vacancy as a nucleation site with the other metal atoms coming from the pristine zirconia instead. In this case, on the oxygen defected surface the agglomeration energies are comparable to those on the pristine zirconia with the exception of the Rh trimer, and Pt tetramer (see ESI† for tabulated values).

Even though e.g. the structure containing the substituted SA and one other metal atom is formally a dimer, it is more structurally analogous to the SA on non-substituted zirconia. Therefore, the calculations on the metal substituted zirconia were performed for structures containing up to 5 Rh or Pt metal atoms, and from here on out the M_N clusters on Zr vacancy containing zirconia will be considered to consist of the N additional metal atoms deposited on top of the metal atom sitting in the Zr vacancy. The SA sitting in the cationic vacancy can be considered as a nucleation site similar to the SA on the surface with an oxygen vacancy. Calculated this way the total agglomeration energy of four free SA onto the nucleation site is −6.56 eV for Rh and −4.90 eV for Pt. The migration of a SA from an ideal zirconia site onto the nucleation site is −1.20 and −0.58 eV exothermic for Rh and Pt, respectively, which indicates that the SA have a stronger affinity to the site with a substituted metal atom than the pure zirconia site. The calculated adhesion energies for the clusters on metal substituted zirconia (see ESI† for tabulated values) are also more exothermic than for the clusters on ideal zirconia, with Rh adhesion being stronger than that of Pt.

3.3 Effect of CO on agglomeration thermodynamics

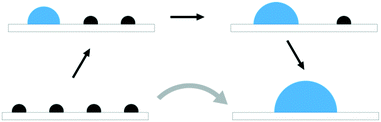
The atom-wise agglomeration process from Rh and Pt single atoms up to 4-atom clusters with and without adsorbed CO is depicted in Fig. 2a and b. In the previous section, the agglomeration of SA was considered as a kind of coalescence of SA into a particle of a certain size. The schematic Fig. 1 illustrates the connection between the two schemes.

Fig. 1 Schematic representation of single atom (black semi-circles) agglomeration into clusters (blue semi-circles). The figures connected by straight black arrows depict atom-wise agglomeration while the curved grey arrow represents coalescence.

In the absence of CO, the addition of each consecutive atom into the cluster is increasingly exothermic as the larger clusters become more and more stable. This indicates that there is a large thermodynamic driving for the agglomeration of SAs. The incorporation of one CO molecule per metal atom (the right-most structure of each row in Fig. 2a and b) dramatically changes the agglomeration thermodynamics. In the case of Rh, the formation of a Rh dimer with two CO adsorbed is more favourable than with no CO, but the formation of trimers and tetramers is much less favourable, though still strongly exothermic. The total agglomeration energy of four single atoms into a Rh₄ cluster is 2.15 eV less exothermic in the presence of CO than in the absence of CO.

Fig. 2 Agglomeration of a) Rh and b) Pt SA species with and without adsorbed CO. Rh, Pt, C, adsorbate O, lattice O, and Zr atoms are coloured blue, violet, dark gray, red, light gray and white, respectively. The curved dark arrows represent the agglomeration process where the cluster grows one atom at a time. The number next to them corresponds to the energy difference between the larger cluster and the smaller cluster plus another single atom species at an infinite separation. The straight horizontal grey arrows represent CO adsorption and the number underneath is the differential adsorption energy in eV.

For Pt species, the difference upon incorporation of CO is even more dramatic than for Rh. The adsorption of two CO molecules onto the dimer causes it to spontaneously dissociate into two Pt–CO complexes. Spontaneous cluster disintegration has recently been reported also for Pt₄ clusters with four adsorbed CO on CeO₂.⁵³ The energy change of +0.29 eV upon bringing the two Pt–CO complexes close together is most likely due to repulsion between the complexes. Three adsorbed CO are not enough to spontaneously dissociate the Pt trimer, however it is 0.38 eV less stable than three infinitely separated Pt–CO complexes, and the middle Pt–CO unit is no longer in contact with the zirconia surface. The CO covered Pt₄ can exist as structures that do not spontaneously dissociate, however they are slightly higher in energy than the partially dissociated structure consisting of CO containing Pt SA and Pt₂ complexes. In total, the agglomeration process (with respect to the lowest energy non-dissociated Pt₄ system) for CO containing Pt is 1.08 eV endothermic, which is a difference of 6.22 eV compared to the case with no adsorbed CO. In order to explain the higher stability of the Pt–CO unit compared to the CO covered clusters, we analysed the density of states plots of Pt, Pt–CO, Rh, and Rh–CO units on ideal zirconia, please Fig. S7 in the ESI.† From the plots, it can be seen that the Pt states located in the zirconia band gap are more significantly modified by the presence of CO than those of Rh. We tentatively ascribe the observed stability of Pt–CO units to enhanced hybridization between Pt and zirconia states in the presence of adsorbed CO.

3.4 CO binding and vibrational frequencies

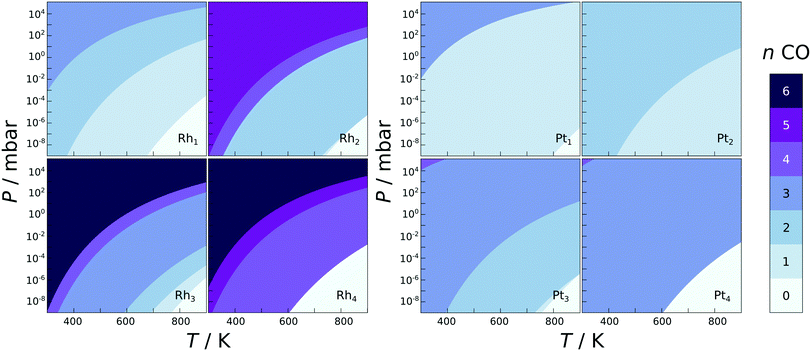
CO stretching frequencies are often used as an indication of the presence of single atoms on the support,^{7,9,35,36,54,55} and here the calculated CO adsorption energies and IR stretching frequencies are reported in the ESI.† CO binds to the single atoms and clusters with adsorption energies for a single CO varying from −0.78 to −3.89 eV, with no clear trend with respect to the structure or chemical composition. The adsorption strengths also vary from one metal atom to the next for all clusters, for example on the Rh₂ the adsorption energy for a single CO on a top site differs by 0.45 eV depending on which atom it is binding to. With the dimer being a perfectly symmetric species, this difference is clearly induced by the support. Location dependent adsorption energies have been previously reported for dissociated water, hydrogen, and CO on the globally optimised zirconia supported Rh and Pt clusters.^47,56 The type of the most favourable adsorption site varies as well, with CO sometimes preferring a top, bridge, or a hollow site. Especially in the case of Pt clusters the CO molecules preferred to form bridges between the metal atoms, almost appearing to hold the clusters together.

In the phase diagrams (Fig. 3), where the most favourable CO coverages are plotted for a range of experimental conditions for M_1–4 clusters on ideal zirconia, it is shown that the single atoms and small clusters incorporate CO even at very low pressures. In fact, all of the species studied here are expected to contain at least one adsorbed CO under ultra high vacuum (P < 10⁻⁹ mbar) at temperatures under 600 K. This indicates that CO adsorption should be accounted for when analysing the stability or reactivity of zirconia supported SAs and clusters, if CO is expected to be present in the gas-phase.

Fig. 3 Phase diagrams showing the most stabilising amount of adsorbed CO on Rh (left) and Pt (right) 1–4 atom clusters as a function of CO pressure and temperature. Note that the Pt₂ species containing 2 CO molecules is no longer a dimer, but two Pt–CO monomers close together on the surface formed from the spontaneous disintegration upon CO adsorption.

Unlike on metal facets, the CO adsorption energy does not depend on the coverage in a smooth manner, but is very unpredictable. For some metal species, such as Pt₃ on ideal zirconia, the differential adsorption energy becomes less exothermic with each adsorbed CO, yet for others, such as Pt₄ on ideal zirconia, the adsorption starts off weaker and becomes more exothermic on average with each added CO until the cluster spontaneously breaks apart. The unpredictable behaviour of CO adsorption is probably due to the extensive restructuring that the particles can undergo upon CO adsorption, as well as the inequivalent nature of the adsorption sites mentioned earlier. The fluxionality of small clusters and its effect on catalytic activity has been discussed recently.^56–61 The non-uniformity of CO adsorption is clearly seen in the phase diagrams (Fig. 3): some CO coverages are never the most stable. For example the Rh₄ and Pt₄ clusters go directly from four and three adsorbed CO to being completely bare at elevated temperatures and low CO pressures. The difference in the adsorption energy of a single CO to a supported SA/cluster and the same SA/cluster in gas-phase frozen to the same geometry, ΔΔE_ads, measures the ligand effect the oxide support has on the adsorption of CO. The ligand effect was evaluated for the M_1–4 clusters (see ESI† for equation used and tabulated values), and was found to vary strongly from one cluster to the next. For most clusters ΔΔE_ads is negative, which indicates a stabilising ligand effect, while for the SA the value is almost always positive, with the exception of the Pt SA on the cation defected zirconia.

The Rh–CO and Pt–CO monomers have one stretching frequency at 1956 and 2037 cm⁻¹ on the ideal zirconia, respectively. The frequency for Pt–CO is close to previously reported experimental values for Pt SA supported on CeO₂ (ref. 55) and FeO_x.⁷ The Rh and Pt SA with two adsorbed CO have the characteristic symmetric and asymmetric modes which are 40 and 30 wavenumbers apart in frequency. The difference between these peaks has been reported as around 70 cm⁻¹ for Rh SA on different supports, including tetragonal zirconia.^9,36 The addition of each consecutive CO adds another stretching frequency, but also shifts the pre-existing CO stretching modes. The bridge bonded CO on clusters have the lowest frequencies (<1900 cm⁻¹), similar to those reported for CO bridge bonded to metal nanoparticles.^7,9,36,55 Interestingly, the stretching frequencies given by Pt₁(CO)₃ species on ideal zirconia are in good agreement with previous experimental vibrational data.⁶² The stretching modes of adsorbed CO are sensitive to the structure of the underlying oxide, which is seen as shifts in the frequencies when the cluster is deposited on oxygen defected or metal substituted zirconia. For example, the stretching frequency of a single CO bound to a Rh SA is lowered by over 60 cm⁻¹ in the presence of an oxygen vacancy, probably due to the CO lying closer to the zirconia surface. Also the two Pt–CO complexes formed upon spontaneous Pt dimer disintegration give two frequencies approximately 40 cm⁻¹ apart that are both shifted from the isolated Pt–CO frequency. The Pt–Pt distance between the complexes is 4.4 Å.

In summary, these CO stretching frequencies of different SA and clusters are quite close together, with the number of bound CO dependent on reaction conditions, it could be difficult to identify which peaks belong to which species. This kind of ambiguity in CO frequencies has been predicted also for ceria supported Pt₈ clusters and SA.⁶³ However, the presence of low frequency peaks could be an indication of the presence of small clusters.

3.5 Agglomeration kinetics

Finally, we consider the kinetics of SA agglomeration which is a complex surface diffusion process with several time scales.⁶⁴ The traditional picture of SA agglomeration is based on either Ostwald ripening or coalescence. In both processes the decrease in the surface energy provides the driving force. Additionally, the Ostwald ripening process assumes a critical particle size at which neither shrinking nor growth takes place; the critical particle size can be understood as an additional thermodynamic barrier separating SAs and small clusters from larger particles.

While the above traditional notions are applicable to nanoparticle growth, for SAs or very small clusters, such as considered in this work, the surface energy is no longer a meaningful concept and cannot even be defined. Indeed, SAs and small clusters belong to the “every-atom-counts” size region where the thermodynamics are no longer extensive.^25,27,28 As a result, the decrease in surface energy can no longer be used as the driving force. To mend this deficiency and to account for the non-extensive thermodynamic nature of SAs and nanoclusters, we combined non-equilibrium thermodynamics and nanothermodynamics to develop a kinetic model for the sintering of SAs and USCs. Unlike previous kinetic models,^13,24,65,66 our model does not rely on the particle-size dependent surface tension or critical particle size and is applicable to arbitrarily small or large particles. Furthermore, it is possible to study the tendency of SAs to grow into cluster or further to larger nanoparticles.

Following the development in the ESI† and the scheme in Fig. 4, the kinetics of particle growth can be characterized using the effective flux from an SA to cluster size R as follows.

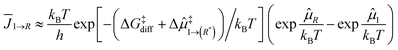where ‘1’ denotes a SA, ΔG^‡_diff is the SA diffusion barrier, Δ[small mu, Greek, circumflex]^‡_1→(R*) is a possible additional thermodynamic barrier from a SA to a critical cluster size R*, and [small mu, Greek, circumflex]_R is the generalised chemical potential which depends on the particle size. As detailed in the ESI,†[small mu, Greek, circumflex](R) takes into account the thermodynamics non-extensitivity resulting in particle size-dependent thermodynamics.

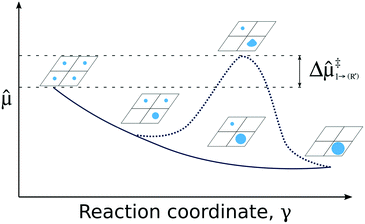Fig. 4 Pictorial presentation of the scheme used for analyzing SA stability. The studied reaction is the agglomeration of SA and the reaction coordinate γ is the SA coverage. Stability of the system along γ is obtained from generalized chemical potentials, [small mu, Greek, circumflex] (see ESI†). The solid line characterizes the evolution of [small mu, Greek, circumflex] without a critical cluster size. The dashed line depicts a situation in which a critical cluster size separates the SAs and the growing cluster inducing an additional kinetic barrier Δ[small mu, Greek, circumflex]^‡.

Even though eqn (1) is derived using a non-equilibrium nanothermodynamic approach, it is remarkably similar to models obtained using a macroscopic description of particle growth kinetics in ref. 13, 24, 65 and 66; the flux is defined as a product of a kinetic term and a thermodynamic driving force which in is due to the generalised chemical potential rather than surface energy of macroscopic models. The timescale for agglomeration is given by the surface diffusion between of SAs or larger clusters. While the SAs can be stabilised by the [small mu, Greek, circumflex]_R*, the driving force for SA agglomeration to clusters or larger particles is extremely large as shown in the ESI.† Therefore, SA agglomeration will be extremely fast and irreversible whenever diffusion is sufficiently fast.

To understand the sintering of zirconia supported Rh/Pt SAs and clusters we consider the pathways presented in Fig. 2a and b. All the quantities used for parametrising eqn (1) are based on DFT-computed values as shown in the ESI.† In the absence of CO, no critical cluster size has been identified and sintering of SAs and clusters to larger particles is always energetically favourable. As shown in the ESI,† forming even larger cluster with 13, 19, and 43 atoms is always favourable and irreversible. We note that it cannot be completely ruled out that a critical size could be found among clusters with 5 to 12, 14 to 18, or 20 to 42 atoms. As there is no energetic penalty for particle growth (Δ[small mu, Greek, circumflex]_R* = 0), ZrO₂(1̄11) is unable to kinetically stabilize Rh/Pt SAs or clusters. Furthermore, the diffusion barrier for Rh/Pt SA on the ideal zirconia terrace is only 0.7/0.9 eV, which can be overcome even at moderate temperatures. On the vacancy containing zirconia, the diffusion barrier will be much larger, since the thermodynamic cost alone of the SA leaving the vacancy is already several eV.

In the presence of CO, sintering of Rh is again spontaneous and no critical cluster size has been found. As a result, CO atmosphere cannot be used to kinetically stabilise Rh SA and clusters on zirconia. The case of Pt is different, as CO adsorption makes agglomeration both thermodynamically (no driving force) and kinetically (Δ[small mu, Greek, circumflex]₂ > 0) unfavourable. As a result CO is expected to suppress Pt agglomeration on zirconia. Interestingly, previous calculations report that TiO₂ supported Rh particles should be more susceptible to CO induced disintegration than Pt particles, owing to the more exothermic formation energies of the Rh–CO complexes.³¹

4 Conclusions

The stability of Rh and Pt single atoms was evaluated on the pristine and anionic/cationic defect containing zirconia. The defected zirconia sites as well as the zirconia edge site stabilise single atoms more compared to the ideal zirconia terrace. Agglomeration of the SAs is strongly thermodynamically favoured in all cases unless unfilled vacancies are left behind by the agglomerating atoms, in which case the process is highly unfavourable. Agglomeration of free Rh SA onto Rh substituent atoms on the zirconia surface is even more exothermic than onto an ideal zirconia site, indicating that they could act as nucleation sites for agglomeration. The presence of CO kinetically and thermodynamically hinders the agglomeration of SA, and in the case of Pt dimers and tetramers induces spontaneous particle disintegration.

The atomistic thermodynamic analysis of the M_N–xCO complexes shows that the SA and clusters are likely to have CO bound to them at a very wide range of temperatures, even under UHV. Computational models involving small clusters and SA should therefore include adsorbed CO if any CO is expected to be present in system of interest. CO binding to the SA is also so strong that it may in some cases be considered a poison. Our results also show that vibrational frequencies of CO adsorbed SAs and small clusters are closely spaced. This makes the application of vibrational spectroscopy to identify of SAs, clusters, and adsorption sites error-prone. Furthermore, using CO as a probe molecule to characterise SAs is troublesome because CO can induce particle disintegration which might not take place under the intended operation conditions without CO. Our combined DFT and thermodynamic analysis shows that CO may significantly affect thermodynamic and kinetic stability and the structure of SAs or small clusters. Therefore, caution is needed when using CO or other common probe molecules to characterise the existence and properties of SAs.

Author contributions

MMK performed the DFT calculations and devised the thermodynamic analysis. MMM developed the non-equilibrium nanothermodynamic model used for assessing kinetic stability. KH conceptualised and supervised the work. All authors participated in planning the research and writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was funded by Academy of Finland projects 277222 (MMK) and 307853 (MMM) and University of Jyväskylä. MMK thanks Dr Sami Malola for fruitful discussions. The electronic structure calculations were made possible by the computational resources provided by the Finnish Grid and Cloud Initiative and the CSC — IT Center for Science, Espoo, Finland (https://www.csc.fi/en/).

Notes and references

1. A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
2. M. Flytzani-Stephanopoulos, Chin. J. Catal., 2017, 38, 1432–1442.
3. Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804.
4. S. Back, J. Lim, N.-Y. Kim, Y.-H. Kim and Y. Jung, Chem. Sci., 2017, 8, 1090–1096.
5. J. Jones, H. Xiong, A. T. DeLaRiva, E. J. Peterson, H. Pham, S. R. Challa, G. Qi, S. Oh, M. H. Wiebenga, X. I. Pereira Hernández, Y. Wang and A. K. Datye, Science, 2016, 353, 150–154.
6. N. Daelman, M. Capdevila-Cortada and N. López, Nat. Mater., 2019, 18, 1215–1221.
7. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641.
8. R. Lang, W. Xi, J.-C. Liu, Y.-T. Cui, T. Li, A. F. Lee, F. Chen, Y. Chen, L. Li, L. Li, J. Lin, S. Miao, X. Liu, A.-Q. Wang, X. Wang, J. Luo, B. Qiao, J. Li and T. Zhang, Nat. Commun., 2019, 10, 234.
9. Y. Kwon, T. Y. Kim, G. Kwon, J. Yi and H. Lee, J. Am. Chem. Soc., 2017, 139, 17694–17699.
10. J. H. Kwak, J. Hu, D. Mei, C.-W. Yi, D. H. Kim, C. H. F. Peden, L. F. Allard and J. Szanyi, Science, 2009, 325, 1670–1673.
11. H. Yan, H. Cheng, H. Yi, Y. Lin, T. Yao, C. Wang, J. Li, S. Wei and J. Lu, J. Am. Chem. Soc., 2015, 137, 10484–10487.
12. M. T. Darby, R. Réocreux, E. C. H. Sykes, A. Michaelides and M. Stamatakis, ACS Catal., 2018, 8, 5038–5050.
13. R. Ouyang, J.-X. Liu and W.-X. Li, J. Am. Chem. Soc., 2013, 135, 1760–1771.
14. Y.-G. Wang, D. Mei, V.-A. Glezakou, J. Li and R. Rousseau, Nat. Commun., 2015, 6, 6511.
15. Q. Liu and Z. Zhang, Catal. Sci. Technol., 2019, 9, 4821–4834.
16. A. S. Bazhenov, M. M. Kauppinen and K. Honkala, J. Phys. Chem. C, 2018, 122, 6774–6778.
17. A. Ruiz Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513.
18. M. T. Darby, M. Stamatakis, A. Michaelides and E. C. H. Sykes, J. Phys. Chem. Lett., 2018, 9, 5636–5646.
19. J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976.
20. J. Resasco, L. DeRita, S. Dai, J. P. Chada, M. Xu, X. Yan, J. Finzel, S. Hanukovich, A. S. Hoffman, G. W. Graham, S. R. Bare, X. Pan and P. Christopher, J. Am. Chem. Soc., 2020, 142, 169–184.
21. P. Christopher, ACS Energy Lett., 2019, 4, 2249–2250.
22. Q. Zhao, B. Liu, Y. Xu, F. Jiang and X. Liu, New J. Chem., 2020, 44, 1632–1639.
23. Y. Tang, C. Asokan, M. Xu, G. W. Graham, X. Pan, P. Christopher, J. Li and P. Sautet, Nat. Commun., 2019, 10, 4488.
24. Y. Dai, P. Lu, Z. Cao, C. T. Campbell and Y. Xia, Chem. Soc. Rev., 2018, 47, 4314–4331.
25. T. L. Hill, Thermodynamics of small systems. Parts I and II, W.A. Benjamin, Inc, 1964.
26. Z. H. Li and D. G. Truhlar, Chem. Sci., 2014, 5, 2605–2624.
27. T. L. Hill, J. Chem. Phys., 1962, 36, 3182–3197.
28. T. L. Hill, Nano Lett., 2001, 1, 273–275.
29. J. Liu, ACS Catal., 2017, 7, 34–59.
30. S. Tosoni and G. Pacchioni, Surf. Sci., 2017, 664, 87–94.
31. B. R. Goldsmith, E. D. Sanderson, R. Ouyang and W.-X. Li, J. Phys. Chem. C, 2014, 118, 9588–9597.
32. A. Suzuki, Y. Inada, A. Yamaguchi, T. Chihara, M. Yuasa, M. Nomura and Y. Iwasawa, Angew. Chem., Int. Ed., 2003, 42, 4795–4799.
33. J.-C. Liu, Y.-G. Wang and J. Li, J. Am. Chem. Soc., 2017, 139, 6190–6199.
34. K. Ding, A. Gulec, A. M. Johnson, N. M. Schweitzer, G. D. Stucky, L. D. Marks and P. C. Stair, Science, 2015, 350, 189–192.
35. H. V. Thang, S. Tosoni, L. Fang, P. Bruijnincx and G. Pacchioni, ChemCatChem, 2018, 10, 2634–2645.
36. J. C. Matsubu, V. N. Yang and P. Christopher, J. Am. Chem. Soc., 2015, 137, 3076–3084.
37. Z. Tang, P. Liu, H. Cao, S. Bals, H. J. Heeres and P. P. Pescarmona, ACS Catal., 2019, 9, 9953–9963.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396.
40. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202.
41. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109.
42. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
43. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
44. V. Korpelin, M. M. Melander and K. Honkala, Manuscript in preparation.
45. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
46. A. S. Bazhenov and K. Honkala, Top. Catal., 2017, 60, 382–391.
47. A. S. Bazhenov and K. Honkala, J. Phys. Chem. C, 2019, 123, 7209–7216.
48. H. Jónsson, G. Mills and K. W. Jacobsen, Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions, Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Singapore, 1998, p. 385.
49. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
50. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
51. S. Smidstrup, A. Pedersen, K. Stokbro and H. Jónsson, J. Chem. Phys., 2014, 140, 214106.
52. T. Mineva, N. Russo and H.-J. Freund, J. Phys. Chem. A, 2001, 105, 10723–10730.
53. Y.-Q. Su, Y. Wang, J.-X. Liu, I. A. Filot, K. Alexopoulos, L. Zhang, V. Muravev, B. Zijlstra, D. G. Vlachos and E. J. Hensen, ACS Catal., 2019, 9, 3289–3297.
54. E. Varga, P. Pusztai, L. Óvári, A. Oszkó, A. Erdőhelyi, C. Papp, H.-P. Steinrück, Z. Kónya and J. Kiss, Phys. Chem. Chem. Phys., 2015, 17, 27154–27166.
55. C. Wang, X.-K. Gu, H. Yan, Y. Lin, J. Li, D. Liu, W.-X. Li and J. Lu, ACS Catal., 2017, 7, 887–891.
56. M. M. Kauppinen, V. Korpelin, A. M. Verma, M. M. Melander and K. Honkala, J. Chem. Phys., 2019, 151, 164302.
57. P. Liu and J. A. Rodriguez, J. Chem. Phys., 2007, 126, 164705.
58. Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458.
59. B. Zandkarimi and A. N. Alexandrova, J. Phys. Chem. Lett., 2019, 10, 460–467.
60. Y. Yang, J. Evans, J. A. Rodriguez, M. G. White and P. Liu, Phys. Chem. Chem. Phys., 2010, 12, 9909–9917.
61. L. Barrio, P. Liu, J. A. Rodriguez, J. M. Campos-Martin and J. L. G. Fierro, J. Phys. Chem. C, 2007, 111, 19001–19008.
62. G. S. Icking-Konert, H. Handschuh, G. Ganteför and W. Eberhardt, Phys. Rev. Lett., 1996, 76, 1047–1050.
63. H. A. Aleksandrov, K. M. Neyman, K. I. Hadjiivanov and G. N. Vayssilov, Phys. Chem. Chem. Phys., 2016, 18, 22108–22121.
64. K. Alexopoulos and D. G. Vlachos, Chem. Sci., 2020, 11, 1469–1477.
65. S. C. Parker and C. T. Campbell, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035430.
66. L. R. Houk, S. R. Challa, B. Grayson, P. Fanson and A. K. Datye, Langmuir, 2009, 25, 11225–11227.

---

Footnote

† Electronic supplementary information (ESI) available: 1) Formation, 2) vacancy formation, 3) agglomeration, and 4) adhesion energies. 5) Atomistic thermodynamics. 6) CO adsorption and vibrational frequencies. 7) Model for kinetic stability. 8) Catalyst model structure geometries. See DOI: 10.1039/d0cy00413h

---