Conformationally adaptive macrocycles with flipping aromatic sidewalls†
Abstract
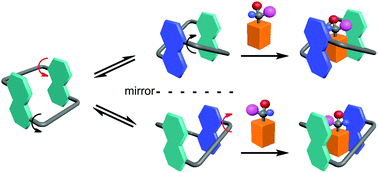
Conformationally adaptive macrocycles possess multiple well-defined conformations through quickly flipping their aromatic sidewalls. The macrocycles combine the binding power of all the conformations. Upon binding a guest, one or a combination of conformations are selected to achieve the maximized binding affinity. In addition, the complex conformational network is responsive to changes in temperature or solvent. It has been demonstrated that these macrocycles have unique properties in chirality sensing, stimuli-responsive self-assembly, and molecular switches. In this tutorial review, we summarize recent advances on conformationally adaptive macrocycles with an emphasis on our own research. We believe that this class of macrocycles will have a bright future in supramolecular chemistry and beyond.


 Please wait while we load your content...
Please wait while we load your content...