Synthesis, optoelectronic properties and applications of halide perovskites
Abstract
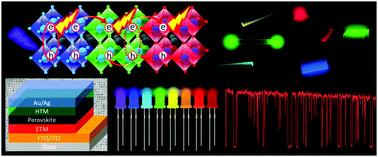
Halide perovskites have emerged as a class of most promising and cost-effective semiconductor materials for next generation photoluminescent, electroluminescent and photovoltaic devices. These perovskites have high optical absorption coefficients and exhibit narrow-band bright photoluminescence, in addition to their halide-dependent tuneable bandgaps, low exciton binding energies, and long-range carrier diffusion. These properties make these perovskites superior to classical semiconductors such as silicon. Most importantly, the simple synthesis of perovskites in the form of high quality films, single crystals, nanocrystals and quantum dots has attracted newcomers to develop novel perovskites with unique optoelectronic properties for optical and photovoltaic applications. Here, we comprehensively review recent advances in the synthesis and optoelectronic properties of films, microcrystals, nanocrystals and quantum dots of lead halide and lead-free halide perovskites. Followed by the classification of synthesis, we address the ensemble and single particle properties of perovskites from the viewpoints of the confinement and transport of charge carriers or excitons. Further, we correlate the charge carrier properties of perovskite films, microcrystals, nanocrystals and quantum dots with the crystal structure and size, halide composition, temperature, and pressure. Finally, we illustrate the emerging applications of perovskites to solar cells, LEDs, and lasers, and discuss the ongoing challenges in the field.


 Please wait while we load your content...
Please wait while we load your content...