Open Access Article
Open Access ArticleA review of defect structure and chemistry in ceria and its solid solutions†
Rafael
Schmitt‡
 a,
Andreas
Nenning‡
a,
Andreas
Nenning‡
 abc,
Olga
Kraynis‡
abc,
Olga
Kraynis‡
 d,
Roman
Korobko
ad,
Anatoly I.
Frenkel
d,
Roman
Korobko
ad,
Anatoly I.
Frenkel
 e,
Igor
Lubomirsky
e,
Igor
Lubomirsky
 d,
Sossina M.
Haile
f and
Jennifer L. M.
Rupp
d,
Sossina M.
Haile
f and
Jennifer L. M.
Rupp
 *abg
*abg
aElectrochemical Materials, Department of Materials, ETH Zurich, Switzerland
bElectrochemical Materials, Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jrupp@mit.edu
cTU Wien, Institute of Chemical Technologies and Analytics, Vienna, 1060, Austria
dDepartment Materials and Interfaces, Weizmann Institute of Science, Rehovot 76100, Israel
eDepartment of Materials Science and Chemical Engineering, Stony Brook University, Stony Brook, NY 11794, USA
fMaterials Science and Engineering, Northwestern University, Evanston, IL, USA
gElectrochemical Materials, Department of Electrical Engineering & Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 24th December 2019
Abstract
Ceria and its solid solutions play a vital role in several industrial processes and devices. These include solar energy-to-fuel conversion, solid oxide fuel and electrolyzer cells, memristors, chemical looping combustion, automotive 3-way catalysts, catalytic surface coatings, supercapacitors and recently, electrostrictive devices. An attractive feature of ceria is the possibility of tuning defect-chemistry to increase the effectiveness of the materials in application areas. Years of study have revealed many features of the long-range, macroscopic characteristics of ceria and its derivatives. In this review we focus on an area of ceria defect chemistry which has received comparatively little attention – defect-induced local distortions and short-range associates. These features are non-periodic in nature and hence not readily detected by conventional X-ray powder diffraction. We compile the relevant literature data obtained by thermodynamic analysis, Raman spectroscopy, and X-ray absorption fine structure (XAFS) spectroscopy. Each of these techniques provides insight into material behavior without reliance on long-range periodic symmetry. From thermodynamic analyses, association of defects is inferred. From XAFS, an element-specific probe, local structure around selected atomic species is obtained, whereas from Raman spectroscopy, local symmetry breaking and vibrational changes in bonding patterns is detected. We note that, for undoped ceria and its solid solutions, the relationship between short range order and cation–oxygen-vacancy coordination remains a subject of active debate. Beyond collating the sometimes contradictory data in the literature, we strengthen this review by reporting new spectroscopy results and analysis. We contribute to this debate by introducing additional data and analysis, with the expectation that increasing our fundamental understanding of this relationship will lead to an ability to predict and tailor the defect-chemistry of ceria-based materials for practical applications.
1 Basic properties and applications of ceria
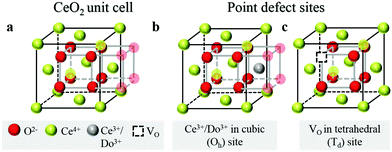
Over the past few decades, the crystal structure, electronic and ionic conductivities, elastic moduli and electromechanical behavior of ceria, CeO2, and its doped derivatives, have been studied and the materials have been found to be suited to a variety of important industrial applications.1 Beyond the functional properties, these oxides are generally inert against reactions and hence are compatible with many materials, both biological and inorganic, they are stable in harsh environments, including temperatures up to at least 2000 °C, and cerium, despite being a lanthanide, is rather abundant in the earth's crust, comparable in abundance to copper.2 These features add to the suitability of this class of materials to a wide range of devices.The properties of ceria are closely linked to its rather stable cubic fluorite (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) crystal structure, Fig. 1a, which has four CeO2 formula units per cubic unit cell. The Ce atoms are arranged in a face centered cubic array, occupying the 4a sites of the Fm
m) crystal structure, Fig. 1a, which has four CeO2 formula units per cubic unit cell. The Ce atoms are arranged in a face centered cubic array, occupying the 4a sites of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, and the oxygen anions fill the eight tetrahedral 8c sites. The arrangement gives 8-fold coordination of Ce and 4-fold tetrahedral coordination of O ions. The properties of the material can be readily manipulated within the framework of this robust crystal structure by extrinsic doping to create solid solutions. In particular, cations of similar size to Ce4+ but with different valence are compensated by the creation of functional point defects. When the dopants are trivalent acceptor cations, henceforth Do, (Fig. 1b), the missing positive charge is compensated by the formation of one extrinsic oxygen vacancy per two dopant elements (Fig. 1c), and the stoichiometry is Ce1−xDoxO2−x/2. Such acceptor doping has been widely exploited for fuel cell development,3,4 because the resulting materials, particularly in the case of Sm and Gd doping, display exceptionally high ionic conductivity.5 Divalent dopants (e.g. Ca, Mg. Ba), though generating a higher concentration of vacancies per dissolved dopant ion, result in uniformly lower conductivities than Sm and Gd dopants6 and therefore have been of much lower technological interest. The case of high valence donor dopants (e.g. Nb5+, Ta5+) has been studied to an even lesser extent, in large part because the solubilities of these species is relatively low (generally on the order of 1 at%), implying limited impact on bulk properties.7–9
m space group, and the oxygen anions fill the eight tetrahedral 8c sites. The arrangement gives 8-fold coordination of Ce and 4-fold tetrahedral coordination of O ions. The properties of the material can be readily manipulated within the framework of this robust crystal structure by extrinsic doping to create solid solutions. In particular, cations of similar size to Ce4+ but with different valence are compensated by the creation of functional point defects. When the dopants are trivalent acceptor cations, henceforth Do, (Fig. 1b), the missing positive charge is compensated by the formation of one extrinsic oxygen vacancy per two dopant elements (Fig. 1c), and the stoichiometry is Ce1−xDoxO2−x/2. Such acceptor doping has been widely exploited for fuel cell development,3,4 because the resulting materials, particularly in the case of Sm and Gd doping, display exceptionally high ionic conductivity.5 Divalent dopants (e.g. Ca, Mg. Ba), though generating a higher concentration of vacancies per dissolved dopant ion, result in uniformly lower conductivities than Sm and Gd dopants6 and therefore have been of much lower technological interest. The case of high valence donor dopants (e.g. Nb5+, Ta5+) has been studied to an even lesser extent, in large part because the solubilities of these species is relatively low (generally on the order of 1 at%), implying limited impact on bulk properties.7–9
Even in the absence of extrinsic dopants, a substantial concentration of point defects can exist in ceria as a result of partial reduction of Ce4+ to Ce3+. In such case, the material has the formula CeO2−δ, where δ is the oxygen non-stoichiometry, and both ionic and electronic conductivity become significant. The reduction is generally favored at high temperatures, low gas-phase oxygen chemical potentials (i.e., low oxygen partial pressures), and on surfaces.10,11 The reversibility and ease of the reduction is implicated in the high catalytic activity of ceria for a variety of redox reactions which are reviewed e.g. by Trovarelli12 or Montini.13 The most prominent technological application in this context is in automotive three-way-catalysts.1,14 In order to simultaneously remove soot, carbon monoxide, and NOx from the exhaust stream, precise control of the oxygen-to-fuel ratio is necessary. Ceria has the capacity to serve as an oxygen buffer by actively varying its oxygen non-stoichiometry, supplying oxygen when required for carbon oxidation, and removing it as necessary for NOx reduction. Another promising use of the oxygen storage capacity of ceria is in solar-driven thermochemical water splitting.15,16 During this cyclic process, ceria releases oxygen at extremely high temperatures (typ. 1500 °C), which can be achieved by solar concentration. Subsequently, the material is cooled to 800–1000 °C, and the oxygen vacancies generated from the prior reduction step are filled with oxygen through a water and CO2 splitting reaction. Though not treated in this review, it is noteworthy that doping with tetravalent cations, Zr4+ or Hf4+, increases the ease by which the reduction of the host material occurs.17,18 This behavior is used to increase the oxygen storage capacity in exhaust catalysts, or to decrease the operating temperature of solar- and thermochemical water splitting.19,20 The partial reduction of ceria in the presence of hydrogen or other fuels furthermore provides advantages for its use as a constituent in composite anodes of solid oxide fuel cells.21–24
While the use of ceria and its doped derivatives in energy and environmental technologies as described above is relatively well-known, the reducibility and mixed conductivity of ceria are also relevant to its applicability in emerging areas such as resistive switching devices25–28 for computation and data storage, and supercapacitors.29 In the medical sector, where ceria has been found to be biocompatible with human tissue, the surface catalytic redox activity has been investigated for potential use in cancer therapy and inhibition of radiation-induced damage.30,31
Because of the extensive range of demonstrated and possible applications of trivalent (rare-earth) doped ceria, the literature is rich with studies connecting the macroscopic properties, particularly transport properties, to the material chemistry32–34 and to the long-range, averaged crystal structure, where the latter is generally determined by conventional X-ray powder diffraction.35,36 In this review we focus on an area of ceria defect chemistry that has received comparatively little attention: defect-induced local distortions and short-range associates. The selection of this topic is motivated by the recognition that several questions regarding the chemo-mechanical and electrostrictive properties of doped ceria remain open.37–39 For example, 10 mol% Gd-doped ceria supported thin films37,38 can develop large electrostrictive stress (up to 500 MPa) and the electrostrictive strain coefficient is surprisingly large at low electric field frequencies. As characterized by Newnham et al. for a large variety of materials,40 the electrostrictive strain coefficient should scale with the ratio of the material elastic compliance to the dielectric permittivity. According to this scaling law, materials with large bulk modulus and dielectric constant 30–55 such as trivalent doped ceria should not produce a large electrostrictive response.41 For example, Y-stabilized ZrO2 has a strain electrostriction coefficient of the order of 10−21 (m2 V−2). However, electrostriction coefficients of ≈10−18−10−16 (m2 V−2), comparable to commercial relaxor materials, have been recorded for substrate supported doped ceria films in a “cantilever” configuration,37,39,42 self-supported membranes,43 as well as for bulk ceramics.44 Moreover, Gd-doped ceria has been shown to be anelastic, meaning that the elastic moduli depend on the rate of deformation.45 These unusual properties, which emerge at trivalent dopant concentrations of ≤20 mol%, are proposed to originate from anisotropic lattice distortions in the near neighbor shells of the cations and oxygen vacancies in an average fluorite structure.38,46
This review draws from the extensive literature derived from thermogravimetric measurements,18,47–51 from which defect association in partially reduced ceria compositions can be inferred, and from local structural measurements, specifically X-ray absorption fine structure (XAFS) spectroscopy and Raman spectroscopy. These spectroscopic methods are exquisitely suited to the detection of non-periodic distortions and can assist in the search for suitable descriptors of the interaction of oxygen anions and vacancies with dopant or Ce3+ ions, e.g. defect associates and lattice distortions. Additional suitable methods for addressing short-range interatomic distances such as neutron and X-ray total scattering analysis using Pair Distribution Function (PDF) were recently reviewed by Coduri et al. in ref. 34. The conclusions from these data will be briefly discussed alongside XAFS results. Similarly, nuclear magnetic resonance (NMR) spectroscopy can give insights into local structural configurations, and conclusions in this area are discussed alongside the Raman spectroscopy results. Other methods like oxygen isotope exchange and depth profiling (IEDP) by secondary ion mass spectroscopy (SIMS) yield valuable complementary information on oxygen exchange and diffusion kinetics, but do not shed light on the local structure considered in this review.52–55
The thermogravimetric measurements, analyzed in conjunction with appropriate defect models, reveal that, as soon as defect concentration become non-negligible, the thermodynamics of reduction of undoped and (to a lesser extent) doped ceria deviate from simple solution behavior. In such case, rather than isolated, non-interacting defects, associates in the form of neutral trimers dominate the defect chemistry.56,57 Raman spectroscopy reveals the emergence of new peaks when defects are introduced into ceria, providing a sensitive tool for investigating local structure. Extended XAFS (EXAFS) spectroscopy has been used to measure the distance from Ce or dopant cations to their nearest neighbors (oxygen anions) or next nearest neighbors (other cations). The average nearest-neighbor distances of doped ceria show that the lattice strongly deviates from fluorite symmetry at the unit cell level.58,59 This stands in a seeming contradiction with the XRD studies which average over all unit cells and indicate fluorite symmetry for acceptor doping levels up to 20 mol%.35,60–62 It is evident that the global average does not provide the full structural description and a multimodal approach, combining the XRD and EXAFS studies to provide a picture of actual structure, is needed. In agreement with the EXAFS findings, Raman spectra of extrinsically doped and reduced undoped ceria, demonstrate additional defect-related Raman modes, indicating that the fluorite symmetry is no longer present on the unit cell level.
Combining the results across methods that are capable of directly probing local cation–oxygen, and oxygen-vacancy related lattice interactions and distortions enables identification of new parameters affecting electro/thermo-chemo-mechanics of ceria solid solutions. In turn, the insights afforded from this framework can reveal the role of defect clustering and local structural distortions on reducibility and the generation of surprisingly large electrostriction. Such factors must be considered when designing ceria based materials for a wide range of applications.
2 Thermodynamic studies of the defect-chemistry of ceria, without and with dopants
We review in this section the state of understanding of the defect-chemistry of ceria as developed largely using thermogravimetric methods and conductivity measurements in combination with defect chemical modeling and more recent atomistic simulations. With such techniques, information on the enthalpies and entropies of defect interactions, as well as candidates for defect clusters are accessible. As we show later in this review, Raman and XAFS spectroscopies can directly reveal the local chemical environment of defects. These techniques provide even deeper insights into the nature, concentration and degree of association of such defects as relevant for fully elucidating the structure–property relationships.Ceria is a wide bandgap semiconductor with an experimentally measured bandgap of ∼6 eV from the valence band with predominantly oxygen 2p character to the conduction band with predominantly cerium 5d character.63 Localized, empty 4f states lie within the gap,64 leading some to describe the bandgap to be ∼3 eV,65 which is, however, the distance from the valence band to the bottom of the empty 4f band. As already noted, doping with tri- or divalent cations introduces extrinsic oxygen vacancies, which balance the effective negative charge of the dopant species. Exposure to high temperature or reducing gas conditions causes a loss of oxygen to the gas phase, generating intrinsic oxygen vacancies. These vacancies are charge-balanced by electronic defects in form of Ce3+ ions and, depending on specific conditions, the concentration on intrinsic defects can dominate bulk properties.50 The reactions and mass action laws characterizing the redox behavior are summarized in Table 1 (eqn (1)–(10)), where the defect species are described using Kroger–Vink notation.66 The electronic defect, 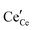 , expressed in these equations describes a cerium ion that has trapped an electron in its vicinity.67,68 The trapping gives rise to a small polaron, i.e., a quasiparticle which appears when an electron interacts with the polarization of its surrounding ions.69 Electronic structure calculations suggest that the polarons fill states that are created as a result of the reduction and lie just below the unoccupied 4f states at a distance of 2 to 2.4 eV from the valence band, as sketched in Fig. 2.64,70,71 Their position is also ∼1 eV below the Fermi level, as experimentally observed in ambient pressure XPS (X-ray photoelectron spectroscopy) measurements on reduced ceria.10,72
, expressed in these equations describes a cerium ion that has trapped an electron in its vicinity.67,68 The trapping gives rise to a small polaron, i.e., a quasiparticle which appears when an electron interacts with the polarization of its surrounding ions.69 Electronic structure calculations suggest that the polarons fill states that are created as a result of the reduction and lie just below the unoccupied 4f states at a distance of 2 to 2.4 eV from the valence band, as sketched in Fig. 2.64,70,71 Their position is also ∼1 eV below the Fermi level, as experimentally observed in ambient pressure XPS (X-ray photoelectron spectroscopy) measurements on reduced ceria.10,72
| Name | Expressiona | Eqn |
|---|---|---|
a Square brackets indicate the fractional (unitless) site occupancies; there are two oxygen and one cation sites per formula unit, electroneutrality equations differ by a factor of 2 when expressed in volumetric concentrations. 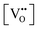 , including intrinsic (int) and extrinsic (ext) contributions, and , including intrinsic (int) and extrinsic (ext) contributions, and 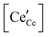 refer to the concentration of vacancies and electronic defects not in associates. refer to the concentration of vacancies and electronic defects not in associates. ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) O2 is the oxygen pressure relative to the standard oxygen pressure of 1 atm. O2 is the oxygen pressure relative to the standard oxygen pressure of 1 atm.
|
||
| Reduction, isolated vacancies |
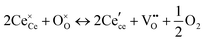
|
(1) |
| Mass action |
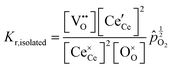
|
(2) |
| Reduction, trimer associates |
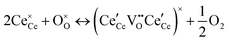
|
(3) |
| Mass action |
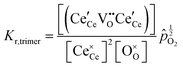
|
(4) |
| Electroneutrality, undoped |
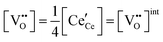
|
(5) |
| Electroneutrality, doped |
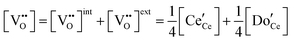
|
(6) |
| Anion site restriction |
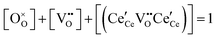
|
(7) |
| Cation site restriction, undoped |
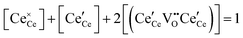
|
(8) |
| Cation site restriction, doped |
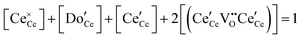
|
(9) |
| Non-stoichiometry |
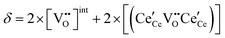
|
(10) |
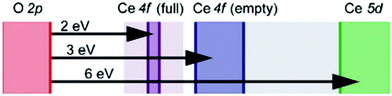 | ||
| Fig. 2 Schematic band diagram of ceria containing electronic defects. The O2p states form the valence band and the Ce5d states the conduction band. The Ce4f states labelled ‘full’ are absent when the material has no electronic defects. Shading is used to indicate uncertainty in the band positions. Reproduced from ref. 64 with permission from AIP Publishing, copyright 2007. | ||
Under conditions in which the non-stoichiometry δ is sufficiently small that defects are non-interacting, the reduction of ceria is described by eqn (1) with the corresponding mass action law, eqn (2).51,68 When the site occupancies of  and
and  are close to 1, the equilibrium constant can be approximated as
are close to 1, the equilibrium constant can be approximated as
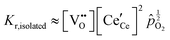 | (11) |
Together with the electroneutrality condition expressed in eqn (5), the above implies vacancy and electronic defect concentrations that vary with oxygen partial pressure according to a power law exponent of −⅙. Experimentally, power law exponents close to this value have been observed in oxygen partial pressure dependent conductivity measurements.68 Such measurements express the thermodynamics because they reflect the variation in the polaron defect (i.e. carrier) concentration. In contrast to transport measurements, thermogravimetric measurements tend to show slightly larger exponents.50,51 This is undoubtedly due to the difficulty in measuring mass changes in the regimes where δ is small, whereas accurate conductivity measurements are readily performed under such conditions.
At high oxygen non-stoichiometry, encountered at low oxygen partial pressure and high temperature, defect interactions become important. The mass action law, eqn (2), in principle, assumes dilute solution behavior and taken alone, is incompatible with such interactions. The problem can be treated by replacing the concentration terms in the mass action equation with activities, or by introducing additional reactions to describe specific types of defect interactions such as associates, as given, for example, in eqn (3). The latter approach has the benefit of revealing the underlying defect-chemistry.
The early literature suggested that the relevant defect interactions in highly reduced ceria were between free electrons and oxygen vacancies, generating singly ionized 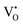 or neutral species
or neutral species 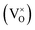 ,68 with the singly ionized defect dominating the behavior. More recent analysis indicates that, instead, associates are formed between
,68 with the singly ionized defect dominating the behavior. More recent analysis indicates that, instead, associates are formed between 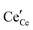 ions and oxygen vacancies.51,70,71,74 Both dimer,
ions and oxygen vacancies.51,70,71,74 Both dimer, 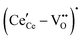 , and trimer,
, and trimer, 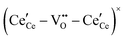 species have been considered, and the preponderance of the data, both experimental and computational (see Fig. 3), indicate the predominance of trimers, reflecting another departure from early interpretations. In many computational studies, the presence of
species have been considered, and the preponderance of the data, both experimental and computational (see Fig. 3), indicate the predominance of trimers, reflecting another departure from early interpretations. In many computational studies, the presence of 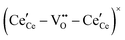 is in fact unremarkable and treated as entirely expected.65,73,75,76 From a global defect chemical perspective,
is in fact unremarkable and treated as entirely expected.65,73,75,76 From a global defect chemical perspective, 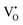 and
and 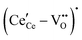 are qualitatively the same, just as
are qualitatively the same, just as 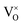 and
and 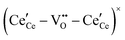 are. However, the local configurations are quite distinct.71
are. However, the local configurations are quite distinct.71
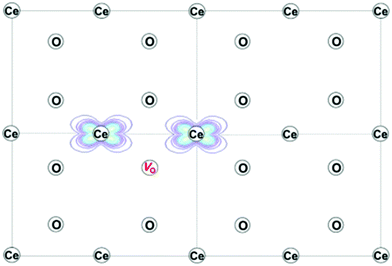 | ||
| Fig. 3 Projection of the computed charge density of reduced ceria on the (110) plane, showing the electronic ground state with localization of two Ce3+ ions next to an oxygen-vacancy, to create the trimer associate. Reproduced from ref. 73 with permission from American Chemical Society, copyright 2016. | ||
Beyond the types of associates described above, some evidence has been put forward for the occurrence of more extended defect clusters, including double-trimers (hexamers) that emerge from a treatment of the experimental thermogravimetric data,56 and oxygen-vacancy pairs that emerge from ab initio calculations.73,75,76 Not surprisingly, the local configurational and macroscopic computational complexity increases dramatically when such extended defects are fully treated, without providing (due to their low concentrations) a qualitatively different picture of the macroscopic transport and non-stoichiometry behavior. Detection of such defects, which are increasingly recognized to impact other types of properties, is best achieved by the local probes discussed in the next chapters.
Returning to the specific defect chemical reactions of Table 1, when the concentrations of species are sufficiently low, chemical activity is adequately represented by concentration, and mass action laws (eqn (2) and (4)) are appropriately expressed in terms of concentration (as written). At small δ, at which 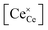 and
and 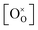 are ∼1, eqn (4) implies that the power law exponent describing the variation in trimer concentration with oxygen partial pressure is −½. The total vacancy concentration will be the sum of the isolated vacancy concentration and the trimer concentration, eqn (10), giving rise to a slope in the double-logarithmic plot of δ vs. pO2 at moderate δ that falls between −⅙ and −½. Such a result is experimentally observed, Fig. 4.50,51,74
are ∼1, eqn (4) implies that the power law exponent describing the variation in trimer concentration with oxygen partial pressure is −½. The total vacancy concentration will be the sum of the isolated vacancy concentration and the trimer concentration, eqn (10), giving rise to a slope in the double-logarithmic plot of δ vs. pO2 at moderate δ that falls between −⅙ and −½. Such a result is experimentally observed, Fig. 4.50,51,74
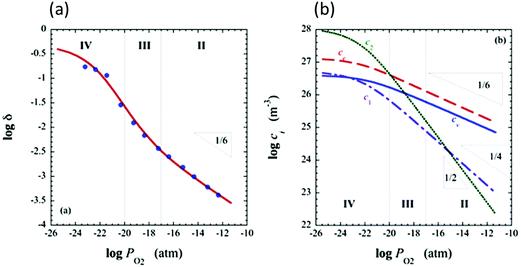 | ||
Fig. 4 Defect chemical modeling of the oxygen partial pressure dependence of non-stoichiometry in (undoped) ceria: (a) comparison of the data from Panlener50 to the model results; and (b) individual defect concentrations, where Cv refers to unassociated oxygen vacancies, Ce to unassociated polarons, C1 to dimers 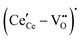 , and C2 to trimers , and C2 to trimers 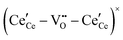 . Slopes shown in (b) are guides to the eye. Modeling reveals three regions of defect behavior: in II isolated vacancies (and isolated polarons) dominate, and the power law exponent is close to −⅙; in III trimers are comparable in importance to isolated defects and the dependence of non-stoichiometry on oxygen partial pressure rises; in IV site saturation effects emerge. Reproduced from ref. 74 with permission from AIP publishing, copyright 2007. . Slopes shown in (b) are guides to the eye. Modeling reveals three regions of defect behavior: in II isolated vacancies (and isolated polarons) dominate, and the power law exponent is close to −⅙; in III trimers are comparable in importance to isolated defects and the dependence of non-stoichiometry on oxygen partial pressure rises; in IV site saturation effects emerge. Reproduced from ref. 74 with permission from AIP publishing, copyright 2007. | ||
A more complete treatment of the defect equilibrium behavior considers the reduction reactions in tandem, as well as site occupancy restrictions. The latter constrain the total concentration of the anionic and cationic species to the number of sites available (for a total fractional concentration of 1 on each type of site), eqn (7) and (8). Bishop et al. employed this framework to evaluate the oxygen partial pressure dependent non-stoichiometry data at 800 °C. The numerically implemented fit reproduces the experimental results well, Fig. 4(a). Due to the inclusion of site restriction effects, the model reproduces the plateau in δ that occurs in the vicinity of 0.5, where the stoichiometry approaches Ce2O3. The analysis furthermore reveals the concentration of each type of species, Fig. 4(b), and yields values of the equilibrium constants, Kr,isolated and Kr,trimer.51
An alternative methodology for treating the redox thermodynamics considers the macroscopic behavior without (immediate) reference to the nature of the defects formed.49,50 The reduction of the undoped material by this formalism is written for an infinitesimal ε, change in state as
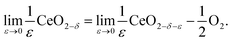 | (12) |
Noting that the chemical potentials of the two solids are identical in the limit ε → 0, the equilibrium constant, Kred for this reaction, becomes
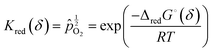 | (13) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) O2 is the oxygen pressure relative to the standard oxygen pressure of 1 atm (see Table 1), and ΔredG° is the standard Gibbs energy of reduction (per mole of O). This equality expresses the value of the oxygen partial pressure that generates an equilibrium non-stoichiometry of δ at a given temperature, and reflects the fact that, under equilibrium, the partial molar Gibbs energy of oxygen in the solid must be equal to that in the gas.
O2 is the oxygen pressure relative to the standard oxygen pressure of 1 atm (see Table 1), and ΔredG° is the standard Gibbs energy of reduction (per mole of O). This equality expresses the value of the oxygen partial pressure that generates an equilibrium non-stoichiometry of δ at a given temperature, and reflects the fact that, under equilibrium, the partial molar Gibbs energy of oxygen in the solid must be equal to that in the gas.
The equilibrium reduction constant of eqn (13), must of course, be related to the mass action constants of Table 1 (eqn (2) and (4)). If isolated defects dominate the reduction at low δ and associates dominate the behavior as δ increases, then it is reasonable to expect that Kred will be a function of non-stoichiometry, gradually changing in value from that defined by Kr,isolated to that defined by Kr,trimer. Considering first the limit of very small δ, the globally and microscopically defined equilibrium constants differ by the term
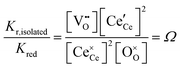 | (14) |
This quantity specifies the number of distinguishable ways to distribute the defects. Recognizing R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω as Sconfig, the configurational entropy associated with the presence of the defects, it becomes apparent that
Ω as Sconfig, the configurational entropy associated with the presence of the defects, it becomes apparent that 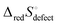 , the entropy for the defect reaction eqn (1), and by analogy that for eqn (3) also, is related to that for the macroscopic reduction of eqn (13), ΔredS°, according to
, the entropy for the defect reaction eqn (1), and by analogy that for eqn (3) also, is related to that for the macroscopic reduction of eqn (13), ΔredS°, according to
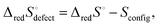 | (15) |
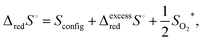 | (16) |
Taking into account the observation that associates become increasingly important as δ increases, it is reasonable to expect that the macroscopic Kred will be a function of non-stoichiometry, gradually changing in value from that defined by Kr,isolated to that defined by Kr,trimer. Thus, one can anticipate that the enthalpy and entropy terms associated with Kred will also gradually vary from those describing the isolated defects to those describing associates. In particular, because the energetics associated with the two very distinct defect reactions eqn (1) (isolated defects) and (3) (trimers) differ significantly, as shown for example, by DFT calculations,71 a dependence of ΔredH° on δ is fully expected. In contrast, the excess entropy may be relatively invariant with non-stoichiometry.
Experimental determination of the enthalpy and entropy of reduction requires reliable thermogravimetric data spanning a wide range in T–![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) O2 space. Following the microscopic approach, one then makes use of the expressions in Table 1 to derive from these data the equilibrium constants for the specific defect reactions of interest at multiple temperatures. In the macroscopic, model-free approach, one extracts effective equilibrium constants at multiple, specified values of δ, {δi}, and for each δi, at multiple temperatures. In both cases, extraction of the enthalpy and entropy terms relies on the linearity of the data when presented as Arrhenius plots of the equilibrium constants. Such linearity implies the temperature independence of the reduction enthalpies and entropies, behavior that is sometimes assumed without verification.
O2 space. Following the microscopic approach, one then makes use of the expressions in Table 1 to derive from these data the equilibrium constants for the specific defect reactions of interest at multiple temperatures. In the macroscopic, model-free approach, one extracts effective equilibrium constants at multiple, specified values of δ, {δi}, and for each δi, at multiple temperatures. In both cases, extraction of the enthalpy and entropy terms relies on the linearity of the data when presented as Arrhenius plots of the equilibrium constants. Such linearity implies the temperature independence of the reduction enthalpies and entropies, behavior that is sometimes assumed without verification.
Despite these challenges, quantification of the redox characteristics of bulk ceria has been rather successful. From an analysis of the thermogravimetric data of Panlener50 within the context of the microscopic model, Tuller and Nowick68 concluded that the enthalpy of reduction in the isolated-defect regime is 451 ± 7 kJ mol−1. The associated-defect regime was analyzed assuming predominance of singly ionized oxygen vacancies. The authors extracted an enthalpy of 397 kJ mol−1, and hence even an imperfect defect model (it is now known that the association is dominated by neutral trimers) reveals the fact that defect association decreases the enthalpy of reduction. Using the macroscopic approach, several studies have shown that the enthalpy of reduction of ceria decreases monotonically from a value of ∼475 kJ mol−1 at small δ, to ∼400 kJ mol−1 at δ ∼ 0.1.48–50,79–82 Thus, the microscopic and macroscopic approaches both reveal that the enthalpy decreases with increasing δ, and the former provides a chemical rational for this trend.
A notable exception to the overall agreement in the literature lies in the work of Takacs et al.,47 who recently re-evaluated the defect-chemistry in the context of thermochemical fuel production in the temperature range of 1300–1500 °C. While these authors reported a monotonically decreasing enthalpy of reduction with δ (consistent with the prior studies), the absolute value of the enthalpy at small δ was substantially higher than obtained in previous reports, see Fig. 5. For the purposes of evaluating the potential of ceria for fuel production via high temperature redox cycles, Takacs et al.47 measured even small non-stoichiometry at 1300–1500 °C. Thus, as suggested by the authors, the discrepancy in absolute enthalpy with respect to the prior literature is likely due to a temperature dependence of this quantity. Notwithstanding this outlying result, there is generally a good understanding of the origin of the enthalpy variation with δ at small to moderate values of δ in CeO2−δ.
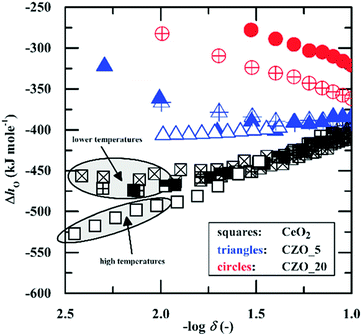 | ||
| Fig. 5 Enthalpy of oxidation of ceria (kJ per mol-O) as a function of non-stoichiometry. Blue and red data markers refer to values for 5 and 10 mol% Zr substituted ceria (denoted as CZO and according number for dopant molar concentration), respectively, and are not considered here. The magnitude of the enthalpy decreases with increasing d. High temperature measurements yield higher enthalpy values (in magnitude) than low temperature measurements. Reproduced from ref. 47, creative commons license 2015. | ||
At large δ a substantial disagreement between the microscopic and macroscopic approaches appears. Whereas the microscopic approach, when limited to defect reactions 1 and 3, inherently predicts a monotonic decrease in the enthalpy of reduction with increasing δ, analysis of the thermogravimetric data within the macroscopic framework shows that the enthalpy rises beyond δ ∼ 0.15 (reaching ∼410 kJ mol−1 at δ = 0.28). Reflecting this disagreement, the model fit for a temperature of 800 °C presented by Bishop et al. using the microscopic defect chemical approach noticeably deviates from the experimental data, under-predicting the vacancy concentration when δ ≳ 0.1.51,56 The probable explanation for a peak in the enthalpy of reduction at stoichiometry CeO1.81 is the onset of a degree of ordering within the single-phase fluorite lattice structure, not accounted for in typical microscopic models. Pair distribution function analysis in conjunction with reverse Monte Carlo modeling of high-resolution neutron powder diffraction data collected at 1000 °C has indeed revealed the presence of oxygen-vacancy pairs with preferential 〈111〉 alignment for ceria of similar oxygen content within the nominally fluorite structure.83 The vacancy arrangement is reminiscent of that encountered in the vacancy ordered phases Ce11O20 and Ce7O12.84
Until recent years, the entropy of reduction of ceria has received somewhat lesser attention than the enthalpy. The experimental data agree that the excess entropy of eqn (15) is small,50 but nevertheless the solid state reduction entropy, 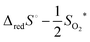 is large enough to render ceria a benchmark material for thermochemical fuel production via redox cycling.15,16 The early literature on ceria assumed the excess entropy was dominated by vibrational effects, as is typical in solid state systems. Recent computational studies suggest that in fact electronic effects, related to the high density of electronic states in the narrow 4f band, may be responsible for the large solid state reduction entropy of ceria.85 The results furthermore caution against parsing the electronic defect contributions to the entropy into configurational and non-configurational terms. The relevance of this behavior to the local defect structure remains to be explored but is potentially significant.
is large enough to render ceria a benchmark material for thermochemical fuel production via redox cycling.15,16 The early literature on ceria assumed the excess entropy was dominated by vibrational effects, as is typical in solid state systems. Recent computational studies suggest that in fact electronic effects, related to the high density of electronic states in the narrow 4f band, may be responsible for the large solid state reduction entropy of ceria.85 The results furthermore caution against parsing the electronic defect contributions to the entropy into configurational and non-configurational terms. The relevance of this behavior to the local defect structure remains to be explored but is potentially significant.
The defect chemical framework, which has been largely successful in describing the redox behavior of bulk, undoped ceria, can be readily applied to doped compositions, where we focus here again on trivalent dopants indicated with overall stoichiometry Ce1−xDoxO2−x/2−δ. As noted above, oxygen vacancies resulting directly from acceptor-doping are designated ‘extrinsic’ and those resulting from reduction are designated ‘intrinsic’. When δ is small 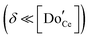 the concentration of extrinsic vacancies is by definition small, and the electroneutrality condition, eqn (6), can be approximated as
the concentration of extrinsic vacancies is by definition small, and the electroneutrality condition, eqn (6), can be approximated as
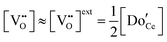 | (17) |
This result, along with eqn (11), implies that the polaron concentration and hence also the intrinsic vacancy concentration in doped ceria will vary with oxygen partial pressure according to a power law exponent of −¼, in contrast to the −⅙ expected for undoped ceria in the low δ limit.
In a broad sense, the experimental thermogravimetric data agree with the predictions of ideal solution behavior in trivalent doped ceria.49,51,77,86 However, because of the difficulty of accurately measuring δ by gravimetry when the δ ≲ 10−3, it is unreasonable to accept thermogravimetric results alone as definitive proof of the defect chemical model. In contrast, conductivity is easily measured in any regime including that producing a low δ, and a power law exponent of −¼ relating conductivity and oxygen partial pressure is routinely reported for doped ceria,87–89 as shown for example in Fig. 6. It is to be emphasized that the power law exponent of −¼ is observed not because the total vacancy concentration is changing, but because the concentration of electrons, which have higher mobility than vacancies, is changing. In light of such experimental results, the high-temperature defect chemical behavior in the dopant dominated-region is largely considered settled. However, it must be noted that charge-neutral associates formed of an oxygen vacancy, a dopant ion, and an electronic defect, so-called mixed trimers, would also lead to an exponent of −¼,51 and the occurrence of such species, possibly even in large concentrations, cannot be ruled out on the basis of the power law exponent alone.
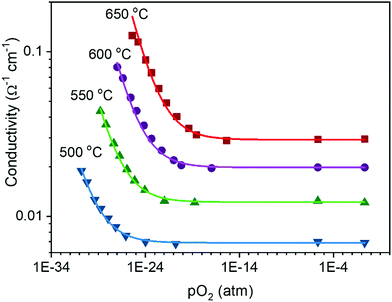 | ||
Fig. 6 Electrical conductivity of 15 mol% Sm doped ceria as a function of oxygen partial pressure at the temperatures indicated. The solid lines are fits to the expression 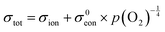 . Under reducing conditions, a power law exponent describing the dependence of conductivity on oxygen partial pressure of −¼ is obtained, consistent with ideal solution behavior. Adapted from ref. 88 with permission from Wiley, copyright 2005. . Under reducing conditions, a power law exponent describing the dependence of conductivity on oxygen partial pressure of −¼ is obtained, consistent with ideal solution behavior. Adapted from ref. 88 with permission from Wiley, copyright 2005. | ||
Beyond power law exponents, much as with undoped ceria, the measured δ(pO2) for doped ceria have been used to determine defect equilibrium constants, evaluate the thermodynamic parameters, and further test the validity of defect chemical models describing the redox behavior. In particular, Bishop has presented a comprehensive study of the behavior of Ce0.9Gd0.1O1.95−δ,51 whereas Hashimoto and coworkers have evaluated both Gd and Sm-doped ceria, at both 10 and 20 mol% doping levels.49,77,86 These dopants generally lower the enthalpy of reduction, relative to that in undoped ceria and decrease the dependence of the enthalpy on non-stoichiometry. Doping with calcium produces a similar transition from non-ideal to ideal solution thermodynamics, i.e., from δ-dependent to δ-independent enthalpy.90 Given the presence of a large concentration of extrinsic vacancies in doped systems, the tendency towards ideal solution behavior (which implies weaker defect-defect interactions) is surprising on first sight. However, ideal solution behavior here means, in fact, a transition from reduction of ideal, isolated defects according to eqn (1), to reduction of ‘ideal’ associates according to eqn (3). Viewed in that context, the onset of ideal behavior with an enthalpy of reduction that is independent of δ is reasonable. At large δ, the onset of a regime in which the non-stoichiometry is relatively insensitive to oxygen partial pressure has been attributed to site restriction effects (eqn (7)–(9)) and the emergence of defect ordering, much as has been suggested for undoped ceria.51,56 The local structure methods described in this review have the potential to resolve these apparent discrepancies.
A key distinction between undoped and doped ceria arises at moderate temperatures and ambient pressures. Under such conditions, the defect concentration in ideally pure ceria approaches zero, whereas in doped ceria eqn (17) continues to apply. However, the extrinsic vacancies generated by doping can become associated with the dopant species. A convenient, first-order formalism for treating such effects in dilute systems is to express trapping according to the reaction91
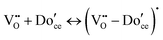 | (18) |
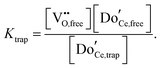 | (19) |
Due to the low cation mobility at the temperatures at which associate formation is thermodynamically driven, appreciable concentrations of the neutral defect 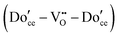 do not occur. In the state of maximum association, typically corresponding to temperatures of ∼300 °C and lower, charge and mass balance requirements imply that half the dopant ions will form associates, trapping all of the available oxygen vacancies, with the remainder of the dopant species remaining isolated. Furthermore, as has been pointed out, at a dopant concentration of just 2 at%, already 30% of the dopant species in a randomly doped ceria host will have a dopant in its nearest neighbor or next nearest neighbor cation shell.92 Thus, the system can only be treated as dilute for very low dopant concentrations.
do not occur. In the state of maximum association, typically corresponding to temperatures of ∼300 °C and lower, charge and mass balance requirements imply that half the dopant ions will form associates, trapping all of the available oxygen vacancies, with the remainder of the dopant species remaining isolated. Furthermore, as has been pointed out, at a dopant concentration of just 2 at%, already 30% of the dopant species in a randomly doped ceria host will have a dopant in its nearest neighbor or next nearest neighbor cation shell.92 Thus, the system can only be treated as dilute for very low dopant concentrations.
Experimentally, dopant-vacancy association has been inferred from ionic conductivity measurements, specifically, from a difference in high and low temperature activities for charge transport and from the existence of a conductivity maximum, as well as a minimum in low temperature activation energy, as a function of dopant concentration.92–95 The temperature dependence of the activation energy results because the vacancies must be thermally activated out of the trap sites. Hence, the activation energy measured at low temperature is a sum of migration and trapping terms, whereas at high temperature, at which all vacancies are liberated from trapping sites, the activation energy is due only to migration effects. Thus, values for the trapping and migration energies can in principle be determined from the difference in the activation energies between the two regions, or more rigorously from the temperature dependence of the apparent activation energy across the regions.
Not immediately predicted by the first order model, but widely observed, is a strong dependence of the empirical activation energy for ion transport on dopant concentration. Specifically, the first order model predicts that in the deeply associated region, in which  , the free (mobile) vacancy concentration is given from eqn (19) by
, the free (mobile) vacancy concentration is given from eqn (19) by 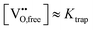 , and is independent of dopant concentration.92 Thus, in order for a dependence on dopant concentration in the activation energy to emerge, either the vacancy trapping energy, or the vacancy migration energy, or both, must depend on the dopant concentration. In light of the relative proximity of dopant species to one another even at very low doping levels, a dependence of the trapping and migration energetics on dopant concentration is not surprising. On the other hand, the complexity of the problem, with a myriad of possible vacancy-dopant configurations, implies that macroscopic conductivity measurements alone do not permit reliable decomposition of the energy contributions to the observed values.
, and is independent of dopant concentration.92 Thus, in order for a dependence on dopant concentration in the activation energy to emerge, either the vacancy trapping energy, or the vacancy migration energy, or both, must depend on the dopant concentration. In light of the relative proximity of dopant species to one another even at very low doping levels, a dependence of the trapping and migration energetics on dopant concentration is not surprising. On the other hand, the complexity of the problem, with a myriad of possible vacancy-dopant configurations, implies that macroscopic conductivity measurements alone do not permit reliable decomposition of the energy contributions to the observed values.
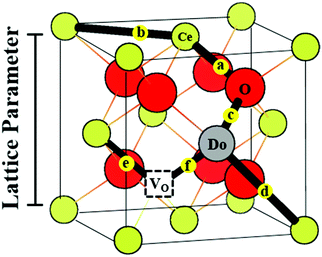
A treatment of the problem of the ionic conductivity maximum in doped ceria has been approached more recently computationally, with an excellent overview reported by Martin and coworkers in 2018.32 By such methods it is possible to differentiate between effects due to trapping of vacancies in defect states and those due to impacts on the overall migration barriers. The former, which establish the equilibrium concentration of defects at a given temperature and doping level, are of particular interest here. Shown in Fig. 7 are DFT (density functional theory) computed association energies for vacancy trapping in doped ceria as a function of dopant species, specifically, as a function of the ionic radius of the rare earth (RE) element.96 For placement of the vacancy in a nearest neighbor site (see Fig. 10 below for the structural arrangement), there is a clear trend in association energy with radius, with elements smaller than Gd preferentially trapping the vacancy at this position, and those larger than Sm repelling the vacancy. The dopants Gd and Sm, known to produce high ionic conductivity in ceria, are neither attractive nor repulsive towards vacancies. A weaker and opposite trend is evident for the next nearest neighbor site, and in this case the trapping is apparently never favored. Significantly, the computation further predicts (not shown) that the magnitude of the defect association energy strongly increases with the number of nearest neighbor RE ions surrounding the vacancy, explaining, in part, the concentration dependence of the ionic conductivity. Thus, computational studies are beginning to shed important light on the local configurations of dopants and oxygen vacancies in doped ceria, although details remain unresolved, and may ultimately depend on processing and the influence of quenching on the cation distributions in the solid.
 | ||
| Fig. 7 Association energy of dopant ion with vacancies as nearest and next nearest neighbors, plotted as function of dopant (RE3+) radius. Adapted from ref. 96 with permission from Royal Society of Chemistry, copyright 2009. | ||
A final area of open questions about the defect-chemistry of ceria lies in the realm of the interfacial properties. Both the internal and external interfaces (i.e., grain boundaries and surfaces, respectively) display strong evidence of enhanced reduction relative to the bulk. For example, thermogravimetric measurements of high surface area ceria, both undoped97 and 10 mol% Gd-doped,56 reveal higher and less oxygen partial pressure dependent non-stoichiometry relative to conventional samples with large particle sizes.56,97,98 The immediate conclusion is that the oxygen-vacancy and Ce3+ concentration is enhanced at the surfaces. Studies of surface oxidation states by near-ambient pressure XPS measurements have directly proven such surface enhancement.10,11,99 Similarly, grain boundaries are often described as positively charged, implying an enhanced vacancy concentration at the grain boundary core, which is charge balanced by a negative space charge region. Within this region, positively charged defects, in particular oxygen vacancies, are depleted.100,101 Support for the space charge model of grain boundaries in ceria derives, in part, from impedance spectroscopic measurements101 in which bulk and grain boundary resistances can be deconvoluted. Because the spatial extent of the space charge region scales with cDo−1/2, where cDo is the volumetric dopant concentration,100,102 space charge effects are particularly important in lightly or undoped ceria, as has been observed experimentally.101,102 The spectroscopic methods reviewed below, which provide access to spatially resolved information about oxidation state and coordination environment, appear well suited for going beyond the inferences from defect model and transport models to enable the unraveling of outstanding questions regarding defect interactions in ceria.
3 Local structure of ceria solid solutions as probed by X-ray absorption spectroscopy
3.1 Introduction to X-ray absorption spectroscopy
X-ray absorption spectroscopy (XAS) is a synchrotron-based technique that provides element-specific information about local atomic and electronic structure of materials. In this method, X-ray photons excite core-level electrons that interact with the nearest neighboring (NN) atoms to the absorbing species. In a typical XAS experiment, the intensity (It) of the X-ray beam transmitted through the sample is measured along with the incident beam intensity I0 as a function of X-ray energy, E. The X-ray absorption coefficient μ(E) is given by the Beer–Lambert law as μ·d = ln(I0/It), where d is the path of the beam through the material (or the sample thickness). A typical XAS spectrum for ceria powder is shown in Fig. 8, taken from ref. 45. A sharp increase in μ(E) occurs when the incident X-ray photon carries sufficient energy to excite an electron from a low-energy bound state in the atom to an upper energy level. This element specific increase is termed an “absorption edge”, and is labeled K, L or M, depending on the principal quantum number n of the initial state from which the excitation occurred. Namely, K corresponds to the 1s state, L (subscripts I–III) corresponds to 2s, 2p1/2 and 2p3/2 states, while M (subscripts I–V) corresponds to 3s, 3p1/2, 3p3/2, 3d3/2 and 3d5/2 states.103 In Fig. 8, the Ce-LIII absorption edge in CeO2 powder appears as a sharp increase in absorption at ∼5724 eV and is due to the transition 2p3/2 → 5d5/2.104 Measurements of the Ce-LIII edge are usually chosen for undoped and doped ceria, due to the scarcity of beamlines that can access the high energy of the Ce-K edge (∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 eV).105–107 The negative slope of the background in Fig. 8 is captured in the Victoreen formula, μ(E) ∼ 1/E3. Measurements can be performed in either transmission or fluorescence mode. The latter is necessitated when the sample is either too thick for transmission, or the concentration of the X-ray absorbing species is too dilute. Fluorescence detection is also beneficial for thin film samples, as it minimizes the signal of the substrate. It is important to note that XAS probes ‘bulk’ properties, where penetration depth is a function of the material X-ray attenuation coefficient at the relevant incident X-ray energy. For example, probing the Ce-LIII edge at ∼6 keV in ceria or doped ceria compounds yields an attenuation length (where the intensity of radiation falls to 1/e of that at the material surface) of 5–10 μm.108,109 The penetration depth increases with the incident energy in proportion to the decrease in absorption given by the Victoreen formula above. It is possible however to probe surface properties (few nm penetration depth) using XAS by setting a grazing incident configuration, where the incident angle is below the angle for total external reflection for the specific material.
450 eV).105–107 The negative slope of the background in Fig. 8 is captured in the Victoreen formula, μ(E) ∼ 1/E3. Measurements can be performed in either transmission or fluorescence mode. The latter is necessitated when the sample is either too thick for transmission, or the concentration of the X-ray absorbing species is too dilute. Fluorescence detection is also beneficial for thin film samples, as it minimizes the signal of the substrate. It is important to note that XAS probes ‘bulk’ properties, where penetration depth is a function of the material X-ray attenuation coefficient at the relevant incident X-ray energy. For example, probing the Ce-LIII edge at ∼6 keV in ceria or doped ceria compounds yields an attenuation length (where the intensity of radiation falls to 1/e of that at the material surface) of 5–10 μm.108,109 The penetration depth increases with the incident energy in proportion to the decrease in absorption given by the Victoreen formula above. It is possible however to probe surface properties (few nm penetration depth) using XAS by setting a grazing incident configuration, where the incident angle is below the angle for total external reflection for the specific material.
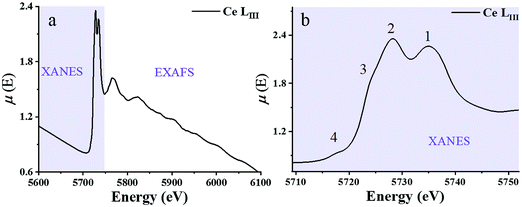 | ||
| Fig. 8 (a) X-ray absorption spectrum at the Ce-LIII edge for a CeO2 powder described in ref. 59μ(E) denotes the X-ray absorption coefficient. XANES and EXAFS regions are indicated. (b) The expanded XANES range of the absorption spectrum, with four main features labeled 1–4 described in the text. Adapted from ref. 45 with permission from Elsevier, copyright 2010. | ||
Historically, XAFS (the fine features emerging in the absorption spectrum) has been divided into two X-ray energy regions: the X-ray absorption near edge structure (XANES) and the extended XAFS (EXAFS). The XANES portion of the spectrum is sensitive to the redox state. It enables quantification of Ce3+vs. Ce4+ valence states and reveals the effect of dopant cations and grain size on the redox chemistry of ceria-based materials. A XANES spectrum includes features from ca. 40 eV below to ca. 50 eV above the absorption edge, the most prominent being the so-called “white line” which appears as a strong peak, positioned at the absorption maximum. (See ref. 110–113 for XANES theory.) The Ce-LIII white line displayed in Fig. 8 reveals four prominent features, which are understood to result from a combination of several effects. Many-body final states (due to mixing of 4f0 and 4f1L final configurations where L represents a hole in the delocalized O 2p band of the ligand oxygen species) give rise to the main peak splitting (generating peaks 1 and 2). Crystal field splitting of the 5d states (Δf ≈ 3.7 eV) gives rise to the shoulder feature denoted as 3. This shoulder also overlaps the white line due to absorption by reduced Ce3+ species.104,114 In high-resolution experiments, examples of which are described below, peaks 2 and 3 are fully resolved, and the splitting of peak 1, again due to crystal field effects, can also be observed.115 Multiple scattering, which provides access to final states at the bottom of the Ce 5d conduction band with delocalized d character, gives rise to the pre-edge feature labeled 4. XANES spectra are thus rich with chemical and structural information. From the positions and relative intensities of peaks 1 and 2 information about local geometry, the number of, and the degree of order in coordinating ligands about the central Ce absorber can be gained.37,38,116 Similarly, analysis of the relative intensity of peak/shoulder 3 can be used to track the extent of reduction of ceria-based materials.117–120
The EXAFS region of the absorption coefficient (which is the focus of the XAFS portion of this review) extends to ca. 1000–1500 eV above the absorption edge and provides information about nearest neighbor bonding environments, such as the coordination numbers, interatomic distances and their disorder. In ceria and other related materials, in which LIII edges are used to measure EXAFS, the useful energy range is limited by the presence of LII edges and can span as little as 300–400 eV (EXAFS region indicated in Fig. 8a). EXAFS features originate from the interference effect110–113 caused by the interaction of the outgoing photoelectron waves ejected from inner core levels by the incoming X-ray radiation, and those scattered back to the absorbing atom by its neighbors. This interference modulates the wavefunction of the final state and, therefore, the probability of absorbing the X-ray photon, according to Fermi's golden rule. This modulation, appearing in the high energy portion of the X-ray absorption spectrum, was recognized by Stern et al.121 as being related to the radial distribution of neighboring atoms around the central absorbing atom. Due to the nature of the photoelectron wave interference that originates from the path difference between the outgoing and backscattered waves, the interference can be constructive or destructive (and thus the fine structure of the absorption coefficient will exhibit a maximum or a minimum), depending on the number (integer or fractional) of wavelengths in the total photoelectron path. For single-scattering events, the path is equal to twice the distance between the absorber and a nearest neighbor atom.122 The information about the environment of the absorber (the number of nearest neighbors, their identities, distances to the absorber and the spread in these distances) can be extracted from the data. This information is both element-specific and local, the latter because of both the bond length disorder that increases with the distance from the absorber and dampens the contribution of higher order coordination shells, and the short photoelectron mean free path.110,111,121–131 Limited by this “nearsightedness”, EXAFS provides “fast” snapshots of the local atomic and electronic environments: the photoexcited states have a very short life-time (∼1 fs), for which the absorption process is much shorter than the typical time scale of atomic vibrations (on the order of ps). Extracting this information from the experimental data is a multi-step process. First, using de Broglie's relationship between the wavenumber and momentum of the wave-particle, the wavenumber k is expressed as:111
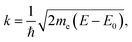 | (20) |
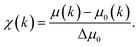 | (21) |
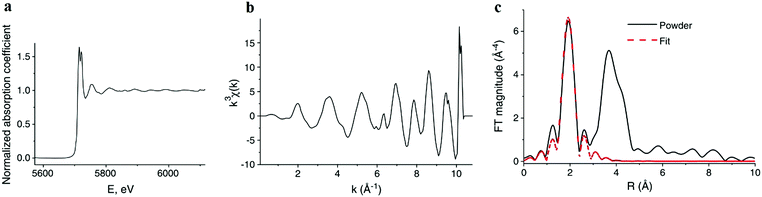 | ||
| Fig. 9 (a) The normalized absorption spectrum at the Ce LIII edge for pure ceria powder. The normalization includes subtraction of a monotonically decreasing background function, causing the difference to Fig. 8a and normalization of the edge step, defined as Δμ0. Δμ0 is the intensity difference between the average pre edge absorption (normalized to 0) to the post edge step absorption of the atom in the absence of neighbours (i.e. no white line or EXAFS features, normalized to 1). (b) The corresponding k3-weighted EXAFS spectrum. (c) The corresponding Fourier transform magnitude of the data and theoretical fit for the first coordination shell of cerium. Adapted from ref. 45 with permission from Elsevier, copyright 2010. | ||
The resulting χ(k) pattern is generally weighted by a factor of kn (n = 1–3) in order to amplify the weaker high-k portion of the signal, as shown in Fig. 9b. Finally, the EXAFS pattern χ(k) is converted to real-space (r-space) by Fourier transformation, and the magnitude of the complex Fourier transform (FT magnitude) is presented, Fig. 9c. The first peak relates to the distribution of nearest neighbor distances to the absorber, e.g. Ce–O in the case of CeO2. Peaks at distances beyond those of the nearest neighbors are usually a combination of single- and multiple-scattering contributions to EXAFS. In order to obtain structural information concerning nearest neighbors and bonding environments, the EXAFS data are fit using non-linear, multiple, least squares regression methods, that we describe below.
Eqn (22), representing the EXAFS spectrum, is a modern form of the original equation, derived by Stern, Sayers, and Lytle.121,126,127
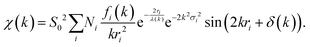 | (22) |
Each unique scattering path i is characterized by ri, defined as the distance between the absorbing atom and the ith scattering atom (for single scattering) and, in general, is equal to half path-lengths for multiple-scattering paths. fi(k) is the “backscattering amplitude”, proportional to the scattering cross section of the photoelectron. This function is element specific since heavier atoms (large Z) will scatter with greater probability than lighter atoms (small Z). For example, Ce atoms scatter more strongly than the rather light oxygen atoms. Another term that depends on the identity of the scattering atom is the photoelectron phase shift δ(k) due to both the absorber and the scattering atom. The term 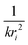 accounts for the spherical nature of the wavefunction. The wavefunctions of the final and initial states of the (Z − 1) electrons that are not excited by the X-ray photon, do not completely overlap. To correct for this effect, which is not accounted for in the single-electron approximation used to derive eqn (22), the “amplitude reduction factor” S02, is introduced. Since this factor, to a first approximation, is only sensitive to the type of the absorbing atom, but not the scattering atoms, it does not depend on k, an approximation which is universally used in data analyses. Equivalent single scattering paths are represented by a multiplication factor Ni representing the coordination number describing the absorber–scatterer geometry. For example, in undoped ceria, all first shell oxygen neighbors of a Ce4+ cation in octahedral coordination (Ni = 8), will contribute approximately the same EXAFS signal. In this respect, one of the challenges in EXAFS analysis is accounting for “multiple scattering” effects that may make significant contributions in materials with high symmetry, such as those with fluorite structure. The difficulty arises because of the high degeneracy of such paths that interfere constructively in high symmetry structures. The mean free path term,
accounts for the spherical nature of the wavefunction. The wavefunctions of the final and initial states of the (Z − 1) electrons that are not excited by the X-ray photon, do not completely overlap. To correct for this effect, which is not accounted for in the single-electron approximation used to derive eqn (22), the “amplitude reduction factor” S02, is introduced. Since this factor, to a first approximation, is only sensitive to the type of the absorbing atom, but not the scattering atoms, it does not depend on k, an approximation which is universally used in data analyses. Equivalent single scattering paths are represented by a multiplication factor Ni representing the coordination number describing the absorber–scatterer geometry. For example, in undoped ceria, all first shell oxygen neighbors of a Ce4+ cation in octahedral coordination (Ni = 8), will contribute approximately the same EXAFS signal. In this respect, one of the challenges in EXAFS analysis is accounting for “multiple scattering” effects that may make significant contributions in materials with high symmetry, such as those with fluorite structure. The difficulty arises because of the high degeneracy of such paths that interfere constructively in high symmetry structures. The mean free path term, 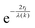 appears due to inelastic scattering processes and the finite core-hole lifetime. This is one of the reasons why EXAFS is a local probe, only characterizing the environment ≤6–8 Å from the absorber. A Debye–Waller type term, e−2k2σi2, describes the suppression of χ(k) due to disorder, including both thermal (dynamic, i.e., vibrational) and static (configurational) disorder. The parameter σi2 is defined as the variance in the interatomic half path length ri, and is often abbreviated as “mean square radial displacement (MSRD)”, or, alternatively, as the EXAFS Debye–Waller factor (DWF). It is important to note that the Gaussian approximation that gives rise to the Debye–Waller term in EXAFS eqn (22) is often not adequate when significant asymmetry of the pair distribution function is present, for example at elevated temperatures132 or in strongly anharmonic materials.133 In those cases, the contribution of the pair distribution function to eqn (22) can be analyzed via cumulant expansion as described by ref. 111 and in ref. 122.
appears due to inelastic scattering processes and the finite core-hole lifetime. This is one of the reasons why EXAFS is a local probe, only characterizing the environment ≤6–8 Å from the absorber. A Debye–Waller type term, e−2k2σi2, describes the suppression of χ(k) due to disorder, including both thermal (dynamic, i.e., vibrational) and static (configurational) disorder. The parameter σi2 is defined as the variance in the interatomic half path length ri, and is often abbreviated as “mean square radial displacement (MSRD)”, or, alternatively, as the EXAFS Debye–Waller factor (DWF). It is important to note that the Gaussian approximation that gives rise to the Debye–Waller term in EXAFS eqn (22) is often not adequate when significant asymmetry of the pair distribution function is present, for example at elevated temperatures132 or in strongly anharmonic materials.133 In those cases, the contribution of the pair distribution function to eqn (22) can be analyzed via cumulant expansion as described by ref. 111 and in ref. 122.
3.2 Local structure of ceria solid solutions as characterized by EXAFS
Being element specific, EXAFS is particularly useful for the study of doped ceria compounds Ce1−xDoxO2−x/2 where x is the nominal molar fraction of the extrinsic dopant on the cationic site, and Do3+ refers to the trivalent dopant atom. In these solid solutions, separately addressing the local environment around cerium and around the aliovalent dopant atoms is essential for understanding the macroscopic defect-related properties such as ionic conductivity,3,134 electrostriction and anelasticity.135 However, the absorption edges of different elements may be too close to each other so that their EXAFS spectra overlap, complicating analyses of both edges. Therefore, to take full advantage of the information contained in an EXAFS spectrum, the absorption edge (LI, LII or LIII) of Ce and Do must be chosen with care in order to separate them as much as possible. The Ce LI, LII and LIII edges occur at ∼6549, ∼6164, and ∼5724 eV, respectively. For example, in Sm3+-doped ceria, the Sm LIII edge located at ∼6719 eV111 is close to the Ce LI, leading to overlap of EXAFS spectra originating from the low energy and high energy edges; therefore, when acquiring data for Sm-doped ceria, it is advantageous to probe the more isolated Sm LII edge at ∼7315 eV instead of the Sm LIII edge.136 In the following sections we review the short-range structural information reported in the literature for ceria solid solutions on the basis of the EXAFS investigations. It is important to note that major discrepancies are reported, even for same dopant cations and concentrations, which we discuss below. To begin explaining these differences, the following factors must be taken into account:(i) The influence of dopant concentration on the short-range structure may be convoluted with microstructural effects because of the role of dopant level on microstructure evolution. For example, a change in doping concentration affects the average grain size through solute drag effects, and consequently the degree of defect segregation and local cation–anion distribution over grain and grain boundaries even for constant processing conditions.33,136
(ii) For equal doping levels, the synthesis route and conditions (e.g., Pechini, solid state or combustion synthesis, etc., temperature, atmosphere) can affect the local density and distribution of dopants in the structure. In turn, these will affect interatomic distances.
(iii) Extracting material parameters from EXAFS data involves multiple stages of data processing, as described in the previous section. Therefore, the fitting process is model dependent.
In summary, in the case of ceria compounds, due to the variety of factors affecting the local structure, it is preferred to focus on the relative trends in the EXAFS derived results rather than absolute values for a specific sample or composition.
As mentioned in the previous section, EXAFS data was collected over the years from ceria materials of different morphologies and preparation methods, however similar trends in EXAFS derived data appear for example for both bulk materials (powders and pellets) and sputter deposited thin films. Thin films differ from bulk ceramics by grain size, shape and orientation, but most notably by the existence of possible anisotropic strain. In such a case the film experiences either compressive (or tensile) strain in parallel to the substrate surface, and the opposite strain perpendicular to it and caused by the Poisson ratio. This type of anisotropic strain can reach up to 0.5% and is retained either intrinsically from the deposition process or as a result of heterogeneous layer stacking,27 or opposed stress patterns in free standing film membranes.137 It is important to stress that this anisotropy is relatively small and does not necessarily deem the unit cell to distort to lower symmetry. This effect can be readily detected and quantified by examining the in- and out-of-plane lattice parameters using XRD, e.g. described in ref. 138. In addition it can be qualitatively detected using Raman spectroscopy, as measured by Rupp and co-workers e.g. see ref. 137. The effect of anisotropic strain on the Raman spectra of doped and undoped ceria thin films is discussed intensively in Section 4.3. The impact of anisotropic strain on the interatomic distances measured by EXAFS was investigated by Kossoy et al.59 for 20 mol% Gd doped, 200–450 nm thick films. Fig. 11 illustrates that while films with no anisotropic strain (strain free) produce first and second shell interatomic distances similar to the equivalent powder control, the presence of anisotropic strain slightly reduces the measured interatomic distances most significantly for the most abundant Ce–O interatomic distance. This effect has to be kept in mind when comparing thin films to bulk pellets and powders in the following sections. The decrease in Ce–O distances due to a lower intrinsic compaction of a film with the presence of anisotropic strain was interpreted as a form of stress relaxation in the Ce first shell environment mediated by nearby oxygen vacancies.
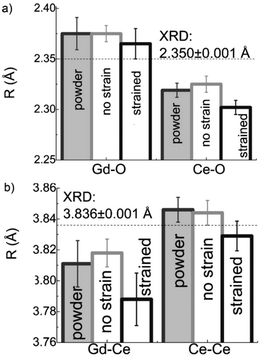 | ||
| Fig. 11 First shell (a) and second shell (b) interatomic distances, as measured by EXAFS for Ce and Gd absorption edges of 20 mol% Gd doped ceria materials. The investigated materials are in the form of powders (>1 μm grain size) and films deposited by magnetron sputtering with and without compressive in plane strain. The equivalent interatomic distance as derived from an XRD measurement of the lattice parameter is given by a dashed line in each panel. Reproduced from ref. 59, with permission from John Wiley & Sons, Inc., copyright 2010. | ||
In addition to capturing the impact of anisotropic strain on local structure, Fig. 11 also introduces the major differences observed using EXAFS around the host cation (Ce) and the dopant cation (Gd) first and second shell environments. The first shell distance Cat–O is greater around Gd as expected from the dopant's larger ionic radius compared to Ce4+, however, counter intuitively the second shell distance is greater around Ce4+. To compare this effect for several doped ceria materials, Fig. 12 summarizes representative first shell Ce–O, Do–O and second shell Ce–Ce, Do–Ce distances obtained by EXAFS studies as functions of Shannon ionic radii for octahedral coordination (N = 8).139 Yb, Er and Sm-doped ceria data are taken from Giannici et al.,136 whereas Y, Gd and La-doped ceria data are taken from Deguchi et al.107 These reports were selected since they include both first and second coordination shells for two doping fractions of 10 and 20 mol% dopant in ceria, thus allowing systematic consideration of the role of the dopant type on the interatomic distances illustrated in Fig. 10, as well as the influence of concentration.
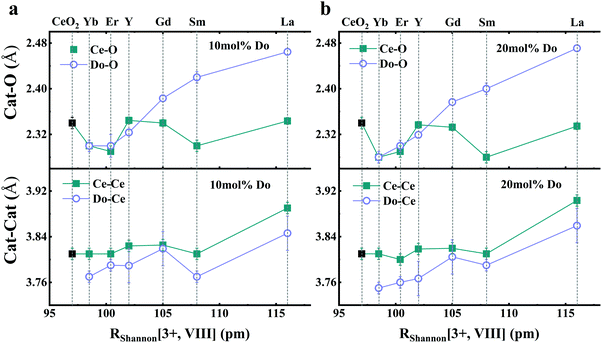 | ||
| Fig. 12 Top panels give the first coordination shell distances for Ce–O (squares) and for dopant atoms Do–O (circles) in ceria solid solutions with 10 mol% (a) and 20 mol% (b) dopant fraction, as a function of Shannon ionic radius RShannon. Bottom panels present the corresponding second coordination shell distances. The top axis indicates the type of doping and the bottom axis shows the ionic radius for octahedral coordination. Y, Er and Sm-doped ceria solutions were prepared using solution combustion synthesis, calcined, sintered and pressed into pellets as described in ref. 136. Y, Gd and La-doped ceria were prepared using a solid state reaction method, calcined sintered and pressed into pellets as described in ref. 107. Materials in both data sets have micro-crystalline grain size. The data used for this figure are summarized in Table S1 of the ESI.† | ||
Considering first the Cat–O distances for small dopants (Yb, Er and Y) the Ce–O and Do–O distances are similar. For dopants with radius above 105 pm (Gd, Sm, La), the Do–O distance is in fact larger than the Ce–O distance and this discrepancy increases with dopant ionic radius. This result is supported by other reports,106,116,140–142 and it is intuitively expected for dopants with larger ionic radius to have larger distance to neighboring oxygen ions. However, even though ionic radii of Yb3+, Er3+ and Y3+ are larger than Ce4+, their first shell radii are very similar to that of Ce, for both 10 and 20 mol% doping. The intuitive interatomic distance relationships arrived at by comparing ionic radii of Ce4+ and Do3+ also do not apply to the second coordination shell. In the bottom panels, describing the second coordination shells around Ce and dopants for 10 and 20 mol% doping, we observe that firstly, Ce–Ce distances are slightly larger than Do–Ce distances, even for the largest trivalent dopants reported for the series i.e., Sm and La. Secondly the second shell environments of Ce and Do are much more similar to each other than the first shell environments. These second shell effects, were also noted by Wang et al.105 for Y and Kossoy et al. for 20 mol% Gd-doped powders,116 as well as for sputter deposited films with and without compressive in-plane strain as described in Fig. 11.59 It can be concluded by EXAFS analysis on trivalent-cation doped ceria solid solutions that: (i) for dopants with RShannon ≥ 105 pm, Ce–O < Do–O while Ce–Ce > Do–Ce. This discrepancy suggests that the lattice is strongly distorted in the vicinity of dopant ions and fluorite symmetry is not preserved on the local level, even when the dopant cation concentration is as little as 10 mol%, where no long-range ordering of defects is observed.33,35 (ii) The smaller discrepancy between the Do and Ce second shells as compared to the first shells, reveals that local lattice distortions, if present, are much more significant in the first shell than the second. (iii) These trends with ionic radius are generally insensitive to dopant concentration in the range 10–20%. A focused evaluation of the role of concentration is presented below.
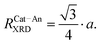 | (23) |
If symmetry is also preserved around all cation sites, a simple weighted average of the constituent individual distances, the real RCat–OEXAFS and that representative of vacancy sites, 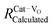 , produces an equation relating XRD and EXAFS results:
, produces an equation relating XRD and EXAFS results:
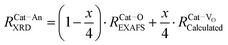 | (24) |
| RCat–OEXAFS = RCe–OEXAFS·(1 − x) + RDo–OEXAFS·x | (25) |
Combining eqn (24) and (25) yields an expression for the Cat–VO distance (which cannot be directly measured), given by
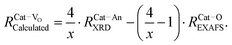 | (26) |
An analysis of literature data, which provide both EXAFS and XRD results, is summarized for Gd and Sm dopants in Fig. 13.
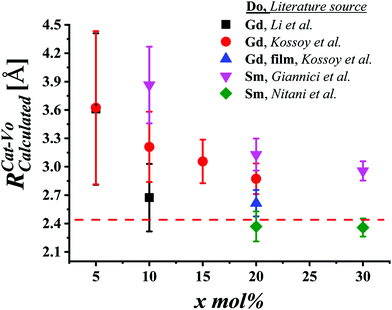 | ||
Fig. 13 Cat–VO distances 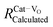 , derived using eqn (26) from combined XRD and EXAFS data, assuming preservation of fluorite Fm , derived using eqn (26) from combined XRD and EXAFS data, assuming preservation of fluorite Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, as a function of dopant mol% (x). The Gd-doped ceria data are taken from Li et al.152 and Kossoy et al.116 for powders, from Kossoy et al.59 for Gd-doped ceria films, and for Sm-doped powders from Giannici et al. and Nitani et al.106,136 The data for the figure are summarized in Table S2 of the ESI.† The dashed line is the numerically computed Cat–VO distance ∼2.45 Å based on the molecular dynamics (MD) estimate from Marroccelli et al.153 m symmetry, as a function of dopant mol% (x). The Gd-doped ceria data are taken from Li et al.152 and Kossoy et al.116 for powders, from Kossoy et al.59 for Gd-doped ceria films, and for Sm-doped powders from Giannici et al. and Nitani et al.106,136 The data for the figure are summarized in Table S2 of the ESI.† The dashed line is the numerically computed Cat–VO distance ∼2.45 Å based on the molecular dynamics (MD) estimate from Marroccelli et al.153 | ||
Inaba et al.154 suggested that the cations in the first coordination shell of the vacancy site move away from it due to electrostatic repulsion. Marrocchelli et al.153 estimated the repulsion of Ce4+ away from the vacancy site in reduced ceria, based on molecular dynamics (MD) calculations, assuming the preservation of fluorite symmetry and using known ionic radii. The result was a shift of the Ce4+ ions away from the vacancy site by ∼0.1 Å. With respect to Ce–O distance of 2.34 Å as calculated from EXAFS for CeO2 (see Fig. 12), the MD based calculation brings the predicts therefore a Cat–VO distance of ∼2.45 Å marked by a dashed line in Fig. 13. Calculation of the Cat–VO distance by eqn (26) produces large error bars at low dopant concentrations due to the appearance of the doping fraction in the denominator. It is none the less clear that available XRD and EXAFS values are for the most part (excluding Nitani et al. data106) unable to produce reasonable Cat–VO distances using the above assumptions, with some values being as large as the second coordination shell radii, at ∼3.8 Å. Importantly, these unphysical values are calculated under the incorrect assumption that the lattice structure of ceria is perfectly preserved in the first coordination shell of defects.
The second cation coordination shell (Cat–Cat) radii can be compared for EXAFS and XRD derived data in a similar fashion and are shown to produce no detectable discrepancy.45 This indicates again that a distortion in the fluorite symmetry is more significant in the cations’ first coordination shells for undoped and doped ceria structures. Recently, Shirbhate et al.155,156 studied more complex ceria systems with mixed dopants, Ce0.85(Sm)0.075(M)0.075O2−δ (where M = Sm, Sr, Gd, Nd, Ca, and Dy), using Rietveld analysis and EXAFS. Here too, local and average first shell distances, were found to be difficult to reconcile. Very low values for the EXAFS Ce–O distances were obtained, compared to values derived from XRD and Rietveld analysis using a fixed fluorite unit cell, again, suggestive of lattice distortions not captured in the XRD results.
It has long been known that for dopants larger than ∼102 pm, such as Gd3+ and Sm3+, the average lattice parameter in the fluorite phase, as obtained using X-ray diffraction methods, increases with doping concentration.157,158 However, several studies conducted on doped ceria using local probes, such as EXAFS,58,107,116,136,140–142 have found that cation–oxygen distances Cat–O, labeled a and c in Fig. 10, do not follow the average lattice parameter and contract as a function of increasing dopant concentration. These results were also supported by X-ray and neutron scattering based PDF measurements.144–146 Ohashi et al. were the first to note this discrepancy for Gd-doped ceria. Shortly thereafter, Yamazaki et al. acquired XAFS data for doped ceria for multiple dopants at several concentrations and reported the Ce–O distance trend presented in Fig. 14.140 According to more recent works,116,136,142 this average reduction in interatomic distances with increasing dopant fraction is accompanied by increasing disorder as indicated by an increase in the σ2 factor (mean square radial displacement), as given in eqn (22).
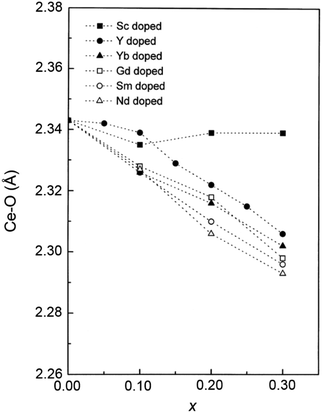 | ||
| Fig. 14 Ce–O interatomic distances in ceria doped with Sc, Y, Yb, Gd, Sm and Nd as a function of nominal dopant fraction x. Adapted from ref. 140 with permission from Elsevier, copyright 2000. | ||
Building on the above observations, we have collected here all available EXAFS data of the type shown in Fig. 14 for various dopants, all approximately within the fluorite range (dopant fraction, x ≤ 0.3). In addition, we have collected complementary XRD lattice parameter data, and derived RCat–OXRD using eqn (23). To a first approximation, the interatomic distances vary linearly with dopant concentration, as exemplified in Fig. 14, prompting us to compute the slopes, Δ[Cat–An]/Δ[x], as a metric for capturing the differences between the local (EXAFS) and average (XRD) trends. We applied linear regression analysis to each data set and extracted the approximate slope in units of Å per mol% dopant. The complete dataset and slopes are provided in the ESI,† Tables S3–S12. The results are presented as a function of the trivalent dopant Shannon ionic radius for 8-coordination139 in Fig. 15. The error bars reflect both the uncertainties in the original data and the nonlinearities in the distance vs. dopant fraction plots33 (which is particularly pronounced in the case of the XRD data of Nd-doped ceria94). The linear fits are intended to demonstrate qualitatively the relative contraction/expansion of the lattice parameter and of the different local environments defined by the dopant choice and concentration in the ceria solid solution.
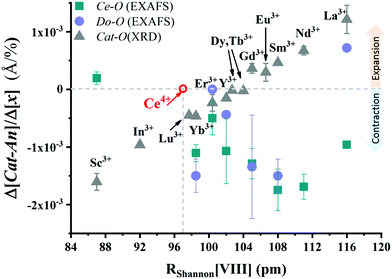 | ||
| Fig. 15 The vertical axis gives values of the slopes extracted from Cat–An distances (Å) as a function of dopant fraction x in mol%, for the assumed fluorite lattice phase (x ≤ 0.3), using linear regression for EXAFS and XRD analysis. Green squares show the values of slopes extracted from first coordination shell distances of Ce measured by EXAFS. Purple circles show the values of slopes extracted from first coordination shell distances of the dopant, measured by EXAFS for the same material. Gray triangles show values of slopes extracted from average Cat–An distances calculated from XRD by using eqn (23). We used XRD and EXAFS data from the same report when available, including XRD data from additional sources: Yb,136,140,157 Er,136,157 Sm,136,140,146,157 Gd.107,116,140,141,159 For dopants where only EXAFS data were available, we collected XRD data from external sources: Sc,140,152 Y,107,140,145 Nd,94,140,157 La.61,107,157 In addition XRD data were added for dopants where EXAFS local data were not available: In,152 Lu,160 Dy,157 Tb, Eu,61 in order to facilitate discussion. Where multiple EXAFS and XRD data sets were available, we averaged the trends. The materials in ref. 145, 146 and 152 have nanocrystalline grains while the data used from other reports includes materials with microcrystalline grains. Materials in refs: Deguchi et al.,107 Varenik et al.,160 Yavo et al.,159 Hong et al.157 and ref. 136 were measured as pellets, other data represents powder samples. The data used to construct this figure are summarized in ESI,† Tables S3 and S12. | ||
The trend from Cat–An data measured by standard XRD (gray triangles) is well described in the literature and qualitatively follows Vegard's law. It clearly shows the linear dependence of lattice expansion (positive values on the vertical axis) and contraction (negative values on the vertical axis) with respect to the dopant ionic radius. Note that contrary to expectation, zero contraction does not coincide with a dopant of ionic radius near Ce4+ (hollow red circle at 97 pm). Intuitively, we would expect the lattice parameter to increase upon addition of a substitutional dopant larger than the host. However, it has been known for some time on the basis of experimental data157 that the critical dopant radius at which expansion/contraction with respect to dopant fraction is at minimum is given by a value of ∼102 pm for ceria. Molecular dynamics (MD) and density functional theory (DFT) simulations later produced a slightly larger critical dopant radius of 105 pm (Gd).153 Indeed, zero expansion in Fig. 15: is observed in the 102–105 pm range for Dy (102.7 pm) and Tb (104 pm) from literature values of up to x ≤ 0.23 and x ≤ 0.18 respectively (see Table S12 in the ESI†). This effect was attributed to an overall contraction in the second nearest neighbor shell about the vacancy, composed of oxygen atoms, moving inwards to compensate for the partial positive charge.153,154 However, referring back to Fig. 12, no expansion is observed in Yb–O, Er–O and Y–O distances compared to Ce–O (although all dopants are slightly larger than Ce), suggesting that contraction in the lattice parameter in these cases does not necessarily originate only from the contraction of oxygen atoms around the vacancy site but is inherent to the dopant environment itself.
Turning to the EXAFS data, for all dopants with RShannon > 97 pm, contraction of Ce–O upon doping (green squares) is observed. The contraction magnitude of Ce–O increases in the dopant radius range between Er and Nd. Sc and Yb (having generally a strong tendency to form Do–VO clusters, i.e. low association energy, [see Fig. 7 and ref. 161]) and La (having the highest association energy of dopants discussed here) lie outside the trend. The behavior of Do–O (purple circles) follows closely the Ce–O trend (green squares), with the exception of La, which is the only cation that reveals expansion of the Do–O distance upon doping. Sc is the only dopant with ionic radius <97 pm (Ce4+) for which EXAFS data are available. It exhibits a significant contraction in lattice parameter, yet no recorded change with x in the local Ce–O distance. As observed by Yamazaki et al.140 using XRD, Sc tends to phase separate as Sc2O3 even for x < 0.3. This may suggest that fewer dopants (and vacancies) are available in the vicinity of Ce which ordinarily contribute to Ce–O bond contraction (N.B. – there are at present no EXAFS data which include Sc–O distances). It is apparent that much experimental, local structural data are missing, particularly for Do–O distances, and for dopants smaller than Ce4+. Obtaining such data with high accuracy can help focus and assist in a discussion of ceria solid solution local structure.
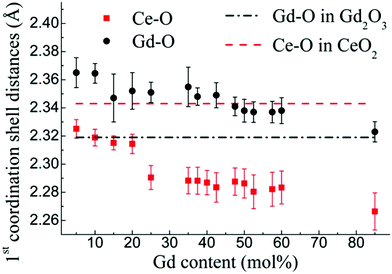 | ||
| Fig. 16 Ce–O and Gd–O distances in Gd-doped ceria from 5 to 95 mol% Gd. The top dashed line (red) indicates the Ce–O distance for undoped CeO2, while the bottom dashed line (black) indicates the average Gd–O distance in Gd2O3. Both Ce–O and Gd–O distances are shown to decrease with Gd content, across the full doping range, with Ce–O displaying a sharp change in slope around 20–25 mol%. Reproduced from ref. 116, with permission from American physical society, copyright 2013. | ||
These regions were defined as “nano-domains” and appear at compositions close to 20 mol% for Gd, and close to 30 mol% for Sm and Lu. These compositions are at the upper doping levels of the fluorite phase, prior to any detection of double-fluorite by XRD. The evidence presented above suggests that local “double-fluorite – like” regions may exist in the lower mol% regions normally identified by XRD as “fluorite”. As the doping fraction increases towards the XRD detectable phase transition, the double-fluorite-like regions may associate, finally generating nano-domains and later domains large enough to be detected by X-ray diffraction.
The missing link, therefore, for accurately constructing the actual local structure of ceria, may be the consideration of local strain fields, containing Ce–O and Do–O bonds which are much shorter than the average Cat–An distance calculated from the fluorite lattice parameter, similar to distinctly different sets of interatomic distances existing in the double-fluorite structure as described in ref. 143 and 167. Several reports presenting evidence in support of this idea can be cited. Deguchi et al.107 suggested, on the basis of Do–Do distances obtained by de-convoluting 2NN EXAFS data for Ce and for Do, that the dopant cation environments resemble the double-fluorite structures in La, Y and Gd-doped ceria. Wang et al.105 found that the Y K-edge EXAFS data in 20 mol% Y-doped ceria is best modeled by a double-fluorite structure. Kossoy et al. suggested, based on the data in Fig. 16, that the Ce environment in Gd-doped ceria resembles the cation-1 site in the double-fluorite phase.
Additional evidence to the existence of double-fluorite-like disorder prior to detection of phase transition were collected in recent years for a series of doped ceria materials using PDF analysis of neutron and X-ray total scattering data. Similarly to EXAFS, PDF analysis can produce short range interatomic distances. However, X-ray scattering data is insensitive to low atomic mass ions such as oxygen and therefore Cat–Cat distances are predominantly detected. These results summarized in a recent review by Coduri et al.34 support the existence of more than one Cat–Cat distance prior to long range detection of the double-fluorite phase in several doped ceria materials. Unlike for EXAFS the identity of the cation is not straightforward to extract, however the analysis supports that the appearance of a longer Cat–Cat distance occurs predominantly around the dopant species. In addition Coduri et al.146 using Rietveld refinement of XRD data, detected a small number of cation positions characteristic of the cation-1 site in double-fluorite, at Sm fractions as small as x = 0.125.
In summary, the appearance of double-fluorite-like local strain fields are related to the decrease in cation ionic radius, as a result of decrease in cation first shell coordination numbers discussed in the previous section. Both effects drive the observed local contraction in Cat–An distances described in Fig. 15. Material properties reported in ceria in recent years, such as electrostriction and anelastic behavior135 demonstrated that local strain fields may be active under applied anisotropic stress or electric field. As a result, advanced XANES and particularly EXAFS techniques were employed in order to observe changes in Cat–O distances in situ under an applied electric field.
3.3 Modulation of local distortion under bias (electro-mechanical activity)
An unusually large electromechanical response at room temperature was first reported for Gd-doped ceria in 2012 by Korobko et al.37 The strain was found to vary as the square of the electric field; the frequency of the response was second harmonic and therefore the material could be classified as electrostrictive. However, as characterized by Newnham et al. for a large variety of electrostrictive materials,40 the electrostrictive strain coefficient should scale with the ratio of the material elastic compliance to the dielectric permittivity. According to this scaling law, materials with large bulk modulus and dielectric constant ∼30168 should not produce a large electrostrictive response. However a response comparable to commercial relaxor materials has been recorded for substrate supported37,39,42 and self-supported43 doped ceria films as well as for bulk ceramics.160 Rather than producing bulk polarization of the material, local, uncorrelated dipolar strain fields were suggested to respond to electric field application.37Techniques allowing for both elemental selectivity and local (first and second shell) structural sensitivity were required in order to test the local strain hypothesis, and to identify the specific lattice sites responsible for strain generation under electric field. XAS techniques, meeting the above requirements, were particularly suitable for the in situ study of doped ceria as a function of applied electric field: conventional XANES,37 high energy resolution fluorescence detection (HERFD)-XANES169 and “difference X-ray absorption fine structure (ΔXANES and ΔEXAFS)”38 were employed. The information obtained from XANES and HERFD-XANES will be briefly summarized while most of the following will focus on the difference EXAFS data. In addition, we emphasized that all in situ experiments involving application of electric field were to this date performed on magnetron sputtered thin films in a plate capacitor configuration. Small film thickness excludes the need to use high voltage in order to achieve the required electric field.
In the first report describing large electromechanical response in substrate supported films of Gd-doped ceria,37 XANES data were collected from the host Ce and dopant Gd species under applied field by scanning the LIII absorption edges of Ce and Gd cations. No difference in the cation XANES spectra could be detected by measuring E-field ON vs. OFF states. However, applying a combined DC and low-frequency AC bias for several hours (poling), induced a change in the Ce XANES “white line” intensity and shape, when compared to the un-poled state. For the Gd LIII edge, no such change was detected. This indicated that NN oxygen ligands to Ce changed conformation as a result of the poling process, providing the first evidence for the existence of local strain, and pointing specifically to the Ce sites as its origin. To obtain structural information during ON and OFF states of the field, the sensitivity of the local structure sampling had to be increased. This was achieved by introducing “in situ differential XAS”.38
XAS spectra for Ce and Gd LIII edges were collected with bias electric field-on (60 kV cm−1) for 45 s and field-off for an additional 45 s. These on/off cycles were repeated 10 times. For each half-cycle (on or off), the spectra were normalized and merged (for more details, see ref. 38). For both the XANES and EXAFS regions of the XAS data, the averaged signals in the “off” state were subtracted from the signals in the “on” state, and the resulting difference spectrum was again averaged over time. A difference XANES signal was obtained for the Ce LIII edge resulting from an intensity increase in the white line upon bias application. No difference in signal was observed for the Gd LIII edge, supporting the result obtained after prolonged modulated field application (poling) in ref. 37, emphasizing that local strain is generated near the Ce cation. The difference XANES signal was qualitatively interpreted as either an increase in the density of unoccupied states of Ce as a result of increased ionic character, stronger configurational order, and/or larger coordination number of neighbors. Most importantly, the largest difference XANES signal for the Ce LIII edge was obtained for a 10 mol% Gd film, which also gave the largest recorded electrostrictive strain coefficient among the measured samples. This emphasized a clear connection between the structural data and the electrostrictive response.
The difference EXAFS signal, Δχ, can be defined as:
| Δχ = χ(Eon) − χ(Eoff) | (27) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) off) = χspectator + χactive(Eon
off) = χspectator + χactive(Eon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) off). χspectator is the contribution to the EXAFS signal from photoelectron scattering paths (see eqn (22)) that do not change under applied bias, while χactive is the contribution from scattering paths that do change. The difference k-weighted EXAFS signal Δχ, averaged as described above, is shown in Fig. 17a as a thick black line, and shows a distinct interference pattern, while a single χon EXAFS signal (collected during 45 s) is plotted in the background. The first strong peak of the radial distribution function (RDF) represents information concerning Ce–O distances (Fig. 17b). By comparing the Ce–O RDF peak for Δχ – representing the active bonds, to the χon RDF (an average of all “on” half-cycles), we can qualitatively see that the active Ce–O bonds are shorter than the spectators. In order to fit Δχ (‘active’ bond signal) and extract the EXAFS parameters, it was necessary to consider the active bond “anharmonicity”. This is accomplished by including higher order terms in the cumulant expansion that give rise to the structural parameters, such as the coordination number N, the effective nearest-neighbor distance r and the Debye Waller factor term e−2k2σ2 of eqn (22). A skew in the radial distribution caused by anharmonicity of the interatomic potential132,133 requires corrections to the Gaussian form of the Debye–Waller factor.122 The third cumulant, C3, characterizes the skew of the radial distribution function and is introduced as a correction to the phase term δ(k) in the EXAFS equation of a single scattering path:
off). χspectator is the contribution to the EXAFS signal from photoelectron scattering paths (see eqn (22)) that do not change under applied bias, while χactive is the contribution from scattering paths that do change. The difference k-weighted EXAFS signal Δχ, averaged as described above, is shown in Fig. 17a as a thick black line, and shows a distinct interference pattern, while a single χon EXAFS signal (collected during 45 s) is plotted in the background. The first strong peak of the radial distribution function (RDF) represents information concerning Ce–O distances (Fig. 17b). By comparing the Ce–O RDF peak for Δχ – representing the active bonds, to the χon RDF (an average of all “on” half-cycles), we can qualitatively see that the active Ce–O bonds are shorter than the spectators. In order to fit Δχ (‘active’ bond signal) and extract the EXAFS parameters, it was necessary to consider the active bond “anharmonicity”. This is accomplished by including higher order terms in the cumulant expansion that give rise to the structural parameters, such as the coordination number N, the effective nearest-neighbor distance r and the Debye Waller factor term e−2k2σ2 of eqn (22). A skew in the radial distribution caused by anharmonicity of the interatomic potential132,133 requires corrections to the Gaussian form of the Debye–Waller factor.122 The third cumulant, C3, characterizes the skew of the radial distribution function and is introduced as a correction to the phase term δ(k) in the EXAFS equation of a single scattering path: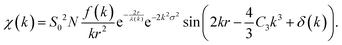 | (28) |
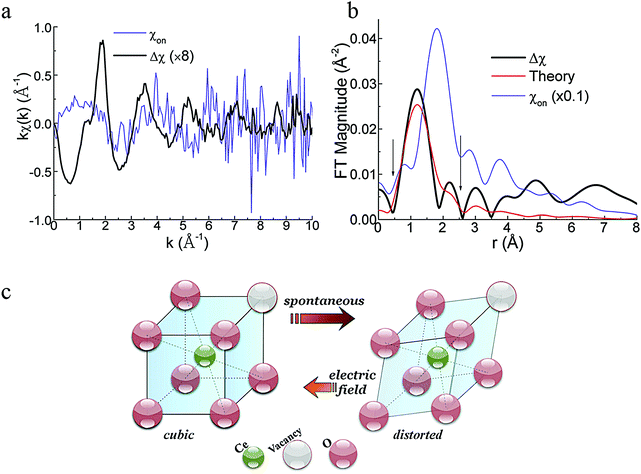 | ||
| Fig. 17 (a) k-Weighted EXAFS χon signal recorded during 45 s of field application (one half cycle), and the difference EXAFS signal Δχ, acquired according to eqn (27), representing the signal due to the “active species”. (b) RDF plot for the general Ce–O bond population represented by χon, and the “active” Ce–O bond population represented by Δχ. (c) An illustration of distorted cation sites (right) in the crystal as a result of decreased coordination number around the cation site from 8 to 7 oxygen atoms. When an electric field is applied, such units change towards the undistorted form, generating macroscopic strain. Adapted from ref. 38 with permission from American Institute of Physics, copyright 2015. | ||
Parameters N, r and C3 were extracted for active Ce–O bonds and spectators. The averaged active Ce–O bonds in the difference EXAFS signal were found to be 2.22 ± 0.09 Å in length, which is 4.6% shorter than the average Ce–O bonds in the material (2.33 ± 0.02 Å). The active bond anharmonicity factor C3 was found to be unusually large (0.210 ± 0.008 Å3), compared to the negligibly small value (0.000 ± 0.002 Å3) for the spectator bonds. Comparison of coordination numbers suggested short bonds comprise ≈3.4% of the total Ce–O bonds. This was consistent with the value of macroscopic strain ≈−6 × 10−4 measured during electrostrictive actuation. Finally, a negative sign in the difference coordination number N for Δχ, indicated that short bonds are not present in the “on” state. The general conclusion from this study is that local distortions (strain fields on the interatomic level) are present in the material prior to field application, comprising, in part, short, anharmonic Ce–O bonds. Upon field application, the distortions are minimized, thus generating measurable macroscopic strain, as illustrated in Fig. 17c. Although the model of the local distortion and the active Ce–O bonds was speculated to resemble the double-fluorite cation-1 site,116 HERFD results, described briefly below, indicated that local distortions prior to field application include a combination of configurations, not necessarily a single, well defined, double-fluorite – like structure.
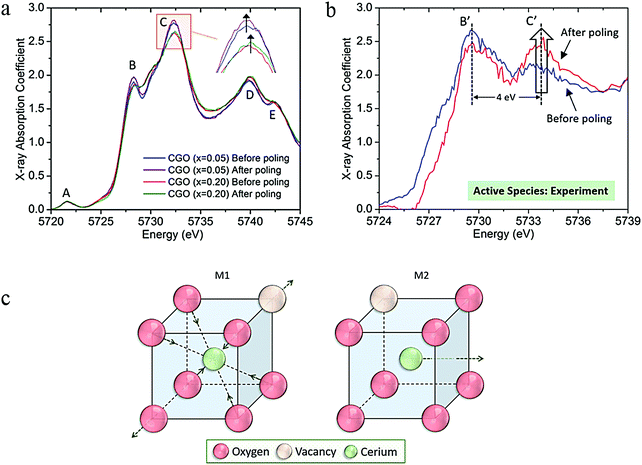 | ||
| Fig. 18 (a) HERFD white lines for the Ce absorption edge of 5 and 20 mol% ceria films, before and after “poling” with a combination of AC and DC fields, Vapplied = VDC + VAC·cos(2πft) [f = 10 mHz, VAC = 0.75 V, VDC = 0.4 V]. (b) Isolating the contribution of the active species to the intensity change in the “white line” peaks. (c) A model which combines two different local distortions is required in order to reproduce the intensity change caused by the active species to the Ce white line. Adapted from ref. 169 with permission from American Institute of Physics, copyright 2016. | ||
3.4 Correlating long range and short range data in a single model approach
Recently, a Reverse Monte Carlo (RMC) based approach was implemented to the analysis of undoped and doped ceria EXAFS data.58,171 The basic principle involves the extraction of a theoretical EXAFS spectrum from a simulated 3D model structure. The structure then continues to evolve through random atomic displacements, until theoretical and experimental spectra reach maximal agreement. The implementation of the RMC approach to EXAFS data improves the ability of data extraction beyond the first and second coordination shells from the EXAFS spectrum and tackles issues like “multiple scattering”.172 Besides the advantages for EXAFS analysis, the potential of an RMC based approach for ceria is the ability to constrain the model with several sets of experimental data, as implemented for amorphous materials in the past,173 representing short, intermediate and long range data, from neutron or X-ray total scattering together with EXAFS, consolidating the apparent inconsistencies between them. For ceria materials RMC models where constructed separately for neutron diffraction data of undoped83 and Nb or Ca doped174 ceria. In a step towards multiscale modeling, Clark et al.171 employed RMC modeling to EXAFS as well as neutron total scattering to model undoped ceria powder material. More recently XRD lattice parameters and EXAFS data were consolidated in a single model structure,58 for a series of Y- and Sm-doped ceria solid solutions. Here sputter deposited thin films were investigated. This allowed the assumption of randomly distributed solid solutions, since deposition on cold substrates reduces the possibility for preferential defect clustering at low doping fractions. The model showed that in order to produce realistic Ce–VO distances and also for the average XRD and local EXAFS experimental data to co-exist in the same crystal structure, first shell (Cat–O) and second shell (Cat–Cat) distances must display bimodal distributions. Specifically, more than one bond population is suggested to exist for Ce–O, Do–O and Ce–Cat distances, where for dopant coordination shells, the split in population was observed even for doping fractions as low as 5 mol%. This finding supports the existence of local double-fluorite like arrangements in the vicinity of a dopant as well as Ce host cations, see discussion in Section 3.2.6. From a functional perspective it supports the existence of local strain fields, able to deform under electric field, as discussed in Section 3.3. In addition, when discussing ion conductivity it implies that a basic diffusion step, a jump of an oxygen-vacancy does not have an equal probability for all six neighboring oxygen sites but may have some “preferential” directions caused by local asymmetry. The above experimental works sample the potential of the RMC approach for constructing multiple scale models for doped ceria materials.3.5 Conclusions from EXAFS: local structure of ceria solid solutions
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. However varying degrees of defect interaction and defect ordering play an important part as well: dopants that are larger than Nd3+ and smaller than Gd3+ display different relationships between the local and average structures. La3+ for example, is larger than Nd3+ and La-doped ceria solid solutions display expansion in the lattice parameter with dopant content. However, contraction in EXAFS-derived Cat–O is observed only for Ce–O distances while La–O follows the symmetry-predicted trend. This also provides evidence that local deformation as a result of oxygen-vacancy formation is present mainly near Ce4+. For dopants with ionic radius smaller than Gd3+, e.g., Y3+, Er3+ and Yb3+ the average and local environments qualitatively agree by producing contraction of lattice parameters as well as Cat–O distances.
m symmetry. However varying degrees of defect interaction and defect ordering play an important part as well: dopants that are larger than Nd3+ and smaller than Gd3+ display different relationships between the local and average structures. La3+ for example, is larger than Nd3+ and La-doped ceria solid solutions display expansion in the lattice parameter with dopant content. However, contraction in EXAFS-derived Cat–O is observed only for Ce–O distances while La–O follows the symmetry-predicted trend. This also provides evidence that local deformation as a result of oxygen-vacancy formation is present mainly near Ce4+. For dopants with ionic radius smaller than Gd3+, e.g., Y3+, Er3+ and Yb3+ the average and local environments qualitatively agree by producing contraction of lattice parameters as well as Cat–O distances.
These observations provided a new approach by suggesting that, through the application of an external electric field in combination with XAS, the state of local strain fields in the vicinity of point-defects could be detected. Local cation environments were probed by XANES,37 EXAFS,38 and HERFD169 before, during and after the application of the electric field under “poling” and low-frequency modulation regimes. These measurements have shown that: (i) a small number of Ce4+ ions have non-fluorite, 1NN oxygen coordination shells containing “active” bonds which can be modified by electric field or stress application; (ii) active Ce–O bonds are strained by ∼−4.6% (at 2.22 Å) with respect to their length in fluorite ceria (2.33 Å); the response to an applied electric field is expansion i.e., return to a cation–anion bond length closer to that expected from fluorite symmetry. The recent experiments described above highlight the role of modulated electric field application to selectively activate minority electroactive bonds, enhancing the sensitivity of XAFS experiments to their environment.38,169,177
4 Raman spectroscopy for probing point-defects and lattice distortions in undoped and doped ceria
Raman spectroscopy is a versatile and readily accessible experimental technique to investigate bonding and short-range order in metal-oxide materials by detecting lattice vibrations. In the following sections, we shall describe how pressure, temperature, oxygen non-stoichiometry, and extrinsic doping influence the Raman spectrum of ceria and its solid solutions, and how this information can be used to understand the defect-chemistry and local defect structures. Raman spectroscopy is also an excellent tool for characterizing the electro-chemo-mechanical properties of ceria, facilitated by in situ application of anisotropic stress or electric fields. In the following, we first introduce the fundamentals of Raman spectroscopy and then provide an overview of the interpretation of Raman spectra in ceria, with focus on point defects induced by aliovalent doping and oxygen non-stoichiometry.4.1 Basics of Raman spectroscopy in solid state compounds
Raman spectroscopy is a form of vibrational spectroscopy that measures the frequency and Raman intensity of lattice oscillation modes in solids.178 It overcomes the major drawback of XRD for oxides, which is the weak X-ray scattering amplitude of oxygen and the relative insensitivity to uncorrelated point-defects. Raman scattering is an inelastic scattering of a photon by a lattice oscillation (phonon). By this process, the frequency of the scattered photon shifts by an amount equal to the phonon frequency, which enables measurement of the frequencies of symmetry permitted interatomic bond vibrations. For the characterization of solids, usually confocal optical microscopes are used, and objective lenses have very high numeric aperture for efficient collection of the rather weak Raman scattering signal. The spatial resolution limit of this detection method is around 500 nm and 1 μm in depth. By depositing plasmonic structures on a substrate, the information depth can be reduced to few nanometers, which is called surface enhanced Raman spectroscopy.179 Another approach for increasing spatial resolution is tip-enhanced Raman spectroscopy (TERS), which uses an Atomic Force Microscope (AFM) tip few nanometers above the sample which enhances the field strength below the tip.180,181 Not only the spatial but also the temporal resolution of Raman spectroscopy can be enhanced by so-called femtosecond stimulated Raman spectroscopy,182,183 which enables the characterization of excited states. These advanced detection modes show the versatility of Raman spectroscopy. In standard configurations, the sample is illuminated with monochromatic light, typically a laser in the near-IR, visible or near-UV range. As shown in Fig. 19, a laser photon excites an electron into a virtual energy level with an extremely short lifetime. Upon relaxation, the emitted photon may have the same energy (elastic (Rayleigh) scattering), or the energy may be shifted by the energy of a phonon mode (Stokes, anti-Stokes scattering).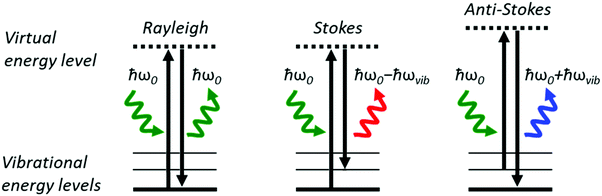 | ||
| Fig. 19 Schematic representation of the energy levels involved in Rayleigh, Stokes, and anti-Stokes Raman scattering. | ||
The macroscopic scattering process is described as follows. The incident laser light may be characterized by the electric field vector ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) of (angular) frequency ω0. Since the wavelength of the light is much longer than interatomic distances, its k-vector can be approximated as zero, described by the equation
of (angular) frequency ω0. Since the wavelength of the light is much longer than interatomic distances, its k-vector can be approximated as zero, described by the equation
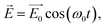 | (29) |
x = x0 + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωvibt). cos(ωvibt). | (30) |
p = α·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . . | (31) |
When atoms in the lattice vibrate around their equilibrium position, the polarizability changes as well, and may be linearized for small amplitude as
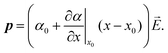 | (32) |
In this sense, Raman scattering occurs through the modulation of the polarizability due to lattice vibration. Inserting eqn (30) and (31) into eqn (32) yields
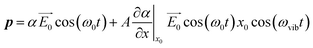 | (33) |
We may rewrite the equation using the trigonometric relation 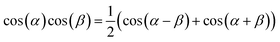 , which yields
, which yields
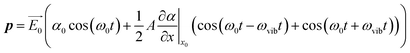 | (34) |
Eqn (34) shows that in addition to the frequency of the incoming light, Raman scattering gives rise to two new frequencies, ω0 − ωvib (Stokes scattering) and ω0 + ωvib (anti-Stokes scattering), whenever the partial derivative of the polarizability 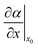 in eqn (32) is non-zero. This defines the selection rule for Raman activity since a vibrational mode is Raman active only if it induces a first order change in the polarizability. In other words, only when a lattice oscillation mode causes variations of the polarizability at the same frequency, this oscillation is first order Raman active.
in eqn (32) is non-zero. This defines the selection rule for Raman activity since a vibrational mode is Raman active only if it induces a first order change in the polarizability. In other words, only when a lattice oscillation mode causes variations of the polarizability at the same frequency, this oscillation is first order Raman active.
Some general features of Raman spectroscopy are relevant for any Raman experiment. (1) Vibrational energy levels are occupied according to Boltzmann statistics, and therefore Stokes scattering from the ground state to an excited state is more intense than anti-Stokes scattering from the less populated excited state. By calculating the ratio of the Stokes and anti-Stokes bands, the sample temperature may be determined.184,185 (2) Only when the lattice oscillation has the same phase for neighboring unit cells, this oscillation is Raman active. In the phonon dispersion curves, this condition is only satisfied at the Brillouin zone center, where the reduced k-vector equals 0, also denoted as Γ. This second condition is the reason why Raman peaks in crystalline solids can be quite narrow. (3) Although the Raman shift of a vibrational mode is independent of the exciting laser wavelength, Raman scattering amplitude may vary strongly with wavelength. Resonant intensity enhancement occurs when the exciting photon energy is close to the energy of an electronic transition, which strongly increases the lifetime of the photo-excited state, also known as resonant Raman scattering.186 Since excitation of real electronic states often also increases fluorescence, resonant enhancement does not increase the signal to background ratio in all cases.
Materials doped e.g. with either Er or Eu often exhibit strong fluorescence signals, which are typically much stronger than the detectable Raman scattering signal.187–189 An example of fluorescence in Er doped Ceria is shown in ESI,† Fig. S2.3. In contrast to Raman scattering, the wavelength of fluorescence signals is independent of the exciting laser wavelength, and in most cases also strongly fluorescent materials can be investigated by selecting the appropriate laser wavelength, as exemplified on measurements by the Rupp group in the ESI,† Section S2.3. Actually fluorescence signals can yield details on the local environment of fluorescent ions and can be effectively used to gain additional local near order information on structures, e.g. see for example on the use of Eu3+ref. 190 for further insights.
As noted above, vibrational modes are only Raman active when a lattice oscillation causes a first order change in the electric polarizability. Raman active vibrations can be predicted by group theory, taking into account the crystallographic symmetries.191 Typically, crystal structures with high symmetry have few Raman active oscillation modes. However, lattice distortions introduced by doping or oxygen-vacancy defects can locally lift the inversion symmetry and therefore introduce Raman activity also for normally inactive oscillation modes. Moreover, the Raman vibrational frequency depends on lattice geometry and bonding, specifically the bond stiffness, atomic mass and coordination number. In the following sections we will discuss these effects for ceria.
As detailed in Section 1, undoped ceria crystallizes in the cubic fluorite Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure (point group m
m structure (point group m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), shown in Fig. 1. Due to the high symmetry of the crystal structure, only one triply degenerate oxygen breathing mode of F2g symmetry at 465 cm−1 is Raman active,192 as shown in Fig. 20. Analogous to infrared spectroscopy, the Raman shift is typically measured in inverse wavelength, with the relation
m), shown in Fig. 1. Due to the high symmetry of the crystal structure, only one triply degenerate oxygen breathing mode of F2g symmetry at 465 cm−1 is Raman active,192 as shown in Fig. 20. Analogous to infrared spectroscopy, the Raman shift is typically measured in inverse wavelength, with the relation 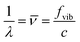 , where λ is the wavelength,
, where λ is the wavelength, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) the wavenumber, fvib the (temporal) vibrational frequency, and c the speed of light.
the wavenumber, fvib the (temporal) vibrational frequency, and c the speed of light.
In crystalline solids, lattice vibration frequencies are typically displayed on phonon dispersion curves. Phonon dispersion curves can be measured by inelastic neutron scattering,193 inelastic X-ray scattering,194 or high-resolution electron energy loss spectroscopy EELS.195 They can also be calculated by density functional theory (DFT).196 The phonon dispersion curves for CeO2 are shown in Fig. 21, where the experimentally measured data are superimposed on the DFT-calculated curves.
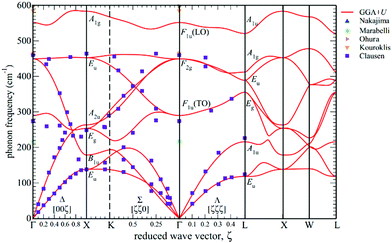 | ||
| Fig. 21 Phonon dispersion curves of CeO2. The data lines were calculated by DFT and the data points measured by inelastic neutron scattering (purple squares), Raman scattering (blue and orange triangles), infrared spectroscopy (brown triangle), and reflectivity (green diamond). Reproduced from ref. 197, with permission from American Physical Society, copyright 2013. | ||
For vibrational spectroscopy, only the Brillouin zone center frequencies, denoted by the point Γ in Fig. 21 are of interest. Other points in the wave vector axis (X, K, L, W) designate edges and corners of the Brillouin zone, but are not of interest here, because in ceria these oscillations produce very weak second order Raman active modes.198 The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (cubic fluorite) of ceria gives rise to six partially degenerate optical phonon modes yielding three frequencies at the Γ point. Out of all optical phonon modes, as noted above, only the triply degenerate F2g mode is Raman active, see Fig. 20.198 The F2g mode is the symmetric breathing vibration of the tetrahedrally-coordinated oxygen ions about the unit cell center. Since cations do not oscillate, the frequency is independent of the cationic mass.61 On the other hand, any variation in bond length or the formation of oxygen-vacancy defects will have a direct impact on the oscillation frequency and are therefore detectable in the Raman spectra.60 The two other optical phonon modes visible in Fig. 21 with Brillouin zone center frequencies corresponding to 270 cm−1 and 595 cm−1 have F1u symmetry and are therefore IR but not Raman-active.
m space group (cubic fluorite) of ceria gives rise to six partially degenerate optical phonon modes yielding three frequencies at the Γ point. Out of all optical phonon modes, as noted above, only the triply degenerate F2g mode is Raman active, see Fig. 20.198 The F2g mode is the symmetric breathing vibration of the tetrahedrally-coordinated oxygen ions about the unit cell center. Since cations do not oscillate, the frequency is independent of the cationic mass.61 On the other hand, any variation in bond length or the formation of oxygen-vacancy defects will have a direct impact on the oscillation frequency and are therefore detectable in the Raman spectra.60 The two other optical phonon modes visible in Fig. 21 with Brillouin zone center frequencies corresponding to 270 cm−1 and 595 cm−1 have F1u symmetry and are therefore IR but not Raman-active.
4.2 Interpretation of temperature or isostatic pressure induced changes in the F2g mode in terms of defect structure and chemistry
Raman spectroscopy is an excellent technique for probing the chemo-mechanics of a solid. Both the isothermal and isobaric Grüneisen parameters, accessible via Raman spectra, describe among other parameters the relationship between unit cell volume and lattice vibrational frequency. The effects of isostatic pressure on Raman spectra have been reviewed by Lucazeau.199 In the Grüneisen model, the frequency of a Raman mode shifts when the lattice expands or contracts. Due to the anharmonicity of the lattice potentials, shorter bonds are stiffer and therefore cause higher oscillation frequencies. For a cubic crystal lattice, the unit cell parameter a0 and vibrational frequency ω0 are related by: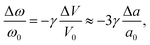 | (35) |
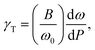 | (36) |
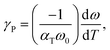 | (37) |
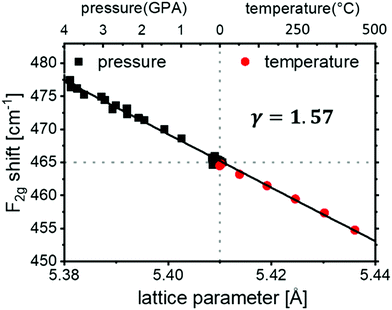 | ||
| Fig. 22 Position of the F2g mode as a function of the lattice parameter in CeO2. Black square data points were measured at high hydrostatic pressure for CeO2 powder, taken from ref. 201, and lattice parameter changes were calculated using a bulk modulus of 230 GPa.202 Red circle data points were measured on heated CeO2 pelletsat ambient pressure and the thermal expansion coefficient was taken from ref. 203, see ESI,† Section S2 for details. | ||
It is important to note that the case presented here is unusual in its ideality. As discussed by Lucazeau,199 the temperature dependent Raman shift can be affected by more than just thermal expansion and may therefore deviate from linearity, as well as from the value for the isothermal Grüneisen parameter. In addition, factors such as multiple scattering processes must be considered in some cases where deviations from the quasi-harmonic approximation are found. These effects are addressed for example in ref. 204 and 205, where nanocrystalline or oxygen-deficient ceria is considered. An additional important point is significant variation of the reported isothermal Grüneisen parameter in the literature, in part due to use of different values for the bulk modulus: some authors used the bulk modulus of ThO2 204 GPa (instead of 230 GPa which was measured for CeO2202) and claim a value of γ = 1.44200 for CeO2 single crystals. For nano-crystalline CeO2 powders, values range from 1.3206 to 1.4.207 For Gd and Sm-doped powders, values range from 1.16 to 1.46.207 It is therefore clear that both the isothermal and isobaric Grüneisen parameters are sensitive to material factors such as grain size and defect concentration (extrinsic and intrinsic) and require further exploration in these parameter ranges.
4.3 The effect of anisotropic strain on Raman spectra
Ceria thin films differ from bulk samples in several aspects. The film thickness is typically much smaller than the information depth of a Raman microscope. Therefore, substrates with no overlapping Raman peaks should be chosen, and acquisition time is conventionally longer than for bulk pellet samples which have a mm-sized sample thickness. The grain size of thin films varies from tens of nanometers in polycrystalline films to very large domains in epitaxial films. This can lead to broadening and red shift of the F2g peak, as observed for nanocrystalline Ceria films with grain size below 50 nm.208Most importantly, thin films are usually strained, due to mechanical interaction with the substrate, even when they are polycrystalline.26,59,209 In epitaxial films, strain is proportional to the mismatch in substrate and film lattice parameters, but also appears in polycrystalline films, due to the deposition process. This strain, can increase or impede the ionic conductivity, e.g. shown by Harrington et al.210 or Schweiger et al.26 and decrease the reduction enthalpy.211 Therefore, knowledge and manipulation of the strain state is of high technological importance.
Raman spectroscopy was shown to be a useful non-destructive tool to assess strain in such devices, or monitor crystallization of amorphous films.212,213 For example, Shi et al.137 probed 20 mol% Gd-doped ceria films, which were partly substrate-supported and partly free-standing membranes. The authors relate a F2g peak shift measured by Raman spectroscopy to variations in the local strain states (compressive vs. tensile). Also Schweiger et al. modulated strain by changing the number of multi-layer interfaces in a hetero-structure consisting of alternating Gd-doped ceria and erbia layers.26,27 For larger strain levels, increased asymmetry of the unit cells was deduced from the Raman spectra and confirmed by high-resolution transmission electron microscopy (HRTEM) at the interfaces.
Even though an effect of anisotropic strain on Raman shifts of ceria films was reported by various authors,26,201,209,212 the effect of strain on vibrational lattice dynamics – and thereby Grüneisen parameters remains only partly understood. Iguchi et al.207 suggested that since films of ceria and doped ceria experience anisotropic stress conditions, the Grüneisen relation as derived from high pressure experiments has to be modified for the biaxial modulus. This approach has also been adapted by Li et al.201 However, deviations from the relation in eqn (35) are also useful to learn about the properties of ceria materials: Kraynis et al.209 directly measured the equivalent Grüneisen parameter for doped ceria thin films, by comparing lattice volume and F2g peak position between strained thin films and relaxed fee-standing membranes. They found that the F2g Raman shift correlates qualitatively with the unit cell volume in agreement with eqn (35), but the equivalent Grüneisen parameter under biaxial strain is much lower than under isostatic pressure. This comparison suggested that the basic assumptions underlying the Grüneisen model (quasi-harmonicity and elasticity) are not preserved in the case of doped ceria thin films under anisotropic strain. This helped emphasize the role of defects when anisotropic stresses are applied to ceria materials, as summarized in a recent review.135
4.4 Investigation of Ceria defect-chemistry by Raman spectroscopy: the effect of reduction and acceptor dopants
Modification of the defect-chemistry of ceria, via either reduction of the undoped material or aliovalent doping to form solid solutions (e.g., with trivalent cations partially replacing Ce4+), markedly influences the Raman spectra: (i) the F2g mode frequency shifts in concert with changes of the lattice constant, (ii) a splitting of the F2g mode occurs and (iii) new modes emerge at both higher and lower wave numbers than that of the dominant F2g mode. These three types of changes are described below in the context of chemical changes induced by reduction and doping.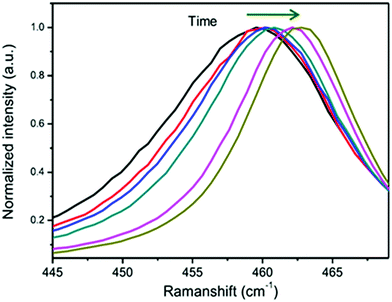 | ||
| Fig. 23 Raman time series during the oxidation of an oxygen non-stoichiometric ceria film in air; the F2g peak position shifts from ∼459 cm−1 to 465 cm−1. Spectra were normalized to F2g peak height. Reproduced from ref. 201 with permission from Elsevier, copyright 2016. | ||
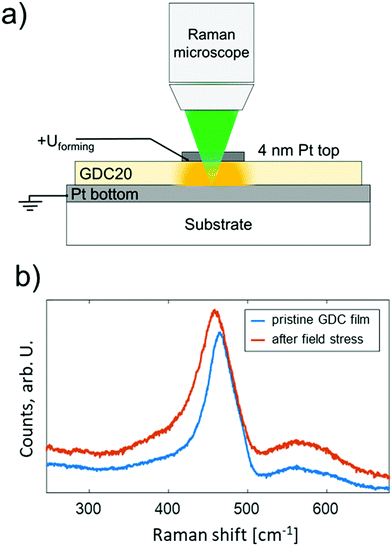 | ||
| Fig. 24 An example of using Raman spectroscopy as a tool for detecting the effect of high electric fields on the defect-chemistry of ceria solid solutions. (a) Cross sectional sketch of the experiment; a Gd0.2Ce0.8O1.9−δ thin film is prepared between two metallic electrodes – due to the very thin top electrode (4 nm Pt), the Raman laser reaches the Gd0.2Ce0.8O1.9−δ film underneath. (b) Normalized Raman spectra before and after application of a high electric field (800 kV cm−1 for 90 minutes). Adapted from ref. 28. | ||
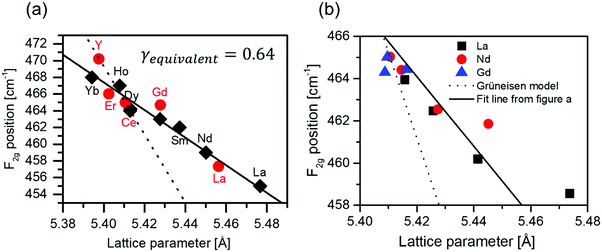 | ||
| Fig. 25 (a) Shift of the F2g Raman mode with respect to the lattice parameter of 20 mol%-doped ceria, where Do = Y, Yb, Er, Ho, Dy, Gd, Sm, Nd, La. The filled red circles represent the Rupp group data measured on polycrystalline pellets, see ESI,† Section S2 for details; the black diamonds are adapted from Pikalova et al.124 The solid line represents a linear fit, revealing an ‘equivalent Grüneisen’ parameter of 0.64. The dotted line shows the fit of the isothermal/isobaric experiments shown in Fig. 22, with a “proper” Grüneisen parameter of 1.57. (b) F2g shift vs. lattice parameter for La, Nd and Gd-doping with varying doping fraction (1–20%), data taken from Mcbride et al.61 The solid line is equal to figure part (a), and the dashed line is again taken from the isothermal/isobaric experiment. | ||
The Grüneisen model is applicable only if average bond lengths scale with the lattice parameter and symmetry is maintained. This is, however not the case, as shown in the EXAFS results in Fig. 12 and 15. Average Cat–O distances (which notably define bond stiffness) have no simple relation to the dopant radius or lattice parameter changes. Moreover, as shown in Fig. 14, the Ce–O distance (as measured by EXAFS) depends on the dopant species, reflecting varying degrees of local strain and suggesting variations in the degree of dopant-vacancy association and extent of non-periodic deviation from the cubic fluorite symmetry. Given these findings from EXAFS, it is not surprising that the Grüneisen model is not valid. On the contrary, it is surprising that a simple linear relationship between the F2g shift and lattice parameter is found at all as function of dopant radius across ten different dopant species. Noteworthy, phonon softening in Sm and Gd doped ceria was also predicted by DFT calculations by Jung et al.218 Varying the concentration of the extrinsic dopant also influences the shift of the ceria F2g Raman mode.25,60,61,217,219 For example, McBride et al. measured Raman shifts and lattice parameters for Gd, Nd and La doped ceria with 3–20 mol% dopant,61 and the data are shown in Fig. 25b. Perhaps not surprisingly, the correlation in this case is not as strongly linear because of effects from both dopant concentration and dopant radius are reflected in the data. Significantly, analogous to variation of the dopant radius, changing the lattice parameter by changing the dopant content causes a much smaller F2g peak shift compared to isostatic pressure. Although for the dopant concentration ranges considered the material remains in the fluorite phase (according to XRD), as already discussed, doping causes local distortions and deviations from fluorite symmetry in a dopant-specific fashion, Fig. 15. Therefore, it is not particularly surprising that a single “equivalent Grüneisen parameter” is an imperfect fit of the data.
An interesting analogy can be drawn between the effects of doping and anisotropic strain effects on ceria Raman spectra. Kraynis et al. studied the Grüneisen parameter of Eu3+ and Sm3+-doped ceria thin films under biaxial strain relaxation.209 Similar to the trivalent doping effect discussed above, a value of 0.4–0.6 was found for the equivalent Grüneisen parameter. Gopal et al. showed that biaxial strain, whether compressive and tensile, increases the reducibility of CeO2 thin films.211 Thus, both trivalent doping and strain will introduce defects into the structure. Under biaxial strain, the bond stiffness no longer changes isotropically. As elaborated in Section 3.2.4 the same is also true in doped systems for local bond distances near oxygen vacancies or dopant ions, where deviations from the cubic fluorite symmetry occur. This causes some analogies in the properties of doped and anisotropically strained ceria.
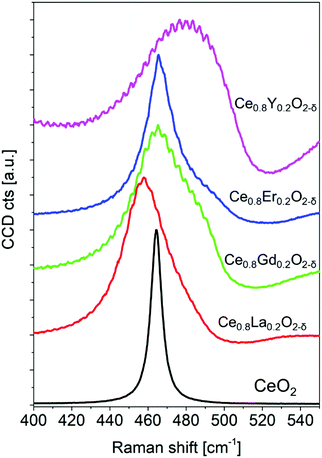 | ||
| Fig. 26 Raman spectra around the F2g peak in ceria pellets doped with 20 mol% La, Gd, Er, and Y, normalised to the F2g peak height established by Rupp group, see ESI,† Section S2 for experimental details. | ||
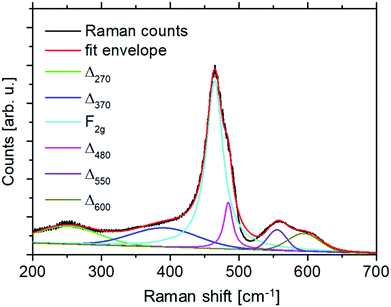 | ||
| Fig. 28 Raman spectrum of a high temperature sintered Ce0.8Gd0.2O1.9 pellet, with peak fit for the F2g vibrational mode and various defect-related Raman peaks, labeled with Δ. Experimental details are in the ESI,† Section S2 measured by Rupp group on polycrystalline pellets. | ||
While the large peak width of the defect bands led to an initial interpretation that they occur due to second-order scattering,61 Nakajima et al. showed by careful evaluation of the temperature dependence of the peak intensities that they are first-order in nature.224 Comparison of different dopants (La3+, Y3+, Zr4+),224 and also Hf4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 led to the observation that the Δ270 and Δ600 peaks are present for all dopants,224 and the Δ600 peak is even found in CeO2 nanocrystals.226,227
19 led to the observation that the Δ270 and Δ600 peaks are present for all dopants,224 and the Δ600 peak is even found in CeO2 nanocrystals.226,227
Although many defect related peaks appear to be rather insensitive to the type of defect, the Δ550 peak is only found when oxygen vacancies are present224 and is therefore a fingerprint for oxygen vacancies.
If we compare the frequency of the defect bands with the phonon dispersion curves for ceria in Fig. 21, we see that aside from the F2g vibration, with phonon frequency of 465 cm−1, two additional phonon branches of F1u (LO) and F1u (TO) symmetry are relevant and have Brillouin zone center frequencies of ∼590 and ∼290 cm−1. These phonon modes are not Raman active in the fluorite structure, which is, however, not preserved in the nearest and next nearest neighbor shells of point-defects, as elaborated in the EXAFS section. Remarkably, not only oxygen vacancies but also zirconia and hafnia dopants, that have a significant ionic radius mismatch, i.e., Zr4+ (0.84 Å) and Hf4+ (0.83 Å), compared to Ce4+ (0.97 Å),69 can be sufficient to activate the Δ600 and Δ270 modes. Although the intensity of defect-related Raman peaks depends strongly on the type of dopant (see Fig. 29a), the Δ600 position appears correlated with the F2g peak position, Fig. 29b, which further supports the relation to the F1u(LO) phonon mode.
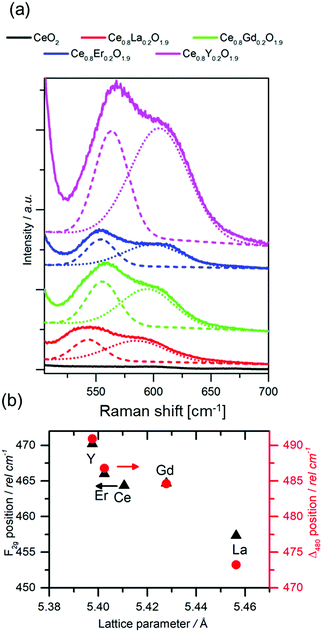 | ||
| Fig. 29 (a) Magnification of the Δ550 and Δ600 Raman modes with peak fit of 20 mol% rare-earth doped ceria with La, Gd, Er, and Y dopants. The intensity was normalized to the F2g peak. (b) Fitted peak positions as a function of dopant radius. See ESI,† Section S2.1 for details from pellets synthesized and measured by Rupp team. | ||
The relative intensity of the defect-related Raman modes is significantly enhanced by using a UV laser for excitation.228,229 In the Δ550, and Δ600 defect region this effect was attributed by the authors primarily to the shallow penetration depth of UV radiation (λ ≈ 365 nm), consequently leading to observation of the defect enriched surface at this excitation wavelength. Recently, also resonant enhancement of these defect modes was observed for undoped and a series of Lu, Gd, Sm and La doped ceria materials.230 A full set of LO mode harmonics (1–6LO) was assigned to undoped ceria. The study emphasized that under resonant conditions the Δ600 defect region is convoluted with the 1LO resonantly enhanced mode and therefore only the vacancy related Δ550 of the two defect bands can be resolved. The enhancement of the Δ550 vacancy related band under the UV excitation, enabled to observe its blue shift as function of dopant mol% for Gd and Sm doped ceria, in contrast to the simultaneous red shift of the F2g mode. This observation is in direct agreement with Fig. 15 where EXAFS derived Ce–O and Do–O distances for Sm and Gd doped ceria contract as function of mol%, while the lattice parameter shows expansion. The correlation of Raman and EXAFS data in this case, indicate that oxygen vacancy defects are likely in the vicinity of the contracting interatomic distances.
To continue the discussion of resonant effects, resonant enhancement in the defect region of Pr-doped ceria was demonstrated with laser wavelength of 514–532 nm.231 This enhancement was attributed to coupling of phonon states to the O2− ⇒ Pr4+ charge transfer, responsible for the absorption maximum in the visible (red/green). The intensity of the defect bands in Ce0.8Y0.2O1.9 can be explained by the small ionic radius of Y, which facilitates association of dopants and oxygen vacancies, as predicted by DFT calculations shown in Fig. 7. Similar results are observed at higher doping concentrations in Gd-doped ceria, where the periodic arrangement of the extrinsic oxygen vacancies leads to a lowering of the crystal symmetry.25,167 The transition occurs at lower dopant concentrations for Yttria-doped Ceria because of the small size of the Y3+ ion, which leads to lattice instabilities relaxed through the structural transition.
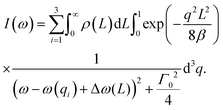 | (38) |
Therein, ω is the angular frequency, i is the number of the phonon branch (1–3) L is the average particle size, ρ(L) is the particle size distribution function and q the phonon wavevector divided by the lattice constant. ω(qi) is the frequency of the F2g phonon mode i as function of the wave vector (see Fig. 21), Δω(L) the F2g red shift due to particle size and Γ0 is the Raman FWHM of the single crystalline material (varying from 7–10 cm−1). The value of β determines the strength of phonon confinement analytic models predict values of β = 1 (Richter et al.240) or β = 2π2 (Campbell et al.239) and other authors treat β as a free fitting parameter, yielding values in the order of 40.237 By combining phonon confinement and particle size distribution, several authors could explain the F2g line shape of pure and doped Ceria nanocrystals.205,208,220,226,237,241 In summary, the effect of crystalline size on Raman spectra (especially the F2g peak) renders Raman spectroscopy as a suited tool to measure Ceria nanoparticle sizes in the range of 3–25 nm.
4.5 Conclusions from Raman spectroscopy
Undoped, oxygen stoichiometric ceria only has one Raman active lattice oscillation mode at 465 cm−1, which is a symmetrical breathing mode of oxygen anions, called the F2g mode. According to the Grüneisen model, compressed bonds are stiffer, so the oscillation frequency, and F2g peak position, depends on the lattice parameter. The F2g position is therefore sensitive to doping, isostatic pressure, temperature and oxygen nonstoichiometry. For obtaining Grüneisen parameters, literature data and some new own measurements were re-evaluated as a function of pressure, strain, temperature or aliovalent doping up to 20 mol%. In all cases, a linear relation of F2g peak shift and lattice parameter is found, although the slopes differ significantly, depending on the origin of lattice contraction and expansion. Doping of ceria introduces non-equivalent Cat–O bonds and other lattice distorions, which were elaborated in the XAFS chapter. Therefore there is no simple, linear relationship between bond lengths and lattice parameter in doped ceria.
In doped, reduced or nanocrystalline ceria, or anisotropically strained thin films, membranes or multilayer film structures, additional modes appear in the Raman spectra, which are characterized as follows. An additional peak appears slightly above the F2g vibration, denoted as the Δ480 mode. It is likely because in ceria containing point defects, Cat–O bonds become non-equivalent.
Additionally, Raman peaks at ∼270 and ∼590 cm−1 appear in ceria containing point defects, probably due to local symmetry reduction, enabling Raman activity of additional LO and TO phonon modes. This sensitivity towards local lattice distortions can provide useful insight into the concentration and association of defects.
Some defect-related peaks are related to specific structural features. A peak at ∼550 cm−1 appears only when oxygen vacancies are present, and is therefore a very good indicator for the latter. For dopant fractions close to or above the transition to double fluorite phase, a peak at ∼370 cm−1 is observed, and indicative for this transition.25,36,60 Generally, the relative intensity of the defect related Raman peaks can be greatly enhanced by using a UV laser for excitation.228–230
We emphasize by careful analysis and additional new standards published herein, that Raman spectroscopy is an excellent technique to probe temperature, strain and point defects and their changes in association and concentration for ceria materials with an easily accessible lab tool.
5 Summary and outlook
Undoped and doped ceria are among the most thoroughly investigated materials of modern lanthanide oxides and are currently in commercial use for a variety of applications. These investigations reveal that many properties of ceria based materials, such as elastic anomalies, strong electrostriction and defect thermodynamics, are not well described by simple models relying on the assumption that fluorite symmetry is preserved around isolated point defects. In the absence of an obvious crystallographic phase transition, standard XRD measurements are insufficient to describe properties that are likely caused by local lattice distortions and/or interacting defects that can develop in the presence of either extrinsic (dopant-induced) or intrinsic oxygen vacancies. This review has focused on experimental studies of the material's thermodynamic properties as well as its local structure and near neighbor ligand bonding patterns as measured by the complementary techniques of synchrotron X-ray absorption fine structure and Raman spectroscopy.By combining these methods, we have presented quantitative evidence from the literature that local structure in acceptor-doped (≤20–30 mol%), or oxygen-nonstoichiometric ceria does indeed deviate from the average fluorite symmetry. Defect thermodynamics, measured by mass changes of oxygen non-stoichiometric ceria, show that point-defects interact at quite low defect concentrations, especially in reduced, undoped ceria. Only models that assume associates such as 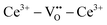 trimers or more extended defect clusters can accurately describe oxygen nonstoichiometry in reduced ceria. For acceptor-doped ceria, the lattice parameter increases or decreases, depending on the ionic radius (Shannon) of the dopant, and a linear relationship of dopant radius and lattice parameter is found.61 Interestingly, the “zero expansion” dopant radius of ∼103 pm is significantly larger than that of Ce4+ (97 pm).61 Also, if fluorite symmetry were preserved at the local level, Ce–O and dopant–O bond lengths should simply scale with the lattice parameter. In contrast, EXAFS data show both Ce–O and dopant–O bond length contraction for ceria doped with ions that cause lattice expansion. Therefore, it is reasonable to conclude that local environments around defects strongly deviate from fluorite symmetry and that these are the source of some of its unusual mechanical properties, such as anelasticity and large electrostriction with the latter having a potential for new industrial applications. These local deviations from fluorite symmetry also mean that the lattice is anisotropically strained and presents opportunity for chemo-mechanical behavior which has not been identified by XRD, which is only sensitive to periodic and non-element specific environments.
trimers or more extended defect clusters can accurately describe oxygen nonstoichiometry in reduced ceria. For acceptor-doped ceria, the lattice parameter increases or decreases, depending on the ionic radius (Shannon) of the dopant, and a linear relationship of dopant radius and lattice parameter is found.61 Interestingly, the “zero expansion” dopant radius of ∼103 pm is significantly larger than that of Ce4+ (97 pm).61 Also, if fluorite symmetry were preserved at the local level, Ce–O and dopant–O bond lengths should simply scale with the lattice parameter. In contrast, EXAFS data show both Ce–O and dopant–O bond length contraction for ceria doped with ions that cause lattice expansion. Therefore, it is reasonable to conclude that local environments around defects strongly deviate from fluorite symmetry and that these are the source of some of its unusual mechanical properties, such as anelasticity and large electrostriction with the latter having a potential for new industrial applications. These local deviations from fluorite symmetry also mean that the lattice is anisotropically strained and presents opportunity for chemo-mechanical behavior which has not been identified by XRD, which is only sensitive to periodic and non-element specific environments.
Also Raman spectroscopy, which is more readily accessible than synchrotron based XAFS, can probe symmetry, local order and bonding environments in ceria and its solid solutions. Structural changes caused by doping and reduction have a strong impact on Raman spectra. Defect-free, fluorite CeO2 has one Raman active phonon mode with F2g symmetry at 465 cm−1, reflecting the symmetric oxygen breathing vibration. A change in lattice parameter, caused by hydrostatic pressure or temperature, induces a linear response in the position of the F2g mode phonon frequency: compressed Ce–O bonds are stiffer and therefore increase the F2g oscillation frequency. From a linear relationship of phonon frequency and unit cell volume (due to quasi-harmonic displacement of ions from their equilibrium positions) the “Grüneisen parameter” can be defined. In the case of doped ceria, an equivalent Grüneisen parameter can be determined by fitting F2g peak position vs. lattice parameter of variously doped ceria solid solutions. This parameter is significantly lower than in the case of applied isostatic pressure or heating. This apparent discrepancy is explained by EXAFS measurements, which clearly reveal that a simple relation of lattice parameter and Ce–O or dopant–O bond length does not exist. This is the reason why the Grüneisen model is not valid for measuring the effect of doping-induced lattice parameter chances via Raman spectroscopy.
Emphasis is also placed on evidence from the literature that, in addition to a shift of the F2g mode for ceria solid solutions with change in either dopant size or concentration, additional Raman modes appear with frequencies around 270, 370, 480, 550 and 600 cm−1. The positions of the modes around 270 and 600 cm−1 coincide with the calculated frequencies of optical phonon modes that are not Raman active in fluorite crystals. As elaborated earlier, doping locally lifts the cubic fluorite symmetry and therefore enables Raman activity of these defect related modes which include information on isolated oxygen point-defects, and also associated defects such as Do–VO–Do trimers. For differentiating between point-defect types, the 550 cm−1 mode in Raman spectra is important, as it only appears in acceptor-doped or reduced ceria, making it a descriptor for oxygen vacancies and their environment. The Raman peak at 370 cm−1 is a good indicator for double fluorite ordering, which appears at higher doping levels (typ. >20 mol%). From combining measurements of oxygen nonstoichiometry, Ce–O bond length by EXAFS and symmetry reduction by Raman spectroscopy, we can conclude that doping of ceria causes strong lattice distortions around point-defects, which are probably the reason for the electro and chemo-mechanical properties.
Finally, although one may have considered that the defect structure and chemistry of ceria and its solid solutions might fall neatly into an ideally cubic description, this review has summarized experimental data from literature that demonstrate that in fact, doped ceria is rich with complexity. Changing perspective by moving away from structure-averaging techniques to quantitative and sensitive complementary methods, which can probe local structure and bonding environments, clearly reveals that, in the vicinity of point-defects, fluorite symmetry is indeed broken to an extent which depends on dopant identity, concentration, and local strain. We are hopeful that in this review, we have succeeded in presenting experimental findings that will assist future research in the field by contributing to tailored design of the defect-chemistry of ceria-based devices for solar-, thermo- and electro-chemistry applications and for industrial uses of giant electrostriction or memristive effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swiss National Science Foundation under the project numbers 155986 (SNSF starting grant) and 138914. Further support was provided by the US National Science Foundation under award number DMR-1505103. JR thanks the Thomas Lord Foundation for support of her Thomas Lord Assistant Professorship at the Department of Materials Science and Engineering (DMSE) at the Massachusetts Institute of Technology. IL and AIF acknowledge the NSF-BSF program grant 2018717. AIF acknowledges support by NSF Grant number DMR-1911592. This work was supported in part by the Israeli Ministry of Science and Technology grant 3-12944. This research is made possible in part by the historic generosity of the Harold Perlman Family. The authors would like to thank Dr Mads Weber for fruitful discussions about Raman spectroscopy and Dr Ellen Wachtel for assistance with editing and scientific discussion.References
- H. Yao and Y. Y. Yao, J. Catal., 1984, 86, 254–265 CrossRef CAS.
- G. Haxel, J. Hedrick and G. Orris, Rare earth elements—critical resources for high technology, US Geological Survey, US Geological Survey, 2002 Search PubMed.
- S. J. Skinner and J. A. Kilner, Mater. Today, 2003, 6, 30–37 CrossRef CAS.
- B. C. Steele, Solid State Ionics, 2000, 129, 95–110 CrossRef CAS.
- J. W. Fergus, J. Power Sources, 2006, 162, 30–40 CrossRef CAS.
- J. Molenda, K. Świerczek and W. Zając, J. Power Sources, 2007, 173, 657–670 CrossRef CAS.
- K. Yashiro, T. Suzuki, A. Kaimai, H. Matsumoto, Y. Nigara, T. Kawada, J. Mizusaki and J. Sfeir, Solid State Ionics, 2004, 175, 341–344 CrossRef CAS.
- R. Heinzmann, I. Issac, J.-P. Eufinger, G. Ulbrich, M. Lerch, J. R. Janek and S. Indris, J. Phys. Chem. C, 2016, 120, 8568–8577 CrossRef CAS.
- T. Charoonsuk, N. Vittayakorn and T. Kolodiazhnyi, J. Alloys Compd., 2017, 695, 1317–1323 CrossRef CAS.
- W. C. Chueh, A. H. McDaniel, M. E. Grass, Y. Hao, N. Jabeen, Z. Liu, S. M. Haile, K. F. McCarty, H. Bluhm and F. El Gabaly, Chem. Mater., 2012, 24, 1876–1882 CrossRef CAS.
- S. C. DeCaluwe, M. E. Grass, C. Zhang, F. E. Gabaly, H. Bluhm, Z. Liu, G. S. Jackson, A. H. McDaniel, K. F. McCarty and R. L. Farrow, J. Phys. Chem. C, 2010, 114, 19853–19861 CrossRef CAS.
- A. Trovarelli, Catal. Rev., 1996, 38, 439–520 CrossRef CAS.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS PubMed.
- J. Kašpar, P. Fornasiero and M. Graziani, Catal. Today, 1999, 50, 285–298 CrossRef.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- J. R. Scheffe and A. Steinfeld, Mater. Today, 2014, 17, 341–348 CrossRef CAS.
- Y. Hao, C.-K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- M. Kuhn, S. Bishop, J. Rupp and H. Tuller, Acta Mater., 2013, 61, 4277–4288 CrossRef CAS.
- J. R. Scheffe, R. Jacot, G. R. Patzke and A. Steinfeld, J. Phys. Chem. C, 2013, 117, 24104–24114 CrossRef CAS.
- F. Call, M. Roeb, M. Schmucker, C. Sattler and R. Pitz-Paal, J. Phys. Chem. C, 2015, 119, 6929–6938 CrossRef CAS.
- W. C. Chueh, Y. Hao, W. Jung and S. M. Haile, Nat. Mater., 2012, 11, 155 CrossRef CAS PubMed.
- W. Jung, J. O. Dereux, W. C. Chueh, Y. Hao and S. M. Haile, Energy Environ. Sci., 2012, 5, 8682–8689 RSC.
- V. A. Rojek-Wöckner, A. K. Opitz, M. Brandner, J. Mathé and M. Bram, J. Power Sources, 2016, 328, 65–74 CrossRef.
- E. P. Murray, T. Tsai and S. Barnett, Nature, 1999, 400, 649 CrossRef CAS.
- R. Schmitt, J. Spring, R. Korobko and J. L. M. Rupp, ACS Nano, 2017, 11, 8881–8891 CrossRef CAS PubMed.
- S. Schweiger, M. Kubicek, F. Messerschmitt, C. Murer and J. L. Rupp, ACS Nano, 2014, 8, 5032–5048 CrossRef CAS PubMed.
- S. Schweiger, R. Pfenninger, W. J. Bowman, U. Aschauer and J. L. Rupp, Adv. Mater., 2017, 29, 1605049 CrossRef PubMed.
- A. Nenning, R. Schmitt, T. Defferriere and J. L. M. Rupp, 2019, to be submitted.
- A. S. Dezfuli, M. R. Ganjali, H. R. Naderi and P. Norouzi, RSC Adv., 2015, 5, 46050–46058 RSC.
- W. Lin, Y.-w. Huang, X.-D. Zhou and Y. Ma, Int. J. Toxicol., 2006, 25, 451–457 CrossRef CAS PubMed.
- R. W. Tarnuzzer, J. Colon, S. Patil and S. Seal, Nano Lett., 2005, 5, 2573–2577 CrossRef CAS PubMed.
- J. Koettgen, S. Grieshammer, P. Hein, B. O. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291–14321 RSC.
- C. Artini, Inorg. Chem., 2018, 57, 13047–13062 CrossRef CAS PubMed.
- M. Coduri, S. Checchia, M. Longhi, D. Ceresoli and M. Scavini, Front. Chem., 2018, 6, 526 CrossRef CAS PubMed.
- C. Artini, M. Pani, M. M. Carnasciali, J. R. Plaisier and G. A. Costa, Inorg. Chem., 2016, 55, 10567–10579 CrossRef CAS PubMed.
- S. Presto, C. Artini, M. Pani, M. Carnasciali, S. Massardo and M. Viviani, Phys. Chem. Chem. Phys., 2018, 20, 28338–28345 RSC.
- R. Korobko, A. Patlolla, A. Kossoy, E. Wachtel, H. L. Tuller, A. I. Frenkel and I. Lubomirsky, Adv. Mater., 2012, 24, 5857–5861 CrossRef CAS PubMed.
- R. Korobko, A. Lerner, Y. Li, E. Wachtel, A. I. Frenkel and I. Lubomirsky, Appl. Phys. Lett., 2015, 106, 042904 CrossRef.
- M. Hadad, H. Ashraf, G. Mohanty, C. Sandu and P. Muralt, Acta Mater., 2016, 118, 1–7 CrossRef CAS.
- R. Newnham, V. Sundar, R. Yimnirun, J. Su and Q. Zhang, J. Phys. Chem. B, 1997, 101, 10141–10150 CrossRef CAS.
- R. Yimnirun, P. J. Moses, R. E. Newnham and R. J. Meyer, J. Electroceram., 2002, 8, 87–98 CrossRef CAS.
- R. Korobko, E. Wachtel and I. Lubomirsky, Sens. Actuators, A, 2013, 201, 73–78 CrossRef CAS.
- E. Mishuk, E. Makagon, E. Wachtel, S. Cohen, R. Popovitz-Biro and I. Lubomirsky, Sens. Actuators, A, 2017, 264, 333–340 CrossRef CAS.
- N. Yavo, O. Yeheskel, E. Wachtel, D. Ehre, A. I. Frenkel and I. Lubomirsky, Acta Mater., 2018, 144, 411–418 CrossRef CAS.
- A. Kossoy, A. I. Frenkel, Y. Feldman, E. Wachtel, A. Milner and I. Lubomirsky, Solid State Ionics, 2010, 181, 1473–1477 CrossRef CAS.
- R. Gerhardt, W.-K. Lee and A. Nowick, J. Phys. Chem. Solids, 1987, 48, 563–569 CrossRef CAS.
- M. Takacs, J. R. Scheffe and A. Steinfeld, Phys. Chem. Chem. Phys., 2015, 17, 7813–7822 RSC.
- B. Iwasaki and T. Katsura, Bull. Chem. Soc. Jpn., 1971, 44, 1297–1301 CrossRef CAS.
- T. Kobayashi, S. R. Wang, M. Dokiya, H. Tagawa and T. Hashimoto, Solid State Ionics, 1999, 126, 349–357 CrossRef CAS.
- R. Panlener, R. Blumenthal and J. Garnier, J. Phys. Chem. Solids, 1975, 36, 1213–1222 CrossRef CAS.
- S. Bishop, K. Duncan and E. Wachsman, Electrochim. Acta, 2009, 54, 1436–1443 CrossRef CAS.
- T. Horita, K. Yamaji, N. Sakai, M. Ishikawa, H. Yokokawa, T. Kawada and M. Dokiya, Electrochem. Solid-State Lett., 1998, 1, 4–6 CrossRef CAS.
- P. Manning, J. Sirman and J. Kilner, Solid State Ionics, 1996, 93, 125–132 CrossRef CAS.
- R. A. De Souza and M. Martin, MRS Bull., 2009, 34, 907–914 CrossRef CAS.
- E. Ruiz-Trejo, J. Sirman, Y. M. Baikov and J. Kilner, Solid State Ionics, 1998, 113, 565–569 CrossRef.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Acta Mater., 2009, 57, 3596–3605 CrossRef CAS.
- S. Kazlauskas, A. Kežionis, T. Šalkus and A. F. Orliukas, J. Mater. Sci., 2015, 50, 3246–3251 CrossRef CAS.
- O. Kraynis, J. Timoshenko, J. Huang, H. Singh, E. Wachtel, A. I. Frenkel and I. Lubomirsky, Inorg. Chem., 2019, 58, 7527–7536 CrossRef CAS PubMed.
- A. Kossoy, A. I. Frenkel, Q. Wang, E. Wachtel and I. Lubomirsky, Adv. Mater., 2010, 22, 1659–1662 CrossRef CAS PubMed.
- C. Artini, M. Pani, M. M. Carnasciali, M. T. Buscaglia, J. R. Plaisier and G. A. Costa, Inorg. Chem., 2015, 54, 4126–4137 CrossRef CAS PubMed.
- J. R. McBride, K. C. Hass, B. D. Poindexter and W. H. Weber, J. Appl. Phys., 1994, 76, 2435–2441 CrossRef CAS.
- D. Horlait, L. Claparede, N. Clavier, S. Szenknect, N. Dacheux, J. Ravaux and R. Podor, Inorg. Chem., 2011, 50, 7150–7161 CrossRef CAS PubMed.
- E. Wuilloud, B. Delley, W. D. Schneider and Y. Baer, Phys. Rev. Lett., 1984, 53, 202–205 CrossRef CAS.
- C. W. M. Castleton, J. Kullgren and K. Hermansson, J. Chem. Phys., 2007, 127, 11 CrossRef PubMed.
- P. R. L. Keating, D. O. Scanlon, B. J. Morgan, N. M. Galea and G. W. Watson, J. Phys. Chem. C, 2012, 116, 2443–2452 CrossRef CAS.
- F. Kröger and H. Vink, J. Phys. Chem. Solids, 1958, 5, 208–223 CrossRef.
- H. Tuller and A. Nowick, J. Phys. Chem. Solids, 1977, 38, 859–867 CrossRef CAS.
- H. L. Tuller and A. S. Nowick, J. Electrochem. Soc., 1979, 126, 209–217 CrossRef CAS.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Surf. Sci., 2005, 576, 217–229 CrossRef CAS.
- T. Zacherle, A. Schriever, R. A. De Souza and M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134104 CrossRef.
- C. Zhang, M. E. Grass, Y. Yu, K. J. Gaskell, S. C. DeCaluwe, R. Chang, G. S. Jackson, Z. Hussain, H. Bluhm and B. W. Eichhorn, ACS Catal., 2012, 2, 2297–2304 CrossRef CAS.
- X. P. Han, N. Amrane, Z. S. Zhang and M. Benkraouda, J. Phys. Chem. C, 2016, 120, 13325–13331 CrossRef CAS.
- K. L. Duncan, Y. Wang, S. R. Bishop, F. Ebrahimi and E. D. Wachsman, J. Appl. Phys., 2007, 101, 044906 CrossRef.
- C. B. Gopal and A. van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 8 Search PubMed.
- G. E. Murgida, V. Ferrari, M. V. Ganduglia-Pirovano and A. M. Llois, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115120 CrossRef.
- S. Wang, H. Inaba, H. Tagawa, M. Dokiya and T. Hashimoto, Solid State Ionics, 1998, 107, 73–79 CrossRef CAS.
- W. Cai and W. D. Nix, Imperfections in crystalline solids, Cambridge University Press, 2016 Search PubMed.
- D. J. M. Bevan and J. Kordis, J. Inorg. Nucl. Chem., 1964, 26, 1509–1523 CrossRef CAS.
- B. Bulfin, L. Hoffmann, L. de Oliveira, N. Knoblauch, F. Call, M. Roeb, C. Sattler and M. Schmucker, Phys. Chem. Chem. Phys., 2016, 18, 23147–23154 RSC.
- O. T. Sorensen, J. Solid State Chem., 1976, 18, 217–233 CrossRef.
- J. Campserveux and P. Gerdanian, J. Solid State Chem., 1978, 23, 73–92 CrossRef CAS.
- S. Hull, S. T. Norberg, I. Ahmed, S. G. Eriksson, D. Marrocchelli and P. Madden, J. Solid State Chem., 2009, 182, 2815–2821 CrossRef CAS.
- E. Kümmerle and G. Heger, J. Solid State Chem., 1999, 147, 485–500 CrossRef.
- S. S. Naghavi, A. A. Emery, H. A. Hansen, F. Zhou, V. Ozolins and C. Wolverton, Nat. Commun., 2017, 8, 285 CrossRef PubMed.
- S. Wang, H. Inaba, H. Tagawa and T. Hashimoto, J. Electrochem. Soc., 1997, 144, 4076–4080 CrossRef CAS.
- W. C. Chueh, W. Lai and S. M. Haile, Solid State Ionics, 2008, 179, 1036–1041 CrossRef CAS.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS.
- S. R. Wang, T. Kobayashi, M. Dokiya and T. Hashimoto, J. Electrochem. Soc., 2000, 147, 3606 CrossRef CAS.
- J. Garnier, R. Blumenthal, R. Panlener and R. Sharma, J. Phys. Chem. Solids, 1976, 37, 368–378 CrossRef.
- J. Kilner, Chem. Lett., 2008, 37, 1012–1015 CrossRef CAS.
- D. Park, J. Griffith and A. Nowick, Solid State Ionics, 1981, 2, 95–105 CrossRef.
- J. Faber, C. Geoffroy, A. Roux, A. Sylvestre and P. Abelard, Applied Physics A, 1989, 49, 225–232 CrossRef.
- I. E. Stephens and J. A. Kilner, Solid State Ionics, 2006, 177, 669–676 CrossRef CAS.
- S. Omar, E. D. Wachsman, J. L. Jones and J. C. Nino, J. Am. Ceram. Soc., 2009, 92, 2674–2681 CrossRef CAS.
- M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2009, 11, 3241–3249 RSC.
- S. Kim, R. Merkle and J. Maier, Surf. Sci., 2004, 549, 196–202 CrossRef CAS.
- J. L. Rupp, A. Infortuna and L. J. Gauckler, J. Am. Ceram. Soc., 2007, 90, 1792–1797 CrossRef CAS.
- C. B. Gopal, F. E. Gabaly, A. H. McDaniel and W. C. Chueh, Adv. Mater., 2016, 28, 4692–4697 CrossRef CAS PubMed.
- X. Guo and R. Waser, Prog. Mater. Sci., 2006, 51, 151–210 CrossRef CAS.
- H. J. Avila-Paredes, K. Choi, C.-T. Chen and S. Kim, J. Mater. Chem., 2009, 19, 4837–4842 RSC.
- A. Tschöpe, S. Kilassonia and R. Birringer, Solid State Ionics, 2004, 173, 57–61 CrossRef.
- R. Jenkins, R. Manne, R. Robin and C. Senemaud, X-Ray Spectrom., 1991, 20, 149–155 CrossRef CAS.
- A. V. Soldatov, T. S. Ivanchenko, S. Dellalonga, A. Kotani, Y. Iwamoto and A. Bianconi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5074–5080 CrossRef CAS.
- Y. R. Wang, H. Kageyama, T. Mori, H. Yoshikawa and J. Drennan, Solid State Ionics, 2006, 177, 1681–1685 CrossRef CAS.
- H. Nitani, T. Nakagawa, M. Yamanouchi, T. Osuki, M. Yuya and T. A. Yamamoto, Mater. Lett., 2004, 58, 2076–2081 CrossRef CAS.
- H. Deguchi, H. Yoshida, T. Inagaki and M. Horiuchi, Solid State Ionics, 2005, 176, 1817–1825 CrossRef CAS.
- J. A. Van Bokhoven and C. Lamberti, X-ray absorption and X-ray emission spectroscopy: theory and applications, John Wiley & Sons, 2016 Search PubMed.
- T. Heenan, D. Brett and P. Shearing, J. Phys.: Conf. Ser., 2017, 012020 Search PubMed.
- D. Koningsberger and R. Prins, X-ray absorption: principles, applications, techniques of EXAFS, SEXAFS, and XANES, John Wiley and Sons, 1988 Search PubMed.
- G. Bunker, Introduction to XAFS: a practical guide to X-ray absorption fine structure spectroscopy, Cambridge University Press, 2010 Search PubMed.
- S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995–3009 CrossRef CAS PubMed.
- P. Durham, J. Pendry and C. Hodges, Comput. Phys. Commun., 1982, 25, 193–205 CrossRef CAS.
- A. Bianconi, A. Marcelli, H. Dexpert, R. Karnatak, A. Kotani, T. Jo and J. Petiau, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 806 CrossRef CAS PubMed.
- G. Gasperi, L. Amidani, F. Benedetti, F. Boscherini, P. Glatzel, S. Valeri and P. Luches, Phys. Chem. Chem. Phys., 2016, 18, 20511–20517 RSC.
- A. Kossoy, Q. Wang, R. Korobko, V. Grover, Y. Feldman, E. Wachtel, A. K. Tyagi, A. I. Frenkel and I. Lubomirsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 054101 CrossRef.
- F. Zhang, P. Wang, J. Koberstein, S. Khalid and S.-W. Chan, Surf. Sci., 2004, 563, 74–82 CrossRef CAS.
- T.-S. Wu, Y. Zhou, R. F. Sabirianov, W.-N. Mei, Y.-L. Soo and C. L. Cheung, Chem. Commun., 2016, 52, 5003–5006 RSC.
- H. Dexpert, R. Karnatak, J.-M. Esteva, J. Connerade, M. Gasgnier, P. Caro and L. Albert, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 1750 CrossRef CAS.
- C. Paun, O. V. Safonova, J. Szlachetko, P. M. Abdala, M. Nachtegaal, J. Sa, E. Kleymenov, A. Cervellino, F. Krumeich and J. A. van Bokhoven, J. Phys. Chem. C, 2012, 116, 7312–7317 CrossRef CAS.
- D. E. Sayers, E. A. Stern and F. W. Lytle, Phys. Rev. Lett., 1971, 27, 1204–1207 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- C. F. J. Konig, J. A. van Bokhoven, T. J. Schildhauer and M. Nachtegaal, J. Phys. Chem. C, 2012, 116, 19857–19866 CrossRef CAS.
- E. Y. Pikalova, A. A. Murashkina, V. I. Maragou, A. K. Demin, V. N. Strekalovsky and P. E. Tsiakaras, Int. J. Hydrogen Energy, 2011, 36, 6175–6183 CrossRef CAS.
- B. K. Teo, EXAFS: basic principles and data analysis, Springer Science & Business Media, 2012 Search PubMed.
- F. W. Lytle, D. E. Sayers and E. A. Stern, Phys. Rev. B: Solid State, 1975, 11, 4825–4835 CrossRef CAS.
- E. A. Stern, D. E. Sayers and F. W. Lytle, Phys. Rev. B: Solid State, 1975, 11, 4836–4846 CrossRef CAS.
- F. De Groot and A. Kotani, Core level spectroscopy of solids, CRC press, 2008 Search PubMed.
- E. Stern and S. Heald, Handbook on synchrotron radiation, 1983, vol. 1, pp. 955–1014 Search PubMed.
- H. Wende, Rep. Prog. Phys., 2004, 67, 2105 CrossRef CAS.
- E. D. Crozier, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 133, 134–144 CrossRef CAS.
- A. I. Frenkel and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 585–588 CrossRef CAS PubMed.
- G. Dalba, P. Fornasini, M. Grazioli, R. Gotter and F. Rocca, Physica B, 1995, 208, 135–136 CrossRef.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef CAS.
- E. Wachtel, A. I. Frenkel and I. Lubomirsky, Adv. Mater., 2018, 30, 1707455 CrossRef PubMed.
- F. Giannici, G. Gregori, C. Aliotta, A. Longo, J. Maier and A. Martorana, Chem. Mater., 2014, 26, 5994–6006 CrossRef CAS.
- Y. Shi, A. H. Bork, S. Schweiger and J. L. M. Rupp, Nat. Mater., 2015, 14, 721–727 CrossRef CAS PubMed.
- A. Kossoy, E. Wachtel and I. Lubomirsky, J. Electroceram., 2014, 32, 47–50 CrossRef CAS.
- R. T. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925–946 CrossRef CAS.
- S. Yamazaki, T. Matsui, T. Ohashi and Y. Arita, Solid State Ionics, 2000, 136, 913–920 CrossRef.
- T. Ohashi, S. Yamazaki, T. Tokunaga, Y. Arita, T. Matsui, T. Harami and K. Kobayashi, Solid State Ionics, 1998, 113, 559–564 CrossRef.
- J. Koettgen and M. Martin, J. Phys. Chem. C, 2019, 123, 6333–6339 CrossRef CAS.
- C. Artini, G. A. Costa, M. Pani, A. Lausi and J. Plaisier, J. Solid State Chem., 2012, 190, 24–28 CrossRef CAS.
- M. Scavini, M. Coduri, M. Allieta, M. Brunelli and C. Ferrero, Chem. Mater., 2012, 24, 1338–1345 CrossRef CAS.
- M. Coduri, M. Scavini, M. Allieta, M. Brunelli and C. Ferrero, Chem. Mater., 2013, 25, 4278–4289 CrossRef CAS.
- M. Coduri, P. Masala, M. Allieta, I. Peral, M. Brunelli, C. A. Biffi and M. Scavini, Inorg. Chem., 2017, 57, 879–891 CrossRef PubMed.
- Y. Rosenberg, V. S. Machavariani, A. Voronel, S. Garber, A. Rubshtein, A. Frenkel and E. Stern, J. Phys.: Condens. Matter, 2000, 12, 8081 CrossRef CAS.
- A. I. Frenkel, E. A. Stern, A. Voronel and S. M. Heald, Solid State Commun., 1996, 99, 67–71 CrossRef CAS.
- A. Frenkel, A. Voronel, A. Katzir, M. Newville and E. Stern, Phys. B, 1995, 208, 334 CrossRef.
- A. Frenkel, E. A. Stern, A. Voronel, M. Qian and M. Newville, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 11662 CrossRef CAS PubMed.
- A. Frenkel, V. S. Machavariani, A. Rubshtein, Y. Rosenberg, A. Voronel and E. Stern, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 9364 CrossRef CAS.
- P. Li, I. W. Chen, J. E. Pennerhahn and T. Y. Tien, J. Am. Ceram. Soc., 1991, 74, 958–967 CrossRef CAS.
- D. Marrocchelli, S. R. Bishop, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2012, 22, 1958–1965 CrossRef CAS.
- H. Inaba, R. Sagawa, H. Hayashi and K. Kawamura, Solid State Ionics, 1999, 122, 95–103 CrossRef CAS.
- S. C. Shirbhate, K. Singh, S. A. Acharya and A. K. Yadav, Ionics, 2017, 23, 1049–1057 CrossRef CAS.
- S. C. Shirbhate, A. K. Yadav and S. A. Acharya, Appl. Phys. Lett., 2016, 108, 143501 CrossRef.
- S. J. Hong and A. V. Virkar, J. Am. Ceram. Soc., 1995, 78, 433–439 CrossRef CAS.
- D. J. Kim, J. Am. Ceram. Soc., 1989, 72, 1415–1421 CrossRef CAS.
- N. Yavo, D. Noiman, E. Wachtel, S. Kim, Y. Feldman, I. Lubomirsky and O. Yeheskel, Scr. Mater., 2016, 123, 86–89 CrossRef CAS.
- M. Varenik, X.-D. Zhang, G. Leitus, N. Yavo, R. Carmieli, E. Wachtel, X. Guo and I. Lubomirsky, Phys. Chem. Chem. Phys., 2018, 20, 27019–27024 RSC.
- S. Grieshammer, B. O. Grope, J. Koettgen and M. Martin, Phys. Chem. Chem. Phys., 2014, 16, 9974–9986 RSC.
- D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518–3521 CrossRef CAS PubMed.
- J. Koettgen, T. Zacherle, S. Grieshammer and M. Martin, Phys. Chem. Chem. Phys., 2017, 19, 9957–9973 RSC.
- F. Ye, T. Mori, D. R. Ou, J. Zou, G. Auchterlonie and J. Drennan, Solid State Ionics, 2008, 179, 827–831 CrossRef CAS.
- P. A. Žguns, A. V. Ruban and N. V. Skorodumova, Phys. Chem. Chem. Phys., 2018, 20, 11805–11818 RSC.
- P. A. Žguns, A. V. Ruban and N. V. Skorodumova, Scr. Mater., 2019, 158, 126–130 CrossRef.
- A. Banerji, V. Grover, V. Sathe, S. Deb and A. Tyagi, Solid State Commun., 2009, 149, 1689–1692 CrossRef CAS.
- V. Shelukhin, I. Zon, E. Wachtel, Y. Feldman and I. Lubomirsky, Solid State Ionics, 2012, 211, 12–19 CrossRef CAS.
- Y. Li, O. Kraynis, J. Kas, T.-C. Weng, D. Sokaras, R. Zacharowicz, I. Lubomirsky and A. I. Frenkel, AIP Adv., 2016, 6, 055320 CrossRef.
- K. O. Kvashnina, S. M. Butorin and P. Glatzel, J. Anal. At. Spectrom., 2011, 26, 1265–1272 RSC.
- A. H. Clark, H. R. Marchbank, T. I. Hyde, H. Y. Playford, M. G. Tucker and G. Sankar, Phys. Scr., 2017, 92, 034002 CrossRef.
- J. Timoshenko, A. Kuzmin and J. Purans, J. Phys.: Condens. Matter, 2014, 26, 055401 CrossRef CAS PubMed.
- J. Wicks and R. McGreevy, J. Non-Cryst. Solids, 1995, 192, 23–27 CrossRef.
- C. I. Hiley, H. Y. Playford, J. M. Fisher, N. C. Felix, D. Thompsett, R. J. Kashtiban and R. I. Walton, J. Am. Chem. Soc., 2018, 140, 1588–1591 CrossRef CAS PubMed.
- A. Frenkel, E. A. Stern, A. Voronel, M. Qian and M. Newville, Phys. Rev. Lett., 1993, 71, 3485 CrossRef CAS PubMed.
- A. I. Frenkel, D. M. Pease, J. I. Budnick, P. Metcalf, E. A. Stern, P. Shanthakumar and T. Huang, Phys. Rev. Lett., 2006, 97, 195502 CrossRef CAS PubMed.
- H. Singh, D. Donetsky, J. Liu, K. Attenkofer, B. Cheng, J. Trelewicz, I. Lubomirsky, E. Stavitski and A. I. Frenkel, Rev. Sci. Instrum., 2018, 89, 045111 CrossRef CAS PubMed.
- T. R. Gilson and P. J. Hendra, Laser Raman Spectroscopy: A Survey of Interest Primarily to Chemists, and Containing a Comprehensive Discussion of Experiments on Crystals, Wiley-Interscience, London, 1970 Search PubMed.
- P. L. Stiles, J. A. Dieringer, N. C. Shah and R. P. Van Duyne, Annu. Rev. Anal. Chem., 2008, 1, 601–626 CrossRef CAS PubMed.
- R. M. Stöckle, Y. D. Suh, V. Deckert and R. Zenobi, Chem. Phys. Lett., 2000, 318, 131–136 CrossRef.
- E. Bailo and V. Deckert, Chem. Soc. Rev., 2008, 37, 921–930 RSC.
- E. Ploetz, S. Laimgruber, S. Berner, W. Zinth and P. Gilch, Appl. Phys. B: Lasers Opt., 2007, 87, 389–393 CrossRef CAS.
- P. Kukura, D. W. McCamant and R. A. Mathies, Annu. Rev. Phys. Chem., 2007, 58, 461–488 CrossRef CAS PubMed.
- P. Larkin, Infrared and Raman Spectroscopy, Elsevier, Oxford, 2011, pp. 7–25 Search PubMed.
- R. Maher, L. Cohen, P. Lohsoontorn, D. Brett and N. Brandon, J. Phys. Chem. A, 2008, 112, 1497–1501 CrossRef CAS PubMed.
- R. S. Drago, Physical methods in chemistry, 1977 Search PubMed.
- J. Joo, T. Yu, Y. W. Kim, H. M. Park, F. Wu, J. Z. Zhang and T. Hyeon, J. Am. Chem. Soc., 2003, 125, 6553–6557 CrossRef CAS PubMed.
- J. Cui and G. A. Hope, J. Spectrosc., 2015, 940172 Search PubMed.
- C. Michael, H. Yuen, V. Sabnis, T. Johnson, R. Sewell, R. Smith, A. Jamora, A. Clark, S. Semans and P. Atanackovic, Opt. Express, 2008, 16, 19649–19666 CrossRef CAS PubMed.
- D. Avram, C. Rotaru, B. Cojocaru, M. Sanchez-Dominiguez, M. Florea and C. Tiseanu, J. Mater. Sci., 2014, 49, 2117–2126 CrossRef CAS.
- M. Tasumi, A. Sakamoto, T. Hieda and H. Torii, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, 2006 Search PubMed.
- M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef PubMed.
- S. F. Parker, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, 2006 Search PubMed.
- B. Eberhard, Rep. Prog. Phys., 2000, 63, 171 CrossRef.
- M. A. Chesters, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, 2006 Search PubMed.
- H. Matsuura and H. Yoshida, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, 2006 Search PubMed.
- J. Buckeridge, D. O. Scanlon, A. Walsh, C. R. A. Catlow and A. A. Sokol, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214304 CrossRef.
- W. H. Weber, K. C. Hass and J. R. McBride, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 178–185 CrossRef CAS PubMed.
- G. Lucazeau, J. Raman Spectrosc., 2003, 34, 478–496 CrossRef CAS.
- G. A. Kourouklis, A. Jayaraman and G. P. Espinosa, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 4250–4253 CrossRef CAS.
- H. Li, P. Zhang, G. Li, J. Lu, Q. Wu and Y. Gu, J. Alloys Compd., 2016, 682, 132–137 CrossRef CAS.
- U. Benedict, J. Alloys Compd., 1995, 223, 216–225 CrossRef CAS.
- S. Stecura and W. J. Campbell, Thermal expansion and phase inversion of rare-earth oxides, Bureau of Mines. College Park Metallurgy Research Center, Md., 1960 Search PubMed.
- S. D. Pandey, J. Singh, K. Samanta, N. D. Sharma and A. Bandyopadhyay, J. Nanomater., 2015, 16, 154 Search PubMed.
- Z. Popović, Z. Dohčević-Mitrović, A. Cros and A. Cantarero, J. Phys.: Condens. Matter, 2007, 19, 496209 CrossRef.
- S. Dogra, J. Singh, N. D. Sharma, K. Samanta, H. Poswal, S. Sharma and A. Bandyopadhyay, Vib. Spectrosc., 2014, 70, 193–199 CrossRef CAS.
- F. Iguchi, S. Onodera, N. Sata and H. Yugami, Solid State Ionics, 2012, 225, 99–103 CrossRef CAS.
- I. Kosacki, T. Suzuki, H. U. Anderson and P. Colomban, Solid State Ionics, 2002, 149, 99–105 CrossRef CAS.
- O. Kraynis, E. Makagon, E. Mishuk, M. Hartstein, E. Wachtel, I. Lubomirsky and T. Livneh, Adv. Funct. Mater., 2019, 29, 1804433 CrossRef.
- G. F. Harrington, L. Sun, B. Yildiz, K. Sasaki, N. H. Perry and H. L. Tuller, Acta Mater., 2019, 166, 447–458 CrossRef CAS.
- C. B. Gopal, M. García-Melchor, S. C. Lee, Y. Shi, A. Shavorskiy, M. Monti, Z. Guan, R. Sinclair, H. Bluhm and A. Vojvodic, Nat. Commun., 2017, 8, 15360 CrossRef PubMed.
- J. L. Rupp, B. Scherrer and L. J. Gauckler, Phys. Chem. Chem. Phys., 2010, 12, 11114–11124 RSC.
- R. Pfenninger, M. Struzik, I. Garbayo, E. Stilp and J. L. Rupp, Nat. Energy, 2019, 4, 475–483 CrossRef CAS.
- S. Ackermann, L. Sauvin, R. Castiglioni, J. L. M. Rupp, J. R. Scheffe and A. Steinfeld, J. Phys. Chem. C, 2015, 119, 16452–16461 CrossRef CAS PubMed.
- K. Lee and J. R. Scheffe, J. Sol. Energy Eng., 2019, 141, 021013 CrossRef CAS.
- E. Sediva, T. Defferriere, N. H. Perry, H. L. Tuller and J. L. Rupp, Adv. Mater., 2019, 1902493 CrossRef PubMed.
- J. L. M. Rupp, E. Fabbri, D. Marrocchelli, J.-W. Han, D. Chen, E. Traversa, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2014, 24, 1562–1574 CrossRef CAS.
- D.-H. Jung, J.-H. Lee, M. E. Kilic and A. Soon, Phys. Chem. Chem. Phys., 2018, 20, 10048–10059 RSC.
- N. Yang, Y. Shi, S. Schweiger, E. Strelcov, A. Belianinov, V. Foglietti, P. Orgiani, G. Balestrino, S. V. Kalinin, J. L. M. Rupp and C. Aruta, ACS Appl. Mater. Interfaces, 2016, 8, 14613–14621 CrossRef CAS PubMed.
- S. Aškrabić, Z. D. Dohčević-Mitrović, M. Radović, M. Šćepanović and Z. V. Popović, J. Raman Spectrosc., 2009, 40, 650–655 CrossRef.
- S. Aškrabić, Z. Dohčević-Mitrović, A. Kremenović, N. Lazarević, V. Kahlenberg and Z. V. Popović, J. Raman Spectrosc., 2012, 43, 76–81 CrossRef.
- V. Grover, A. Banerji, P. Sengupta and A. K. Tyagi, J. Solid State Chem., 2008, 181, 1930–1935 CrossRef CAS.
- R. Korobko, S. K. Kim, S. Kim, S. R. Cohen, E. Wachtel and I. Lubomirsky, Adv. Funct. Mater., 2013, 23, 6076–6081 CrossRef CAS.
- A. Nakajima, A. Yoshihara and M. Ishigame, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13297–13307 CrossRef CAS PubMed.
- T. Tsuchiya, S. Miyoshi, Y. Yamashita, H. Yoshikawa, K. Terabe, K. Kobayashi and S. Yamaguchi, Sci. Technol. Adv. Mater., 2013, 14, 045001 CrossRef PubMed.
- Z. D. Dohčević-Mitrović, M. J. Šćepanović, M. U. Grujić-Brojčin, Z. V. Popović, S. B. Bošković, B. M. Matović, M. V. Zinkevich and F. Aldinger, Solid State Commun., 2006, 137, 387–390 CrossRef.
- Z. Wu, M. Li, J. Howe, H. M. Meyer and S. H. Overbury, Langmuir, 2010, 26, 16595–16606 CrossRef CAS PubMed.
- T. Taniguchi, T. Watanabe, N. Sugiyama, A. K. Subramani, H. Wagata, N. Matsushita and M. Yoshimura, J. Phys. Chem. C, 2009, 113, 19789–19793 CrossRef CAS.
- M. Guo, J. Lu, Y. Wu, Y. Wang and M. Luo, Langmuir, 2011, 27, 3872–3877 CrossRef CAS PubMed.
- O. Kraynis, I. Lubomirsky and T. Livneh, J. Phys. Chem. C, 2019, 123, 24111–24117 CrossRef CAS.
- A. Westermann, C. Geantet, P. Vernoux and S. Loridant, J. Raman Spectrosc., 2016, 47, 1276–1279 CrossRef CAS.
- Y. Ikuma, S. Nagasawa, N. Hayashi and M. Kamiya, J. Jpn. Soc. Powder Powder Metall., 2005, 52, 599–602 CAS.
- C. Artini, M. M. Carnasciali, J. R. Plaisier, G. A. Costa and M. Pani, Solid State Ionics, 2017, 311, 90–97 CrossRef CAS.
- M. Ando, I. Oikawa, S. Ohki, M. Tansho, T. Shimizu, H. Maekawa and H. Kiyono, Chem. Lett., 2012, 42, 57–59 CrossRef.
- I. Heinmaa, T. Joon, H. Kooskora, J. Pahapill and J. Subbi, Solid State Ionics, 2010, 181, 1309–1315 CrossRef CAS.
- N. Kim and J. F. Stebbins, Chem. Mater., 2007, 19, 5742–5747 CrossRef CAS.
- J. E. Spanier, R. D. Robinson, F. Zhang, S.-W. Chan and I. P. Herman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245407 CrossRef.
- A. Apostolov, I. Apostolova and J. Wesselinowa, Solid State Commun., 2018, 279, 17–21 CrossRef CAS.
- I. Campbell and P. M. Fauchet, Solid State Commun., 1986, 58, 739–741 CrossRef CAS.
- H. Richter, Z. Wang and L. Ley, Solid State Commun., 1981, 39, 625–629 CrossRef CAS.
- Z. Popović, Z. Dohčević-Mitrović, M. Šćepanović, M. Grujić-Brojčin and S. Aškrabić, Ann. Phys., 2011, 523, 62–74 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cs00588a |
| ‡ Shared first-co-authorship, these authors have equally contributed to this manuscript. |
| This journal is © The Royal Society of Chemistry 2020 |