Microhydration of substituted diamondoid radical cations of biological relevance: infrared spectra of amantadine⁺-(H₂O)_{n = 1–3} clusters

Abstract

Hydration of biomolecules and pharmaceutical compounds has a strong impact on their structure, reactivity, and function. Herein, we explore the microhydration structure around the radical cation of the widespread pharmaceutical drug amantadine (C₁₆H₁₅NH₂, Ama) by infrared photodissociation (IRPD) spectroscopy of mass-selected Ama⁺W_{n = 1–3} clusters (W = H₂O) recorded in the NH, CH, and OH stretch range of the cation ground electronic state. Analysis of the size-dependent frequency shifts by dispersion-corrected density functional theory calculations (B3LYP-D3/cc-pVTZ) provides detailed information about the acidity of the protons of the NH₂ group of Ama⁺ and the structure and strength of the NH⋯O and OH⋯O hydrogen bonds (H-bonds) of the hydration network. The preferred sequential cluster growth begins with hydration of the two acidic NH protons of the NH₂ group (n = 1–2) and continues with an extension of the H-bonded hydration network by forming an OH⋯O H-bond of the third W to one ligand in the first hydration subshell (n = 3), like in the W₂ dimer. For n = 2, a minor population corresponds to Ama⁺W₂ structures with a W₂ unit attached to Ama⁺via a NH⋯W₂ H-bond. Although the N–H proton donor bonds are progressively destabilized by gradual microhydration, no proton transfer to the W_n solvent cluster is observed in the investigated size range (n ≤ 3). Besides the microhydration structure, we also obtain a first impression of the structure and IR spectrum of bare Ama⁺, as well as the effects of both ionization and hydration on the structure of the adamantyl cage. Comparison of Ama⁺ with aliphatic and aromatic primary amine radical cations reveals differences in the acidity of the NH₂ group and the resulting interaction with W caused by substitution of the cycloalkyl cage.

---

1. Introduction

Amantadine (Ama, 1-tricyclo[3.3.1.1^3,7]decylamine, 1-adamantylamine, 1-aminoadamantane, C₁₆H₁₅NH₂) is the amino derivative of adamantane (C₁₀H₁₆, Ad), which is the parent molecule of the diamondoids (also called polymantanes),^1,2 a fundamental class of saturated sp³-hybridized hydrocarbon molecules. These rigid and stress-free cycloalkanes are nanometer-sized H-passivated nanodiamonds, which are thermodynamically and chemically highly stable and perfectly size-selectable.^3–5 Diamondoids are therefore an important class of hydrocarbon molecules, with a variety of applications in materials and polymer sciences, molecular electronics, astrochemistry, chemical synthesis, and medical sciences.^6–14 Concerning pharmaceutical applications, Ama is one of the best known commercially available diamondoid, because it is successfully marketed as an antiviral and antiparkinson drug under the brand names Symmetrel® (Ama·HCl), Gocovri®, Symadine®, and Osmolex ER®.^15–18 The antiviral properties result from the ability of the drug to prevent the virus from entering the host cell by blocking the ion channel. The drug interferes with a viral protein, M2 (an ion channel), which is needed for the virus to become “uncoated” as soon as it is absorbed into the cell by endocytosis.¹⁹ However, its use for influenza is no longer recommended due to drug resistance.^20,21 The mechanism of its antiparkinsonian effect is not yet fully understood at the molecular level, but the drug increases dopamine release from the nerve endings of brain cells, together with a stimulation of the norepinephrine response.^22–24 Moreover, it also has NMDA receptor antagonistic effects.^25,26 Ama is also under discussion for the treatment of fatigue in multiple sclerosis, depression, and cocaine dependence.^27–29 The methylated derivative, memantine or Namenda®, was amongst the top 100 sold drugs worldwide, with sales of more than 10⁹ US$ in the year 2013.³⁰ Herein, we study microhydrated clusters of the Ama⁺ cation, Ama⁺W_n (W = water = H₂O), to characterize the intermolecular interaction of this biomolecular cation with W at the molecular level. In addition to its pharmaceutical importance, Ama and particularly its radical cation is also of relevance in the context of astrochemistry. In particular, due to their high stability, diamondoids are postulated to be highly abundant in the interstellar medium.^31–36 The large fraction of primary amines detected in interstellar space suggests a significant abundance of Ama and its radical cation, whereby the latter is produced by ionizing radiation. Microhydrated clusters of Ama⁺ are relevant to investigate the chemical reactivity of diamondoid radical cations in interstellar ice grains, in which ionizing radiation may induce photochemical reactions of organic molecules leading to molecules with higher complexity (e.g., ethers, alcohols).^37,38

Neutral Ama has a structure with C_s symmetry and consists of a primary pyramidal amino group (NH₂) attached to the adamantyl backbone (C₁₀H₁₅), which grants the molecule the special chemical properties of diamond-like structures.^26,39 The geometric, vibrational, and electronic properties of Ama have been characterized by infrared (IR), Raman, and electron momentum spectroscopy.^40–42 Moreover, the Ama⋯DNA interaction has been studied by Raman spectroscopy.⁴³ In contrast to neutral Ama, there are no studies on the Ama⁺ cation so far, with the notable exception of low-resolution electron momentum spectra yielding approximate energies for the electronic states.⁴¹ The latter study reveals that ionization of Ama into the ground electronic state of the cation occurs by removal of one electron from the nonbonding N lone pair of the amino group, with a rough estimation of the vertical ionization energy of 8.6 eV.

Herein, we analyse IR photodissociation (IRPD) spectra of size-selected Ama⁺W_n clusters with n = 1–3 generated in a molecular beam with the aid of quantum-chemical dispersion-corrected density functional theory (DFT) calculations at the B3LYP-D3/cc-pVTZ level, with the major goal of characterizing the initial steps of the microhydration process of this important diamondoid cation. This dual experimental and computational approach has been well established in our laboratory for the study of microhydrated cations,^38,44–68 and provides direct access to the interaction potential between the cation and the solvent molecules. The Ama⁺W_n cluster system has been chosen for the following reasons. (1) No spectroscopic studies are available for both Ama⁺ and any of its clusters. Hence, our Ama⁺W_n data provide a first impression of the interaction of this biological ion with neutral solvent molecules at the molecular level. The IRPD spectra recorded in the informative OH, NH, and CH stretch range serve as a very sensitive probe of the ion–ligand interaction potential with respect to both binding site and interaction strength, as well as the structure of the hydrogen-bonded (H-bonded) solvent network. In addition, the cluster data also provide information about the properties of the Ama⁺ monomer ion, such as the acidity of its N–H bonds. (2) In previous work, we characterized the structure and bonding in the bare adamantane cation (Ad⁺)³⁵ and its monohydrated cluster (Ad⁺W).³⁸ Ionization of Ad with tetrahedral symmetry (T_d) from the triply-degenerate bonding t₂ highest occupied molecular orbital (HOMO), which is delocalized over the Ad cage, results in a Jahn–Teller distorted cation with C_3v symmetry, with one very acidic C–H bond along the C₃ axis.³⁵ Formation of the CH⋯O H-bond in the Ad⁺W monohydrate activates this C–H bond even further. Thus, microhydration of cationic diamondoids can have a profound impact on their structure, IR spectrum, and chemical reactivity, and the magnitude of these effects may differ largely from that observed for related simple cationic hydrocarbons such as CH₄⁺.³⁸ As ionization of Ama into the cation ground state occurs by removal of an electron from the N lone pair and not from the adamantyl cage, H → NH₂ substitution will have a big impact on the structure of the diamondoid cation, as well as its interaction with ligands. (3) Microhydration of aromatic amine radical cations has been studied before by IRPD spectroscopy and computations, and examples relevant for the present work include aniline (AN⁺W_n)^69,70 and aminobenzonitrile (ABN⁺W_n).⁵⁵ Surprisingly, no experimental data are available for the microhydrated methylamine cation (CH₃NH₂⁺), the most simple aliphatic amine cation, so that all information relies on recent computational data for CH₃NH₂⁺W_n ≤ 5.⁷¹ Comparison of Ama⁺ with AN⁺, ABN⁺, and CH₃NH₂⁺ reveals the differences of an aromatic, aliphatic, and cycloaliphatic substituent on the acidity and intermolecular interaction of the NH protons of primary amine cations. Cationic NH₂ and NH groups of primary and secondary amines are known to form strong NH⋯O ionic H-bonds with W ligands and larger W_n clusters.^{54,55,57,69–73} A particular question to be addressed is thus the competition between the formation of the H-bonded solvent network (which is strongly favoured by nonadditive cooperative three-body interactions) and interior cation hydration with individual ligands binding by simple charge–dipole forces (suffering from noncooperative three-body forces).⁴⁴ A further issue to be addressed is the question of proton transfer to solvent. As the proton affinity of W_n clusters strongly increases with cluster size n (PA = 691, 808, 862, 900, 904, and 908 kJ mol⁻¹ for n = 1–6),^74–78 proton transfer from the NH group of the cation to the W_n solvent cluster can occur above a critical size n_c.^44,56,67,79 The critical size depends strongly on the structure of the molecule, functional groups, the charge and protonation state, and the way of generating the clusters. For example, for protonated benzaldehyde (C₇H₇O⁺W_n) proton transfer to the solvent is observed for n ≥ n_c = 3,⁵⁶ and for protonated benzonitrile at n_c = 2,⁶⁷ whereas in AN⁺W_n it occurs for n ≥ 6 or n > 12, depending on the way the clusters are generated.^69,70 Calculations for CH₃NH₂⁺W_n predict no proton transfer up to n = 5.⁷¹ Our analysis of the IRPD spectra of Ama⁺W_n provides information on the interaction strength of the NH⋯O H-bonds, the structure of the microhydration shell (H-bonded solvent network vs. interior ion solvation), and the degree of N–H bond activation by hydration.

2. Experimental and computational techniques

IRPD spectra of Ama⁺W_n with n = 1–3 are recorded in a tandem quadrupole mass spectrometer coupled to an electron ionization cluster source described elsewhere.^44,80 Briefly, the clusters are produced in a pulsed supersonic plasma expansion by electron and/or chemical ionization of Ama (Sigma Aldrich, >97%) close to the nozzle orifice and subsequent three-body clustering reactions. The expanding gas mixture is generated by passing Ar carrier gas (5 bar) through a reservoir containing solid Ama. To produce hydrated Ama⁺ clusters, distilled water is added into the gas line just before the sample reservoir. A typical mass spectrum of the ion source in the mass range m/z 115–220 is shown in the ESI† (Fig. S1). The chemical composition of the mass-selected Ama⁺W_n clusters is confirmed by collision-induced dissociation (CID) spectra (Fig. S2, ESI†), which show the exclusive loss of W ligands. The generated Ama⁺W_n parent clusters are mass selected by a first quadrupole and irradiated in an adjacent octopole with a tunable IR laser pulse (ν_IR) of an optical parametric oscillator pumped by a nanosecond Q-switched Nd:YAG laser. The IRPD spectra are recorded in the spectral range of 2700–3800 cm⁻¹ to cover the informative CH, NH, and OH stretch modes. The IR laser pulses are characterized by an energy of 2–5 mJ in the considered spectral range, a repetition rate of 10 Hz, and a bandwidth of 2 cm⁻¹. The laser frequency is calibrated to better than 1 cm⁻¹ using a wavemeter. Resonant vibrational excitation of Ama⁺W_n induces evaporation of a single W ligand. Resulting Ama⁺W_n−1 fragment ions are selected by a second quadrupole and monitored as a function of the laser frequency to obtain the IRPD spectra of Ama⁺W_n. The ion source is triggered at twice the laser frequency to allow for a separation of laser-induced Ama⁺W_n − 1 fragments from those produced by metastable decay. All IRPD spectra are normalized for frequency-dependent variations in the photon flux.

Dispersion-corrected DFT calculations are carried out at the B3LYP-D3/cc-pVTZ level for the Ama, Ama⁺, and W monomers and the Ama⁺W_n clusters to determine their structural, vibrational, and energetic properties.⁸¹ This computational approach has proven to provide reliable results for the monohydrated adamantane cation (Ad⁺W) and is an efficient compromise between computing time and accuracy.³⁸ In particular, spin contamination for the open-shell Ama⁺ radical cation is negligible at this DFT level, with values of 〈S²〉−0.75 below 0.005 and 10⁻⁴ before and after annihilation, respectively. This is in contrast to MP2/aug-cc-pVTZ calculations, with a significantly higher contamination of 〈S²〉−0.75 = 0.04 and 0.0006 before and after annihilation, respectively. All coordinates are relaxed in the search for stationary points, and their nature as minima or transition states is verified by harmonic frequency analysis. Relative energies and equilibrium dissociation energies (E_e, D_e) are corrected for harmonic zero-point vibrational energy to yield E₀ and D₀ values. If not stated otherwise, the binding energies are computed for dissociation into the relevant Ama⁺W_n − 1 fragment isomer and W. The total binding energies (D^total₀) are calculated with respect to Ama⁺ and separated W ligands (Table S1, ESI†). Free energies (G) are obtained at room temperature (T = 298.15 K, Table S1, ESI†). Cartesian coordinates and energies of all structures are available in the ESI.† Harmonic frequencies are scaled by factors of 0.9630 and 0.9491 for OH and NH/CH stretch frequencies, respectively. These factors are derived from fitting calculated harmonic OH stretch frequencies of W and CH/NH stretch frequencies of Ama to available experimental values.^42,82 Such a dual scaling factor procedure accounts for the somewhat different anharmonicities of the OH and CH/NH stretch modes. To calculate harmonic combination bands and overtones, harmonic frequencies below 2000 cm⁻¹ (fingerprint range) are scaled by a factor of 0.9672. This factor results from fitting the calculated harmonic OH and NH bending frequencies of W and Ama to experimental values.^42,82 For Ama⁺W, additional anharmonic calculations are performed.⁸¹ Computed IR stick spectra are convoluted with Gaussian line profiles (fwhm = 10 cm⁻¹). Natural bond orbital (NBO) analysis is employed to evaluate the charge distribution and charge transfer in Ama⁺W_n, as well as the second-order perturbation energies (E⁽²⁾) of donor–acceptor orbital interactions involved in the H-bonds.^83,84

3. Experimental results

A typical mass spectrum of the electron ionization source is shown in Fig. S1 (ESI†). The molecules present in the source (Ama, W, Ar) form different cluster combinations including the desired Ama⁺W_n clusters. The mass spectrum is dominated by W_nH⁺, Ama⁺ and its fragment ions, and hydrated Ama⁺W_n clusters. As mentioned above, the CID spectrum of Ama⁺W_n reveals only the loss of W ligands, which confirms the cluster composition and excludes unwanted isobaric mass contaminations. While the CID spectra reveal the loss of 1 to n W ligands, the IRPD process leads to the loss of only a single W ligand, because the relatively high hydration energies are comparable to the IR photon energy (D₀ ∼ hν_IR).

The IRPD spectra of Ama⁺W_n with n = 1–3 are compared in Fig. 1, and the observed transitions are listed in Table 1, along with their vibrational assignments. The investigated spectral range (2700–3800 cm⁻¹) covers free and bound OH stretch modes of the W ligands (A–D, ν_OH, 3400–3800 cm⁻¹), free and bound NH stretch modes of the amino group of Ama⁺ (E–H, ν_NH, 2800–3500), aliphatic CH stretch modes of the Ama⁺ cage (I and J, ν_CH, 2800–3000 cm⁻¹), and combination and overtone bands of the OH, NH, and CH₍₂₎ bend fundamentals (K and L, 2900–3300 cm⁻¹). The IRPD spectra show a clear dependence on the cluster size n and thus provide insight into the details of the hydration motif with respect to both the water binding site and the structure of the solvation network.

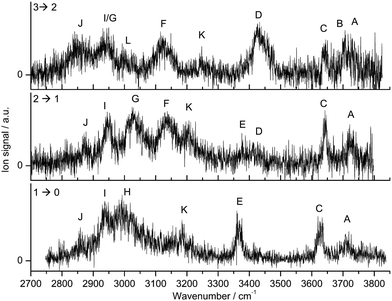Fig. 1 IRPD spectra of Ama⁺W_{n = 1–3} in the 2700–3800 cm⁻¹ range recorded in the W loss channel. The spectral range investigated covers CH, NH, and OH stretch fundamentals. The positions, widths, and assignments of the transitions observed (A–L) are listed in Table 1.

Table 1 Positions, widths (fwhm in parenthesis) and vibrational assignments of the transitions observed in the IRPD spectra of Ama⁺W_{n = 1–3} (Fig. 1)^a

Peak	Mode	Ama^+W	Ama^+W2	Ama^+W3
a All values are given in cm^−−1. b Combination or overtone band.
A	ν OH ^a	3717 (28)	3721 (24)	3730 (20)
B	ν OH ^f			3707 (12)
C	ν OH ^s	3627 (31)	3642 (17)	3644 (21)
D	ν OH ^b		3413 (30)	3426 (86)
E	ν NH ^f	3368 (27)	3376 (28)
F	ν NH ^b a		3137 (68)	3116 (97)
G	ν NH ^b s		3027 (58)	2944 (45)
H	ν NH ^b	2992 (66)
I	ν CH2	2937 (35)	2949 (37)	2944 (45)
J	ν CH	2858 (20)	2874 (29)	2840 (40)
K		3187 (20)	3206 (32)	3247 (15)
L				2993 (20)

---

The IRPD spectrum of the Ama⁺W monohydrate contains clear signatures for the predominant presence of a single H-bonded isomer, in which W binds as an acceptor in an NH⋯O ionic H-bond to one of the acidic NH groups of Ama⁺. Such a structure is expected from the strong charge–dipole forces between the Ama⁺ cation and dipolar W, which dominate the long-range part of the intermolecular attraction. The two coupled free OH stretch modes of W appear at 3717 (A, ν₃ = ν_OH^a, antisymmetric OH stretch) and 3627 cm⁻¹ (C, ν₁ = ν_OH^s, symmetric OH stretch) with a width of about 30 cm⁻¹. Their redshifts of 39 and 30 cm⁻¹ from the corresponding transitions of bare W (ν₃ = 3756 cm⁻¹, ν₁ = 3657 cm⁻¹), as well as the IR enhancement of ν₁ are typical for cation–W clusters.^{44,51,63,64,67} Only a single band appears in the spectral range of the free NH stretch modes of Ama⁺ (3300–3450 cm⁻¹), which is readily assigned to the remaining free NH group of the H-bonded Ama⁺W dimer (E, ν_NH^f, 3368 cm⁻¹). The absence of a second intense free NH stretch band implies that nearly all detected Ama⁺W isomers feature a strong NH⋯O ionic H-bond involving the amino group, which shifts the resulting bound NH stretch (ν_NH^b) down to the spectral range 2800–3100 cm⁻¹. In this range, it couples strongly with NH, OH, and CH₍₂₎ bend overtones (via anharmonic Fermi resonances) as well as CH stretch fundamentals (via local mode mixing), giving rise to a broad vibrational multi-band pattern in the IRPD spectrum. A similar complex pattern has previously been observed for a variety of monohydrated cationic dimers with a NH⋯O ionic H-bond such as formanilide, acetanilide, hydroxyindole, or pyrrole.^{54,57,60–62} As the ν_NH^b band is expected to carry the highest IR oscillator strength, it is assigned to the broad band H at 2992 cm⁻¹ with a width of 66 cm⁻¹. Its large redshift of 376 cm⁻¹ from ν_NH^f is a measure of the strength of the NH⋯O H-bond. The interpretation of the sharper bands I, J, and K at 2937, 2858, and 3187 cm⁻¹ are less obvious. By comparison with the Ad⁺W spectrum,³⁸ bands I and J are assigned to CH stretch modes, while band K is attributed to a combination or overtone band.

Most transitions in the IRPD spectrum of Ama⁺W₂ show only small changes in frequency and intensity compared to the n = 1 spectrum, with the major exception that the transitions in the free NH stretch range disappear almost completely (e.g., E), while the intense transition H in the bound NH stretch range now splits into the doublet F and G. Thus, the coarse structure of the Ama⁺W₂ spectrum demonstrates the predominant presence of an isomer, in which the two W ligands bind separately to the two NH groups of Ama⁺ leading to the formation of two equivalent NH⋯O H-bonds. In line with this interpretation, bands A and C at 3721 and 3642 cm⁻¹ are attributed to ν_OH^a and ν_OH^s of the individual uncoupled W ligands. Their redshifts from the transitions of bare W, 35 and 15 cm⁻¹, are slightly smaller than those for n = 1, because of the noncooperative (i.e., anticooperative) three-body effects typical for interior ion solvation.^44,55 Peaks F and G at 3137 and 3027 cm⁻¹ are then readily assigned to bound antisymmetric and symmetric NH stretch modes, ν_NH^b_a and ν_NH^b_s, respectively. The centre of the two bands at 3082 cm⁻¹, which is a measure for the strength of the N–H bonds, is blueshifted by 90 cm⁻¹ from ν_NH^b of n = 1 (H), confirming that the NH⋯O H-bonds in n = 2 are indeed weaker than in n = 1. Peaks J and I at 2874 and 2949 cm⁻¹ assigned to CH stretch modes are also slightly blueshifted from the corresponding n = 1 transitions, consistent with their mixing with the NH stretch modes. Band K at 3206 cm⁻¹ also has a somewhat higher frequency than in n = 1. The weak bands E and D at 3376 and 3413 cm⁻¹ are clear spectral signatures of a less abundant isomer, in which a H-bonded W₂ dimer is attached to one of the acidic NH groups of Ama⁺. This isomer has a remaining free NH stretch mode (ν_NH^f) assigned to band E, and this band is slightly blueshifted by 8 cm⁻¹ compared to that of n = 1. Band D is attributed to the bound OH stretch mode of the W₂ dimer corresponding to the OH donor in the OH⋯O H-bond (ν_OH^b). Its frequency is drastically reduced from the corresponding transition in bare W₂ (3601 cm⁻¹),⁸⁵ because of the large cooperativity of the H-bonded network, which arises from the strong polarisation forces induced by the nearby positive charge of Ama⁺. The weak intensities of bands D and E indicate that this isomer is far less abundant than the isomer in which both NH groups of Ama⁺ are solvated by a single W. As a result, the free uncoupled OH stretch of the proton donor (ν_OH^f) expected near 3700 cm⁻¹ is not visible.

The appearance of the Ama⁺W₃ spectrum is consistent with a predominant isomer, in which one NH group of Ama⁺ is solvated by W and the other one by W₂. As a result, the bands associated with the W₂ ligand become very prominent in the OH stretch range, and the characteristic bound and free OH stretch modes of the proton donor W molecule are clearly apparent at 3426 (D, ν_OH^b) and 3707 cm⁻¹ (B, ν_OH^f), while the free OH stretch modes of the acceptor occur at 3730 (A, ν_OH^a) and 3644 cm⁻¹ (C, ν_OH^s). The ν_OH^a/s modes of the single W ligand overlap with bands A and C. The fact that band E disappears completely for n = 3 implies that at this cluster size both NH bonds of the NH₂ group are fully solvated, and that isomers with a free N–H bond and one N–H bond solvated with W₃ are below the detection limit. The bound NH stretch modes are now quite decoupled, because of asymmetric solvation of the NH₂ group with W and W₂. Because W₂ has a much higher proton affinity than W (808 and 691 kJ mol⁻¹),^74,75 the NH⋯W₂ H-bond is much stronger than the NH⋯W H-bond, giving rise to a larger redshift in ν_NH^b. Thus, band F at 3116 cm⁻¹ is assigned to ν_NH^b of the NH⋯W moiety, while band G at 2944 cm⁻¹ is attributed to ν_NH^b of the NH⋯W₂ unit. Band J at 2840 cm⁻¹ is broader and redshifted compared to the n = 2 spectrum, while band I overlaps with band G. There are weaker bands L and K at 2993 and 3247 cm⁻¹, whose interpretation is again less obvious. In summary, the IRPD spectra of Ama⁺W_n with n = 1–3 can be interpreted with a predominant sequential cluster growth, in which the two acidic NH protons of the amino group of Ama⁺ are first solvated by single W ligands via NH⋯O ionic H-bonds (n = 1–2), before further W molecules are attached to the initial W ligands via the formation of an OH⋯O bonded network (n = 3). In order to identify more precise structural motifs, DFT calculations are employed in Section 4.

4. Computational results and assignments

4.1. Ama, Ama⁺, and W

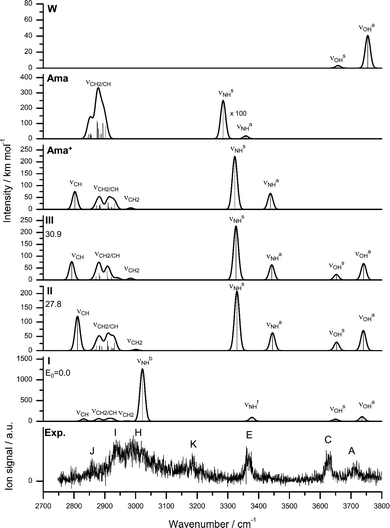
In an effort to determine the structures responsible for the IRPD spectra, quantum chemical calculations are performed at the B3LYP-D3/cc-pVTZ level. The calculated structures of the Ama, Ama⁺, and W monomers are shown in Fig. 2. The structure of Ama (C_s) in its ¹A′ ground electronic state consists of a pyramidal NH₂ group (θ_CNX = 124° with the dummy atom X located on the C₂ axis of the NH₂ group) attached to an adamantyl cage (C₁₀H₁₅), which has slightly different binding parameters compared to Ad arising from H → NH₂ substitution (Fig. S3, ESI†).^35,38 Especially the C–C bond adjacent to the NH₂ group in the C_s plane is significantly longer than in Ad (r_CC = 1.544 vs. 1.538 Å). The NH₂ group in Ama has similar binding parameters (θ_HNH = 106.4°, r_NH = 1.015 Å, r_CN = 1.467 Å) as in CH₃NH₂ (θ_HNH = 106.4°, r_NH = 1.013 Å, r_CN = 1.465 Å, Fig. S4, ESI†). The calculated structure and IR spectrum of Ama (Fig. 3) is consistent with previous computational and experimental data.^41,42,86,87 Concerning W, the O–H bond parameters in its ¹A₁ ground state (r_OH = 0.961 Å, ν_1/3 = 3658/3754 cm⁻¹) agree well with the experimental data (0.9578 Å, 3657/3756 cm⁻¹).^88,89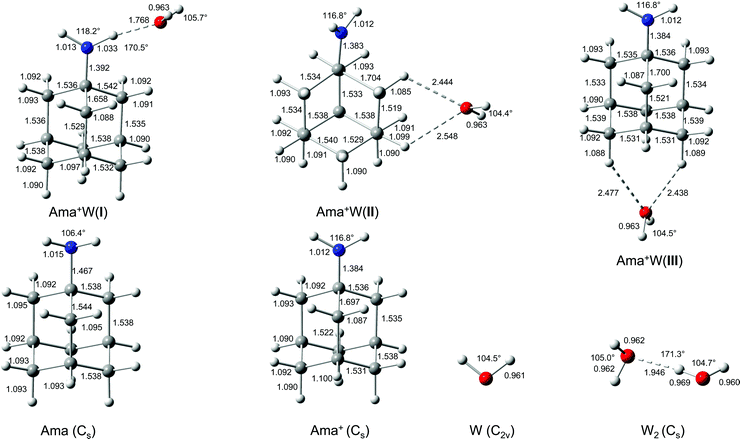

Fig. 2 Calculated equilibrium structures (in Å and degrees) of W, W₂, Ama, Ama⁺, and Ama⁺W(I–III) in their ground electronic state (B3LYP-D3/cc-pVTZ).

Fig. 3 IRPD spectrum of Ama⁺W compared to linear IR absorption spectra of W, Ama, Ama⁺, and Ama⁺W(I–III) calculated at the B3LYP-D3/cc-pVTZ level. The positions of the transition observed in the IRPD spectrum of Ama⁺W and their vibrational assignment are listed in Table 2. Differences in relative energy (ΔE₀) are given in kJ mol⁻¹ for isomers I–III.

Ionization of Ama into the ground electronic state of Ama⁺ (²A′, C_s) occurs by removal of one electron from the HOMO, which is largely described by the nonbonding a′ lone pair orbital of N, as illustrated by the orbitals of Ama⁽⁺⁾ shown in Fig. S5 (ESI†).⁴¹ As a result, the pyramidal NH₂ group becomes essentially planar upon ionization (θ_CNX = 170.7°, close to the NH₃ case with θ_HNX = 180°), with the NH₂ plane being perpendicular to the symmetry plane. As a result, the NH₂ angle opens up from 106 to 117°. Due to the increasing conjugation of the nitrogen lone pair orbital, the bond order of the C–N bond increases substantially from 1 to ∼1.5, as illustrated by the massive bond contraction of 83 mÅ. Ionization increases the charge on the NH₂ group by Δq = 474 me, which is substantially smaller than in the related CH₃NH₂⁽⁺⁾ molecule, because of enhanced charge delocalization into the adamantyl cage (Fig. S6, ESI†). Nonetheless, q_NH2 = 313 me remains on the NH₂ group in Ama⁺ (as compared to 597 me in CH₃NH₂⁺), making this binding site highly attractive for the W ligands. Ionization slightly contracts the N–H bonds by 3 mÅ, leading to significantly higher frequencies (∼40/80 cm⁻¹) for the free symmetric and antisymmetric NH stretch normal modes (ν_NH^s = 3322 vs. 3285 cm⁻¹ and ν_NH^a = 3438 vs. 3358 cm⁻¹, Fig. 3 and Table 2). Ionization also increases the positive charge of the NH protons to q_H = 405 me, which drastically enhances the IR intensity of the NH stretch modes (by two orders of magnitude). Because the charge on the NH protons is much higher than on all CH protons (206–232 me), the resulting rather acidic N–H bonds are excellent H-bond donors for NH⋯O ionic H-bonds with W. Most of the C–C bonds of the Ama cage remain nearly unchanged. The notable exception is the C–C bond adjacent to the C–N bond denoted C–C^ext (which elongates by 153 mÅ), because it lies in the symmetry plane and thus can conjugate with the in-plane lone pair of N. The next adjacent C–C^adj bond in the C_s plane shortens by a smaller amount (16 mÅ) because of the increased distance from the N lone pair, thus damping the conjugation effects. Ionization increases the variation of the C–H bond lengths drastically from 1.092–1.095 Å (Δr_CH = 3 mÅ) in Ama to 1.087–1.100 Å in Ama⁺ (Δr_CH = 13 mÅ). As a result, the single broad and unresolved intense convoluted band of the coupled ν_CH(2) stretch vibrations in the computed IR spectrum of Ama splits for Ama⁺ into four better resolved and more widely spread bands, including one intense peak of the isolated ν_CH mode at 2803 cm⁻¹, two broader peaks of ν_CH/CH2 modes at 2882 and 2914 cm⁻¹, and one weak peak of the isolated ν_CH2 mode at 2984 cm⁻¹ (Table 2). The isolated low and high frequency transitions result from the long and short C–H bonds at the C atoms in the symmetry plane of Ama⁺, where the HOMO is concentrated. The adiabatic computed ionization energy of 7.95 eV corresponds well with the measured vertical value of 8.6 eV, derived from low-resolution electron momentum spectra.⁴¹

Table 2 Computed vibrational frequencies (in cm⁻¹, B3LYP-D3/cc-pVTZ) of Ama, Ama⁺, W, and Ama⁺W(I) compared to experimental values of Ama⁺W (Fig. 3)^a

Mode	Ama	Ama^+	W	Ama^+W(I)	Ama^+W exp.
a IR intensities in km mol^−1 are given in parentheses. The computational data for isomers II and III are available in Table S2 (ESI). The experimental frequencies with width (fwhm in parenthesis) are assigned to the most dominant vibrations. b Harmonic value. c Result of anharmonic calculation.
ν CH	2845 (13)	2803 (76)		2831 (59)	J 2858 (20)
ν CH2	2848 (30)	2870 (4)		2869 (11)
ν CH2	2853 (39)	2874 (16)		2879 (12)
ν CH2	2854 (29)	2882 (16)		2881 (14)
ν CH2	2855 (18)	2884 (20)		2882 (22)
ν CH2	2856 (25)	2887 (10)		2884 (14)
ν CH2/νCH	2875 (119)	2910 (5)		2906 (23)
ν CH2/νCH	2876 (105)	2911 (28)		2909 (14)
ν CH2/νCH	2880 (66)	2912 (1)		2911 (14)
ν CH2/νCH	2884 (26)	2913 (10)		2915 (7)
ν CH2	2888 (12)	2922 (6)		2919 (5)
ν CH2	2889 (33)	2922 (11)		2922 (7)
ν CH2	2894 (102)	2927 (4)		2923 (12)
ν CH2	2898 (5)	2932 (27)		2927 (36)	I 2937 (35)
ν CH2	2903 (80)	2984 (7)		2973 (7)
ν NH ^b				3022 (1267)	H 2992 (66)
2βCH2				2960^b	I 2937 (35)
				2940 (12)^c
β NH + βOH				3187^b	K 3187 (20)
				3167 (136)^c
ν NH ^f				3378 (95)	E 3368 (27)
ν NH ^s	3285 (3)	3322 (223)
ν NH ^a	3358 (0.2)	3438 (67)
ν OH ^s			3658 (3)	3650 (51)	C 3627 (31)
ν OH ^a			3754 (40)	3736 (110)	A 3717 (28)

---

4.2. Ama⁺W

The Ama⁺ cation offers three main attractive binding sites for dipolar W, which can be attached either to the NH₂ group (isomer I) or to the side (II) or bottom (III) of the Ama⁺ cage (Fig. 2 and Table S1, ESI†). The computed IR spectra of all Ama⁺W isomers are compared in Fig. 3 to the experimental IRPD spectrum and to those calculated for Ama, Ama⁺, and W. The position and widths of the transitions observed in the IRPD spectrum of Ama⁺W are listed in Table 2, along with their vibrational assignments. While W forms in the most stable isomer I a strong NH⋯O ionic H-bond to the NH₂ group (E₀ = 0), it is attached in II and III to the Ama⁺ cage by substantially weaker charge–dipole forces resulting in much higher relative energies (E₀ = 27.8 and 30.9 kJ mol⁻¹). All structures have a favourable charge–dipole configuration, with the electronegative O atom of W pointing toward the Ama⁺ cation. Due to the low ionization energy of Ama and the higher proton affinity of the amantandinyl radical as compared to W (IE = 7.95 vs. 12.6 eV, PA = 960 vs. 691 kJ mol⁻¹)^42,74 neither charge nor proton transfer occurs upon monohydration.

In the Ama⁺W(I) global minimum, W forms a strong and nearly linear NH⋯O H-bond (170.5°) to the NH₂ group, with a bond length of 1.768 Å and a high binding energy of D₀ = 61.4 kJ mol⁻¹ (Fig. 2). The barrier for internal W rotation around its C₂ rotational axis is relatively high (V_b = 3.28 kJ mol⁻¹ or 274 cm⁻¹) and the pyramidal angle of the amino group is nearly unchanged from that in bare Ama⁺ (θ_CNX = 170.1°). Upon monohydration, the N–H bond is stretched by 21 mÅ and the NH₂ bond angle increases by 1.4° to 118.2°. As a result, its bound NH stretch frequency shifts down to ν_NH^b = 3022 cm⁻¹ along with a drastic enhancement in IR intensity (by a factor 6), as is typical for RNH₂⁺-W dimers.⁵⁵ The redshift of 358 cm⁻¹ from the average NH stretch frequency of Ama⁺ (ν_NH^av = 3380 cm⁻¹) is a direct measure of the strength of the H-bond. The remaining free N–H bond does not change its strength (≤1 mÅ) resulting in a less intense ν_NH^f mode at 3378 cm⁻¹, essentially unshifted from ν_NH^av (Δν_NH = 2 cm⁻¹). The NBO charge analysis shows that formation of the H-bond involves a charge transfer of 38 me from Ama⁺ to W and a second order perturbative energy of E⁽²⁾ = 33.9 kJ mol⁻¹ for the donor–acceptor interaction between the lone pairs of O and the antibonding σ* orbital of the N–H donor bond. As a result, the O–H bonds of W elongate by 2 mÅ and the W bond angle increases by 1.2°. Further, the free OH stretch modes ν_OH^s and ν_OH^a experience redshifts of 8 and 18 cm⁻¹ and a substantial IR intensity enhancement (factor 17 and 3). These effects are typical for the formation of cation–W clusters.⁴⁴ Apart from the NH₂ group, monohydration has also a certain impact on the structure of the Ama⁺ cage. Because of partial charge transfer from Ama⁺ to W, the molecule gets more neutral again, and as a result the structural effects upon ionization of Ama are somewhat reduced. For example, the strongly contracted C–N bond upon ionization is slightly elongated again by 8 mÅ upon hydration, the C–C^ext bond contracts by 39 mÅ, and the C–C^adj bond elongates by 7 mÅ. As a result, the low-frequency ν_CH mode is blueshifted by 28 cm⁻¹ to 2831 cm⁻¹, while the remaining CH and CH₂ stretch frequencies do not change much (Fig. 3).

There is a large energy gap of ∼30 kJ mol⁻¹ between the global minimum I and the next two local minima II and III. Due to their high relative energy, they are not observed experimentally and we do not discuss them in detail here. Briefly, W binds in II and IIIvia CH⋯O contacts to two CH₂ groups of Ama⁺ with low binding energies of D₀ = 33.6 and 30.6 kJ mol⁻¹, respectively. The Ama⁺⋯W bonds in II and III are essentially based on electrostatic charge–dipole forces with long intermolecular distances of more than 2.4 Å. Because of the strongly nonlinear CH⋯O contacts, there is little contribution from H-bonding. As a result, charge transfer is minor (Δq < 9 me) and E⁽²⁾ ≤ 2 kJ mol⁻¹. Due to this weak intermolecular bonding, complex formation in II and III has much less impact on the structures of both monomer units than for I. Consequently, the resulting IR spectra are essentially an addition of those of W and Ama⁺ in the considered spectral range, with characteristic intense free NH stretch bands at ∼3330 and ∼3440 cm⁻¹ (Fig. 3 and Table S2, ESI†).

The comparison of the measured IRPD spectrum of Ama⁺W with the linear IR spectra computed for isomers I–III in Fig. 3 immediately demonstrates the predominant abundance of the most stable structure I, because of the observation of only a single free intense NH stretch band between 3300 and 3450 cm⁻¹. Based on the achieved signal-to-noise ratio and the computed oscillator strengths, the absence of the two bands of the free and fully coupled intense NH stretch modes of the unperturbed NH₂ group of II and III near ∼3330 and ∼3440 cm⁻¹ provides an estimate of the upper limit of their abundance as ∼15%. Thus, the whole observed spectrum is fully attributed to isomer I whose computed spectrum agrees well with the measured one. Specifically, bands E and H at 3368 and 2992 cm⁻¹ are readily assigned to the free and bonded NH stretch bands predicted at ν_NH^f = 3378 cm⁻¹ and ν_NH^b = 3022 cm⁻¹. Both frequencies are close to those found for the related ABN⁺W dimer at 3433 and 3040 cm⁻¹, a complex with a similar NH⋯O H-bond between a cationic amine and W.⁵⁵ Moreover, due to the larger redshifts of the free OH stretch frequencies of isomer I, the observed bands C and A at 3627 and 3717 cm⁻¹ agree better with those predicted for I (3650 and 3736 cm⁻¹) than for II and III. Peak J (2858 cm⁻¹) and I (2937 cm⁻¹) are attributed to the ν_CH/CH2 modes of the adamantyl cage, and these agree indeed well with the corresponding bands measured for Ad⁺ (2868/2875 and 2954/2942 cm⁻¹).^35,38 While J is assigned to the intense ν_CH mode predicted at 2831 cm⁻¹, peak I is associated with several overlapping CH₂ modes. If only the most intense CH₂ mode (2927 cm⁻¹, I = 36 km mol⁻¹) is taken into account, the deviation is only 10 cm⁻¹. The high intensity of peak I cannot be explained by a fundamental mode of isomer I and is probably enhanced from signal of the intense band H (ν_NH^b). Possibly, an overtone of a CH₂ bending mode at 1480 cm⁻¹ (anharmonic: 2β_CH = 2940 cm⁻¹) may gain intensity by a Fermi resonance with the strongly IR active ν_NH^b mode at 3022 cm⁻¹ and thus contribute further to the intensity of band I. The isolated peak K at 3187 cm⁻¹ can also not be explained by a fundamental transition of isomer I but may be associated with a combination band β_NH + β_OH at 3187 cm⁻¹ of the symmetric (1578 cm⁻¹) and antisymmetric (1609 cm⁻¹) coupled OH and NH bending modes. The anharmonic vibrational calculation of the IR spectrum of Ama⁺W(I) supports such a scenario and predicts the combination band β_NH + β_OH at 3167 cm⁻¹ with high intensity (I = 136 km mol⁻¹).

4.3. Ama⁺W₂

The IRPD spectrum of Ama⁺W₂ detailed in Fig. 1 (Table 1) shows only very weak activity in the free NH stretch range, providing a strong indication that both NH donors of the NH₂ group of Ama⁺ are hydrated in the predominant isomer. The weak band E near 3350 cm⁻¹ (ν_NH^f) may be taken as evidence for minor isomers in which only one of the N–H bonds is solvated. The absence of any signal in the range of ν_NH^s and ν_NH^a near 3350 and 3450 cm⁻¹ suggests that the population of isomers with a completely free NH₂ group is below the detection limit. Consequently, we investigated computationally only isomers in which one or both NH groups are hydrated. Indeed, based on the Ama⁺W dimer potential, such isomers are expected to be by far lowest in energy. The structures of the five isomers found are shown in Fig. 4 and Table S1, ESI.† Their calculated IR spectra are compared in Fig. 5 to the IRPD spectrum of Ama⁺W₂ and the IR spectra computed for Ama⁺, W, and W₂ (Table 3 and Table S3, ESI†).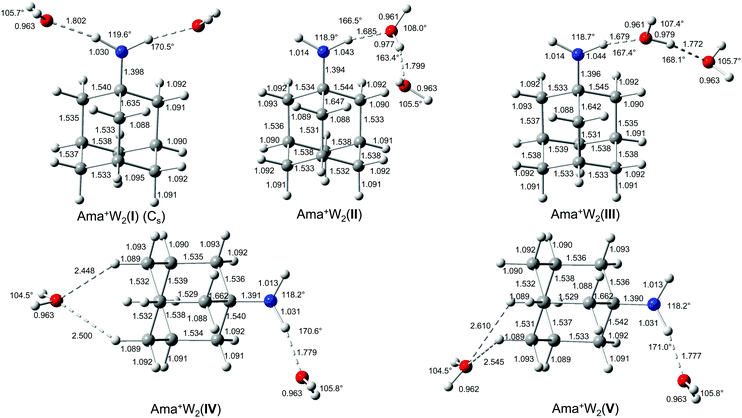

Fig. 4 Calculated equilibrium structures (in Å and degrees) of Ama⁺W₂(I–V) in their ground electronic state (B3LYP-D3/cc-pVTZ).

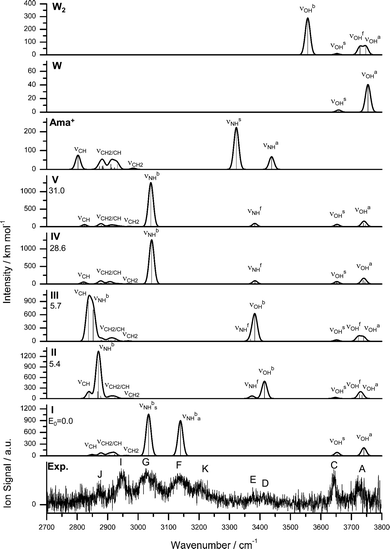Fig. 5 IRPD spectrum of Ama⁺W₂ compared to linear IR absorption spectra of Ama⁺, W, W₂, and Ama⁺W₂(I–V) calculated at the B3LYP-D3/cc-pVTZ level. The positions of the transition observed in the IRPD spectrum of Ama⁺W₂ and their vibrational assignment are listed in Table 3. Differences in relative energy (ΔE₀) are given in kJ mol⁻¹ for isomers I–V.

Table 3 Computed vibrational frequencies (in cm⁻¹, B3LYP-D3/cc-pVTZ) of Ama⁺, W₂, and Ama⁺W₂(I–III) compared to experimental values of Ama⁺W₂ (Fig. 5)^a

Mode	Ama^+	W2	Ama^+W2(I)	Ama^+W2(II)	Ama^+W2(III)	Ama^+W2 exp.
a IR intensities in km mol^−1 are given in parentheses. The experimental frequencies with width (fwhm in parenthesis) are assigned to the most dominant vibrations. The computational data for isomers IV and V are available in Table S3 (ESI).
ν CH	2803 (76)		2849 (36)	2839 (201)	2837 (896)	J 2874 (29)
ν CH2	2870 (4)		2876 (0.4)	2868 (199)	2868 (15)	J 2874 (29)
ν CH2	2874 (16)		2876 (17)	2877 (75)	2878 (14)
ν CH2	2882 (16)		2877 (27)	2879 (13)	2879 (33)
ν CH2	2884 (20)		2880 (25)	2881 (16)	2882 (16)
ν CH2	2887 (10)		2881 (9)	2887 (7)	2885 (8)
ν CH2/νCH	2910 (5)		2904 (39)	2904 (28)	2903 (27)
ν CH2/νCH	2911 (28)		2907 (23)	2909 (10)	2909 (12)
ν CH2/νCH	2912 (1)		2909 (1)	2911 (16)	2911 (23)
ν CH2/νCH	2913 (10)		2915 (3)	2912 (10)	2912 (7)
ν CH2	2922 (6)		2917 (0.03)	2918 (7)	2917 (10)
ν CH2	2922 (11)		2919 (12)	2919 (7)	2919 (5)
ν CH2	2927 (4)		2921 (24)	2924 (40)	2924 (39)
ν CH2	2932 (27)		2923 (46)	2933 (15)	2935 (8)	I 2949 (37)
ν CH2	2984 (7)		2962 (12)	2970 (4)	2967 (10)
2βCH2			2958			I 2949 (37)
ν NH ^b				2870 (1094)	2853 (711)	J 2874 (29)
ν NH ^b s			3034 (1065)			G 3027 (58)
ν NH ^b a			3139 (901)			F 3137 (68)
β NH + βOH			3191			K 3206 (32)
ν NH ^f				3374 (75)	3369 (51)	E 3376 (28)
ν NH ^s	3322 (223)
ν NH ^a	3438 (67)
ν OH ^b		3557 (290)		3415 (494)	3383 (612)	D 3413 (30)
ν OH ^s		3653 (10)	3652 (48)	3647 (33)	3651 (33)	C 3642 (17)
ν OH ^s			3653 (41)			C 3642 (17)
ν OH ^f		3728 (65)		3727 (124)	3722 (111)	A 3721 (24)
ν OH ^a		3747 (68)	3741 (5)	3735 (100)	3740 (100)	A 3721 (24)
ν OH ^a			3741 (201)			A 3721 (24)

---

In the Ama⁺W₂(I) global minimum structure with C_s symmetry, both N–H bonds of the NH₂ group are symmetrically monohydrated by a single W ligand in form of nearly linear NH⋯O ionic H-bonds (170.5°). Due to noncooperative effects typical for internal ion solvation, the binding energy of D₀ = 56.9 kJ mol⁻¹ is slightly lower (by 7.3%) than that of the corresponding Ama⁺W(I) dimer (D₀ = 61.4 kJ mol⁻¹). As a result, the H-bond is slightly longer (1.802 vs. 1.768 Å) and described by a lower orbital interaction energy (E⁽²⁾ = 29.4 vs. 33.9 kJ mol⁻¹) and smaller charge transfer (34 vs. 38 me, Fig. S7, ESI†). Consequently, the intramolecular N–H bonds in n = 2 are less stretched than in n = 1 (1.030 vs. 1.033 Å) and the NH₂ angle increases further (119.6° vs. 118.2°). The pyramidal character of the amino group is not much affected (θ_CNX = 171.1°). Due to symmetric water solvation of both N–H bonds, both NH stretch frequencies shift down to 3034 (ν_NH^b_s) and 3139 cm⁻¹ (ν_NH^b_a) along with a strong increase in IR intensity. Their centre frequency (3137 cm⁻¹) is somewhat higher than ν_NH^b in n = 1 (3022 cm⁻¹) due to the weaker NH⋯O H-bonds in n = 2. Just as with Ama⁺W(I), the O–H bonds in W are elongated by 2 mÅ and the W bond angle is increased by 1.2°. This effect shifts the ν_OH^s and ν_OH^a modes to 3653 and 3741 cm⁻¹ along with an increase in IR intensity. Upon addition of two W molecules to Ama⁺, the C–N bond becomes further elongated (1.398 Å), while the C–C^ext bond contracts further (1.635 Å). These two geometry effects are amplified by the second W ligand.

In the slightly less stable isomers II and III of Ama⁺W₂ (E₀ = 5.4 and 5.7 kJ mol⁻¹), a H-bonded W₂ dimer is attached to the NH₂ group via a NH⋯O ionic H-bond. These isomers correspond to the formation of a H-bonded solvent network, which is strongly cooperative in nature. The orientation of the W₂ unit differs slightly in the two isomers, because they are stabilized by weak secondary CH⋯O contacts involving two different CH₂ groups adjacent to the CNH₂ moiety (2.579 and 2.626 Å for II and III). Because the proton affinity of W₂ is much larger than for W (808 vs. 691 kJ mol⁻¹),^74,75 the NH⋯W₂ H-bonds in II and III are much stronger and shorter than the NH⋯W H-bonds in isomer I of n = 1 (and also n = 2), with R = 1.685/1.679 (II/III) vs. 1.768 Å, respectively. As a result, charge transfer to the solvent is increased from 38 to 57/60 me, while E⁽²⁾ increases from 33.9 to 46.8/51.8 kJ mol⁻¹. Due to the stronger H-bond, the bound N–H bond elongates from 1.033 to 1.043/1.044 Å, which shifts its ν_NH^b frequency from 3022 cm⁻¹ further down to 2870/2853 cm⁻¹. In case of III, this leads to strong mode mixing with the CH stretch mode at 2837 cm⁻¹, which thus gains substantial IR activity from the NH stretch mode. The free N–H bond of II and III elongates only slightly by the addition of the second W ligand (by 1 mÅ), leading to a small decrease in ν_NH^f (by 4 and 9 cm⁻¹). The presence of the nearby Ama⁺ charge causes, via strongly cooperative three-body polarization forces, the OH⋯O H-bond in the W₂ unit in II and III to be much stronger and shorter than in bare W₂ (1.799/1.772 Å vs. 1.946 Å). The binding energy of the terminal W ligand of D₀ = 51.6/51.3 kJ mol⁻¹ exceeds by far the one in bare neutral W₂ (19.7 kJ mol⁻¹) and reaches almost the strength of the NH⋯O ionic bonds in isomer I (56.9 kJ mol⁻¹). The large cooperativity in total binding energy amounts to 11% for II/III, and makes these isomers energetically competitive with I. The OH⋯O H-bond in III is somewhat stronger and more linear (168.1 vs. 163.4°) than in II, with a larger redshift in the bound OH stretch frequency from bare W₂ (ν_OH^b = 3383/3415 vs. 3557 cm⁻¹), which places this band with high intensity into the vicinity of the free NH stretch bands of Ama⁺. These frequencies are in line with the bond lengths of the O–H proton donor bond (0.979/0.977 vs. 0.969 Å). The corresponding free O–H bond remains largely unchanged and produces an uncoupled ν_OH^f band at 3727/3722 cm⁻¹, while the ν_OH^s and ν_OH^a bands of the terminal W acceptor ligands are predicted at 3647/3651 and 3735/3740 cm⁻¹. The C–N bonds (1.394 Å, 1.396 Å) are shorter and the extended C–C^ext bonds (1.647 Å, 1.642 Å) are longer compared to Ama⁺W₂(I), which however has no big influence on the CH₂ frequencies.

There is a large energy gap of 23 kJ mol⁻¹ between III and the higher energy Ama⁺W₂ isomers IV and V at E₀ = 28.6 and 31.0 kJ mol⁻¹, so that we do not discuss them in detail. Briefly, both isomers have one W attached to the NH₂ group (D₀ = 59.2 and 56.8 kJ mol⁻¹ for IV and V) and one to the CH₂ groups on the opposite side of the Ama⁺ cage (D₀ = 28.4 and 25.9 kJ mol⁻¹). They result essentially by an addition of isomers I + II and I + III of the n = 1 cluster. Because the two W ligands do not interact much, their intermolecular bonding and resulting IR spectra in the NH and OH stretch range are similar to that of isomer I of n = 1.

Comparison of the IRPD spectrum of Ama⁺W₂ to the calculated spectra in Fig. 5 demonstrates good agreement with that of the most stable isomer I with respect to both band positions and intensities. The lack of strong signals in the free NH stretch range (3300–3500 cm⁻¹) provides strong evidence that in the predominantly observed isomer both N–H bonds of Ama⁺ are solvated, which exclusively occurs in I. The resulting two bound NH stretch bands ν_NH^b_s and ν_NH^b_a of the two equivalent NH⋯O H-bonds are assigned to the intense bands G (3027 cm⁻¹) and F (3137 cm⁻¹), with deviations of only 7 and 2 cm⁻¹ from the predicted values. These transitions are also consistent with ν_NH^b_s (3073 cm⁻¹) and ν_NH^b_a (3195 cm⁻¹) of ABN⁺W₂.⁵⁵ The bands C and A at 3642 and 3721 cm⁻¹ are then attributed to the free OH stretch modes ν_OH^s and ν_OH^a with deviations of 10 and 20 cm⁻¹, which is acceptable concerning the widths of the transitions (17 and 24 cm⁻¹). Peak J (2874 cm⁻¹) can again be assigned to the lowest CH stretch mode predicted at 2849 cm⁻¹, and its observed blueshift of 16 cm⁻¹ by hydration with the second W is well reproduced by the calculated shift (18 cm⁻¹). Band I is again composed of overlapping unresolved CH and CH₂ stretching modes. When considering the most intense mode (2923 cm⁻¹, 46 km mol⁻¹), the deviation is merely 26 cm⁻¹. It is also possible that again an overtone of a CH₂ bending mode predicted at 2958 cm⁻¹ may add to the intensity via Fermi resonance with the ν_NH^b_s mode. Like for n = 1, band K cannot be explained by any fundamental mode of Ama⁺W₂(I) and any other Ama⁺W₂ isomer but can again be attributed to a combination band β_NH + β_OH at 3191 cm⁻¹ of the symmetric (1577 cm⁻¹) and antisymmetric (1614 cm⁻¹) coupled bending OH and NH modes.

The remaining weak but clearly discernible bands D and E at 3413 and 3376 cm⁻¹ occur in the free NH stretch and/or bound OH stretch range can clearly not be attributed to a fundamental mode of isomer I. Hence, they are taken as spectroscopic signature for the presence of the low-energy local minima II and III. While bands D and E perfectly match ν_OH^b (3415 cm⁻¹) and ν_NH^f (3374 cm⁻¹) of II, with deviations of less than 3 cm⁻¹, their relative intensities suggest an additional overlapping contribution of ν_NH^f/ν_OH^b of III (3369/3383 cm⁻¹) to band E. The calculated free OH stretch modes of II and III (ν_OH^s, ν_OH^f, ν_OH^a) also match with peaks C and A. The bound ν_NH^b modes of II/III are strongly shifted into the CH stretch range (2870 and 2853 cm⁻¹) and can possibly be assigned to peak J with a deviation of only 4 cm⁻¹ and unstructured signal between 2800 and 2850 cm⁻¹. The population of II and III may roughly be estimated as <20% and <10% of I by considering the achieved signal-to-noise ratio and the computed and observed IR intensities of peaks D, F, and the background in the 2800–2850 cm⁻¹ range. While the higher energy isomers IV and V cannot readily be excluded spectroscopically, a significant population may be excluded by their rather low stability (E₀ > 30 kJ mol⁻¹).

4.4. Ama⁺W₃

Increasing the number of W ligands to three leads to the nine possible isomers I–IX for Ama⁺W₃ generated from the low energy isomers of n = 2 (Table S1, ESI†). The most important structures (I–VI) are shown in Fig. 6 and the remaining ones (VII–IX) are available in Fig. S8 (ESI†). Their computed IR spectra are compared in Fig. 7 to the experimental IRPD spectrum (Table 4 and Fig. S4, ESI†). The position of the transitions observed in the IRPD spectrum of Ama⁺W₃ and their vibrational assignment are listed in Table 4. Because of the many isomers, we will not discuss their structures and properties in detail. The cooperative and noncooperative three-body effects resulting from the formation of a solvent network and interior ion solvation, respectively, are discussed for n = 2. Their impact on structure, energy, charge transfer, orbital interactions, and the IR spectrum of the n = 3 isomers are consistent with these three-body interactions.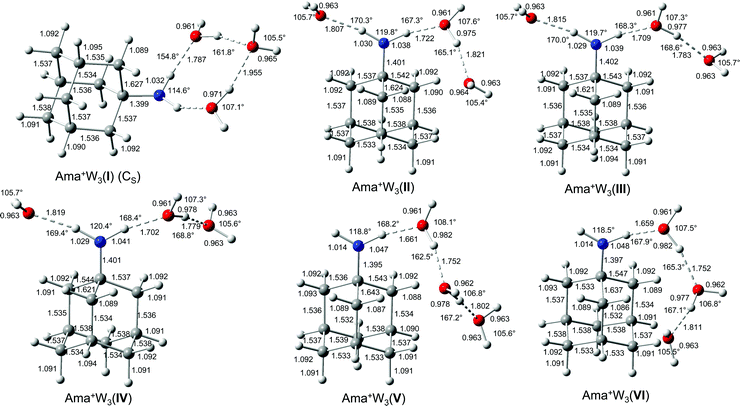

Fig. 6 Calculated equilibrium structures (in Å and degrees) of Ama⁺W₃(I–VI) in their ground electronic state (B3LYP-D3/cc-pVTZ). The structures of isomers VII–IX are shown in Fig. S8 (ESI†).

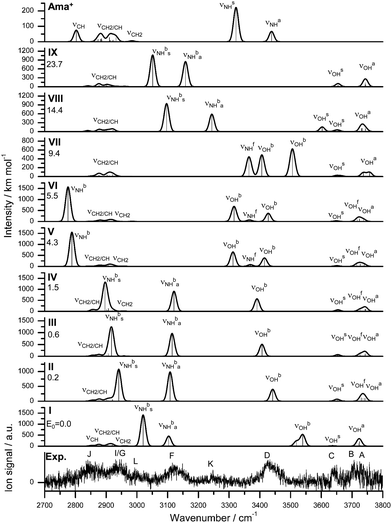Fig. 7 IRPD spectrum of Ama⁺W₃ compared to linear IR absorption spectra of Ama⁺ and Ama⁺W₃(I–IX) calculated at the B3LYP-D3/cc-pVTZ level. The positions of the transition observed in the IRPD spectrum of Ama⁺W₂ and their vibrational assignment are listed in Table 4. Differences in relative energy (ΔE₀) are given in kJ mol⁻¹.

Table 4 Computed vibrational frequencies (in cm⁻¹, B3LYP-D3/cc-pVTZ) of Ama⁺W₃(II-IV, VIII) compared to experimental values of Ama⁺W₃ (Fig. 7)^a

Mode	Ama^+	Ama^+W3(II)	Ama^+W3(III)	Ama^+W3(IV)	Ama^+W3(VIII)	Ama^+W3 exp.
a IR intensities in km mol^−1 are given in parentheses. The computational data for the other isomers are available in Table S4 (ESI). The experimental frequencies with width (fwhm in parenthesis) are assigned to the most dominant vibrations.
ν CH	2803 (76)	2855 (36)	2856 (49)	2856 (84)	2840 (35)	J 2840 (40)
ν CH2	2870 (4)	2875 (14)	2875 (16)	2874 (19)	2872 (4)
ν CH2	2874 (16)	2876 (11)	2875 (20)	2876 (21)	2875 (18)
ν CH2	2882 (16)	2876 (27)	2876 (16)	2878 (6)	2877 (21)
ν CH2	2884 (20)	2880 (21)	2879 (19)	2880 (21)	2878 (20)
ν CH2	2887 (10)	2885 (8)	2883 (11)	2883 (4)	2883 (22)
ν CH2/νCH	2910 (5)	2902 (43)	2901 (39)	2901 (91)	2900 (36)
ν CH2/νCH	2911 (28)	2906 (25)	2905 (23)	2904 (34)	2906 (26)
ν CH2/νCH	2912 (1)	2909 (15)	2907 (113)	2907 (128)	2914 (8)
ν CH2/νCH	2913 (10)	2912 (5)	2912 (8)	2913 (7)	2917 (6)
ν CH2	2922 (6)	2915 (4)	2915 (9)	2916 (3)	2918 (5)
ν CH2	2922 (11)	2918 (20)	2919 (14)	2920 (39)	2922 (31)
ν CH2	2927 (4)	2921 (56)	2920 (21)	2922 (16)	2923 (42)	I 2944 (45)
ν CH2	2932 (27)	2930 (13)	2931 (11)	2925 (20)	2932 (1)
ν CH2	2984 (7)	2964 (6)	2958 (13)	2957 (15)	2990 (3)
ν NH ^b s		2941 (1072)	2917 (1137)	2896 (1172)	3097 (949)	G 2944 (45)
						L 2993 (20)
νNH^bs					3097 (949)	F 3116 (97)
ν NH ^b a		3108 (989)	3114 (967)	3121 (914)		F 3116 (97)
ν NH ^b a					3244 (588)	K 3247 (15)
β NH + βOH		3193				K 3247 (15)
ν NH ^s	3322 (223)
ν NH ^a	3438 (67)
ν OH ^b		3442 (404)	3407 (510)	3391 (571)		D 3426 (86)
ν OH ^s					3603 (157)
ν OH ^s		3648 (32)	3653 (33)	3654 (46)	3645 (27)	C 3644 (21)
ν OH ^s		3654 (42)	3654 (40)	3654 (24)	3655 (43)	C 3644 (21)
ν OH ^f		3730 (114)	3726 (104)	3726 (100)		B 3707 (12)
ν OH ^a		3735 (95)	3742 (90)	3742 (97)	3731 (105)	A 3730 (20)
ν OH ^a		3742 (102)	3743 (108)	3743 (99)	3732 (113)	A 3730 (20)
ν OH ^a					3744 (102)	A 3730 (20)

---

In the global minimum I with C_s symmetry, the W ligands form a cyclic ring involving the NH₂ group via four H-bonds, leading to a total binding energy of D^total₀ = 167.6 kJ mol⁻¹, accompanied by a charge transfer of 78 me from Ama⁺ to W₃ (Fig. S9, ESI†). Two W ligands act as single-donor single-acceptor molecules in NH⋯O and OH⋯O H-bonds, while the bridging terminal W ligand closes the ring as double-acceptor ligand in OH⋯O H-bonds. To close the solvation ring, the NH⋯O and OH⋯O H-bonds have to be quite nonlinear and the two single-donor single-acceptor ligands have to rotate into the plane of the NH₂ group. Thus, although this isomer has four intermolecular H-bonds, the steric strain makes it only slightly more stable than the next isomers II–IV by 0.2 to 1.5 kJ mol⁻¹, although the latter isomers have only three H-bonds. The low binding energy of the outer W, D₀ = 49.3 kJ mol⁻¹, is consistent with the long OH⋯O H-bonds (1.955 Å). These correlate with relatively high bound OH stretch frequencies of ν_OH^b = 3519 and 3539 cm⁻¹, which makes them a characteristic IR fingerprint of this cyclic isomer (Fig. 7). In the only slightly less stable isomers II–IV with E₀ = 0.2, 0.6, and 1.5 kJ mol⁻¹ (D^total₀ = 166.1–167.4 kJ mol⁻¹), the two N–H bonds of the NH₂ group are solvated by W and W₂ leading to a weaker NH⋯W and stronger NH⋯W₂ ionic H-bond. They differ mainly in the orientation and binding parameters of the W₂ unit (r_OH = 0.975–0.978 Å, R_OH⋯O = 1.783–1.821 Å), which leads to somewhat different frequencies of their ν_OH^b modes (3442, 3407, 3391 cm⁻¹, Fig. 7). Moreover, they differ slightly in their N–H bond lengths (1.030/1.038, 1.029/1.039, 1.029/1.041 Å), which results in different ν_NH^b frequencies. The frequencies of ν_NH^b_a (NH⋯W) occur in a narrow range between 3108 and 3121 cm⁻¹, while ν_NH^b_s (NH⋯W₂) varies more strongly between 2941 and 2896 cm⁻¹. Overall, the binding energies of the terminal W ligand (D₀ = 47.7, 48.6, 49.0 kJ mol⁻¹) and the total charge transfer from Ama⁺ to the solvent are quite similar (81, 86 and 87 me, Fig. S9, ESI†).

In isomers V–VII of Ama⁺W₃ with E₀ = 4.3, 5.5, and 9.4 kJ mol⁻¹ (D^total₀ = 163.3, 162.2, 158.3 kJ mol⁻¹), a W trimer is attached to the NH₂ group via a NH⋯O H-bond in either a linear (V/VI) or branched (VII) fashion, while the other N–H bond remains free. Isomers V and VI differ only slightly in the orientation of the W₃ chain, mainly by different ways to optimize the weak CH⋯O contacts (five between 2.5 and 3.0 Å), and thus have similar bonding parameters and IR spectra. Hence, we will discuss only V in more detail. The linear W₃ chain has two OH⋯O H-bonds (1.752 and 1.802 Å), resulting in two intense ν_OH^b modes at 3313 and 3415 cm⁻¹. The terminal W ligand has a lower binding energy of D₀ = 50.3 kJ mol⁻¹ and the total charge transfer (70 me) to the solvent is lower than for II–IV. The rather short and strong NH⋯O H-bond (1.661 Å) results from the high proton affinity of W₃ (862 kJ mol⁻¹)⁷⁸ and produces a strongly redshifted ν_NH^b band at 2789 cm⁻¹ because of the substantial elongation of the N–H bond (1.047 Å). The free ν_NH^f mode occurs at 3369 cm⁻¹ between the two more intense ν_OH^b bands. Isomer VII with the branched W₃ unit is slightly less stable than V/VI because it can develop less CH⋯O contacts. Due to reduced cooperativity, its OH⋯O bonds are slightly longer and weaker (1.768 and 1.856 Å, D₀ ∼ 45 kJ mol⁻¹) resulting in higher-frequency ν_OH^b bands at 3406 and 3506 cm⁻¹, which occur both to the blue of ν_NH^f =3365 cm⁻¹. Because the W ligands are closer to the Ama⁺ charge, charge transfer to W₃ is somewhat higher (85 me, Fig. S9, ESI†). The resulting stronger NH⋯O H-bond (1.590 Å) causes a strong elongation of the N–H donor bond to 1.060 Å, and the corresponding ν_NH^b mode (2589 cm⁻¹) is shifted out of the investigated frequency range.

For completeness, we also computed two structures VIII and IX corresponding to interior ion solvation, in which three individual W ligands bind to the NH₂ group (via NH⋯W H-bonds with 1.8–2.0 Å) and the Ama⁺ cage (via charge–dipole forces and CH⋯W contacts with 2.3–2.5 Å). They result essentially from adding one W to the cage of isomer I of n = 2. These are relatively high in energy (E₀ = 14.4 and 23.7 kJ mol⁻¹), because they lack the cooperativity effect of the formation of a H-bonded solvent network observed in isomers I–VII. VIII is slightly more stable than IX because it has a weak OH⋯O contact (2.02 Å), producing a slightly redshifted ν_OH^s band at 3603 cm⁻¹ in the free OH stretch range. Otherwise, their IR spectra are dominated by the two bound NH stretch bands between 3000 and 3250 cm⁻¹ (Fig. 7).

The IRPD spectrum of Ama⁺W₃ is compared in Fig. 7 to those calculated for isomers I–IX. At first glance, the best match between experimental and computed spectra is observed for II–IV, in which the NH₂ group is hydrated by NH⋯W and NH⋯W₂ H-bonds. These isomers are expected from the predominant observation of isomers I and II of the n = 2 cluster. Clearly, there is no spectroscopic signature for the formation of isomer I, which is computed as global minimum on the n = 3 potential at T = 0 K (E₀ = 0). In particular, the characteristic ν_OH^b modes of the cyclic W₃ ring (3519 and 3539 cm⁻¹) and the most intense ν_NH^b_s band at 3020 cm⁻¹ are absent. The population of I is estimated to be below 20% of II by considering the achieved signal-to-noise ratio and the computed IR intensities. The lack of detection of the cyclic isomer can be rationalized by considering entropic effects, which favour the more flexible chain structures over the more rigid cyclic solvation ring. Indeed, free energy calculations at 300 K show that I lies above II by ΔG = 5.1 kJ mol⁻¹. Such entropic effects changing the order of isomers are not observed for the n ≤ 2 clusters (Table S1, ESI†). A major contribution of isomers V–VII to the IRPD spectrum can be excluded because of the mismatch of their predicted spectra in the range of the bound NH and OH stretch modes (ν_NH^b, ν_OH^b). For example, the population of V is estimated to be ≤15% of that of II. Similarly, VIII and IX can be excluded because of the disagreement in the ν_NH^b range and their high relative energy (E₀ > 14 kJ mol⁻¹).

Out of the energetically and spectroscopically favourable isomers II–IV, the most stable structure II (concerning both E₀ and G) shows by far the best agreement with the IRPD spectrum, with maximum, mean, and summed deviations of 23, 11, and 10 cm⁻¹, respectively. The IR spectra of the similar structures III and IV are also in good accord with the IRPD spectrum, but the frequency deviations are larger and thus we will not discuss them in further detail. Peaks A–C at 3730, 3707, and 3644 cm⁻¹ are attributed to the various free OH stretch modes of II (ν_OH^a, ν_OH^f, ν_OH^s). B and D at 3426 cm⁻¹ corresponds well to ν_OH^b predicted at 3442 cm⁻¹, and is close to the corresponding mode measured for ABN⁺W₃ (3402 cm⁻¹).⁵⁵ Bands F and G at 3116 and 2944 cm⁻¹ are attributed to ν_NH^b_a and ν_NH^b_s predicted at 3108 and 2941 cm⁻¹, and their observed shifts upon addition of the third W ligand (21 and 83 cm⁻¹) agree well with the computed trend (31 and 93 cm⁻¹). This assignment is also consistent with ν_NH^b_s (2919 cm⁻¹) and ν_NH^b_a (3180 cm⁻¹) measured for ABN⁺W₃.⁵⁵ Similar to Ama⁺W₂, peak J at 2840 cm⁻¹ is attributed to a ν_CH mode, while I (2944 cm⁻¹) arising from ν_CH2 modes overlaps with band G (ν_NH^b_s) in the n = 3 spectrum. Again, the origin of peaks K (3247 cm⁻¹) and L (2993 cm⁻¹) remains unclear. They cannot be explained by fundamental modes and thus are ascribed to combination bands or overtones. For example, K could again be assigned to the combination band β_NH + β_OH of the symmetric (1583 cm⁻¹) and antisymmetric (1610 cm⁻¹) coupled NH and OH bending modes, although the observed blueshift of peak K to 3247 cm⁻¹ is not reproduced by the harmonic calculation.

5. Further discussion

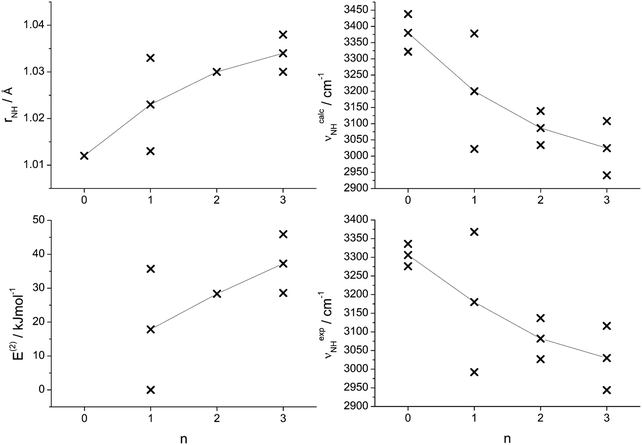
The analysis of the IRPD spectra of Ama⁺W_n in the CH, NH, and OH stretch range with the aid of B3LYP-D3 calculations provides a consistent picture of the sequential cluster growth of this fundamental diamondoid amine cation. All main bands in the IRPD spectra can readily be assigned to the energetically most stable isomer I, except for Ama⁺W₃ where free energies must be considered and then isomer II becomes more stable than I at room temperature by 5 kJ mol⁻¹. For n ≤ 2, the W ligands preferentially bind to the acidic protons of the NH₂ group via strong and nearly linear NH⋯O ionic H-bonds, corresponding to interior ion solvation. The H-bonds in n = 2 are slightly weaker than in n = 1 due to noncooperative effects typical for interior ion solvation. Hence, for n = 2 a local minimum with a H-bonded W₂ dimer attached to the NH₂ group becomes competitive because of strong cooperative effects of the H-bonded solvent network (E₀ = 5.4 kJ mol⁻¹) and thus is observed as a minor isomer. Starting from n = 3, the microhydration network expands as a H-bonded W_n network incorporating the acidic NH₂ group. Such H-bonded isomers appear energetically favoured over other isomers, in which the Ama⁺ cage is progressively solvated by single W ligands via cation–dipole forces supported by weak CH⋯O contacts. The calculated binding energies for the identified Ama⁺W_n clusters decrease as D₀ = 61.4 > 56.9 > 54.4 kJ mol⁻¹ for n = 1–3, and a linear extrapolation to larger cluster sizes would suggest that for n > 8 internal ion solvation becomes more favourable than the extension of the solvation network (Fig. S10, ESI†). However, this prediction is in contradiction to the observed sublimation enthalpy of bulk ice of 51.0 kJ mol⁻¹,⁹⁰ suggesting that larger Ama⁺W_n clusters also prefer structures with the hydrophobic adamantyl cage residing at the surface of the water solvent network. Clearly, structural isomers in which W ligands are attached to the adamantyl cage via charge–dipole forces supported by weak CH⋯O contacts are much less stable than those with hydration around the NH₂ group. The computed hydration energies for n = 1–3 (54–61 kJ mol⁻¹) exceed by far the absorbed IR photon energy (hν < 48 kJ mol⁻¹ = 4000 cm⁻¹), indicating that under the employed single-photon absorption conditions, using an unfocused IR laser beam, only cluster ions with significant internal energy can undergo the IRPD process. This result can also explain the widths of the transitions and the contributions of entropy necessary for the evaluation of the energetic order of the isomers. Although there is progressive partial charge transfer from Ama⁺ to the W_n solvent cluster, most of the charge in [AmaW_n]⁺ remains on Ama⁺ because of the large disparity in the ionization energy of Ama (computed as 7.95 eV) and W_n (>10 eV),⁷⁹ justifying the notation Ama⁺W_n in the considered size range. Similarly, the computed proton affinity of the amantadinyl radical (PA = 960 kJ mol⁻¹) is substantially higher than that of W_n clusters (PA = 691, 808, 862, 900, 904, and 908 kJ mol⁻¹ for n = 1–6),^74–78 suggesting that no proton transfer to solvent occurs for small polyhydrates of Ama⁺, although the tendency for proton shift from Ama⁺ to W_n gradually increases with n.

The detailed evolution of the properties of the N–H bonds of the predominantly observed Ama⁺W_n clusters as a function of n are compared in Fig. 8. These include the calculated individual and averaged free and bound N–H bond lengths (r_NH^f, r_NH^b), the corresponding calculated and experimental individual and averaged free and bound NH stretch frequencies (ν_NH^f, ν_NH^b), and the E⁽²⁾ energies for the NH⋯O H-bonds. In general, the experimental and theoretical frequencies agree quantitatively in terms of both, absolute values and incremental changes, which confirms the given isomer assignments. These diagrams show monotonous trends for all averaged values with increasing degree of hydration. As n increases, the intermolecular NH⋯O H-bonds become stronger due to the increasing proton affinity of the solvent cluster, as illustrated by the rising E⁽²⁾ energies. As a result, the intramolecular N–H bonds become weaker and longer and this trend directly transfers in the reduction of the NH stretch frequencies. However, the N–H bonds are far from being broken by the solvent at the considered cluster size range.

Fig. 8 Plots of various calculated and experimental properties of the N–H bonds of the most stable Ama⁺W_n clusters as a function of the cluster size n: calculated N–H bond lengths (r_NH); calculated second-order perturbation energies (E⁽²⁾) of donor–acceptor orbital interactions involved in the H-bonds; calculated and experimental NH stretch frequencies (ν_NH). Crosses indicate individual data points, whereas connected points correspond to averaged values.

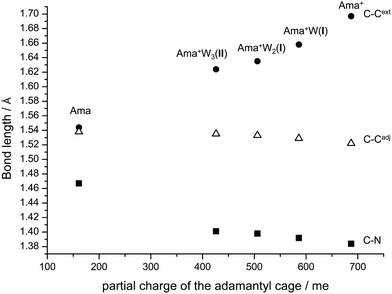
Apart from the NH₂ group, there are further structural changes induced by hydration and the resulting charge transfer to the solvent. To illustrate the major effects on the distortion of the Ama⁺ cage as a function of progressive solvation, the most affected C–C and C–N bond lengths of Ama⁽⁺⁾ and the observed most stable Ama⁺W_n clusters are plotted in Fig. 9 as a function of the partial charge on the adamantyl cage. Ionization of Ama increases the partial charge on this cage from 161 to 687 me. As a result, the C–C^ext bond in the C_s plane is strongly elongated, while the C–C^adj and C–N bonds are shortened. The charge of the cage decreases again with addition of each W ligand, and thus the trends induced by ionization are progressively reversed. However, this process slows down with each additional W ligand so that a complete return to the properties of neutral Ama by hydration is unlikely, because of the disparity in the ionization energies of Ama and W_n (IE = 10.12 ± 0.15 eV for liquid water).⁹¹

Fig. 9 Plot of the bond lengths of the extended C–C bond (C–C^ext), the adjacent C–C bond (C–C^adj), and the C–N bond of Ama, Ama⁺, and the most stable structures of Ama⁺W_1–3 as a function of the partial charge of the adamantyl cage to illustrate that the bond lengths of Ama⁺ approach those of neutral Ama upon progressive hydration.

It is instructive to compare the results of Ama⁺W_n with those obtained previously for microhydration of other primary amine cations, such as aromatic amines (e.g., AN, ABN)^55,69 or aliphatic amines (e.g., CH₃NH₂).⁷¹ Microhydration of AN⁺W_n and ABN⁺W_n shows the same preferential cluster growth as Ama⁺W_n. However, the N–H bonds in AN⁺ and ABN⁺ are less acidic, leading to weaker NH⋯O H-bonds than in Ama⁺W_n. For example, the redshifted bound NH stretch bands occurs at ν_NH^b = 3105, 3040, and 2992 cm⁻¹ for the monohydrates of AN⁺, ABN⁺, and Ama⁺. As a result, the IR spectra of AN⁺W and ABN⁺W are not complicated by the anharmonic interaction of ν_NH^b with CH stretch modes. Furthermore, because of smaller charge transfer to the solvent, the IRPD spectra of the dehydrates of AN⁺ and ABN⁺ reveal isomer I as a single isomer without any population of the minor isomers II and III as observed for Ama⁺.

In an effort to study the effects of replacing the cycloalkyl cage by a simple linear alkyl group on the hydration of aliphatic amine cations, we compare in the following Ama⁺W_n with CH₃NH₂⁺W_n, which is the simplest alkylamine cation with a comparable microhydration process.⁷¹ Although the latter clusters are rather simple, no IRPD spectra have been reported yet, and the only information available comes from computational studies at the MP2/6-311+G(2d,p) level.⁷¹ Because the MP2 level often suffers from spin contamination when applied to radical cations and because we like to compare directly with our data on Ama⁺W_n, we computed herein the properties of CH₃NH₂⁺W_n at the B3LYP-D3 level (Fig. S4, ESI†). In general, the B3LYP-D3 results are consistent with previous MP2 results.⁷¹ The ionization energy of CH₃NH₂ is substantially higher than for Ama (8.9 vs. 7.9 eV) and the calculated proton affinity of CH₃NH is lower than for C₁₀H₁₅NH (896 vs. 960 kJ mol⁻¹).⁹² The major difference between Ama⁺ and CH₃NH₂⁺ is that the HOMO orbital is largely delocalized over the Ama cage, while in CH₃NH₂⁺ it is essentially the localized nitrogen p orbital perpendicular to the CNH₂ plane. Hence, the positive charge on the NH₂ group is much higher in CH₃NH₂⁺ (q_NH2 = 597 vs. 313 me) leading to more acidic NH protons (r_NH = 1.020 vs. 1.012 Å). As a result, the NH⋯O H-bonds in CH₃NH₂⁺W_n are substantially stronger than in Ama⁺W_n. For example, the NH⋯O H-bond in CH₃NH₂⁺W has a higher binding energy than Ama⁺W(I), associated with a shorter H-bond, larger orbital interactions, higher charge transfer to solvent, and stronger intramolecular deformation (D₀ = 88.7 vs. 61.4 kJ mol⁻¹, R_NH⋯O = 1.613 Å vs. 1.768 Å, E⁽²⁾ = 62.4 vs. 33.8 kJ mol⁻¹, Δq = 68 vs. 38 me, Δr_NH = 39 vs. 21 mÅ). On the other hand, the C–N bond elongation is reduced (Δr_NH = 3 vs. 8 mÅ), because of the lacking orbital delocalization. The hydration motif in CH₃NH₂⁺W₂ is quite similar to that of Ama⁺W₂(I), but again with shorter and stronger NH⋯O H-bonds (D₀ = 73.0 vs. 56.9 kJ mol⁻¹, R_NH⋯O = 1.695 Å vs. 1.802 Å, E⁽²⁾ = 44.7 vs. 29.3 kJ mol⁻¹, Δq = 97 vs. 68 me, r_NH = 1.045 Å vs. 1.030 Å). A similar trend is also observed for n = 3, where in CH₃NH₂⁺W₃ the NH⋯O (1.587 vs. 1.722 Å) and OH⋯O H-bonds (1.715 vs. 1.821 Å) of the W₂ unit are also shorter than in Ama⁺W₃(II), based on the higher total binding energy (D^total₀ = 216 vs.167 kJ mol⁻¹) and the larger charge transfer to the solvent (Δq = 120 vs. 81 me).

6. Concluding remarks

In summary, we combined IRPD spectroscopy of size-selected Ama⁺W_n clusters with n ≤ 3 in the sensitive OH, NH, and CH stretch range with DFT calculations at the B3LYP-D3/cc-pVTZ level to determine the first steps in the microhydration process around the radical cation of this important pharmaceutical molecular drug. Significantly, these spectra provide the first spectroscopic information about the Ama⁺ cation and any Ama⁺L_n cluster with neutral ligands L. Thus, they yield a first impression about the acidity of its NH₂ group and its interaction with solvent molecules. The salient results may be summarized as follows.

(1) In agreement with previous experimental and computational evidence, ionization of Ama into the ground state of the cation is achieved by removal of an electron from the nonbonding lone pair of the N atom of the NH₂ group, which has a′ symmetry in the C_s point group. As a result, the pyramidal NH₂ group in neutral Ama becomes essentially planar upon ionization, much like for NH₃. As this orbital is significantly delocalized into the adamantyl cage, ionization also strongly affects the lengths of the neighbouring C–N and C–C bonds lying in the symmetry plane. These structural changes of the NH₂ group and the adamantyl cage are further modulated by sequential microhydration because the formation of the NH⋯O H-bonds is accompanied by partial charge transfer from Ama⁺ to W_n.

(2) The measured IRPD spectra of Ama⁺W_n can essentially be assigned to the energetically most favourable structures for a given cluster size obtained by the DFT calculations, whereby for n = 3 the free energies have to be considered. The preferred sequential cluster growth starts with the hydration of the two acidic NH protons of the NH₂ group via strong NH⋯O ionic H-bonds (n = 1–2) and continues with further extension of the H-bonded solvent network by the formation of a W₂ unit via an OH⋯O H-bond (n = 3). Clearly, structural isomers in which W ligands are attached to the adamantyl cage via charge–dipole forces supported by weak CH⋯O contacts are much less stable than those with hydration around the NH₂ group. However, for n = 2 a minor additional isomer with a W₂ dimer attached to the NH₂ group is detected, because the nearby Ama⁺ charge strongly enhances the binding energy of the W₂ dimer via polarization effects. The formation of a cyclic hydration structure for n = 3, computed to be the global minimum at T = 0 K, can be excluded by spectroscopy, and indeed this structure becomes destabilized by 5 kJ mol⁻¹ compared to the observed structure when considering free energies. Overall, the IRPD spectra and calculations reveal a similar solvation process as observed previously for related RNH₂⁺W_n clusters,^55,69,70 in which also the formation of a H-bonded network is favoured over internal ion solvation.⁵⁵ While the formation of the H-bonded solvation network is strongly favoured by cooperative three-body interactions, the tendency for interior ion solvation is somewhat reduced by noncooperative three-body induction forces.

(3) In general, the solvent increasingly attracts the acidic NH protons of Ama⁺ as the number of W ligands increases. Although the N–H bonds are progressively destabilized by gradual microhydration, no proton transfer to the solvent is observed for n ≤ 3, which is in line with the proton affinities of C₁₀H₁₅NH and W_n. From the increasing proton affinity of the W_n, such a proton transfer may only occur for large n (n ≫6). Similarly, charge transfer from Ama⁺ to W_n increases with n, but remains below 0.1 e due to the large discrepancy between the ionization energies of Ama and W_n.

(4) From comparison of computational spectroscopic data, we conclude that the acidity of the NH₂ group in RNH₂⁺ cations increases in the order aniline < amantadine < methylamine, because of decreasing charge delocalization and resulting stronger H-bonds.

For a more detailed investigation of the bare Ama⁺ cation, experiments with weakly bound rare gas ligands are currently underway.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This study was supported by Deutsche Forschungsgemeinschaft (grant DO 729/8).

References

1. S. Landa and V. Machacek, Collect. Czech. Chem. Commun., 1933, 5, 1–5.
2. J. Kirschbaum, Analytical Profiles of Drug Substances, Elsevier, 1983, pp. 1–36.
3. R. C. Fort and P. v. R. Schleyer, Chem. Rev., 1964, 64, 277–300.
4. J. E. Dahl, S. G. Liu and R. M. K. Carlson, Science, 2003, 299, 96–99.
5. P. v. R. Schleyer, J. Am. Chem. Soc., 1957, 79, 3292.
6. J. E. P. Dahl, J. M. Moldowan, Z. Wei, P. A. Lipton, P. Denisevich, R. Gat, S. Liu, P. R. Schreiner and R. M. K. Carlson, Angew. Chem., Int. Ed., 2010, 49, 9881–9885.
7. H. Schwertfeger, A. A. Fokin and P. R. Schreiner, Angew. Chem., Int. Ed., 2008, 47, 1022–1036.
8. P. R. Schreiner, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, S. Schlecht, J. E. P. Dahl, R. M. K. Carlson and A. A. Fokin, Nature, 2011, 477, 308.
9. W. L. Yang, J. D. Fabbri, T. M. Willey, J. R. I. Lee, J. E. Dahl, R. M. K. Carlson, P. R. Schreiner, A. A. Fokin, B. A. Tkachenko and N. A. Fokina, Science, 2007, 316, 1460–1462.
10. A. A. Fokin and P. R. Schreiner, Chem. Rev., 2002, 102, 1551–1594.
11. L. Wanka, K. Iqbal and P. R. Schreiner, Chem. Rev., 2013, 113, 3516–3604.
12. D. F. Blake, F. Freund, K. F. M. Krishnan, C. J. Echer, R. Shipp, T. E. Bunch, A. G. Tielens, R. J. Lipari, C. J. D. Hetherington and S. Chang, Nature, 1988, 332, 611.
13. R. S. Lewis, E. Anders and B. T. Draine, Nature, 1989, 339, 117.
14. O. Pirali, M. Vervloet, J. E. Dahl, R. M. K. Carlson, A. Tielens and J. Oomens, Astrophys. J., 2007, 661, 919.
15. W. L. Davies, R. R. Grunert, R. F. Haff, J. W. McGahen, E. M. Neumayer, M. Paulshock, J. C. Watts, T. R. Wood, E. C. Hermann and C. E. Hoffmann, Science, 1964, 144, 862–863.
16. R. S. Schwab, A. C. England, D. C. Poskanzer and R. R. Young, JAMA, 1969, 208, 1168–1170.
17. G. Hubsher, M. Haider and M. S. Okun, Neurology, 2012, 78, 1096–1099.
18. K. Spilovska, F. Zemek, J. Korabecny, E. Nepovimova, O. Soukup, M. Windisch and K. Kuca, Curr. Med. Chem., 2016, 23, 3245–3266.
19. J. Hu, R. Fu and T. A. Cross, Biophys. J., 2007, 93, 276–283.
20. WHO, Summary of influenza antiviral susceptibility surveillance findings, 2010–2011. Retrieved 2019.
21. A. S. Monto and N. H. Arden, Clin. Infect. Dis., 1992, 15, 362–367.
22. R. P. Grelak, R. Clark, J. M. Stump and V. G. Vernier, Science, 1970, 169, 203–204.
23. L.-O. Farnebo, K. Fuxe, M. Goldstein, B. Hamberger and U. Ungerstedt, Eur. J. Pharmacol., 1971, 16, 27–38.
24. P. F. Vigtlander and K. E. von; Moore, Science, 1971, 174, 408–410.
25. J. Kornhuber, M. Weller, K. Schoppmeyer and P. Riederer, J. Neural Transm., 1994, 43, 91–104.
26. A. A. Spasov, T. V. Khamidova, L. I. Bugaeva and I. S. Morozov, Pharm. Chem. J., 2000, 34, 1–7.
27. T. J. Murray, Can. J. Neurol. Sci., 1985, 12, 251–254.
28. K. M. Kampman, J. R. Volpicelli, A. I. Alterman, J. Cornish and C. P. O’Brien, Am. J. Psychiatry, 2000, 157, 2052–2054.
29. J. Kornhuber, W. Retz and P. Riederer, J. Neural Transm., Suppl., 1995, 46, 315–324.
30. F. Weber and S. Gottfried, Nachr. Chem., 2014, 62, 997.
31. L. J. Allamandola, S. A. Sandford, A. G. Tielens and T. M. Herbst, Science, 1993, 260, 64–66.
32. T. Henning and F. Salama, Science, 1998, 282, 2204–2210.
33. O. Guillois, G. Ledoux and C. Reynaud, Astrophys. J., Lett., 1999, 521, L133.
34. M. Steglich, F. Huisken, J. E. Dahl, R. M. K. Carlson and T. Henning, Astrophys. J., 2011, 729, 91.
35. A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., Int. Ed., 2012, 51, 4925–4929.
36. P. B. Crandall, D. Müller, J. Leroux, M. Förstel and O. Dopfer, Astrophys. J., Lett., 2020, 900, L20.
37. L. J. Allamandola, M. P. Bernstein, S. A. Sandford and R. L. Walker, Space Sci. Rev., 1999, 90, 219–232.
38. M. George, M. Förstel and O. Dopfer, Angew. Chem., Int. Ed., 2020, 59, 12098–12104.
39. J. C. Garcia, J. F. Justo, W. V. M. Machado and L. V. C. Assali, J. Phys. Chem. A, 2010, 114, 11977–11983.
40. L. Rivas, S. Sanchez-Cortes, J. Stanicova, J. V. García-Ramos and P. Miskovsky, Vib. Spectrosc., 1999, 20, 179–188.
41. I. V. Litvinyuk, Y. Zheng and C. E. Brion, Chem. Phys., 2000, 261, 289–300.
42. P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, NIST Standards and Technology, Gaithersburg, MD, 20889, 2011, http://webbook.nist.gov.
43. J. Staničová, G. Fabriciová, L. Chinsky, V. Šutiak and P. Miškovský, J. Mol. Struct., 1999, 478, 129–138.
44. O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168.
45. O. Dopfer and M. Fujii, Chem. Rev., 2016, 116, 5432–5463.
46. N. Solcà and O. Dopfer, Chem. Phys. Lett., 2001, 347, 59–64.
47. N. Solcà and O. Dopfer, Chem. – Eur. J., 2003, 9, 3154–3161.
48. O. Dopfer, N. Solcà, J. Lemaire, P. Maitre, M.-E. Crestoni and S. Fornarini, J. Phys. Chem. A, 2005, 109, 7881–7887.
49. H.-S. Andrei, N. Solcà and O. Dopfer, ChemPhysChem, 2006, 7, 107–110.
50. S. Chakraborty, A. Patzer, A. Lagutschenkov, J. Langer and O. Dopfer, Chem. Phys. Lett., 2010, 485, 49–55.
51. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2020, 124, 1134–1151.
52. K. Tanabe, M. Miyazaki, M. Schmies, A. Patzer, M. Schütz, H. Sekiya, M. Sakai, O. Dopfer and M. Fujii, Angew. Chem., Int. Ed., 2012, 124, 6708–6711.
53. I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S.-S. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 74307.
54. J. Klyne, M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3148–3164.
55. M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, J. Chem. Phys., 2014, 141, 214301.
56. O. Dopfer, A. Patzer, S. Chakraborty, I. Alata, R. Omidyan, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2014, 140, 124314.
57. J. Klyne, M. Schmies, M. Fujii and O. Dopfer, J. Phys. Chem. B, 2015, 119, 1388–1406.
58. M. Schütz, K. Sakota, R. Moritz, M. Schmies, T. Ikeda, H. Sekiya and O. Dopfer, J. Phys. Chem. A, 2015, 119, 10035–10051.
59. A. Bouchet, M. Schütz and O. Dopfer, ChemPhysChem, 2016, 17, 232–243.
60. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986.
61. J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092–3108.
62. J. Klyne and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 2706–2718.
63. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 32262–32271.
64. K. Chatterjee and O. Dopfer, Chem. Sci., 2018, 9, 2301–2318.
65. K. Chatterjee and O. Dopfer, J. Chem. Phys., 2018, 149, 174315.
66. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2019, 123, 7637–7650.
67. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 25226–25246.
68. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2020, 22, 13092–13107.
69. Y. Inokuchi, K. Ohashi, Y. Honkawa, N. Yamamoto, H. Sekiya and N. Nishi, J. Phys. Chem. A, 2003, 107, 4230–4237.
70. M. Alauddin, J. K. Song and S. M. Park, Int. J. Mass Spectrom., 2012, 314, 49–56.
71. S.-K. Jiang, D. Yang, X.-T. Kong, C. Wang, X.-Y. Zang, H.-J. Zheng, G. Li, H. Xie, W.-Q. Zhang and X.-M. Yang, Chin. J. Chem. Phys., 2020, 33, 31–36.
72. S. Scheiner, Hydrogen bonding: a theoretical perspective, Oxford University Press, 1997.
73. G. A. Jeffrey and W. Saenger, Hydrogen bonding in biological structures, Springer, 2012.
74. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
75. D. J. Goebbert and P. G. Wenthold, Eur. J. Mass Spectrom., 2004, 10, 837–845.
76. A. Courty, M. Mons, J. Le Calvé, F. Piuzzi and I. Dimicoli, J. Phys. Chem. A, 1997, 101, 1445–1450.
77. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Chem. Phys. Lett., 2004, 399, 412–416.
78. R. Knochenmuss, Chem. Phys. Lett., 1988, 144, 317.
79. L. Belau, K. R. Wilson, S. R. Leone and M. Ahmed, J. Phys. Chem. A, 2007, 111, 10075–10083.
80. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
81. M. Frisch, et al., Gaussian 09, version D.01, Gaussian, Inc, Wallingford, CT, 2009.
82. T. Shimanouchi, Tables of Molecular Vibrational Frequencies Consolidated, National Bureau of Standards, Washington, DC, 1972, pp. 1–160, vol. I.
83. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.
84. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
85. F. Huisken, M. Kaloudis and A. Kulcke, J. Chem. Phys., 1996, 104, 17–25.
86. C. Parlak and Ö. Alver, Chem. Phys. Lett., 2017, 678, 85–90.
87. P. C. Yates, T. J. Hill and M. Kaur, J. Mol. Struct., 1992, 258, 299–313.
88. A. G. Császár, G. Czakó, T. Furtenbacher, J. Tennyson, V. Szalay, S. V. Shirin, N. F. Zobov and O. L. Polyansky, J. Chem. Phys., 2005, 122, 214305.
89. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman Spectra of Polyatomic Molecules, Krieger Publishing Company, Malabar, Florida, 1991.
90. S. Heiles, R. J. Cooper, M. J. DiTucci and E. R. Williams, Chem. Sci., 2017, 8, 2973–2982.
91. C. F. Perry, P. Zhang, F. B. Nunes, I. Jordan, A. Conta and H. J. von Wörner, J. Phys. Chem. Lett., 2020, 11, 1789–1794.
92. D. H. Aue and M. T. Bowers, Gas phase ion chemistry, Elsevier, 1979, pp. 1–51.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05299j

---