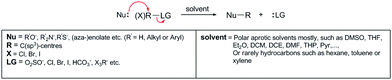
Open Access Article
Open Access ArticleAn analysis of electrophilic aromatic substitution: a “complex approach”†
Nikola
Stamenković
 a,
Nataša Poklar
Ulrih
a,
Nataša Poklar
Ulrih
 a and
Janez
Cerkovnik
a and
Janez
Cerkovnik
 *b
*b
aUniversity of Ljubljana, Biotechnical Faculty, Department of Food Science and Technology, Jamnikarjeva 101, 1000 Ljubljana, Slovenia
bUniversity of Ljubljana, Faculty of Chemistry and Chemical Technology, Department of Chemistry and Biochemistry, Večna pot 113, 1000 Ljubljana, Slovenia. E-mail: janez.cerkovnik@fkkt.uni-lj.si
First published on 7th January 2021
Abstract
Electrophilic aromatic substitution (EAS) is one of the most widely researched transforms in synthetic organic chemistry. Numerous studies have been carried out to provide an understanding of the nature of its reactivity pattern. There is now a need for a concise and general, but detailed and up-to-date, overview. The basic principles behind EAS are essential to our understanding of what the mechanisms underlying EAS are. To date, textbook overviews of EAS have provided little information about the mechanistic pathways and chemical species involved. In this review, the aim is to gather and present the up-to-date information relating to reactivity in EAS, with the implication that some of the key concepts will be discussed in a scientifically concise manner. In addition, the information presented herein suggests certain new possibilities to advance EAS theory, with particular emphasis on the role of modern instrumental and theoretical techniques in EAS reactivity monitoring.
Introduction to electrophilic aromatic substitution
Brief historical overview of electrophilic aromatic substitution
Electrophilic aromatic substitution (EAS) is one of the most researched and common reactions in organic chemistry today. Furthermore, EAS is one of the most useful reactions in the field of synthesis of aromatic compounds.The first report of the EAS reaction that yielded products like those that we know today dates back to the late 19th century, by Henry Armstrong,1 in which, the reaction was characterized as a general type of substitution that was different from those that took place at the C(sp3) reactive site. As such, Armstrong set out certain postulates of this hitherto unknown reaction, with his definition of the reaction intermediate, the (reaction) complex, and the concept of a transition state. Of course, at that time, these terms were poor in information regarding their significance for this type of newly discovered reaction. Thus, it was that, with the further development of organic and synthetic organic chemistry, these terms were theoretically and experimentally defined and determined, and introduced into theory as valid terms.
In the middle of the 20th century, Wheland further explored and deepened the concept of the Armstrong (reaction) complex in EAS, and named it the σ-complex. Indeed, today, the σ-complex is also known as the Wheland complex, as it was first defined by Wheland.2 It is also important to note that today the term ‘Wheland intermediate’ is used in the same way as ‘Wheland complex’, as synonymous with the term σ-complex.
Historically, the transition state has been studied by many well-known scientists, with Hammett, Cram, and Curtin, to name but a few, who have made solid contributions to the development of the theory and concept of the transition state.
Basic postulates of substitution as a transform in retrosynthetic analysis
Substitution is one of the oldest reactions in both organic and inorganic chemistry, and over time, it has become an extremely important form of transformation. With the introduction of the concept of retrosynthetic analysis into the theory of synthetic organic chemistry by Corey, the concept of transformation was changed into that of transform.3 Thus, a transform relates to any type of reaction in the synthesis of a compound. In this regard, substitution is defined, in modern chemical science, as a type of transform, which implies that in such a type of reaction there is a reactant.A ‘reactant’ is a term that is used to describe a chemical species that is introduced into a reaction and is responsible for its initiation.
What characterize the substitution reaction (as well as many other reactions) are the physico-chemical parameters that define its course. Most often, these involve the concepts of enthalpy change, entropy, and Gibbs free energy (i.e., ΔH, ΔS, and ΔG, respectively); however, there are also the concepts of energy barrier, collision factor, Gibbs free transitional state energy, and dihedral and nucleophilic attack angles (Ea, f, ΔG‡, αd, and αnuc, respectively). In addition to these, there are other computer theoretical parameters that are more complex both in their definition and in their calculation.
All of these physico-chemical parameters are equally important in considering and determining the mechanism of any particular type of reaction, including the substitution reaction. Substitution involves the simple modification of an atom, an atomic group, or a part of a molecule at a specific reactive site. Therefore, in addition to these physico-chemical and computer-theoretical parameters, the substitution reaction will depend on the type and nature of any specific reactive site.
In general, reactive sites in the substitution reaction are carbon atoms, although they can also comprise individual heteroatoms, such as nitrogen, the halogen elements (except fluorine), oxygen, and certain transition metals, such as rhodium, palladium, zinc, and copper. However, substitution on heteroatoms has been less investigated and is of less importance for organic synthesis and therefore for EAS reactions as well.
Carbon reactive sites show very diverse reactivity in substitution reactions in organic chemistry. The most reactive are the C(sp3) sites, which, due to their geometry and the nature of their bond with substituents, can receive nucleophilic electrons during substitution particularly rapidly and efficiently (Scheme 1). In doing so, the product of such a reaction also has a stereochemical outcome, which is often called the Walden inversion (Scheme 2). The reactivities of the C(sp2) and C(sp) sites are different, as a function of the reactant involved. The general view is that these two types of sites are less reactive than the C(sp3) sites due to the increased electron density that arises from the increased bond order, such that their activation requires a catalyst or a much stronger nucleophile. This claim is the basis for the study of the reactivities of reactants in the EAS reactions (transforms).
General mechanistic considerations in electrophilic aromatic substitution
Electrophilic aromatic substitution carries in its name the main elements of the mechanistic studies of this reaction: an ‘electrophile’, an ‘aromatic compound’, and a ‘substitution’. All three of these terms are of great importance when it comes to EAS, on the basis of the complexity of aromatic compounds in relation to other compounds.Aromatic compounds (or ‘aromatics’) are characterized by their specific chemical inertness compared to other reactive sites or compounds. They have an aromatic nucleus on which the EAS reaction takes place. It is typical for aromatics to have the so-called closed π-electron system, which can be characterized as an ‘effect’ in mechanistic EAS studies. This effect can be further characterized as stabilizing or destabilizing,4 bearing in mind the quantity known as the electron-flow coefficient, or the inductive coefficient. This coefficient quantifies the flow of electrons through all σ-bonds and π-bonds through the molecular map on which the reactive site(s) are located. The π-electron system in aromatics is of the conjugate type, such that these π-electrons can move through the molecular system via resonance. However, it must be emphasized that, in their own way, each of the three terms mentioned (i.e., electrophile, aromatic compound, and substitution) controls the outcome of the reaction, the course of the reaction, the product yield of such a reaction, and the regioselectivity of the reaction, as EAS is only characteristic of aromatic nuclei.
To consider the participation and contribution of electrophiles and aromatic compounds in EAS and to consider and analyze in more depth the substitution that takes place in the EAS process, it is necessary to give a brief graphical overview of the EAS process. For the purposes of introducing the EAS mechanism, a concrete example of benzene (PhH) with a specific electrophile (E+) is considered.
Addition mechanism
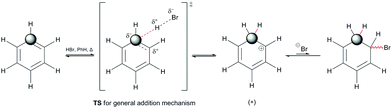
The reactivity of benzene was tested in two different ways to determine its true reactivity. The dilemmas that arose at the time were concerned with the presence of double bonds, which were speculated to react separately as well as to react independently of each other, depending on the conditions. To perform the reaction on one double bond chemoselectively, the conditions of the reaction system had to be adjusted so that the amount of the electrophile was a little less than the unit amount of the particular double bond on the benzene nucleus (<0.33 eq.), while the catalysts were in much larger amounts.The first way that benzene can react is by electrophilizing the unit double bond of the benzene nucleus, without any further chemical modification of the aromatic nucleus itself. This implies a key concept when considering the mechanism of this reaction – the loss of aromaticity of the aromatic compound! The loss of aromaticity here refers to the formation of the C(sp3) sites and also to the destabilization of the molecular system. Therefore, this aromatic compound would no longer be aromatic, nor would it have a system of conjugated double bonds.4a–c An example of an addition reaction to a benzene reactant follows on from an alkene addition reaction (Scheme 3). Therefore, the general characteristics of the mechanism that characterizes the addition reaction to alkenes would also characterize the addition reaction to benzene.
Scheme 3 indicates three key aspects: the appearance of an anti-aromatic reactive species that has a carbocationic site in the α-position; the formation of a C(sp3) site that has highly acidic H-atoms; and the transition state (Scheme 3, TS), where the electrostatic potential map indicates the possibility of the formation of nonplanar polarization of the observed double bond.5 Nonplanar polarization of a single double bond is a phenomenon that accompanies the formation of a C(sp3) site on such a compound. To explain this polarization, analogous allenic or other nonaccumulated diene protonated systems can be considered, where their orbital image indicates the presence of an orbital outside one plane (Fig. 1), which can partially ‘support’ the existence of the phenomena of nonplanar proton abstraction in such a transition state.6 The transition state in Scheme 3 is characterized by the ‘capturing’ of protons from the HBr molecules, where nonplanar double-bond polarization leads to polarization of the π-electron cloud of benzene, and the generation of a carbanion reactive orbital, which is planar with the rest of the π-electron cloud in the molecule at the moment of its generation. According to the relevant data on the characterization of this transient state, the most approximate theoretical studies at the MP2 level were performed on the superacid system C6H6–HBr–AlBr3, which showed that the newly generated C(sp3) site is still planar, while the reactive carbon orbital (the highest occupied molecular orbital; HOMO) is at an angle (αHOMO) of approximately 90° < αHOMO ≤ 109.28° (±3.00°) relative to the proton position.7,21 This explains the appearance of a nonplanar transition state during the protonation of benzene molecules (Fig. 2). In favor of this, the example of naphthalene protonation (i.e., the simplest molecule in the group of polycyclic aromatic hydrocarbons) under superacid conditions produces the protonated naphthyl cation, where the C(sp3) site is generated at the C-1 position.8
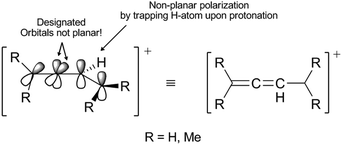 | ||
| Fig. 1 Orbital view of 1,3-dienyl-2-cation. The arrows indicate orbitals that are out of plane and also where nonplanar polarization has taken place.6 | ||
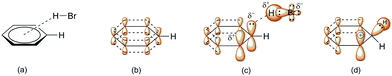 | ||
| Fig. 2 Interaction of benzene with hydrobromic acid: (a) formation of the (angular) π-complex;9d (b) orbital representation of the p-orbital in benzene; (c) simplified ηn-model of polarization (n = 1, 2) of one part of the π-electron cloud of benzene during the formation of the π-complex (the carbanionic highest occupied molecular orbital [HOMO] is planar at this moment);6,9d and (d) angular deformation of the HOMO during the formation of the σ-complex and free p-orbital formation. | ||
During the formation of the intermediate species from the indicated transition state, the carbocationic species is unstable for two reasons: the carbocation drastically lowers the energy of the electrophilic orbital (i.e., as the lowest unoccupied molecular orbital [LUMO]; Scheme 3, the site adjacent to that marked by the sphere), and there is the absence of a nonnucleophilic counterion (i.e., the presence of a bromide ion). The estimated acidity of this arenium ion is about −2.9 in ionic liquid systems9a (the extrapolated acidity of this species in an aqueous system is −24),9b,c which indicates that the bromide can have both nucleophilic and basic characteristics in further reactions. The further course of the reaction is such that the feedback reaction is favored, and that the aromatic nucleus and the molecules of hydrobromic acid are regenerated, notwithstanding the greatly increased electrophilicity of the carbonation of the protonated benzene. The problem of reversibility of the reaction can be solved by using a catalytic system or by an increase in temperature in the presence of an aprotic polar solvent (most frequently, MeCN, DCM [DCE], and THF). Both solutions are operational, bearing in mind that in the experimental sense each has its own convenience. The catalytic system establishes a favorable two-component entropic system, in which alternating and mutual stabilization of the proton and the nucleophilic acid residue occurs (here as the bromide ion). In addition, the catalytic system conditions the angular deformation of the carbanionic orbital in the transition state, which promotes additional stabilization of the catalyst–benzene relationship. On the other hand, an increase in temperature to reflux temperatures (i.e., 65–85 °C) in the presence of an aprotic polar solvent reduces the level of proton stabilization, while it also favors stabilization of the nucleophilic acid residue. This thus reduces the total proton acidity, while the nucleophilic character of the acid residue remains slightly altered, but is still favorable for nucleophilic attack.
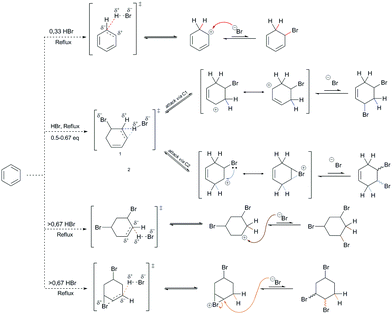
As part of the further discussions of the mechanism of EAS, it is important to note the importance of the structure indicated in Scheme 3 using an asterisk. The transition state provides an insight into the orbital arrangement and reactivity of the proton, as an electrophile, but this structure provides an insight into the reactivity of the benzene nucleus during the EAS reaction. When talking about the reactivity of EAS, it is important to consider the term σ-complex. In the literature, and as indicated above, the σ-complex is also referred to as the Wheland complex or the Wheland intermediate. For σ-complex, it is important to emphasize the characteristic and subtle relationship between the intensity of the electrophilicity and the acidity of the benzene nucleus, as mentioned in the example above. Further disintegration of this complex will strictly depend not only on the conditions in which the reaction takes place, but also on the types and relationships of the participants in the reaction. The existence of nucleophilic species with a possible basic character will show in experimental and theoretical terms that the reaction takes place in the direction of proton abstraction from this complex. However, it must also be said that, as learnt over the last few years, the electrophilicity of the nonaromatic benzene nucleus can be controlled. The difference in Gibbs free energy (ΔGf) of the addition product represents an excellent benchmark when estimating the outcome of an EAS reaction or addition to the benzene nucleus. In this regard, the products of monoaddition (i.e., 5-bromocyclohexa-1,3-diene [BChex]; Fig. 3a), di-addition (i.e., 3,5-dibromocyclohex-1-ene[3,5-DBChex]; Fig. 3b1; 4,5-dibromocyclohex-1-ene [4,5-DBChex]; Fig. 3b2), and tri-addition (1,3,5-tribromo-cyclohexane [1,3,5-TBCy]; Fig. 3c1; 1,3,4-tribromo-cyclohexane [1,2,4-TBCy]; Fig. 3c2) are possible products in the PhH–HBr reactive system.
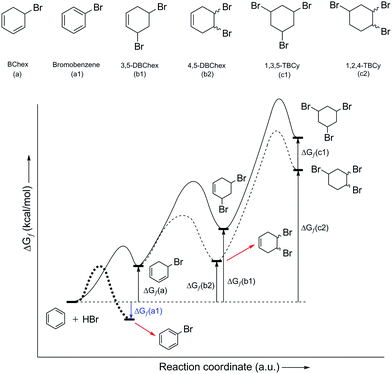 | ||
| Fig. 3 Possible products in the benzene addition reaction with HBr (above), and energy profile of the HBr addition reaction with benzene (below). ΔGf(a1) is the Gibbs free energy value of bromobenzene (bold dashed line for its energy profile path), an EAS product (using Br2 and HBr as a catalytic system,10 as an exception from the electrophilic addition process), presented here as a comparison to the other counterparts in the electrophilic addition process. | ||
The theoretical possibility for the creation of all five of these products gives a different picture through the interpretation of the energy values of each of these possible products, as shown in Fig. 3. Namely, the di-addition and tri-addition products (i.e., 1,5-DBChex, 1,2-DBChex, 1,3,5-TBCy, 1,2,4-TBCy) have very low probabilities of formation due to the particularly high energy barriers for the alternating successive protonation–nucleophilic attack reactions that occur during the subsequent addition reactions and that are higher than those that occur during the EAS reaction. It is important to note that the electrophilicity and the acidity of the protonated addition products during di-addition and tri-addition with HBr correlate inversely with the rate of proton abstraction (kabs), such that the reverse reactions (i.e., debromination) become (slightly) less favored. In contrast, a monoaddition product (BChex) would be expected to have a very high probability of formation. However, it was first experimentally confirmed that in the PhH–HBr system the reverse reaction after protonation was favored! The reason for such a reaction course lies precisely as mentioned above, that the protonated benzene (i.e., the σ-complex) is very unstable and that proton abstraction occurs much faster than the addition of bromide to the carbocation site. Theoretically, the addition process itself can be explained whereby, although bromide would attack the carbocation site before proton abstraction and form a suitable intermediate, this intermediate would be very thermodynamically unstable and would lead to successive tandem proton abstraction and bromide departure, which would regenerate the aromatic system. The structures of all five of the products are shown in Fig. 3, while the indicated differences in reactivity are shown through the reactions in Scheme 4 and the energy profiles in Fig. 3.
It should be emphasized that, according to the reactivity parameter, similar processes of the hydrogenation of benzene have already been developed, and that these methodologies have been successfully applied in the laboratory and in industry (i.e. catalytic hydrogenation).
In the previous example, one theoretical possibility for the reactivity of benzene (i.e., the benzene nucleus) was considered in detail, which has generally been rejected due to a lack of experimental and/or computational evidence. The second way in which aromatic nuclei can react will be discussed below, with the same PhH–HBr system taken into further consideration for reactivity. To explain the reactivity of the benzene nucleus, there is a need to first look at the terms ‘π-complex’ and ‘σ-complex’, which have already been mentioned. As a compound within this system, benzene has very unusual energy stability and thus many different ways in which it can react with reactants. The structure was discovered by the German chemist Kekulé in the 19th century whose representation is still used by the scientific community. It consists of two canonical resonance structures, which explain the unusual stability observed: a six-membered ring with (ideal) angles of 120° (±2°) within which three conjugate double bonds are ‘positioned’. The conjugation of the double bonds can be used to indicate and explain the unusual level of stability of this molecule. For these double bonds, experimental and computational tests have shown that they have electrons that move in the p-orbitals that are positioned to allow an uninterrupted and constant flow of electrons through this entire p-orbital system. This thus defines these double bonds as the so-called ‘electron ring’. This electron ring contains six electrons that form an ‘electron cloud’, which explains the significantly reduced reactivity of benzene. By hybridizing all of the carbon orbitals in this ring and rearranging them, whereby the electron cloud is formed, it can be concluded that these six electrons are π-electrons.
From this, it can be concluded consequently that π-electrons actually contribute to the nucleophilicity of the benzene nucleus. To activate this π-electron cloud, it is necessary that there is an electrophilic species in the reactive system that can allow substitution on this benzene ring. The proton from HBr is an electrophilic species,10 although, during the formation of the σ-complex, the newly formed species would contain two identical electrophiles. This would characterize the reaction as reversible on the basis of the identical probability of abstraction of two protons at the newly generated C(sp3) site. This leads to the conclusion that the electrophile should be a nonproton species that can react with a benzene electron cloud. This is solved by the addition of catalysts to sufficiently reduce the energy of the LUMO of the potential electrophile, thereby disturbing the stability of the π-electron cloud by reacting with a given electrophile in this catalytic system. The σ-complex thus formed can then undergo proton abstraction by the nucleophilic or basic species present in the system and shift the equilibrium toward the reaction product. When the reacting electrophile is different from the proton during the nucleophilic attack of benzene on it to obtain a substitution product, the reaction is known as EAS.4 The basic catalytic systems that are used in EAS reactions include Lewis acids,11–14 which in principle coordinate the electrophile to make it more electrophilic for the attack of the benzene nucleus. Recent research has indicated that proton catalytic systems can also efficiently undergo EAS reactions, which opens up a new field for research into the mechanism of the EAS reaction.10 Newer catalytic systems will be discussed later, and for the needs of the general mechanism of electrophilic aromatic substitution, and in relation to the aforementioned, we will use the modified system of Lewis acid–electrophile–benzene (LA–E+–PhH).
Electrophile–electrophile substitution – electrophile differentiation
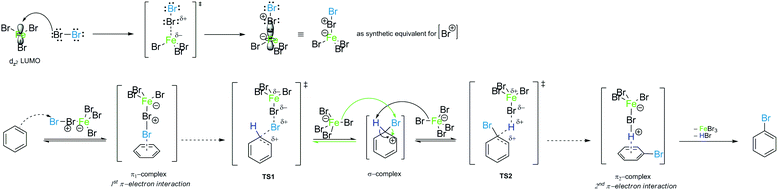
Thus far, we have been concerned specifically about the potential mechanism of addition, which in mechanistic terms has similarities with the EAS reaction, although they actually differ from each other in only one step: the differentiation of electrophiles15a during the reaction. Electrophile differentiation means that an electrophile of similar reactivity is added to a benzene nucleus, such as a proton. This has already been mentioned above in terms of the EAS response mechanism (see Section 2.1), but it is now important to clarify this. The generation of different electrophiles can undoubtedly lead to different yields and outcomes in EAS reactions on the benzene considered here. These will depend on the experimental experience and on the methodology applied during the realization (i.e., execution) of these types of synthetic transforms. Scheme 5a shows the general EAS reaction, while Scheme 5b1 and b2 show the complete mechanism of the EAS reaction.4,15b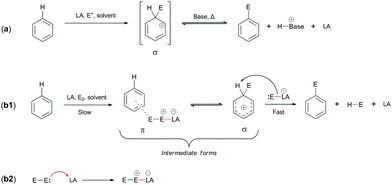 | ||
| Scheme 5 General mechanisms of electrophilic aromatic substitution (EAS): (a) general response of EAS and (b1 and b2) general mechanism of EAS, in relation to reaction (a).15b | ||
We have used the PhH–HBr system mentioned above to explain the mechanism of benzene addition. However, as can be seen from Scheme 5b1 and b2, the addition of a catalyst leads the reaction in a different direction. To explain this direction, it is necessary to emphasize that both the electrophile and the catalyst are completely different from the HBr molecules.
The only difference between the addition reaction and the electrophilic–aromatic substitution is in the nature of the final product. Mechanistically, the reactions are very similar, but the addition reaction has a product that loses aromaticity and consequently isomerizes very quickly to an aromatic form, which is particularly favorable for the feedback reaction. Instead, the EAS reaction regenerates aromaticity and a substituted compound on the aromatic compound is obtained (as the name of the reaction itself indicates).
It can be seen from Scheme 5 that the EAS reaction also goes through the formation of π-complexes and σ-complexes,16–23 which explains the gradual destabilization of the aromatic system. First, a π-complex is formed, which is thermodynamically less stable and rapidly isomerizes to the corresponding σ-complex.42 The stability of the π-complex is characterized by both the quality of the electrophile present and the coordination of the π-electron with this electrophile. This coordination is usually established slowly, so the formation of a π-complex is slow, and mobile π-electrons bind to free hybrid orbitals (if there are any). This results in a reduction in the energy of the transition state and also in potentially a more stable intermediate.24 If there is no empty hybrid orbitals on the electrophile here, then the coordination takes place via the counter σ/π (σ*/π*) orbitals. By binding over against the connecting orbitals, the energy of the transition state increases due to the energy requirements and differences between the HOMO of benzene/arenes and the LUMO of the electrophile. Theoretically, the energy of the HOMO of benzene is constant, while the LUMO of the electrophile is variable, as a function of its stabilization by an additional agent. The addition of a catalyst that lowers the energy of the LUMO is a solution, which thus requires the presence of this chemical species that would position the electrons from the electrophile in its empty nonhybrid orbital, thus making the LUMO more reactive.
In experimental terms, Lewis acids have been shown to be the best chemical species for this purpose, as they show a good yield–selectivity ratio (i.e. ratio that defines catalyst applicability [i.e. Lewis acid(s)] versus yield achieved using this methodology). Theoretically, the most suitable Lewis acids are transition metal halides or metalloids and also carbonyl transition metal complexes.19 The structural aspect of the halides of metalloids and p-block metals has shown that the efficiency of electrophile complexation for this reactant is very favorable for the further course of the EAS reaction, which makes the electrophile sufficiently electrophilic for the EAS reaction to take place. Very strong Lewis acids are most commonly used for this purpose, such as SbCl5 or SbCl3, AlCl3 or AlBr3, and BCl3 or BF3. Chlorides of iron(III), gallium(III), and titanium(IV)25 are also used for the electrophilic aromatic substitution reactions, as are also ferrocenes and carbonyl complexes of chromium(0), manganese(0), rhenium(0), and tungsten(0).26 In general, due to the steric characteristics of ferrocenes and carbonyl complexes, they are mainly less used in these EAS reactions (they are more often used in EAS reactions on hetero-aromatic reactants). Here, the most commonly used acids are AlCl3 or AlBr3, SbCl5 or SbCl3, and FeBr3.
If, on the other hand, we turn our attention to π-complexes, it can also be said that the more aromatic the π-electrons associated with a particular electrophile, the greater the stability of the resulting π-complex. A qualitative measure of the stability of such a complex can, therefore, be related to the number of coordinated π-electrons of the aromatic reactant, which is characterized by the measure of hapticity (ηn, where n is the number of coordinated carbon atoms), which will be discussed further later. It is necessary to mention for now that only π-complexes are characterized by coordinate connections. The nature of the coordinate bond in π-complexes with η number >1 can be characterized as a higher-level coordinate bond, the affinity of which will depend on the number and type of substituents on the observed aromatic compound. Through rapid isomerization and transition to the σ-complex, all coordinate connections of a higher level are theoretically broken more rapidly, with the formation of one, much stronger, σ connection. It must also be emphasized that the coordinate bond is caused by inhomogeneity in the π-electron cloud of aromatics, and that this increases the probability that, in the subsequent presence of electrophiles, the aromatic will react according to the scheme shown above. Such coordinate connections are also characterized as connections in which charge transfer takes place, so that a charge transfer complex is created.19 Růžičková and co-workers recently conducted a study in which they characterized the frozen π-complex of toluene with the hydronium ion (H3O+). This characterization is currently difficult to implement mainly because of the rapid isomerization to the corresponding σ-complex.27 In terms of reactivity in EAS reactions, the hydronium ion is a very ‘ungrateful’ chemical species that can be used as a source of protons and can also assist in the easy formation of H–π-complexes, which would serve as activating species in EAS transforms. In explaining the nature of protons and complementary coordinate species, Reed provided an insight into the structure of differently hydrated and solvated protons28 and also into the potential source of protons with fewer nucleophilic counterions. This provides a potential direction in which the possibility of easier formation of H–π-complexes in EAS transforms might be further developed.
Characterization of σ-complexes in electrophilic aromatic substitution
In this sense, σ-complexes differ because their stability is higher from the kinetic aspect, considering the possibility of stabilization and isolation of these species. Certain types of σ-complexes have been characterized as their salts via NMR spectroscopy. Some of these salts have been shown to be stable even at high temperatures,29 which leaves the possibility for these complexes to be chemically modeled as a function of the presence of different electrophiles. It can be seen from Scheme 5b1 that the stability of the σ-complex depends on whether the EAS product will be formed or whether the starting species (i.e., reactants) will be regenerated. Therefore, it is very important to choose which electrophiles and counterions will stabilize the resulting σ-complex. The electrophile should not be a proton unless the counterion is a nonnucleophilic conjugate base. A nonnucleophilic conjugate base will generally shift the equilibrium between the π-complex and the σ-complex to the σ-complex. Such an equilibrium shift to the right will be particularly pronounced if the intensity of the stabilization of the analog π-complex is higher.During the nonplanar polarization of the π-bond, the dihedral angle of the benzene ring (θ) is very small, from 2.0° to 4.5°, so it can be said that the benzene ring in the σ-complex retains its planarity, while the angle between the C–H and C–E bonds is modified, as 90.0° (±3.0°) to 109.2° (±3.0°). An angle measurement error of ±3.0° originates from the minimum deviation of the dihedral angle (θ) and from the data on the basis of which the angles were calculated. The angle that encloses the electrophile with σ(C–H) in most systems still retains an angle of 100.0° to 109.2°, which can be related to the path of attack of nucleophiles on carbonyl compounds: the Bürgi–Dunitz angle (103–107°).5a
Deformation of such a HOMO leads to the formation of a C(sp3) site, as already mentioned, while the C(sp2)–E bond is shortened relative to the same bond in the π-complex.20Fig. 4 shows the ratio of the angles that overlap the electrophile and the hydrogen atom, with respect to the plane axis (i.e., the benzene nucleus).
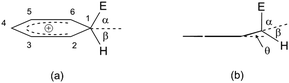 | ||
| Fig. 4 (a) σ-Complex of benzene (benzenium ion). (b) dihedral angle that encloses the C1 atom with the remainder of the benzenium ion. The angles α and β are formed during the formation of the C(sp3) site with the electrophile (α) and hydrogen (β), while the θ angle indicates the dihedral angle.29 | ||
The instrumental characterization of these two intermediate species (i.e., σ-complex, π-complex) was aggravated until the beginning of the 21st century. However, to date, some advances in certain characterization techniques have been made, such that it is possible to observe and characterize the clear presence of σ-complexes in electrophilic aromatic substitution, while for π-complexes this is reduced to the possibility of characterization, but in relation to the stability of the corresponding σ-complex. This is also explained by the increased stability of a given σ-complex as a function of the equilibrium of the transformation of the π-complex into a σ-complex, and also by the characteristic energy balance of the connections that are broken and created in these two types of complexes.
In this regard, nuclear magnetic resonance (NMR) and infrared (IR) spectroscopy have been developed for characterization, hoping that the relevant data can be obtained using these two methods. A more stable C–E connection is monitored as a function of time (dt) and its total energy (dH2 or dG2) in relation to the choice of one of the two methods indicated. These dependences have been shown to be effective in both the experimental and theoretical senses, so they have been taken for the approximate determination of the energy of this σ-complex and also for monitoring the mentioned C–E bond.30 The corresponding C–H bond has been shown to weaken over time, which can be revealed using 1H NMR and also 13C NMR spectra. This weakening of the C–H bond is accompanied by the appearance of an adjacent carbon site where its δC values far exceed the δC values for aldehydes and ketones (190–210 ppm) and also for intra-hydrogen bonded 1,3-ketoenols (180–200 ppm). Peaks that occur at 260–367 ppm in 13C NMR spectra correspond to new highly magnetically deflected sites.18 However, peaks located at 150–190 ppm were seen in the 13C NMR spectra of the σ-complexes, which can be explained by the presence of appropriate substituents that stabilize the positive charge and also by the structure of these complexes.21,31 Their appearance in 13C NMR spectra is characterized by the appearance of moderately strong or weak singlets, even when using distortionless enhancement by polarization transfer 13C NMR and similar techniques. In contrast, C(sp3) sites are characterized by a large decrease in the displacement value (δC) relative to the analogous core values before the formation of this σ-complex. Their values, which closely correlate with the identity of the electrophiles, vary from 40 ppm to 90 ppm. These large differences in δC are reflected only in the diversity of the electrophiles that can participate in EAS reactions and that are stable enough to react here. These complexes are generally recorded at temperatures from −78 °C to −100 °C, mainly due to their relative instabilities, while recording above room temperature is impossible due to thermal decomposition of the test substance! As it is possible to interpret the stability of species as a function of the NMR time scale, the general relation dδC/dt can be used to characterize the stability of the complex and also the strength of the C–E bond, as mentioned above, which can be used to effectively monitor the isodesmic changes.
The IR spectra provide another option to monitor and characterize the instrumental σ-complex, as a function of the second derivative of the dependence of the vibration frequency of the connection (d2ν) on the thermodynamic properties of the bond (dH2 or dG2). As the frequency of vibration of the connection when using IR is usually represented as an inverse value (i.e., a wave number), the function of the dependence of the thermodynamic parameters is observed in relation to the change in the wave number. According to Hooke's law, the wave number will depend on the strength of the bond if the atoms in the bond considered are viewed as unit particles of the oscillatory system. In σ-complexes under IR spectroscopy stability monitoring studies, pattern changes occur; it has been shown that the wave number of the C–H bond of the benzene nucleus decreases with time as the complex is formed, which characterizes the formation of the C(sp3) center along with the loss of the C(sp2) center. At the same time, a C–E bond is formed, the wave number of which increases with time. This thus creates a strong enough bond that is polar enough such that the electrophile addition reaction is not reversible. The polarity of the bond changes proportionally with the change in the wave number, which can be further related to the hydrogen acidity for these C–H bonds at different reactive sites. The typical values of the aromatic C(sp2)–H bond (3020–3050 cm−1) as a function of time decrease (to 2600–2800 cm−1),21,32 which corresponds to the overtone peaks of aldehydes (2700–2800 cm−1) or to C(sp3)–H bonds. As the aldehyde does not form during the formation of the σ-complex, it can only be characterized as a transformation of the reactive site. In addition to these two methods, X-ray spectroscopy can also provide insights into the structure of the σ-complex formed.18
Characterization of π-complexes in electrophilic aromatic substitution
In methodological terms, the characterization of the π-complexes is very limited and very specific. This implies that very strict and extreme conditions are needed for a π-complex to be characterized, provided that it survives as a species very shortly in solutions (10−12 to >10−15 s) and that some of these complexes can be isolated, which significantly prolongs the life of this species (e.g., from a few minutes to a few days or weeks). UV/Vis spectroscopy has been shown to be an effective technique to relatively easily and quickly record and ‘capture’ the π-complex,3 provided that the ratio of the recording time and the quality of the data obtained are good. Modified UV/Vis spectrophotometers with diode-array technology can record spectra over a few milliseconds, while laser-induced spectrophotometers can record very unstable intermediates that have a lifetime of femtoseconds,21 which corresponds to the lifetime of this π-complex. Given that a very small number of π-complexes have been recorded due to their labile chemical nature, the characteristic absorption maxima (λmax) vary between 343 (±3) nm and 530 (±1) nm. This can also be used to determine the reaction kinetics and thus the reaction mechanism. However, the results obtained using UV/Vis spectroscopy are very narrowly defined in their interpretations, because they are very dependent on the type of solvent used, the thickness and type of cuvette, and the concentration of the substance or type. These four parameters make it much more difficult to reconcile the data, so further mechanistic analysis is limited by this, and further mathematical analysis of UV/Vis spectra (e.g., first and second derivatives of the function by dG and dt; see above) can only characterize the strength of individual π-coordinate bonds in these complexes with certain electrophiles. To date, data have been obtained for several very potent heteroatomic electrophiles, such as H+, Cl+, Br+, and NO+, and also for some reactive carbon electrophiles, such as Me+.21,34,35 This presentation of the data indicates another conclusion that should be addressed, that is, it has been reported that the absorption maxima increase with increasing substitution on the attacking nucleophile (e.g., benzene/aryl). Also, these maxima are slightly sharpened with increase in the electrophilicity of the selected electrophile, and also the molar absorption coefficients do not change significantly with a change in substitution and the selected electrophile!21,33 This conclusion might discourage monitoring of the changes and stabilities of these complexes or intermediates through successive transition states. Therefore, other characterization techniques have been sought, precisely for the reasons of reliability and verification of the information obtained via UV/Vis spectroscopy.It has also been shown that X-ray spectroscopy and IR spectroscopy can be very useful in solving the structures of these complexes. It should be noted that X-ray spectroscopy can be used when more stable π-complexes are studied, while for those that are less stable it is better to use UV/Vis, and especially IR, spectroscopy; due to quantum excitation of the vibrational levels of electrophiles, this can provide data even for relatively unstable π-complexes. In particular, in π-complex analysis, the multiple photon dissociation technique with IR spectroscopy37,38 has been shown to provide reliable data for these types of coordinate bonds.36,38b Bearing in mind that the energies and lengths of these coordinate connections change as a function of time, it is possible to efficiently monitor the changes in the wave numbers as a function of time. As the energy and length of a bond are proportionally related to the overall stability of this type of (coordinate) bond, modified dependence of the function of the wave number change on the change in Gibbs energy per unit time can be introduced.
Such a mathematical model has already been presented in terms of the σ-complex (see above); however, in this section, this is discussed again on the basis that the characterization of the π-complex is more delicate than that of the analogous σ-complexes, and so this should be mentioned here as well. It can be set in two ways so that its solution follows the course of the reaction, and thus of the reaction coordinate and reaction mechanisms (see eqn (1a), (1b), (2a) and (2b) below). These mathematical models are prototype conceptual models for the prediction of reaction mechanisms through instrumental means (IR specifically), and it can be assumed that the relative errors will be relatively large at the start. Of note, if theoretical predictions are made, those for vibrational constants (k; Hooke's equation) and wave numbers (ν) will largely depend on the choice of the theory. In the course of research to date, the B3LYP hybrid theory in general has proven to be the most accurate for the prediction of these values. Modified hybrid theories, such as B3P86, B3PW91 and BLYP, have also shown comparable results.32,36,40 The use of basic sets in the corresponding theories mentioned has proven to be decisive, considering the diversity and function of the basic sets in computational chemistry. Therefore, sets with diffuse functions and also sets with selected d-diffuse functions have shown better results than rigid ones (e.g., 6-311+G**; 6-31G*, 6-31G**).32,36,39,40 In addition to the B3LYP hybrid theory, the classical Hartree–Fock theory with density-functional modification (HF/DF) has provided some accurate data regarding the benzene nitrosation reaction.39 Of course, other theories have also provided appropriate data, such as those of MINDO, MP2, HF, and CISD, although their errors in the estimated values of the parameters monitored are generally larger than those of B3LYP and HF/DF.39,40 For example, the nitrosation reaction, in which the π-complex is perhaps the most researched according to the literature, can provide not only insights into the characteristics and possibilities of π-complex characterization, but also some substantial (key) characteristics for EAS reactivity, as well as potential new possibilities in chemoselectivity of the substituted benzene nuclei.
Starting from the wave number (ν) and Gibbs free energy:
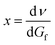 | (1a) |
This can be differentiated by dGf, respectively: 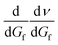 , which gives
, which gives
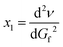 | (1b) |
Thus each changes as the function of time is characterized by two points in the two-dimensional coordinate system as an ordered pair (x, x1)!
If the first derivative is considered as a local minimum/maximum of a function, then the flow of this function is determined by the first and second partial derivatives, as a function of time (t) and transmissibility/transmission (in IR spectroscopy, T), as a fixed reference parameter:
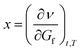 | (2a) |
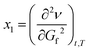 | (2b) |
Eqn (1a) and (1b) are the basic equations from which the analogous eqn (2a) and (2b) are derived, which also include the third common parameter. This more approximately determines the position of x and x1 (points in the coordinate system that describe the reaction flow, as a function of local maxima/minima and as changes in the function flow, respectively) in the two-dimensional coordinate space of the energy diagram.
Therefore, the binding of a π-electron to an electrophile is, it can be said, essential for further development of the EAS reaction, in a mechanistic sense, together with the concept of the stability of its analogous σ-complex, which has already been discussed. The stability of the π-complex as highlighted in Scheme 5b1 is in very delicate microscopic equilibrium with the σ-complex,42 making such a coordinative relationship very important in this type of discussion. For this reason, the role of hapticity in the characterization of the π-complex must be further discussed. Fig. 5 shows possible models of the π-complex formed with a given electrophile (E+).
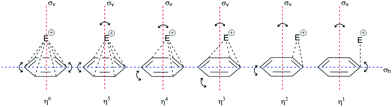 | ||
| Fig. 5 Three-dimensional representations of the π-complex of benzene with electrophiles as a function of the electrophilic displacement from the vertical plane of reflection (σv) and the horizontal plane of reflection (σh). The complexes of all hapticities undergo deformation, both in the ring and in the position of the electrophile in relation to the σh plane of reflection (i.e., so-called planar distortion).19,41 | ||
The structure of the π-complex is defined by the coordination of carbon atoms for a given electrophile. There are six carbon atoms on the benzene nucleus, and hence there are six potential sites. To date, the characterized complexes with hapticities (η) of 1, 2, and 6 and hypervalent order of hapticity have shown greater stability than other species of the same type of complex.19,41 In the terminology of organometals and EAS, hyperhapticity refers to values of η that are >6, and this is accompanied by greater molecular complexity, from which it can be said that hyperhapticity is shown only by certain types of aryl compounds. These types usually include conjugated unsaturated compounds, the substituents of which are unsaturated chains, although it is possible to form hyperhaptive π-complexes with isolated unsaturated bonds in such an aryl compound, where the stability is less than analogous hyperhaptive complexes with conjugated unsaturated bonds. The presence of a triple bond does not (significantly) affect the stability of the π-complex as a double bond. Part of the reason for this is the stiffness of the triple bond, as well as the additional s-character in the C(sp) atoms in this bond. The increased electronegativity of the C(sp) atoms (2.8 < χ ≤ 3.1)44 shows increased electron mobility, which in the theoretical model can disrupt the homogeneity of the π-electron cloud and thus the stability of the corresponding π-complexes. Although data on the thermodynamic or kinetic properties of such π-conjugate complexes have not been published to date to the best of our knowledge, according to current knowledge, conclusions can be drawn that would justify the hypotheses related to these types of complexes. These could be supported by hybrid theories used to calculate the zero energy of lower hapticity complexes and also used to calculate the total enthalpy and free energy (i.e., zero-point energy, sum of electronic and thermal enthalpies/free energies, respectively).41
If the concept of unsaturation is introduced into the thesis of hapticity in EAS, a clear trend can be seen where the increase in the index of hydrogen deficiency (or the double bond equivalents) is accompanied by an increase in the hapticity, along with a general proportional increase in the thermodynamic stability of these π-complexes. Indeed, in the general interpretation of the stability of π-complexes, this trend is manifested, but only in hyperhaptive π-complexes; on the other hand, in the case of ‘regular’ hapticity complexes, this trend is not so precisely and correctly defined,18 even when general considerations of stability are introduced.43 That is to say, complexes with η of 3, 4, and 5 are less frequently characterized and are more likely to be characterized when there are multiple electron-donating substituents on the benzene nucleus, wherein this number is generally ≥3 row-linked substituents, in strong activating groups (e.g., OH, OR, NR2, CR2−, M; R = H, alkyl), or more than three sequentially or alternately arranged substituents, in moderately strong groups (e.g., O-esters, N-amides, OCN, SR; R = H, alkyl). This conclusion arises because of the effective balance between the two effects that define the stability of these types of complexes: the electron-donor power of the substituents involved and the level of stabilization of this complex by coordination bonds. It has already been mentioned that the more the coordinate bonds in the π-complex, the more stable it is: some η4 and η5 complexes show a certain degree of structural deformation during the construction of the π-complex (the term ‘planar distortion’ is also used; Fig. 6) due to the possibility of deformation of the homogeneity and shape of the π-cloud, which is shown in Fig. 5 as the absence of coordination with the electrophile. This disrupts not only the stability of this complex, but can also result in a negative trend of enthalpy–entropy compensation for a number of such types of complexes, which does not favor the thermodynamic product. From the kinetic point of view, such complexes can be generated19 whereby their lifespan is shorter than those of the more stable η1, η2, or η6 π-complexes. With some metal cations, such as tantalum (Ta2+/3+), it has been reported that even stable η6 complexes can show some deformation of the benzene nucleus, which even depends on the charge of the electrophiles (tantalum cations, in this case), which means that all of the complexes have the possibility of planar distortion.19 Electron-acceptor substituents mainly destabilize the π-complex and do not favour its formation. Some of the more stable types of complexes listed above can survive very briefly and isomerize very rapidly to the corresponding σ-complexes,41 where the effects of substituents on the benzene nucleus in electrophilic aromatic substitution reactions are reflected, as also for the overall influence of such substituents on the reactivity of the benzene nucleus.
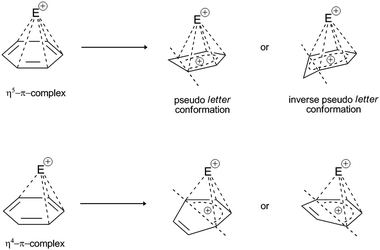 | ||
| Fig. 6 Possible deformations (i.e., planar distortions) of the η4 and η5 π-complexes in the presence of a coordinated electrophile. Deformations of the benzene ring can take place in one (vertical) plane, which impairs the enthalpy stability of the complex. For the η5-complex, due to a partial positive charge on the noncoordinated C-atom, the inverse pseudo-conformation of the latter is retained, which further destabilizes the enthalpy complex. Such deformations have been experimentally determined for E+:lanthanide complexes, Ti, Zr, Fe, Ru, Co, and Ni.45–49 | ||
Course of electrophilic aromatic substitution as a function of transition-state energy ratios: determining the rate-limiting step
To round off the part concerning the mechanistic aspects of EAS, we return to the concrete PhH–HBr system. To explain the mechanism of EAS for this example (according to Scheme 5), the Lewis acid must be taken into account and also the corresponding electrophile. Hydrobromic acid cannot be used as an electrophile due to redistribution of electron density, which favors the polarization of the H–Br bond (see above). For this reason, elemental (liquid) bromine will be used as the corresponding electrophile, FeBr3 as the corresponding Lewis acid, and benzene as the relevant aromatic nucleophile.Elemental bromine (Br2) is a non-polar molecule, the bond within which can be broken in two ways:
(1) Using a very strong nucleophile that can polarize the bromine atom in a Br2 molecule (e.g. lithium– or magnesium–halogen exchange transform), which will make the original σ*-orbitals more susceptible to electron reception. This method of activating the antibonding σ-orbitals is possible due to the higher coefficient of polarizability of the Br2 molecule and the reduced coefficient of chemical hardness (ηs)50 and also due to the high coefficient of nucleophilicity and the reaction sensitivity factor51 of the corresponding strong nucleophile. Within the interpretation of this method, strong nucleophiles can be functionalized carbon nucleophiles, such as metal enolates,52–64 Grignard reagents,65–67 organolithiums,68–70 (highly) activated aromatics,62,63,71–76 nitrogen nucleophiles,77–79 and in some cases (e.g., in a narrowed choice of solvents) alkali metal oxides. Therefore, it is important to emphasize that, together with the parameters of acidity (i.e., ΔGacid, pKa[solv.]), chemical hardness50b,c and chemical potential (μ)80 are the basic and main parameters when considering the choice of nucleophiles81 and electrophiles for this method.
(2) Photochemically, using rays of shorter wavelength (λ) than those in the visible region of the electromagnetic spectrum. These are mainly the wavelengths of the UV region of the electromagnetic spectrum (180 < λ < 250 nm), which excites the binding electrons of both bromine atoms so much so that the vibrational levels of these electrons are disturbed, and the electrons are brought into a state of excitement. When they are in the excited state, σ-binding orbitals become half-filled orbitals (i.e., SOMO); these have much higher energies than the binding energies and are also much more unstable, which results in a significant increase in the reactivity of these species. These are characterized as free radicals, and it has been experimentally shown that free radicals trigger the reaction by reacting with the corresponding atoms in the reactant, making the reactant very reactive to the electrophile. Photochemical induction of reactivity requires either irradiation of molecules, as already mentioned, or introduction of the so-called initiator molecules. These initiator molecules contain a characteristic energy-labile bond, which under the action of an energy quantum (hν) decomposes homolytically, to give a reactive radical, which initiates the initiation phase.4 As for the hydrogen radical (H˙), the bromine radical (Br˙)82 will react with the species that has the highest affinity for the electron and where the bond will be the most stable. As it is generally more difficult to predict reactivity in radicals compared to analogous ionic species, in the theory of EAS, this method is not so mechanistically obvious. This is because the characteristic step of initiation is the abstraction of a proton or a corresponding substituent if the conditions are met from an electronic point of view, which generates the corresponding phenyl or aryl radical.83
Iron is a relatively electropositive element, with an electronegativity value according to Pauling (χP) of 1.83 (±0.03). This implies that, as a rough conclusion, for any element where χP > 1.83 and which forms a compound behind iron, a map of its electrostatic potential shows a relative local electron deficit on the iron/atom. This means further that, through its σ-bonds, iron transfers electrons to this more electronegative element, with which it builds a compound, i.e., that it has a more pronounced positive inductive effect in a given compound. Therefore, the iron atom/ion in the same compound will carry a partial positive charge, which will depend on the element with which it builds the compound and also on the oxidation state of the iron atom. The FeBr3 molecule is such an example, in which not only the polarization of the Fe–Br bond is more pronounced but also the type of valence orbitals of iron: the two main factors that give a favorable picture when discussing the efficiency of a molecule such as a Lewis acid. The triple partial charge on the iron atom in FeBr3 indicates increased electrophilicity of the iron atom, which lowers the energy of the LUMO and makes it available to electrophiles with a relatively low HOMO, such as the Br2 molecule. On the other hand, the Fe3+ ion has an electronic configuration of [Ar]3d5, which indicates the stability of this ion, although the 18e-rule is also violated, with 11 electrons on the iron atom in FeBr3. This emphasizes that the bond order in this molecule is a little lower than 1, which, in the theory of EAS, results in a more diffuse redistribution of the electron density and easier generation of electrophiles. An additional aspect that confirms these conclusions is that, by forming a p–d bond between electrophiles and iron ions/atoms, the electron density on the electrophile decreases to some extent through an additional σ-formed bond84a due to the polarizability of iron d-orbitals.84b,c A similar type of analysis can be applied to other types of Lewis acids85a–e and also to Brønsted acids! This analysis shows that transition metal halides are a good choice as catalysts (or catalytic systems) for the EAS reaction.
As indicated above, elemental (liquid) bromine, Br2, is a nonpolar molecule with a bond order of 1. Due to the nonpolarity of the σ-bond, the bromine molecule is a relatively poor electrophile in EAS reactions. Therefore, the use of FeBr3 as the catalyst has shown its good chemical properties relative to the reactivity of bromine molecules in EAS reactions.84,85a,c,d It must also be emphasized that the electrophilicity of Br2 is affected not only by Lewis transition metal acids in EAS reactions, but also by other species that function as catalysts via other mechanistic pathways. These species are very similar in chemical terms to the Lewis acids of transition metals, but bromination (and in the general case, halogenation) takes place indirectly.85b,c,e–j However, such delicate differences in the mechanisms of the EAS reaction in the couplings mentioned are even more delicate when the reactivities of elemental bromine in different solvents or oxidants are taken into account.86,87 These mechanistic principles of the catalyst-neutral electrophilic source coupling with these types of catalysts will be explained below.
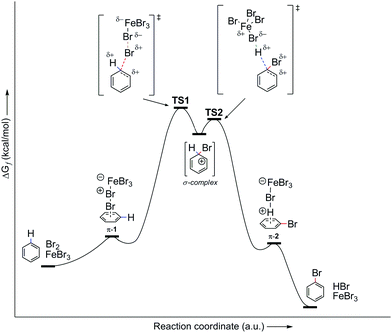
However, let us look at the example given in the previous paragraph (i.e., PhH–Br2–FeBr3). To better understand the EAS reaction of this system, the energy profile of the reaction should also be considered, as shown in Fig. 7. From this, it can be seen that the energies of the transition states are greater than both the reactant and the product, and are also higher than that of the main intermediate, the σ-complex. The TS1 and TS2 transition states in Fig. 7 are a reflection of the electrostatic reactivities of benzene and the given electrophile/electrophilic coupling (Br2·FeBr3), which thus achieves the preliminary binding of electrophiles to the nucleophile molecule via the π-electron cloud, to create the first π-complex. When the π-complex was mentioned previously here, it was not indicated that two types of π-complexes can occur mechanistically: the first is characterized as the so-called early transition state, and the second as the so-called late transition state. In kinetic and thermodynamic terms, these two types of π-complexes are very similar, and in EAS reactions they are very close to each other, in relation to the reaction coordinate. However, due to the small differences they show, in terms of both the leaving group and the entire reaction system related to the two complexes, they can be considered as separate. The energy profile of this reaction system will show the structures of both of these π-complexes, as well as explain the differences between the general scheme of the EAS mechanism as presented in Scheme 5 and this scheme as presented in Fig. 8.
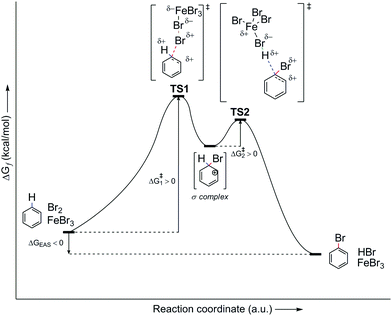 | ||
| Fig. 7 Energy profile of the PhH–Br2–FeBr3 reaction system, as the general energy profile without including the π-complexes. TS, transition state. | ||
By comparing Scheme 5 and Fig. 7, and according to the analysis of the general reaction system for EAS, it can be seen that the comparison is incomplete and that certain information and details are missing within the interpretations. Thus, the use of a catalytic system reduces the total energy of the system, where ΔG is negative. Despite the large energy barriers for the TS1 and TS2 transition states, it can be seen from Fig. 7 that the product creation function from transition state 2 (TS2) shows a steeper energy curve. This steeper curve gives a mathematical indication that the reaction proceeds faster and that further hypothetical energy barriers are smaller, such that they can be overcome (if they indeed exist). For the reaction system itself, this indicates that it can change more spontaneously, as a function of time. This also indicates the nature of the intermediate in that part of the reaction coordinate, and it can also give a qualitative idea of what the reaction products would look like. Furthermore, and perhaps more importantly, this indicates the geometric properties of the intermediates involved. On the other hand, in the earlier reaction stages, the energy change curve is not so steep for the reaction coordinate, which can also be seen in Fig. 7. This relatively (or slightly) flatter energy curve in this profile suggests a lower level of spontaneity for the reaction, which is logical from the aspect of its entropy gradient. Thus, in the earlier stages of the reaction, the entropy of the system is only gradually reduced, which brings the system into a state of greater order. The greater order of the system is not characterized by pronounced spontaneity of change, to thus respect the Laws of Thermodynamics. A system that reaches a higher level of order through a constant balance of systemic physico-chemical phases spontaneously transforms into its disordered phase, while releasing a certain amount of energy as a function of time. This energy release also results in the formation of a multi-reaction type system, as is the case with the reaction system analyzed in Fig. 7 and 8.
The analysis of the energy profiles between Fig. 7 and 8, when compared to the example of the reaction system used here, corresponds to the part of the energy profile between transition state 1 (TS1) and the σ-complex. This part of the reaction coordinate where the σ-complex is located is characterized as the local minimum of the EAS energy profile. In Fig. 8, this is characterized by a small drop in the system energy, and the ratio of the number of reactive species is also of importance. Transition state 1 is characterized by the dynamic formation-breaking of bonds within the electrophile considered (Br2), the catalyst that is already coordinated (FeBr3), and the benzene nucleus, as the corresponding nucleus here. The previously indicated nonplanar polarization of the π-electron cloud of the benzene now results in the binding of one bromine atom to the carbon site of the benzene, which changes the length of the three relevant bonds in this part of the reaction coordinate: d(C(sp2)–Br1), d(Br1–Br2), and d(Br2–Fe). No matter how much these bond lengths change, this transient state is characterized by one reaction system, in which all three species are connected at the same time, which can be used as an argument for the decrease in the entropy gradient of the EAS reaction system. However, the very large internal energy of this transient state is released spontaneously, which breaks the Br1–Br2 bond to generate the corresponding σ-complex and the [FeBr4]− counterion. The moment the σ-complex is formed, the energy decreases, as the entropy gradient increases. This increases primarily due to the increased disorder of the system, which is mainly caused by the increase in the number of reactive species. As there was one reactive species in transition state 1, in the form of a reaction subsystem, the counterions and complexes in the next step mean a doubling of the number of reactive species in this part of the reaction coordinate.
Then, noting that the σ-complex is an unstable reactive species and that [FeBr4]− is a source of nucleophilic bromine, the EAS reaction does not end with the formation of the σ-complex, as has been shown experimentally.88a In the second phase of the EAS reaction, this σ-complex that is under the influence of the field of the anti-aromatic benzene ion is further polarized at the newly formed C(sp3) site. This σ-complex contains bromine and hydrogen, which have both been shown to be potential electrophiles, whereby their electrophilic affinities depend on their internal properties as well as on the conditions under which the reaction takes place. If there is a source of nucleophilic species, the competition between the reactivities of hydrogen and bromine on the σ-complex will be balanced. If there is a good base, this will deprotonate the σ-complex and give the EAS reaction product. If there is a species that has an ambifunctional role (i.e., can act as both a nucleophile and a base), the reactivity will again be competitive between the hydrogen and bromine atoms. The outcome for this part of the reaction will result in the appearance of another energy barrier in the given reaction. This barrier will be considerably smaller and will be bridged using even very weak bases (see σ-complex/benzenium ion acidity in the paragraph above; Scheme 6). In agreement with this, it should be noted here that the EAS reaction is reversible at this stage, when there is a possibility of competitive reactions with effects on one reactive species, as the σ-complex in this case. As in this step the bromine atom on the σ-complex is more electron protected at the valence level (as opposed to the hydrogen atom, which has no additional electrons of its own), the abstraction of the H-atom versus the Br-atom is more likely. If this is the case, the bromide from the tetrabromoferrate(III) ion will undergo preliminary binding to the H-atom from the σ-complex, giving a second or later transition state. In relation to the overall reaction coordinate, the features of the later transition state are that all of the reactive species have lower energies in relation to the other (earlier) parts of the reaction coordinate. Furthermore, the energy barriers are significantly lower compared to those from the earlier coordinate. This leads to the conclusion that the reaction after the formation of transition state 2 takes place spontaneously, which is mainly the outcome in EAS reactions, in a mechanistic sense. Transition state 2 is characterized by the coordination of bromides for the hydrogen atoms of the σ-complex, with the lengthening of the C(sp3)–H bond. This leads to a steeper curve for this part of the coordinate, the EAS reaction (as characterized by the great spontaneity of this part of the reaction). This conclusion can be further argued by looking at the structures of TS1 and TS2. As already mentioned, to form the σ-complex, the electrophilic species needed to approach and induce the polarization of the π-electron cloud of benzene under the action of the catalytic system. Only then can this reaction take place, the further course of which would depend on the intensity of the electrophilicity of the electrophile used and the catalytic system. Then, on the other hand, when passing through transition state 2, the modification of the reactive species refers exclusively to the preferential extension of the characteristic C(sp3)–H bond! Therefore, this is an excellent introduction to the analysis of another factor of the EAS reaction: the occurrence and reactivity of the corresponding π-complexes along the reaction coordinate.
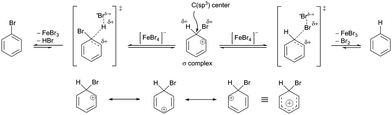 | ||
| Scheme 6 Two modes of reactivity of the σ-complex as a function of the tetrabromoferrate(III)-ion ([FeBr4]−) (top) and the resonant structure of the σ-complex with the resonant hybrid (bottom). | ||
To date, there have been no indications of the influence of π-complexes on reactivity and reactive species in EAS. However, as was noted at the beginning of this analysis, the energy profiles differ in their forms, depending on whether they are considered completely (i.e., with all transition types included) or incompletely (i.e., with only appropriate transition states). The following should thus be inserted into the whole narrative so far, in the thermodynamic sense: there would be no transition state 1 if there was no appropriate species that can lead to its formation through energy compensation. Fig. 8 shows the complete energy profile of the PhH–Br2–FeBr3 reaction system. A simple comparison of Fig. 7 and 8 shows that there are small changes in the early and later parts (regions) of the reaction coordinate, which have their own energy barriers. These small changes correspond to the formation of the corresponding π-complexes, in the experimental sense.
These π-complexes are mechanistically significant for the analysis of the complete mechanism of electrophilic aromatic substitution because the ratio of their energies defines the slopes of the curve in the early and late transition states and thus the energies of the corresponding transition states 1 and 2. When it comes to π-complexes, they can be related to the determination of the slowest reaction step and the definition of the EAS reaction rate, i.e., by defining the EAS reaction in a kinetic sense. Analysis of the reaction curves in Fig. 8 shows that, in the early region of the reaction coordinate, π-complex 1 (π-1) has a small energy barrier, i.e., the formation of this species is characterized by a small positive ΔG. However, given that the driving force is what constantly ‘pushes’ species to undergo a certain chemical change as a function of time, the preliminary binding of the π-electron cloud to the electrophilic coupling will be favored, to form π-1. This will then continue the process of polarization of the Br1–Br2 connection, to bring the system to transition state 1. Next, the reaction proceeds as previously described until transition state 2. Transition state 2 is a specially defined guiding force for the reaction, which makes the transformation process in this transition state isodesmic, whereby the leaving group is brought to a position in which it only sporadically binds to the (at present) reaction product of EAS: bromobenzene. The leaving group is formally a proton, and experimentally a hydrobromic acid, which favors the formation of π-complex 2 (π-2). This complex is similar, although lower in energy, to its analog π-1,88b and this subtle difference in the energies of these two species lies in the species bound to the benzene nucleus, as well as the nature of the newly formed product. Bromobenzene, as discussed further below, is a little less reactive than benzene, which makes it less favorable for binding any type of electrophile in the initial or final step of the reaction. On the other hand, a proton is a slightly better electrophile than a bromonium ion (Br+), mainly due to the aforementioned difference in the shielding effect, which is more pronounced with bromine than with hydrogen. Due to this situation in terms of these reactivities and electrophiles, π-2 will be more stable than π-1, so the influence of the counterion will have a significant impact on the stability of the π-complex, and the type of connection that the electrophile makes with the counterion will thus have an impact on the slope of the curves in the early and late regions of the reaction coordinate. It can be noted that, in theoretical terms, the stability of π-1 depends in principle on the slope of the curve in the early region of the reaction coordinate, and thus the lowest step in the reaction will be determined by comparison of the energies of π-1 and π-2, not considering them kinetically or thermodynamically. The theory of the transition state states that the part of the energy curve that leads to the transition state with the highest energy (or energy barrier, ΔG‡) defines the slowest step in the reaction (i.e., is rate limiting), as well as the overall reaction rate. Therefore, studying the energy of these complexes in parallel made it possible to determine which step in the EAS reaction would be the slowest. From the details above, it can be seen that while there are only very small differences in the energies of these two complexes, π-2 is slightly lower in energy than π-1. This means that the slowest step will be the reaction that involves π-1, and therefore this reaction will be bimolecular, i.e., its reaction rate will depend on both electrophiles (El) and nucleophiles (Nu), as bromine and benzene, respectively. As it is the electrophile that determines the stability of the π-1 type, this means that in the general case the expression for the reaction rate will be consistent with the bimolecular notation shown in eqn (3):88,89
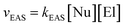 | (3) |
This corresponds to eqn (4) for specific examples of reaction systems in an electrophilic aromatic substitution reaction:
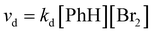 | (4) |
It should only be noted here that the π-complexes by themselves cannot be the ones that determine the course of the reaction because they are not at the top of the reaction curve that determines the reaction rate. According to the above mentioned considerations and analysis, and in agreement with Scheme 5, the mechanism of bromination of benzene in the presence of a Lewis acid can be derived as presented in Scheme 7.
Conclusions
From the aspect of synthetic and physical organic chemistry, the EAS reaction is one of the most researched and applied synthetic transformations in the chemical sciences today. However, over the years, the EAS has been characterized and defined from several different angles, such that a relatively large amount of research has been published on this topic. Despite the fact that now EAS is a very broad topic, this review seeks to present this reaction from the point of view of qualitative physical organic chemistry, with reference to the role of the chemical species that control the flow of EAS. This presentation provides a relatively new point of view on this very widespread and often-applied transform. The results presented and argued throughout this literature review are also in line with the theoretical experimental research that has been additionally argued and published over the last decade, also considering that which has not been strictly related to EAS.84a,90–94Therefore, based on the above analysis, certain conclusions can be summarized as follows:
• The mechanism of EAS implies the use of a catalytic system, except in some cases with highly activated (nucleophilic) nuclei;
• EAS cannot be characterized as a reaction of hydrohalic acid addition, even at elevated temperatures and pressures, or with the addition of a catalyst;
• From the foregoing discussion of electrophilic addition, it is evident that benzene or aromatic derivatives cannot under any circumstances be subjected to successive addition of hydrogen halides;
• The EAS reaction is characterized by π-complexes and σ-complexes, and also by the loss of aromaticity of the benzene nucleus during the formation of the σ-complexes!
• There are the so-called early and late transition states, which depend on the changes in the reaction coordinate of the EAS energy profile, which themselves depend on the corresponding π-complexes that lead to (in the early transition state) or are formed (in the late transition state) in the transition to the reaction product;
• The π-complexes follow the Hammond postulate (according to Scheme 7) and map the reactants or reaction products, depending on their position along the reaction coordinate;
• The rate of the EAS response depends on the formation of the early transition state.
Also, bearing in mind the possibility of mathematical correlation with mechanistic studies of EAS and of the π-complexes and σ-complexes in EAS, and the definition of their stability, the following additional conclusions can be drawn:
• It is possible to determine the stability of the complexes using theoretical (computational) means;
• It is possible to realize the correlation between theoretical and experimental results for a generally larger number of electrophiles, within the limits of the relative error that can range from 1% to 20%, based on the available experimental results. These correlations are defined through computational models and the combination and application of different (functional) theories, so that it is possible to progressively reduce the value of these relative errors.
• It is possible to carry out (complex) mathematical–chemical relations to monitor the mechanisms of EAS by instrumental means through the definition of the first and second derivatives of the approximate function of the transformation curve in the reaction diagram!
• The course of the mechanism can be monitored not only on the basis of theoretical (computational) methods, but also on the basis of instrumental methods (e.g., mainly using IR, NMR, and, possibly, UV/Vis spectroscopy), according to the parameters given in eqn (1a) and (1b), which can also be monitored and evaluated experimentally;
• Based on the proposed mathematical models, a realistic insight into a completely new possibility of mechanistic characterization is created through a thermodynamic approach.
• Thermodynamic mechanistic approaches formulate a new model that connects the kinetic and thermodynamic aspects of the reaction, so such a model can be considered to be useful and also one of the key factors for further development of the physical organic chemistry today. Preliminary evaluation of this approach to certain new methodologies95–100 on EAS systems provides very positive responses. These leave a very clear motive for further improvement of the general theory of these mechanisms in the physical and organic chemical sciences and in other areas of the chemical sciences, such as biochemistry, organometal chemistry, and bioinorganic chemistry.
Thus, with a view to advance the research in this field, it can be said that although a relatively small number of π-complexes have been tested to date, to our knowledge, the results presented here along with our conclusions can be considered to be encouraging, bearing in mind that EAS, as a transform, is still of great interest to many researchers with emerging new techniques.101–103
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Slovenian Research Agency (Research Core Funding Grants P1-0230 and P4-0121). The authors also thank the reviewers for very insightful comments.Notes and references
- W. J. Russell, Proc. Chem. Soc., London, 1890, 6, 95–106 RSC.
- (a) G. W. Wheland, J. Chem. Phys., 1934, 2, 474–481 CrossRef CAS; (b) G. W. Wheland, Advanced organic chemistry, Wiley, New York, 2nd edn, 1949, p. 799 Search PubMed.
- E. J. Corey and X.-M. Chelg, The Logic of Chemical Synthesis, Wiley & Sons, New York, 1995, p. 464 Search PubMed.
- (a) P. C. Vollhardt and N. E. Shore, Organic Chemistry: Structure and Function, W. H. Freeman and Company, New York, 6th edn, 2011, p. 1374 Search PubMed; (b) P. Y. Bruice, Organic Chemistry, Prentice Hall, 2003, 4th edn, p. 1344 Search PubMed; (c) J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press, New York, 2001, p. 1516 Search PubMed.
- During polarization process, short-living carbanion is being formed which turns out to be tetrahedral and attack proton via Bürgi–Dunitz angle. For further information, see: (a) H. U. Bürgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Tetrahedron, 1974, 30, 1563–1572 CrossRef; (b) S. K. Singh and A. Das, Phys. Chem. Chem. Phys., 2015, 17, 9596–9612 RSC; (c) R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846 CrossRef CAS.
- G. A. Olah, G. K. Surya Prakash, Á. Molnár and J. Sommer, Superacid Chemistry, Wiley & Sons, Hoboken, 2nd edn, 2009, p. 867 Search PubMed.
- F. Scholz, D. Himmel, L. Eisele, W. Unkrig and I. Krossing, Angew. Chem., Int. Ed., 2014, 53, 1689–1692 CrossRef CAS.
- I. Alata, R. Omidyan, M. Broquier, C. Dedonder, O. Dopfer and C. Jouvet, Phys. Chem. Chem. Phys., 2010, 12, 14456–14458 RSC.
- (a) F. Scholz, D. Himmel, L. Eisele, W. Unkrig, A. Martens, P. Schliter and I. Krossing, Chem. – Eur. J., 2015, 21, 7489–7502 CrossRef CAS; (b) R. A. More O’Ferrall, Advances in Physical Organic Chemistry, 2010, vol. 44, pp. 19–122 Search PubMed; (c) T. C. Cheng, B. Bandyopadhyay, J. D. Mosley and M. A. Duncan, J. Am. Chem. Soc., 2012, 134, 13046–13055 CrossRef CAS; (d) S. A. Cooke, G. K. Corlett, C. M. Evans and A. C. Legon, Chem. Phys. Lett., 1997, 272, 61–68 CrossRef CAS.
- B. Galabov, G. Koleva, S. Simova, B. Hadjieva, H. F. Schaefer III and P. V. R. Schleyer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10067–10072 CrossRef CAS.
- P. Shaykhutdinova, S. Keess and M. Oestreich, in Organosilicon Chemistry, ed. T. Hiyama and M. Oestreich, Wiley-VCH, Verlag, 2019, p. 568 Search PubMed.
- (a) Y. Yamamoto, J. Org. Chem., 2007, 72, 7817–7831 CrossRef CAS; (b) Y. Yamamoto, J. Org. Chem., 2008, 73, 5210 CrossRef CAS.
- (a) S. Kobayashi, T. Busujima and S. Nagayama, Chem. – Eur. J., 2000, 6, 3491–3494 CrossRef CAS; (b) M. Santelli and J. M. Pons, Lewis Acids and Selectivity in Organic Synthesis, CRC Press, Boca Raton, 1996, p. 352 Search PubMed.
- Y. Nishii, M. Ikeda, Y. Hayashi, S. Kawauchi and M. Miura, J. Am. Chem. Soc., 2020, 142, 1621–1629 CrossRef CAS.
- (a) J. Kong, B. Galabov, G. Koleva, J.-J. Zou, H. F. Schaefer III and P. V. R. Schleyer, Angew. Chem., Int. Ed., 2011, 50, 6809–6813 CrossRef CAS; (b) M. B. Smith and J. March, March's advanced organic chemistry, Wiley, Hoboken, 6th edn, 2007, p. 2377 Search PubMed.
- S. L. Matlow and G. W. Wheland, J. Am. Chem. Soc., 1955, 77, 3653–3655 CrossRef CAS.
- D. V. Banthorpe, Chem. Rev., 1970, 70, 295–322 CrossRef CAS.
- V. F. Sidorkin, E. P. Doronina and E. F. Belogolova, Organometallics, 2012, 31, 7511–7521 CrossRef CAS.
- S. M. Hubig, S. V. Lindeman and J. K. Kochi, Coord. Chem. Rev., 2000, 200–202, 831–873 CrossRef CAS.
- R. Van Lommel, S. L. C. Moors and F. De Proft, Chem. – Eur. J., 2018, 24, 7044–7050 CrossRef CAS.
- S. M. Hubig and J. K. Kochi, J. Org. Chem., 2000, 65, 6807–6818 CrossRef CAS.
- (a) E. Kleinpeter and A. Koch, J. Phys. Chem. A, 2019, 123, 4443–4451 CrossRef CAS; (b) M. J. S. Dewar, J. Chem. Soc., 1946, 777–781 RSC.
- D. A. Lawlor, D. E. Bean, P. W. Fowler, J. R. Keeffe, J. S. Kudavalli, R. A. More O’Ferrall and S. Nagaraja Rao, J. Am. Chem. Soc., 2011, 133, 19729–19742 CrossRef CAS.
- Case of organosilicon cations; electrons are coordinated to vacant Si-orbital in transition state (upon transition from π- to σ-complex).
- Lewis acidities of bromides and chlorides bonded to the same metal ion differ very slightly, thus making bromide a very convenient Lewis acid as well.
- A. Jayaraman and B. T. Sterenberg, Organometallics, 2014, 33, 522–530 CrossRef CAS.
- Z. Růžičková, J. Holub, P. Melichar, J. Moncol, D. A. Wann, J. Fanfrlík, A. Růžička and D. Hnyk, Eur. J. Org. Chem., 2016, 4473–4475 CrossRef.
- C. A. Reed, Acc. Chem. Res., 2013, 46, 2567–2575 CrossRef CAS.
- C. A. Reed, K.-C. Kim, E. S. Stoyanov, D. Stasko, F. S. Tham, L. J. Mueller and P. D. W. Boyd, J. Am. Chem. Soc., 2003, 125, 1796–1804 CrossRef CAS.
- These are simplified functions, aiming to clarify the mathematical purpose of the functions indicated. If the time is being monitored, then the main function is described as (where δE is the experimentally determined shift in the NMR spectrum of given element); or, if monitored as a function of basic thermodynamic properties or number of formed and broken bonds, then: or (T – Transmission in the IR spectrum).
- The aforementioned small dihedral angles can be speculated upon for the instability increase of these carbcationic sites.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- T. Brinck and M. Ljiljenberg, in Arene Chemistry: Reaction Mechanisms and Methods for Aromatic Compounds, ed. J. Mortier, Wiley & Sons, Hoboken, 2016, p. 992 Search PubMed.
- E. K. Kim and J. K. Kochi, J. Am. Chem. Soc., 1991, 113, 4962–4974 CrossRef CAS.
- E. Bosch and J. K. Kochi, J. Org. Chem., 1994, 59, 5573–5586 CrossRef CAS.
- B. Chiavarino, M. Elisa Crestoni, S. Fornarini, J. Lemaire, P. Maître and L. MacAleese, J. Am. Chem. Soc., 2006, 128, 12553–12561 CrossRef CAS.
- G. VonHelden, D. Van Heijnsbergen and G. Meijer, J. Phys. Chem. A, 2003, 107, 1671–1688 CrossRef CAS.
- (a) J. Oomens, A. G. G. M. Tielens, B. G. Sartakov, G. von Helden and G. Meijer, Astrophys. J., 2003, 591, 968–985 CrossRef CAS; (b) J. Oomens, A. J. A. Van Roij, G. Meijer and G. von Helden, Astrophys. J., 2000, 542, 404–410 CrossRef CAS.
- S. Skokov and R. A. Wheeler, J. Phys. Chem. A, 1999, 103, 4261–4269 CrossRef CAS.
- (a) N. Dechamps, P. Gerbaux, R. Flammang, G. Bouchoux, P.-C. Nam and M.-T. Nguyen, Int. J. Mass Spectrom., 2004, 232, 31–40 CrossRef CAS; (b) S. R. Gwaltney, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 3273–3283 CrossRef CAS.
- S. G. Davies and T. D. McCarthy in Comprehensive Organometallic Chemistry II, ed. E.W. Abel, F. G. A. Stone and G. Wilkinson, Pergamon, Oxford, 1995, vol. 12, p. 1039, and references therein Search PubMed.
- D. Lenoir, Angew. Chem., Int. Ed., 2003, 42, 854–857 CrossRef CAS.
- H. C. Brown and J. D. Brady, J. Am. Chem. Soc., 1952, 74, 3570–3582 CrossRef CAS.
- I. Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley & Sons, West Sussex, 2010, p. 529 Search PubMed.
- I. L. Fedushkin, M. N. Bochkarev, H. Schumann and L. Esser, J. Organomet. Chem., 1995, 489, 145–151 CrossRef CAS.
- M. Jang and J. E. Ellis, Angew. Chem., Int. Ed. Engl., 1994, 33, 1973–1975 CrossRef.
- A. S. Batsanov, Y. T. Struchkov, G. P. Zolnikova, I. I. Kritskaya and D. N. Kravtsov, Dokl. Akad. Nauk SSSR, 1987, 293, 614–616 CAS.
- H. F. Klein, K. Ellrich, S. Lamac, G. Hull, L. Zsolnai and G. Hutter, Z. Naturforsch., B: J. Chem. Sci., 1985, 40, 1377–1382 Search PubMed.
- R. Boese, A. Stanger, P. Stellberg and A. Shazar, Angew. Chem., Int. Ed. Engl., 1993, 32, 1475–1477 CrossRef.
- (a) R. G. Parr and W. Yang, Density-functional theory of atoms and molecules, Oxford University Press, New York, 1989, p. 352 Search PubMed; (b) W. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS; (c) R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- Several papers that are in process of preparation.
- X. Wang, A. Hao and T. Wang, Preparation of 2,4-dibromo-1,5-glutaraldehyde Compound Disinfectant used in Paper Currency. Faming ZhuanliShenqingGongkaiShuomingshu, CN 1271518 A 20001101, 2000.
- B. Ziobro, Process for the preparation of 4′-(bromoacetyl) methanesulfonanilide, Pol. PL 187575 B1 20040831, 2004.
- H. Y. Choi and D. Y. Chi, Org. Lett., 2003, 5, 411–414 CrossRef CAS.
- Y. Ling, S. Yang, X. Yang, Y. Sun and L. Zhang, Method for synthesizing (2E)-1-(4-hydroxyphenyl)-5-phenyl-2-penten-1-one, Faming ZhuanliShenqing, CN 102249885 A 20111123, 2011.
- H. J. Harwood, Chem. Rev., 1962, 62, 99–154 CrossRef CAS.
- L. A. Bigelow and R. S. Hanslick, Org. Synth., 1933, 13, 38 CrossRef CAS.
- B. U, Y. Bao, H. Li, Y. Wang, X. Li, ZhongguoYiyaoGongyeZazhi, 2001, vol. 32, p. 374.
- K. M. Aitken and R. A. Aitken, Tetrahedron, 2008, 64, 5217–5220 CrossRef CAS.
- N. L. Drake and J. Bronitsky, J. Am. Chem. Soc., 1930, 52, 3715–3720 CrossRef CAS.
- A. Alix, C. Lalli, P. Retailleau and G. Masson, J. Am. Chem. Soc., 2012, 134, 10389–10392 CrossRef CAS.
- F. Sabuzi, G. Pomarico, B. Floris, F. Valentini, P. Galloni and V. Conte, Coord. Chem. Rev., 2019, 385, 100–136 CrossRef CAS.
- I. Saikia, A. J. Borah and P. Phukan, Chem. Rev., 2016, 116, 6837–7042 CrossRef CAS.
- A. Podgoršek, S. Stavber, M. Zupan and J. Iskra, Green Chem., 2007, 9, 1212–1218 RSC.
- L. I. Zakharkin, V. V. Gavrilenko and B. A. Paley, J. Organomet. Chem., 1970, 21, 269–272 CrossRef CAS.
- M. S. Kharasch and O. Reinmuth, Grignard Reactions of Nonmetallic Substances, Prentice Hall, New York, 1954, p. 1332 Search PubMed.
- X. Creary, J. Org. Chem., 1980, 45, 2727–2729 CrossRef CAS.
- W. H. Glaze, C. M. Selman, A. L. Ball Jr. and L. E. Bray, J. Org. Chem., 1969, 34, 641–644 CrossRef CAS.
- G. K. Köbrich and W. Goyert, Tetrahedron, 1968, 24, 4327–4342 CrossRef.
- J. B. Wakefield, The Chemistry of Organolithium Compounds, Pergamon Press, Oxford, 1974, p. 332 Search PubMed.
- O. A. Attanasi, S. Berretta, G. Favi, P. Filippone, G. Mele, G. Moscatelli and R. Saladino, Org. Lett., 2006, 8, 4291–4293 CrossRef CAS.
- C. M. Brewster and J. C. Harris, J. Am. Chem. Soc., 1930, 52, 4866–4872 CrossRef CAS.
- A. Becker, N. Kornberg and B. Croitoru, Process for Preparing p-Bromophenol and Related Compounds, Ger. Offen. Patent Appl. DE 3742515 A1 19880714, 1988.
- S. C. Puri, S. M. Anand and C. K. Atal, Indian J. Chem., 1985, 24B, 294–295 CAS.
- D. Guo, Z. Wan, Y. Xiao and D. Liu, Huaxue Shijie, 1987, 28, 300–302 CAS.
- M. B. Smith, L. (Chen) Guo, S. Okeyo, J. Stenzel, J. Yanella and E. LaChapelle, Org. Lett., 2002, 4, 2321–2323 CrossRef CAS.
- A. Palmieri, S. V. Ley, K. Hammond, A. Polyzos and I. R. Baxendale, Tetrahedron Lett., 2009, 50, 3287–3289 CrossRef CAS.
- S. Gronert, J. M. Garver, C. M. Nichols, B. B. Worker and V. M. Bierbaum, J. Org. Chem., 2014, 79, 11020–11028 CrossRef CAS.
- H. I. Bloemink and A. C. Legon, J. Chem. Phys., 1995, 103, 876–882 CrossRef CAS.
- P. Atkins and J. de Paula, Physical Chemistry for the Life Sciences, W. H. Freeman & Company, New York, 2nd edn, 2011, p. 618 Search PubMed.
- Electrofuge influence over aromatics is tightly related to the choice of an electrophile. For ionic type of reactions, see: (a) A. Bravo, F. Fontana, B. Dordi and F. Minisci, J. Org. Chem., 2000, 65, 3880–3882 CrossRef CAS; (b) S. Ni, M. A. E. A. A. A. E. Remaily and J. Franzén, Adv. Synth. Catal., 2018, 360, 4197–4204 CrossRef CAS; (c) B. Huang, Y. Zhao, C. Yang, Y. Gao and W. Xia, Org. Lett., 2017, 19, 3799–3802 CrossRef CAS; (d) D. Azarifar, K. Khosravi, Z. Najminejad and K. Soleimani, J. Iran. Chem. Soc., 2012, 9, 321–326 CrossRef CAS.
- J. Liao, L. G. Huey, D. J. Tanner, F. M. Flocke, J. J. Orlando, J. A. Neuman, J. B. Nowak, A. J. Weinheimer, S. R. Hall, J. N. Smith, A. Fried, R. M. Staebler, Y. Wang, J.-H. Koo, C. A. Cantrell, P. Weibring, J. Walega, D. J. Knapp, P. B. Shepson and C. R. Stephens, J. Geophys. Res., 2012, 117, D00R16, DOI:10.1029/2011JD016641.
- (Linked to ref. 81) For free radical type of reactions, see: (a) D. R. Motati, D. Uredi, A. G. Burra, J. P. Bowen, F. R. Fronczek, C. R. Smith and E. B. Watkins, Org. Chem. Front., 2020, 7, 1095–1106 RSC; (b) W.-K. Tang, F. Tang, J. Xu, Q. Zhang, J.-J. Dai, Y.-S. Feng and H.-J. Xu, Chem. Commun., 2020, 56, 1497–1500 RSC; (c) C. Minero, V. Maurino, E. Pelizzetti and D. Vione, Environ. Sci. Pollut. Res., 2006, 13, 212–214 CrossRef CAS.
- (a) A. M. Andrievsky and M. V. Gorelik, Russ. Chem. Rev., 2011, 80, 421–428 CrossRef CAS; (b) S. A. Cotton, J. Coord. Chem., 2018, 71, 3415–3443 CrossRef CAS; (c) N. V. Bausk, S. B. Érenburg, N. F. Yudanov and L. N. Mazalov, J. Struct. Chem., 1997, 37, 913–919 CrossRef.
- (a) Y. Nishina and K. Takami, Green Chem., 2012, 14, 2380–2383 RSC; (b) K. Kikushima, T. Moriuch and T. Hirao, Tetrahedron Lett., 2010, 51, 340–342 CrossRef CAS; (c) Y.-L. Ren, B. Wang, X.-Z. Tian, S. Zhao and J. Wang, Tetrahedron Lett., 2015, 56, 6452–6455 CrossRef CAS; (d) A. D. Darwish, P. R. Birkett, G. John Langley, H. W. Kroto, R. Taylor and D. R. M. Walton, Fullerenes, Nanotubes, Carbon Nanostruct., 1997, 5, 705–726 CAS; (e) S. Uemura, A. Onoe and M. Okano, Bull. Chem. Soc. Jpn., 1974, 47, 147–150 CrossRef CAS; (f) K. Huthmaher and F. Effenberger, Synthesis, 1978, 693–694 CrossRef; (g) R. K. Sharma and C. Sharma, Tetrahedron Lett., 2010, 51, 4415–4418 CrossRef CAS; (h) L. Kumar, T. Mahajan and D. D. Agarwal, Green Chem., 2011, 13, 2187–2196 RSC; (i) R. M. Al-Zoubi and D. G. Hall, Org. Lett., 2010, 12, 2480–2483 CrossRef CAS; (j) M. Naresh, M. A. Kumar, M. M. Reddy, P. Swamy, J. B. Nanubolu and N. Narender, Synthesis, 2013, 1497–1504 CAS.
- J. D. Sivey, M. A. Bickley and D. A. Victor, Environ. Sci. Technol., 2015, 49, 4937–4945 CrossRef CAS.
- (a) J. D. Sivey, J. S. Arey, P. R. Tentscher and A. L. Roberts, Environ. Sci. Technol., 2013, 47, 1330–1338 CrossRef CAS; (b) J. D. Sivey, J. S. Arey, P. R. Tentscher and A. L. Roberts, Environ. Sci. Technol., 2013, 47, 8990 CrossRef CAS.
- (a) R. Bruckner, Advanced Organic Chemistry, Elsevier, 2002, p. 636 Search PubMed; (b) D. J. R. Duarte, M. M. de las Vallejos and N. M. Peruchena, J. Mol. Model., 2010, 16, 737–748 CrossRef CAS.
- (a) M. Liljenberg, J. H. Stenlid and T. Brinck, J. Phys. Chem. A, 2018, 122, 3270–3279 CrossRef CAS; (b) L. Lu, H. Liu and R. Hua, Org. Lett., 2018, 20, 3197–3201 CrossRef CAS.
- H. Mayr and A. R. Ofial, Acc. Chem. Res., 2016, 49, 952–965 CrossRef CAS.
- B. Galabov, S. Ilieva, G. Koleva, W. D. Allen, H. F. Schaefer III and P. V. R. Schleyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 37–55 CAS.
- B. Galabov, D. Nalbantova, P. von R. Schleyer and H. F. Schaefer III, Acc. Chem. Res., 2016, 49, 1191–1199 CrossRef CAS.
- C. H. Cheon and H. Yamamoto, Chem. Commun., 2011, 47, 3043–3056 RSC.
- B. Galabov, G. Koleva, H. F. Schaefer III and P. von R. Schleyer, J. Org. Chem., 2010, 75, 2813–2819 CrossRef CAS.
- N. Sablon, F. De Proft and P. Geerlings, Chem. Phys. Lett., 2010, 498, 192–197 CrossRef CAS.
- M. Franco-Pérez, P. W. Ayers and J. L. Gázquez, Theor. Chem. Acc., 2016, 135, 199–206 Search PubMed.
- N. Sablon, F. De Proft and P. Geerlings, J. Phys. Chem. Lett., 2010, 1, 1228–1234 Search PubMed.
- (a) C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS; (b) M. D. Driver, M. J. Williamson, J. L. Cook and C. A. Hunter, Chem. Sci., 2020, 11, 4456–4466 RSC.
- J. Chakkamalayath, K. R. S. Chandrakumar and S. K. Ghosh, J. Phys. Chem. A, 2020, 124, 3770–3777 CrossRef CAS.
- (a) P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS; (b) E. Matito and M. V. Putz, J. Phys. Chem. A, 2011, 115, 12459–12462 CrossRef CAS.
- J. C. Kromann, J. H. Jensen, M. Kruszyk, M. Jessing and M. Jørgensen, Chem. Sci., 2018, 9, 660–665 RSC.
- A. Tomberg, M. J. Johansson and P.-O. Norrby, J. Org. Chem., 2018, 84, 4695–4703 CrossRef.
- Y. Guan, C. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green and K. F. Jensen, ChemRxiv, 2020 DOI:10.26434/chemrxiv.12907316.v1.
Footnote |
| † Dedicated to Professor B. Plesničar on his 80th birthday. |
| This journal is © the Owner Societies 2021 |