Ground and excited electronic states of AuH₂via detachment energies on AuH₂⁻ using state-of-the-art relativistic calculations

Abstract

Photoelectron spectroscopy (PES) is a well-known technique which provides unique information about the electronic structure of anionic and neutral species of simple molecules containing heavy elements; however, the detailed interpretation of the resulting experimental spectra can be very complex and theoretical support is mandatory. In this work, based on the available vibrationally resolved PES experiments for gold dihydride (Liu, H.-T. et al., Chem. Sci., 2012, 3, 3286), we have employed several relativistic theoretical approaches with the aim of reproducing experimental photoelectron Detachment Energies (DEs) of AuH₂⁻ to give a neutral open-shell molecule, AuH₂. The results are discussed in terms of relativistic effects, orbital relaxation and electron correlation. In order to reproduce accurate DEs it has been necessary to include all these effects in a consistent manner at a high degree of accuracy, by means of the equation-of-motion coupled-cluster theory (EOM-IP-CCSD) based on the relativistic exact two-component Hamiltonian (Shee A. et al. J. Chem. Phys., 2018, 174113). This method has also been applied for investigating the ground and low-lying electronic potential energy surfaces of the neutral open shell AuH₂ species. The equilibrium geometry of the AuH₂ ground state is found to be bent, which is fully consistent with the experimental findings, while all the excited states, including the first, which was previously suggested to have a slightly bent structure, are found to be linear. In the linear centrosymmetric nuclear configuration (which corresponds to the equilibrium geometry of the anion, AuH₂⁻), we find that the first excited state and ground state are very close in energy and the ground state is characterized by an unexpected symmetry breaking in the direction of the asymmetric stretching, due to the pseudo-Jahn–Teller effect. This effect depends on the energy difference between these two electronic states and disappears when the spin–orbit coupling is neglected. The picture that emerges here is intriguing and demonstrates that the interpretation, for which the vibronic transitions that were previously assigned to a slightly bent structure of the first excited state needs to be revised and that a full rationalization of the PES spectra would require the explicit inclusion of the nuclear dynamical effects, beyond the Born–Oppenheimer (BO) approximation. From a methodological point of view, the relativistic EOM-IP-CCSD method results are highly accurate and capable of giving a well-balanced description of the anionic and neutral species, which is a key aspect for the interpretation of the PES spectra in open-shell heavy element compounds.

---

Gold complexes have received increasing attention^1–3 since the late 1980s, when Haruta and his co-workers demonstrated their catalytic potentialities⁴ (for an early history of catalysis by gold see ref. 5). In this context, gold hydrides are very important species,⁶ since they are believed to be key intermediates in gold catalysis.^7–9 Moreover, since gold is considered as a local maximum of relativistic effects in the periodic table,¹⁰ great attention has been paid to the physical and chemical properties of gold's simplest compounds, with AuH being often a target prototypical gold complex for investigating these effects^11–16 and benchmarking relativistic quantum chemistry methods. Unfortunately, gold dihydride (AuH₂) has not received the same amount of attention, mainly due to the difficulties in generating this open-shell species experimentally. In its ground state the AuH₂ molecule was predicted to have a bent structure,^17,18 in contrast to its closed-shell anion (AuH₂⁻), which is linear. A potential energy surface for Au reacting with the H₂ molecule has also been reported.¹⁹ The first experimental characterization of the open-shell molecule AuH₂ was performed in a hydrogen solid matrix by Andrews et al.^20,21 using infrared spectroscopy. These seminal works, where a joint experimental and theoretical approach was employed, confirmed that the ground state structure of AuH₂ is bent and that the system is expected to be long-lived (compared to other coinage metal compounds) because of a large barrier to dissociation into Au + H₂. This kind of information is important since the AuH₂ molecule (together with the other coinage metal dihydrides) may be of actual interest for the development of hydrogen storage devices.²⁰ These works gave useful information concerning the ground state of gold dihydride and its stability. Nevertheless, not much was reported concerning its low-lying excited states. A turning point is the more recent work by Liu et al., where AuH₂ has been characterized by means of photoelectron spectroscopy (PES) in its ground and low-lying excited states.²² PES is a widely used experimental approach for investigating heavy element compounds.^23–28 The experiment was performed in the gas phase and consisted in removing an electron from the AuH₂⁻ anion in its ground state by using a laser beam. In this way, the AuH₂ molecule was generated in its ground and excited states and its formation was revealed by collecting the ejected electrons. Liu et al. obtained a detailed picture of the electronic structure of AuH₂ by combining the experimental PES information with quantum mechanical calculations. First of all, the Vertical Detachment Energies (VDE) for the ground and first five excited states of the neutral AuH₂ molecule were determined with high accuracy. Furthermore, because of the high resolution of the experimental spectrum, it was possible to analyze the vibrational progression and determine the Adiabatic Detachment Energy (ADE) for the ground state of AuH₂. The latter contains information concerning the geometrical relaxation of the system from the Franck–Condon region (i.e. geometry of the anion) to the most stable nuclear configuration of the ground state of AuH₂. Despite its apparent simplicity, it is challenging to reproduce the VDE by theoretical calculations, because it requires that the anionic and neutral species are described in a well-balanced manner. In order to reproduce the experimental VDEs and to assign the bands of the PES spectrum, it is mandatory to introduce relativity (including spin–orbit coupling) and electron correlation in the calculation at a high level of accuracy. For this reason, Liu et al. resorted to a multi-step theoretical approach based on a combination of ab initio methods. The approach included scalar-relativistic effects using pseudopotentials and the spin–orbit (SO) coupling as a perturbation. In particular, the SO splitting was calculated on the basis of the complete active space self-consistent field (CASSCF) method with the diagonal matrix elements replaced by the individual state energies evaluated at the unrestricted coupled cluster level with the full single and double excitations and estimating the triples contribution via perturbation theory [UCCSD(T)]. The CASSCF calculations were performed with an active space of 13 electrons in 8 valence orbitals (Au 5d, Au 6s and H 1s) denoted CASSCF (13e, 8o). The assignment of the experimental PES bands was facilitated by the fact that the AuH₂⁻ anion is linear with D_∞h symmetry, thus the VDE signal (associated with ground and excited states of AuH₂) were labeled with the spectroscopic terms of centrosymmetric linear molecules. Moreover, by analyzing the vibrational progression of the ground state PES band, it was seen how this progression corresponds to a bending mode and thus it was once again confirmed (see also the work by Andrews et al.²¹) that the AuH₂ ground state is bent. Calculations agreed with the previous findings in locating the equilibrium bond angle at about 129 degrees. The absence of any vibrational progression in the bands from B to E (i.e. bands concerning the second to fifth excited states) led to the conclusion that the corresponding states maintain a linear geometry. A more intriguing issue came out when analyzing band A, i.e. of the first excited state. Indeed, for a laser energy close to the resonance, some anomalous weak vibrational bands in the spectrum at lower energies with respect to the VDE suggested that the structure of the first excited state could be characterized by a double-well resulting in a minimum energy bent structure, with a very small deviation from linearity. Nevertheless, none of the calculations performed so far found a bent structure for this electronic state. Liu et al. suggested that the application of more accurate theoretical methods to treat the electron correlation and relativistic effects (i.e. including SO coupling in a variational manner) would shed light on this issue and find a more stringent link between the given interpretation of the experimental data and the theoretical findings.

In this work we have employed various theoretical methods which include relativistic effects and electron correlation with increasing accuracy for the evaluation of the electron detachment energies of AuH₂⁻ to reproduce the experimental PES and to give detailed information about the ground and excited states of the AuH₂ molecule. The role of relativistic effects, orbital relaxation and electron correlation has been analyzed in detail. In order to include both relativistic effects and the electron correlation in a consistent manner, we have also applied the recently developed and current state-of-the-art relativistic approach for the prediction of the detachment energies, the relativistic ionization-potential-equation-of-motion coupled cluster approach,²⁹ based on the exact two-component (X2C) Dirac–Coulomb–Gaunt Hamiltonian using a molecular mean-field approach³⁰ (hereafter simply referred to as “X2C-EOM-CCSD”). This method has been also employed for investigating the Adiabatic Potential Energy Surfaces (APESs) of the ground and excited electronic states of AuH₂. This will shed light on the peculiarities of gold dihydride's electronic structure and reveal intriguing features of the ground state potential energy surface in order to build a bridge between the interpretation of the experimental spectra and the theoretical calculations.

1 Theory and computational details

The key quantities theoretically used to interpret photoelectron spectra and probe the electronic structure of molecules are the Detachment Energies (DE), which can be defined as:

DE = E_neutral − E_anion (1)

Two different types of detachment energy can be distinguished. The Vertical Detachment Energy (VDE) is defined as the energy needed to eject an electron from the anion in its ground state without relaxing its internal degrees of freedom (the geometry of the neutral species is kept frozen at the ground state geometry of the anion). The Adiabatic Detachment Energy (ADE) is defined as the minimal energy required to remove an electron from the anion ground state to produce the neutral molecule. The ADE is accordingly calculated by considering the electronic states of the neutral molecule at their minimum nuclear configurations. This is clearly lower than the VDE value because here the system is allowed to relax its geometry from the anion structure (i.e. the nuclear arrangement it has in the Franck–Condon region) to its vibronic ground state. For a stringent comparison with experimental ADE one should add to the electronic contribution also the 0–0 vibrational transition correction which corresponds to the difference in the vibrational zero-point energy between the anion and the neutral molecule.

In this work, various theoretical methods have been employed for the prediction of the VDEs. The methods have been chosen according to their computational complexity and with the specific aim of emphasizing those contributions (such as relativistic effects, orbital relaxation and electron correlation) which are required to obtain accurate VDEs.^31,32 The simplest approach is to approximate the VDEs using Koopmans’ theorem (KT).³³ This requires a simple Hartree–Fock (HF) calculation on the anion and may be considered as a useful reference since it includes neither the orbital relaxation nor electron correlation (usually, these two factors tend to cancel each other when dealing with valence ionization³⁴). The ΔSCF approach³⁵ has been applied to include the effect of the orbital relaxation (i.e. the response of the electronic structure to a hole created in the occupied orbitals³²). In this case VDEs are calculated as in eqn (1) where the energies of the neutral molecule (ground and excited states) are computed by forcing the occupation of the orbitals and then by self-consistently solving the HF or the Kohn–Sham (KS) equation with this excited state population. In these cases in which this procedure properly converges, this approach remains computationally very cheap with the advantage that the orbital relaxation is included in the calculations. With the ΔSCF approach the electron correlation can be neglected (in the case of ΔHF) or included through an exchange–correlation functional at the Kohn–Sham level (ΔKS). Reliable results for the VDEs can be obtained within the framework of the Ionization-Potential-Equation-of-Motion Coupled Cluster (EOM-IP-CCSD)^36,37 method, which is known to include in a consistent manner both the orbital relaxation and electron correlation. The method has a computational cost comparable to that of the CCSD method for the ground state (scaling is approximately N⁶).³⁶ We refer interested readers to a few pedagogical reviews which explain how the EOM (and EOM-IP) theory works and illustrate its applicability on typical target systems.^38–41

Unless otherwise stated, all the reported calculations have been carried out using the relativistic quantum chemistry code DIRAC^42,43 (released 2018) which implements all the methods mentioned above in combination with accurate relativistic Hamiltonians. In particular, in order to investigate the impact of relativistic effects on VDEs we employed exact 2-component^44–48 (X2C) and 4-component (4c) Hamiltonians, with the latter also in its spinfree (SF) form.⁴⁹

Dyall's Gaussian-type basis sets of different qualities, double-, triple-, and quadruple-zeta with polarization functions (dyall.dzp, dyall,tzp, dyall.qzp respectively) for both gold⁵⁰ and hydrogen⁵¹ were employed for the KT, ΔHF and ΔKS calculations. In the ΔKS case the PBE⁵² exchange–correlation functional was applied. The SCF convergence on the excited state of the AuH₂ molecule was obtained by overlap selection.^42,43 Correlated EOM-IP-CCSD calculations are based on the recent relativistic formulation²⁹ and have been carried out using both Dyall valence (dyall.vdz, dyall.vtz, and dyall.vqz) and core-valence (dyall.cvdz, dyall.cvtz, and dyall.cvqz) basis sets.^50,51 For the former calculations the 5s, 5p, 5d and 6s electrons for Au are correlated, whereas for the latter the n = 4 shell electrons of Au were included in the active space as well. The X2C-Dirac–Coulomb–Gaunt (DCG) Hamiltonian has been employed in the molecular mean field (mmf) approach.³⁰ This method (in the following simply referred to as “X2C-EOM-CCSD”) represents an excellent compromise between a good accuracy and a reasonable computational cost; the latter has been shown to yield results largely indistinguishable from their 4-component counterparts.²⁹ The X2C-EOM-CCSD approach has been used for the numerical optimization of the minimum energy structures of the AuH₂ molecule in its ground and (five) low-lying excited states and to investigate selected cuts of Adiabatic Potential Energy Surfaces (APESs). The calculation of the expectation values of the electric dipole moment for the ground state of AuH₂ was carried out using analytical gradients as implemented in ref. 53. For calculating the VDEs, the geometry from ref. 22 has been used for AuH₂⁻ (r_Au−H = 1.647 Å; α_H−Au−H = 180 degrees).

We mention that some test calculations have also been applied including the relativistic effects through the approximate scalar (SR) and spinOrbit (SO) 2-component ZORA Hamiltonians,^54–56 for which the Amsterdam Density Functional (ADF) program package^57–59 was used, together with Slater-type double- (DZ), triple- (TZ2P) and quadruple-zeta (QZ4P) basis sets. In particular this code has been used to estimate the zero-point-energy (ZPE) and the 0–0 vibrational correction to the ADE.

2 Results and discussion

2.1 Vertical detachment energies (VDEs)

As mentioned, VDEs obtained with high accuracy in the experiment by Liu et al.²² represent an ideal reference in order to establish a suitable theoretical protocol, based on first principles, for the quantitative estimation of these observables. Our results are summarized in Fig. 1, where the VDEs are reported using different theoretical methods and compared with the experimental data taken from ref. 22. The numerical data are also reported in Table 1, together with the percent error with respect to the experimental data.

Fig. 1 Gray and green diamonds correspond to VDEs estimated using Koopmans’ theorem (KT) at the 4-component (4c-KT) and spin-free (SF-KT) levels, respectively. Black and orange crosses correspond to the 4c-ΔKS and 4c-ΔHF calculations, respectively. The basis set for all the latter is dyall.tzp. Blue dots represent X2C-EOM-CCSD calculations using the dyall.vtz basis set. Red bars represent experimental values from ref. 22.

Table 1 VDEs (in eV) for AuH₂⁻ calculated at different levels of theory. The basis set for KT and ΔHF(KS) calculations is dyall.tzp, whereas for X2C-EOM-CCSD calculations it is dyall.vtz. For each calculated value, the percent error with respect to the experimental reference is reported in parentheses

State/exp. band	SF-KT	4c-KT	4c-ΔHF	4c-ΔKS	X2C-EOM-CCSD	Exp.^a
a Experimental VDEs (Exp.) are taken from ref. 22.
^2Σ^+1/2u/X	3.982 (8.3)	4.021 (9.3)	3.386 (7.9)	4.013 (9.1)	3.667 (0.3)	3.678
^2Σ^+1/2g/A	3.676 (5.8)	3.599 (7.8)	2.299 (41.1)	3.848 (1.4)	3.790 (2.9)	3.904
^2Δ5/2g/B	6.398 (38.1)	5.699 (22.9)	2.900 (37.4)	4.850 (4.6)	4.731 (2.1)	4.635
^2Π3/2g/C	6.640 (38.8)	5.878 (22.8)	3.021 (36.9)	4.823 (0.8)	4.825 (0.8)	4.785
^2Π1/2g/D	6.640 (15.4)	6.933 (20.5)	4.128 (28.3)	5.832 (1.5)	5.765 (0.3)	5.745
^2Δ3/2g/E	6.398 (2.9)	7.566 (21.5)	4.477 (28.0)	6.450 (3.7)	6.275 (0.8)	6.22

---

All calculations have been carried out at the linear equilibrium geometry of anion AuH₂⁻, taken from ref. 22 (r_Au−H = 1.647 Å; α_H−Au−H = 180 degrees). For the sake of simplicity, we keep the same notation used in ref. 22 and label the VDEs using both the experimental bands (X, A, B, C, D and E in energy order) and the spectroscopic terms of the linear centrosymmetric molecules reported as ^2Σ+1Λ_Ωu/g. It should be noted that the first two transitions (corresponding to the ground and first excited states of AuH₂) are challenging to assign unambiguously and represent a stringent test for our calculations (these two states are of different parity and are very close in energy, the experimental energy difference is only 0.24 eV).

Now, focusing on the results, we begin with the analysis of the VDE values based on Koopmans’ theorem (KT). As shown in Fig. 1 and Table 1, the VDEs have been calculated both at the 4c level (4c-KT) and in a spinfree framework (SF-KT). Similar data can be obtained with the 2-component scalar and spinOrbit ZORA Hamiltonian, see Table S1 in the ESI.† The results show that the inclusion of SO coupling is fundamental even for a qualitative description of these quantities. Indeed, concerning the higher-energy detachments (i.e. bands from B to E), when SO coupling is included, the experimental VDE trend is nicely reproduced. The method is able to give the correct assignment of these electronic states even if the calculated VDEs are shifted at somewhat higher energy. In a SF framework, a completely different trend is observed. In this case, the C/D states (and the B/E states) become degenerate since they correspond to the doublet components of the ²Π states (and ²Δ states). This clearly prevents the proper energy order and the correct assignment states. Although the 4c-KT method has only to be considered as a first approximation it is noteworthy that the calculated energy splitting for the C/D and B/E states (numerical values are 1.05 eV and 1.86 eV, respectively) agrees surprisingly well with the experimental values (0.96 eV and 1.59 eV). The inclusion of SO coupling has a positive impact on the results for high energy states (i.e. bands from B to E), nevertheless, the situation is different at lower energies (X and A bands). The highest level calculations from ref. 22 showed that the band X should be related to the electronic state of the ungerade symmetry, corresponding to the ²Σ⁺_1/2u state. In our 4c-HF calculations, the AuH₂⁻ HOMO is an orbital of symmetry σ_1/2g, whereas the HOMO−1 has a σ_1/2u symmetry, thus the application of KT gives a ground state of the incorrect symmetry (²Σ⁺_1/2g). Indeed, there is a swap in energy between the HOMO and the HOMO−1 molecular orbitals of the anion. The 4c-KT method is clearly a too simple approach for an accurate estimation of DEs.

For the evaluation of the orbital relaxation effect, we use the 4c-ΔHF approach. The experimental trend is qualitatively reproduced for bands B-E, although the calculated VDE values are now shifted at lower energies; nevertheless the 4c-ΔHF method still fails to provide the correct energy order of the two lowest-energy states (bands X-A). In general, the error in the higher energy states is increased dramatically, probably because the error compensation (between the orbital relaxation and electron correlation contributions), typically expected in the KT framework, is now missing. The 4c-ΔKS calculations show how including both the orbital relaxation and electron correlation significantly improves the agreement with the experimental values. Unfortunately, the energy swap of the lower-energy states still remains and the method fails to reproduce the correct symmetry of the AuH₂ ground state. This finding suggests that a more accurate treatment of the electron correlation is needed for reproducing these quantities. The results reported in Fig. 1 and Table 1 show that the X2C-EOM-CCSD method works exceptionally well. First of all, the order of the electronic states found here fully supports the assignment reported in ref. 22, where, as mentioned in the introduction, a multi-step theoretical recipe was specifically applied to include scalar relativistic effects, electronic correlation and spin-orbit coupling in a balanced way. Our results unambiguously confirm that the ground state of AuH₂ at the linear centrosymmetric configuration (i.e. at the minimum energy of the anion) is the electronic state ²Σ⁺_1/2u (ungerade symmetry). The computed VDEs are in very good agreement with the experimental data; indeed, as it can be seen, the percent errors for calculated VDEs are in the range of 2.9–0.3% (Table 1). In addition to this, it must be pointed out that the results displayed in Table 1 can be consistently improved. Indeed, as shown in Table 2, one can increase both the quality of the basis set and the number of active electrons. It is evident from the data how increasing simultaneously both of these factors can lead to an even more stringent agreement with the experimental results. For instance, when the electrons of the shell with n = 4 of gold are correlated and a core-valence quadruple-zeta (cvqz) quality basis set is used, the error can be further reduced (the percent errors are in the range of 0.1–1.4%, which corresponds to an absolute error below 0.06 eV). The error on the VDEs for the experimental reference values was estimated in the order of 0.02–0.03 eV.²² The results are consistent (with only a slight increase of the percent error), also if we apply the basis set extrapolation techniques (data labeled as v∞z and cv∞z in Table 2). In particular we have used the three-parameter exponential formula (see eqn (20) in ref. 32) already employed to estimate the ionization energies’ complete basis set limit.³²

Table 2 VDEs (in eV) for AuH₂⁻ calculated with the X2C-EOM-CCSD method by varying both the number of correlated electrons (i.e. only 5d and 6s electrons, all n = 5 shell and 6s electrons or all n = 4 and n = 5 shells plus 6s electrons) and the basis set (valence and core-valence Dyall basis set of double-, triple- and quadruple-zeta quality). Complete basis set extrapolation data are also reported (see the text for details). For each calculated value, the percent error with respect to the experimental reference is reported in parentheses. Experimental data taken from ref. 22 (the numerical values are also reported in Table 1 of this work for easy reference)

State/exp. band	Active electrons and basis set
	5d + 6s				5s5p5d + 6s				4s4p4d5s5p5d + 6s
	vdz	vtz	vqz	v∞z	vdz	vtz	vqz	v∞z	cvdz	cvtz	cvqz	cv∞z
^2Σ^+1/2u/X	3.454	3.667	3.714	3.727	3.458	3.673	3.725	3.742	3.462	3.678	3.727	3.741
	(6.1)	(0.3)	(1.0)	(1.3)	(6.0)	(0.1)	(1.3)	(1.7)	(5.9)	(0.0)	(1.3)	(1.7)
^2Σ^+1/2g/A	3.574	3.790	3.873	3.925	3.462	3.734	3.839	3.905	3.478	3.748	3.849	3.909
	(3.8)	(2.9)	(0.8)	(0.5)	(11.3)	(4.3)	(1.7)	(0.2)	(10.9)	(4.0)	(1.4)	(0.1)
^2Δ5/2g/B	4.457	4.731	4.858	4.968	4.126	4.496	4.667	4.814	4.142	4.513	4.667	4.814
	(3.8)	(2.1)	(4.1)	(7.2)	(11.0)	(3.0)	(0.7)	(3.9)	(10.6)	(2.6)	(0.9)	(3.9)
^2Π3/2g/C	4.551	4.825	4.950	5.055	4.238	4.595	4.771	4.942	4.254	4.619	4.781	4.910
	(4.9)	(0.8)	(3.4)	(3.8)	(11.4)	(4.0)	(0.3)	(3.3)	(11.1)	(3.6)	(0.1)	(2.6)
^2Π1/2g/D	5.500	5.765	5.884	5.981	5.259	5.593	5.764	5.943	5.274	5.621	5.773	5.891
	(4.3)	(0.3)	(2.4)	(4.1)	(8.5)	(2.6)	(0.3)	(3.4)	(8.2)	(2.1)	(0.5)	(2.5)
^2Δ3/2g/E	5.999	6.275	6.404	6.521	5.731	6.097	6.276	6.450	5.746	6.118	6.286	6.396
	(3.5)	(0.8)	(2.9)	(4.8)	(7.9)	(1.9)	(1.0)	(3.7)	(7.6)	(1.6)	(1.1)	(2.8)

---

2.2 Adiabatic potential energy surfaces (APESs) of the ground and low-lying excited states of AuH₂

At this point, we already showed that the X2C-EOM-CCSD approach is a suitable and accurate theoretical tool for quantitatively probing the electronic structure of AuH₂. Our principal aim here is to characterize in detail the ground and low-lying electronic excited states of AuH₂, including their minimum energy nuclear configurations, and provide accurate ADEs. The latter are typically more difficult to extract from experiments than VDEs. Furthermore, we will analyze the first excited state of AuH₂, which was suggested by Liu et al.²² to possess a double well in the direction of the bending mode that would be consistent with a slightly bent structure, but that previous theoretical calculations were not able to predict. In their seminal work Liu et al. suggested that only those theoretical methods that included relativistic effects and the electron correlation at a high level of accuracy could be useful for optimizing the geometry of this state, and therefore, for fully rationalizing the experimental data. The X2C-EOM-CCSD approach seems particularly suitable for answering this open question. Since an analytic gradient is not available in the current implementation of the method, we probe the potential energy surfaces resorting to single point energy calculations along selected cuts of the APES. We have preliminary optimized the Au–H bond length in a linear and centrosymmetric configuration (the results are reported in Table S2 in the ESI†). The results show that the optimal bond length is about 1.64 Å, almost independently of the specific electronic state (it ranges from 1.64 to 1.66 Å, for ²Σ⁺_1/2u and ²Π_3/2g, respectively). Thus, by freezing the bond length, we have performed a first scan in the bending direction (see Fig. 2). Numerical data are reported in Table S3 of the ESI.† In the ESI† we also report the results obtained using a small basis set (dyall.vdz) for comparison (see Fig. S1 and Table S4 in the ESI†). Our results for the ground state matches completely with the experimental data and confirms previous calculations:^17,21,22 this state is found to be bent and the minimum bond angle has been calculated very close to 130 degrees (the system has a C_2v symmetry and using the spin-free notation we can label this electronic state as ²B₂). For the second to fifth excited states, the photoelectron spectrum showed no vibrational progressions for the corresponding detachment bands and for this reason these states are expected to be linear (they maintain the linear structure as that of the anion and so they have a small nuclear relaxation). Our calculations confirm this picture and these states present a minimum at 180 degrees (the corresponding spectroscopic terms are those of the centrosymmetric linear configuration: ²Δ_5/2g, ²Π_3/2g, ²Π_1/2g and ²Δ_3/2g). The interpretation given in the PES experiment suggested a slightly bent structure for the first excited state, nevertheless, as can be seen clearly in Fig. 2, this excited state of gold dihydride is found to be linear. Even scanning the adiabatic potential energy surface finely in the vicinity of the 180 degrees does not modify this picture: the minimum energy of the first excited state is found in its linear configuration. We mention that this result does not qualitatively depend on the quality of the basis set employed (for a comparison using different basis sets see Fig. S2 and Tables S5, S6 in the ESI†). One possible pitfall of the above calculations may be the fact that we used a frozen Au–H bond length (fixed it at 1.64 Å). In order to relax also this last constraint, a larger 3D scan of the first excited state has been performed, where bond length (Au–H) and bond angle (H–Au–H) have been varied simultaneously. The results are shown in the ESI† (see Fig. S3). Based on these findings, we can confidently say that the X2C-EOM-CCSD approach predicts a linear geometry for the first excited state of gold dihydride, which somehow contrasts with the conclusions derived by Liu et al.²² based on the analysis of the PES spectra. We will return on possible reasons of this apparent inconsistency at the end of this section.

Fig. 2 X2C-EOM-CCSD calculated cuts of the APESs in the bending direction for AuH₂ (the Au–H bond length frozen at 1.64 Å) in its ground and first five excited states. Basis set: dyall.vtz. The energy has been shifted relatively to the minimum energy. The electronic states are labeled with spectroscopic terms of the centrosymmetric linear configuration corresponding to the bending angle of 180 degree.

By performing the scan of the APES along both the bond length (maintaining the constraint that the two Au–H remain at the same length) and the bond angle at the X2C-EOM-CCSD level, analogously to what we have done for the first excited state, we have found the equilibrium geometries and the ADEs for all electronic states associated with the experimental bands. The results are reported in Table 3. Concerning the AuH₂ ground state, the geometry found here matches quite well the one previously calculated by Liu et al.²² with a bond length of 1.605 Å and a bond angle of 129.2 degrees. Moreover, the ADE value is very close to the one that was determined experimentally and also reported in Table 3. We mention that our theoretical estimate of ADE does not include the 0–0 vibrational correction (the difference in the ZPE of anion AuH₂⁻ and of AuH₂ at the respective equilibrium geometries). This contribution is relatively small; an estimate at the DFT level gives about 0.03 eV (see Table S7 in the ESI†). Concerning the excited states, even though we have no experimental reference to validate our results, we find that ADEs have only slightly smaller values compared to the VDE values. This is consistent with the small geometrical rearrangements of AuH₂ in these electronic states with respect to the anion. The difference between VDE and ADE (Δ_VDE−ADE) can be considered as a stringent test for the ability of our calculations to describe the potential energy surface in a well-balanced and consistent manner. We find that the calculated Δ_VDE−ADE (0.687 eV) agrees extremely well with the experimental one (0.637 eV). The difference is 0.05 eV, which further demonstrates the consistency of the calculated APESs.

Table 3 X2C-EOM-CCSD calculated equilibrium geometries (the Au–H bond length in Å) and Adiabatic Detachment Energies (ADEs) (in eV) for the ground and first five excited states of gold dihydride. Dyall.vtz basis set was used. The equilibrium bond lengths (Å) and angles (degrees) have been determined through polynomial fits

State/PES band	Bond angle (degrees)	Bond length (Å)	Calculated ADE (eV)	Exp. ADE^a (eV)
a Experimental data taken from ref. 22.
^2B2/X	129.8	1.59	2.98	3.030
^2Σ^+1/2g/A	180.0	1.63	3.72	—
^2Δ5/2g/B	180.0	1.64	4.49	—
^2Π3/2g/C	180.0	1.65	4.60	—
^2Π1/2g/D	180.0	1.66	5.60	—
^2Δ3/2g/E	180.0	1.64	6.10	—

---

All the results reported above witness the accuracy of the X2C-EOM-CCSD computational protocol in describing the features of gold dihydride's electronic states, in close agreement with the experiment. The only discrepancy that still remains concerns the first excited state, which was expected to be characterized by a slightly bent equilibrium geometry. Returning to the experimental work of Liu et al.,²² we have to observe that the bent structure for the first excited state was drawn on the basis of the presence of a fine structure PES spectrum that emerges at slightly lower energies with respect to the signal assigned to the VDE of the first excited state (band A, in Fig. 3 and Table 1 of ref. 22). These fine band structures are made of three or four vibrational states spaced from about 500 to 200 cm⁻¹ with an increasing anharmonicity and were associated with some bound nuclear states of the bending mode. However, if this would be the case, the energetic range would be consistent with the presence of a double-well in the excited state with a barrier larger than 1600 cm⁻¹ (about 0.2 eV), which is clearly far beyond the accuracy we expect from our level of theory and thus, it would have been easily revealed by our calculations. So, we have to conclude that, on the basis of our extensive theoretical study, the interpretation for which the first excited states should present a bent structure needs to be revised. Furthermore, as a matter of fact the vibrational progression, previously assigned to the first excited state of AuH₂ observed in the experiment, occurs at an energy which is between the VDEs of the ground and the first excited state (3.67 and 3.90 eV, respectively) and has a spread of about 0.2 eV, which is really consistent with the small energy difference between these two quasi-degenerate states. We therefore suggest that the mentioned vibrational progression is not a sign of the presence of a bent structure of the first excited state, but may be more likely related to the dynamical effect of the nuclei, which arises from the presence of quasi-degenerate adiabatic states (for which the Born–Oppenheimer approximation cannot be fulfilled).⁶⁰ In such situations, the fine details of the PES spectra can only be extracted using appropriate nuclear dynamics coupling models based on the results of high-level electronic structure methods.^32,60 Precisely because the non-adiabatic dynamics is expected to be very sensitive even to the fine details of the adiabatic potential energy surfaces, especially in the Franck–Condon region, it is highly desirable to investigate whether the presence of these quasi-degenerate states may give peculiar and unexpected features of their topology. In particular, in the following section we will demonstrate that the pseudo-Jahn–Teller effect^61,62 gives rise to a symmetry breaking in the adiabatic potential energy surface of the ground state, thus that, right in the Franck–Condon region (i.e. in the linear arrangement), the most stable configuration of AuH₂ is a non-centrosymmetric structure with unequal Au–H bond lengths.

Fig. 3 3D plot of the ground (lower sheet) and first excited (upper sheet) state APESs of AuH₂ in the direction of the asymmetric stretching. Calculations have been performed at the X2C-EOM-CCSD level. Basis set: dyall.vdz. The energy has been shifted relatively to the minimum.

2.3 Symmetry breaking and pseudo-Jahn–Teller effect in the AuH₂ linear configuration

A number of linear triatomic open-shell molecules, such as ABA systems (with A and B from IA and VIIA groups respectively),⁶³ ZnCl₂⁺,^64,65 CuCl₂,⁶⁶ and the more debated BNB,⁶⁷ present a linear non-centrosymmetric structure. The distortion from the centrosymmetric symmetry of these linear molecules arises from the symmetry breaking (SB) consequence of the pseudo-Jahn–Teller effect (PJTE), where a significant vibronic coupling is present in near-degenerate electronic states.^61,62 In the ESI,† we briefly reviewed the main points of the theory behind the PJTE that may be useful for discussing our results. For further insights into PJTE theory, the reader may refer to ref. 61–63 and 68 and, for an even more specific analysis of PJTE in the linear X–Y–X systems, Sections 3.1 and 3.2 of ref. 62. For the PJTE treatment by means of quantum chemistry methods (including the EOM-IP-CCSD method) we refer the reader to a detailed discussion reported in ref. 69. Other relevant works showing the specific application of the EOM-IP-CCSD method for describing PJTE, open-shell systems and quasidiabatic states are ref. 70–72.

The PJTE takes place only when the two (quasi-degenerate) electronic states have symmetry properties which are compatible with the symmetry of the nuclear displacement. In particular, the necessary condition in order to have the PJTE is Γ = Γ′ × Γ′′, where Γ is the irreducible representation of the nuclear displacement and Γ′ and Γ′′ are the irreducible representations to which the lower and higher energy coupled states belong in the high symmetry configuration. The other important factor to have a significant PJTE is the electronic coupling parameter (Δ), which is defined as half of the energy separation between the two coupled states in their high symmetry configuration. The closer these states are in energy (small Δ), the stronger the vibronic coupling is and an actual SB may occur. For gold dihydride in its linear configuration (D_∞h symmetry) we have that the ground (²Σ⁺_1/2u) and first excited state (²Σ⁺_1/2g) are very close in energy and are likely to undergo symmetry breaking along the coordinate of the asymmetric stretching (Σ⁺_u symmetry). Note that the necessary condition in order to have the PJTE is fulfilled whether one uses the spin-free notation or the full picture including SO coupling (double group symmetry). In the spin-free framework one only considers spatial symmetry and the direct product of the involved electronic states (Σ⁺_g × Σ⁺_u) gives Σ⁺_u, which is the symmetry of the antisymmetric stretch. In the full picture the direct product of electronic states (E_1/2,g × E_1/2,u) gives Σ⁺_u + Σ⁻_u + Π_u which also includes the symmetry term of the antisymmetric stretch. For an interesting discussion about the impact of SO coupling on the selection rules for PJTE see ref. 73. Since in our case the PJTE can take place by symmetry, the system may be stable in a configuration with unequal Au–H separation, and unstable (saddle point) in the centrosymmetric configuration. At first glance, this seems to be an exotic situation; however, as already mentioned above, it has been observed for a number of linear triatomic open-shell molecules of general formula X–Y–X.^62–67

So we have used the X2C-EOM-CCSD approach for investigating the APES along the asymmetric stretching coordinate. The method is expected to be accurate to describe the PJTE.^38,69,70 The CI-like form of the EOM excitation operator enables access to multi-configurational open-shell wave functions, including degenerate and nearly degenerate states, as well as interacting states of different character.³⁸ The notorious issue of coupled-cluster theory to treat conical intersections^74–76 between states of the same symmetry is not expected to play a role here. The numerical examples of Kohn et al.⁷⁴ showed that this problem arises only very close to the intersection (within an energy range of ±0.02 eV). This is clearly not the case in point here, in that the involved electronic states have different symmetry for the high symmetry nuclear configuration and their energy gap is above 0.15 eV. For the sake of completeness, we mention that the problem of EOM with treating conical intersections between states of the same symmetry has recently found a solution within the framework of similarity-constrained theory.⁷⁶ The selected cut of the potential energy surface has been worked out by scanning several distances between the two terminal hydrogen atoms (R_H–H′) and by varying the single Au–H bond lengths asymmetrically (the asymmetric displacement with respect to the centrosymmetric structure is indicated as ΔR).

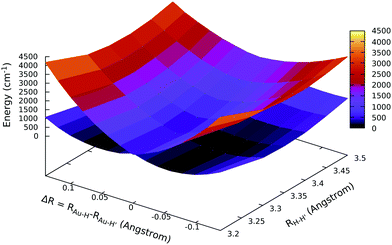
Surprisingly, the results support our hypothesis: the ground state APES of gold dihydride is not centrosymmetric around its linear configuration (as demonstrated by the lower sheet in Fig. 3, showing a double-well APES for the ground state), whereas the first excited state is linear and centrosymmetric. We find the minimum equilibrium structure to be at R_H–H′ = 3.3 Å with the minimum energy asymmetric displacement being ΔR = 0.06 Å. For a more quantitative perspective on the energies, we also performed calculations with larger basis sets (i.e. vtz, vqz, with n = 5 and 6s electrons correlated) and by correlating more electrons (i.e. cvtz, cvqz basis, with n = 4, n = 5 and 6s electrons correlated) by keeping fixed the overall R_H–H′ distance at 3.3 Å. As shown in Table 4, a SB is always observed, with the minimum energy asymmetric displacement being ΔR = 0.06 Å. Both the PJTE stabilization energy separating the minimum energy asymmetric structure from the centrosymmetric one (E_PJTE) and the electronic coupling parameter Δ change, becoming smaller and greater respectively; indeed, the most accurate calculations we performed (i.e. with a cvqz basis set) yield an E_PJTE of 31 cm⁻¹, which is small, yet is perfectly compatible with previous data referred to other systems in which the same phenomenon takes place.⁶² One of the most important and straightforward parameters for the evaluation of the PJTE (see eqn (S3)–(S6) in the ESI†) and SB is the electron coupling parameter, Δ, which can be directly evaluated from the APES. We see, in Table 4, how actually this value is related to the depth of the double-well: when, with smaller basis-sets, we have a greater PJTE stabilization energy, we observe a smaller Δ and vice versa with a larger basis set. One may argue that this symmetry breaking could be an artefact of the calculation; nevertheless, we have means to point out that we avoid artificial SB. First of all, as already mentioned, the X2C-EOM-CCSD method, which is based on EOM-IP-CCSD, is an accurate approach since it recovers most of the necessary correlation needed for treating these phenomena.^{37,38,65,69,70}

Table 4 PJTE stabilization energy separating the centrosymmetric configuration and the distorted one (E_PJTE), electronic coupling parameter (Δ) and asymmetric displacement at the minimum energy configuration (ΔR) for the gold dihydride ground state calculated at the X2C-EOM-CCSD level with different Dyall valence (dyall.vdz, dyall.vtz, and dyall.vqz) and core-valence (dyall.cvtz and dyall.cvqz) basis sets

Basis set	vdz	vtz	vqz	cvtz	cvqz
E PJTE (cm^−1)	268	126	34	150	31
Δ (cm^−1)	23	221	466	186	472
ΔR (Å)	0.06	0.06	0.06	0.06	0.06

---

Furthermore, as commonly used in the literature, in order to demonstrate that the SB is a real effect and not an artefact of the calculations is to ascertain that the wavefunction modifies its character continuously as the geometrical parameters are modified along a symmetry breaking mode. Thus, for the linear AuH₂ molecule, we calculate the expectation values of the dipole moment for the ground state at different asymmetric displacement (ΔR). A real SB should feature a zero dipole moment when ΔR = 0 and a continuous curve for other values of ΔR^65,67 (reflecting a wavefunction which varies continuously as a consequence of the physical mixing of the coupled electronic states). This criterion is fully respected by our calculations: the dipole moment expectation value is zero at ΔR = 0 and as the geometry undergoes distortion the corresponding dipole varies with continuity as shown in the previous cited examples.^65,67 The numerical data are reported in the ESI,† see Table S8.

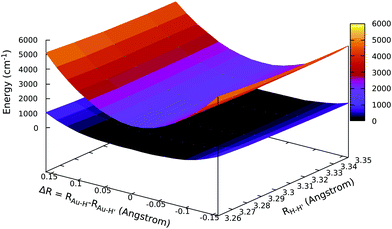
We have shown that the PJTE is very sensitive to the energy separation of the electronic states at their highest symmetric configuration (Δ parameter). Since AuH₂ is a heavy-element containing molecule (to our knowledge the first that displays a SB in the asymmetric stretching direction due to PJTE), it is interesting to investigate whether the distortion in the asymmetric direction can be affected by spin–orbit coupling. The answer to this question can be given by scanning the APESs with the EOM-IP-CCSD approach, using a spinfree Hamiltonian in order to switch off spin–orbit interaction. The spinfree APESs are reported in Fig. 4, where, by using a spinfree Hamiltonian in the calculations, there is no evidence of a SB in the asymmetric stretching direction. Indeed, the APES for the ground state is found to be very flat, but both the ground and first excited state's APESs show a minimum at ΔR = 0, i.e. the minimum configuration is the centrosymmetric one when spin–orbit coupling is neglected. This finding is surprisingly in that the symmetry analysis just reported above shows that PJTE is also allowed within the spinfree framework. A more quantitative perspective can be obtained by considering the electronic coupling parameter (and therefore the separation of the two states at ΔR = 0, 2Δ). Indeed, as shown in Table 4, where relativistic effects (including spin–orbit coupling) are considered, the separation between these ground and first excited states in their linear nuclear configuration (when using the same computational setup, i.e. the dyall.vtz basis set) is less than 1000 cm⁻¹ (2Δ = 932 cm⁻¹). In the case of spinfree calculations instead, switching off the spin–orbit interaction, the separation is much larger and almost the double (1724 cm⁻¹). This is consistent with the PJTE theory, where to larger Δ should correspond weaker couplings between states.

Fig. 4 3D plot of the ground (lower sheet) and first excited (upper sheet) state APESs of AuH₂ in the direction of the asymmetric stretching. Calculations have been performed at the EOM-IP-CCSD level by switching off the spin–orbit coupling effect with a spinfree Hamiltonian. Dyall.vtz basis set was used. The energy has been shifted relatively to the minimum.

3 Conclusions

A very detailed photoelectron spectroscopy (PES) experiment was previously reported, in which the electronic structure of AuH₂ was extensively probed. Detachment energies (DEs) were determined with high accuracy and, coupled with ab initio calculations, the ground state of AuH₂ was found to be bent. The first excited state was also supposed to be slightly bent due to the presence in the spectrum of a small vibrational progression which was associated with a bending mode, although, to this day, every theoretical approach tested yielded a linear structure. In this work, based on this highly accurate experiment as a reference, we have applied several methods for reproducing the experimental DEs of AuH₂, by taking into account the factors that may influence calculations, such as relativistic effects, orbital relaxation and the electron correlation. The X2C-EOM-CCSD method, which includes the electronic correlation at the EOM-IP-CCSD level and relativistic effects based on the X2C-Dirac–Coulomb–Gaunt Hamiltonian using a molecular mean-field approach, is found to be highly accurate in both reproducing the correct order of the experimental PES bands and the DE values. The method has been used for describing the Adiabatic Potential Energy Surfaces of gold dihydride's ground and a few low-lying excited states. For the ground state, for which detailed information concerning its structure and DEs was available, the X2C-EOM-CCSD approach yields a very accurate adiabatic potential energy surface, whose features tightly match the experimental findings. Indeed, both the bending angle and the Adiabatic Detachment Energies (ADEs) were reproduced with high accuracy (typical error is of the order of 0.03–0.06 eV). All the other excited states (including the first) are found to be linear. The picture that emerges from our theoretical investigation is intriguing and gives a new perspective on the features of this peculiar gold complex.

In particular, on the basis of our X2C-EOM-CCSD calculations we have demonstrated that the interpretation which suggested for a slightly bent structure of the first excited state of AuH₂ needs to be revised. The first excited state in AuH₂ is found to be linear and, in this nuclear configuration (which also corresponds to the equilibrium geometry of the anion, AuH₂⁻, and characterizes the vertical detachment process), it is quasi-degenerate with the ground electronic state. Surprisingly, these states are found to be coupled by the pseudo-Jahn–Teller effect (PJTE) which induces a symmetry breaking along the asymmetric stretching coordinate, for which the centrosymmetric nuclear configuration becomes a saddle point and the asymmetric configuration (two Au–H bonds with different lengths) is the most stable. Even though similar triatomic open-shell molecules have been reported to be affected by this phenomenon, this is, to our knowledge, the first reported example of a heavy-metal-containing molecule affected by PJTE in the direction of the asymmetric stretching. Since AuH₂ is a heavy metal containing compound, the role of the spin–orbit coupling has been analyzed. Its effect is to reduce the energy gap between these quasi-degenerate states and to enhance the PJTE. Interestingly, thus, we have shown how the symmetry breaking is observed only when the calculations accurately account for spin–orbit coupling. Our findings strongly suggest that the mentioned vibrational progression observed in the reference experiment is not a sign of the presence of a bent structure of the first excited state, but, more likely, may be related to the dynamical effect of the nuclei, due to the presence of quasi-degenerate adiabatic states (for which the Born–Oppenheimer approximation may not be fulfilled) in the Franck–Condon region associated with the photodetachment process. It is clear that in order to confirm the last hypothesis a full treatment of the nuclear degrees of freedom would be required. The latter, together with the surprising symmetry breaking reported here, paves the way for further theoretical and experimental investigation on the peculiar electronic structure of AuH₂, which is a simple molecular system only in appearance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Ministero Istruzione dell’Università e della Ricerca (MIUR) and the University of Perugia are acknowledged for the financial support through the program “Dipartimenti di Eccellenza 2018–2022” (grant AMIS).

Notes and references

1. A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936.
2. C. H. Christensen and J. K. Nørskov, Science, 2010, 327, 278–279.
3. A. M. Echavarren, A. S. K. Hashmi and F. D. Toste, Adv. Synth. Catal., 2016, 358, 1347.
4. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408.
5. G. Bond, Gold Bull., 2008, 41, 235–241.
6. H. Schmidbaur, H. G. Raubenheimer and L. Dobrzańska, Chem. Soc. Rev., 2014, 43, 345–380.
7. A. S. K. Hashmi, Angew. Chem., Int. Ed., 2005, 44, 6990–6993.
8. H. Ito, T. Saito, T. Miyahara, C. Zhong and M. Sawamura, Organometallics, 2009, 28, 4829–4840.
9. S. Labouille, A. Escalle-Lewis, Y. Jean, N. Mézailles and P. Le Floch, Chem. Eur. J., 2011, 17, 2256–2265.
10. P. Pyykkö, Chem. Rev., 1988, 88, 563–594.
11. V. Kellö and A. J. Sadlej, Theor. Chim. Acta, 1995, 92, 253.
12. P. Schwerdtfeger, J. R. Brown, J. K. Laerdahl and H. Stoll, J. Chem. Phys., 2000, 113, 7110–7118.
13. H. A. Witek, T. Nakijima and K. Hirao, J. Chem. Phys., 2000, 113, 8015–8025.
14. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
15. P. Pyykkö, Inorg. Chim. Acta, 2005, 358, 4113–4130.
16. P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967.
17. K. Balasubramanian and M. Z. Liao, J. Phys. Chem., 1988, 92, 361–364.
18. K. Balasubramanian and M. Z. Liao, J. Phys. Chem., 1989, 93, 89–94.
19. M. Yuan, W. Li, J. Yuan and M. Chen, Int. J. Quant. Chem., 2018, 118, e25493.
20. L. Andrews and X. Wang, J. Am. Chem. Soc., 2003, 125, 11751–11760.
21. L. Andrews, X. Wang, L. Manceron and K. Balasubramanian, J. Phys. Chem. A, 2004, 108, 2936–2940.
22. H.-T. Liu, Y.-L. Wang, X.-G. Xiong, P. D. Dau, Z. A. Piazza, D.-L. Huang, C.-Q. Xu, J. Li and L.-S. Wang, Chem. Sci., 2012, 3, 3286.
23. X.-B. Wang and L.-S. Wang, J. Am. Chem. Soc., 2000, 122, 2096–2100.
24. T. Waters, X.-B. Wang and L.-S. Wang, Coord. Chem. Rev., 2007, 251, 474–491.
25. P. D. Dau, J. Su, H.-T. Liu, D.-L. Huang, J. Li and L.-S. Wang, J. Chem. Phys., 2012, 137, 064315.
26. C.-G. Ning, X.-G. Xiong, Y.-L. Wang, J. Li and L.-S. Wang, Phys. Chem. Chem. Phys., 2012, 14, 9323.
27. H.-T. Liu, X.-G. Xiong, P. Diem Dau, Y.-L. Wang, D.-L. Huang, J. Li and L.-S. Wang, Nat. Commun., 2013, 4, 2223.
28. J. Su, P. D. Dau, Y.-H. Qiu, H.-T. Liu, C.-F. Xu, D.-L. Huang, L.-S. Wang and J. Li, Inorg. Chem., 2013, 52, 6617–6626.
29. A. Shee, T. Saue, L. Visscher and A. Severo Pereira Gomes, J. Chem. Phys., 2018, 149, 174113.
30. J. Sikkema, L. Visscher, T. Saue and M. Iliaš, J. Chem. Phys., 2009, 131, 124116.
31. L. S. Cederbaum, W. Domcke, J. Schirmer and W. V. Niessen, Correlation Effects in the Ionization of Molecules: Breakdown of the Molecular Orbital Picture, John Wiley & Sons, Ltd, 2007, pp. 115–159.
32. A. B. Trofimov, D. M. P. Holland, I. Powis, R. C. Menzies, A. W. Potts, L. Karlsson, E. V. Gromov, I. L. Badsyuk and J. Schirmer, J. Chem. Phys., 2017, 146, 244307.
33. T. Koopmans, Physica, 1934, 1, 104–113.
34. J. A. Pople, P. V. Schleyer, W. J. Hehre and L. Radom, Ab Initio Molecular Orbital Theory, John Wiley & Sons, Inc., 1986.
35. P. S. Bagus and H. F. Schaefer, J. Chem. Phys., 1971, 55, 1474–1475.
36. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
37. J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944.
38. A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462.
39. J. D. Watts, An Introduction to Equation-of-Motion and Linear-ResponseCoupled-Cluster Methods for Electronically Excited Statesof Molecules, ed. M. K. Shukla and J. Leszczynski, Springer, Netherlands, Dordrecht, 2008, pp. 65–92.
40. R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138.
41. K. Sneskov and O. Christiansen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 566–584.
42. DIRAC, a relativistic ab initio electronic structure program, Release DIRAC18 (2018), written by T. Saue, L. Visscher, H. J. Aa. Jensen, and R. Bast, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, E. D. Hedegård, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther, and S. Yamamoto (available at https://doi.org/10.5281/zenodo.2253986, see also http://www.diracprogram.org).
43. T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher, I. A. Aucar, R. Di Remigio, K. G. Dyall, E. Eliav, E. Fasshauer, T. Fleig, L. Halbert, E. D. Hedegård, B. Helmich-Paris, M. Iliaš, C. R. Jacob, S. Knecht, J. K. Laerdahl, M. L. Vidal, M. K. Nayak, M. Olejniczak, J. M. H. Olsen, M. Pernpointner, B. Senjean, A. Shee, A. Sunaga and J. N. P. van Stralen, J. Chem. Phys., 2020, 152, 204104.
44. H. J. Aa. Jensen, 2005, Douglas-Kroll the Easy Way, Talk at Conference on Relativistic Effects in Heavy Elements - REHE, Mülheim, Germany, April, 2005. Available at ht tps://doi.org/10.6084/m9.figshare.12046158.
45. W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102.
46. M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102.
47. W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104.
48. T. Saue, ChemPhysChem, 2011, 12, 3077–3094.
49. K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127.
50. K. G. Dyall, Theor. Chem. Acc., 2004, 112, 403–409.
51. K. G. Dyall, Theor. Chem. Acc., 2016, 135, 128.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
53. A. Shee, L. Visscher and T. Saue, J. Chem. Phys., 2016, 145, 184107.
54. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
55. E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293.
56. K. G. Dyall and E. van Lenthe, J. Chem. Phys., 1999, 111, 1366–1372.
57. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
58. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
59. E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, O. Baseggio, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Stener, M. Swart, D. Swerhone, G. te Velde, V. Tognetti, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2014, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com.
60. H. Köppel, W. Domcke and L. S. Cederbaum, Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, John Wiley & Sons, Ltd, 2007, vol. 57, pp. 59–246.
61. U. Öpik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A, 1957, 238, 425–447.
62. I. B. Bersuker, Chem. Rev., 2013, 113, 1351–1390.
63. W. Grochala and R. Hoffmann, J. Phys. Chem. A, 2000, 104, 9740–9749.
64. C. W. Bauschlicher, M. Rosi and S. R. Langhoff, Chem. Phys., 1990, 146, 237–243.
65. W. Zou, I. B. Bersuker and J. E. Boggs, J. Chem. Phys., 2008, 129, 114107.
66. W. Zou, D. Xu, P. Zajac, A. L. Cooksy, I. B. Bersuker, Y. Liu and J. E. Boggs, J. Mol. Struct., 2010, 978, 263–268.
67. Y. Liu, W. Zou, I. B. Bersuker and J. E. Boggs, J. Chem. Phys., 2009, 130, 184305.
68. I. B. Bersuker, Chem. Rev., 2001, 101, 1067–1114.
69. A. I. Krylov, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, 2017, ch. 4, pp. 151–224.
70. J. F. Stanton, J. Chem. Phys., 2001, 115, 10382–10393.
71. J. F. Stanton and J. Gauss, Adv. Chem. Phys., John Wiley & Sons Ltd, 2003, ch. 2, pp. 101–146.
72. T. Ichino, J. Gauss and J. F. Stanton, J. Chem. Phys., 2009, 130, 174105.
73. L. V. Poluyanov and W. Domcke, J. Chem. Phys., 2012, 137, 114101.
74. A. Köhn and A. Tajti, J. Chem. Phys., 2007, 127, 044105.
75. E. F. Kjønstad, R. H. Myhre, T. J. Martínez and H. Koch, J. Chem. Phys., 2017, 147, 164105.
76. E. F. Kjønstad and H. Koch, J. Phys. Chem. Lett., 2017, 8, 4801–4807.

---

Footnote

† Electronic supplementary information (ESI) available: A brief summary of the basic theory of the pseudo Jahn–Teller effect, vertical detachment energies calculated using 2-component scalar and spin–orbit ZORA Hamiltonian, X2C-EOM-CCSD calculated energies using different basis sets and dipole moments in different geometrical arrangements of AuH₂. See DOI: 10.1039/d0cp05204c

---