Investigating the influence of relativistic effects on absorption spectra for platinum complexes with light-activated activity against cancer cells

Abstract

We report the first systematic investigation of relativistic effects on the UV-vis spectra of two prototype complexes for so-called photo-activated chemotherapy (PACT), trans–trans–trans-[Pt(N₃)₂(OH)₂(NH₃)₂] and cis–trans–cis-[Pt(N₃)₂(OH)₂(NH₃)₂]. In PACT, design of new drugs requires in-depth understanding of the photo-activation mechanisms. A first step is usually to rationalize their UV-vis spectra for which time-dependent density functional theory (TD-DFT) is an indispensable tool. We carried out TD-DFT calculations with a systematic series of non-relativistic (NR), scalar-relativistic (SR), and four-component (4c) Hamiltonians. As expected, large differences are found between spectra calculated within 4c and NR frameworks, while the most intense features (found at higher energies below 300 nm) can be reasonably well reproduced within a SR framework. It is also shown that effective core potentials (ECPs) yield essentially similar results as all-electron SR calculations. Yet the underlying transitions can be strongly influenced by spin–orbit coupling, which is only present in the 4c framework: while this can affect both intense and less intense transitions in the spectra, the effect is most pronounced for weaker transitions at lower energies, above 300 nm. Since the investigated complexes are activated with light of wavelengths above 300 nm, employing a method with explicit inclusion of spin–orbit coupling may be crucial to rationalize the activation mechanism.

---

I. Introduction

The use of platinum complexes in cancer therapy is among the most influential results of medicinal inorganic chemistry. Three simple platinum complexes are today approved worldwide for chemotherapy (cisplatin, carboplatin, and oxaliplatin), while three additional complexes (nedaplatin, lobaplatin, and heptaplatin) are approved in a few countries.¹ All these complexes are square planar with Pt(II) centers and the activity against cancer cells is caused by the labile nature of Pt(II). Yet, this labile nature also causes severe side-effects (e.g., nausea and chronic kidney disease), limiting the use of Pt(II)-based medicine. Another limitation is due to cancer cells with intrinsic or developed resistance. Complexes with fewer side-effects and different mechanisms to harm cancer cells are therefore sought for.

Recent investigations have a focus on pro-drugs, i.e., biologically inactive complexes that can be activated at the site of the tumor. For platinum, good candidates for pro-drugs are octahedral, low-spin d⁶ Pt(IV) complexes, which are kinetically stable (non-labile), compared to their d⁸ Pt(II) counterparts. Different activation mechanisms have been used: one strategy has been to rely on bio-reducing reagents, such as ascorbic acid or glutathione, reducing Pt(IV) to Pt(II).^2,3 An alternative is to use light-activation in what have become known as photo-activated chemotherapy (PACT) or photodynamic therapy (PDT).^4–6 The PACT process involves an initial electronic excitation of the pro-drug, followed by a chemical transformation (e.g. a reduction) into an active form. In this way, PACT differs from PDT, which employs a chemical substance (denoted photo-sensitizer) to form an electronically excited state, which in turn induces generation of reactive oxygen species (ROS), harmful to cancer cells. The PACT process is not as far in development as PDT for clinical use,⁷ but PACT offers advantages for cells with low oxygen levels,⁸ which are among the most resistant to therapy.^7,9

For complexes involved in PACT (and similar for PDT), theoretical methods are often required to understand the (usually complex) activation mechanisms. Time-dependent density functional theory (TD-DFT) is a powerful tool to investigate the initial process of excitation and to analyze the character of the excited states generated upon radiation. In several studies, TD-DFT has been used with great insight to explain the experimentally observed photochemistry of platinum complexes used in PACT.^10–17 In one case, several DFT functionals were also benchmarked against complete active space second-order perturbation theory (CASPT2) and it was concluded that range-separated functionals reproduce both experiment and CASPT2 results best.¹⁸

Surprisingly, none of these investigations have focused on the importance of relativistic effects, in particular concerning explicit inclusion of spin–orbit coupling. Instead, relativistic effects have usually been included indirectly through effective core potentials (ECPs) combined with a non-relativistic Hamiltonian. In one instance, relativistic effects have also been included through Douglas–Kroll–Hess to second order (DKH2), focusing on scalar-relativistic (SR) parts.¹⁸ The lack of systematic studies of relativistic effects can perhaps be attributed to that TD-DFT implementations first relatively recently were developed for a large arsenal of relativistic Hamiltonians. Yet, several formulations of relativistic TD-DFT^19–21 ranging from four-component (4c) Dirac–Kohn–Sham^22–24 to various two-component frameworks^24–28 exist today.

In this paper, we systematically investigate TD-DFT in non-relativistic (NR), scalar relativistic (SR) and four-component (4c) frameworks for complexes involved in PACT. The relativistic methods are also compared to the frequently employed ECPs. As targets, we employ two prototypical complexes (here denoted trans-Pt and cis-Pt), shown in Fig. 1. These two complexes are both active against tumors upon radiation with light^29–32 and are among the first reported platinum complexes for use in PACT. They are further the simplest among a number of related complexes which subsequently have shown similar photo-activity.^{11–17,33–38} Their exact mechanism of photo-activation is not known in detail. However, the UV-vis spectra in combination with TD-DFT calculations^10,30 have shown that both trans- and cis-Pt complexes display ligand-to-metal charge-transfer (LMCT) excitations. The population of the resulting states leads to decomposition, likely through multiple pathways,^38–40 including dissociation of N₃⁻ and/or NH₃ ligands, generation of O₂, and reduction to Pt(II). Possibly the photoreactions also involve triplet states which have been shown to be dissociative.^10,13

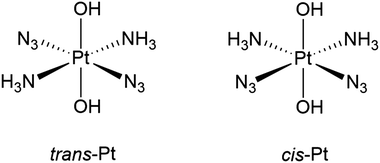Fig. 1 Lewis structures of trans–trans–trans-[Pt(N₃)₂(OH)₂(NH₃)₂] (trans-Pt) and cis–trans–cis-[Pt(N₃)₂(OH)₂(NH₃)₂] (cis-Pt) investigated in this paper.

We will compare our results to experimental UV-vis spectra as well as known light-induced reactivity. However, since we do not include solvent interactions, this comparison can only be qualitative. Intriguingly, the complexes in Fig. 1 only have intense transitions in high-energy parts of the spectra (285 and 256 nm for trans- and cis-Pt, respectively).^10,29–31 Yet, the light-induced reactivity has been achieved in regions without strong absorption. For instance trans-Pt react with DNA or DNA models (guanosine 5′monophosphate) upon exposure of light at 365–366 nm and 647 nm³⁰ (although the latter only slugishly), while cis-Pt reacts after exposure to light at both 365–366 nm, 458 nm, and 647 nm.^29,31,33 Our investigation therefore focuses on both high-energy parts of the spectra (approximately 250–300 nm) where the complexes absorb strongly, as well as lower-energy parts (above 300 nm) where the transitions are weaker, yet potentially important for anti-cancer activity.

II. Computational details

The structures of trans–trans–trans-[Pt(N₃)₂(OH)₂(NH₃)₂] (denoted trans-Pt) and cis–trans–cis-[Pt(N₃)₂(OH)₂(NH₃)₂] (denoted cis-Pt) were optimized with Turbomole 7.1,⁴¹ employing the TPSS⁴² functional and a def2-SV(P) basis set.⁴³ Calculations in Turbomole were sped up by expanding the Coulomb interactions in an auxiliary basis set (the resolution-of-identity approximation),^44,45 employing standard def2-SV(P) auxiliary basis sets. The calculated UV-vis spectra were obtained from these structures, employing TD-DFT with NR, SR and 4c Hamiltonians in the DIRAC program.^20,46 The four component (4c) calculations were carried out within a Dirac–Kohn–Sham framework, using a Dirac–Coulomb Hamiltonian with (SS|SS) integrals replaced by interatomic SS energy corrections.⁴⁷ The TD-DFT calculations were carried out with the def2-SV(P)^43,48,49 basis set for the ligands and the dyall.v2z⁵⁰ basis set for the platinum atom. The basis set for Pt was employed uncontracted. We initially tested the effect of employing a completely uncontracted basis set, but since the obtained spectra were close to identical to calculations with contracted basis sets, all calculations reported here employed contracted basis sets for the ligands. The NR and SR calculations employed the same basis set but invoked the Lévy-Leblond,⁵¹ and Dyall's spin-free^52,53 Hamiltonians, respectively. An additional set of calculations were carried out in the DALTON program⁵⁴ employing the same basis set on the ligands, but replacing the basis set on Pt with an ECP. For this purpose, the cc-pVDZ-PP⁵⁵ basis set was chosen.

Previous CASPT2 calculations favoring range-separated functionals¹⁸ led us to employ the range-separated CAM-B3LYP⁵⁶ functional for the UV-vis spectra. However, to test if our conclusions would change with the more extensively employed global hybrid B3LYP^57–59 functional, we additionally repeated the calculations with B3LYP (for calculations with ECPs only spectra calculated with CAM-B3LYP are shown). All TD-DFT calculations within the DIRAC program (relativistic and non-relativistic) were performed with 80 roots. The NR calculations with an ECP in DALTON employed 25 roots for singlet excitations and 20 roots triplet excitations. The spectra obtained were broadened using a Gaussian convolution with a broadening factor of 0.3 eV. Assignments of transitions were based on analyses of the response vectors for each transition, in combination with visual inspection. The density of states with non-zero intensities is too high to warrant discussion of each transition (particular for the 4c calculations). Therefore, we have divided the spectra into regions (1–6 for trans-Pt and 1–9 for cis-Pt) from which we discuss the most intense transitions although we show all transitions (within the chosen energy intervals) in the spectra. We have as far as possible attempted to group the transitions in regions according to their character so that the regions are comparable across different Hamiltonians and functionals. However, one-to-one correspondence could not always be achieved (especially when comparing functionals). Selected transition energies, oscillator strengths, and assignments are given (in terms of contributing orbitals) for each region in the ESI,† Tables S1–S12. Regarding the NR calculations they led, as could be expected, to large errors and will therefore only be discussed in the ESI.† The ECP calculations are also only shown in the ESI† (Fig. S17 and S18) since they yielded spectra that were close to identical to the SR framework.

Many of the discussed transitions are of similar character and to avoid tedious repetition, we will use the short-hand notation π → d for the ligand-to-metal charge transfer (LMCT) transitions between π-orbitals on N₃⁻ to orbitals of platinum d-character. Transitions between orbitals of d-character are denoted d → d, while transitions from orbitals with p-character (lone pairs) on the OH⁻ oxygen are denoted p → d. This nomenclature has also been employed in the ESI.† In addition to Tables S1–S12 (ESI†), selected orbital densities are displayed in the ESI,† Fig. S1–S12. Note that although we throughout the paper use the term orbitals, the 4c calculations rather employ spinors, which differ from orbitals in SR and calculations with ECPs (and also NR calculations) by having both α- or β-spin parts. Most spinors have a Mulliken population over 0.9 of either the α- or the β-part, but some will be more mixed. We will occasionally define orbitals (spinors) with a mixing degree lower than 0.9 as “spin-mixed” (α and β populations of the orbitals are also reported in the ESI†).

III. Results

We compare the spectra calculated with 4c and SR Hamiltonians (or ECPs) for the individual trans- and cis-complexes in Sections 3.2 and 3.3, after first briefly discussing the optimized structures (Section 3.1). In the final (Section 3.4), we compare 4c and SR results with experimental spectra and light-induced reactivity.

A. Optimized structures

The optimized structures of trans-Pt and cis-Pt complexes are shown in Fig. 2 and selected structural parameters are reported together with experimental values^29,30 in Table 1 (coordinates of the structures are provided in the ESI†). The results are overall in good agreement with both experimental and earlier computational studies¹⁸ (where several other functionals were employed). This good correspondence is illustrated by the fact that the main difference is the Pt–N–N and N–N–N angles for trans-Pt, which only deviate about 3° from the experimental results (previous DFT results have deviations around 2°–4°). The differences for cis-Pt complex are even smaller. The bonds from the platinum center to NH₃ ligands are also slightly elongated, compared to previous results.¹⁸ This elongation is seen for both isomers; for instance the B3LYP result from ref. 18 for the trans-Pt complex is 2.087 Å versus 2.101 Å for TPSS (the corresponding numbers for cis-Pt are 2.046 Å versus 2.057/2.063 Å). Yet, these elongations can still be considered minor.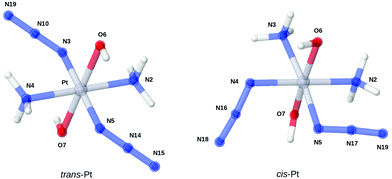

Fig. 2 Optimized structures of the two studied complexes. Bond distances and angles are shown in Table 1.

Table 1 Selected structural parameters for the optimized structures of trans-Pt and cis-Pt (numbers refer to Fig. 2)

trans-Pt
Bonds (Å)	Pt–N2/Pt–N4	Pt–N3/Pt–N5	Pt–O6/Pt–O7
Calc.	2.072	2.101	2.053
Exp.	2.036	2.045	2.006

---

Angles (°)	N2–Pt–N3/N4–Pt–N5	N2–Pt–O6/N4–Pt–O7	N3–N10–N19/N5–N14–N15
Calc.	84.9	79.6	177.1
Exp.	88.8	88.5	174.5

---

cis-Pt
Bonds (Å)	Pt–N2/Pt–N3	Pt–N4/Pt–N5	Pt–O6/Pt–O7
Calc.	2.136/2.117	2.057/2.064	2.047/2.053
Exp.	2.022/2.043	2.037/2.037	2.005/2.008

---

Angles (°)	N2–Pt–N5/N3–Pt–N4	N2–Pt–O6/N3–Pt–O7	N4–N16–N18/N5–N17
Calc.	89.7/81.8	92.8/93.2	174.5/175.9
Exp.	89.6/89.4	89.2/89.6	172.9/175.5

---

Both of the complexes have approximate octahedral coordination environments, i.e., we only see slight deviations from the 90° bond-angles around platinum, as we expect for a symmetric molecule. The complex closest to octahedral symmetry is naturally the trans-complex and symmetry forbidden excitations in higher symmetry (e.g. C_i as used in ref. 18) are likely to be affected (this will be apparent when comparing the spectra of trans- and cis-complex below).

B. UV-vis spectra with 4c and scalar relativistic Hamiltonians for trans-Pt

CAM-B3LYP results. The spectra obtained with 4c and SR Hamiltonians are shown in Fig. 3. Note that transitions of higher energy are significantly more intense than transitions of lower energy and accordingly, Fig. 3(a and b) display high- and low-energy parts of the spectrum separately (with regions 1–6 marked). The full spectrum is shown in Fig. 3(c).

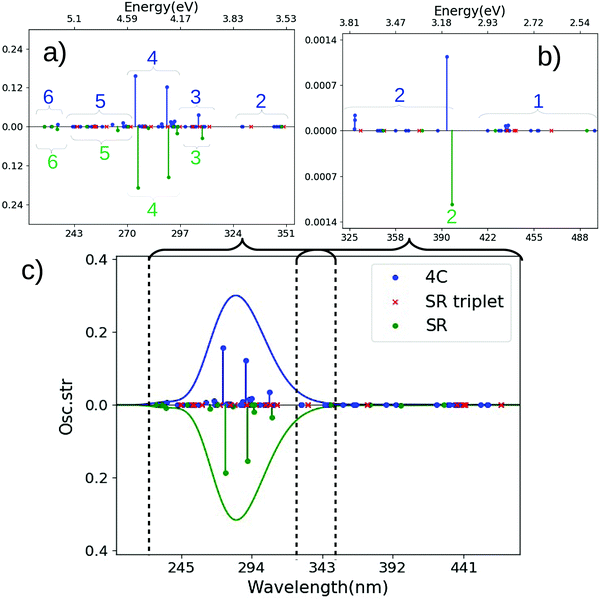
Fig. 3 Spectra for trans-Pt calculated with CAM-B3LYP and SR or 4c Hamiltonians. (a and b) are magnified for 215–305 nm and 305–480 nm. (c) Shows the full spectrum. The SR calculation is always shown along a mirrored y-axis for clarity. Assignments of main transitions within regions 1–6 are provided in Tables S1 and S3 (ESI†).

At high energies (5.71–4.59 eV or 217–270 nm) a number of transitions of low intensity are found for the 4c calculation, labeled 6 and 5 in Fig. 3(a). These transitions are mainly of LMCT character and contain a mixture of transitions from p- and π-orbitals (on OH⁻ and N₃⁻, respectively) to a d-orbital on platinum. The most intense transition (found in region 5 at 4.95 eV or 250 nm) is mainly of π → d character (cf. Table S1, ESI†). We note that all transitions in region 5 also involve (to varying degree) transitions from the oxygen lone-pairs to the metal center (p → d).

The transitions labeled 4 mainly consist of an intense transition of π → d character (cf. Tables S1, ESI†). No intense transitions are found immediately after region 4 in the 4c-CAM-B3LYP calculation, although a few transitions with intensities close to zero can be seen in this region (denoted 3 in Fig. 3(a)).

The SR calculation qualitatively reproduce the most intense features of the high-energy region, although the density of states (as expected) is higher in the 4c calculation. The characters of the transitions labeled 6–3 are to large degree similar in 4c and SR calculations, respectively (cf. Tables S1 and S3, ESI†). For instance, the most intense transition in the spectrum (region 4) is in both cases of π → d LMCT character.

Reproducing the most intense feature in the spectrum is sufficient to provide a seemingly correct description of the full spectrum as seen from Fig. 3(c). However, important differences between 4c and SR calculations occur in both high- and low-energy parts of the spectrum. We have already noted that the density of states was significantly higher in 4c calculations, but the differences become more pronounced for the lower-energy part in Fig. 3(b): in the 4c calculation, region 2 is a mixture of π → d and p → d transitions of which the most intense (at 3.46 eV or 358 nm) is of π → d character, while region 1 has a number of less intense (mainly π → d) transitions around 3.08–2.75 eV (402–451 nm). Although the most intense transitions in region 2 occur at similar energies in the SR calculation (3.43 eV or 361 nm) – and also have π → d LMCT character – a closer investigation shows that the involved transitions are different: in the 4c calculation they either involve spin-mixed orbitals (cf. Table S1 and Fig. S1, ESI†) or have dominantly triplet character, none of which can be reproduced by the SR calculation due to lack of spin–orbit coupling. The same is also true for the transitions labeled 1, where no transitions with intensity occur in the SR calculation. We have labeled triplet excitations from the SR calculations with red crosses in Fig. 3, showing the triplet states do occur the regions 2 and 1. Yet, apart from the lack of intensity, they also occur without splitting and therefore cover a more located part of the two regions (the same is true for regions 6–3 in the high-energy parts of the spectrum). This illustrates that many transitions (due to spin–orbit coupling) have low, but non-zero intensity in the 4c calculation as opposed to the SR (and NR) calculation(s). These differences will be more pronounced in the cis-Pt complex discussed below.

We finally note that the spectrum obtained within a SR framework are largely reproduced by an ECP, including the position of triplet excitations (see Fig. S17, ESI†).

B3LYP results. Since B3LYP has been employed extensively for complexes involved in PACT,^5,10,11,60 we repeated the above calculations with the B3LYP functional. The resulting spectra are shown in Fig. 4. Focusing on 4c-B3LYP and 4c-CAM-B3LYP calculations in Fig. 3 and 4, we see that B3LYP generally predicts a higher number of intense transitions, particular in the high-energy region (this is most evident in regions 4 and 3). A similar observation was made by Solokov and Schaefer,¹⁸ comparing the range-separated ωB97 and ωB97X functionals with several hybrid and pure GGA functionals (with ECPs accounting for relativistic effects). As far as it is possible to compare the regions between the two functionals, B3LYP generally red-shifts the most intense transitions about 0.2–0.4 eV. The intense transitions in region 4 appear at 4.52–4.21 eV (274–294 nm) and is (as for CAM-B3LYP) comprised mostly of π → d transitions and to less degree of p → d transitions (cf. Table S4, ESI†).

Fig. 4 Spectra for trans-Pt calculated with B3LYP and SR or 4c Hamiltonians. (a and b) are magnified for 220–355 nm and 328–500 nm. (c) Shows the full spectrum. The SR calculation is always shown along a mirrored y-axis for clarity. Assignments of main transitions within regions 1–6 are provided in Tables S4 and S6 (ESI†).

The region immediately after 4 contains (contrary to 4c- and SR-CAM-B3LYP), transitions with significant intensity: the region is denoted 3 in Fig. 4(a) and the intense transitions in the 4c- and SR-B3LYP calculations (at 4.05 and 4.02 eV or 306 and 308 nm) have p → d character.

Regarding the changes between 4c- and SR frameworks, no conclusions change by employing B3LYP: most of the intense transitions in the high-energy parts are similar for 4c and SR-B3LYP calculations, while the low-energy parts differ in SR and 4c frameworks (as seen for CAM-B3LYP). Thus, also for B3LYP the transitions in regions 2 and 1 (of π → d character) are considerably spin mixed in the 4c framework. Accordingly, several transitions in region 2 do not occur in the SR-calculation and intense transitions in region 1 are entirely missing. For the triplet excitations we also see the same as for CAM-B3LYP: in Fig. 4(a), the triplet excitations (with zero intensity) also occur in regions 1 and 2 (and also in regions 6–3), but they cover only rather localized parts of these regions.

C. UV-vis spectra with 4c and scalar relativistic Hamiltonians for cis-Pt

CAM-B3LYP results. The spectra obtained with 4c and SR frameworks are shown in Fig. 5. They contain significantly more transitions with relatively high intensities, compared to trans-Pt, and have therefore been divided into nine regions 1–9, shown in Fig. 5(a and b). Although we did not employ symmetry in our calculations, the higher number of intense transitions for cis-Pt was also discussed by Sokolov and Schaefer,¹⁸ who employed C_i symmetry for the trans-Pt complex. Thereby they could show that four out of the five lowest transitions are symmetry forbidden. As discussed in a previous section of this paper, the obtained symmetry is quite close to octrahedral in our calculations and the higher number of excitations for the cis-Pt complex is therefore not surprising.

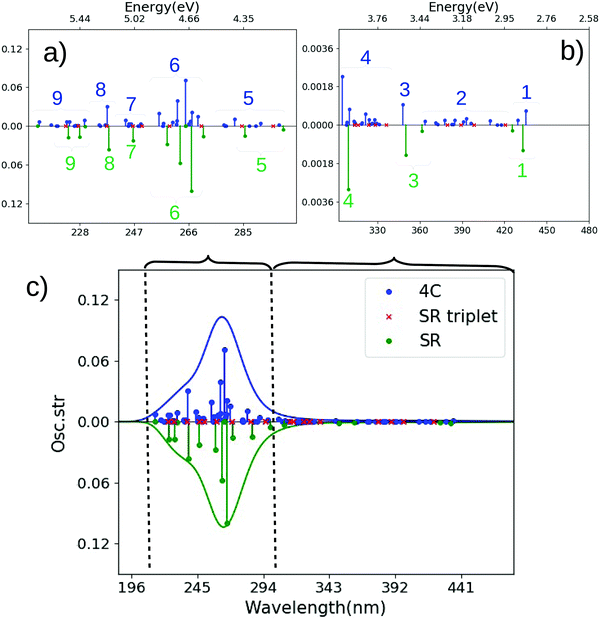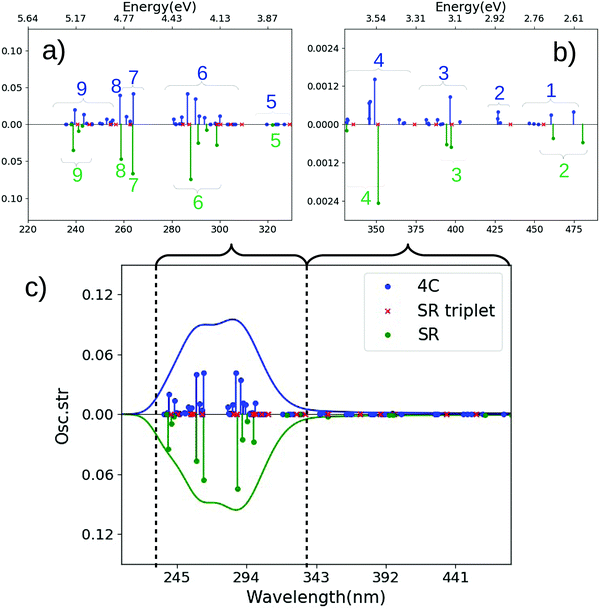
Fig. 5 Comparison of spectra for cis-Pt calculated with CAM-B3LYP and SR or 4c Hamiltonians. (a and b) are magnified for 210–306 nm and 306–480 nm. (c) Shows the full spectrum. The SR calculation is always shown along a mirrored y-axis for clarity. Assignments of main transitions within regions 1–9 are provided in Tables S7 and S9 (ESI†).

We first discuss the transitions at highest energy in the 4c calculations, labeled 9–7 (5.80–5.40 eV or 214–230 nm). The transitions labeled 9 involve almost exclusively transitions of d → d character, consistent with their low intensity, while 8 involves a mixture of transitions with d → d and π → d (LMCT) character. The next group of transitions (7 at 5.08–4.98 eV or 244–249 nm) in Fig. 5(a) have relatively low intensities; the most intense transition has π → d character. Meanwhile, the most intense transitions in the spectrum are found in region 6, at 4.85–4.61 eV (256–269 nm), followed by several transitions of lower intensity (5) at 4.46–4.26 eV (278–291 nm). Both regions 6 and 5 are of LMCT character with a mixtures of π → d and p → d transitions, where region 5 has larger weight of the former and region 6 has larger weight of the latter.

The SR calculation overall reproduces the most dominant features of the spectrum in the high-energy parts, as seen for trans-Pt. However, also for cis-Pt there are important differences: as expected, spin–orbit coupling gives rise to significantly higher density of states in the 4c calculation and many of these states have significant intensity, cf.Fig. 5(a). The higher density of states is evident for all groups of transitions in the high-energy regions (9–6), but perhaps most pronounced for region 6: in the 4c calculation this region has five intense transitions (and a number of less intense ones), whereas the SR calculation only has four intense transitions in this region. Analyzing the underlying transitions shows that their character in 4c and SR calculations corresponds fairly well to each other (π → d and p → d). However, the transitions in the 4c framework have both large triplet character and contain spin-mixed orbitals (see Table S10 and Fig. S4, ESI†), causing the differences between 4c and SR (as well as NR) frameworks. Closer investigation of Fig. 5(a) shows that triplet excitations (shown as red crosses) also occur in region 6 within an SR framework but have (as expected) no intensity and do not split.

In the low-energy parts of the spectrum (regions 1–4, Fig. 5(b)), the first group of transitions (4) at 4.07–3.78 eV (305–328 nm) in the 4c calculation is a mixture of transitions with π → d and p → d characters; the next region (3 at 3.56 eV; 348 nm) is of p → d character. Region 2 consists of many low-intensity LMCT transitions (of mixed π → d and p → p character) at 3.28–3.02 eV (378–410 nm). The last region (1 at 2.89–2.84 eV or 430–435 nm) is of LMCT character (π → d). In these parts of the spectrum we also see differences between 4c and SR calculations: region 4 at 4.01 eV (310 nm) in the SR calculation is almost exclusively of π → d character, compared to a mix between π → d and p → d in the 4c counterpart. Further, the transitions in region 4 involve orbitals that are significantly spin-mixed (and some are also of dominant triplet character) in the 4c calculations, cf. Table S7 and Fig. S4 (ESI†). Accordingly, region 4 has a number of relatively intense transitions, not seen in the SR calculation (but note that several triplet excitations are found in region 4). The character of transitions in regions 3 (mainly p → d) and 1 (π → d) in the SR calculation corresponds reasonably well with the 4c calculation, while no (intense) transitions occur in region 2 in the SR (or NR) calculation. From the 4c calculation, the underlying transitions in region 2 are found to be considerably spin-mixed, explaining the lack of intensity for the transitions in the NR and SR calculations. Only one triplet excitation is seen in region 2 (and similar for region 1) for the SR calculation.

B3LYP results. Spectra calculated with 4c and SR Hamiltonians and B3LYP are given in Fig. 6. We also here divide the spectrum into nine regions 1–9 (cf.Fig. 6(a and b)). We start by comparing 4c-B3LYP with 4c-CAM-B3LYP in the high-energy regions 9–5, cf.Fig. 6(a) and 5(a). The underlying transitions are roughly similar with the two functionals (cf. Tables S7 and S11, ESI†), although they on several occasions are predicted more intense with B3LYP, particular for regions 9–7. To the extend comparison between the regions is possible, they are generally red-shifted (between 0.2–0.5 eV) in the 4c-B3LYP calculations, compared to 4c-CAM-B3LYP.

Fig. 6 Spectra for cis-Pt calculated with B3LYP and SR or 4c Hamiltonians. (a and b) are magnified for 220–330 nm and 330–490 nm. (c) Shows the full spectrum. The SR calculation is always shown along a mirrored y-axis for clarity. Assignments of main transitions within regions 1–9 are provided in Tables S10 and S12 (ESI†).

The energy-shifts of 0.2–0.5 eV between B3LYP and CAM-B3LYP remains for the low-energy part of the spectrum (regions 4–1, Fig. 6). Yet, 4c-B3LYP calculations obtain roughly the same character for the transitions as for CAM-B3LYP (i.e. LMCT-transitions of p → d and π → d character).

The changes in the spectra from SR-B3LYP to 4c-B3LYP are similar as seen for CAM-B3LYP: the most intense features of the spectrum (regions 9–5) from the 4c calculation are reproduced, and the transitions are of similar character. Also for B3LYP, a number of transitions with significant intensity are not seen in the SR calculation due to the lack of spin–orbit coupling. We highlight again region 6 which (as for CAM-B3LYP) in the 4c framework contains both transition with dominant triplet character and orbitals that are considerably spin mixed (cf. Table S10 and Fig. S10, ESI†). Ultimately, this leads to five intense transitions (and several more of lower intensity), compared to only four in the SR calculation. Few triplet excitations also are found in region 6 for the SR-B3LYP calculation (the same was the case for SR-CAM-B3LYP). A similar scenario is found for the lower-energy regions (4–1); as for 4c-CAM-B3LYP the transitions in these regions are considerably spin-mixed and region 2 completely lack transitions with intensity in SR (and NR) calculations.

D. Comparison with experiment

Before comparing our calculated spectra with the experimental counterparts, it should be emphasized that the comparison is complicated by that the experiments were performed in water, while our calculations did not include solvent interactions. Hence, our comparison should be taken with some care, as solvent effects can alter the spectra significantly. We note however, that our calculations are in qualitative agreement with the experimental spectra: the experimental spectrum of trans-Pt has one strong absorption (without structure) at 285 nm (4.35 eV) assigned as a π → d LMCT transition.³⁰ The charge-transfer character of this excitation would suggest that employing a range-separated functional is most appropriate since regular GGA functionals can be associated with large errors for charge-transfer excitations.⁶¹ However, the errors are mainly seen for transitions involving orbitals with small spatial overlap and we therefore report a diagnostic denoted Λ⁶² for selected transitions (in the ESI,†cf. Tables S3, S6, S9 and S12). The Λ-value is directly related to the spatial overlap of the involved orbitals; typically problematic transitions have low Λ-value and an estimate of 0.3 was given from a small benchmark study of organic molecules in ref. 62. The complexes we investigate here are quite different from the benchmark in ref. 62, but we will use their value as a rough guideline.

Judging only from most intense transitions at 4.51 eV (275 nm) with 4c-CAM-B3LYP and at 274 nm (4.52 eV) with 4c-B3LYP, little difference is seen for the two functionals: 4c- and SR-B3LYP calculations obtain a range of transitions with high intensities around the experimental peak at 285 nm (regions 4 and 3 from 4.05–4.52 eV or 274–306 nm, cf.Fig. 3 and 4). Meanwhile, the range-separated functional only obtain one intense transition (cf.Fig. 3). The experimental resolution does not allow us to conclude whether CAM-B3LYP or B3LYP performs best for the trans-Pt complex. For the most intense transitions in regions 4 and 3, we obtain Λ-values around 0.4 for B3LYP (see Tables S3 and S6, ESI†). This is here considered sufficiently low to indicate that the transitions are affected by employing a range-corrected functional.

For the cis-Pt complex, the difference between B3LYP and experiment is more pronounced than for the trans-Pt complex in the high-energy regions: the B3LYP calculation predicts either three (NR-B3LYP) or two (4c- and SR-B3LYP) intense bands while the experimental spectrum³⁰ contains only one band (single peak at 256 nm or 4.84 eV). Using 4c-B3LYP as example, regions 7–8 at 4.80–4.70 eV (259–264 nm) corresponds well with experiment, while the almost equally intense transitions at 4.36 eV or 284 nm (region 6) is not reflected in the experimental spectrum. We note however, that the Λ-values (0.5–0.6, see Table S12, ESI†) do not per se signal a problematic charge-transfer excitation. Yet, the 4c- (or SR-) CAM-B3LYP calculation shows closer resemblance to experiment with one transition having significantly higher intensity than all other transitions (region 6 at 4.68 eV or 264 nm for the 4c calculation). Previous investigations have reached the same conclusions regarding range-separated functionals^10,18 and in one case also shown that range-separated functionals are closer to the CASPT2 benchmarks.¹⁸ Hence, in the discussion of the lower energy parts (where direct comparison with experimental UV-vis spectra is not possible), we focus on 4c- and SR-CAM-B3LYP (similar conclusions are obtained from comparing 4c and ECP calculations). In both trans- and cis-complexes, we find that, the LMCT (π → d and p → d) transitions extend into the regions above 300 nm but with much lower intensity (as also found in previous studies, see e.g.ref. 18). Light-induced activity has been observed for trans-Pt around 365 nm (3.40 eV)^30,40 which corresponds well with regions 1–3 with transitions in the range 4.02–2.83 eV (308–438 nm). In particular, the 4c-CAM-B3LYP calculation have a π → d transition at 3.46 eV (359 nm; region 2) which fits well with induced reactivity at 366 nm. While the SR calculation also displays a transition in this region (e.g. in region 2 at 3.43 eV), the 4c calculation reveals that the density of states (with non-zero intensity) in this region is higher than in the SR calculation as the excitations of triplet character are split through spin–orbit coupling. Thus, several more states may participate in the photo-induced reactivity than expected from the SR (or NR) calculation. It is also noted that the π → d transitions in region 2 were found to be considerably spin mixed (the same is true for regions 1 and 3), which is not captured by the SR (or NR) calculation.

The cis-Pt complex reacts with DNA after exposure to light at 366 nm and 458 nm.^29,31,33 From the spectra calculated with 4c-CAM-B3LYP (see Fig. 5) we see that regions 3 (3.56 eV or 348 nm) and 2 (3.28–3.02 eV or 378–411 nm) in the 4c calculations have transitions that corresponds well with 366 nm (3.39 eV). However, as seen for trans-Pt, these regions are considerably spin mixed in the 4c calculation and hence has a denser manifold of states (especially for region 2), compared to the SR calculation. Including triplet excitations in the SR calculations shows indeed excitations in region 2 but neither density of states nor the intensities are reproduced (as expected). Similar arguments holds for both singlet and triplet excitations in region 1 (2.89–2.85 eV or 429–435 nm) in the 4c-CAM-B3LYP calculation, where several transitions correspond well with light-induced reactivity at 458 nm (2.7 eV).

Finally, we note that photo-induced reactivity at 647 nm has been reported for both complexes^29,30,33 but no transitions were found in this region (for any of the complexes). Thus, the activity induced from light of this wavelength cannot be explained from our current calculations. A possible explanation may be that transitions in this region only occur due to further breaking of symmetry associated with either vibrations or solvent interactions.

IV. Conclusion

Using TD-DFT, we have carried out a systematic investigation of the effect of using NR, SR and 4c Hamiltonians in calculations of UV-vis spectra on two Pt(IV) complexes, known to have light-activated activity against cancer cells. We have additionally compared the SR results to the more frequently used ECPs. We have used both B3LYP and the long-range corrected CAM-B3LYP functionals, but the changes between NR, SR and 4c Hamiltonians are similar for the two functionals, ensuring that our conclusions are not merely artifacts from the functional choice. For both functionals, we find that (as might have been expected) a NR Hamiltonian does not reproduce the spectra obtained within a 4c framework. The SR calculations perform better (the ECPs essentially deliver identical results to the all-electron SR calculations). In fact, employing a SR Hamiltonian (or an ECP) is sufficient to reproduce the main features of the experimental spectra, which are dominated by one strong absorption peak. However, the 4c-calculations show that the underlying transitions are not always properly reproduced in the SR calculations, due to the lack of spin–orbit coupling: thus, intense bands in the higher energy parts (below 300 nm) as well as transitions of lower intensity (above 300 nm) can be considerably spin mixed and/or contain transitions of triplet character. This cannot be properly reproduced with SR/ECPs or NR Hamiltonians.

Seeing that incident light with wavelength above 300 nm is usually employed to photo-activate trans-Pt and cis-Pt, inclusion spin–orbit coupling seems pertinent to fully understand the activation mechanism. For instance, the 4c-CAM-B3LYP calculations predict a dense manifold of states with low, yet non-zero intensities in regions around 366 nm (a wavelength use to activate both complexes). These transitions either have triplet character and/or involve significantly spin-mixed orbitals (and a similar scenario occurs for cis-Pt around 458 nm).

Since the effects of spin–orbit coupling are seen in all regions of the spectra (and independent of the employed functional), we believe our conclusions will remain if solvent effects are modeled (which was not done in our current study). Yet, solvent effects are expected to be important and currently their omission complicates an assessment of the best functional by comparison to experiment. Our results here in combination with earlier CASPT2 results¹⁸ slightly favor the CAM-B3LYP functional over B3LYP. We plan to investigate the solvent effect in a forthcoming paper, employing a recent extension of the so-called polarizable embedding model.⁶³

We finally note that although our present results show that it is advantageous to include spin–orbit coupling in investigations of Pt complexes used for PACT, it is probably not necessary to use a 4c framework; we anticipate that various two-component methods will be sufficient.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. D. H. acknowledges financial support from the European Commission (MetEmbed, Project No. 745967) and the Villum Foundation (Young Investigator Program, Grant No. 29412).

References

1. T. C. Johnstone, K. Suntharalingam and S. J. Lippard, The next generation of platinum Drugs: targeted Pt(II) agents, nanoparticle delivery, and Pt(IV) prodrugs, Chem. Rev., 2016, 116, 3436–3486.
2. M. D. Hall and T. W. Hambley, Platinum(IV) antitumour compounds: their bioinorganic chemistry, Chem. Rev., 2002, 232, 49–67.
3. N. Graf and S. J. Lippard, Redox activation of metal-based prodrugs as a strategy for drug delivery, Adv. Drug Delivery Rev., 2012, 64, 993–1004.
4. J. S. Butler and P. J. Sadler, Targeted delivery of platinum-based anticancer complexes, Curr. Opin. Chem. Biol., 2013, 17, 175–188.
5. N. J. Farrer, L. Salassa and P. J. Sadler, Photoactivated chemotherapy (PACT): the potential of excited-state d-block metals in medicine, Dalton Trans., 2009, 10690–10701.
6. S. Bonnet, Why develop photoactivated chemotherapy?, Dalton Trans., 2018, 47, 10330–10343.
7. S. B. Brown, E. A. Brown and I. Walker, The present and future role of photodynamic therapy in cancer treatment, Lancet Oncol., 2004, 5, 497–508.
8. H. Chen, J. Tian, W. He and Z. Guo, H₂O₂-activatable and O₂-evolving nanoparticles for highly efficient and selective photodynamic therapy against hypoxic tumor cells, J. Am. Chem. Soc., 2015, 137, 1539–1547.
9. W. R. Wilson and M. P. Hay, Targeting hypoxia in cancer therapy, Nat. Rev. Cancer, 2011, 11, 393–410.
10. L. Salassa, H. I. A. Phillips and P. J. Sadler, Decomposition pathways for the photoactivated anticancer complex cis,trans,cis-[Pt(N₃)₂(OH)₂(NH₃)₂]: insights from DFT calculations, Phys. Chem. Chem. Phys., 2009, 11, 10311–10316.
11. F. S. Mackay, N. J. Farrer, L. Salassa, H.-C. Tai, R. J. Deeth and S. A. Moggach, et al., Synthesis, characterisation and photochemistry of Pt(IV) pyridyl azido acetato complexes, Dalton Trans., 2009, 2315–2325.
12. N. J. Farrer, J. A. Woods, L. Salassa, Y. Zhao, K. S. Robinson and G. Clarkson, et al., A Potent Trans-Diimine Platinum Anticancer Complex Photoactivated by Visible Light, Angew. Chem., Int. Ed., 2010, 49, 8905–8908.
13. A. F. Westendorf, L. Zerzankova, L. Salassa, P. J. Sadler, V. Brabec and P. J. Bednarski, Inuence of pyridine versus piperidine ligands on the chemical, DNA binding and cytotoxic properties of light activated trans,trans,trans-[Pt(N₃)₂(OH)₂(NH₃)(L)], J. Inorg. Biochem., 2011, 105, 652–662.
14. A. F. Westendorf, J. A. Woods, K. Korpis, N. J. Farrer, L. Salassa and K. Robinson, et al., Antitumor platinum complex that kills human cancer cells by an apoptosis-independent mechanism, Mol. Cancer Ther., 2012, 11, 1894–1905.
15. Y. Zhao, J. A. Woods, N. J. Farrer, K. S. Robinson, J. Pracharova and J. Kašpárková, et al., Diazido mixed-amine platinum(IV) anticancer complexes activatable by visible-light form novel DNA adducts, Chem. – Eur. J., 2013, 19, 9578–9591.
16. Y. Zhao, N. J. Farrer, H. Li, J. S. Butler, R. J. Mcquitty and A. Habtemariam, et al., De novo generation of singlet oxygen and ammine ligands by photoactivation of a platinum anticancer complex, Angew. Chem., Int. Ed., 2013, 125, 13878–13882.
17. E. Shaili, L. Salassa, J. A. Woods, G. Clarkson, P. J. Sadler and N. J. Farrer, Platinum(iv) dihydroxido diazido N-(heterocyclic)imine complexes are potently photocytotoxic when irradiated with visible light, Chem. Sci., 2019, 10, 8610–8617.
18. A. Y. Sokolov and H. F. Schaefer III, Ground and excited state properties of photoactive platinum(IV) diazido complexes: Theoretical considerations, Dalton Trans., 2011, 40, 7571–7582.
19. W. Liu and Y. Xiao, Relativistic time-dependent density functional theories, Chem. Soc. Rev., 2018, 47, 4481–4509.
20. T. Saue, R. Bast, A. S. P. Gomes, H. J. A. a. Jensen, L. Visscher and I. A. Aucar, et al., The DIRAC code for relativistic molecular calculations, J. Chem. Phys., 2020, 152, 204104.
21. M. Repiský, S. Komorovský, M. Kadek, L. Konecny, U. Ekström and E. Malkin, et al., ReSpect: Relativistic spectroscopy DFT program package, J. Chem. Phys., 2020, 152, 184101.
22. J. Gao, W. Liu, B. Song and C. Liu, Time-dependent four-component relativistic density functional theory for excitation energies, J. Chem. Phys., 2004, 121, 6658.
23. J. Gao, W. Zou, W. Liu, Y. Xiao, D. Peng and B. Song, et al., Time-dependent four-component relativistic density-functional theory for excitation energies. II. The exchange-correlation kernel, J. Chem. Phys., 2005, 123, 054102.
24. R. Bast, H. J. A. a. Jensen and T. Saue, Relativistic adiabatic time-dependent density functional theory using hybrid functionals and noncollinear spin magnetization, Int. J. Quantum Chem., 2009, 109, 2091–2112.
25. F. Wang, T. Ziegler, E. Van Lenthe, S. Van Gisbergen and E. J. Baerends, The calculation of excitation energies based on the relativistic two-component zeroth-order regular approximation and time-dependent density-functional with full use of symmetry, J. Chem. Phys., 2005, 122, 204103.
26. D. Peng, W. Zou and W. Liu, Time-dependent quasirelativistic density-functional theory based on the zeroth-order regular approximation, J. Chem. Phys., 2005, 123, 144101.
27. M. Kühn and F. Weigend, Implementation of two-component time-dependent density functional theory in TURBOMOLE, J. Chem. Theory Comput., 2013, 19, 5341–5348.
28. F. Egidi, J. J. Goings, M. J. Frisch and X. Li, Direct atomic-orbital-based relativistic two-component linear response method for calculating excited-state fine structures, J. Chem. Theory Comput., 2016, 12, 3711–3718.
29. P. Müller, B. Schröder, J. A. Parkinson, N. A. Kratochwil, R. A. Coxall and A. Parkin, et al., Nucleotide cross-linking induced by photoreactions of platinum(iv)-azide complexes, Angew. Chem., Int. Ed., 2003, 42, 335–339.
30. F. S. Mackay, J. A. Woods, H. Moseley, J. Ferguson, A. Dawson and S. Parsons, et al., A photoactivated trans-diammine platinum complex as cytotoxic as cisplatin, Chem. – Eur. J., 2006, 12, 3155–3161.
31. P. J. Bednarski, R. Grünert, M. Zielzki, A. Wellner, F. S. Mackay and P. J. Sadler, Light-activated destruction of cancer cell nuclei by platinum diazide complexes, Chem. Biol., 2006, 13, 61–67.
32. M. Imran, W. Ayub and I. S. Butler, Rehman Zu. Photoactivated platinum-based anticancer drugs, Coord. Chem. Rev., 2018, 376, 405–429.
33. J. Kašpárková, F. S. Mackay, V. Brabec and P. J. Sadler, Formation of platinated GG crosslinks on DNA by photoactivation of a platinum(IV) azide complex, J. Biol. Inorg. Chem., 2003, 8, 741–745.
34. F. S. Mackay, J. A. Woods, P. Heringová, J. Kašpárková, A. M. Pizarro and S. A. Moggach, et al., A potent cytotoxic photoactivated platinum complex, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20743–20748.
35. J. Pracharova, L. Zerzankova, J. Stepankova, O. Novakova, N. J. Farrer and P. J. Sadler, et al., Interactions of DNA with a new platinum(IV) azide dipyridine complex activated by UVA and visible light: relationship to toxicity in tumor cells, Chem. Res. Toxicol., 2012, 25, 1099–1111.
36. Y. Min, J. Li, F. Liu, E. K. L. Yeow and B. Xing, Near-infrared light-mediated photoactivation of a platinum antitumor prodrug and simultaneous cellular apoptosis imaging by upconversionluminescent nanoparticles, Angew. Chem., Int. Ed., 2014, 53, 1012–1016.
37. A. Gandioso, E. Shaili, A. Massaguer, G. Artigas, A. González-Canto and J. A. Woods, et al., An integrin-targeted photoactivatable Pt(IV) complex as a selective anticancer pro-drug: synthesis and photoactivation studies, Chem. Commun., 2015, 51, 9169–9172.
38. C. Imberti, P. Zhang, H. Huang and P. J. Sadler, New designs for phototherapeutic transition metal complexes, Angew. Chem., Int. Ed., 2020, 59, 61–73.
39. L. Ronconi and P. J. Sadler, Unprecedented carbon-carbon bond formation induced by photoactivation of a platinum(iv)-diazido complex, Chem. Commun., 2008, 235–237.
40. L. Ronconi and P. J. Sadler, Photoreaction pathways for the anticancer complex trans,trans,trans-[Pt(N₃)₂(OH)₂(NH₃)₂], Dalton Trans., 2011, 40, 262–268.
41. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: the program system TURBOMOLE, Chem. Phys. Lett., 1989, 162, 165–169.
42. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: nonempirical meta-generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91, 146401.
43. A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
44. K. Eichkorn, T. Oliver, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary basis sets to approximate Coulomb potentials, Chem. Phys. Lett., 1995, 240, 283–290.
45. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials, Theor. Chem. Acc., 1997, 97, 119–124.
46. T. Saue, L. Visscher, H. J. A. Jensen and R. Bast, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, E. D. Hedegård, T. Helgaker, J. Henriksson, M. Iliaš, C. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Salek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther and S. Yamamoto, DIRAC, a relativistic ab initio electronic structure program, Release DIRAC18, 2018,  DOI:10.5281/zenodo.2253986, see also http://www.diracprogram.org.
47. L. Visscher, Approximate molecular relativistic Dirac-Coulomb calculations using a simple Coulombic correction, Theor. Chim. Acta, 1997, 98, 68–70.
48. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-adjustedab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77, 123–141.
49. F. Weigend and R. Ahlrichs, Energy-adjustedab initio pseudopotentials for the second and third row transition elements, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
50. K. G. Dyall and A. S. P. Gomes, Revised relativistic basis sets for the 5d elements Hf-Hg, Theor. Chem. Acc., 2009, 125, 97.
51. J. M. Lévy-Leblond, Nonrelativistic particles and wave equations, Commun. Math. Phys., 1967, 6, 286–311.
52. K. G. Dyall, An exact separation of the spin-free and spin-dependent terms of the Dirac-Coulomb-Breit Hamiltonian, J. Chem. Phys., 1994, 100, 2118–2127.
53. L. Visscher and T. Saue, Approximate relativistic electronic structure methods based on the quaternion modified Dirac equation, J. Chem. Phys., 2000, 113, 3996–4002.
54. J. M. H. Olsen, S. Reine, O. Vahtras, E. Kjellgren, P. Reinholdt and K. O. Hjorth Dundas, et al., Dalton Project: A Python platform for molecular- and electronic-structure simulations of complex systems, J. Chem. Phys., 2020, 152, 214115.
55. D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf-Pt, J. Chem. Phys., 2009, 130, 164108.
56. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
57. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
58. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
59. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
60. C. Garino and L. Salassa, The photochemistry of transition metal complexes using density functional theory, Philos. Trans. R. Soc., A, 2013, 371, 20120134.
61. A. Dreuw and M. Head-Gordon, Failure of time-dependent density functional theory for long-range charge-transfer excited states: the zincbacteriochlorin-bacteriochlorin and bacteriochlorophyll-spheroidene complexes, J. Am. Chem. Soc., 2004, 126, 4007–4016.
62. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128(4), 044118,  DOI:10.1063/1.2831900.
63. E. D. Hedegård, R. Bast, J. Kongsted, J. M. H. Olsen and H. J. A. Jensen, Relativistic polarizable embedding, J. Chem. Theory Comput., 2017, 13, 2870–2880.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05143h

---