Chaotic oscillations, dissipation and mirror symmetry breaking in a chiral catalytic network
Received
28th September 2020
, Accepted 11th November 2020
First published on 12th November 2020
Abstract
Catalytic reaction networks consist of molecular arrays interconnected by autocatalysis and cross-catalytic pathways among the reactants, and serve as bottom-up models for the design and understanding of molecular evolution and emergent phenomena. An important example of the latter is the emergence of homochirality in biomolecules during chemical evolution. This chiral symmetry breaking is triggered by bistability and bifurcation in networks of chiral replicators. Spontaneous mirror symmetry breaking (SMSB) results from hypercyclic connectivity when the chirality and enantioselectivity of the replicators are taken into account. Heretofore, SMSB has been generally understood as involving chemical transformations yielding scalemic outcomes as non-equilibrium steady states (NESS). Here, in marked contrast, we consider the chaotic regime, in which steady states do not exist. The dissipation, or entropy production, is chaotic as is the exchange entropy. The rate of change of the total system entropy, governed by the entropy balance equation, is also chaotic. Subsequent to the mirror symmetry breaking transition, the time averaged entropy production is minimized in the final chaotic chiral state with respect to the former chaotic racemic state. The chemical forces (i.e., the affinities) evolve in time so as to lower the sum of the entropy production and the exchange entropy, in compliance with the general evolution criterion extended to reaction networks subject to volumetric open flow.
1 Introduction
Complex systems in nature are appropriately modeled as open networks,1,2 where energy, raw materials and reactants are continuously being pumped in, and reactants and products are prone to dissipation and decay. Replicators and catalytic reaction networks are prime examples of such systems and are fundamental to the origin of life and for its capacity to evolve. The study of chemical networks exhibiting emergent phenomena is at the core of Systems Chemistry research.3–5 The design and analysis of such schemes can shine light on early chemical evolution processes that led to emergent properties in prebiotic environments. One such basic emergent property is chiral symmetry breaking: biology exhibits homochirality. That is, only one of the two enantiomers of amino acids and sugars are used in proteins and nucleic acids in biochemistry. Non-equilibrium thermodynamic studies of chemical replicators able to lead to chiral symmetry breaking provide crucial information on the origin of homochirality and life, and in compliance with the underlying physico-chemical mechanisms and constraints.
Autocatalysis is significant for life,6–8 because it sustains self-reproduction in the nucleic acid and protein domains. The emergence of autocatalysis during the formation of the first replicators represents a crucial stage in chemical evolution. On the other hand, since biological replication is enantioselective, a spontaneous mirror symmetry breaking (SMSB) scenario of enantioselective autocatalysis occurring at the same stage of abiotic evolution, rather than during the latter stage of the emergence of replicators (e.g., pre-RNA- or RNA-world9,10 or even for the simultaneous emergence of RNA and DNA11), is a reasonable unifying hypothesis which has been put forward and elaborated in ref. 12. The need to understand the origin of biological homochirality makes the study of such chiral chemical networks especially interesting and relevant. Moreover, the significance of such a SMSB reaction network is that it does not imply heterochiral inhibiting reactions, such as in the Frank model,13 and as a result, the emergence of biological homochirality could already be included, both theoretically and experimentally, in current models of the selection and evolution of biological replicators. These results12 suggest an abiotic scenario of a simultaneous emergence of biological homochirality during the formation of replicator networks with catalytic activity.
Spontaneous mirror symmetry breaking (SMSB) or absolute asymmetric synthesis (AAS) refer to the transformation of achiral or racemizing initial products to final chiral reaction products in detectable enantiomeric excesses, in the absence of chiral polarizations or external chiral forces and influences. Typically, both SMSB and AAS are understood as processes yielding non-racemic outcomes manifested as non-equilibrium steady states (NESS).14–17 However, final state stationarity is not a necessary condition for chiral symmetry breaking. In this paper, we consider a catalytic network studied previously for its rich repertoire of periodic and complex chaotic dynamics.1,2 We extend that model (without the error tail) to encompass two enantiomeric sets of replicators coupled solely through their mutual competition for a common resource: the activated monomers. The ensuing chiral replicator network is placed within a well-stirred open flow reactor. Then, through high-precision numerical simulations, we demonstrate how SMSB can take place between two chaotic dynamic states. In the initial chaotic racemic state, the pair of enantiomeric concentrations for each replicator is described by an identical temporal series. Adding a small initial perturbation to any one of the enantiomers provokes a mirror symmetry breaking transition. The final chiral state is described by chaotic temporal series for only one of the two enantiomers of each replicator. The chirality of the final enantiomer so selected can depend on the way the initial fluctuations are distributed. The oppositely handed enantiomers are completely extinguished, leading to 100% homochirality in the final dynamic state. Although the individual replicator concentrations oscillate in a quasi-periodic random fashion, the enantiomeric excess is completely stationary. The final chiral sign is selected deterministically from the initial conditions, in spite of underlying chaotic dynamics.
The question of the origin of biological homochirality requires an understanding of the non-equilibrium thermodynamic conditions that may condition and lead to deviations from the racemic composition. Non-equilibrium thermodynamics provides fundamental insights on key properties of wide classes of systems at a macroscopic level of description in which the entropy production, measuring the dissipation released by the irreversible processes taking place within the system, plays a central role.18 We study in detail the entropy production and entropy exchange associated with the racemic to chiral transition in going from one chaotic regime to another. This leads to a description of the entropy production, the entropy exchanged with the environment, and the total entropy balance involving the former and the latter for both the racemic and homochiral chaotic states. The entropy production and exchange are given by chaotic temporal series. Although the system never reaches a stationary state, the time-averaged entropy production is minimized for the final chaotic chiral state with respect to that of the former chaotic racemic state. The general evolution criterion for chemical reactions subject to open volumetric flow is obeyed,19 indicating that the chemical forces, or affinities, evolve so as to lower the rate of change of the net system entropy.
2 General model with error tail
We give a brief review of the general catalytic network,1,2 on which the chiral model in Section 3 is based, to highlight and distinguish the similarities and differences between the two.
The general model consists of n species Xi, (1 ≤ i ≤ n) that individually self-replicate via non-catalytic and catalytic action, catalyzing the replication of other species. Faulty replication produces error mutants Xe which are assumed to be kinetically indistinguishable among themselves. This aggregate error-species (denoted as the error-tail) undergoes non-catalyzed self-replication, but has no effect on the catalytic species. A constant population (CP) constraint sets up a competition among all reactants including the error tail. The corresponding kinetic reactions can be represented as follows, where Ai is the amplification factor, Kji the kinetic constants for catalytic replication, and 0 ≤ Q ≤ 1 is the quality factor, (1 − Q) is the mutation rate:
| |  | (1) |
| |  | (2) |
| | 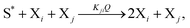 | (3) |
| |  | (4) |
| | 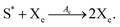 | (5) |
Energy-rich substrate monomers S* are continuously injected into the system, and the product S resulting from the degradations:
| |  | (6) |
| |  | (7) |
| |  | (8) |
represent energy-poor monomers that do not provide substrate for replication. The CP constraint

on the concentrations leads to an output flux
ϕ.
Fig. 1 shows the general model.
 |
| | Fig. 1 Schematic diagram of the fully connected catalytic model for n replicators Xi including the error tail Xe.1,2 Solid circular arrows designate autocatalytic replication; straight arrows cross-catalytic replication. Broken circular arrows: non-catalytic replication. Reproduced from ref. 1 with permission from Elsevier. | |
3 Chiral replicator network
The hypercycle model20 solves the problem of how to perform replicator selection, that is, how to achieve exponential growth dynamics based on quadratic autocatalysis. Recently, we have shown that heterocatalytically coupled enantioselective replicators are able to yield spontaneous mirror symmetry breaking (SMSB) in a number of networks of varying complexity, and this implies enantiomeric selection in the case of chiral replicators.12,21,22 In terms of real chemical systems, we note that cross-chiral catalysis has been recently reported for D- and L-RNA mixed systems.23 Thus, if homochiral cross catalysis can be experimentally demonstrated in RNA type models (D-RNA catalyzing D-RNA, and L-RNA catalyzing L-RNA) then these would provide an explicit chemical realization of networks such as the one considered here. The chemical network could also, for example, represent an ecological network of genomes in symbiosis and the model's purpose would be to justify the coexistence of populations of distinct sequences.
We consider a volumetric open flow scheme Fig. 2 similar to those analyzed in ref. 12, which maintains the reactions out of equilibrium. Such an open flow configuration was shown to lead to SMSB, in the presence of tiny chiral perturbations, and for various numbers of chiral replicators. Here, activated monomers S flow in with a predetermined fixed input concentration [S]in, whereas the unconsumed monomers together with the instantaneous concentrations of the replicators established within the well-stirred reactor flow out, such that reactor volume V is kept constant. Let q be the volume of solution flowing per unit time in and out of the reactor. Then the open flow chemical reaction scheme for the i, j = 1,…, n replicator enantiomers Li, Di is:
| |  | (9) |
| |  | (10) |
| |  | (11) |
| |  | (12) |
| |  | (13) |
| |  | (14) |
The noncatalytic replication
eqn (9) proceeds with amplification
Ai, whereas the kinetic constants
Kji govern the auto- and cross-catalytic replication
eqn (10). Activated monomers are input to the reactor with a fixed concentration
(11), whereas all the species flow out of the reaction domain with their specific instantaneous concentrations
(12)–(14) as established within the well-stirred reactor.
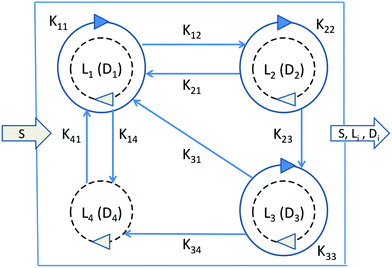 |
| | Fig. 2 Network graph of the n = 4 open-flow chiral replicator model used in the numerical analysis. Monomers S flow in with a fixed concentration [S]in, whereas the unused monomers S and all the replicator enantiomers Li, Di, i = 1, 2, 3, 4 flow out with their instantaneous concentrations as established within the well-stirred reactor. Solid circular arrows designate autocatalytic replication; straight arrows cross-catalytic replication. Broken circular arrows: non-catalytic replication. The values of the kinetic constants employed are given in eqn (23), the same used in ref. 1 and 2. | |
The above scheme eqn (9)–(14) implies the following set of 2n + 1 differential rate equation for the concentrations of the replicator enantiomers:
| |  | (15) |
| | 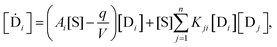 | (16) |
and for the concentration of the monomers:
| |  | (17) |
The system rapidly settles down (in about one second for the simulation parameters employed below) to a state of constant total population (CP), but constancy in the total chemical mass does not imply however that the system is in a steady state (e.g., see the chaotic temporal series below). In this CP state, the total system concentration evolves to equalize to the fixed input monomer concentration:
| |  | (18) |
| |  | (19) |
It is worth emphasizing that this CP condition is arrived at dynamically, and is not imposed as an additional constraint, as was done originally in
ref. 1 and 2. This condition
eqn (19) leads to competition among all the reactants, which is therefore an emergent property of the network.
3.1 Scaling relations
By scaling the concentrations ([Li],[Di],[S],[S]in) → λ([Li],[Di],[S],[S]in) by λ > 0, the dynamical equations eqn (15)–(17) can be made invariant by a corresponding re-scaling of the flow rate, amplification and catalytic matrix as follows:| | ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) = λq, = λq, | (20) |
| | ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ji = λ3Kji, ji = λ3Kji, | (22) |
and by redefining the time scale by τ = λ−1t. This shows that there is wide range of concentrations and reaction rate constants which lead to identical dynamics. We can exploit this scaling freedom to choose concentrations in order to decrease the time scale of the initial transient behavior and the onset of the chaotic dynamics. We exploit this freedom and choose the replicator concentrations to be of the same order as those employed in ref. 1 and 2 to facilitate comparison with the complex behavior displayed by non-chiral replicator networks considered previously.
4 Chaotic racemic state
The lowest dimension of the original achiral model capable of generating complex behavior corresponds to n = 4 catalytic species.1,2 It included an error tail and was subjected to an imposed CP constraint. We verify numerically that this complex chaotic behavior emerges as well for our chiral model eqn (9)–(14) and Fig. 2, which dispenses with the error tail and operates under open volumetric flow, see eqn (11)–(14) above. For this, we employ the same catalytic matrix Kji and amplification vector Ai2 as introduced in ref. 1:| |  | (23) |
Recall these values can be scaled up by appropriate re-scalings of the species concentrations, as mentioned above, see eqn (20)–(22).
The first thing we need to check is if the chiral version of the hypercyclic model in ref. 1 is capable of chaotic dynamics. The answer is in the affirmative. Strictly racemic initial conditions [Li]0 = [Di]0 for i = 1,…., 4 lead to a racemic outcome. This racemic outcome is chaotic. The corresponding temporal series in the concentrations of both the enantiomers of all the catalytic species is shown in Fig. 3. Although each enantiomer exhibits a complex temporal behavior, the enantiomeric excess eei = ([Li] − [Di])/([Li] + [Di]) for each pair of replicator enantiomers is strictly zero (eei = 0) once the constant population regime eqn (19) is reached. The temporal series of each enantiomer is identical to that of its mirror image, as to be expected in a strictly mirror symmetric reaction network. In other words, the enantiomeric excess is vanishing and moreover is stationary in the chaotic racemic state.
 |
| | Fig. 3 Chaotic time series in the concentrations of the four catalytic species for the racemic outcome: [Li] = [Di], for i = 1, 2, 3, 4. For racemic initial conditions: [Li]0 = [Di]0, and using a working precision of 30 significant digits. Initial values are [L1]0 = 2 × 102, [L2]0 = [L3]01 = 1 × 102, [L4]0 = 10; and [S]0 = 1 × 102. | |
5 Chaotic time series: chiral symmetry breaking
Chiral symmetry can be broken by including a tiny initial perturbation in any of the enantiomers. Here, we perturb the initial concentration of the L1 replicator by 10−4 M. Generally speaking, a positive perturbation in a given handedness will lead to chiral amplification in all the enantiomers of that same handedness, and for all the replicators. For example, a small positive fluctuation in L1 will lead to amplification in all the Li and extinction in all the Di, see Fig. 4. Conversely, an initial tiny positive fluctuation in any of the Di enantiomers will lead to a homochiral outcome for all the D-enantiomers and full extinction in all the L-enantiomers. In the case of SMSB, the temporal series for the surviving L-enantiomers are qualitatively similar to those corresponding to the racemic outcome, except for a notable increase by an approximate factor of two in the maxima of the amplitudes of the chaotic oscillations: compare Fig. 3 (racemic outcome) with Fig. 4 (scalemic outcome). The mirror symmetry breaking bifurcation is displayed in Fig. 5, in which we plot the time dependence of the sum of the concentrations of the L replicators and that of the D-replicators.
 |
| | Fig. 4 Chaotic time series in the concentrations of the four catalytic species for the homochiral outcome: [Li] > 0, [Di] ≈ 0, for i = 1, 2, 3, 4. Note the maximum amplitudes for each species is approximately twice that of the same species in the racemic outcome, see Fig. 3. | |
 |
| | Fig. 5 The chiral symmetry breaking bifurcation. Top branch (blue) the sum of the concentrations of the L-replicators  , bottom branch (red) the sum of the concentrations of the D-replicators, , bottom branch (red) the sum of the concentrations of the D-replicators,  . . | |
6 Entropy production, exchange and balance
The entropy production 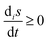 reveals the rate of dissipation and
reveals the rate of dissipation and  represents the exchange or net transport of entropy to the environment.24 The matter fluxes that drive entropy production, and are involved in entropy exchange with the environment, are crucial for determining the thermodynamic stability of any open system. Aspects of chemical stability can be characterized and quantified in terms of this non-equilibrium thermodynamic state function25 and is fundamental for understanding the thermodynamics of evolution.26
represents the exchange or net transport of entropy to the environment.24 The matter fluxes that drive entropy production, and are involved in entropy exchange with the environment, are crucial for determining the thermodynamic stability of any open system. Aspects of chemical stability can be characterized and quantified in terms of this non-equilibrium thermodynamic state function25 and is fundamental for understanding the thermodynamics of evolution.26
The entropy production rate (per unit volume) for an out-of-equilibrium chemical reaction system is expressed as a sum over all species α, of products of generalized forces Fα and generalized flows Jα for the internal reactions:24–26
| |  | (24) |
where
T is the absolute temperature. Given that the reaction scheme
eqn (9) and (10) involves strictly irreversible transformations, the standard prescription
24–26 for the forces assuming (micro)-reversible transformations leads to logarithms of the ratio of the forward and reverse reaction rates. These logarithms clearly diverge in the approximation of strictly zero reverse reaction. To overcome this unphysical feature, we employ the prescription, originally due to Onsager,
27 in which the chemical forces
Fα are defined as the difference of the standard chemical potential of a species with respect to its equilibrium value (the latter is the value reached when the driven system is isolated, that is, removed from the open flow):
| |  | (25) |
where
R is the gas constant. This relative chemical potential shifts the reference point from the Gibbs energy of formation to the equilibrium state of the system (and for ideal solutions, where the activity is equal to the concentration, a valid approximation for dilute solutions
28). Using this we obtain:
29| |  | (26) |
| |  | (27) |
| |  | (28) |
The concentrations [X
eq] correspond to those resulting from shutting off the volumetric flow, and after which the system has reached its total chemical mass which is equal to [S]
in,
eqn (19). The generalized flows
Jα are given by the rate of change of concentration of each species due to the internal transformations (that is, excluding the input and output flows:
eqn (11)–(14)):
| | JLi = [![[L with combining dot above]](https://www.rsc.org/images/entities/char_004c_0307.gif) i]|q=0, i]|q=0, | (29) |
the explicit expressions can be read off from
eqn (15)–(17) upon setting
q = 0. Substituting these redefined forces and fluxes into
eqn (24) leads to a finite expression for the entropy production provided, of course, that the equilibrium concentrations do not vanish: [L
ei] > 0, [D
ei] > 0, [S
e] > 0. We will see below that this prescription does yield a positive result for
eqn (24), as to be expected for the entropy production, or rate of dissipation.
For a system with k species, denoting their instantaneous concentration by ck, the entropy, per unit volume, exchanged with the environment is given by ref. 30, where ck,in denote the input concentrations:
| |  | (32) |
The concentrations
ck,eq are determined from mass conservation: they correspond to isolating the reactor from the open flow after reaching the chemical mass of the racemic chaotic state. In our case, they correspond to the species concentrations averaged over the chaotic racemic state.

can have any sign. For our open flow model, this gives
| |  | (33) |
From the above expressions (24), it follows that the entropy production per unit volume is given by
| |  | (34) |
The sum of the entropy production and exchange terms satisfy the entropy balance equation
25 where

is the rate of change of total or net system entropy per unit volume:
| | 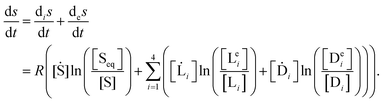 | (35) |
Note that the net change of entropy

vanishes identically at a non-equilibrium stationary state (NESS), if indeed such a state existed, since stationarity itself implies [Ṡ] = [
![[L with combining dot above]](https://www.rsc.org/images/entities/char_004c_0307.gif) i
i] = [Ḋ
i] = 0, and hence the entropy production and exchange are balanced between themselves, that is, they mutually compensate each other in stationary states: thus

. On the other hand, if the system is an a dynamic state, as for example regular or chaotic temporal oscillations, then the total change in entropy will not generally vanish

, and consequently the entropy production and exchange terms are not mutually compensated. Such is the case here, and we calculate the entropy production and exchange entropy (per unit volume) for both the chaotic racemic and chaotic chiral outcomes: see
Fig. 6 (the chaotic racemic outcome) and
Fig. 7 (the chaotic scalemic outcome). The total rate of change of entropy (the entropy balance equation:
eqn (35)) is presented in
Fig. 8.
 |
| | Fig. 6 Chaotic time series for the exchange entropy eqn (33) (left) and for the internal entropy production eqn (34) (right) for the racemic outcome. Units are J K−1 L−1 s−1. | |
 |
| | Fig. 7 Chaotic time series for the exchange entropy eqn (33) (left) and for the internal entropy production eqn (34) (right) for the chiral outcome. Units are J K−1 L−1 s−1. Note the maximum amplitude of entropy production is lowered in the mirror symmetric broken state with respect to that of the racemic state: compare to Fig. 6. | |
 |
| | Fig. 8 Chaotic time series for the total net entropy change per unit volume, eqn (35), (the entropy balance: the sum of entropy production and exchange entropy) for the racemic outcome (left) and for the chiral outcome (right). Units are J K−1 L−1 s−1. | |
Comparison of the range of numerical values spanned for the maximum amplitudes of the internal entropy production  between the racemic and chiral regimes indicates that it is diminished for the latter with respect to the former. That is, the entropy production is lowered in absolute terms for the chiral regime. This implies that the time-average of the entropy production is also minimized for the chaotic chiral regime with respect to the chaotic racemic regime:
between the racemic and chiral regimes indicates that it is diminished for the latter with respect to the former. That is, the entropy production is lowered in absolute terms for the chiral regime. This implies that the time-average of the entropy production is also minimized for the chaotic chiral regime with respect to the chaotic racemic regime:  , where angular brackets denote averaging with respect to a specified time interval.
, where angular brackets denote averaging with respect to a specified time interval.
7 Role of the chemical forces: the general evolution criterion
Glansdorff and Prigogine derived a general evolution criterion (GEC) for macroscopic physical systems subject to prescribed boundary conditions. This criterion takes the form of an inequality for an expression which is the sum of a surface integral (involving the boundary conditions pertinent to the system) plus a volume integral (involving the physical processes taking place within the bulk system).25,31,32 When time independent boundary conditions are invoked, the surface integral contribution vanishes, and the resultant inequality governs the time evolution of the so-called generalized forces involved in the bulk processes taking place within the system volume.
For the case of chemical reaction systems, a long-standing approximation has been to assume fixed or “clamped” external concentrations, primarily in order to simplify greatly the mathematical analysis. In this approximation, the GEC states that the generalized forces F (here, the chemical affinities) evolve in such a way so as to lower the entropy production. That is, the evolution of the chemical forces tends to lower the dissipation. This kinetic approximation of clamped concentrations for the chemical species exchanges with the environment overlooks the role of the boundary conditions of open flow systems for the correct description of non-equilibrium stationary states.33
In open volumetric flow systems however (as in Fig. 2), the affinities, or chemical forces, depend on both the internal bulk system reactions as well as on the matter fluxes entering and leaving the system, just as in open flow reactors. In this more general and realistic setting, where chemical species are free to enter and to exit the reactor volume with their instantaneous time-dependent concentrations, the GEC becomes the statement that all the chemical forces evolve in such a way† to lower the sum of the entropy production plus the exchange entropy.19 For the open-flow scheme considered here, this more encompassing criterion is the statement that
| |  | (36) |
If we shut off the volumetric mass flow
q = 0, the exchange entropy terms vanishes identically:
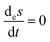
, and this reduces to the original Glansdorff and Prigogine GEC, which holds for the clamped approximation, as commented above. From the final line we see that the overall expression vanishes only for either an equilibrium or non-equilibrium stationary state. If the driven system possesses no stationary states, then the temporal derivative of the system net entropy with respect to the rate of change of the forces
F (the affinities) is thus strictly negative definite.
We validate this predicted behavior eqn (36) for chaotic dynamics by evaluating the expression given on the final line. We note that for chaotic dynamics, in the absence of stationary states, the inequality is obeyed: see Fig. 9 for the chaotic racemic behavior prior to mirror symmetry breaking and Fig. 10 for the chaotic chiral behavior subsequent to the mirror symmetry breaking transition. The chemical forces of both the internal reactions and those driving the matter flows evolve in unison so as to lower the balance of entropy, that is, the sum of (i) the entropy production due to irreversible transformations  and (ii) the entropy exchanged with the environment
and (ii) the entropy exchanged with the environment  , leading to
, leading to  .
.
 |
| | Fig. 9 The derivative, of the sum of the entropy production and entropy exchange (per unit volume), with respect to the time dependence of the forces F, or chemical affinities eqn (36), and for the chaotic racemic outcome. Units are J K−1 L−1 s−2. Note that 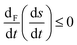 , in compliance with the general evolution criterion. , in compliance with the general evolution criterion. | |
 |
| | Fig. 10 The derivative, of the sum of the entropy production and entropy exchange (per unit volume), with respect to the time dependence of the forces F, or chemical affinities eqn (36), and for the chaotic chiral outcome. Units are J K−1 L−1 s−2. Note that 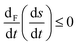 , in compliance with the general evolution criterion. , in compliance with the general evolution criterion. | |
The only rigorous theorem determining what path a far from equilibrium dynamical system follows is the general evolution criterion.25 An explicit example of a simple chemical model which can end up producing either a minimum or maximum of entropy in a final stable state was discussed in ref. 19 (see Fig. 2 there). This system, enantioselective autocatalysis of order 0.1 < n ≤ 2 possesses a stable racemic, an unstable scalemic and a stable scalemic state for certain autocatalytic orders. Depending on the sign of the fluctuation about the unstable scalemic state, and for orders in the range 1.6 < n < 1.7, the system can evolve to either the stable racemic (which therefore maximizes the entropy production with respect to that of the unstable scalemic) or it can evolve to the stable scalemic state, which therefore minimizes the entropy production, again, with respect to that of the unstable scalemic. Nevertheless, the General Evolution Criterion (GEC) is obeyed for all these alternative outcomes.19
8 Conclusions
Within the framework of non-equilibrium non-linear thermodynamics of irreversible processes24,25 mirror symmetry breaking can occur for specific system parameters and when the system is maintained out of equilibrium with its surroundings.14 The racemic state becomes metastable along the so-called thermodynamic branch and the intrinsic statistical chiral fluctuations perturb the system, provoking a transition to one of two energetically degenerate final chiral states: a bifurcation to ordered scalemic states takes place with a consequent decrease in the symmetry, and for which the production of entropy is minimized with respect to the former racemic configuration. This bifurcation trend together with the minimization of entropy production has been confirmed via numerical simulations for a variety of model chemical systems capable of reaching non-equilibrium steady states;22,33–37 here we show it holds as well for chaotic dynamics.
Enantioselective hypercycles enable quadratic (first-order) autocatalysis to achieve the enantioselective behavior of cubic (second-order) autocatalysis and therefore may lead to SMSB. Most importantly, whereas typically SMSB refers to when a system transits from a racemic to a chiral final stationary state (for specific reaction parameters and thermodynamic configurations that keep the system out of equilibrium), here we have demonstrated that that a spontaneous racemic to chiral transition can take place for non-stationary final chaotic states. In dynamic states the net entropy production is not necessarily perfectly compensated by the exchange entropy, as would be the case for stationary states. Nevertheless, the average entropy production is minimized for the final chiral chaotic state with respect to the average taken over the initially racemic chaotic state.
Entropy production, i.e., the rate of dissipation, entropy exchange, and entropy balance are fundamental concepts in the thermodynamic characterization of far-from-equilibrium open systems. Many years ago, Glansdorff and Prigogine established a general inequality for the entropy production valid for the entire range of macroscopic physics and for fixed boundary conditions.24–26,31 Their now classic result states that the temporal change of the forces proceeds always in a way as to lower the value of the entropy production: this is known as the General Evolution Criterion (GEC).
We have validated the extension of the GEC to volumetric open-flow systems exhibiting chaotic dynamics. This inequality governs the joint evolution of both the internal reactions taking place within the system volume and the matter fluxes that the system exchanges with its environment. We validate this theorem for a chiral catalytic network possessing non-equilibrium chaotic states that lie off the thermodynamic branch, of interest regarding the emergence of biological homochirality in systems unable to reach stationarity. This result opens up a new window for the design of models and simulations for the study of the dynamics of complex systems and their interactions with the environment.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the research grant CTQ2017-87864-C2-2-P (MINECO), Spain.
References
- M. Andrade, J. N. no, F. Morán, F. Montero and G. Mpitsos, Phys. D, 1993, 63, 21–40 CrossRef.
- J. Nuño, M. Andrade, F. Morán and F. Montero, Bull. Math. Biol., 1993, 55, 385–415 CrossRef.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285–366 CrossRef CAS.
- G. Ashkenasy, T. Hermans, S. Otto and A. Taylor, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
-
M. Kisakürek, The Emergence of Systems Chemistry, Natural and Life Sciences, Zurich, 1st edn, 2018 Search PubMed.
- S. Kauffman, J. Theor. Biol., 1986, 119, 1–24 CrossRef CAS.
-
M. Eigen, J. McCaskill and P. Schuster, The Molecular Quasi-Species in Advances in Chemical Physics, John Wiley, New York, 1st edn, 2007, vol. 75 Search PubMed.
- W. Hordijk, J. Hein and M. Steel, Entropy, 2010, 12, 1733–1742 CrossRef CAS.
- W. Gilbert, Nature, 1986, 319, 618 CrossRef.
-
G. Joyce and L. Orgel, The RNA World, Cold Spring Harbor Laboratory Press, New York, 3rd edn, 2006 Search PubMed.
- S. Bhowmik and R. Krishnamurthy, Nat. Chem., 2019, 11, 1009–1018 CrossRef CAS.
- J. Ribó, J. Crusats, Z. El-Hachemi, A. Moyano and D. Hochberg, Chem. Sci., 2017, 8, 763–769 RSC.
- F. C. Frank, Biochim. Biophys. Acta, 1953, 11, 459–463 CrossRef CAS.
- J. M. Ribó, C. Blanco, J. Crusats, Z. El-Hachemi, D. Hochberg and A. Moyano, Chem. – Eur. J., 2014, 20, 17250–17271 CrossRef.
- J. Crusats, D. Hochberg, A. Moyano and J. M. Ribó, ChemPhysChem, 2009, 12, 2123–2131 CrossRef.
- C. Blanco, J. M. Ribó, J. Crusats, Z. El-Hachemi, A. Moyano and D. Hochberg, Phys. Chem. Chem. Phys., 2013, 15, 1546–1556 RSC.
- C. Blanco, J. Crusats, Z. El-Hachemi, A. Moyano, D. Hochberg and J. M. Ribó, ChemPhysChem, 2013, 14, 2432–2440 CrossRef CAS.
-
S. deGroot and P. Mazur, Non-equilibrium Thermodynamics, Dover, New York, 2011 Search PubMed.
- J. M. Ribó and D. Hochberg, Phys. Chem. Chem. Phys., 2020, 22, 14013–14025 RSC.
-
M. Eigen and P. Schuster, The Hypercycle: a Principle of Natural Self-Organization, Springer-Verlag, Berlin, 1st edn, 1979 Search PubMed.
- J. Ribó, D. Hochberg, J. Crusats, Z. El-Hachemi and A. Moyano, J. R. Soc., Interface, 2017, 14, 20170699 CrossRef.
- D. Hochberg and J. M. Ribó, Life, 2019, 9, 1–16 CrossRef.
- J. T. Sczepanski and G. F. Joyce, Nature, 2014, 515, 440–442 CrossRef CAS.
-
D. Kondepudi and I. Prigogine, Modern Thermodynamics From Heat Engines to Dissipative Structures, Wiley, Chichester, 2nd edn, 2014 Search PubMed.
-
P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, New York, 1st edn, 1971 Search PubMed.
-
G. Nicolis and I. Prigogine, Self-Organization in Nonequilibrium Systems, Wiley, New York, 1st edn, 1977 Search PubMed.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS.
-
J. W. E. Acree, Thermodynamic Properties of Non-Electrolyte Solutions, Academic Press, New York, 1st edn, 1984 Search PubMed.
-
K. Banerjee and K. Bhattachrayya, 2013, 1–15, arXiv: 1309.0960v1.
- D. Hochberg and J. M. Ribó, Phys. Chem. Chem. Phys., 2018, 20, 23726–23739 RSC.
- P. Glansdorff and I. Prigogine, Physica, 1954, 20, 773–780 CrossRef.
- P. Glansdorff and I. Prigogine, Physica, 1964, 30, 351–374 CrossRef.
- J. Ribó and D. Hochberg, Symmetry, 2019, 11, 814 CrossRef.
- M. Mauksch and S. Tsogoeva, ChemPhysChem, 2008, 9, 2359–2371 CrossRef CAS.
- R. Plasson and H. Bersini, J. Phys. Chem. B, 2009, 113, 3477–3490 CrossRef CAS.
- C. Blanco, J. M. Ribó, J. Crusats, Z. El-Hachemi, A. Moyano and D. Hochberg, Phys. Chem. Chem. Phys., 2013, 15, 1546–1556 RSC.
- D. Kondepudi and Z. Mundy, Symmetry, 2020, 12, 769 CrossRef.
Footnote |
| † A proof of the generalized GEC for chemical reactions subject to volumetric open-flow will be given elsewhere. |
|
| This journal is © the Owner Societies 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Antonio
Sánchez Torralba
*a,
Antonio
Sánchez Torralba
 b and
Federico
Morán
bc
b and
Federico
Morán
bc


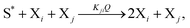

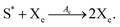



 on the concentrations leads to an output flux ϕ. Fig. 1 shows the general model.
on the concentrations leads to an output flux ϕ. Fig. 1 shows the general model.









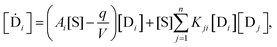



![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) = λq,
= λq,![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ji = λ3Kji,
ji = λ3Kji,


 , bottom branch (red) the sum of the concentrations of the D-replicators,
, bottom branch (red) the sum of the concentrations of the D-replicators,  .
.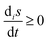 reveals the rate of dissipation and
reveals the rate of dissipation and  represents the exchange or net transport of entropy to the environment.24 The matter fluxes that drive entropy production, and are involved in entropy exchange with the environment, are crucial for determining the thermodynamic stability of any open system. Aspects of chemical stability can be characterized and quantified in terms of this non-equilibrium thermodynamic state function25 and is fundamental for understanding the thermodynamics of evolution.26
represents the exchange or net transport of entropy to the environment.24 The matter fluxes that drive entropy production, and are involved in entropy exchange with the environment, are crucial for determining the thermodynamic stability of any open system. Aspects of chemical stability can be characterized and quantified in terms of this non-equilibrium thermodynamic state function25 and is fundamental for understanding the thermodynamics of evolution.26





![[L with combining dot above]](https://www.rsc.org/images/entities/char_004c_0307.gif) i]|q=0,
i]|q=0,
 can have any sign. For our open flow model, this gives
can have any sign. For our open flow model, this gives

 is the rate of change of total or net system entropy per unit volume:
is the rate of change of total or net system entropy per unit volume: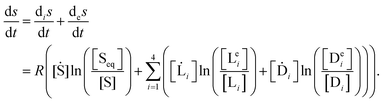
 vanishes identically at a non-equilibrium stationary state (NESS), if indeed such a state existed, since stationarity itself implies [Ṡ] = [
vanishes identically at a non-equilibrium stationary state (NESS), if indeed such a state existed, since stationarity itself implies [Ṡ] = [![[L with combining dot above]](https://www.rsc.org/images/entities/char_004c_0307.gif) i] = [Ḋi] = 0, and hence the entropy production and exchange are balanced between themselves, that is, they mutually compensate each other in stationary states: thus
i] = [Ḋi] = 0, and hence the entropy production and exchange are balanced between themselves, that is, they mutually compensate each other in stationary states: thus  . On the other hand, if the system is an a dynamic state, as for example regular or chaotic temporal oscillations, then the total change in entropy will not generally vanish
. On the other hand, if the system is an a dynamic state, as for example regular or chaotic temporal oscillations, then the total change in entropy will not generally vanish  , and consequently the entropy production and exchange terms are not mutually compensated. Such is the case here, and we calculate the entropy production and exchange entropy (per unit volume) for both the chaotic racemic and chaotic chiral outcomes: see Fig. 6 (the chaotic racemic outcome) and Fig. 7 (the chaotic scalemic outcome). The total rate of change of entropy (the entropy balance equation: eqn (35)) is presented in Fig. 8.
, and consequently the entropy production and exchange terms are not mutually compensated. Such is the case here, and we calculate the entropy production and exchange entropy (per unit volume) for both the chaotic racemic and chaotic chiral outcomes: see Fig. 6 (the chaotic racemic outcome) and Fig. 7 (the chaotic scalemic outcome). The total rate of change of entropy (the entropy balance equation: eqn (35)) is presented in Fig. 8.



 between the racemic and chiral regimes indicates that it is diminished for the latter with respect to the former. That is, the entropy production is lowered in absolute terms for the chiral regime. This implies that the time-average of the entropy production is also minimized for the chaotic chiral regime with respect to the chaotic racemic regime:
between the racemic and chiral regimes indicates that it is diminished for the latter with respect to the former. That is, the entropy production is lowered in absolute terms for the chiral regime. This implies that the time-average of the entropy production is also minimized for the chaotic chiral regime with respect to the chaotic racemic regime:  , where angular brackets denote averaging with respect to a specified time interval.
, where angular brackets denote averaging with respect to a specified time interval.
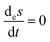 , and this reduces to the original Glansdorff and Prigogine GEC, which holds for the clamped approximation, as commented above. From the final line we see that the overall expression vanishes only for either an equilibrium or non-equilibrium stationary state. If the driven system possesses no stationary states, then the temporal derivative of the system net entropy with respect to the rate of change of the forces F (the affinities) is thus strictly negative definite.
, and this reduces to the original Glansdorff and Prigogine GEC, which holds for the clamped approximation, as commented above. From the final line we see that the overall expression vanishes only for either an equilibrium or non-equilibrium stationary state. If the driven system possesses no stationary states, then the temporal derivative of the system net entropy with respect to the rate of change of the forces F (the affinities) is thus strictly negative definite.
 and (ii) the entropy exchanged with the environment
and (ii) the entropy exchanged with the environment  , leading to
, leading to  .
.
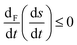 , in compliance with the general evolution criterion.
, in compliance with the general evolution criterion.
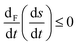 , in compliance with the general evolution criterion.
, in compliance with the general evolution criterion.
