Open Access Article
Open Access ArticleElectron spectroscopy and dynamics of HBr around the Br 1s−1 threshold†
Nacer
Boudjemia
 *a,
Kari
Jänkälä
*a,
Kari
Jänkälä
 a,
Ralph
Püttner
a,
Ralph
Püttner
 b,
Tatiana
Marchenko
cd,
Oksana
Travnikova
cd,
Renaud
Guillemin
cd,
Loïc
Journel
b,
Tatiana
Marchenko
cd,
Oksana
Travnikova
cd,
Renaud
Guillemin
cd,
Loïc
Journel
 cd,
Iyas
Ismail
cd,
Dimitris
Koulentianos‡
cd,
Iyas
Ismail
cd,
Dimitris
Koulentianos‡
 ce,
Satoshi
Kosugi
gh,
Yoshiro
Azuma
gh,
Minna
Patanen
ce,
Satoshi
Kosugi
gh,
Yoshiro
Azuma
gh,
Minna
Patanen
 a,
Marko
Huttula
a,
Denis
Céolin
d,
Maria Novella
Piancastelli
a,
Marko
Huttula
a,
Denis
Céolin
d,
Maria Novella
Piancastelli
 cf and
Marc
Simon
cf and
Marc
Simon
 cd
cd
aNano and Molecular Systems Research Unit, University of Oulu, P.O. Box 3000, 90014 Oulu, Finland. E-mail: nacer.boudjemia@oulu.fi
bFachbereich Physik Freie Universität Berlin, Arnimallee 14, D-14195 Berlin, Germany
cSorbonne Université, CNRS, Laboratoire de Chimie Physique-Matière et Rayonnement, LCPMR, F-75005, Paris, France
dSynchrotron SOLEIL, L'Orme des Merisiers, Saint-Aubin, BP 48, F-91192 Gif-sur-Yvettes Cedex, France
eDepartment of Physics, University of Gothenburg, Origovägen 6B, SE-412 96 Gothenburg, Sweden
fDepartment of Physics and Astronomy, Uppsala University, SE-75120 Uppsala, Sweden
gDepartment of Materials and Life Sciences, Sophia University, Tokyo 102-8554, Japan
hDepartment of Physics, Tokyo Gakugei University, 4-1-1 Nukuikita-machi, Koganei, Tokyo 184-8501, Japan
First published on 12th November 2020
Abstract
A comprehensive electron spectroscopic study combined with partial electron yield measurements around the Br 1s ionization threshold of HBr at ≅13.482 keV is reported. In detail, the Br 1s−1 X-ray absorption spectrum, the 1s−1 photoelectron spectrum as well as the normal and resonant KLL Auger spectra are presented. Moreover, the L-shell Auger spectra measured with photon energies below and above the Br 1s−1 ionization energy as well as on top of the Br 1s−1σ* resonance are shown. The latter two Auger spectra represent the second step of the decay cascade subsequent to producing a Br 1s−1 core hole. The measurements provide information on the electron and nuclear dynamics of deep core-excited states of HBr on the femtosecond timescale. From the different spectra the lifetime broadening of the Br 1s−1 single core-hole state as well as of the Br(2s−2,2s−12p−1,2p−2) double core-hole states are extracted and discussed. The slope of the strongly dissociative HBr 2p−2σ* potential energy curve is found to be about −13.60 eV Å−1. The interpretation of the experimental data, and in particular the assignment of the spectral features in the KLL and L-shell Auger spectra, is supported by relativistic calculations for HBr molecule and atomic Br.
1 Introduction
Availability and opportunity of combining a high-photon-energy source with a high-resolution hemispherical energy analyzer, such as the hard X-ray photoelectron spectroscopy (HAXPES) end station at GALAXIES beamline,1,2 SOLEIL synchrotron, has opened new avenues for the investigation of photoionization and photoexcitation dynamics.3,4 A similar spectroscopic set-up has been developed also recently at SPring-8 in Japan by Oura et al.5 These new possibilities allow, for example, studying nuclear dynamics on the sub-femtosecond time scale for K-shell ionization and relaxation of heavy element containing molecules via normal Auger, absorption-like and resonant Auger (RAS) spectroscopies. In the present work we concentrate on the Br K-edge (≅13.48 keV) in the HBr molecule.Electronic states related to the Br K-edge excitation have been a subject of investigation in the past. As an example, a study on the relative intensities and energies of Br KLL Auger spectrum was reported by Erman et al.6 Photoabsorption spectra of Br2 around the K-edge were measured and supported with ab initio theory by Kincaid et al.7 In that work the first high-resolution extended X-ray-absorption fine structure (EXAFS) spectrum of Br around the K-edge was presented. Other studies were carried out by D'Angelo et al.,8 on the double-electron excitation channels at the Br K-edge of HBr and Br2. Recently, non-dipole asymmetries of Br K-shell photoelectrons have been reported by Southworth et al.9 In addition, photoabsorption spectrum of gaseous HBr up to 50 eV above the K-edge has been studied in ref. 10.
In isolated molecules, excitation of an electron from the core to the lowest unoccupied molecular orbital (LUMO) can induce fast nuclear dynamics if the state has a steep dissociative potential energy surface. Core-excited states are also highly unstable electronically, characterized by a very short lifetime, ranging typically from a few femtoseconds to even tens of attoseconds. They decay rapidly by emitting photons or electrons via radiative or non-radiative processes, respectively. Thus, nuclear dynamics and the decay of the core-excited state can be in competition, and the photon energy dependence of these processes has been utilised to probe ultra-fast nuclear dynamics using the so-called core-hole clock spectroscopy (CHCS).11–16 The most relevant techniques for CHCS studies are resonant inelastic X-rays scattering (RIXS) and resonant Auger spectroscopy (RAS). A detailed description and a comparison of RIXS and RAS techniques are reported by Marchenko et al. in ref. 17.
Studies of nuclear dynamics of deep core orbitals of molecules containing heavy atoms are quite scarce. This is due to limited availability of high-resolution X-ray sources that can handle gaseous samples. If an electron in hydrogen halide molecules, HX (X = F, Cl, Br or I), is promoted to LUMO, the molecule is put into a strongly dissociative state because of LUMO's antibonding character. The electronic lifetime of core-excited states can be comparable to molecular dissociation time, occurring on a femtosecond timescale. Therefore, the excited electronic state can decay when the system is already, or becoming, atomic-like, and the study of the electronic decay can yield information on nuclear dynamics. In a pioneering study of HBr with angle-resolved photoelectron spectroscopy conducted by Morin et al.,11 observation of large and sharp resonant Auger peaks showed direct experimental evidence of repulsive character of Br(3d−1σ*) state and a competition between atomic and molecular resonant Auger decay. Similar results have been reported later by Aksela et al. in the case of the HCl molecule,18,19 showing evidence of ultrafast dissociation following excitation to the σ* orbital. In addition, similar behavior has been reported for H2O, O2, NH3, SF6, CF4, and CH3Cl molecules, see e.g..20–23 However, to our knowledge, dynamics involving a very deep K-edge above 10 keV have not been performed so far. It is important to note that such a deep core hole results in a dissociation of the molecule in the timescale of several femtoseconds. However, in the present work we focus on the first two decay steps which occur on a timescale of less than 1 fs. For this timescale, and based on the results presented below, 0.1 Å was estimated as an upper limit for the internuclear distance elongation, which implies that dissociation should take place during the subsequent decay processes. Despite the small bond elongation we observe indication of the initiated dissociation process.
In this article we study the photoabsorption spectrum measured in partial electron yield mode as a function of photon energy including the 1s → σ* resonance, the Br 1s photoelectron spectrum and the subsequent HBr1+ → HBr2+ and HBr2+ → HBr3+ Auger decay spectra. The recorded resonant Auger spectra as a function of photon energy provide insight into the molecular dynamics following HBr(1s−1) excitation. The extracted information is related to the line narrowing below the core-hole-lifetime broadening and to the anomalous dispersion of 2p−2σ* spectral lines showing an S-like dispersion as a function of photon energy. The 2p−2 double-core-hole (DCH) lifetime is determined to be about 2 times shorter in comparison to 2p−1 single-core-hole (SCH) lifetime using a simplified form of the Kramers–Heisenberg cross section equation,17 and the value is confirmed by the results from a fit of KLL normal Auger electron lines. The slope of the potential energy curve (PEC) of 2p−2σ* states populated from the Auger relaxation of 1s−1σ* states is estimated to be −13.60 eV Å−1. In addition, relaxation of the Rydberg state 1s−15p is studied.
The analysis of experimental photoelectron and Auger spectra are supported by relativistic molecular Dirac–Fock and atomic multi-configuration calculations for HBr and Br, respectively. The calculations are in good agreement with the experimental results.
2 Experiment
The experiments were carried out at the GALAXIES beamline,1,2 of the SOLEIL Synchrotron in Saint Aubin close to Paris, France. The data were recorded with a Scienta EW4000 hemispherical deflection energy analyser by applying different modes. The electron spectrometer was mounted in perpendicular position to the beam and parallel to the linear polarization of the synchrotron light, with a gas cell mounted at the bottom of the main chamber. The photoelectron and KLL Auger spectra were measured with photon energies of 13.8 and 13.6 keV, respectively. The HBr1+ → HBr2+ → HBr3+ Auger spectra (HBr0+ → HBr1+ → HBr2+ at σ* resonance) were recorded using photon energies of 13.55, 2.3 and 13.47 keV. These values are for above and below the HBr 1s ionization threshold, and on the top of the HBr 1s−1σ* resonance, respectively. The resonant KLL Auger 2D-map and the X-ray absorption measurements were carried out in partial electron yield mode, scanning the photon energy from 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 to 13
467 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 eV with a step of 0.5 eV, and a kinetic energy window of 10
483 eV with a step of 0.5 eV, and a kinetic energy window of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160–10
160–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 eV.
320 eV.
During the measurements the target pressure in the main chamber was about 2 × 10−5 mbar. The energy resolution of the electron energy analyzer was about 1 eV with a pass energy of 500 eV and a slit width of 800 μm. Based on the fit of a Ar 1s−1 photoelectron spectrum the photon bandwidth is estimated to be 2.5 eV at the photon energy of 13.8 keV. The kinetic-energy scale of the electron-energy analyzer was calibrated using the Ar KLL and KLM Auger spectra.24,25 The kinetic energy scale of the spectrometer in the range of 9700–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 eV was also calibrated with Ar KLL and KLM Auger spectra, due to lack of more appropriate calibration lines. The photon energy was calibrated using the Ar 1s photoelectron line.25
300 eV was also calibrated with Ar KLL and KLM Auger spectra, due to lack of more appropriate calibration lines. The photon energy was calibrated using the Ar 1s photoelectron line.25
3 Calculations
The molecular calculations were carried out using the DIRAC code26 to obtain the HBr(1s−1) ionization energy and HBr(1s−1σ*) excitation energies within the Δ-SCF framework using the Dyall's triple-ξ basis set.27 A H–Br bond length of 1.41 Å in the ground state was taken as a fixed value from literature.28 The molecular calculations were carried out using the relativistic Dirac–Coulomb Hamiltonian and correcting the values further with Breit and quantum electrodynamics (QED) corrections from atomic GRASP2k code,29 as discussed in ref. 30.In addition, relativistic atomic calculations within a configuration–interaction Dirac–Fock framework using the GRASP2K code29 were carried out. The inherently relativistic calculations included also Breit interaction and QED corrections (self-energy, vacuum polarization) as subsequent perturbations.
The Auger spectra subsequent to K and L-orbital photoionization, photoexcitation, KL-emission and KLL-Auger decay were simulated by including all relevant energetically allowed final states obtainable from the ground state configuration of atomic Br. The photoionization cross-sections and radiative transition rates were calculated in a dipole approximation with a length gauge using PHOTO and REOS components of the RATIP package,31 respectively.
Auger decay rates were calculated using the FAC code,32 which uses the same theoretical framework as GRASP2K and provides about the same state energies. The FAC code was used for calculating the Auger rates due to its reliability and considerably shorter execution times in comparison to GRASP2K and RATIP.
4 The photoabsorption spectrum around the Br 1s−1 threshold
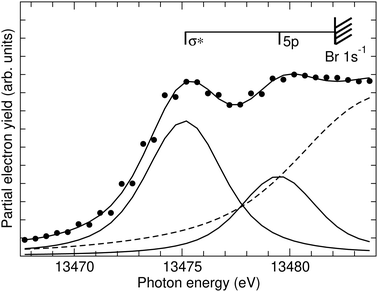
Fig. 1 shows the absorption spectrum of HBr in the photon energy region of 13467.5 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 eV measured using the partial electron yield method. A fit to the spectrum consists of two peaks indicated by solid subspectra, namely Br
489 eV measured using the partial electron yield method. A fit to the spectrum consists of two peaks indicated by solid subspectra, namely Br  and Br 1s−15p, and an arctan-function which accounts for higher Rydberg states and the continuum cross section. Note that the higher molecular states are assigned to np Rydberg states since for 3d absorption they can be classified in Rydberg series,33,34i.e. they experience the HBr+ ion as an almost point-like charge distribution; a more detailed argumentation why Br 1s and Br+ absorption spectra are closely related to each other are given below.
and Br 1s−15p, and an arctan-function which accounts for higher Rydberg states and the continuum cross section. Note that the higher molecular states are assigned to np Rydberg states since for 3d absorption they can be classified in Rydberg series,33,34i.e. they experience the HBr+ ion as an almost point-like charge distribution; a more detailed argumentation why Br 1s and Br+ absorption spectra are closely related to each other are given below.
For the two distinct spectral features the same lifetime broadening, represented by a Lorentzian function, is used resulting in a value of Γ = 2.66(34) eV full width at half maximum (FWHM). The spectral features are also convoluted with a Gaussian width of 2.50 eV in order to account for the photon bandwidth; this value is obtained from fitting the Ar 1s−1 photoelectron line recorded at a photon energy in the same range and it has an estimated error of ±100 meV. The Br  transition was also convoluted with a second Gaussian in order to simulate broadening due to the dissociative character of the excited state. In fits where the respective parameter was free it turned out that ≅1 eV can be considered as an upper limit. Since this value agrees with the respective broadening observed in the Br 3d−1 photoion yield spectrum33,34 it was used as fixed parameter in the fits performed to obtain the Br 1s−1 lifetime broadening. Note that molecular properties like potential energy curves, geometry, or term values mainly depend upon the valence-shell structure, but not upon a particular core hole; this is reflected in the equivalent-core or Z + 1 approximation. As a consequence, in core-level photoabsorption the final-state orbital is most important for these properties. Therefore we can expect similar values for e.g. the Br
transition was also convoluted with a second Gaussian in order to simulate broadening due to the dissociative character of the excited state. In fits where the respective parameter was free it turned out that ≅1 eV can be considered as an upper limit. Since this value agrees with the respective broadening observed in the Br 3d−1 photoion yield spectrum33,34 it was used as fixed parameter in the fits performed to obtain the Br 1s−1 lifetime broadening. Note that molecular properties like potential energy curves, geometry, or term values mainly depend upon the valence-shell structure, but not upon a particular core hole; this is reflected in the equivalent-core or Z + 1 approximation. As a consequence, in core-level photoabsorption the final-state orbital is most important for these properties. Therefore we can expect similar values for e.g. the Br  and the Br
and the Br  states. Following the same argument, only one Lorentzian is used for the Br 1s−15p state as no vibrational excitations are observed for the Br 3d−15p states.33,34 The two peaks labelled as Br
states. Following the same argument, only one Lorentzian is used for the Br 1s−15p state as no vibrational excitations are observed for the Br 3d−15p states.33,34 The two peaks labelled as Br 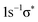 and Br 1s−15p are found at hν = 13475.1(1) eV and hν = 13479.5(2) eV, respectively. From the latter value and the term values of the Br 3d−15p resonances33,34 the threshold energy can be estimated to be hν = 13482.1(3) eV. Note that the statistical error bars refer to relative distances. In addition, the energies are subject to an additional error of ≅2 eV due to the calibration of the energy scale.
and Br 1s−15p are found at hν = 13475.1(1) eV and hν = 13479.5(2) eV, respectively. From the latter value and the term values of the Br 3d−15p resonances33,34 the threshold energy can be estimated to be hν = 13482.1(3) eV. Note that the statistical error bars refer to relative distances. In addition, the energies are subject to an additional error of ≅2 eV due to the calibration of the energy scale.
Table 1 summarises experimental and calculated Br 1s−1 binding energy and Br 1s−1σ*/4p/5p excitation energies for molecular HBr as well as atomic Br. The molecular calculations carried out with the Dirac code are in good agreement with the values extracted from the experiment. In addition, the experimental values are supported by the atomic calculations carried out using the GARSP2K code for neutral atomic Br and for Kr-like anion (not shown here). The results show an interesting behaviour, namely that the experimental Br 1s−1 binding energy value agrees much better with the value obtained for neutral atomic Br rather than Br−. This can be understood from the electronegativity of both Br and H atoms. The electronegativity values of Br and H are 2.96 and 2.2, respectively. The values are given in dimensionless Pauling scale.35 Therefore the difference between the two electronegativity values is 0.76, which defines a mildly polar covalent bond type, where the Br atom has only a slight negative charge Brδ−. This explains why Br appears as “Br-like” in the HBr molecule. In addition, the calculated atomic Br 1s−15p excitation energy is found to be in agreement with the experimental energy value obtained for HBr 1s−15p. This due to the fact that the 5p orbital in the HBr molecule has a strong Rydberg character, as reflected also on KLL Auger spectra, see Section 6.2.
| Bromine 1s−1 | Bromine 1s → σ*/4p | Bromine 1s → 5p | ||||
|---|---|---|---|---|---|---|
| HBr | Br | HBr | Br | HBr | Br | |
| Dirac | 13480.90 | — | 13475.50 | — | 13478.81 | — |
| GRASP2K | — | 13481.65 | — | 13468.68 | — | 13479.13 |
| Experiment | 13482.1(3) | — | 13475.1(1) | — | 13479.5(2) | — |
5 The Br 1s−1 photoelectron spectrum
The Br 1s−1 photoelectron spectrum measured using a photon energy of hν = 13.8 keV is displayed in Fig. 2. The red line through the data points represents the results of a fit analysis, which was performed to extract a second value for the Br 1s−1 core-hole lifetime width. In the fit analysis it has been taken into account that the Br 1s−1 core hole decays, according to the present calculations, see below, by 61% by X-ray emission, by 31% by KLL Auger decay and by 8% by KLY Auger decay, with the major contribution by KLM Auger decay; note that throughout this publication we use X = L, M, N and Y = M, N. Because of this, Br 1s−1 main peak is described with three contributions, namely a Lorentzian lineshape (black solid subspectrum) for the X-ray emission as well as a post-collision interaction (PCI) lineshape36 for both the KLL (blue solid subspectrum) and KLM (orange solid subspectrum) contributions. The intensities are weighted according to the above given percentages and all three contributions are described with the same parameter for the lifetime broadening. Moreover, to describe the PCI lineshapes, an average kinetic energies of 10 and 11.55 keV for the KLL and KLM Auger transitions respectively were used. Finally, four Gaussians were employed to describe the shake-up satellite structures; they are indicated by the dashed black subspectrum. The lineshapes were convoluted with a Gaussian of 2.7 eV to account for the photon bandwidth of 2.5 eV and the spectrometer resolution of 1.0 eV. To estimate the error bars, the Gaussian lineshape describing the experimental resolution was varied by ±0.1 eV.The thin vertical dashed line serves as guide to the eye to stress that the three contributions to the main line show different line profiles due to PCI shifts and distortions. From the fit we obtained Γ1s−1 = 2.37(10) eV, which we combined with Γ1s−1 = 2.66(34) eV from the absorption spectrum to Γ1s−1,exp = 2.40(12) eV. This value is slightly lower than the theoretical result of Γ1s−1,theo = 2.52 eV reported in ref. 37. Moreover, the obtained value is 0.25 eV lower than the value of Γ1s−1 = 2.65(14) eV recently obtained for Kr,38 which agrees well with the difference of 0.23 eV calculated by Krause and Oliver.37
In the energy region around 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 eV shake-up satellite structures are visible. The spectral structures match, beside the larger lifetime broadening and, therefore, the less pronounced structures, quite well the satellite structures of the Cl 2p−1 spectrum of HCl.39 In the latter spectrum the satellites are explained with transitions originating to the 4σ, 5σ, and 2π valence orbitals,39 which suggests that the similar structures in HBr are due to shake-up transitions to the valence orbitals 7σ, 8σ, and 4π. A detailed discussion of the shake structures in HBr is beyond the scope of this article. However, as will be discussed below, their presence is relevant for the interpretation of the Br KLL Auger spectrum.
500 eV shake-up satellite structures are visible. The spectral structures match, beside the larger lifetime broadening and, therefore, the less pronounced structures, quite well the satellite structures of the Cl 2p−1 spectrum of HCl.39 In the latter spectrum the satellites are explained with transitions originating to the 4σ, 5σ, and 2π valence orbitals,39 which suggests that the similar structures in HBr are due to shake-up transitions to the valence orbitals 7σ, 8σ, and 4π. A detailed discussion of the shake structures in HBr is beyond the scope of this article. However, as will be discussed below, their presence is relevant for the interpretation of the Br KLL Auger spectrum.
6 The Auger spectra
6.1 The Br KLL normal Auger decay
Fig. 3 shows the Br KLL Auger spectrum of HBr subsequent to HBr 1s−1 photoionization at hν = 13.6 keV measured with an experimental resolution of 1 eV, together with relativistic calculation carried out for neutral atomic-Br. The small shift seen in the energy positions is most likely due to the average energy level scheme used in the calculation. The calculated spectrum is built-up from the singly ionised Br+ (1s−1) state, that undergo a KLL Auger relaxation to Br2 +, giving rise to 2s−2, 2s−12p−1 and 2p−2 final states. This allows an assignment of the diagram lines in full agreement with literature.6 Note, that transitions to the 2p−2(3PJ) final states are forbidden in pure LS coupling and are absent in lighter atoms such as neon.40 The presence of the final states 2p−2(3P0,2) in the Auger spectrum indicates, together with the splitting of the transitions to the final states 2s−12p−1(3P0,3P1,3P2), significant spin–orbit interaction for the Br 2p shell. Note, that the transitions to the final states 2p−2(3P0) and 2p−2(3P2) gain intensity from configuration interaction with the final states of the same value of J, namely 2p−2(1S0) and 2p−2(1D2). In contrast to this, the closest state for 2p−2(3P1) that can mix with it is 2s−12p−1(3P1), which is about 200 eV higher in energy, which makes mixing negligible.40 | ||
| Fig. 3 The experimental and calculated Br KLL Auger spectrum of HBr including the assignment of the diagram lines. | ||
To our knowledge, the present spectrum is the first Br KLL Auger spectrum reported in the literature since the work of Erman and coworkers published in 1965.6 In their work, the 1s−1 core hole in a 79Br atom was formed by an electron-capture decay of 79Kr and the experiment had a resolution of 10 eV, which is rather modest by modern standards.
The Br KLL Auger transitions were fitted in order to extract the lifetime broadenings of the Br 2p−2, 2s−12p−1 and 2s−2 double core-hole (DCH) states. In the analysis it was assumed that all DCH states of the Br 2p−2 configurations show the same lifetime broadening. For the 2s−12p−1 configurations the present calculations suggest different lifetimes for the individual states. In particular, for the 2s−12p−1(3P) states similar lifetime broadenings are calculated, while for the 2s−12p−1(1P) state a significantly larger value was obtained. Following these results we assumed in the fit analysis the same lifetime broadening for the 2s−12p−1(3P) states and a different one for the 2s−12p−1(1P) state.
The upper panel of Fig. 4 shows the Br 1s−1 → 2p−2 Auger transitions. All the four diagram lines Br 1s−1 → 2p−2(1S0,1D2,3P0,3P2) show a slight asymmetry with a tail towards higher kinetic energies. This is due to PCI and therefore the lines are fitted with PCI lineshapes36 and convoluted with a Gaussian of 1 eV FWHM in order to account for the spectrometer resolution. This procedure resulted in a linewidth of Γ = 5.12(10) eV. By subtracting the lifetime broadening of the 1s−1 core hole, Γ1s−1 = 2.40(12) eV, we obtain Γ2p−2 = 2.72(22) eV. Note that in the fit analysis the kinetic energy of the photoelectron was treated as a free parameter resulting in Ekin,PE ≅ 340 eV, which is much larger than the actual value of ≅120 eV. This is due to the fact that we approximated the line with one PCI-lineshape of 5.12(10) eV width. A correct treatment of the spectral feature would be a PCI-lineshape with the linewidth of the Br 1s−1 photoline convoluted with a Lorentzian of the linewidth of the Br 2p−2 double core hole final states;41 however, this is not implemented in the fit program and the additional error caused by this approximation is small compared to the uncertainty in the lifetime broadening of the Br 1s−1 core hole.
The Br 1s−1 → 2s−12p−1(1P1,3P0,3P1,3P2) Auger lines are shown in the middle panel of Fig. 3. As mentioned above, in the fit two different parameters for the linewidths were used, namely one for the Br 1s−1 → 2s−12p−1(1P1) transition and one for the Br 1s−1 → 2s−12p−1(3P) transitions. Since for the latter transitions, the lifetime broadenings are found to be slightly larger than Br 1s−1 → 2p−2(1S0,1D2,3P0,3P2), both were fitted with Lorentzian and PCI lineshapes. However, the values for the intensities and widths resulted in practically identical χ2-values and the parameters turned out to differ only within the error bars. Moreover, in the fit using a PCI lineshape for the photoelectron, a kinetic energy of Ekin,PE ≅ 750 eV was obtained; this indicates a rather Lorentzian-like lineshape. As the main difference between the two approaches, for the Br 1s−1 → 2s−12p−1(3P) transitions the fit using PCI lineshapes provided 0.40(3) eV lower Auger energies than the fit using symmetric Lorentzian lineshapes. We consider this value a guide value for the size of systematic errors due to the simplified description of the lineshapes, see above.
For the Br 1s−1 → 2s−12p−1(1P1) transition, only a Lorentzian lineshape was used. In detail, for the Br 1s−1 → 2s−12p−1(1P1) transition a total width of 7.35(60) eV and for the Br 1s−1 → 2s−12p−1(3P) transitions a total width of 5.56(50) eV were obtained. From these values the double core hole lifetime widths of Γ2s−12p−1(1P1) = 4.95(72) eV and Γ2s−12p−1(3P) = 3.16(62) eV were derived. For the Br 1s−1 → 2s−2(1S0) Auger transition displayed in the lower panel of Fig. 3 a width of 10.60(21) eV is obtained, resulting in a lifetime broadening of Γ2s−2 = 8.20(33) eV.
In the present work the Br2+ DCH lifetime widths were also calculated by assuming an Auger relaxation of Br2+ initial states to Br3+ final states. From the calculations the following widths are obtained: Γ2p−2(1S0,1D2,3P0,2) = 2.72 eV, Γ2s−12p−1(1P1,3P0,1,2) = 9.37, 5.94, 6.57 and 5.33 eV, respectively, and Γ2s−2(1S0) = 11.58 eV. For the state 2p−2(1S0,1D2,3P0,3P2) perfect agreement with the experiment is found. For the states with holes in the 2s level, the theoretical results show clearly the same tendency, but they are systematically too large.
In the following we compare the L-shell DCH lifetime broadenings with the values of the single core-hole (SCH) states calculated by Krause and Oliver,37 which are Γ2s−1 = 4.11 eV, Γ2p1/2−1 = 1.21 eV, and Γ2p3/2−1 = 1.08 eV. The result provides DCH/SCH linewidth ratios of 2.00(0.08) for the 2s orbital and 2.39(21) for the Γ2p3/2−1 = 1.08 orbital. The value for the 2s orbital agrees within the error bars with the expected ratio of 2 for deeper core holes.42 The value of the 2p orbital is somewhat larger, however, still smaller than the ratios close to three obtained for shallow core levels, namely Ne 1s with a ratio of 2.9(1)42 and Ar 2p with a ratio of 2.8(2).43 For the 2s−12p−1 DCH the situation is more complex. The sum of the 2s−1 and the 2p−1 lifetime broadenings of ≅5.25 eV agrees within the error bars with the value of Γ2s−12p−1(1P1) = 4.95(72) eV for the singlet state. It is, however, significantly larger than the value of Γ2s−12p−1(3P) = 3.16(62) eV for the triplet states. This can at least partially be understood by the fact that the L1L2,3Y Coster–Kronig Auger probability of the 2s−1 vacancy is significantly reduced due to the presence of the 2p−1 hole. We want to point out that in a naive picture the spin of the holes are parallel in the triplet states and antiparallel in the singlet state. As a result, in the triplet states only two 2s−1 electrons can fill the 2s hole without spin–flip, while in the singlet state three 2p electrons are available for filling the 2s hole; this might explain the larger linewidth for transitions to the latter state. For argon it has also been observed that the lifetime broadening of the 1s−12p−1 DCH states is smaller than the sum of the broadening of the single core-hole states44 and it was also explained with a reduced Auger rate due to a reduced number of 2p electrons which are involved in the main Auger decay channel.
In all panels of Fig. 4 the dashed solid black lines indicate the background, which predominantly consists of features related to the Auger decay of photoionization shake-up satellite states. Practically for all diagram lines a shake satellite structure shifted by about 10 eV to lower kinetic energies can be observed. A similar observation has been made, for example, for the KLL Auger spectrum of H2S45 and Ar46 where the corresponding satellites could unambiguously be assigned to Auger decays of the satellite lines in the photoelectron spectrum. Shake processes during the Auger decay were found at kinetic energies which are lower by ≅15 to 30 eV with respect to the diagram lines and they turned out to have considerably lower intensities. This suggests to assign the spectral features found at kinetic energies about 10 eV below those of the diagram lines as Auger processes of the photoelectron satellites presented in Fig. 2 and the spectral feature at ≅10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 205 eV to a shake process during the Br 1s−1 → 2p−2(1D2) Auger decay.
205 eV to a shake process during the Br 1s−1 → 2p−2(1D2) Auger decay.
Additional results of the fit are accurate values for the energy splitting and relative intensity ratios between the different diagram lines. These results are summarised in Table 2, together with the present theoretical results. The numbers in parentheses indicate the statistical error bars. Generally, a good agreement is observed. In more detail, the theoretical splitting between the states is somewhat larger than the experimental values. For the relative intensities a good agreement is observed, with the exception of the Br−1 → 2s−2 transition showing an experimental values 3 times larger than the theoretical one. The fit model is, however, limited by the description of the shake structures in the Auger spectrum, since the exact contributions of these structures to the spectrum are unknown. We estimate that this can lead to systematic errors for the intensity ratio in the order of 10% of the given relative value, while the energy positions are essentially unaffected.
| Final state | E Auger (eV) | E rel (eV) | Relative intensity (arb. units) | |||
|---|---|---|---|---|---|---|
| Exp. | Calc. | Exp. | Calc. | Exp. | Calc. | |
| 2p−2(3P2) | 10285.1 | 10281 | 56.16(5) | 56 | 0.23(1) | 0.23 |
| 2p−2(3P0) | 10265.9 | 10260 | 37.04(13) | 35 | 0.06(1) | 0.04 |
| 2p−2(1D2) | 10228.9 | 10225 | 0 | 0 | 1.00 | 1.00 |
| 2p−2(1S0) | 10176.3 | 10169 | -52.60(10) | −56 | 0.08(1) | 0.06 |
| 2p−12p−1(3P2) | 10076.6 | 10069 | −152.30(34) | −156 | 0.05(1) | 0.09 |
| 2p−12p−1(3P1) | 10056.3 | 10048 | −172.62(33) | −177 | 0.09(2) | 0.13 |
| 2p−12p−1(3P0) | 10028.6 | 10021 | −200.35(46) | −204 | 0.03(1) | 0.04 |
| 2p−12p−1(1P1) | 10001.4 | 9990 | −227.57(16) | −235 | 0.26(2) | 0.26 |
| 2s−2(1S0) | 9820.4 | 9811 | −408.54(20) | −414 | 0.16(1) | 0.05 |
6.2 The HBr KLL resonant Auger decay
In Fig. 5(a) the resonant KLL Auger spectra as a function of photon energy is recorded as a 2D-map, where the intensities are represented by the color scale. The 2D-map is measured in the kinetic energy range of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160–10
160–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 eV with a step width of 0.25 eV and in the photon energy range of 13
320 eV with a step width of 0.25 eV and in the photon energy range of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467–13
467–13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 eV with a step width of 0.5 eV. Using photons with energy lower than the 1s binding energy of 13
484 eV with a step width of 0.5 eV. Using photons with energy lower than the 1s binding energy of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 eV, a predominantly resonant Auger decay of the type
482 eV, a predominantly resonant Auger decay of the type| γ + HBr → HBr*(1s−1V) → HBr* + (2p−2V) + eKLL− | (1) |
| γ + HBr → HBr+(1s−1) + eph− → HBr2+(2p−2) + eKLL− | (2) |
 | ||
| Fig. 5 The panel (a) shows a 2D-map of the resonant KLL Auger decay. The x-axis shows the Auger energies and the y-axis the photon energy used for excitation. An integration along the x-axis results in the absorption spectrum shown in Fig. 1. The intensities are shown in color scale. The two dashed horizontal black lines represent the resonance energies of 1s−1σ* and 1s−15p, (compare to Fig. 1). The dashed horizontal red line represents the 1s−1 ionization threshold. The tilted vertical black solid lines with an S-shape at the 1s−1σ* resonance energy indicate the kinetic energy dispersion of the 2p−2σ* final state. The tilted vertical linear red solid lines indicate the kinetic energy dispersion of 2p−25p Rydberg states. In the lower panels (b) and (c) the experimental HBr and the calculated atomic Br KLL resonant Auger spectra measured and calculated on top of the 1s−15p and 1s−1σ* resonances are shown. The intensity maxima are set to 1. | ||
The vertical tilted solid black and red lines show the kinetic energy dispersion of the 2p−2σ* and 2p−25p final states, respectively. Around the lower horizontal dashed line representing the resonance energy of the Br 1s−1σ* excitation, the black line exhibits an S-shape behavior. This S-shape indicates nuclear motion in the Br 1s−1σ* state due to the dissociative character of the σ* orbital. In this case, part of the photon energy is spent for the movement of nuclei and is not available for the emitted Auger electron. Note that these S-shaped features are not pronounced in Fig. 5(a). For the 2p−2(1D2)σ* final state it can be seen more clearly in the panel (a) of Fig. 6. For the 2p−25 p Auger final states mainly populated via 1s−15p, a tilted linear red line in the upper panel of the Fig. 5(a) indicates a normal (linear) kinetic energy dispersion. This can be understood by assuming that the states are non-dissociative,48 see Section 4.1.
 | ||
| Fig. 6 The kinetic energy dispersion (a) with exchanged axes in comparison to Fig. 5(a) and the full width at half maximum (FWHM) (b) of the 1s−1σ* → 2p−2(1D2)σ* transition as a function of the incident photon energy in the energy range of the 1s−1σ* resonance. Error bars are from the fits of the experimental spectra using Voigt profiles. The red lines are the results of fit using eqn (3) and the blue lines are the results of the convolution of the eqn (3) with an additional Gaussian of 2.7 eV to simulate the experimental resolution. | ||
The calculated resonant KLL Auger spectra subsequent to 1s−15p and 1s−14p resonant excitations in the Br atom are shown as red lines in panels (b) and (c) of Fig. 5, respectively. The resonant KLL Auger final states are built-up by assuming an excitation of an electron from 1s to 4p, to mimic the excitation of the electron from the 1s orbital to the σ* (LUMO), and an excitation from 1s to 5p, to mimic the transition to the higher Rydberg orbitals in the HBr molecule. These states undergo resonant Auger spectator decay, mainly to the 2p−2(3P2,3P0,1D2,1S0)np final states.
The simulated spectra shown in the panels (b) and (c) of Fig. 5 are in a good agreement with the experiment in terms of the intensity features. The kinetic energy of the 1s−15p → 2p−25p resonant Auger transitions displayed in panel 5(b) shows a mismatch between experiment and theory comparable to the one for the 1s−1 → 2p−2 normal Auger transitions visible in Fig. 3. This similar energy mismatch confirms that the 5p orbital can be simulated by atomic calculations, i.e. it has a strong Rydberg character. Contrary to this, the agreement of the energy positions of the experimental 1s−1σ* → 2p−2σ* and the theoretical 1s−14p → 2p−24p resonant Auger transitions displayed in panel 5(c) is much better. We consider this finding coincidental and refer to the fact that an excitation to the molecular valence orbital σ* is compared with an atomic excitation; this difference compensates by accident the energy mismatch inherent to the 1s−1 → 2p−2 transition. Note that the theoretical 1s−14p → 2p−24p transition represents the Auger decay at long bond distances, i.e. after dissociation, while the bond elongation during the Br 1s−1 core-hole lifetime is practically zero. The spectral features in panel (b) of Fig. 5 show an asymmetric lineshape and a larger width compared to the calculated Br atomic spectrum. The reason for this is the presence of a number of unresolved 1s−15p → 2p−2np shake-up Auger transitions with n > 5. Such a behaviour has been observed also for Xe in ref. 49. Note that the shake processes during Auger decay have not been taken into account in the calculations.
The black points in Fig. 6(a) and (b) display the anomalous kinetic energy dispersion and the linewidth of the 1s−1σ* → 2p−2(1D2)σ* transition, respectively. The data points have been obtained by fitting the line with a Voigt profile where both Gaussian and Lorentzian widths were free parameters. More specifically, the data were fitted using a simplified form of the generalized Kramers–Heisenberg formula.50 The equation is frequently used to describe RIXS cross sections in the case of dissociative intermediate states. The simplified form for the present case is extracted from ref. 17 as
 | (3) |
Fig. (7) indicates the relation between the different quantities used in the eqn (3), in which ω and ω′ are the incident photon energy and the kinetic energy of the resonant Auger electron, respectively. Moreover, ε = Ef − ΔUf is the nuclear kinetic energy at r → ∞, Ef, reduced by the potential energy difference ΔUf = Uf(re) − Uf(r → ∞) with Uf(re) and Uf(r → ∞) being the potential energy of the final state at the equilibrium distance re and at r → ∞, respectively. Note that ε = 0 for excitations at the equilibrium distance, and is negative for excitations at larger internuclear distances. Δf = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) foa0, is the Franck–Condon factor, where
foa0, is the Franck–Condon factor, where ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) fo is the absolute value of the gradient of the PEC of the dissociative final state at re and a0 is the width of the Franck–Condon distribution between the ground and the final state. ωco is the energy of the vertical transition from the ground (o) to the intermediate state (c) and ωfo is the energy of the vertical transition from ground state (o) to the final state (f). Γc,f are the lifetime broadenings of the intermediate and final states.
fo is the absolute value of the gradient of the PEC of the dissociative final state at re and a0 is the width of the Franck–Condon distribution between the ground and the final state. ωco is the energy of the vertical transition from the ground (o) to the intermediate state (c) and ωfo is the energy of the vertical transition from ground state (o) to the final state (f). Γc,f are the lifetime broadenings of the intermediate and final states.
 | ||
| Fig. 7 Rough schematic diagram indicating the different used parameters in the eqn (3). | ||
In the present case the cross section reduces to a product of a Gaussian function representing the bound-free FC factors and two Lorentzian functions that account for the core-excited intermediate and final states lifetimes Γc and Γf, respectively. Note that eqn (3) needs to be further convoluted with a Gaussian describing the instrumental resolution for direct comparison with the experiment. Eqn (3) is obtained in the Franck–Condon and Born–Oppenheimer approximations. Furthermore, in the present case both final and intermediate states are strongly dissociative, but, due to the short lifetime of the 1s core-excited state, ∼280 as, nuclear propagation in the intermediate state has been neglected. For more details, see ref. 17.
The fits were performed by fixing the parameters as follows: Γc = 2.40(12) eV, ω0 = 2648.975 cm−1 (which gives a0 = 0.11 Å from a0 = [ħ/μω0]1/2), μ = 0.99 amu, re = 1.41 Å, ωco = 13475.5 eV and ωfo = 3236.5 eV. Γf and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) fo were set as free parameters.
fo were set as free parameters.
From the fits, the value of Γf = 2.50(5) eV as the DCH lifetime for Br(2p−2) can be found. The obtained value for the 2p−2σ* final states agrees within the error bars with the one obtained for the 2p−2 final states of Γ2p−2 = 2.72(22) eV. The value for the 2p−2σ* final states gives a DCH/SCH ratio of 2.23 by taking the Br 2p−1 SCH width to be 1.12 eV37,51 as an average from 2p1/2 and 2p3/2 SCH lifetimes. The obtained ratio from the fitting method is thus in good agreement with the τ2p−1 ∼ 2τ2p−2 ratio extracted from the normal KLL Auger spectrum, see above.
Concerning the Frank–Condon (FC) factor Δf a value of 1.5 eV has been obtained, giving rise to Ffo(2p−2) = −13.60(10) eV Å−1 as a slope of the Br(2p−2σ*) PEC. The reflected behaviour on the kinetic energy peak dispersion and the line narrowing in the Fig. 6 is a manifestation of nuclear dynamic effects across the 1s−1σ* resonance, where a part of the photon energy is transferred to the nuclei in the HBr molecule leading to the elongation and breaking of H–Br bond as stated above.
Fig. 8 shows the PEC of the 2p−2σ* state as a function of H-Br distance using the following equation from ref. 17, where the dissociative potential Uf(r) can be described by an exponential shape
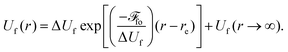 | (4) |
Here, the value of Uf(re) ≅ 3236.5 eV is known from the experiment. For Uf(r → ∞) a value of ≅3234.6 eV is used. It is estimated as a sum of atomic Br 2p−24p(1D2) binding energy of 3230.8 eV (calculated using GRASP2K) and the experimental H–Br dissociation energy of about 3.8 eV.52
The PEC at the FC zone shows strong dissociative character for the 2p−2σ* states. The obtained slope value is reasonable in comparison to the slopes of 2p−2σ* PEC obtained for H–Cl and CH3–Cl, where the values are −14.5 eV Å−115 and −11.10(30) eV Å−117 respectively.
6.3 L-shell Auger decay of HBr
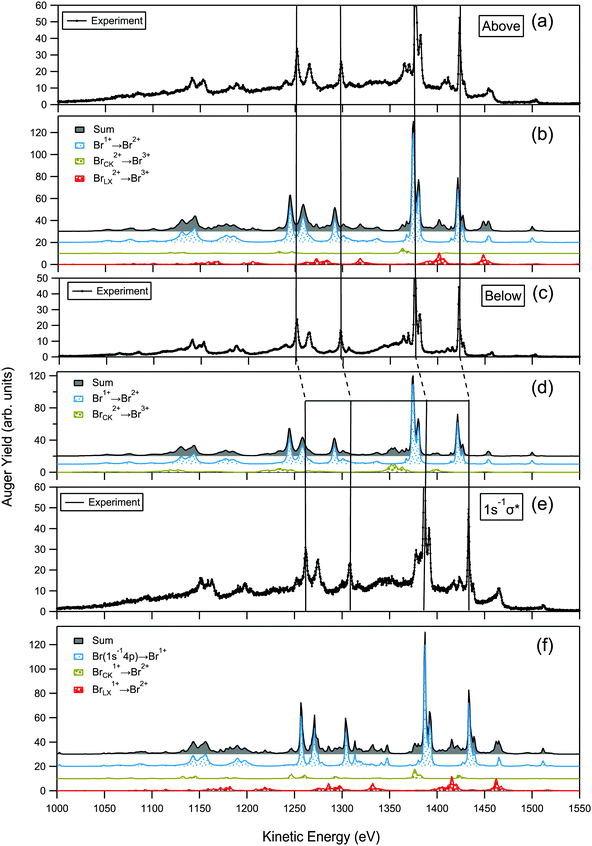
Panels (a), (c) and (e) of Fig. 9 show the experimental Auger spectra of HBr in the electron kinetic energy range of 1000–1550 eV, i.e. the decay of L single core-holes formed by direct ionization or KL X-ray emission and LX double core-holes with X = L, M, N formed by KLX Auger decay or LLY (Y = M, N) Coster–Kronig decay. Consequently, the spectra comprise LYY, LX–XXY, and LY–XYY Auger decays. The Auger spectra are measured above (Fig. 9a) and below (Fig. 9c) the K-edge, as well as at the 1s−1σ* resonance (Fig. 9e). Panels (b), (d) and (f) show the corresponding theoretical spectra calculated for atomic Br. The Auger spectra are very similar to the respective spectra recorded from atomic Kr,38,53,54 except for the fact that the Kr spectrum is shifted by ≅85 eV to higher kinetic energies. Therefore it is possible to identify the main features of the present spectra in more detail by comparison to Fig. 2 and Table 2 of ref. 38. The similarity is due to the fact that the studied Auger decay takes place between deep core orbitals, which causes the overall shape of the spectra to be similar between Br and Kr.The above K-edge spectrum displayed in Fig. 9(a) and the resonant (spectator) Auger spectrum in Fig. 9(e) show very similar structure and differ only by an energy shift of the latter spectrum to higher kinetic energies by ≅10 eV. This is due to the fact that the L-shell holes are populated by the same pathways. Comparison of the spectra in panels (a) and (c) recorded above and below the K-edge, however, shows subtle differences in the peak intensities. Similar differences have been observed for atomic 1s−1 ionization spectra of Xe55 and Kr38 as well as in I 1s−1 ionization of CH3I and CF3I in ref. 56. These differences can be understood by different population pathways leading to the L-hole states by ionization below and above the 1s−1 threshold. In the following the pathways will be discussed in detail.
Using a photon energy below the HBr 1s ionization threshold, the L-hole states can be populated only by direct photoionization of L1,2,3 orbitals. Thus the population of the initial states of Auger decay are described by the photoionization branching ratios of L1,2,3 orbitals. Note that, L2,3 states can in principle be populated by L1 → L2,3 fluorescence decay. This channel is, however, negligible in comparison to the L1XY Auger decay so that we can write
| γ + Br → Br+(2s−1,2p−1) + eph | (5) |
The most prominent relaxation pathway of Br+(2s−1,2p−1) ionic states is LMY Auger decay, where Y = M, N, in the energy region under discussion. The Contribution of this path is displayed in panel 9(d) as the Br1+ → Br2+ subspectrum. In addition, 2s−1 and 2p1/2−1 core hole states can decay via L1L2,3Y and L2L3Y Coster–Kronig processes, respectively. The kinetic energy of Coster–Kronig Auger electrons is well below the currently studied energy range, but it leads to double-hole states where one of the holes is in the 2p orbital. These states can decay further by emitting an electron into the studied kinetic energy range, see below for the description 2p hole decay.
Using a photon energy above the HBr 1s ionization threshold or a photon energy around the HBr 1s−1σ* resonance leads predominantly to a hole in the K-shell. Above threshold, the probability for creating a K-hole is 86%, an L1-hole is 8% and an L2,3-hole is 6%. Eqn (6) shows the three K-hole decay paths that lead to one or two L-holes
 | (6) |
As it can be seen from eqn (6), above the K-edge the experimentally observed population of L-holes is mainly a result of the K-hole decay, not direct photoionization. 61% of the initial K-hole states decay via KL X-ray emission to HBr+ (2p−1) states (Note that 2s−1 cannot be reached by KL-emission), about 31% decays via KLL Auger decay to HBr2+(2s−2,2s−12p−1,2p−2) states and about 8% Auger decays to HBr2+(2s−1,2p−1)nl−1, where n = 3, 4. As expected, the probabilities are similar to those reported for atomic Kr in ref. 38.
As stated above, the HBr 2p core hole predominantly decays via LMY Auger. The corresponding transitions are indicated by the blue subsepctra in the panels (b), (d) and (f) of Fig. 9 and are related to Br1+ → Br2+ transitions in case of photoionization and Br0 → Br1+ transitions in case of resonant excitations. The Br 2p1/2−1 core hole can also relax via Coster–Kronig decay to Br (2p3/2−1Y−1) states. The corresponding olive subspectra are also shown in Fig. 9 and indicated by BrCK2+ → Br3+ for the ionization process as well as by BrCK1+ → Br2+ for resonant excitation. The differences between the olive subspectra in panels (b), (f) and (d) can be explained by the small contribution from Br 2s−1 initial states in the above K-shell and resonant 1s−1σ* cases. It should also be noted, that despite different L-hole population mechanisms, the shapes of spectra recorded above and below the K-edge are remarkably similar. The reason is that KL2/KL3 fluorescence ratio is nearly identical to the high energy limit of the σ2p1/2/σ2p3/2 photoionization ratio, and the fact that the main features contributing to the spectra in Fig. 9 are originating from L2,3MY Auger decay.
The states populated by KLX Auger decay can relax via further Auger decay by filling a hole in the L-shell. The contribution of this decay is displayed in Fig. 9(b) by the red subspectrum labeled BrLX2+ → Br3+ and in Fig. 9(f) by the red subspectrum labeled BrLX1+ → Br2+. As discussed above, the main contributions originate from the case X = L, i.e. they are a result of a KLL Auger decay. Note that LY, initial states of the BrLX2+ → Br3+ or BrLX1+ → Br2+ subspectrum might be also partly populated by the Coster–Kronig decay of Br 2p1/2−1 states, however, their contributions are minor.
The experimental Auger energy line positions of the HBr molecule produced by singly ionized K and L-shells are found to be centered around the calculated neutral atomic-Br Auger spectra as shown in Fig. 2, and Fig. 9(a and c). The reason can be understood from the fact that the deep core orbitals are atomic-like because of the small difference in the electronegativity between H and Br atoms as discussed in Section 5. However, the Auger energies originating from the decay of the 1s−1σ* resonance displayed in Fig. 9 panel (e) are found to be in agreement with calculated resonant atomic-Br (1s−14p) Auger spectrum displayed in the Fig. 9 panel (f). At these times scales (hundreds of attoseconds), the agreement is coincidental, see Section 6.2.
7 Conclusions
A detailed study of the Br 1s−1 resonant excitations and ionization of HBr and of the subsequent two first steps of the Auger decay, namely the relaxation of K and L-holes, has been performed with state-of-the-art experimental resolution. Complementary relativistic multiconfigurational Dirac–Fock calculations for atomic Br and HBr molecule have been performed.We presented an analysis of the partial electron yield photoabsorption spectrum in the energy range from 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 to 13
460 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 eV. The analysis allowed us to extract precise excitation energies of the 1s−1σ* and 1s−15p resonances. Moreover, from this and analysis of the Br 1s photoelectron spectrum, a value of 2.40(12) eV was derived for the lifetime broadening. From the fit analysis of the normal KLL Auger spectrum the Auger energies, the relative intensities and the DCH lifetime widths of 2s−2, 2s−12p−1 and 2p−2 have been derived. The 2s level Γ2s−2 ≅ 2·Γ2s−1 was found as expected for deep core levels. For the 2p level the ratio turned out to be ≅2.4, which is between the values of 2 expected for deep core levels and ≅3 observed for shallow core levels. Finally, different lifetime broadenings were found for the 2s−12p−1(1P) state and the 2s−12p−1(3P) states.
490 eV. The analysis allowed us to extract precise excitation energies of the 1s−1σ* and 1s−15p resonances. Moreover, from this and analysis of the Br 1s photoelectron spectrum, a value of 2.40(12) eV was derived for the lifetime broadening. From the fit analysis of the normal KLL Auger spectrum the Auger energies, the relative intensities and the DCH lifetime widths of 2s−2, 2s−12p−1 and 2p−2 have been derived. The 2s level Γ2s−2 ≅ 2·Γ2s−1 was found as expected for deep core levels. For the 2p level the ratio turned out to be ≅2.4, which is between the values of 2 expected for deep core levels and ≅3 observed for shallow core levels. Finally, different lifetime broadenings were found for the 2s−12p−1(1P) state and the 2s−12p−1(3P) states.
The analysis of the resonant Auger spectra as a function of the photon energy provides evidence of strong repulsive character of the 1s−1σ* state due to the antibonding character of the σ* orbital. The analysis of the kinetic energy and linewidth of the 1s−1σ* → 2p−2σ*(1D2) transition shows anomalous dispersion (S-shape) and line narrowing as a function of the photon energy. This finding is interpreted as a signature of ultrafast nuclear dynamics. The anomalous dispersion and the linewidth narrowing were fitted with the aid of a simplified Kramers–Heisenberg formula, and the HBr 2p−2 DCH lifetime has been extracted and found to be comparable to the value obtained from the analysis of the normal KLL Auger spectrum. The HBr 2p−2σ* potential energy curve has been reconstructed, and its slope at the equilibrium distance of the ground state was estimated to be −13.60 eV Å−1.
Finally, we presented an analysis of the L-shell Auger spectra measured with photon energies below and above 13.482 keV, i.e. the Br 1s ionization energy as well as on top of the 1s → σ* resonance. The latter two spectra represent predominately the second step of the decay cascade subsequent to Br 1s excitation or ionization. Below threshold only singly ionized L-hole initial states are produced by direct ionization. Above threshold L2,3 holes in singly ionized HBr are induced by KL X-ray emission and L-holes in doubly ionized HBr by the KLX Auger processes; the same processes lead in case of a resonant 1s → σ* excitation to L-holes in neutral and singly ionized HBr, respectively. The main differences of the intensities measured below threshold, above threshold and on the resonance are related to the population of the L1-hole in singly ionized HBr. For the Br 1s−1 core hole the KL-emission rate is larger than the Auger emission rate with a ratio of 61 to 39%. The analysis of the Auger kinetic energy peak positions resulting from the deep core-excited and ionized 1s−1σ*, 1s−15p and 1s−1 states shows mainly decays via molecular Auger spectator/participator processes, due to the short lifetime of the states, in comparison to the nuclear dynamics.
Author contributions
M. S. and T. M. elaborated the research plan, T. M., O. T., R. G., L. J., I. I., D. K., S. K., Y. A., D. C., R. P., M. N. P., and M. S., participated and performed the measurement, N. B. K. J, T. M., M. P., and R. P performed the data analysis, N. B., K. J., and M. H., performed the theoretical calculations, N. B, K. J., R. P., and M. N. P., wrote the paper and all authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from the European Unions's Horizon 2020 research and innovation programme under Marie Skoldowska-Curie agreement no. 713606. Academy of Finland is acknowledged for funding. Experiments were performed on GALAXIES beamline at SOLEIL Synchrotron, France (Proposal No. 99170136).References
- D. Céolin, J. Ablett, D. Prieur, T. Moreno, J.-P. Rueff, T. Marchenko, L. Journel, R. Guillemin, B. Pilette and T. Marin, et al. , J. Electron Spectrosc. Relat. Phenom., 2013, 190, 188–192 CrossRef.
- J.-P. Rueff, J. Ablett, D. Céolin, D. Prieur, T. Moreno, V. Balédent, B. Lassalle-Kaiser, J. Rault, M. Simon and A. Shukla, J. Synchrotron Radiat., 2015, 22, 175–179 CrossRef CAS.
- M. Simon, R. Püttner, T. Marchenko, R. Guillemin, R. K. Kushawaha, L. Journel, G. Goldsztejn, M. N. Piancastelli, J. M. Ablett and J.-P. Rueff, et al. , Nat. Commun., 2014, 5, 1–5 Search PubMed.
- M. N. Piancastelli, T. Marchenko, R. Guillemin, L. Journel, O. Travnikova, I. Ismail and M. Simon, Rep. Prog. Phys., 2019, 83, 016401 CrossRef.
- M. Oura, T. Gejo, K. Nagaya, Y. Kohmura, K. Tamasaku, L. Journel, M. N. Piancastelli and M. Simon, New J. Phys., 2019, 21, 043015 CrossRef CAS.
- P. Erman, I. Bergström, Y. Chu and G. Emery, Nuclear Phys., 1965, 62, 401–409 CrossRef CAS.
- B. M. Kincaid and P. Eisenberger, Phys. Rev. Lett., 1975, 34, 1361–1364 CrossRef CAS.
- P. D'Angelo, A. Di Cicco, A. Filipponi and N. V. Pavel, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 2055–2063 CrossRef.
- S. Southworth, R. Dunford, E. Kanter, B. Krässig, L. Young, L. LaJohn and R. Pratt, Radiat. Phys. Chem., 2006, 75, 1574–1577 CrossRef CAS.
- R. Hauko, J. Padežnik Gomilšek, A. Kodre, I. Arčon and G. Aquilanti, Phys. Rev. A: At., Mol., Opt. Phys., 2019, 99, 062501 CrossRef CAS.
- P. Morin and I. Nenner, Phys. Rev. Lett., 1986, 56, 1913 CrossRef CAS.
- O. Björneholm, S. Sundin, S. Svensson, R. R. T. Marinho, A. Naves de Brito, F. Gel'mukhanov and H. Ågren, Phys. Rev. Lett., 1997, 79, 3150–3153 CrossRef.
- R. Feifel, F. Burmeister, P. Sałek, M. N. Piancastelli, M. Bässler, S. L. Sorensen, C. Miron, H. Wang, I. Hjelte, O. Björneholm, A. Naves de Brito, F. K. Gel'mukhanov, H. Ågren and S. Svensson, Phys. Rev. Lett., 2000, 85, 3133–3136 CrossRef CAS.
- F. Gel'mukhanov and H. Ãgren, Phys. Rep., 1999, 312, 87–330 CrossRef.
- O. Travnikova, T. Marchenko, G. Goldsztejn, K. Jänkälä, N. Sisourat, S. Carniato, R. Guillemin, L. Journel, D. Céolin and R. Püttner, et al. , Phys. Rev. Lett., 2016, 116, 213001 CrossRef.
- O. Travnikova, N. Sisourat, T. Marchenko, G. Goldsztejn, R. Guillemin, L. Journel, D. Céolin, I. Ismail, A. Lago and R. Püttner, et al. , Phys. Rev. Lett., 2017, 118, 213001 CrossRef CAS.
- T. Marchenko, G. Goldsztejn, K. Jänkälä, O. Travnikova, L. Journel, R. Guillemin, N. Sisourat, D. Céolin, M. Žitnik and M. Kavčič, et al. , Phys. Rev. Lett., 2017, 119, 133001 CrossRef CAS.
- H. Aksela, S. Aksela, M. Ala-Korpela, O. Sairanen, M. Hotokka, G. Bancroft, K. Tan and J. Tulkki, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6000 CrossRef CAS.
- H. Aksela, S. Aksela, M. Hotokka, A. Yagishita and E. Shigemasa, J. Phys. B: At., Mol. Opt. Phys., 1992, 25, 3357 CrossRef CAS.
- I. Hjelte, M. Piancastelli, R. Fink, O. Björneholm, M. Bässler, R. Feifel, A. Giertz, H. Wang, K. Wiesner and A. Ausmees, et al. , Chem. Phys. Lett., 2001, 334, 151–158 CrossRef CAS.
- O. Björneholm, M. Bässler, A. Ausmees, I. Hjelte, R. Feifel, H. Wang, C. Miron, M. Piancastelli, S. Svensson and S. Sorensen, et al. , Phys. Rev. Lett., 2000, 84, 2826 CrossRef.
- I. Hjelte, M. Piancastelli, C. M. Jansson, K. Wiesner, O. Björneholm, M. Bässler, S. Sorensen and S. Svensson, Chem. Phys. Lett., 2003, 370, 781–788 CrossRef CAS.
- P. Morin and C. Miron, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 259–266 CrossRef CAS.
- L. Avaldi, G. Dawber, R. Camilloni, G. King, M. Roper, M. Siggel, G. Stefani and M. Zitnik, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 3953 CrossRef CAS.
- M. Breinig, M. H. Chen, G. E. Ice, F. Parente, B. Crasemann and G. S. Brown, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 520 CrossRef CAS.
- H. J. A. Jensen, R. Bast, T. Saue, L. Visscher, V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, T. Helgaker, J. Henriksson, M. Iliaš, C. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther and S. Yamamoto, DIRAC, a relativistic ab initio electronic structure program. Release DIRAC16, 2016. See http://www.diracprogram.org Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447 Search PubMed.
- P. Bunker, J. Mol. Spectrosc., 1972, 42, 478–494 CrossRef CAS.
- P. Jönsson, X. He, C. F. Fischer and I. Grant, Comput. Phys. Commun., 2007, 177, 597–622 CrossRef.
- J. Niskanen, K. Jänkälä, M. Huttula and A. Föhlisch, J. Chem. Phys., 2017, 146, 144312 CrossRef CAS.
- S. Fritzsche, Comput. Phys. Commun., 2012, 183, 1525–1559 CrossRef CAS.
- M. F. Gu, Can. J. Phys., 2008, 86, 675–689 CrossRef CAS.
- R. Püttner, M. Domke, K. Schulz, A. Gutiérrez and G. Kaindl, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2425 CrossRef.
- R. Püttner, Y.-F. Hu, E. Nommiste, G. Bancroft and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 032513 CrossRef.
- A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221 CrossRef CAS.
- G. B. Armen, J. Tulkki, T. Aberg and B. Crasemann, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 5606 CrossRef.
- M. O. Krause and J. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329–338 CrossRef CAS.
- N. Boudjemia, K. Jänkälä, R. Püttner, T. Gejo, L. Journel, Y. Kohmura, M. Huttula, M. N. Piancastelli, M. Simon and M. Oura, Phys. Rev. A: At., Mol., Opt. Phys., 2020, 101, 053405 CrossRef CAS.
- V. Carravetta, H. Ågren, D. Nordfors and S. Svensson, Chem. Phys. Lett., 1988, 152, 190–195 CrossRef CAS.
- V. Schmidt, Electron spectrometry of atoms using synchrotron radiation, Cambridge University Press, 1997, p. 73 Search PubMed.
- R. Guillemin, S. Sheinerman, R. Püttner, T. Marchenko, G. Goldsztejn, L. Journel, R. Kushawaha, D. Céolin, M. N. Piancastelli and M. Simon, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 012503 CrossRef.
- G. Goldsztejn, T. Marchenko, R. Püttner, L. Journel, R. Guillemin, S. Carniato, P. Selles, O. Travnikova, D. Céolin and A. Lago, et al. , Phys. Rev. Lett., 2016, 117, 133001 CrossRef CAS.
- M. Žitnik, R. Püttner, G. Goldsztejn, K. Bučar, M. Kavčič, A. Mihelič, T. Marchenko, R. Guillemin, L. Journel and O. Travnikova, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2016, 93, 021401 CrossRef.
- R. Püttner, G. Goldsztejn, D. Céolin, J.-P. Rueff, T. Moreno, R. K. Kushawaha, T. Marchenko, R. Guillemin, L. Journel and D. W. Lindle, et al. , Phys. Rev. Lett., 2015, 114, 093001 CrossRef.
- R. Püttner, D. Céolin, R. Guillemin, R. K. Kushawaha, T. Marchenko, L. Journel, M. N. Piancastelli and M. Simon, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 93, 042501 CrossRef.
- R. Püttner, P. Holzhey, M. Hrast, M. Žitnik, G. Goldsztejn, T. Marchenko, R. Guillemin, L. Journel, D. Koulentianos, O. Travnikova, M. Zmerli, D. Céolin, Y. Azuma, S. Kosugi, A. Föhlisch, M. N. Piancastelli and M. Simon, to be submitted, 2020.
- D. Céolin, T. Marchenko, R. Guillemin, L. Journel, R. K. Kushawaha, S. Carniato, S.-M. Huttula, J. P. Rueff, G. B. Armen, M. N. Piancastelli and M. Simon, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 022502 CrossRef.
- G. Goldsztejn, T. Marchenko, D. Céolin, L. Journel, R. Guillemin, J.-P. Rueff, R. K. Kushawaha, R. Püttner, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2016, 18, 15133–15142 RSC.
- R. Püttner, K. Jänkälä, R. K. Kushawaha, T. Marchenko, G. Goldsztejn, O. Travnikova, R. Guillemin, L. Journel, I. Ismail, B. Cunha de Miranda, A. F. Lago, D. Céolin, M. N. Piancastelli and M. Simon, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 96, 022501 CrossRef.
- H. A. Kramers and W. Heisenberg, Z. Phys., 1925, 31, 681–708 CrossRef CAS.
- J. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS.
- L. O. Werme, T. Bergmark and K. Siegbahn, Phys. Scr., 1972, 6, 141–150 CrossRef CAS.
- A. Kovalík, V. Gorozhankin, A. Novgorodov, A. Minkova, M. Mahmoud and M. Ryšavý, J. Electron Spectrosc. Relat. Phenom., 1992, 58, 49–66 CrossRef.
- M. N. Piancastelli, K. Jänkälä, L. Journel, T. Gejo, Y. Kohmura, M. Huttula, M. Simon and M. Oura, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 95, 061402 CrossRef.
- N. Boudjemia, K. Jänkälä, T. Gejo, K. Nagaya, K. Tamasaku, M. Huttula, M. N. Piancastelli, M. Simon and M. Oura, Phys. Chem. Chem. Phys., 2019, 21, 5448–5454 RSC.
Footnotes |
| † CCDC. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cp04787b |
| ‡ Present address: Chemical Sciences and Engineering Division, Argonne National Laboratory, 9700 S Cass Avenue, Lemont, IL 60439, USA. |
| This journal is © the Owner Societies 2020 |