Addition of carbon-centered radicals to aromatic antioxidants: mechanistic aspects

Abstract

Several recent studies have shown that the rates of formation of adduct radicals between carbon-centred radicals and aromatic molecules are virtually diffusion-controlled and reversible. This contrasts with “radical addition”, the well-known multistep reaction in preparative organic chemistry where the rate-determining initial formation of radical adducts is perceived to be several orders of magnitude slower and virtually irreversible. Using pulse radiolysis and spectroscopic analysis, we have now re-examined parts of this complex mechanism. The results have significant implications for biological systems: electron-rich, aromatic structures may act like buffers for radicals, moderating their reactivity resulting in a much slower reaction determining the overall rate of oxidation. In vivo, an organism would gain time for an appropriate antioxidant reaction.

---

Introduction

Oxidative stress is a common consequence of modern industrialized life, widely held to be responsible for the initiation or aggravation of many diseases and other deleterious conditions in humans.¹ It is defined as a condition in which the challenge by free radicals and other oxidants exceeds the defensive capacity of the organism. While humans and other aerobic organisms are equipped with a range of endogenous antioxidant systems selected for defense against deleterious oxidative processes, these defenses are clearly inadequate under oxidative stress. Since oxidative stress is strongly associated with deleterious health conditions, there is a well-recognized need for supplementation of the endogenous defenses with additional antioxidants. They should be widely available, effective, readily administered and inexpensive. To fill this need, there is a vast choice of commercially available antioxidant supplements, many of which claim to provide defense against free radicals, frequently without scientific justification.

In fact, there is a large group of natural products with significant beneficial effects on health demonstrated in many careful studies, which were for many years partly explained by their antioxidant properties.² Flavonoids and other plant-derived polyphenols form a group of over 8000 identified compounds, with over 500 forming part of human diet.³ While their ability to act as antioxidants by donating electrons to free radicals and other oxidizing agents is well known, later quantitative work identified two principal reasons why they were unlikely to compete with the physiological endogenous antioxidants such as ascorbate or GSH in vivo. First, the concentrations of ingested polyphenols in tissues apparently only reach at best micromolar levels and, second, their reactions with radicals are relatively slow.

There are now significant doubts about the validity of both these conclusions. On the concentrations in vivo, the accuracy of the commonly used spectrophotometric and LC-MS techniques has been questioned, with poor agreement in inter-laboratory estimates of even standard single polyphenols and their metabolites. Measurements of these compounds and their metabolites in tissues are likely to be even more subject to error, with the general caution that the obtained values are likely to be significantly underestimated.^3–5 The second reservation, slowness of the reactions of polyphenols with radicals, is at least partly due to differences in the understanding of the term antioxidant. Oxidation is defined by IUPAC as ‘the complete, net removal of one or more electrons from a molecular entity’.⁶ Accordingly, most chemists would think of antioxidant action exclusively in terms of electron-transfer. The requirement of complete electron transfer leads to low reaction rates of the flavonoids (Fl(OH)₂) and polyphenols (PPH) generally because it involves a large entropic barrier imposed by the need for exchange of protons:⁷

Fl(OH)₂ + R˙ → Fl(OH)O˙ + RH (1)

Fl(OH)O˙ + H₂O → Fl(O⁻)O˙ + H₃O⁺ (2)

As an example of typical reaction kinetics, the rate constants of reactions of 12 flavonoids with superoxide radicals (O₂˙⁻/HO₂˙) lie in the range of only ∼3 × 10² to 4.1 × 10⁵ M⁻¹ s⁻¹ in spite of a very large redox potential difference.^8,9 In contrast to the chemical definition, for biologists an antioxidant is defined by its ability to inhibit deleterious oxidative processes partially or completely, regardless of the mechanism. The practical advantage of the biological approach lies in that it measures the quality of an antioxidant solely by its effectiveness in lowering the activity of damage-inducing oxidants; this may well be sufficient to eliminate the consequences of oxidative stress under physiological conditions. It will be shown that both the chemical and biological definitions of antioxidant action are illustrated by the reactions of polyphenols with C-centered radicals.

The possibility of a potential role of polyphenols as effective in vivo antioxidants in reactions not involving transfer of electrons was suggested by results reported in 2014 by Nauser and Carreras, who described a fast reversible addition reaction of carbon-centered radicals to histidine.¹⁰ Reaction kinetics were investigated by pulse radiolysis because formation of the adducts was virtually diffusion-controlled, with rate constants 2–3 orders of magnitude higher than in processes involving complete electron transfer. Importantly also, formation of the adducts resulted in significant lowering of the reactivity of the radicals.

The chemistry of polyphenols and their oxidation by radicals have been extensively studied. Most of the results were obtained in alkaline solutions, where the compounds are more soluble.¹¹ This implies deprotonation of at least one phenolic group, which would accelerate the transfer of electrons.⁷ Kinetics measurements at high pH would, therefore, yield an upper limit for the respective electron transfer reactions at neutral pH. However, results of measurements in alkaline solutions cannot be simply extrapolated to physiological conditions, reducing their relevance to biological systems; it will be shown that the mechanism of the radical–polyphenol reaction appears to change significantly around pH 8. In order to test the antioxidant potential of polyphenols under conditions approaching the physiological, we reported recently on radical addition of carbon-centered amino acid radicals to several polyphenols at neutral pH.¹² We confirmed the results of the earlier studies with histidine by finding a close to diffusion-controlled rates of formation of the adducts with a range of polyphenols, resulting in drastic lowering of the reactivity of amino acid radicals. The reactions were reversible, with equilibrium constant of 5 × 10⁴ M⁻¹ in the case of morin. Adduct formation did not involve electron-transfer or the breaking of bonds.¹³ The process leading finally to the repaired radical and formation of a phenoxyl radical (PPO˙) can be represented by reaction (3), with the marked stages corresponding to the biological and chemical definitions of antioxidant action (see above):

Observation of the reaction rate difference of several orders of magnitude between formation of the adducts (biological definition) and the final products (chemical definition) required the availability of fast and sensitive pulse radiolysis technology and was missed in earlier studies. At present there is no information on the intermediate steps following the formation of the complex.

Addition of radicals to aromatic centers is long known¹⁴ and “nucleophilic radical addition”, where carbon-centered radicals are used to add aliphatic side chains to aromatic centers, has been used in organic chemical synthesis since the pioneering work of Minisci in the 1970s.^15–18 Minisci interpreted his experimental product yields and distribution in terms of a mechanism in which formation of a radical adduct was the rate-determining step, followed by a very fast oxidation process, for example by a transition metal ion, resulting in in the final product.¹⁵ The studies of aromatic radical adduct by Nauser et al. revealed a significant complexity of the mechanism of these reactions, particularly at pH values relevant to living organisms.^10,12,13,19

In an effort to deepen our understanding of the details of the reaction mechanism and to provide a critical test of our initial data, we have now investigated by pulse radiolysis the response of the adducts of the flavonoid morin and amino acid radicals to varying conditions, such as concentration and pH. We also extended the study to additional amino acids and polyphenols. Interpretation of the data was challenging, but the difficulties were not unique: when Minisci investigated the addition of electron-rich radicals to electron-poor aromatic structures, many of the findings had to be rationalized by an educated guess. However, as we were observing the initial fast processes and loss of radical reactivity instead of formation of the products, our findings contribute to the overall mechanistic picture of radical addition reactions, adding some new pieces to the puzzle.

Experimental

Pulse radiolysis

Experiments were carried out in the pulse-radiolysis facility at the ETH described previously.²⁰ Briefly, samples were irradiated with 50 ns/2 MeV electron pulses delivered by the electron accelerator. As light-source a 75 W Xe-arc lamp was used. For wavelength selection appropriate order-sorting filters and a 300 mm Czerny–Turner monochromator with 150 l mm⁻¹ gratings (blazed either at 300 nm or at 500 nm) and a slit width of 1 mm were chosen. Prepared samples were taken up in gas-tight syringes and were introduced into the measurement cell through a PEEK capillary. The quartz measurement cell had an optical pathlength of 6 cm.

Sample preparation

To prepare stock solutions, the polyphenols were dissolved under argon. Polyphenols with slow dissolution kinetics were dissolved at high pH and then brought back to neutral pH within one minute by addition of HCl (diluted from 37%, pro analysi, source: Merck, Zug, Switzerland). Morin (95%) was purchased from Adipogen (Liestal, Switzerland), rutin (98%) from ABCR (Karlsruhe, Germany), gallic acid from Cayman Chemical Company (Ann Arbor, USA), catechin (>98%) from Sigma (Zug, Switzerland), and epigallocatechin gallate was a kind gift from Dr J. Vinson. For the chemical structures of the (poly-)phenols used, see Table 1. Stock solutions of the polyphenols were used within 2–3 h after preparation. Stock solutions of the amino-acid derivatives (Bachem, Bubendorf, Switzerland) were prepared from the pure chemicals and MilliQ water (Millipore, Switzerland) and kept under argon. Phosphate buffer was prepared with NaH₂PO₄ and Na₂HPO₄ (puriss. pro analysi) from Fluka (Buchs SG, Switzerland) according to the Henderson–Hasselbach calculation. Because the pH of phosphate buffer around neutral is concentration dependent, slight corrections were applied by addition of NaOH (made from pellets, Ph. Eur. II, source: Siegfried, Zofingen, Switzerland) or HCl.

Table 1 Structures of (poly-)phenols used

Name	Structure
Catechin
Gallate
Epigallocatechin gallate
Morin
Rutin

---

Before use, glassware, syringes and tubing were first rinsed with dilute HNO₃ (to mobilise transition-metal ions) and then with MilliQ water. We chose not to immerse any pH-electrode into our samples before the experiments. Pulse-radiolysis experiments can be very sensitive to even nanomolar traces of contaminations, especially transition metal ions. Working in an inorganic chemistry lab, we could not exclude presence of such contaminations on and in our electrodes. We controlled approximately correct pH with the leftover solution that could not be taken up into the syringe. These drops were put on a pH-paper for control. Appropriate pH-papers were used (depending on expected pH) from Riedel-de-Haen (Reinach, Switzerland), Merck, Fluka, and Macherey-Nagel (Oensingen, Switzerland). Solutions that were not used up completely were measured with a pH meter after the experiments.

With the stock solutions, 10 ml batches were prepared in Schlenk tubes where they were deaerated and saturated with the required gas. Deaeration was carried out by repeated evacuation to 20 mbar to prevent boiling at ambient temperature, stirring and refilling with argon or N₂O. After at least 6 cycles, the sample was equilibrated with the required gas or gas mixture at atmospheric pressure.

Evaluation of results

Absorbed energy doses are given in J kg⁻¹ ≡ Gy (gray). The electron pulses decomposed water in the irradiated solutions, generating 2.7 × 10⁻⁷ M Gy⁻¹ of reducing electrons (e_aq⁻), 2.8 × 10⁻⁷ M Gy⁻¹ oxidizing hydroxyl radicals (HO˙), and 0.6 × 10⁻⁷ M Gy⁻¹ of hydrogen atoms (H˙).²¹ In solutions saturated with 24 mM N₂O, the e_aq⁻ were converted to HO˙, approximately doubling their yield.

Results

The reaction of amino acid alkyl radicals with morin

1. Near-neutral pH: kinetics and spectra. The results shown in Fig. 1 were generated by pulse irradiating N₂O saturated solution of 10 mM AcAlaNH₂, 50 μM morin, pH 7 with doses of approximately 8 Gy. Approximately 5 μM of AcAla˙NH₂ radicals then reacted with the morin. The 200 fold concentration excess of the amino acid ensured that 98% of the primary radicals generated reacted with the amino acid, leaving the morin intact.

Fig. 1 Upper panel: Irradiation of N₂O saturated solution of 10 mM AcAlaNH₂, 50 μM morin, pH 7, with doses of approximately 8 Gy. Kinetics traces at 575 nm (blue) and 700 nm (red). Middle panel: Corresponding transient spectra for 10 μs (black), 50 μs (blue), and 500 μs (green) after irradiation. Lower panel: Kinetics trace at 550 nm 50 μM morin, pH approximately 7.4, irradiation dose 10 Gy, oxidized by HO˙ radicals (N₂O saturated solution), red trace, or oxidized by peroxyl radicals (in presence of 10 mM AcAlaNH₂, 80% N₂O, 20% O₂), blue trace. In the latter case, the total radical yield is approximately 15% higher – the trace has been scaled accordingly.

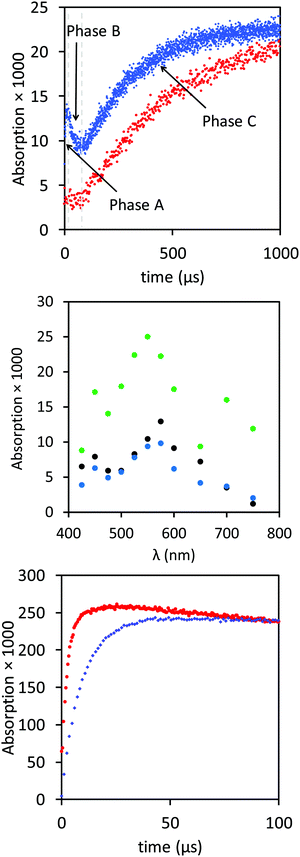
Time vs. absorption trace at 575 nm showed three phases in the first millisecond after the pulse (Fig. 1, upper panel, blue trace), in agreement with an earlier report: Phase A, a fast absorption increase (0–5 μs), followed by a brief decay in Phase B (10–100 μs) and a slow increase in Phase C.¹¹ Phase A was attributed to a fast equilibrium reaction of AcAla˙NH₂ radicals forming an adduct with the morin. The kinetics of Phase B were second order (see below). Associated with the reaction in Phase C, there was an absorption increase at 700 nm (Fig. 1, upper panel) which was slower than at 575 nm. During the first two phases, the absorption at 700 nm was small. The build-up at 700 nm may be associated with a reaction consecutive to the 3rd phase observed at 550 nm. Importantly, concomitant with the build-up in Phase C, there was also a shift of the absorption band from 575 nm to 550 nm (Fig. 1, middle panel). In the presence of 20% oxygen (0.2 mM) and 80% N₂O (20 mM) or 10% oxygen (0.1 mM) and 90% N₂O (22 mM), Phase C was suppressed: under such conditions an absorption at 550 nm was observed and reached maximum after approximately 20 μs, with k_obs = 2 × 10⁵ s⁻¹. The calculated extinction coefficient was identical to the one derived for N₂O-saturated solution of 50 μM morin in 10 mM phosphate buffer at pH 7.4 irradiated in the absence AcAlaNH₂,¹² provided a correction was applied for the appropriate radiochemical yield of HO˙ for the respective solutions (Fig. 1, lower panel).²²

2. Near-neutral pH: stochiometry. When a sample of 100 μM morin and 20 mM AcAlaNH₂ in 10 mM phosphate buffer at pH 7.5 was repeatedly irradiated with ∼13 Gy pulses, the build-up of Phase C became progressively weaker and its rate was lowered with each pulse (Fig. 2, upper panel). Also, the time-dependent absorbance changes at 700 nm disappeared gradually. Something was consumed. More and more, the decay of Phase B dominated the kinetics trace. Phases B and C could be separated because the kinetics of Phase B were of second order and practically unaffected by repeated pulsing. Therefore, the background signal, i.e. Phase B, is best fitted in the first 400 μs, after repeated pulsing. This background could then be subtracted from the other kinetics traces, and the build-up rate constants of Phase C derived (Fig. 2, lower panel) from the corresponding traces. As long as there was “enough” morin left intact, we observed a linear drop in reaction rate. At very low remaining concentration of still intact morin, its consumption by the irradiation leveled off (Fig. 2, lower panel).

Fig. 2 Response of samples of 100 μM morin and 20 mM AcAlaNH₂ in 10 mM phosphate buffer at pH 7.5 to repeated irradiation with 13 Gy pulses. Upper panel: Kinetics traces detected at 550 nm: number of pulses before measurement is shown above the x-axis (0 represents the fresh solution), with the corresponding kinetic traces from 0 on the top to 8 on the bottom. Lower panel: The corresponding apparent rate constants of Phase C absorbance growth.

In the experimental results shown in Fig. 2, approximately 7–8 μM of radicals were produced per pulse.²² The results show that 73% of the reactivity of 100 μM morin in Phase C could be quenched by 5 successive irradiations. Apparently, the stochiometry of Phase C was not 1 : 1 for the radical : morin ratio. This was corroborated by experiments in which 15 mM AcLysNH₂ and 75 μM morin were pulse irradiated with doses that produced 3–90 μM AcLys˙NH₂. The data showed unambiguously that the relative yield of product in Phase C strongly decreased with increasing dose, i.e. with the starting concentration of radicals (Fig. 3, upper panel). A decrease in the relative yield can be rationalized qualitatively by the influence of competing radical recombination reactions whose occurrence increased with the radiation dose. It is, however, surprising that the absolute yield of absorbance dropped sharply when the concentration of amino acid radicals was larger than that of morin (Fig. 3, upper panel, brown trace, 152 Gy, 93 μM radicals). Under such conditions, the shape of the kinetics trace changed completely which indicates a change of the mechanism of the morin–radical reaction. Notably, this is the only trace that cannot reflect a smaller stochiometry than 1 : 1 of [radicals] : [morin] ratio, with morin not in excess. The initial absorbance in Phase A, 3 μs after pulse, was strictly linear with the amount of radicals produced, with one exception, where [AcLys˙NH₂] > [morin] (Fig. 3, lower panel).

Fig. 3 Pulse irradiation of N₂O saturated solutions of 15 mM AcLysNH₂ and 75 μM morin with variable doses between 5 and 150 Gy. Upper panels: Traces for 5 Gy (black), 9 Gy (blue), 19 Gy (green), 27 Gy (orange), 47 Gy (red) and 152 Gy (brown) detected at 550 nm. Lower panel: Plot of initial absorption (3 μs after pulse) vs. initial radical concentration.

3. Near-neutral pH: thermodynamics. For a more detailed investigation of Phase B, we chose to pre-condition the samples by repeated pulsing, in order to suppress Phase C.¹² Both the first and second Phases of the kinetics were unaffected by repeated irradiation of the solution, even if the total amount of radicals exceeded the initial morin concentration by a wide margin, with [radical]_tot > 10[morin]_initial.¹² If the morin concentration was varied, given a fixed ratio [morin] : [AcAla] of 1 : 200, the rate of this decay was inversely proportional to the initial morin concentration (Fig. 4, upper panel). In other words, a non-consumed substructure of morin inhibited the radical decay in Phase B. The kinetics corresponded to a recombination of radicals engaged in a fast equilibrium reaction with morin with an equilibrium constant of (4 ± 3) × 10⁵ M⁻¹ (for details see ref. 10, ESI). That is almost one order of magnitude higher than the value derived from the build-up kinetics.¹² It should be noted that in our current determination the K_eq value was calculated by dividing the slope of the measurement by the offset and that since the latter was small, the result carried a large relative error. Note also that the pH-determination in our experiments had an accuracy of ±0.2 (for implications see below).

Fig. 4 Dependence of the apparent rate constant of Phase B on the morin concentration (upper panel) and the amino acid (lower panel). Upper panel: [morin] : [AcAla] = 1 : 200, pH 7.4. Lower panel: 75 μM morin, 15 mM amino acid derivative, pH 7.4. All data base on kinetics traces recorded at 550 nm.

In further tests, 15 mM solutions of different amino acid derivatives and 75 μM morin at pH (7.4 ± 0.2) were saturated with N₂O and then pulse irradiated. The results were similar to those with AcAla, but with different observed rate constants. Apparent rate constants of Phase B were thus derived for solutions that had been irradiated multiple times (Fig. 2, lower panel), in analogy with results in Fig. 2 (upper panel).

Influence of pH

We found that the kinetics of morin reacting with AcAla˙NH₂ were very sensitive to the conditions of the preparation. It is known that such reactions are pH dependent and that autoxidation of polyphenols during preparation may be an issue, especially if they are dissolved at high pH. Therefore, experiments used for quantitative intercomparison of results have always been carried out using samples prepared from the same stock solutions of polyphenol, buffer and AcAlaNH₂ that have all been kept under argon. In addition, the experiments were carried out with the same concentration ratio of chemicals and within 2–3 hours after preparation of the polyphenol stock solution. This minimized differences in pH and in possible impurities in the samples due to degradation. In order to qualitatively survey the response of our experiments to pH changes, we conducted a series of experiments changing the pH between 3 and 9 while keeping the concentration of morin (25 μM) and AcAlaNH₂ (5 mM) constant (Fig. 5). Qualitatively, we observed that at 550 nm Phases A and B did become less prominently visible above pH 7 and were obscured almost completely at pH 9 by the strong absorption of Phase C. With increasing pH the associated build-up of Phase C was also accelerated and more prominent and absorption at 700 nm was also more prominent. At pH 9.4 the kinetics trace was clearly sigmoidal and still had a positive slope at 1.5 ms, in clear contrast to the measurement at 550 nm, where at the same time the slope was negative.

Fig. 5 Dependence of the kinetics traces on pH: N₂O saturated solutions of 25 μM morin and 5 mM AcAlaNH₂ were pulse-irradiated with doses of approximately 10 Gy and the results normalized to 1 Gy. Upper panel: Detection wavelength 550 nm. The solutions were at pH of 9.4, 7.9, 7.1, 6.0, 4.7 and 3.7 (from top to bottom at 1500 μs). The traces shown are averages of 4 experiments (except for pH 4.7). Lower panel: Detection wavelength 700 nm. Solutions had a pH of 9.4, 7.9, 7.1 and 3.7 from top to bottom. Traces represent single experiments.

The reaction of amino acid alkyl radicals with rutin, gallate, catechin and epigallocatechin gallate

Reactions of the flavone morin were subsequently compared with those of other polyphenols. Qualitative experiments were carried out with rutin, a glycosylated flavone, and with flavonoid epigallocatechin gallate (EGCG) as well as its related substructures catechin and gallate. The pulse-irradiated solutions were saturated with N₂O and contained 75 μM polyphenol, 15 mM AcAlaNH₂ and 20 mM buffer. No spectra were collected. Except for catechin, kinetics traces between were recorded between 500 nm and 575 nm. For catechin the detection wavelength was 300–350 nm (see below).

Experiments with rutin yielded qualitatively similar traces to morin under the same conditions (Fig. 6). It is unsurprising that the different positions of the hydroxy groups in the B-ring of the flavone (ortho vs. para dihydroxy) as well as glycosylation of the C-ring would have an influence on rate constants and extinction coefficients. For example, the build-up in Phase C appeared to be slower in the case of rutin.

Fig. 6 Kinetics traces detected at 550 nm. Red: N₂O saturated solution of 15 mM AcAlaH₂ and 75 μM rutin, pH 7.4, irradiated with 32 Gy. Blue: N₂O saturated solution of 15 mM AcAlaNH₂ and 75 μM morin, pH 7.5, irradiated with 23 Gy.

We found that catechin, gallate and EGCG also reacted with AcAla˙NH₂, as shown by the kinetics traces. With catechin, no distinct traces in the visible range could be observed. However, the decay observed at 310 nm, where the spectrum of AcAla˙NH₂ has a shoulder,²⁰ was significantly slowed down (data not shown). Gallate had a similar effect on the traces measured in the UV, but there was also an absorbance build-up detected in the visible region (Fig. 7, red trace). EGCG showed a response to radicals similar to that of morin and rutin, with 3 different reaction phases visible in the kinetics traces (Fig. 7, blue trace). The slow absorbance build-up of Phase C was faster than with gallate.

Fig. 7 Pulse irradiation N₂O saturated solution of 15 mM AcAlaNH₂ and, red trace: 75 μM gallate with 61 Gy, or, blue trace: 75 μM EGCG irradiated with 28 Gy. Both kinetics traces were recorded at 500 nm.

Discussion

Our previous study of the fast formation of adduct of carbon-centered radicals and polyphenols (PPH) suggested that the initial step was followed by a series of reactions, presumed to reflect stepwise stabilization of the adducts.¹² We have now carried out additional experiments and analysis as part of a study of the mechanism of this sequence of reactions.

Under the conditions employed, pulse radiolysis generated hydroxyl radicals which were scavenged by an amino acid, producing a C-centered radical AA˙. It seems beyond doubt that reactions (4) and (5) governed the initial phase of our experiments. Subsequently many reactions were possible, but their occurrence cannot be conclusively established with the available data. However, some of our experimental results allow comments on reactions (6)–(14):

2AA˙ → products (4)

AA˙ + PPH ⇌ [AA⋯PPH]˙ (5)

AA˙ + PPH → AAH + PP˙ (6)

[AA⋯PPH]˙ → AAH + PP˙ (7)

[AA⋯PPH]˙ + PPH ⇌ [PPH⋯AA⋯PPH]˙ (8)

AA˙ + O₂ → AA-O₂˙ (9)

AA-O₂˙ + PPH → AA-O₂H + PP˙ (10)

PP˙ + O₂ → PP-O₂˙ (11)

PP-O₂˙ → PP_ox + O₂˙⁻ (12)

[AA⋯PPH]˙ + O₂ → AA-PPH-O₂˙ (13)

AA-PPH-O₂˙ → AA-PP + HO₂˙ (14)

The range of possible reactions indicates the complexity of the mechanism of the reactions following the well-documented formation of the complex [AA⋯PPH]˙. Already 20 years ago we were cautioned in personal communications by W. Bors that the mechanism of the kinetics of reaction of radicals with polyphenols would be very complicated and that sample preparation would be difficult, particularly in solutions close to pH 7. After the conclusion of our study, we entirely concur. However, the finding of very high rates of formation of adducts of polyphenols and carbon-centered radicals in neutral solutions, with consequent lowering of the reactivity of the radicals, made such reactions potentially relevant to biological systems and their study desirable.¹² While the complexity of the mechanism imposes a limit on the assignment of relative significance to the individual reactions, some general useful conclusions should be possible. We therefore investigated the details of the chemistry of polyphenol–radical adducts near pH 7, in order to test whether polyphenols are likely to fulfil the role of effective antioxidants in vivo.

Possible role of contaminants

The possibility that impurities in the supplied chemicals affected the reproducibility of experimental results cannot be excluded, although none had claimed purity of less than 98%. It is also possible that autoxidation during sample preparation and small changes in pH between samples from different stock solutions may be partly responsible. However, we need to emphasize that such variations did at no point change the qualitative or even the semiquantitative results. Other than impurities in the chemicals, oxygen is always a strong candidate as contaminant. One of the major problems in our experiment setup is that it allows for up to 10 μM O₂ in any fresh solution. For most experiments this could be considered fully anaerobic, but in radical chemistry even low amounts of oxygen may lead to problems in the high microsecond timescale, for example by reactions (9)–(12). Repeated irradiation consumes oxygen. Indeed, repeated irradiation did change signals, but the changes could not be explained by the presence of oxygen alone. In pulse radiolysis, because of the slow kinetics of H₂O₂, the peroxide is usually the sink, i.e. when two electrons are consumed per O₂. Three irradiations with a dose of 10 Gy should have consumed oxygen quantitatively if oxygen had been the sole reason for Phase C. This is not consistent with our results. Based on control experiments with deliberately introduced 100 and 200 μM O₂, we would have expected the kinetics of Phase C to be faster than observed if reactions (9) and (10) had been the sole cause of Phase C. In the “absence” of oxygen, we also observed an absorption maximum at 700 nm which we did not observe when electron-transfer experiments (reactions (6) or (12)) were carried out (data not shown). Interestingly, Filipe et al. reported formation of a 700 nm band when exposing quercetin, a flavonoid, to Br₂˙⁻ in positively charged CTAB-micelles (Fig. 3A in ref. 23) but not in Triton X100 (Fig. 3B in ref. 2). Could partial oxidation of the CTAB by Br₂˙⁻ with the production of carbon-centred radicals be involved?

Adduct formation

It is known that radical addition to aromatic moieties is in principle a two-step process: first, a π-adduct is formed that has to change to σ-adduct before stable products may be produced by a second electron transfer:

AA˙ + PPH ⇌ [AA⋯PPH]_π˙ (π adduct) (5a)

[AA⋯PPH]_π˙ ⇌ [AA⋯PPH]_σ˙ (σ adduct) (5b)

For the case of hydroxyl radical addition to benzoic acid, Ashton and Buxton²⁴ reported a barrierless formation of the π-complex (K_eq = 3000 M⁻¹) and an activation energy of approximately 1 kJ mol⁻¹ for the strongly exothermic formation of the σ-complex. Given the high rate constant k₅ of reaction (5) with polyphenols¹² and His^10,19 the kinetics of carbon radical addition to aromatic centers may well also be barrierless, corresponding to the formation of the π-complex. With a less favourable transformation of the C-centered adduct into the σ-complex than with HO˙ adduct, the activation energy may increase. However, with HO˙ and benzoic acid, the rate constant k_−5a was about 10⁹ s⁻¹,²⁴ while the rate constant for k₋₅ with His was in the order of several times 10⁶ s⁻¹ for normal alkyl radicals and 10⁵ s⁻¹ for strong electrophiles.¹⁹ For the amino acid alkyl radicals and polyphenol additions, we estimated it to be in the order of 10⁴–10⁵ s⁻¹. It seems, therefore, that our observed reaction (5) represents adequately the overall radical–polyphenol addition reaction.

After the initial reaction of AcAla˙NH₂ with morin (Phase A, Fig. 1) the absorption maximum changed from 575 nm to 550 nm within half a millisecond. Concomitantly, there was a new absorption maximum evolving at 700 nm. A maximum absorbance at 550 nm was reported for one-electron oxidation of morin¹² and, therefore, could indicate phenoxyl radical formation. After 1 ms the absorption at 550 nm band started to bleach while the one at 700 nm was still growing, indicating that the bands stemmed from different species and different processes. That would imply at least one additional process occurring within the first millisecond at pH 7.

There was a stoichiometric consumption of the reactive species or reactive groups involved in Phase C of the reaction cascade (Fig. 2). Like the band at 550 nm, this observation may indicate involvement of a redox process, as suggested in the early literature on radical reactions with polyphenols (reviewed in ref. 25). In contrast to equilibria, oxidation processes require irreversible stoichiometric consumption of reactants. Interestingly, the drop in reactivity of the adducts implies the consumption of two equivalents of morin per radical: fresh solutions showed a rate constant of Phase C of k = 7.5 × 10³ s⁻¹, with the initial six 13 Gy pulses causing a rate constant drop of 1.1 × 10³ s⁻¹ per pulse (Fig. 2, lower panel). While a dose of 13 Gy produced 7–8 μM carbon-centered radicals, the reactivity drop implies a destruction of about 14–15 μM morin. “Strange” reactions often point to the presence of impurities in the solutions. However, the persistent and reproducible lack of the expected stochiometry for all polyphenol samples investigated does not support this hypothesis. In addition, the observation of a reaction stochiometry different than 1 : 1 for reactions of radicals and aromatic molecules is not unique. A reaction with two aromatic centres per radical is similar to earlier findings with the reaction of alcohol radicals and His, where at elevated His concentrations more than one His participated in the reaction.¹⁰ There was an obvious mechanism change if [radical] > [morin] with Phase C not observed any more (Fig. 3, upper panel, brown trace). However, for experiments with more than 2 morin molecules per radical, i.e. with a dose <50 Gy, the kinetics traces were qualitatively similar and we expect a similar mechanism, in keeping with the notion of a 1 : 2 [radical] : [morin] stochiometry. These observations, however, do not prove conclusively that a 1 : 2 stochiometry applied for Phase C. It may also be only effective at later times, i.e. at the product formation step (reaction (6)). Importantly, because of the high reactant concentrations needed for these experiments, current data do not allow extrapolation of our observations to possible similar reactions in vivo.

At a fixed concentration of 75 μM morin, the measured absorbance in Phase A was linear with the radical concentration, provided [morin] > [radical] (Fig. 3, lower panel). If, however, [radical] > [morin], [morin] was the determining concentration as visualized by the red dot at 75 μM in the plot. This again supports our previous notion that the initial reaction (Phase A) strictly followed a 1 : 1 stochiometry. Further insight into the mechanism can be gained from Fig. 4, upper panel. The reactive center involved in the formation of the adduct (Phase A) was not consumed:¹² when morin had been degraded by repeated irradiation so that Phase C was completely suppressed, the apparent rate constant of the decay in Phase B, k_{obs,Phase B}, was inversely proportional to the initial concentration of morin. This is indicative of a mechanism analogous to adducts of carbon-centered radicals with histidine:¹⁰ Phase B is governed by the recombination reaction (4) and equilibrium (5). Mathematics shows that the observed recombination rate k_{obs,Phase B} then is dependent on k₄ and K₅:

k_4,obs = k₄/ε/l (15)

ε represents the difference of molar absorptivity between reactants and products, l the optical pathlength. While reaction (4) is an elementary reaction, strictly limited for reactions of AA˙, Phase B is an overall reaction linked to “all radicals”, i.e. [AA⋯morin]˙ and AA˙ and

[[AA⋯morin]˙] = [AA˙] × K₅ × [morin] (16)

[AA˙]_tot = [AA˙] + [[AA⋯morin]˙] = [AA˙] × (1 + K₅ × [morin]) (17)

with K₅ the equilibrium constant of reaction (5), [AA˙]_tot the amount of “amino-acid related” radicals directly or indirectly involved in Phase B, and k_obs (eqn (15) and (20)) the slope derived from the linearization of a second-order kinetics trace, 1/Abs vs. t. Even though all amino-acid related radicals ([AA˙]_tot) will eventually react viareaction (4), only a part ([AA˙]) is in a reactive form (eqn (17)). Therefore, k_Phase B, the experimentally observed overall rate constant of Phase B, is smaller than k₄ and decreases with increasing morin concentration. The integration of the second order rate law for reaction (4) and the observed overall reaction, Phase B, yield:

1/[AA˙] − 1/[AA˙]_(t=0) = k₄ × t (18)

1/[AA˙]_tot − 1/[AA˙]_tot(t=0) = k_Phase B × t = (1/[AA˙] − 1/[AA˙]_(t=0))/(1 + K₅ × [morin]) (19)

k_{obs,Phase B} = k_4,obs/(1 + K₅ × [morin]) (20a)

1/k_{obs,Phase B} = (1 + K₅ × [morin])/k_4,obs = (1 + K₅ × [morin]) × ε × l/k₄ (20b)

Fig. 4, lower panel, shows that the kinetics traces of Phase B decay depended on the nature of the amino acid radical. The morin concentration, the optical pathlength l and k₄ were by design the same for all these experiments. As we do not expect the extinction coefficient to change much between adducts,¹⁰ we suspect the equilibrium constant for adduct formation, K₅, to depend on the radical. This is not surprising: earlier work with His showed the equilibrium constant to depend on the electrophilicity of the radical¹⁹ and we also expect steric factors and charge to play a role.

Some of the reproducibility problems mentioned above can be explained by results of qualitative experiments with morin at varying pH (Fig. 5): the observed response of the samples was strongly pH-dependent. The data recorded at 550 nm imply two pH-equilibria involved in the reactions, one between pH 5 and 6 and one around pH 8. All parameters seemed to be affected: kinetics, spectra and perhaps even the mechanisms. Whether the experiments were carried out with different flavonoids (Fig. 6 and 7) or different amino acid radicals (Fig. 1, 3 and 4) at around pH 7, the qualitative overall observations were the same. We take this as indication that the same types of relevant reaction mechanisms are likely to govern the chemistry at a given pH region. If true, that would imply that our data would be representative for the family of (iso-)flavonoids at physiological pH. This, in turn, would support a significant antioxidant role for the aromatic metabolome made up of the wide range of endogenous metabolites and ingested aromatic compounds.¹²

Electron transfer

While our results do not support electron-transfer as the major process in the reaction sequence following formation of the initial adduct (reaction (3)), we also cannot rule it out as minor reaction: the maximum shift from 575 nm to 550 nm at pH 7.4 in Phase C may well be indicative of an electron transfer. That would parallel our findings with carbon-centred radicals with those of earlier papers on electron transfer with other radicals. However, the absorptivity of the deaerated samples in Phase C at 550 nm was less than 30% of that observed with peroxyl or hydroxyl radicals. If electron transfer did indeed occur, the efficiency of the process would be low. When we repeatedly irradiated the same sample, with a repetition rate of approx. 1 min⁻¹, we observed that absorbance of the solutions did not change permanently. That means that all absorptions seen above 400 nm were transient and bleached fully within some 30 s. We concluded that none on these “Phases” were directly associated with product formation. In agreement with earlier assumptions¹² this is consistent with a complicated multi-step mechanism, with more than 4 reactions.

There is indication that more than one polyphenol was consumed per radical under our experimental conditions. There is, however, no convincing explanation yet on what that would mean on a mechanistic level. There may be some chain reaction involved or annulation reactions might be a reason. We carried out control experiments to detect possible influence of contaminations and failed. However, as long as there is no good hypothesis for a mechanism, we cannot completely rule out contamination as contributor to Phase C.

The mechanism of radical addition

Minisci et al. used radical clock experiments to establish the reaction mechanism.¹⁷ As with every kinetics experiment, data analysis depends on the mechanistic assumptions made. With radical clock experiments the standard assumption is of two irreversible reactions with rate constants derived as from a competition reaction by determining the reaction yields. Therefore an undetected, (almost) diffusion-controlled and reversible initial (π-)adduct formation, may skew the interpretation. If the “trapping” reaction of one of the two reactions is reversible, determination of the rate constants of elementary reactions from product yields becomes questionable. As Ashton and Buxton²⁴ pointed out, product distribution is governed by the conversion of π-adduct to σ-adduct with known directing effects. Our data suggest (vide supra), that for carbon-centered radicals even this step is largely reversible.

The terminology of “nucleophilic radical addition” for the Minisci reaction is questioned by the fast initial adduct formation, as in ref. 12, because the addition step is electrophilic: the stronger the electrophilicity of the incoming radical, the larger the equilibrium constant of the addition reaction.¹⁹ Such behavior might have been predicted from Minisci's statement “the radical must be oxidative in nature”, i.e. a good electron acceptor, which characterizes an electrophile. This statement does not question the vast amount of data on the kinetics of the addition product formation, the yields of stable products, or the product distribution, which are determined by the electron deficiency at the reaction site. It does, however, change the perception of the mechanism involved. If the equilibrium constants of the adducts increase with the electrophilicity of the incoming radical, one may assume that they would increase with the electron-excess of the aromatic structures. This seems to be the case. Why then would the Minisci reaction require electron-poor aromatic systems?¹⁸ While the reaction of a strong electrophile with an electron-rich aromatic structure is thermodynamically favorable, strong electrophiles are usually good oxidants, with electron-rich aromatic structures more easily oxidized than electron-poor ones. There is a good probability of an electron-transfer process, for example by elimination of the reduced radical (see reaction (7) or the reaction of HO˙ with phenols²⁶), competing with the formation of the desired final product of the synthesis. That may prohibit practical use for preparative purposes. If our hypothesis is true, electron-rich aromatic structures might act like buffers for radicals, moderating their reactivity. Thermodynamics dictate that such spontaneous reaction must result in lowering of the activity of the adduct-forming radicals. In biological systems, adduct formation would therefore constitute an antioxidant reaction. It would be additionally beneficial, after initially buffering of a potentially harmful damaged site, by repairing it in reaction (7) at a later stage. Secondly, more stable intermediates would slow down the possibly rate determining oxidation process, yielding the final product. In vivo, an organism would gain time for an appropriate antioxidant reaction, i.e. to reduce the radical, for example by ascorbate. In a preparative environment, recombination of radicals may outcompete the formation of stable addition products. That said, we do not pretend to be able to present a comprehensive alternative to Minisci's model of radical addition. We do disagree with the first step in his mechanism based on direct observations of initial intermediates, a technique not used in his work. That raises again the question on the nature of the rate-determining step which appeared settled. However, our disagreement leaves the practical use and implications of Minisci's work untouched.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We are grateful to Prof. D. Günther for provision of the pulse radiolysis facility. This research was supported by ETH Zürich and by Macquarie University. It did not receive any specific grant from funding agencies in the public, commercial, or non-profit sectors.

References

1. B. Halliwell and J. M. C. Gutteridge, Free Radicals in Biology and Medicine, Oxford University Press, Oxford, 3rd edn, 1999.
2. D. Del Rio, A. Rodriguez-Mateos, J. P. E. Spencer, M. Tognolini, G. Borges and A. Crozier, Dietary (Poly)phenolics in Human Health: Structures, Bioavailability, and Evidence of Protective Effects Against Chronic Diseases, Antioxid. Redox Signaling, 2012, 18(14), 1818–1892.
3. J. A. Rothwell, M. Urpi-Sarda, M. Boto-Ordoñez, R. Llorach, A. Farran-Codina, D. K. Barupal, V. Neveu, C. Manach, C. Andres-Lacueva and A. Scalbert, Systematic analysis of the polyphenol metabolome using the Phenol-Explorer database, Mol. Nutr. Food Res., 2016, 60(1), 203–211.
4. C. Manach, G. Williamson, C. Morand, A. Scalbert and C. Rémésy, Bioavailability and bioefficacy of polyphenols in humans. I. Review of 97 bioavailability studies, Am. J. Clin. Nutr., 2005, 81(1 Suppl), 230S–242S.
5. J. I. Ottaviani, R. Y. Fong, G. Borges, H. Schroeter and A. Crozier, Use of LC-MS for the quantitative analysis of (poly)phenol metabolites does not necessarily yield accurate results: Implications for assessing existing data and conducting future research, Free Radical Biol. Med., 2018, 124, 97–103.
6. P. Muller, Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994), Pure Appl. Chem., 1994, 66(5), 1077–1184.
7. S. V. Jovanovic, Y. Hara, S. Steenken and M. G. Simic, Antioxidant Potential of Gallocatechins. A Pulse Radiolysis and Laser Photolysis Study, J. Am. Chem. Soc., 1995, 117(39), 9881–9888.
8. S. V. Jovanovic, S. Steenken, M. Tosic, B. Marjanovic and M. G. Simic, Flavonoids as Antioxidants, J. Am. Chem. Soc., 1994, 116(11), 4846–4851.
9. S. V. Jovanovic, S. Steenken, Y. Hara and M. G. Simic, Reduction potentials of flavonoid and model phenoxyl radicals. Which ring in flavonoids is responsible for antioxidant activity?, J. Chem. Soc., Perkin Trans. 2, 1996,(11), 2497–2504.
10. T. Nauser and A. Carreras, Carbon-centered radicals add reversibly to histidine – implications, Chem. Commun., 2014, 50(92), 14349–14351.
11. W. Bors and M. Saran, Radical Scavenging by Flavonoid Antioxidants, Free Radical Res. Commun., 1987, 2(4–6), 289–294.
12. T. Nauser and J. M. Gebicki, Fast reaction of carbon free radicals with flavonoids and other aromatic compounds, Arch. Biochem. Biophys., 2019, 674, 108107.
13. T. Nauser and J. M. Gebicki, Antioxidants and Radical Damage in a Hydrophilic Environment – Chemical Reactions and Concepts, Essays Biochem., 2020, 61(1), 67–74.
14. L. M. Dorfman, I. A. Taub and R. E. Bühler, Pulse Radiolysis Studies. I. Transient Spectra and ReactionRate Constants in Irradiated Aqueous Solutions of Benzene, J. Chem. Phys., 1962, 36, 3051–3061.
15. F. Minisci, F. Fontana and E. Vismara, Substitutions by nucleophilic free radicals: A new general reaction of heteroaromatic bases, J. Heterocycl. Chem., 1990, 27(1), 79–96.
16. A. Citterio, F. Minisci and V. Franchi, Nucleophilic character of the alkyl radicals. 19. 1a Absolute rate constants in the homolytic alkylation of protonated heteroaromatic bases by n-butyl and tert-butyl radicals, J. Org. Chem., 1980, 45(23), 4752–4757.
17. A. Citterio, F. Minisci, O. Porta and G. Sesana, Nucleophilic character of the alkyl radicals. 16. Absolute rate constants and the reactivity-selectivity relationship in the homolytic aromatic alkylation, J. Am. Chem. Soc., 1977, 99(24), 7960–7968.
18. F. Minisci, R. Bernardi, F. Bertini, R. Galli and M. Perchinummo, Nucleophilic character of alkyl radicals: VI: A new convenient selective alkylation of heteroaromatic bases, Tetrahedron, 1971, 27(15), 3575–3579.
19. N. Santschi and T. Nauser, An Experimental Radical Electrophilicity Index, ChemPhysChem, 2017, 18(21), 2973–2976.
20. T. Nauser, G. Casi, W. H. Koppenol and C. Schöneich, Reversible Intramolecular Hydrogen Transfer between Cysteine Thiyl Radicals and Glycine and Alanine in Model Peptides: Absolute Rate Constants Derived from Pulse Radiolysis and Laser Flash Photolysis, J. Phys. Chem. B, 2008, 112(47), 15034–15044.
21. G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, Critical Review of Rate Constants for Reactions of Hydrated Electrons, Hydrogen Atoms and Hydroxyl Radicals (˙OH/˙O⁻) in Aqueous Solution, J. Phys. Chem. Ref. Data, 1988, 17(2), 531–886.
22. R. H. Schuler, L. K. Patterson and E. Janata, Yield for the Scavenging of OH Radicals in the Radiolysis of N₂O-Saturated Aqueous Solutions, J. Phys. Chem., 1980, 84, 2088–2089.
23. P. Filipe, P. Morlière, L. K. Patterson, G. L. Hug, J. C. Mazière, C. Mazière, J. P. Freitas, A. Fernandez and R. Santus, Mechanisms of flavonoid repair reactions with amino acid radicals in models of biological systems: a pulse radiolysis study in micelles and human serum albumin, Biochim. Biophys. Acta, 2002, 1572(1), 150–165.
24. L. Ashton and G. V. Buxton, Temperature Dependence of the Rate of Reaction of OH with Some Aromatic Compounds in Aqueous Solution, J. Chem. Soc., Faraday Trans., 1995, 91(11), 1631–1633.
25. C. A. Rice-Evans, N. J. Miller and G. Paganga, Structure-antioxidant activity relationships of flavonoids and phenolic acids, Free Radical Biol. Med., 1996, 20(7), 933–956.
26. S. Steenken and P. Neta, Transient Phenoxyl Radicals: Formation and Properties in Aqueous Solutions, in Phenols, ed. Z. Rappoport, Wiley, Chichester, UK, 2003.

---