Theoretical insights into the effect of size and substitution patterns of azobenzene derivatives on the DNA G-quadruplex

Abstract

Introducing photoswitches into the DNA G-quadruplex provides excellent opportunities to control folding and unfolding of these assemblies, demonstrating their potential in the development of novel nanodevices with medical and nanotechnology applications. Using a quantum mechanics/molecular mechanics (QM/MM) scheme, we carried out a series of simulations to identify the effect of the size and substitution patterns of three azobenzene derivatives (AZ1, AZ2 and AZ3) on the excitation energies of the two lowest excited states of the smallest photoswitchable G-quadruplex reported to date. We demonstrated that the size and the substitution pattern do not affect the ultrafast cis–trans photoiomerization mechanism of the azobenzene derivatives significantly, in agreement with the experiment. However, molecular dynamics simulations revealed that while AZ2 and AZ3 G-quadruplexes are structurally stable during the simulations, the AZ1 G-quadruplex undergoes larger structural changes and shows two ground state populations that differ in the azobenzene backbone adopting two different conformations. AZ1, with para–para substitution pattern, provides more flexibility to the whole G-quadruplex structure compared to AZ2 and AZ3, and can thus facilitate the photoisomerization reaction between a nonpolymorphic, stacked, tetramolecular G-quadruplex and an unstructured state after trans–cis isomerization occurring in a longer time dynamics, in agreement with the experimental findings. The QM/MM simulations of the absorption spectra indicated that the thermal fluctuation plays a more crucial role in the main absorption band of the azobenzene derivatives than the inclusion of the G-quadruplex, implying that the influence of the G-quadruplex environment is minimal. We propose that the latter is attributed to the position of the azobenzene linkers in the G-quadruplexes, i.e. the edgewise loops containing the azobenzene moieties that are located above the G-quartets, not being fully embedded inside or involved in the stacked structure. Our theoretical findings provide support to a recent study of the photoresponsive formation of photoswitchable G-quadruplex motifs.

---

1 Introduction

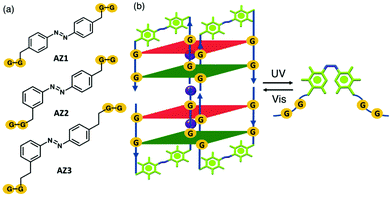
G-quadruplexes are important non-canonical DNA structures formed by stacking of G-quartets; a planar structure of four guanine bases linked by a Hoogsteen hydrogen bond network.^1–3 Such structures are stabilized in the presence of K⁺ or Na⁺ cations located between the G-quartets. G-quadruplexes have attracted considerable attention because of their potential as therapeutic targets for cancer.^4,5 For example, stabilization of the G-quadruplex within telomeric DNA and oncogene promoter regions can inhibit telomere elongation in cancer cells and oncogene transcription or translation, respectively.^6–9 Besides the biological applications, G-quadruplex structures can be utilized as interesting building blocks in nanodevices¹⁰ and optomechanical molecular motors¹¹ as their folding and unfolding can be controlled in the presence of external stimuli such as, light,¹² pH,¹³ metal cations^14,15 and small molecules.^16–18 Light is a promising external trigger which has multiple advantages including high precision, eco-friendliness, spatiotemporal control and non-invasiveness features.^19,20 The introduction of photolabile groups into G-quadruplex structures is one of the most widely used methods to regulate G-quadruplex formation.^21,22 Moreover, azobenzene derivatives have been employed in G-quadruplexes which can reversibly either fold or unfold upon light irradiation.^12,23 Heckel and co-workers developed the smallest photocontrollable DNA switch reported to date, i.e. a photoswitchable G-quadruplex in which two sets of two guanosines were connected through photoswitchable azobenzene derivatives, AZ1, AZ2, and AZ3 as part of the backbone structure (Fig. 1a).²³ This structure is a tetrameric G-quadruplex consisting of two stacked dimeric G-quadruplex units in which residues G1/G4 and G2/G5 are in syn and anti conformations along their glycosidic bonds. The size of the azobenzene derivatives, as G-quadruplex backbones, are the same for AZ1 and AZ2, but with different substitution patterns, i.e. para–para vs. para–meta, respectively. AZ3 with a para–meta substitution pattern is a double homologue of AZ2. On the basis of their findings, the antiparallel G-quadruplex can be formed for all three azobenzenes in the presence of K⁺ ions within the G-quartets when the azobenzene linkers are in a trans conformation. In addition, spectroscopic data strongly suggest that only the G-quadruplex containing AZ1 (para–para substitution pattern) linker can enable photoswitching between a nonpolymorphic, stacked, tetramolecular G-quadruplex and an unstructured state after trans–cis isomerization of the azobenzene units (Fig. 1b). A primary mechanistic question to ask is why only AZ1 shows a defined and robust structural behavior, leading to a reversible G-quadruplex photoswitch between the folded and the unfolded G-quadruplex and not the other two, i.e. para–meta substitution pattern AZ2 and its double homologue AZ3.

Fig. 1 (a) The structures of the three azobenzene units in the trans isomer, G refers to the guanosine moieties and (b) schematic representation of the photoswitchable G-quadruplex structure with azobenzene residues (AZ1) in green color. K ⁺ cations are presented as purple spheres.

Extensive theoretical studies have been performed on the photoisomerization of azobenzene and its derivatives, both in the gas phase and in solution.^24–38 In addition, photoswitching of the azobenzene within DNA/RNAs has been also reported.^39–43 However, to the best of our knowledge, the photoisomerization mechanism of the azobenzene derivatives and their spectroscopic properties within a G-quadruplex structure have not yet been explored computationally. For example, the effect of the size and substitution patterns of the azobenzene linkers (e.g. AZ1, AZ2, and AZ3 here) on the reversible photoswitching of G-quadruplex remained unclear. In this study, we applied mixed classical and quantum mechanical simulations to investigate the effect of different azobenzene derivatives on the spectroscopic properties of the photoswitchable G-quadruplexes. The results provide a basis for the interpretation of the experimental findings and describe the effect that the size and substitution patterns of the azobenzene units might have on the photoisomerization reaction, and whether or not there is a difference in their short-time dynamics that might potentially influence the G-quadruplex folding and unfolding that occurs in a longer time scale.

The paper is organized as follows: in Section 2, we describe the computational methods. Results from gas-phase calculations of azobenzene derivatives are presented in Section 3.1 whereas details of molecular dynamics (MD) simulations and QM/MM calculations are presented in Sections 3.2 and 3.3, respectively. Finally, Section 4 summarizes our concluding remarks.

2 Computational methods

The G-quadruplex structure with AZ1 (PDB code 2N9Q)²³ was used as a starting structure for constructing the model system. The Parmbsc0⁴⁴ force field was selected for G-quadruplex nucleobases. Recent studies have reported that the Parmbsc0 is a valid force field for DNA simulations,^45–47 in particular for the simulations within the ns timescale. For atoms in the azobenzene, since it is a non-standard molecule, parameters were defined using the Generalized Amber Force Field (GAFF).⁴⁸ Partial atomic charges of all azobenzene derivatives atoms were assigned with the restrained electrostatic potential (RESP)⁴⁹ at the HF/6-31G* level of theory. The GAFF parameters and charges for azobenzene derivatives are described in Tables S1–S4 (ESI†). The G-quadruplex structure was inserted into a water box extending to 10 Å buffer in each direction. To study the effect of different water models and ion parameters, three different combinations of water models and counterion parameters were used for solvation and neutralization of the negative charge of the system, respectively: group (1) Amber-adapted Åqvist⁵⁰ (AA) K⁺ with the TIP3P water model⁵¹ which has been used in many simulations, group (2) Joung and Cheatham⁵² (JC) K⁺ with SPC/E water model⁵³ and group (3) JC KCl with the SPC/E water model which have been suggested as a safe choice for G-quadruplex MD simulations.⁵⁴ The Lennard-Jones parameters for counterions and explicit water models used in the simulations are summarized in Table S5 (ESI†). The solvated structure was subjected to 2500 steps of energy minimization using the steepest descent algorithm. Then, the minimized structure was equilibrated under an NVT ensemble (300 K) for 1 ns followed by 2 ns NPT equilibration (1 atm) using a velocity rescaling thermostat^55,56 and a Parrinello–Rahman barostat^57,58 (τ_T = 0.1 ps, τ_P = 1 ps). The cut off for van der Waals and electrostatic interactions was set to 10.0 Å. The long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method⁵⁹ and the LINCS algorithm⁶⁰ was used to fix all bonds. Finally, the MD production run was performed in an NPT ensemble for 200 ns. Furthermore, the PDB code 2N9Q was adapted for G-quadruplex structures containing AZ2 and AZ3, and a similar simulation setup has been used for their MD production runs. All MD simulations were performed using the GROMACS 2018.2 package.⁶¹ Additionally, the conformational space of the G-quadruplex in the trajectory was clustered using the GROMOS algorithm.⁶² The 90 structures from each MD production run (total of 270 configurations) were selected for the subsequent QM/MM simulations. The snapshots were extracted by sampling the MD trajectories every 2.2 ns in a duration of 2–200 ns.

The QM/MM simulations were carried out using the Q-Chem electronic structure program^63,64 using structures from the MD simulations and the Parmbsc0 point charges. The interactions between QM and MM atoms were defined using the electrostatic embedding scheme⁶⁵ in which the partial charges of MM atoms were used in the QM Hamiltonian as a one-particle operator. Hydrogen link-atoms were used to cap the dangling bonds when the QM and MM regions were separated. To avoid over-polarization, the charges on MM₁ atoms are evenly distributed in the adjacent bound MM atoms such that the total charge is conserved. The QM region includes one azobenzene residue in the G-quadruplex structures. The rest of the G-quadruplex, three potassium ions, counterions and water molecules were considered in the MM region presented by fixed atomic point charges. The vertical excitation energies were calculated at the time-dependent density functional level of theory (TD-DFT)⁶⁶ using the ωB97X-D functional and the cc-pVDZ⁶⁷ basis set.

In order to identify the effect of the size and substitution pattern on the photoisomerization mechanisms of the azobenzene derivatives, quantum chemical calculations were performed for both isolated cis and trans isomers of azobenzene derivatives, along the trans–cis isomerization reaction coordinate using the spin–flip TDDFT (SF-TDDFT) method. Despite numerous studies on the photoisomerization reaction of isolated azobenzenes,^24–38 to the best of our knowledge, the photoisomerization mechanism of azobenzene with different substitution patterns, as those considered here, has not yet been explored, in particular using the SF-TDDFT method. The ground-state geometries of AZ1, AZ2 and AZ3 were optimized in the gas phase with DFT^68,69 using the ωB97X-D exchange–correlation (xc) functional⁷⁰ along with the cc-pVDZ basis set including Grimme's dispersion correction.⁷¹ The vertical excitation energies of the S₁ and S₂ excited states and the corresponding excited-state optimized geometries were calculated using spin–flip TDDFT (SF-TDDFT)/cc-pVDZ employing the ωB97X-D and B5050LYP functionals. Relaxed potential energy surface (PES) scans were performed for the ground state (S₀) at the SF-TDDFT(B5050LYP)/cc-pVDZ level of theory that is constrained geometry optimizations by fixing the CNNC dihedral angle in the azobenzene derivatives over a range of 0–180°. In addition, minimum-energy crossing points (MECPs) between S₁/S₀ and S₂/S₁ were located using the branching plane updating method⁷² at the SF-TDDFT(B5050LYP)/cc-pVDZ level of theory. An effective state-tracking algorithm, based on a maximum-overlap criterion as implemented in the Q-Chem program suite,^63,73 is used to check the spin-contamination problem in SF-TDDFT calculations. All quantum mechanical calculations have been performed using the Q-Chem electronic structure program.^63,64 Cartesian coordinates of all the relevant structures are given in the ESI.†

3 Results and discussion

3.1 Photoisomerization reactions of AZ1, AZ2 and AZ3 derivatives in the gas phase

In order to understand how the size and substitution patterns of the azobenzene unit can affect its photoisomerization reactions, we begin by analyzing the ground (S₀) and excited (S₁ and S₂) states potential energy surfaces (PESs) of the isolated azobenzene derivatives. We applied the SF-TDDFT method to explore potential energy surfaces of the AZ1, AZ2 and AZ3 along photoisomerization reactions (CNNC dihedral), by locating critical geometries of the S₀, S₁ and S₂, such as various minima, transition states, and MECPs between S₁/S₀ and S₂/S₁. The geometry parameters including CNNC dihedral (ϕ), two NNC bond angles (θ) and NN bond length are summarized in Table 1.

Table 1 Optimized geometry parameters of the S₀, S_1 min, S_2 min, and MECPs CI_S0/S1 and CI_S1/S2. ΔE (in eV) refers to the energies relative to the (S_0 min) of the trans isomer. Bond length d_N=N is given in angstroms (Å), and bond angles θ and dihedral angle ϕ are given in degrees. Note that the experimentally reported parameters^74–76 are related to the azobenzene without substitution

Molecule	Geometry	trans				cis
		ϕ	θ	d N=N	ΔE	ϕ	θ	d N=N	ΔE
AZ1	S0	179.5	114.4/114.6	1.247	0	6.8	122.6/122.6	1.241	0.74
	S1 min	133.4	126.8/126.8	1.243	2.44	133.8	126.8/126.8	1.243	2.44
	S2 min	179.7	112.8/112.9	1.305	3.73	92.9	125.8/125.8	1.248	2.94
	CIS1/S0	92.5	119.4/138.4	1.243	2.32	92.2	119.3/138.4	1.243	2.32
	CIS2/S1	179.8	114.7/114.6	1.329	3.14	45.9	117.4/117.3	1.468	4.31
AZ2	S0	179.6	114.3/114.6	1.246	0	6.7	122.6/122.6	1.241	0.72
	S1 min	135.2	126.9/127.1	1.242	2.43	134.4	127.0/126.8	1.242	2.42
	S2 min	180.0	112.7/114.3	1.323	3.61	92.9	125.3/126.6	1.247	2.92
	CIS1/S0	92.5	119.3/139.2	1.242	2.32	92.0	119.2/137.2	1.245	2.30
	CIS2/S1	180.0	114.2/114.3	1.331	3.15	53.2	118.2/115.6	1.487	4.32
AZ3	S0	179.2	114.5/114.4	1.247	0	6.3	122.4/122.5	1.241	0.72
	S1 min	136.1	127.2/127.1	1.241	2.41	135.7	127.0/127.1	1.242	2.42
	S2 min	180.0	112.7/114.3	1.322	3.62	92.9	123.6/126.6	1.247	2.92
	CIS1/S0	92.2	119.5/137.3	1.245	2.28	92.2	119.5/137.2	1.244	2.28
	CIS2/S1	179.9	114.1/114.3	1.332	3.15	52.1	115.4/118.4	1.487	4.32
Azobenzene^74–76	S0	180	113.6/113.6	1.260	—	8.0	121.9/121.9	1.253	0.6^77
		180	113.9/113.9	1.247	—

---

The ground state optimized geometries of para-substituted and meta-substituted azobenzene derivatives (AZ1, AZ2 and AZ3) are in good agreement with experimental results^74–77 as well as previous theoretical studies^78–80 reported for azobenzene without substitution. For the S₁ minimum structure, previous theoretical studies using the complete active space self-consistent field (CASSCF) methods^37,79–82 showed that the optimized CNNC dihedral angle (ϕ) is 180° for the trans isomer of the azobenzene molecule, respectively. In contrast, the previous SF-TDDFT work⁷⁸ using the BHHLYP functional showed a non-planar geometry for the trans S_1 min (ϕ = 143.8°). Our results indeed revealed a non-planar S_1 min for all three azobenzene derivatives studies here, with the corresponding CNNC dihedral, for trans isomer, of being 133.4°, 135.2° and 136.1° for AZ1, AZ2 and AZ3, respectively. Since the S₁ excited state corresponds to an n–π* transition and the triplet reference state in SF-TDDFT includes the HOMO (π) and LUMO (π*), the SF results cannot describe the S₁ state properly and show different results compared to the CASSCF methods. As is clear from Table 1, the geometry optimizations of the S₁ state starting from trans and cis isomers, are both converged to the same local minimum for AZ1 (2.44 eV energy), and to slightly different local minima for AZ2 (2.43 eV for trans and 2.42 eV for cis). In contrast, the S₂ geometry optimizations of the trans and cis isomers converged to different local minima; i.e. the trans isomers converged to a planar structure (ϕ = 180°), while the cis isomers converged to a non-planar structure with ϕ of 92.9°. The S₂ optimized geometries obtained here are in good agreement with CASSCF results.^30,83

The vertical excitation energies of the lowest two singlet states (S₁ and S₂) for azobenzene derivatives obtained by SF-TDDFT (various functionals), as well as experimental and previous theoretical results using wave function based methods are summarized in Table 2. The CASPT2//CASSCF results³⁰ show the closest agreements with the experimental results.^84,85 Comparing the performance of SF-TDDFT results with wave function-based methods, it is evident that functionals containing a larger amount of Hartree–Fock exchange, i.e. the B5050LYP functional with 50% Hartree–Fock exchange, provide a closer agreement with the computed CASPT2//CASSCF(12–14)/6-31G* values (difference of ≈0.5 for both S₁ and S₂). It should be pointed out that in general post-Hartree Fock methods are especially sensitive to the nature of the basis set and including the polarization and diffusion functions can influence the vertical excitation energies of S₁ and S₂ states. Note that for all levels of theories, the order of the states remains the same; S₁ being the dark (nπ*) state and S₂ being the bright (ππ*) state for all cis and trans isomers studied here.

Table 2 Vertical excitation energies of S₁ and S₂ states for AZ1, AZ2 and AZ3. The energies are given in eV. Note that ref. 28, 33, 72, 75 and 77 refer to the azobenzene without substitution

Molecule	Method	trans		cis
		S1	S2	S1	S2
AZ1	SF-ωB97X-D/cc-pVDZ	3.09	3.49	3.02	4.34
	SF-B5050LYP/cc-pVDZ	3.07	3.73	3.05	4.40
AZ2	SF-ωB97X-D/cc-pVDZ	3.08	3.54	3.04	4.36
	SF-B5050LYP/cc-pVDZ	3.05	3.78	3.06	4.40
AZ3	SF-ωB97X-D/cc-pVDZ	3.07	3.53	3.02	4.34
	SF-B5050LYP/cc-pVDZ	3.05	3.77	3.07	4.42
Azobenzene	5SA-CASSCF(6,6)/6-31G^86	3.08	5.80	3.77	5.99
	CASPT2//CASSCF(12–14)/6-31G*^30	2.53	4.23	2.72	4.49
	SA3-CAS(10,8)/6-31G*/6-31G^35	3.24	—	3.36	—
	MR-CISD^81	3.11	5.39	3.95	6.12
Azobenzene	Experiment (gas phase)^84,85	2.82	4.12	2.92	4.68

---

The photoisomerization dynamics are typically controlled by the energies of the minima of the various surfaces, various conical intersection seams and MECPs along these seams. Here we determined two MECPs that play a crucial role in the trans–cis photoizomerization of the azobenzene derivatives studies here, namely, CI between S₁ and S₂ (CI_S2/S1) and CI between S₁ and S₀ (CI_S1/S0).

CI_S2/S1. The trans and cis S_0 min geometries served as the starting point for the corresponding MECP optimization calculations. The optimized geometric parameters and their relative energies with respect to S_0 min of the trans isomer are listed in Table 1. Starting from the trans isomers, the optimization converged to a minimum, CI_S2/S1, with an energy of 3.15 eV, and a planar structure (ϕ = 180°) with structural parameters being very similar to those obtained for the S_2 min: the CNNC dihedral difference of ≈0.0°, NNC angle difference of 1.9°, but 0.59 eV higher in energy. The latter indicates that CI_S2/S1, for all three azobenzenes considered here, is located in the close vicinity of the S_2 min. However, starting from the cis isomers, we converge to minima, with energies being around 0.8 eV lower than that of the Franck–Condon (FC) point of the corresponding cis isomers and around 1.4 eV higher than that of the corresponding . Additionally, the structural parameters substantially differ from the corresponding 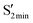; e.g., the CNNC dihedral angles for are 45.9°, 53.2° and 52.1° for AZ1, AZ2 and AZ3, respectively, while the dihedral angle of 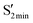is around 93° for all three derivatives.

CI_S1/S0. The trans and cis S_0 min geometries served as the starting point for the corresponding MECP optimization calculations. Interestingly, both trans and cis optimizations converged to the same S₁/S₀ crossing points with a dihedral angle of around 92° and energy of around 2.3 eV (see Table 1). Please note that CI_S1/S0 is around 0.13 eV lower than the S_1 min, but with different dihedral angles (92° vs. 135°).

To shed further light on the cis–trans photoizomerization, the PESs for the S₀, S₁ and S₂ along the CNNC dihedral angle (ϕ) for AZ1 are depicted in Fig. 2. Analogous figures for AZ2 and AZ3 can be found in Fig. S2 (ESI†). It is evident that the S₀ PES has two minima connected through the transition state with 1.8 eV (41.51 kcal mol⁻¹) energy barrier at ϕ = 90°. This large barrier excludes the thermal cis–trans isomerization as a plausible reaction and further confirms that the photoisomerization being the operative mechanism. After photo-excitation to the bright S₂ state, the trans isomer quickly relaxes to the first excited state (S₁) passing the CI_S2/S1 (at ϕ = 180°), through which internal conversion occurs. This behaviour is typical when the CI is accessible from the FC region without significant energy barriers which is the case here. From this critical point, the system undergoes vibrational relaxation towards S_1 min and from there evolves directly towards CI_S1/S0 (at ϕ = 92° with an energy of 2.32 eV for AZ1/AZ2 and 2.28 eV for AZ3), without significant energy barriers (keeping in mind the excess vibrational energy after photoexcitation), which triggers an ultra-fast internal conversion process and provides a funnel of fast access to the ground state, in which the system can evolve either to the S₀ of the cis or the trans isomer. A similar photoconversion mechanism occurs upon photoexcitation of the cis isomer of azobenzene derivatives, namely, after internal conversion through at 45.9°, 53.2° and 52.1° for AZ1, AZ2 and AZ3, respectively, the system will undergo a vibrational relaxation directly towards CI_S1/S0 (at about 92°), that act again as a doorway for an ultrafast internal conversion to the ground state, on which the system can again evolve to the S₀ of the cis or the trans isomer. The similar photodynamics observed for the AZ1, AZ2, and AZ3 derivatives indicate that the size and the substitution pattern does not affect the ultra-fast cis–trans photoiomerization mechanism of the azobenzene unit significantly. The latter is in line with the experimental observation, in which all three AZ1, AZ2, and AZ3 undergo photoisomerization and G-quadruplex formation.

Fig. 2 Schematic representation of the PESs of AZ1 photoisomerization mechanism as function of the CNNC dihedral angle. The ground state (S₀), first (S₁) and second (S₂) excited states are shown in blue, red and green. The S₀ curve is a PES scan along the dihedral angle obtained from SF-B5050LYP/cc-pVDZ. The S₁ and S₂ curves are obtained through a connection of the excited states optimized geometries and MECPs (shown in purple) calculated at the SF-B5050LYP/cc-pVDZ level of theory.

3.2 MD simulations

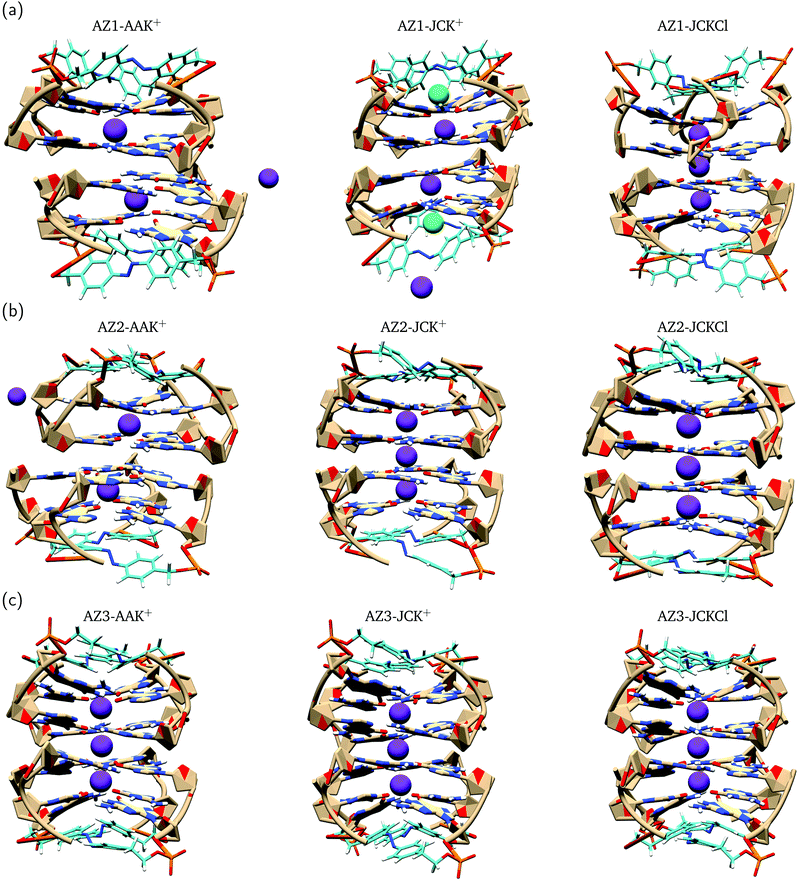
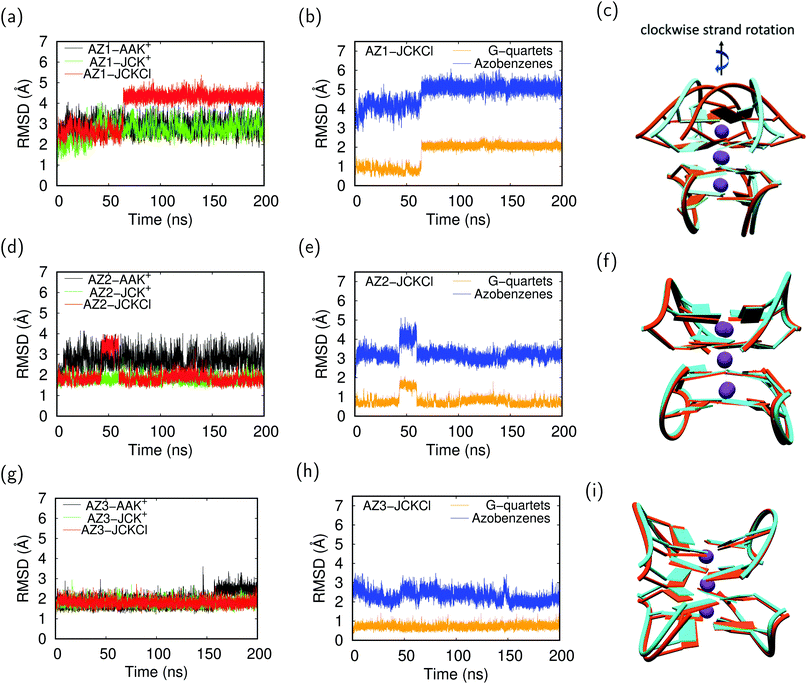
Previous MD simulations on G-quadruplex structures indicated the role of different ion parameters and water models on the simulation results.^54,87 In order to determine the optimal parameters for our system, we used three parameter combinations, i.e. AAK⁺, JCK⁺ and JCKCl as described in Section 2. Throughout the following discussion, we compare the effect of these parameters on the movement of K⁺ ions within the channel and structural stability of the G-quadruplexes during 200 ns MD production runs.

AZ1 simulations. Fig. 3a shows representative structures obtained from the clustering analysis of the three simulations that differ from one another in their ion/water parameters (see Section 2). It is clear that, for the AZ1-AAK⁺ simulation, one of the K⁺ cations escapes from the G-quadruplex channel into bulk water. Inspection of MD trajectories shows that at the beginning of the simulation, the top K⁺ moves up from the channel and stays above the upper G-quartet. Afterwards, at around 8 ns simulation, the middle K⁺ ion occupies the empty coordination site of the top K⁺ resulting in the escape of the K⁺ by passing through the upper G-quartet. The position of the middle ion remains unoccupied during the rest of the simulation time (see Fig. S3 for further details, ESI†). In the case of AZ1-JCK⁺, an ion movement is observed at 26 ns in which the bottom ion leaves its position and then the middle ion replaces it after around 2 ns, thereby facilitating the expulsion of the K⁺ from the channel at 34 ns (see Fig. S4, ESI†). In contrast to the AZ1-AAK⁺ simulation, after the exit of the ion from the channel, two K⁺ ions from the bulk (shown as green in Fig. 3a) move to align near upper and lower G-quartets until the end of simulation. Interestingly, no ion movement is observed for the AZ1-JCKCl simulation that mimics the experimental conditions (i.e. 100 mM KCl concentration).

Fig. 3 Representative structures obtained via clustering analysis for (a) AZ1, (b) AZ2 and (c) AZ3 G-quadruplexes using AAK⁺, JCK⁺ and JCKCl parameters. The internal ions in the G-quadruplex channel and external ions are represented in purple and green, respectively.

To evaluate the conformational stability of each G-quadruplex using different ion/water parameters, we analyzed the root mean square deviation (RMSD) of these systems along the MD trajectories with respect to the initial structures. In addition, we calculated the RMSDs for the G-quartets and the azobenzene backbone, separately, to understand which part of the G-quadruplex is most affected during the simulations. The RMSD graphs and their average values are presented in Fig. 4 and Table 3, respectively. The RMSD graphs for the AZ1 G-quadruplex reveals that despite the fact that the stabilizing ions are very unstable in the AZ1-AAK⁺ and AZ1-JCK⁺ simulations (see Fig. 3a), the overall system including the G-quartets and azobenzene backbones are relatively stable (Fig. 4a). In contrast, for AZ1-JCKCl simulation, an increase in RMSD is observed after around 64 ns which is mainly attributed to the clockwise rotation of two strands (Fig. 4c). As seen from Table 3, the average values for AZ1-JCKCl simulation is 3.80 Å with a standard deviation of 0.83. As is clear in Fig. 4b, the RMSDs for the azobenzene backbone are notably larger than the those for the G-quartets, which can be attributed to the fact that azobenzene residues that are part of the G-quadruplex backbones are not involved in the stacked G-quartet structures and thus can move freely. Notably, the same behaviour is observed for three independent 200 ns MD runs. Furthermore, the per-atom root mean square fluctuation (RMSF) of the all G-quadruplexes in JCKCl simulations were calculated and plotted in Fig. 5 to understand the structural fluctuation of AZ1, AZ2 and AZ3. According to the RMSF plots, AZ1 fluctuates slightly more than AZ2 and AZ3, showing that AZ1 with high RMSD and RMSF values can adopt two different conformations (see Fig. 5). It is evident that the AZ1 linker, with the para–para substitution pattern, offers a suitable balance between the rigidity and the flexibility of the overall structure that not only allows the formation of the G-quadruplex but also allows the conformational flexibility of the AZ1 backbone (Fig. 4c).

Fig. 4 RMSDs as a function of simulation time. (a, d and g) All atoms of the G-quadruplexes in different simulation groups described in the text. (b, e and h) G-quartets and azobenzenes in JCKCl simulations. Superimposed structures of (c) the representative structures of the two different ground state populations of the AZ1 and (f and i) the two random snapshots of AZ2 and AZ3, in JCKCl MD simulations.

Table 3 Average RMSDs (Å) and their standard deviation values for AZ1, AZ2 and AZ3 G-quadruplexes in JCKCl simulations

System	RMSD	Standard deviation
AZ1-JCKCl	3.80	±0.83
AZ2-JCKCl	1.94	±0.48
AZ3-JCKCl	1.80	±0.17

---

Fig. 5 The per-atom RMSFs of AZ1, AZ2 and AZ3 G-quadruplexes in JCKCl simulations.

AZ2 simulations. A similar ion mobility is observed for AZ2-AAK⁺ simulation compared to AZ1-AAK⁺ simulation; however the ion leaves the channel through the bottom G-quartet at around 6 ns of simulation (see Fig. 3b and Fig. S5 for further details, ESI†). In the AZ2-JCK⁺ simulation, all three K⁺ ions remain stable within the G-quartets throughout the simulation (Fig. 3b) which is different from AZ1-JCK⁺ (Fig. 3a). Similar to the trend observed for AZ1-JCKCl, the ions remain stable during the simulation that mimics the experimental conditions (100 mM KCl concentration). Fig. 4 displays the RMSD plots for the AZ2 G-quadruplex. It is evident that the total RMSD increases from about 2 Å for AZ2-JCK⁺ to about 3 Å for AZ2-AAK⁺ which is clearly due to the escape of the ion from the G-quadruplex channel in the AZ2-AAK⁺ simulation. The RMSD for the AZ2-JCKCl simulation indicates a jump in the period from 42 to 59 ns (see Fig. 4e), which is mainly attributed to the deviation of the two strands of the G-quadruplex with respect to the initial reference structure. However, after 60 ns, the RMSD drops and the AZ2 linker and the G-quartets remain stable for the rest of the simulation. Similar to AZ1 simulations, the RMSDs for the azobenzene backbone are notably larger than the those for G-quartets (Fig. 4e). According to the RMSF plot in Fig. 5, AZ2 shows slightly less flexibility compared to the AZ1 in JCKCl simulations.

AZ3 simulations. Under three different simulations, i.e. AZ3-AAK⁺, AZ3-JCK⁺, and AZ3-KCl simulations, the K⁺ ions stay stable within G-quartets during the course of the simulations (see Fig. 3c). Similar to AZ2, the RMSD stays stable for AZ3-JCKCl simulation that resembles that in the experimental conditions (Fig. 4g). It should be noted that the RMSDs for the azobenzene backbone in the AZ3-JCKCl simulation (Fig. 4h) are smaller that those obtained for AZ1 and AZ2 simulations (Fig. 4b–e), reflecting the smaller variations of the AZ3 backbone compared to AZ1 and AZ2. Furthermore, the RMSF plot in Fig. 5 for AZ3-JCKCl show less flexibility compared to the other two azobenzene derivatives. This means that, despite the fact that the AZ3 backbone possesses a longer side chain (double homologue of the AZ2) and is expected to have more flexibility, the AZ1 and AZ2 backbones, with shorter side chains, undergo larger fluctuations than AZ3, with AZ1 with para–para substitution being the most flexible one.

In sum, it is clear that ion movements and structural stability of the G-quadruplexes are significantly affected by the ion/water parameters. It should be mentioned that using AAK⁺ ion/water parameters shows the escape of ions from the G-quadruplex channel which is an artifact as previously reported for the typical G-quadruplex simulations.⁸⁸ Interestingly, under experimental conditions (100 mM KCl concentration) and using the JC parameters, ions remain stable for all three AZ1, AZ2 and AZ3 G-quadruplexes throughout 200 ns simulations. In addition, the simulations were stable until 500 ns and we did not observe any changes (see Fig. S7, ESI†). Our results show that while the AZ2 and AZ3 are structurally stable during the MD runs (see Fig. 4f and i), for the AZ1 G-quadruplex, we observed two ground state populations that differ by the azobenzene backbone orientations, leading to more conformational changes (see Fig. 4c). Introduction of azobenzene derivatives with the para–para substitution pattern into the G-quadruplex, i.e. AZ1, provides an appropriate balance between the rigidity and the flexibility of the overall structure. The latter can be considered as the main factor favoring photoisomerzation reaction of AZ1 compared to AZ2 and AZ3 between a nonpolymorphic, stacked, tetramolecular G-quadruplex and an unstructured state after trans–cis isomerization occurring in a longer time dynamics, in agreement with experimental findings.²³ It should be pointed out that the new version of AMBER force field for DNA (parmbsc1)⁵⁴ and ion/water parameters^52,89 in future studies might accomplish improved agreement with experiments.

3.3 QM/MM simulations

To better understand the effect of the G-quadruplex on the absorption spectra of the azobenzene derivatives, we calculated vertical excitation energies for 90 snapshots, taken from the JCKCl MD simulations, within QM/MM, framework. The average excitation energies of the first two absorption bands (S₁ and S₂) of the azobenzene derivatives in the presence and absence of the point charges of the rest of the DNA are summarized in Table 4 alongside experimental values and the corresponding values for the quantum mechanically optimized isolated azobenzene derivatives. Furthermore, natural transition orbital (NTO) analysis shows that for all the snapshots the S₁ is the dark nπ* state while the S₂, with a noticeable oscillator strength, is the bright ππ* (the state-averaged NTO involved in the transitions are shown in Fig. S6, ESI†). As one can see in Table 4, the excitation energies of the S₁ state for the single optimized structures are in perfect agreement with experimental values (difference of about 0.02 eV) and inclusion of the G-quadruplex environment along with taking the thermal fluctuation into account (average over 90 snapshots) do not significantly affect the excitation energies. The average excitation energies of the S₁ state for AZ1 with and without point charges differ by 0.02 eV with a standard deviation about 0.2 eV. In the case of AZ2 and AZ3, the inclusion of the point charge environment does not change the average excitation energies of S₁ state (2.72 eV with a standard deviation about 0.2 eV). However, the excitation energies of the S₂ state (ππ*) for the single optimized structures are smaller than the corresponding experimental values (4.24, 4.20 and 4.28 eV for AZ1, AZ2 and AZ3, respectively, vs. 4.96 eV). Interestingly, taking only the thermal fluctuation into account (QM/MM average energies using 90 snapshots), without the inclusion of the G-quadruplex environment, blue-shifts the S₂ excitation energies relative to the gas-phase value (≈0.35 eV), thus getting closer to the experimental value. Furthermore, the inclusion of the G-quadruplex environment, does not have a significant effect on the S₂ excitation energies relative to the average energies calculated using structures obtained from 90 MD snapshots (e.g. 4.71 vs. 4.70 for AZ2), implying that the influence of the environment, presented by fixed point charges, in the S₂ excitation energies is minimal. We propose that the latter can be attributed to the position of the azobenzene linkers in the G-quadruplexes (see Fig. 1), i.e. the edgewise loops containing the azobenzene moieties that are located above the G-quartets, not being fully embedded inside or being involved in the stacked structure. In sum, the average excitation energies of the S₂ state for AZ1, AZ2 and AZ3 is about 4.7 eV with standard deviation 0.3–0.4 confirming the broad distribution of the peak maxima in the absorption spectra.

Table 4 Excitation energies calculated for AZ1, AZ2 and AZ3 with and without MM charges using TDDFT(ωB97X-D)/cc-pVDZ. The energies are given in eV

QM	MM	S1	S2
a Using a single gas-phase optimized structure of AZ1, AZ2 and AZ3. b Average energies calculated using QM/MM structures obtained from 90 MD snapshots. c Ref. 23.
AZ1^a	—	2.84	4.24
AZ1^b	All	2.67 ± 0.23	4.67 ± 0.38
AZ1^b	—	2.65 ± 0.21	4.77 ± 0.26
AZ2^a	—	2.83	4.30
AZ2^b	All	2.72 ± 0.19	4.71 ± 0.40
AZ2^b	—	2.72 ± 0.19	4.70 ± 0.28
AZ3^a	—	2.82	4.28
AZ3^b	All	2.72 ± 0.19	4.74 ± 0.29
AZ3^b	—	2.72 ± 0.18	4.70 ± 0.28
Experiment^c	All	2.82	4.96

---

The experimental findings²³ show that AZ1, AZ2 and AZ3 G-quadruplexes have a similar absorption spectrum (red in Fig. 6), that exhibits two bands, the less intense band (S₁) corresponding to 2.82 eV (440 nm) and the most intense band (S₂) at 4.96 eV (250 nm). Here, the resulting excitation energies were convoluted with Gaussian of suitable full width at half maximum (FWHM) of the corresponding experimental spectrum, to account for instrumental resolution and other broadening effects that are not accounted in our MD snapshots. The calculated spectra are plotted in Fig. 6. The comparison between theory and experiment shows a very satisfactory qualitative, partly quantitative, agreement. In the computed spectra for AZ1, AZ2 and AZ3, two peaks are present, but they are red-shifted by about 0.1 eV and 0.5 eV for S₁ and S₂, respectively compared to the corresponding experimental peaks.

Fig. 6 Absorption spectra of AZ1, AZ2 and AZ3 obtained by a Gaussian convolution of the excitation energies of 90 MD simulation snapshots. The experimental spectrum is shown in red which is taken from ref. 23.

4 Conclusions

In summary, we investigated the effect of the size and substitution pattern of the azobenzene derivatives on their spectroscopic properties within the smallest G-quadruplex structure using hybrid quantum classical simulations.

We applied the SF-TDDFT method to explore the photoisomerization mechanism of the azobenzene derivatives in the gas phase. The calculations reveal that all three derivatives have similar photoisomerization reactions which occur via three consecutive steps; (i) S₀ → S₂ excitation, (ii) rapid decay from S₂ to S₁ passing the CI_S2/S1, (iii) decay to the ground state of the trans or cis isomer via CI_S1/S0. The similar photodynamics observed for the AZ1, AZ2, and AZ3 derivatives indicates that the size and the substitution pattern do not affect significantly the ultra-fast cis–trans photoiomerization mechanism of the azobenzene unit, in line with the experimental observation.

The MD simulations performed under different ion/water parameters and concentrations revealed that the structural stability of the G-quadruplex and the ion mobility in the channel are very sensitive to the these parameters. Using the combination of Åqvist parameters for the K⁺ and TIP3P water models (AAK⁺), we observed the escape of ions from the G-quadruplex channel which is not in the agreement with the reported ion residence lifetime.^90,91 With the same water model, using the JC ion parameter under 100 mM KCl concentration (JCKCl), i.e. experimental conditions, the K⁺ ions remain tightly bound in the G-quadruplex channel during the simulations. Moreover, under JCKCl conditions, AZ2 and AZ3 G-quadruplex are structurally stable during the simulations, while AZ1 shows two ground state populations that differ by the azobenzene backbone adopting two different conformations, leading to more conformational variation. In fact, introducing the azobenzene derivative with para–para substitution pattern into the G-quadruplex (i.e. AZ1) provides more flexibility to the structure compared to AZ2 and AZ3 and can thus facilitate the photoisomerization reaction between a nonpolymorphic, stacked, tetramolecular G-quadruplex and an unstructured state after trans–cis isomerization occurring in a longer time dynamics, in agreement with experimental findings.²³

The simulation of the absorption spectra of the azobenzene derivatives within the QM/MM framework showed that the thermal fluctuation plays a more significant role in the excitation energy of the S₂ than the inclusion of the G-quadruplex, implying that the influence of the environment, presented by fixed point charges, is minimal. We suggest that the latter can be attributed to the position of the azobenzene linkers in the G-quadruplexes, i.e. the edgewise loops containing the azobenzene moieties that are located above the G-quartets, not being involved in the stacked structure. Our theoretical findings provide atomistic insights into the recent experimental study of the photoresponsive formation of photoswitchable G-quadruplex motifs at the atomic level, thus providing design principles for developing azobenzene-based photocontrollable DNA G-quarduplexes relevant for novel nanodevices with medical and nanotechnology applications. It would be very important to study the photoisomerization reactions of azobenzene derivatives within G-quadruplex and work in this direction is in progress in our group.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is part of Innovational Research Incentives Scheme Vidi 2017 with project number 016.Vidi.189.044, which is (partly) financed by the Dutch Research Council (NWO).

Notes and references

1. S. Burge, G. N. Parkinson, P. Hazel, A. K. Todd and S. Neidle, Nucleic Acids Res., 2006, 34, 5402–5415.
2. S. Neidle, Curr. Opin. Struct. Biol., 2009, 19, 239–250.
3. S. Neidle and S. Balasubramanian, Quadruplex nucleic acids, Royal Society of Chemistry, 2006, vol. 7.
4. R. Hänsel-Hertsch, M. Di Antonio and S. Balasubramanian, Nat. Rev. Mol. Cell Biol., 2017, 18, 279–284.
5. S. Neidle, FEBS J., 2010, 277, 1118–1125.
6. M. L. Bochman, K. Paeschke and V. A. Zakian, Nat. Rev. Genet., 2012, 13, 770.
7. H. J. Lipps and D. Rhodes, Trends Cell Biol., 2009, 19, 414–422.
8. A. Ou, J. W. Schmidberger, K. A. Wilson, C. W. Evans, J. A. Hargreaves, M. Grigg, M. L. OMara, K. S. Iyer, C. S. Bond and N. M. Smith, Nucleic Acids Res., 2020, 48, 5766–5776.
9. K. G. Moghaddam, A. H. de Vries, S. J. Marrink and S. Faraji, Biophys. Chem., 2019, 253, 106220.
10. F. Wang, X. Liu and I. Willner, Angew. Chem., Int. Ed., 2015, 54, 1098–1129.
11. M. McCullagh, I. Franco, M. A. Ratner and G. C. Schatz, J. Am. Chem. Soc., 2011, 133, 3452–3459.
12. X. Wang, J. Huang, Y. Zhou, S. Yan, X. Weng, X. Wu, M. Deng and X. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5305–5309.
13. D. Miyoshi, S. Matsumura, W. Li and N. Sugimoto, Nucleosides, Nucleotides Nucleic Acids, 2003, 22, 203–221.
14. T. Li, S. Dong and E. Wang, J. Am. Chem. Soc., 2010, 132, 13156–13157.
15. D. M. Engelhard, J. Nowack and G. H. Clever, Angew. Chem., Int. Ed., 2017, 56, 11640–11644.
16. D. P. Gonçalves, R. Rodriguez, S. Balasubramanian and J. K. Sanders, Chem. Commun., 2006, 4685–4687.
17. D. P. Gonçalves, S. Ladame, S. Balasubramanian and J. K. Sanders, Org. Biomol. Chem., 2006, 4, 3337–3342.
18. R. Rodriguez, G. D. Pantos, D. P. Gonçalves, J. K. Sanders and S. Balasubramanian, Angew. Chem., Int. Ed., 2007, 46, 5405–5407.
19. A. S. Lubbe, W. Szymanski and B. L. Feringa, Chem. Soc. Rev., 2017, 46, 1052–1079.
20. W. Szymanski, J. M. Beierle, H. A. Kistemaker, W. A. Velema and B. L. Feringa, Chem. Rev., 2013, 113, 6114–6178.
21. S. Lena, P. Neviani, S. Masiero, S. Pieraccini and G. P. Spada, Angew. Chem., Int. Ed., 2010, 49, 3657–3660.
22. S. Ogasawara and M. Maeda, Angew. Chem., Int. Ed., 2009, 48, 6671–6674.
23. J. Thevarpadam, I. Bessi, O. Binas, D. P. Gonçalves, C. Slavov, H. R. Jonker, C. Richter, J. Wachtveitl, H. Schwalbe and A. Heckel, Angew. Chem., Int. Ed., 2016, 55, 2738–2742.
24. H. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825.
25. T. Schultz, J. Quenneville, B. Levine, A. Toniolo, T. J. Martnez, S. Lochbrunner, M. Schmitt, J. P. Shaffer, M. Z. Zgierski and A. Stolow, J. Am. Chem. Soc., 2003, 125, 8098–8099.
26. M. Böckmann, N. L. Doltsinis and D. Marx, J. Phys. Chem. A, 2010, 114, 745–754.
27. C. Ciminelli, G. Granucci and M. Persico, Chem. – Eur. J., 2004, 10, 2327–2341.
28. A. Toniolo, C. Ciminelli, M. Persico and T. Martnez, J. Chem. Phys., 2005, 123, 234308.
29. M. Böckmann, C. Peter, L. D. Site, N. L. Doltsinis, K. Kremer and D. Marx, J. Chem. Theory Comput., 2007, 3, 1789–1802.
30. I. Conti, M. Garavelli and G. Orlandi, J. Am. Chem. Soc., 2008, 130, 5216–5230.
31. T. Cusati, G. Granucci and M. Persico, J. Am. Chem. Soc., 2011, 133, 5109–5123.
32. O. Weingart, Z. Lan, A. Koslowski and W. Thiel, J. Phys. Chem. Lett., 2011, 2, 1506–1509.
33. J. A. Gamez, O. Weingart, A. Koslowski and W. Thiel, J. Chem. Theory Comput., 2012, 8, 2352–2358.
34. Y. Harabuchi, M. Ishii, A. Nakayama, T. Noro and T. Taketsugu, J. Chem. Phys., 2013, 138, 064305.
35. M. Pederzoli, J. Pittner, M. Barbatti and H. Lischka, J. Phys. Chem. A, 2011, 115, 11136–11143.
36. T. Pancur, F. Renth, F. Temps, B. Harbaum, A. Krüger, R. Herges and C. Näther, Phys. Chem. Chem. Phys., 2005, 7, 1985–1989.
37. A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234–3243.
38. P. Tavadze, G. Avendaño Franco, P. Ren, X. Wen, Y. Li and J. P. Lewis, J. Am. Chem. Soc., 2018, 140, 285–290.
39. D. Rastädter, M. Biswas and I. Burghardt, J. Phys. Chem. B, 2014, 118, 8478–8488.
40. M. Biswas and I. Burghardt, Biophys. J., 2014, 107, 932–940.
41. D. Wu, Y.-T. Wang, W.-H. Fang, G. Cui and W. Thiel, Chem. – Asian J., 2018, 13, 780–784.
42. S.-H. Xia, G. Cui, W.-H. Fang and W. Thiel, Angew. Chem., 2016, 128, 2107–2112.
43. P. Mondal, G. Granucci, D. Rastädter, M. Persico and I. Burghardt, Chem. Sci., 2018, 9, 4671–4681.
44. A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829.
45. M. P. Long, S. Alland, M. E. Martin and C. M. Isborn, Phys. Chem. Chem. Phys., 2020, 22, 5584–5596.
46. H. W. Kim, Y. M. Rhee and S. K. Shin, Phys. Chem. Chem. Phys., 2018, 20, 21068–21074.
47. A. K. Sahoo, B. Bagchi and P. K. Maiti, J. Chem. Phys., 2019, 151, 164902.
48. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
49. T. Fox and P. A. Kollman, J. Phys. Chem. B, 1998, 102, 8070–8079.
50. J. Aqvist, J. Phys. Chem., 1990, 94, 8021–8024.
51. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
52. I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041.
53. H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
54. M. Havrila, P. Stadlbauer, B. Islam, M. Otyepka and J. SÌŒponer, J. Chem. Theory Comput., 2017, 13, 3911–3926.
55. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
56. H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
57. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
58. S. Nosé and M. Klein, Mol. Phys., 1983, 50, 1055–1076.
59. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
60. B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
61. B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
62. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. Van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240.
63. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215.
64. A. I. Krylov and P. M. Gill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 317–326.
65. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
66. Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818.
67. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
68. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
69. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
70. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
71. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
72. S. Maeda, K. Ohno and K. Morokuma, J. Chem. Theory Comput., 2010, 6, 1538–1545.
73. K. D. Closser, O. Gessner and M. Head-Gordon, J. Chem. Phys., 2014, 140, 134306.
74. D. L. Beveridge and H. Jaffe, J. Am. Chem. Soc., 1966, 88, 1948–1953.
75. J. Bouwstra, A. Schouten and J. Kroon, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1121–1123.
76. T. Tsuji, H. Takashima, H. Takeuchi, T. Egawa and S. Konaka, J. Phys. Chem. A, 2001, 105, 9347–9353.
77. E. V. Brown and G. R. Granneman, J. Am. Chem. Soc., 1975, 97, 621–627.
78. L. Yue, Y. Liu and C. Zhu, Phys. Chem. Chem. Phys., 2018, 20, 24123–24139.
79. L. Yu, C. Xu and C. Zhu, Phys. Chem. Chem. Phys., 2015, 17, 17646–17660.
80. L. Yu, C. Xu, Y. Lei, C. Zhu and Z. Wen, Phys. Chem. Chem. Phys., 2014, 16, 25883–25895.
81. T. Ishikawa, T. Noro and T. Shoda, J. Chem. Phys., 2001, 115, 7503–7512.
82. P. Cattaneo and M. Persico, Phys. Chem. Chem. Phys., 1999, 1, 4739–4743.
83. J. Casellas, M. J. Bearpark and M. Reguero, ChemPhysChem, 2016, 17, 3068–3079.
84. H. Fliegl, A. Köhn, C. Hättig and R. Ahlrichs, J. Am. Chem. Soc., 2003, 125, 9821–9827.
85. J.-Å. Andersson, R. Petterson and L. Tegnér, J. Photochem., 1982, 20, 17–32.
86. C. Xu, L. Yu, F. L. Gu and C. Zhu, Phys. Chem. Chem. Phys., 2018, 20, 23885–23897.
87. M. Rebič, A. Laaksonen, J. Sponer, J. Uličný and F. Mocci, J. Phys. Chem. B, 2016, 120, 7380–7391.
88. M. RebicÌŒ, A. Laaksonen, J. Sponer, J. Uličný and F. Mocci, J. Phys. Chem. B, 2016, 120, 7380–7391.
89. S. Mamatkulov and N. Schwierz, J. Chem. Phys., 2018, 148, 074504.
90. D. Bhattacharyya, G. Mirihana Arachchilage and S. Basu, Front. Chem., 2016, 4, 38.
91. E. Largy, J.-L. Mergny and V. Gabelica, The Alkali Metal Ions: Their Role for Life, Springer, 2016, pp. 203–258.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04392c

---