Cryogenic ion trap vibrational spectroscopy of the microhydrated sulfate dianions SO₄²⁻(H₂O)₃₋₈

Abstract

Infrared photodissociation spectra of the D₂-tagged microhydrated sulfate dianions with three to eight water molecules are presented over a broad spectral range that covers the OH stretching and H₂O bending modes of the solvent molecules at higher energies, the sulfate stretching modes of the solute at intermediate energies and the intermolecular solute librational modes at the lowest energies. A low ion temperature combined with messenger-tagging ensures well-resolved vibrational spectra that allow for structure assignments based on a comparison to harmonic and anharmonic IR spectra from density functional theory (DFT) calculations. DFT ab initio molecular dynamics simulations are required to disentangle the broad and complex spectral signatures of microhydrated sulfate dianions in the OH stretching region and to identify systematic trends in the correlation of the strength and evolution of the solute–solvent and solvent–solvent interactions with cluster size. The onset for the formation of the second solvation shell is observed for n = 8.

---

1. Introduction

The sulfate dianion, SO₄²⁻, is among the best studied anions, since it plays an important role in diverse areas such as in atmospheric processes, e.g. sulfate aerosol formation and chemistry in the upper troposphere, in the regulation of metabolic and cellular processes, or in astrogeochemistry.^1–3 Due to its compact, doubly charged nature, the interaction of sulfate with water is strong and consequently it is classified as one of the most cosmotropic anions in the Hofmeister series.⁴ A fundamental understanding of its role in nature relies on a molecular-level understanding of how its intrinsic properties are influenced by solvation. Gas phase spectroscopy of mass-selected ions is particularly useful in obtaining such information, since it allows studying solvation one solvent molecule at a time. Microhydrated sulfate dianions, SO₄²⁻(H₂O)_n, represent important model systems, since they are amenable to high level electronic structure calculations.^5–9

Blades and Kebarle reported the first mass spectrometric studies on gaseous SO₄²⁻(H₂O)_n clusters.⁵ They showed that at least three water molecules are necessary to stabilize the dianion, while smaller clusters are prone to either electron autodetachment or proton transfer and formation of HSO₄⁻ and OH⁻.⁵ Wang and co-workers used anion photoelectron spectroscopy to provide an estimate of the repulsive Coulomb barrier and hydration energies for up to n = 40.^7,10–12 Williams and co-workers then studied dissociation pathways and energetics up to n = 17 by mass spectrometric means.¹³ Infrared multiple photon photodissociation (IRMPD) spectra of cryogenically-cooled SO₄²⁻(H₂O)_3–24 ions at ∼20 K measured in the mid-IR range (550 to 1800 cm⁻¹) provided a more detailed insight into the evolution of the cluster structures with size.¹⁴ Photoelectron spectra of cold anions¹⁵ as well as IRMPD spectra in the O–H stretching region¹⁶ yielded new insights, initially for n ≤ 7 and later also for clusters up to n = 80.^9,17,18 However, the structural assignments for individual cluster sizes remained controversial. For example, the structure of SO₄²⁻(H₂O)₆ was initially predicted to be of C₃ symmetry,¹⁰ then T_d symmetry¹⁴ and later, a mixture of both isomers was proposed.¹⁶ Multiple possible structures have also been discussed for n = 5.^{10,14,15,19,20} Such controversial assignments can be resolved using isomer-specific detection schemes. This was demonstrated recently using cryogenic ion trap vibrational spectroscopy (CIVS) in combination with messenger-tagging and the IR²MS² excitation scheme.²¹ This yields data with enhanced signal-to-noise ratio and resolution that can be interpreted without complications from multiple photon processes, rovibrational hot bands or population of multiple isomers. With respect to the structure of SO₄²⁻(H₂O)₆, the initial assignment to a single C₃-isomer was confirmed.²¹

Early computational studies on microhydrated sulfate dianions focused on determining minimum-energy structures and fragmentation/hydration energies of smaller clusters using either density functional theory (DFT)^10,16,22 or MP2 calculations^14,23 as well as exploring their dynamic properties using DFT ab initio molecular dynamics (AIMD) simulations.^19,24,25 Subsequent investigations focused on larger clusters,^18,26,27 the relationship between charge distribution and stability²⁸ and the performance of density functionals.²⁹ In 2011, a systematic analysis of the hyperpotential surfaces for n = 3 to 7 predicted an energetic reordering of low-lying minimum-energy structures.³⁰ These were subsequently analyzed using high-level electronic structure calculations including coupled cluster theory and estimates of basis set effects up to the complete basis set limit.³¹

Using the same techniques as in our previous CIVS study on the microhydrated sulfate hexamer, SO₄²⁻(H₂O)₆,²¹ we now extend this study to the analysis of the vibrational spectra of SO₄²⁻(H₂O)_n with n = 3 to 8. Our analysis allows for new insights into the structural evolution of microhydrated sulfate dianions with the degree of hydration and how this evolution manifests itself in the particular cluster's IR signature. We consider cold ion data over a broad spectral range in our interpretation and disentangle it using static as well as dynamic computational approaches to account for strong anharmonicities that dominate many of the observed vibrational transitions. After a careful analysis of the structures up to n = 8, we discuss the difficulties in interpreting spectra in the often neglected OH stretching region and approaches to derive more detailed information from this spectral range.

2. Methods

2.1. Experimental methods

IRPD experiments were performed using the 6 K ion trap triple mass spectrometer described previously.^32,33 In brief, microhydrated sulfate dianions are produced in a nanospray ion source from a 20 mM solution of sulfuric acid in a 1 : 1 water/acetonitrile mixture. A mass spectrum of this solution is shown in Fig. S1 of the ESI.† The beam of anions is skimmed, collimated in a gas-filled radio frequency (RF) ion guide, mass-selected using a quadrupole mass filter and focused in a RF ring-electrode ion trap, held at a temperature in-between 6 and 300 K using a closed-cycle helium cryostat. To allow for continuous ion loading and ion thermalization, the trap is continuously filled with buffer gas, either He (for bare ions) or D₂ (for messenger-tagged ions). Many collisions of the trapped ions with the buffer gas provide gentle cooling of the internal degrees of freedom close to the ambient temperature. This typically avoids the production of kinetically trapped species, although there are exceptions.³⁴ At sufficiently low ion-trap temperatures, ion-messenger complexes SO₄²⁻(H₂O)_n(D₂)_z are formed via three-body collisions.^35,36 D₂ binds to the hydrated sulfate dianions with energies below 6.5 kJ mol⁻¹. Every 100 ms, all ions are extracted from the ion trap and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted double-focussing reflectron time-of-flight (TOF) tandem photofragmentation mass spectrometer. The ion packet is accelerated into the reflectron stage, ions spread out in space according to their mass-to-charge ratio (m/z) and are refocused at the initial extraction region. Prior to reacceleration towards the MCP detector, ions with a particular m/z value are irradiated by a properly timed, widely wavelength tunable IR laser pulse (bandwidth: 2.5 cm⁻¹), supplied by an optical parametric oscillator/amplifier (LaserVision: OPO/OPA/AgGaSe₂) laser system.³⁷ An IRPD spectrum is measured by continuously scanning the laser wavelength, which is monitored online using a HighFinesse WS6-600 wavelength meter, with a scan speed such that an averaged TOF mass spectrum (over 50 laser shots) is obtained every 2 cm⁻¹. Typically, at least three scans are measured and averaged and the photodissociation cross section σ_IRPD is determined as described previously.^32,33 We measured IRPD spectra in two spectral regions, from 700 to 1800 cm⁻¹ and from 2800 to 3800 cm⁻¹.

2.2. Computational methods

Electronic structure calculations were performed using the Gaussian 16 rev. A.03 programme.³⁸ For cluster sizes n = 3 to 7 we used previous published geometries^15,27,30 as initial guesses. For SO₄²⁻(H₂O)₈ we used the AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Applications) force field with the TINKER software programme for molecular mechanics and dynamics simulation to explore the energy surface. AMOEBA model parameters for water and sulfate are taken from the publication of Lambrecht et al.³⁰ The previous and newly found geometries were used for geometry optimization with subsequent frequency analysis using the B3LYP functional³⁹ in combination with the 6-311++G(3df,3pd)^40,41 basis set. For specific structures we performed anharmonic frequency calculations using the second-order vibrational perturbation theory (VPT2) method as implemented by Bloino and Barone.⁴² The reported harmonic and anharmonic vibrational frequencies are not scaled. The influence of dispersion interactions was considered by using the D3 version of Grimme's dispersion correction with Becke–Johnson damping.⁴³ All CCSD(T) energies were taken from the literature.³¹

In AIMD simulations, the electronic energy and atomic forces are obtained within the framework of DFT, while the atomic motion is treated within Newtonian mechanics, as implemented in the CP2K package.⁴⁴ The wave functions are expanded in a double zeta Gaussian basis set, while the electron density is expanded in Gaussians and auxiliary plane waves (GPW)⁴⁵ with an energy cut-off at 350 Rydberg for the electron density. The atomic cores are modelled by the Goedecker–Teter–Hutter (GTH) type pseudopotentials.^46–48 The exchange and correlation energy is calculated using the BLYP functional^49,50 in combination with Grimme's D3 dispersion correction.⁴³ A cluster ion is put at the centre of a periodic cubic box, and the effects of the periodic charge density images are corrected by the decoupling technique developed by Martyna and Tuckerman.⁵¹ The box length is 16 to 20 Å depending on the cluster size. The convergence criterion for the SCF electronic procedure is set to be 10⁻⁷ a.u. at each time step. For molecular dynamics, the temperature is controlled by a Nose–Hoover thermostat,⁵² with a time step of 0.5 fs. An equilibration period of up to 15 ps is performed first, while a production run for data collection at 100 K lasts more than 100 ps. A vibrational spectrum can be directly simulated by the Fourier transform of the dipole time-correlation function (DTCF).⁵³

For labelling of structures we use the system proposed by Lambrecht et al.:³⁰ the label of each individual structure of SO₄²⁻(H₂O)_n is given by the n.s.w-l notation, where n refers to the number of water molecules, s to the number of sulphate-water hydrogen bonds (HBs) and w to the number of water–water HBs. Within each n.s.w category the structures are sorted according to increasing electronic energy, as determined by Lambrecht et al.,³⁰ and indicated with number l (l = 1, 2,…).

2.3. Classification schemes

Sulfate dianion hydration is governed by the presence of three coordination sites on each of the four O atoms on the tetrahedral vertices yielding a total of twelve nucleophilic coordination sites. In order to discuss the formation of the hydrogen-bond (HB) network around the sulfate dianion core two classification schemes prove helpful. First, individual water molecules within the cluster can be designated according to their role as HB acceptor (A) or donor (D).⁵⁴ In maximum coordination, a water molecule accepts two and provides two HBs and is consequently labelled as an AADD-H₂O. Note, the total number of HBs per water molecule is typically less than four in smaller clusters like those discussed here. Second, solvent moieties can be labelled according to the size of the HBed network, i.e. as W_1–4 (see Fig. 1).⁵⁵ In general, the HB network structure of a microhydrated ion is determined by a balance between solute–solvent and solvent–solvent interactions. For multiply charged ions, like the sulfate dianion, the ion–water interaction typically dominates over water–water interactions for small n, while the formation of water rings and more extended HB networks is favored for larger n.

Fig. 1 Four characteristic binding motifs found in microhydrated sulfate dianions: (a) W₁, (b) W₂, (c) W₃ and (d) W₄ + W₁ (shown semi-transparent). W₄ only appears in combination with other motifs. Note, the depicted structural motifs are not necessarily stable with respect to electron autodetachment.

The simplest motif, W₁, consists of a single DD-water molecule donating two HBs to SO₄²⁻. An ADD- and a DD-H₂O molecule linked by a single inter-water HB comprise the W₂ motif, which donates three HBs to SO₄²⁻. Within the W₃ motif, three ADD-H₂O molecules form a ring, interconnected by three equatorial inter-water HBs, and the three axial OH groups each donate a HB to SO₄²⁻. The W₄ motif contains a four-membered water ring and is typically part of a larger HB network such that each water molecule is at least threefold coordinated (e.g. four ADD-H₂O's). The W₃/W₄ motifs differ from the smaller motifs in that they contain significant inter-water interactions.

3. Results and discussion

The IRPD spectra of D₂-tagged SO₄²⁻(H₂O)_n dianions with n = 3 to 8, measured in the spectral region from 3800 down to 650 cm⁻¹, are shown in Fig. 2. Band positions and assignments are listed in Table 1. The IRPD spectrum for n = 6 has been reported previously.²¹ The observed features are grouped into seven spectral regions containing the OH stretching (A to D, 3700 to 3000 cm⁻¹), D₂ stretching (E, 2970 to 2850 cm⁻¹), water bending (F, 1770 to 1670 cm⁻¹), sulfate stretching (G, 1140 to 1020 cm⁻¹) and water wagging modes (H, <900 cm⁻¹). The OH stretching region is further divided into regions covering the free and quasi-free§ OH stretching modes (A, >3615 cm⁻¹) as well as OH stretching modes involved in very weak (B, 3615 to 3500 cm⁻¹), weak (C, 3500 to 3300 cm⁻¹) and medium strength (D, 3300 to 3000 cm⁻¹) HBs.⁵⁴

Fig. 2 (a) IRPD spectra of D₂-tagged SO₄²⁻(H₂O)_n for n = 3 to 8 covering the fingerprint (650 to 1800 cm⁻¹) and OH stretching (2800–3800 cm⁻¹) spectral regions. (b) Expanded view of the spectral region covering the antisymmetric sulfate stretching modes (1000 to 1150 cm⁻¹). The weighted mean (dotted line) and the spectral width (double arrow) are shown (see Table S1, ESI†). The spectrum for n = 6 has been reported previously.²¹

Table 1 Band positions (in cm⁻¹) and assignments of the features observed in the IRPD spectra of D₂-tagged SO₄²⁻(H₂O)_n for n = 3 to 8 shown in Fig. 2

Label	n = 3	n = 4	n = 5	n = 6	n = 7	n = 8	Assignments
A						3640	OH stretch
							(W3) O–H⋯O (AADD)
B			3562	3559	3556	3546	OH stretch
			3534	3528	3525	3514	(W3) O–H⋯O (ADD)
						3456	(W4) O–H⋯O (ADD)
C	3274	3344	3399	3455	3466	3476	OH stretch
	3220	3327	3374				(W1) O–H⋯O (SO4)
	3200
D			3086	3174	3221	3240	OH stretch
						3119	(W3) O–H⋯O (SO4)
							(W4) O–H⋯O (SO4)
E	2881	2907	2930	2944	2943	2946	D2 stretch
			2921	2928
F	1741	1714	1710	1710	1718	1697	water bend
				1694	1696
G	1105	1076	1106	1090	1117	1124	antisymmetric sulfate stretch
	1076		1079		1092	1094
	1049		1063		1066	1065
H			806	771	758	770	water wag

---

3.1. Qualitative analysis of the spectra

3.1.1. OH stretch region. Based on the general appearance of the IRPD spectra in the OH stretching region three size ranges, namely n < 5, n = 5–7 and n > 7, are identified. All spectra (n = 3 to 8) exhibit bands in region C, attributed to OH oscillators involved in weak HBs. These are characteristic for the presence of isolated DD-H₂O molecules as part of the W₁ motif.²¹ Bands in region B and D, characteristic of OH stretching modes involved in very weak water–water and medium strength anion–water HBs, hinting at the appearance of ADD-H₂O molecules as part of a three-membered water rings (W₃ motif), are only observed for n ≥ 5.²¹ In this size range the bands in region B are rather narrow and remain at the same position with increasing cluster size. In contrast, the bands in region D are broader and reveal a marked size-dependence: they shift to higher wavenumber with increasing n. This is expected, since an increasing number of water molecules compete for the attractive interaction with the dianionic core. A quasi-free OH stretching band is only observed in the n = 8 spectrum, which also reveals a new feature below 3200 cm⁻¹ in region D, suggesting the appearance of a water binding motif not present in the smaller clusters. We will show further below that this is the W₄ motif in n = 8.

3.1.2. D₂ stretch region. A narrow peak in region E is observed in all the IRPD spectra and assigned to the D₂ stretching vibration of the tag. The IR-forbidden transition in isolated D₂ (at 2994 cm⁻¹)⁵⁶ gains in intensity in a polar environment. The effect is largest for n = 3 and decreases with increasing n, as the charge density on the sulfate core is more and more delocalized over an extended water network, in return reducing the polarization of the D₂ molecule.

3.1.3. Water bend region. The excitation of water bending vibrations is observed in region F. These features shift to lower wavenumbers with increasing microhydration, from 1741 (n = 3) to 1697 cm⁻¹ (n = 8), but remain considerably above the water bending band of pure water (1595 cm⁻¹).⁵⁷ For n > 4 analysis of the band profile suggests (at least) two bands contribute to this feature, confirming the presence of a more heterogeneous water network in the larger clusters starting at n = 5.

3.1.4. Sulfate stretch region. Spectral region G contains the antisymmetric sulfate stretching modes and is very sensitive to the distribution of water molecules around the dianion.¹⁴ Bare SO₄²⁻ has T_d symmetry, with its four sulfate stretching modes divided into two representations: a totally symmetric, IR-forbidden mode ν_S; and the IR-active, triply degenerate antisymmetric stretching mode ν_AS, resulting in a single, intense IR feature. Upon solvation of SO₄²⁻ by water molecules, the threefold degeneracy of ν_AS can be lifted, depending on the symmetry of the solvation shell, and up to three peaks, corresponding to the three components of ν_AS, are observed, while the IR intensity for exciting ν_S remains very small.¹⁴

In qualitative agreement with the previous IRMPD measurements,¹⁴ but with substantially better resolution and signal-to-noise ratio, we observe a single dominant narrow peak for n = 4, a slightly broader one for n = 6, while three features are found for the n = 3, 5, 7 and 8, suggesting that the latter ones exhibit a less symmetric solvation environment. The extent of the splitting is found to be largest in n = 8 and n = 3 (≥72 cm⁻¹). In an attempt to quantify the influence of microhydration on the ν_AS band, we determined the mean, intensity-weighted band position x̄_S as well as the bandwidth Δx_S, the latter corresponding to the width covering 90% of the IR intensity (see Table S1 in the ESI†).

3.1.5. Water libration region. Water wagging modes are excited in the spectral region below 900 cm⁻¹ (region H in Fig. 2). They are observed for all cluster sizes, but gain in intensity for n ≥ 5. A clear trend in band position is not observed. The measured bands are considerably sharper than in the previously published IRMPD spectra. It is known that in bulk solutions these libration modes of solvent water molecules are related to long range collective motions and are sensitive to the fluctuation in the HB network.^58–60 In hydrated bicarbonate clusters, the wagging features were found to be more prominent for n ≥ 6, when there were significant inter-water HB connections.⁶¹ Hence, the present IRPD spectra confirm the presence of such inter-water HBs, presumably as part of ADD binding motifs,²¹ for hydrated sulfate clusters with n ≥ 5.

A comparison of the present IRPD spectra of D₂-tagged SO₄²⁻(H₂O)_n to IRMPD spectra of bare SO₄²⁻(H₂O)_n dianions¹⁴ measured in the mid-IR spectral region for n = 3 to 8 is found in the ESI† in Fig. S2. Overall, qualitative agreement is found between the two types of spectra, in particular with respect to the band positions, confirming that ions with the same structural motifs are probed. Moreover, the messenger-tag effect on band position and the energetic ordering of the isomers is small and probably negligible. The present spectra are characterized by a better spectral resolution, colder ions and hence narrower bands (see e.g. the spectra for n = 3, 6 and 8). The relative intensities agree, in general, but on closer inspection, e.g., the antisymmetric sulfate stretching bands for n = 5 and n = 8 reveal some differences, probably related to differences in the respective ion internal temperature. Note, weaker bands appear clearer in the present IRPD spectra.

Summarizing, the analysis of the experimental IRPD spectrum of microhydrated sulfate dianions suggests that the n = 4 dianion contains the most symmetric solvation shell followed by n = 6, while the structures of the n = 3 and n = 8 dianions are the least symmetric. Isolated water molecules (W₁ motif) are present in all the anions studied and this is the only type of water molecule for n = 3 and n = 4. For larger n, ADD motifs are also present and evidence for the appearance of a new motif is found for n = 8.

3.2. Assignment of IRPD spectra

3.2.1. IRPD spectra assignment protocol. The assignment of the IRPD spectra of microhydrated sulfate dianions based exclusively on a comparison to simulated harmonic IR spectra is complicated by the presence of pronounced anharmonic and entropic effects in these systems, as we recently demonstrated for SO₄²⁻(H₂O)₆.²¹ However, it is computationally demanding to compute anharmonic spectra for all these systems and, indeed, the harmonic spectra do contain useful information in specific spectral regions. It therefore proves helpful to start by defining a general four-step protocol for the assignment of the IRPD spectra, testing it on the smaller systems (n < 6) and then applying it to the interpretation of the spectra of larger clusters.

First, we order the lowest energy isomers using the highest quality electronic energies available from the literature and corrected them with ZPEs calculated with B3LYP+GD3BJ/6-311++G(3df,3pd), including dispersion forces.⁴³ For n = 3 to 6 these are the electronic CCSD(T)/CBS energies (CBS: interpolation to the complete basis set limit) from ref. 31. We find that the lowest energy isomer for n = 3 to 6 coincides with the one identified in the IRPD spectra in contrast to previous reports. For the larger systems (n > 6) we have to revert to ZPE-corrected B3LYP+GD3BJ/6-311++G(3df,3pd) energies, which are less accurate and therefore do not necessarily yield the correct energy ordering. We therefore try to consider all isomers that lie within 10 kJ mol⁻¹ of the lowest energy isomer for n > 6.

Second, we compare the IRPD spectrum of the corresponding D₂-tagged anion to harmonic IR spectra, derived from B3LYP frequencies and intensities, of low-energy isomers of the corresponding untagged anion. Messenger-tag effects are neglected here based on the comparison of the IRPD spectra of the D₂-tagged and the IRMPD spectra of the bare dianions (see above). Indeed, our calculations confirm that tagging has little influence on the sulfate modes, but the shape of the OH stretching bands can be influenced significantly (see Fig. S4, ESI†). We find that only the sulfate stretching (1150 to 1000 cm⁻¹) and, to a much lesser extent, the water bending (1750 to 1650 cm⁻¹) regions are sufficiently diagnostic to exclude a particular isomer from the group of potential candidates based on the comparison to the harmonic spectra.

Third, we compare the IRPD spectrum to B3LYP/VPT2 anharmonic spectra of potential candidates. In favorable cases the general agreement is improved over the comparison to harmonic spectra and allows for the assignment of the remaining features, in particular in the mid-IR region of the spectrum, including overtone and combination bands. Finally, to confirm the structure assignment and to better characterize the spectroscopic signatures of hydrogen bonding in the OH stretching region, AIMD simulations are performed. Note, these simulations typically do not yield a “perfect” agreement, but do allow for important insights into the factors governing the underlying mechanism responsible for the broadening of the bands in question. In those cases where the more elaborate calculations required for the last two steps are not available, performing the first two steps typically already allows for a tentative assignment.

3.2.2. SO₄²⁻(H₂O)₄. We start with the n = 4 system, for which the harmonic as well as both type of anharmonic calculations, the (static) VPT2 and the (dynamic) AIMD approaches, yield consistent results. The structures, relative energies and harmonic IR spectra of five low-energy isomers are compared to the experimental IRPD spectrum in Fig. 3. The VPT2 IR and DTCF spectra of the lowest energy isomer are also shown.

Fig. 3 Comparison of the experimental and computed vibrational spectra of SO₄²⁻(H₂O)₄: (a–e) harmonic B3LYP/6-311++G(3df,3pd) IR spectra of five low energy isomers of bare SO₄²⁻(H₂O)₄, (f) B3LYP/VPT2 IR spectrum of 4.8.0-1, (g) DTCF spectrum of 4.8.0-1 and (h) the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₄. Minimum-energy structures, molecular symmetry groups and ZPE-corrected relative CCSD(T) electronic energies (in kJ mol⁻¹) are also shown.

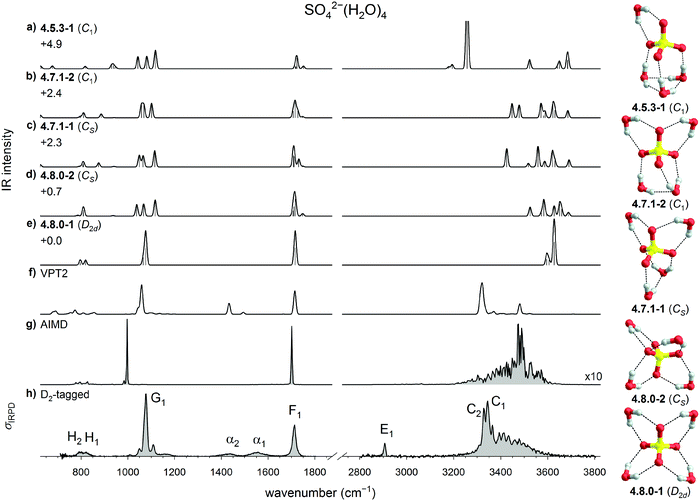
The lowest energy isomer is the highly symmetric D_2d structure 4.8.0-1, which adopts a 4W₁ motif. A second, less symmetric 4W₁ structure (4.8.0-2, C_s) is found less than 1 kJ mol⁻¹ higher in energy. These are followed by the two W₂ + 2W₁ structures 4.7.1-1 (+2.3 kJ mol⁻¹, C_s) and 4.7.1-2 (+2.4 kJ mol⁻¹, C₁), which are the lowest energy structures containing an inter-water HB. The first W₃ + W₁ structure (4.5.3-1, C₁) is predicted at +4.9 kJ mol⁻¹.

The comparison with the harmonic spectra in the sulfate stretching region (see Fig. 3a–e) allows no doubt that the predominant structure observed in the present experiments is the highly symmetric 4.8.0-1 structure, whose IR spectrum is the only one that recovers the single, narrow feature G₁. The two weak absorption features close to G₁ at 1051 and 1108 cm⁻¹, which were also observed in the previous IRMPD study, are attributed to the presence of one or more less abundant, lower symmetry isomers. It is remarkable that in the previous theoretical analysis³¹ three isomers with slightly lower energy (4.7.1-1, 4.8.0-2, and 4.7.1-2) were predicted, each associated with a characteristic triplet of peaks in this spectral region (see Fig. 3b–d), which can account for these two weaker features, but these are limited to contributing less than 20% to the overall IR signal, based on the predicted harmonic IR intensities. Bands F₁, H₁ and H₂ are in reasonable agreement with the water bending and two water wagging modes, respectively, of 4.8.0-1, confirming our assignment. Note, none of the harmonic spectra come even close to reproducing the IR signature in the 3000 to 4000 cm⁻¹ region, demonstrating that harmonic OH stretching frequencies and intensities are, at first glance, not diagnostic and anharmonic effects need to be considered here.

The anharmonic VPT2 spectrum of 4.8.0-1 is shown in Fig. 3f. It represents a significant improvement over the harmonic spectrum in several regards. First, the OH stretching modes are red-shifted, such that the corresponding bands with the highest intensity now nearly coincide. Second the intensity ratio of bands G₁/F₁ increases, closer to the experimentally observed intensity ratio. Third, the experimental features α₁ and α₂ are qualitatively reproduced, suggesting that these can be attributed to combination bands of water wagging modes. Additional combination bands are also predicted in the spectral region below 900 cm⁻¹.

The largest remaining discrepancy between the IRPD spectrum and the VPT2 spectrum of 4.8.0-1 is related to the width of the hydrogen-bonded OH stretching feature, which extends from 3200 to 3600 cm⁻¹. This is qualitatively recovered when considering dynamic effects as part of an AIMD simulation. Unfortunately, the stability of the 4W₁ motif is underestimated by AIMD, i.e., when the simulation temperature is raised above 30 K, 4.8.0-1 becomes unstable and isomerizes into W₂ + 2W₁ structures. However, a DTCF spectrum for 4.8.0-1 can still be obtained by running AIMD at 30 K and this spectrum is shown in Fig. 3g. The width of this feature is indeed reproduced, confirming a pronounced stretch/rock coupling of the DD water molecules, which we discuss in more detail further below. The exact intensity profile, however, is not obtained, suggesting that (i) nuclear quantum effects^21,62 and (ii) better functionals, which reproduce the potential surface more accurately, may be required to obtain quantitative agreement.

3.2.3. SO₄²⁻(H₂O)₃. The structures and relative energies of the five lowest energy structures are shown and their harmonic IR spectra are compared to the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₃ in Fig. 4. The energetic ordering of the isomers is identical to that previously reported.³¹ The C₂-structure 3.6.0-1 represents the global ground state. The three isomers lowest in energy all are 3W₁ structures. These are followed by the two W₂ + W₁ structures 3.5.1-2 (+5.1 kJ mol⁻¹, C₁) and 3.5.1-1 (+5.2 kJ mol⁻¹, C_s) and the W₃ structure 3.3.3-1 (+5.1 kJ mol⁻¹, C₃). The barrier between the two lowest energy isomers is 9 kJ mol⁻¹.

Fig. 4 Comparison of experimental and computed vibrational spectra of SO₄²⁻(H₂O)₃: (a–f) harmonic B3LYP/6-311++G(3df,3pd) IR spectra of six low energy isomers of bare SO₄²⁻(H₂O)₃, (g) B3LYP/VPT2 IR spectrum of 3.6.0-1 and (h) the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₃. Minimum-energy structures, molecular symmetry groups and ZPE-corrected relative CCSD(T) electronic energies (in kJ mol⁻¹) are also shown.

The IRPD spectrum exhibits an evenly spaced triplet of peaks in the sulfate stretching region, characteristic of a low symmetry structure. This pattern is in agreement with the harmonic spectrum of 3.6.0-1, and disagrees with the spectra of the higher symmetric 3W₁ and W₃ isomers 3.6.0-2, 3.6.0-3, and 3.3.3-1. It also agrees less well with the W₂ + W₁ isomers 3.5.1-2 and 3.5.1-1. The remaining IRPD features in the mid-IR region can be assigned, once static anharmonic effects are considered. The VPT2 IR spectrum of 3.6.0-1 not only reproduces the form and relative intensity of the water bending band at 1741 cm⁻¹, but also identifies bands α₁ and α₂ as combination bands and overtones for the three water wagging modes and the minor feature at 1026 cm⁻¹ as a combination of the SO₄ bend (∼600 cm⁻¹) and water rocking modes (∼400 cm⁻¹). Remarkably, this VPT2 spectrum also qualitatively reproduces the position of the broad feature in OH stretching region (3170 to 3600 cm⁻¹), suggesting a tentative assignment of features C₁ (3405 cm⁻¹) to symmetric and C₃ (3220 cm⁻¹) to antisymmetric OH stretching modes, while C₂ (3280 cm⁻¹) is associated with combination bands of the antisymmetric OH stretching modes with low frequency intermolecular sulfate–water stretches. Interestingly, also for n = 3 the all-W₁ structure (3.6.0-1) is found to be quite fragile with respect to isomerization in the AIMD simulations; It transforms into the W₃ structure 3.3.3-1 at temperatures higher than 20 K and the corresponding DTCF spectrum is therefore not shown in Fig. 4.

3.2.4. SO₄²⁻(H₂O)₅. The five lowest energy n = 5 structures and their relative energies are shown in Fig. 5. A large variety of qualitatively different structural isomers is observed. Isomers exhibiting the three different motifs W₃ + 2W₁ (5.7.3-1), W₂ + 3W₁ (5.9.1-1) and 5W₁ (5.10.0-1) are predicted within less than 1 kJ mol⁻¹ of each other. Moreover, 2W₂ + W₁ (5.7.3-2) and W₃ + W₂ (5.6.4-5) structures are calculated within 7 kJ mol⁻¹. Structure 5.7.3-1 (C₁) represents the global ground state and lies 0.8 kJ mol⁻¹ below 5.9.1-1 (C_s).

Fig. 5 Comparison of experimental and computed vibrational spectra of SO₄²⁻(H₂O)₅: (a–e) harmonic B3LYP/6-311++G(3df,3pd) IR spectra of five low energy isomers of bare SO₄²⁻(H₂O)₅, (f) B3LYP/VPT2 IR spectrum of 5.7.3-1, (g) DTCF spectrum of 5.7.3-1 and (h) the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₅. Minimum-energy structures, molecular symmetry groups and ZPE-corrected relative CCSD(T) electronic energies (in kJ mol⁻¹) are also shown.

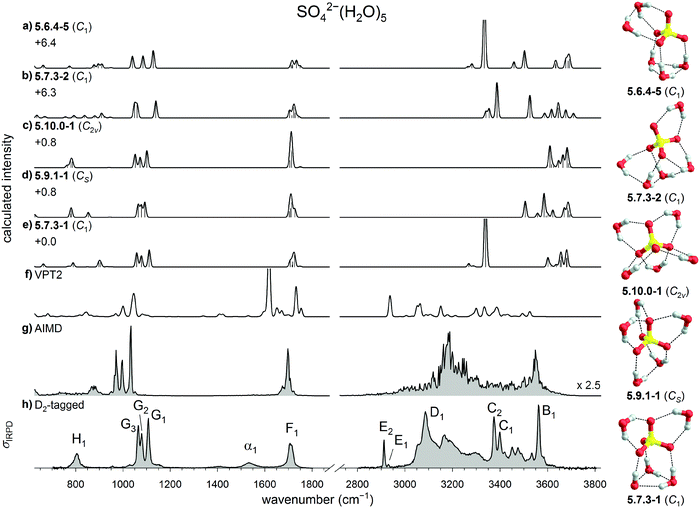
The harmonic IR spectra of the five lowest energy n = 5 structures are compared to the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₅ in Fig. 5. Due to the overall low symmetry of the n = 5 isomers the assignment is not as straight forward as for the other n ≤ 6 systems. Inspection of the sulfate antisymmetric stretch triplet suggests an assignment to either the 5.7.3-1 (Fig. 5e) or 5.10.0-1 isomer (Fig. 5c), which both reproduce the relative peak spacings and intensities satisfactorily. Both of these harmonic spectra also recover the width of the water bend band F₁, whereas the relative intensity (with respect to bands G_1–3) is better reproduced by the 5.7.3-1 spectrum. However, this spectrum predicts two low-intensity wagging bands, one from the ADD-water (W₃ motif) and the other from the DD-water (W₁ motif), at 903 cm⁻¹ and 790 cm⁻¹, respectively. The latter is nearly absent from the present IRPD spectrum. Indeed, the absence of this band in the previously published IRMPD spectrum had resulted in exclusion of this isomer in the previous study.¹⁴ More recently, however, we showed that dynamic effects, which are present in all of the systems, lead to a substantial broadening of the DD-water wagging bands, while the ADD water wags are less affected and therefore more easily identified.²¹ The number of observed water wagging bands does therefore not allow for a conclusive assignment and additional information is required.

As we noted already in Section 3.1.1, the IRPD spectrum shows a characteristically broad OH stretch absorption features extending down to 3000 cm⁻¹. This feature cannot be rationalized by an all-W₁ motif, like 5.10.0-1, but rather requires the presence of stronger inter-water HBs, like in 5.7.3-1. To find additional evidence we turn to the anharmonic calculations. The VPT2 results (see Fig. 5f) are not conclusive. While they do predict broad IR activity in the OH stretching region, i.e. down to 2900 cm⁻¹, the agreement in the fingerprint region that is present at the harmonic level is surprisingly lost. The results of the AIMD simulations, on the other hand, do lend additional support to the 5.7.3-1 assignment. The corresponding DTCF spectrum indeed qualitatively recovers most of the features of the IRPD spectrum across the complete spectral range. Moreover, it is characterized by a sharp feature at ∼3550 cm⁻¹ and strong IR activity around 3200 cm⁻¹ and below. These features are characteristic signatures of the W₃ motif and correspond to excitation of equatorial (B₁) and axial (D₁) OH-stretches in the IRPD spectrum. Compared to the IR signature of W₃ in the n = 6 spectrum, D₁ shifts to the red by ∼90 cm⁻¹ and is broader, in line with the expectation that the W₃–SO₄²⁻ interaction is stronger in n = 5 than in n = 6.²¹ More extensive inter-water HB interactions in n = 5 also lead to the increase in intensity of the water wagging band (H). However, also this spectrum does not show quantitative agreement. For instance, the experimental bands C₁ and C₂ are not satisfactorily reproduced by this AIMD simulation. That, in particular, these bands show a marked temperature-dependence is known from our previous study²¹ on n = 6 and confirmed by the temperature-dependent IRMPD spectra of SO₄²⁻(H₂O)₅ measured from 6 to 150 K (see Fig. S3, ESI†). The marked broadening with increasing temperature is attributed to efficient excitation of large amplitude motion of the two W₁ motifs. Isomer-selective measurements (Fig. S5, ESI†), similar to those previously discussed for n = 6,²¹ demonstrate that indeed only a single isomer is probed. Note, these double resonance measurements are sensitive to laser-induced population changes that are maintained longer than the delay between the two IR laser pulses (∼10⁻⁵ s). The IR spectra of more quickly interconverting isomers cannot be isolated using this technique.

3.2.5. SO₄²⁻(H₂O)₆. Results for the n = 6 complex have been presented and analyzed previously.²¹ The structures of all cluster sizes will be compared later in the paper.

3.2.6. SO₄²⁻(H₂O)₇. As highly accurate electronic energies are only available up to n = 6,³¹ we re-optimized 39 possible isomers of SO₄²⁻(H₂O)₇ reported in ref. 30 using the B3LYP+GD3BJ/6-311++G(3df,3pd) method. The six lowest energy structures and their relative B3LYP energies are shown in Fig. 6. Comparison of B3LYP energies with the highly accurate theoretical results available for smaller clusters showed deviation of ±3 kJ mol⁻¹ in relative energies and we therefore we do not expect these energies to predict the energetic order reliably. The lowest energy isomer predicted is 7.6.7-1, in which all water molecules are part of a single HBed network. Minimally higher in energy are two 2W₃ + W₁ and a W₄ + W₃ isomers.

Fig. 6 Comparison of experimental and computed vibrational spectra of SO₄²⁻(H₂O)₇: (a–f) harmonic B3LYP/6-311++G(3df,3pd) IR spectra of six low energy isomers of bare SO₄²⁻(H₂O)₇ and (g) the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₇. Minimum-energy structures, molecular symmetry groups and ZPE-corrected relative B3LYP electronic energies (in kJ mol⁻¹) are also shown.

Fig. 6 compares the experimental IRPD spectra for n = 7 to the harmonic IR spectra of these energetically low-lying isomers. Inspection of the sulfate stretch region allows to eliminate 7.6.7-1 and 7.7.7-1 from the list of possible candidates. Best agreement is found for 7.8.6-1 and 7.8.6-2. Both have nearly identical IR spectra and only differ in the orientation of the two W₃ motifs relative to each other. The higher energy isomer 7.8.6-12, which shows comparably good agreement in the sulfate stretch region, does not contain an undistorted W₃ motif, but a quasi-free OH moiety, for which no evidence is found in the experimental spectrum. Such a quasi-free OH oscillator was observed for n = 8 and is discussed in the following section. The presence of feature D in the OH stretching region, just like for the IRPD spectra of n = 5 and n = 6, lends further support for the presence of W₃ motifs and thus an assignment to either 7.8.6-1 or 7.8.6-2. Compared to the IRPD spectrum of n = 6, peak B is shifted to the red by only 3 cm⁻¹, indicating that the equatorial and inter-water HBs in W₃ remain about the same. Peak D, on the other hand is shifted to the blue by 47 cm⁻¹, indicating further weakening of the axial HB solvating SO₄²⁻. Unlike the spectrum for n = 5, there is no strong peak around 3400 cm⁻¹, and probably no contribution from W₂. Peaks C₁ and C₂ are likely due to the W₁-motif.

3.2.7. SO₄²⁻(H₂O)₈. Since there is no pool of potential structures available for SO₄²⁻(H₂O)₈, we performed MD simulations to generate structural candidates, of which 24 structures were then calculated more precisely. The six lowest energy isomers are shown in Fig. 7, the five lowest of them lie within 3 kJ mol⁻¹. All of these structures contain eight inter-water HBs. 8.9.7-x and 8.7.9-x structures are more than 5.0 kJ mol⁻¹ higher in energy compared to the lowest energy isomer. The two lowest energy isomers share a common motif, not observed for the structures assigned to the spectra of all smaller (n < 8) systems. The motif consists of a quasi-planar W₄ ring as part of cube spawned by eight O-atoms, three from the sulfate dianion and the rest from five water molecules. The individual structures differ in the arrangement of the remaining water molecules, which can assemble in the form of additional W₁, W₃, and W₄ units.

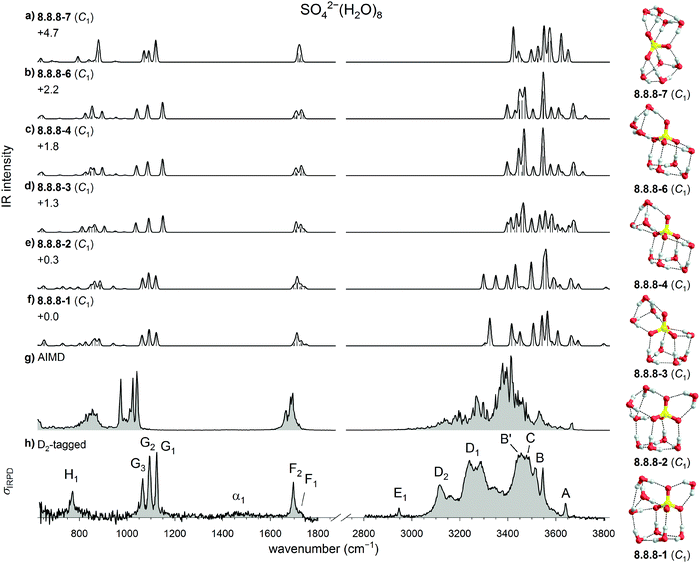Fig. 7 Comparison of experimental and computed vibrational spectra of SO₄²⁻(H₂O)₈: (a–f) harmonic B3LYP/6-311++G(3df,3pd) IR spectra of six low energy isomers of bare SO₄²⁻(H₂O)₈ (g) DTCF spectrum of 8.8.8-1 and (h) the IRPD spectrum of D₂-tagged SO₄²⁻(H₂O)₈. Minimum-energy structures, molecular symmetry groups and ZPE-corrected relative B3LYP electronic energies (in kJ mol⁻¹) are also shown. The labels in the OH stretch region are based on the trends shown in Fig. 1.

Inspection of the sulfate stretching region for n = 8 (see Fig. 7) reveals that the IR spectra of the two lowest energy structures 8.8.8-1 and 8.8.8-2 yield much better agreement with the experimental IRPD spectrum than the those of the next three isomers (see Table S7, ESI†). As already noted in Section 3.1.1, the monotonic blue-shift of band D in the n = 5 to n = 7 spectra does not continue for n = 8. This features actually splits into two components, D₁ and D₂, of which the first falls in line with the previously described blue-shift and the other appears at the same position as for n = 5. This must be due to the W₄ motif of the 8.8.8 isomers. Note, there is now one water molecule that is not directly HBed to SO₄²⁻. In this sense, n = 8 represents the onset for the formation of the second solvation shell, with some HBs strengthened, as indicated by the blue-shift of band D₂. Other HBs are weakened, as indicated by the first appearance of a band as high as 3640 cm⁻¹ (A₁) and attributed to excitation of a quasi-free OH stretch oscillator involved in an unusually long (2.5 Å) equatorial W₃-HB. Bands B₁ (3546 cm⁻¹) and D₁ (3240 cm⁻¹) are also attributed to this W₃ motif.

Further support for this assignment comes from the AIMD simulation involving the 8.8.8-1. The corresponding DTCF spectrum is shown in Fig. 7 and nicely reproduces the above mentioned five features in the OH-stretch region. Moreover, these simulations show that this structure is stable up to 200 K, after which the W₁ moiety forms a new HB to another water molecule, while the other motifs remain stable.

3.3. Microhydration trends

The present results show that caution is required in using individual harmonic IR spectra in the OH stretching region for a structure assignment. However, they remain helpful in identifying qualitative trends when they are viewed as part of a series of spectra, as shown in Fig. 8. The spectral evolution with cluster size of band D, which is associated with the W₃ motif, is highlighted by the gray-shaded bar. The observed experimental pattern is indeed consistent with the trend predicted in the harmonic spectra, i.e. the evolution of W₁-only structures (n = 3, 4) over isolated W₃-structures (n = 5–7) to structures with more extended hydrogen-bonded networks (n ≥ 8):
The W₃ motif appears first for n = 5. Additional water molecules weaken the interaction with the three-membered water ring and therefore strengthen the OH bonds oriented towards the sulfate dianion and hence the corresponding vibrational frequencies are shifted systematically to higher wavenumbers. This trend is stopped at n = 8 with the first appearance of a W₄ motif, which perturbs and weakens the interaction between sulfate and the W₃-ring.

Fig. 8 Comparison of the IRPD spectra (left) to the corresponding harmonic B3LYP IR spectra (right) of the assigned structures for SO₄²⁻(H₂O)_n (n = 3–8) in the OH stretching region. The gray-shaded areas highlight IR-active bands associated with the W₃ motif.

Overall, the present IRPD spectra are qualitatively different from those of comparable systems, like microhydrated halide⁶³ or perchlorate anions.⁶⁴ In particular, the present spectra are characterized by broader and more red-shifted OH stretching bands. This is a direct result of the stronger ion–water interactions in microhydrated sulfate dianions, which leads to marked coupling of the OH oscillators with low frequency modes, in particular, of isolated DD-H₂O molecules,^65,66 but also of water molecules that are part of larger HBed networks.^67,68 Moreover, the water bending features are found at higher frequencies compared to the corresponding bands in the spectra of hydrated perchlorate anions (1650 to 1680 cm⁻¹).⁶⁴

It is also interesting to compare the evolution of the antisymmetric stretch frequencies ν_AS of the tetrahedral core with the degree of microhydration. In microhydrated sulfate dianions the observed splitting of the ν_AS peaks is significantly smaller than in the perchlorate monoanion,⁶⁴ directly reflecting the tendency of water molecules to distribute around a sulfate dianion, while they aggregate on one side of the perchlorate anion. The more symmetric microhydration represents another manifestation of the stronger solute–solvent interactions in the microhydrated sulfate dianions. However, the present results also highlight that the most stable structures are not obtained by exclusively maximizing the number of dianion–water HBs, but the formation of stable three- and four-membered water rings containing strong water–water interactions also needs to be considered.^16,18

4. Conclusions

D₂-tagging microhydrated sulfate dianions introduces a new level of spectral quality in the IRPD spectra of SO₄²⁻(H₂O)_3–8 compared to previous IRMPD measurements, which enables a more reliable determination of band positions and improved structural assignments. The structures identified here by CIVS confirm most of the original assignments made by Wang et al. for n = 4 to 7 based on photoelectron spectra of cold anions, except that for n = 5.¹⁵ Our assignments also differ from those of Lambrecht et al. for n = 4 and n = 5.³⁰

The basic building blocks found in sulfate microhydration up to n = 8 are the four motifs W_1–4. Their stability results from a competition between the formation slightly stronger sulfate–water HBs with cooperativity-driven formation of water–water HBs. The presence of water rings leads to a characteristic but complex IR fingerprint in the spectral region below 3300 cm⁻¹ due to OH oscillators of ADD-H₂Os HBed to the dianion core. OH oscillators involved in water–water HBs are found above 3450 cm⁻¹. A quasi-free OH oscillator is observed for n = 8, i.e., at smaller sizes than previously predicted.²⁷ SO₄²⁻(H₂O)₈ also represents the smallest cluster containing a water molecule not directly bound to the sulfate dianion core and therefore the onset for the formation of a second hydration shell (before the first one is completed). This observation is in agreement with the notion that charge transfer from the dianion core to the water network is complete at n = 7.²⁸

We emphasize that the comparison of harmonic spectra to experimental IR spectra for individual cluster sizes typically does not lead to a conclusive structure assignment, but that series of predicted harmonic spectra remain helpful in identifying trends. Static anharmonic calculations can be helpful in assigning IR bands, in particular in the fingerprint region, but molecular dynamics simulations are required to attempt to disentangle the wealth of information contained in the OH stretching region.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the German Research Foundation (DFG) as part of the individual research Grant No. AS133/3-1 “Spectroscopic Characterization of Salt Dissolution in Microhydrated Cluster Ions and at the Water/Vapor Interface.” ZFL thanks the support from the National Natural Science Foundation of China (Grant No. 21473151) and from CUHK through a Direct Grant (3132676). J. W. is grateful for a Freigeist Fellowship of the Volkswagen Foundation. The authors are thankful to Alexandra Giermann (Universität Leipzig) for her assistance in preparing and handling sulfuric acid solutions. K. R. A. acknowledges instrumental support from the Fritz-Haber-Institute of the Max-Planck Society.

References

1. V. Ramanathan, P. J. Crutzen, J. T. Kiehl and D. Rosenfeld, Science, 2001, 294(5549), 2119.
2. A. Lee, P. A. Dawson and D. Markovich, Int. J. Biochem. Cell Biol., 2005, 37(7), 1350.
3. S. W. Squyres, J. P. Grotzinger, R. E. Arvidson, J. F. Bell, W. Calvin, P. R. Christensen, B. C. Clark, J. A. Crisp, W. H. Farrand, K. E. Herkenhoff, J. R. Johnson, G. Klingelhöfer, A. H. Knoll, S. M. McLennan, H. Y. McSween, R. V. Morris, J. W. Rice, R. Rieder and L. A. Soderblom, Science, 2004, 306(5702), 1709.
4. Y. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10(6), 658.
5. A. T. Blades and P. Kebarle, J. Am. Chem. Soc., 1994, 116(23), 10761.
6. W. R. Cannon, B. M. Pettitt and J. A. McCammon, J. Phys. Chem., 1994, 98(24), 6225.
7. X.-B. Wang, X. Yang and L.-S. Wang, Int. Rev. Phys. Chem., 2002, 21(3), 473.
8. K. R. Asmis and D. M. Neumark, Acc. Chem. Res., 2012, 45(1), 43.
9. M. J. DiTucci, C. N. Stachl and E. R. Williams, Chem. Sci., 2018, 9(16), 3970.
10. X.-B. Wang, J. B. Nicholas and L.-S. Wang, J. Chem. Phys., 2000, 113(24), 10837.
11. X. B. Wang, X. Yang, J. B. Nicholas and L. S. Wang, Science, 2001, 294(5545), 1322.
12. X. Yang, X.-B. Wang and L.-S. Wang, J. Phys. Chem. A, 2002, 106(33), 7607.
13. R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2003, 107(50), 10976.
14. J. Zhou, G. Santambrogio, M. Brümmer, D. T. Moore, L. Wöste, G. Meijer, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2006, 125(11), 111102.
15. X.-B. Wang, A. P. Sergeeva, J. Yang, X.-P. Xing, A. I. Boldyrev and L.-S. Wang, J. Phys. Chem. A, 2009, 113(19), 5567.
16. M. F. Bush, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129(8), 2220.
17. J. T. O'Brien, J. S. Prell, M. F. Bush and E. R. Williams, J. Am. Chem. Soc., 2010, 132(24), 8248.
18. F. Thaunay, A. A. Hassan, R. J. Cooper, E. R. Williams, C. Clavaguéra and G. Ohanessian, Int. J. Mass Spectrom., 2017, 418, 15.
19. B. Gao and Z.-F. Liu, J. Chem. Phys., 2005, 123(22), 224302.
20. Y. Miller, G. M. Chaban, J. Zhou, K. R. Asmis, D. M. Neumark and R. B. Gerber, J. Chem. Phys., 2007, 127(9), 94305.
21. H. Knorke, H. Li, Z.-F. Liu and K. R. Asmis, Phys. Chem. Chem. Phys., 2019, 21(22), 11651.
22. C.-G. Zhan, F. Zheng and D. A. Dixon, J. Chem. Phys., 2003, 119(2), 781.
23. C. C. Pye and W. W. Rudolph, J. Phys. Chem. A, 2001, 105(5), 905.
24. B. Gao and Z.-F. Liu, J. Chem. Phys., 2004, 121(17), 8299.
25. P. Jungwirth, J. E. Curtis and D. J. Tobias, Chem. Phys. Lett., 2003, 367(5–6), 704.
26. F. Thaunay, C. Clavaguéra and G. Ohanessian, Phys. Chem. Chem. Phys., 2015, 17(39), 25935.
27. L. C. Smeeton, J. D. Farrell, M. T. Oakley, D. J. Wales and R. L. Johnston, J. Chem. Theory Comput., 2015, 11(5), 2377.
28. M. Kulichenko, N. Fedik, K. V. Bozhenko and A. I. Boldyrev, J. Phys. Chem. B, 2019, 123(18), 4065.
29. N. Mardirossian, D. S. Lambrecht, L. McCaslin, S. S. Xantheas and M. Head-Gordon, J. Chem. Theory Comput., 2013, 9(3), 1368.
30. D. S. Lambrecht, G. N. I. Clark, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. A, 2011, 115(41), 11438.
31. D. S. Lambrecht, L. McCaslin, S. S. Xantheas, E. Epifanovsky and M. Head-Gordon, Mol. Phys., 2012, 110(19–20), 2513.
32. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34(1), 1.
33. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35(3), 507.
34. T. K. Esser, H. Knorke, F. Siro-Brigiano, D. R. Galimberti, K. R. Asmis, M.-P. Gaigeot and J. M. Lisy, Phys. Chem. Chem. Phys., 2018, 20(45), 28476.
35. M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119(24), 12700.
36. D. J. Goebbert, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Phys. Chem. A, 2009, 113(20), 5874.
37. W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10(9), 1716.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, Gaussian Inc., Wallingford, CT, 2016.
39. A. D. Becke, J. Chem. Phys., 1993, 98(7), 5648.
40. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72(1), 650.
41. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80(7), 3265.
42. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136(12), 124108.
43. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32(7), 1456.
44. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167(2), 103.
45. G. Lippert, J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103(2), 124.
46. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703.
47. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(7), 3641.
48. M. Krack, Theor. Chem. Acc., 2005, 114(1), 145.
49. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098.
50. C. Lee, Q. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785.
51. G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110(6), 2810.
52. S. Nosé, J. Chem. Phys., 1984, 81(1), 511.
53. D. A. McQuarrie, Statistical Mechanics, Harper and Row, New York, 1976, ch. 21.
54. J.-C. Jiang, Y.-S. Wang, H.-C. Chang, S. H. Lin, Y. T. Lee, G. Niedner-Schatteburg and H.-C. Chang, J. Am. Chem. Soc., 2000, 122(7), 1398.
55. H. Li, X. Kong, L. Jiang and Z.-F. Liu, Phys. Chem. Chem. Phys., 2018, 20(42), 26918.
56. P. J. Brannon, C. H. Church and C. W. Peters, J. Mol. Spectrosc., 1968, 27(1–4), 44.
57. T. Shimanouchi, Tables of molecular vibrational frequencies, National Bureau of Standards, Washington, DC, 1980.
58. M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(27), 12068.
59. M. Heyden, J. Sun, H. Forbert, G. Mathias, M. Havenith and D. Marx, J. Phys. Chem. Lett., 2012, 3(16), 2135.
60. M. Śmiechowski, J. Sun, H. Forbert and D. Marx, Phys. Chem. Chem. Phys., 2015, 17(13), 8323.
61. E. Garand, T. Wende, D. J. Goebbert, R. Bergmann, G. Meijer, D. M. Neumark and K. R. Asmis, J. Am. Chem. Soc., 2010, 132(2), 849.
62. M. R. Fagiani, H. Knorke, T. K. Esser, N. Heine, C. T. Wolke, S. Gewinner, W. Schöllkopf, M.-P. Gaigeot, R. Spezia, M. A. Johnson and K. R. Asmis, Phys. Chem. Chem. Phys., 2016, 18(38), 26743.
63. W. H. Robertson and M. A. Johnson, Annu. Rev. Phys. Chem., 2003, 54, 173.
64. J. T. Kelly, M. Mayer, A. C. Kennedy, C. Schemel and K. R. Asmis, J. Chem. Phys., 2018, 148(22), 222840.
65. E. M. Myshakin, K. D. Jordan, E. L. Sibert and M. A. Johnson, J. Chem. Phys., 2003, 119(19), 10138.
66. N. Heine, E. G. Kratz, R. Bergmann, D. P. Schofield, K. R. Asmis, K. D. Jordan and A. B. McCoy, J. Phys. Chem. A, 2014, 118(37), 8188.
67. M. A. Boyer, O. Marsalek, J. P. Heindel, T. E. Markland, A. B. McCoy and S. S. Xantheas, J. Phys. Chem. Lett., 2019, 10(5), 918.
68. N. Yang, C. H. Duong, P. J. Kelleher, A. B. McCoy and M. A. Johnson, Science, 2019, 364(6437), 275.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04386a

‡ These authors contributed equally.

§ With quasi-free we mean OH stretches involved in HBs with HB length larger than 2.5 Å.

---