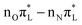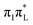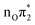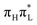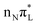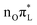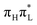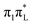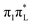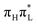Open Access Article
Open Access ArticleQuantum dynamics of the ππ*/nπ* decay of the epigenetic nucleobase 1,5-dimethyl-cytosine in the gas phase†
Martha
Yaghoubi Jouybari
a,
Yanli
Liu
b,
Roberto
Improta
 *c and
Fabrizio
Santoro
*c and
Fabrizio
Santoro
 *a
*a
aCNR-Consiglio Nazionale delle Ricerche, Istituto di Chimica dei Composti Organo Metallici (ICCOM-CNR), SS di Pisa, Area della Ricerca, via G. Moruzzi 1, I-56124 Pisa, Italy. E-mail: fabrizio.santoro@pi.iccom.cnr.it
bSchool of Physics and Optoelectronics Engineering, Ludong University, 264025 Yantai, Shandong, P. R. China
cCNR-Consiglio Nazionale delle Ricerche, Istituto di Biostrutture e Bioimmagini (IBB-CNR), via Mezzocannone 16, I-80136 Napoli, Italy. E-mail: robimp@unina.it
First published on 21st October 2020
Abstract
We study the ultrafast dynamics of 1,5-dimethyl-cytosine, a model for 5-methyl-cytidine, after photoexcitation to the first two bright ππ* states, focusing on the possible population transfer to dark nπ* states. To that end we propagate the initial wave packets on the coupled potential energy surfaces of the seven lowest energy excited states modelled with a diabatic linear vibronic coupling (LVC) model, considering all the vibrational coordinates. Time-evolution is computed by the multilayer version of the multiconfigurational time dependent Hartree (ML-MCTDH) method. The LVC Hamiltonian is parametrized with time-dependent density functional theory (TD-DFT) calculations adopting PBE0 and CAM-B3LYP functionals, which provide a different energy gap between the lowest energy nπ* states and the spectroscopic ππ* state. Population of the lowest ππ* flows to a dark nπ* state which involves a lone pair (LP) of the carbonyl oxygen (nOπ*), but the extent of such transfer is much larger according to PBE0 than to CAM-B3LYP. Photoexcitation to the second bright state gives rise to much richer dynamics with an ultrafast (50 fs) complete decay to the lowest ππ*, to nOπ* and to another nπ* in which the excited electron comes from the LP of the ring nitrogen. We perform a detailed analysis of the vibronic dynamics both in terms of normal modes and valence coordinates (bond lengths and angles). The comparison with the analogous dynamics in 1-methyl-cytosine, a model for cytidine, provides insights into the effect of methylation at carbon 5 on the electronic and nuclear dynamics.
1 Introduction
5-Methyl-cytosine (5-Me-Cyt) is the most important epigenetic DNA base (it can constitute up to 5% of the human genome),1–3 and plays a key role in many cellular processes, from cell differentiation to gene expression.4 Moreover, it has been identified as a mutational hotspot related to cancer development.5,6 In particular it is more prone than cytosine (Cyt), its parent base, to undergo photodimerization.7–10 Therefore, the photoactivated dynamics of 5-Me-Cyt and the 5-methyl(deoxy)cytidine (5-Me-dCyd) nucleoside present in DNA has been rather extensively studied by experiments9,11–16 and calculations.10,13,16–21 Methyl substitution at position 5 has been shown to increase the excited state lifetime of Cyt by almost one order of magnitude, i.e. in water from ≤1 ps to 6–9 ps.11,12,14,15,18 A similar trend is found also for jet-cooled molecules in the gas phase.16 This result has been related to the non-radiative decay path of the lowest energy bright transition, which is HOMO → LUMO ππ* excitation for Cyt, 5-Me-Cyt and 1,5-diMe-Cyt (often used as a model for 5-Me-dCyd).16,18 It involves the so-called C5–C6 ethylenic Conical Intersection (CoI), characterized by the motion of the C5 and C6 substituents out from the molecular plane; the associated energy barrier, very small for Cyt, is increased by 5-methylation.16,18 A methyl in position 5 also suppresses a deactivation channel,14,15 with a characteristic time of ∼30 ps, identified for Cyt and (deoxy)Cytidine (dCyd) in water14,15 and in chloroform,22 and assigned to a dark nπ* transition.18 Actually, different computational models predict that, for both Cyt and 5Me-Cyt, two ‘dark’ nπ* states, involving the lone pair of N3 and O7, fall in the energy range of the two lowest energy ππ* transitions. On the other hand, according to a recent experimental study in water,15 another long-living excited state (persisting up to the ns) is populated in 5-Me-dCyd and not in dCyd, and it has been associated to a dark nπ* state. Moreover, this channel should be active when exciting 5-Me-dCyd at 290 nm (i.e. in a region where only the lowest energy bright state should absorb) and not at 240 nm (where the population of the second lowest bright state should be maximum).15Therefore, there are several indications that methylation at position 5 should affect the interplay between bright and dark excited states in cytosine. The present study focuses on this process, though a direct comparison with the available experimental results is not possible because the solvent effect is not considered and the simulation time is too short. Besides the physical chemical interest for Cyt molecules, the presence of long living dark nπ* states in nucleobases can be critical also for the photoreactivity of DNA and the damage of the genetic code. Finally, in DNA, 5Me-Cyt in principle could be involved in the Proton Coupled Electron Transfer processes that are shown to be operative when cytosine is Watson–Crick paired with guanine.23,24
We use as a model 1,5-diMe-Cyt (see the inset in Fig. 1 with atom labelling) and perform Quantum Dynamical (QD) simulations based on a Linear Vibronic Coupling (LVC) Hamiltonian. To that end, we exploit a general diabatization procedure of time-dependent density functional theory (TD-DFT) calculations presented in a very recent study,25 and thereby applied to simulate the photoactivated dynamics of Cyt and 1-Me-Cyt, i.e. the parent compounds of 1,5-diMe-Cyt. Our LVC Hamiltonian is parameterized against the results obtained by two widely used DFT functionals, i.e. CAM-B3LYP and PBE0, selected because they provide a different description of the lowest energy excited states of 1,5-diMe-Cyt in the FC region. Moreover, we study the photoactivated dynamics starting from the two lowest energy bright excited states. In this way, we shall obtain insights into the main factors that can affect the population transfer between bright and dark states, like the energy gap (interesting information because the latter is sensitive also to the environment) and the excitation wavelength.
This study also provides the opportunity to investigate in detail the interplay between the dynamics of the electronic populations and the vibrational modes. In fact, a QD on a simple LVC model is very attractive for a model analysis because it is exact but is also easy to interpret since the driving forces for vibrational dynamics are very well identified, as discussed in the next sections. Moreover, the analysis of a small heterocyclic compound, such as 1,5-diMe-Cyt, with strongly delocalized normal modes will provide instructive insights into how simple dynamics in a normal-mode picture translates into a complex one when considering the time-evolution of bond lengths and bond angles. These latter are, in fact, the coordinates more often used by chemists to interpret the structural rearrangements induced by light absorption.
2 Computational details
We adopted density functional theory (DFT), using CAM-B3LYP26 and PBE027,28 functionals and the 6-31+G(d,p) basis set. Excited-state calculations were performed with TD-DFT with the same functionals and basis set. In order to parameterize the LVC Hamiltonians, whose expression is given in Section S2 of the ESI,† we adopted the methodology presented in ref. 25 and used reference states computed in Cs symmetry as this allows decoupling by symmetry ππ* (A′) and nπ* (A′′) states. We focused on the keto-amino tautomer and included in our LVC model the lowest 7 excited states comprising the first two bright transitions and all the close by states. In ground-state (GS) optimizations in Cs symmetry a small imaginary frequency, i93 cm−1 and i150 cm−1 according to CAM-B3LYP and PBE0, respectively, was found corresponding to the pyramidalization of the nitrogen of the amino group. Slightly distorted true minima were located by displacing the geometry along the imaginary modes, but they are only negligibly more stable than the Cs stationary points (2.0 cm−1 for CAM-B3LYP and 9.4 cm−1 for PBE0). Therefore imaginary frequencies were neglected by simply turning them to real. Checks in Section S3.2 of the ESI† show that even removing such modes or assigning them arbitrary small values (<100 cm−1) the time evolution of the electronic populations does not change significantly. As already done in previous works (ref. 25 and 29), tight SCF convergence with 10−6 a.u. threshold is used for TD-DFT energy calculations. Full-dimensionality QD calculations considering all the 51 normal modes were performed with the multilayer version of the multiconfigurational time dependent Hartree (ML-MCTDH) method.30–32 We used a variable mean field (VMF) with a Runge–Kutta integrator of order 5 and accuracy 10−7, like in the provided examples for S2/S1 dynamics of pyrazine with 24 normal modes.33 As a primitive basis set we adopted an Hermite DVR representation as we already did for similar systems.25,29,34,35 ML-trees and convergence tests of the ML-MCTDH propagation with respect to the dimension of the primitive basis set and the number of single particle functions are reported in Section S3.1 of the ESI.† The LVC model assumes that all diabatic PESs are harmonic with the same vibrational frequencies of S0. This is clearly an approximation, so that the parameters of the Hamiltonian will depend in principle on the expansion point. We tested the reliability of our predictions comparing those obtained with LVC models expanded at the minima of the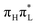 state and the two lowest nπ* states with CAM-B3LYP or by introducing a quadratic correction along a single mode, namely the C
state and the two lowest nπ* states with CAM-B3LYP or by introducing a quadratic correction along a single mode, namely the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching. The results of these analyses are discussed in Sections S3.4 and S3.5 of the ESI.† Excited state minima are characterized by few imaginary modes (see Section S1 of the ESI†), but they do not enter into the LVC parameterization since it is based on GS normal coordinates. Cartesian coordinates of all optimized structures are reported in Section S1 of the ESI.†
O stretching. The results of these analyses are discussed in Sections S3.4 and S3.5 of the ESI.† Excited state minima are characterized by few imaginary modes (see Section S1 of the ESI†), but they do not enter into the LVC parameterization since it is based on GS normal coordinates. Cartesian coordinates of all optimized structures are reported in Section S1 of the ESI.†
All electronic calculations were done with Gaussian 16,36 LVC Hamiltonians were parameterized with an in-house code interfaced with Gaussian and available upon request and ML-MCTDH simulations were performed with Quantics.37,38
3 Results
3.1 Excited states at the ground-state minimum
Here we give a concise description of the lowest energy excited states in the GS minimum (FC point). Additional details, including the plot of Kohn–Sham (KS) and natural transition orbitals (NTOs) are reported in Section S1 of the ESI.† As reported in Table 1, both CAM-B3LYP and PBE0 predict two bright ππ* transitions below 6 eV. The lowest energy excited state (S1) corresponds to HOMO → LUMO excitation, and therefore will be labeled as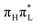 . The other bright state, ∼1 eV higher in energy, can be described as an excitation to the LUMO from the second lowest energy π orbital (π1); therefore it is labeled
. The other bright state, ∼1 eV higher in energy, can be described as an excitation to the LUMO from the second lowest energy π orbital (π1); therefore it is labeled 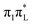 . In addition to two states with πRydberg character, three nπ* transitions, involving the lone pairs (LP) of N3 and O7, fall close to
. In addition to two states with πRydberg character, three nπ* transitions, involving the lone pairs (LP) of N3 and O7, fall close to  and
and  . As shown by the corresponding NTOs (Fig. S3 of the ESI†), according to CAM-B3LYP S2 and S5 mainly correspond, respectively, to an excitation to the LUMO from the lone pair (LP) of N3
. As shown by the corresponding NTOs (Fig. S3 of the ESI†), according to CAM-B3LYP S2 and S5 mainly correspond, respectively, to an excitation to the LUMO from the lone pair (LP) of N3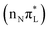 or of O7 (hereafter
or of O7 (hereafter  ). S7 corresponds to the transition from the O7 LP to a higher π* state
). S7 corresponds to the transition from the O7 LP to a higher π* state  , and therefore will be labeled as
, and therefore will be labeled as  . According to PBE0 (see Fig. S11 of the ESI†), S2 and S3 correspond instead to the symmetric and antisymmetric combinations of
. According to PBE0 (see Fig. S11 of the ESI†), S2 and S3 correspond instead to the symmetric and antisymmetric combinations of  and
and 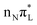 , whereas S7 is still assigned to
, whereas S7 is still assigned to  . From the quantitative point of view, the relative stability of
. From the quantitative point of view, the relative stability of  with respect to the first nπ* state is ∼0.1 eV larger according to CAM-B3LYP. Comparison with Cyt and 1-Me-Cyt25 shows that methylation mostly affects the relative stability of
with respect to the first nπ* state is ∼0.1 eV larger according to CAM-B3LYP. Comparison with Cyt and 1-Me-Cyt25 shows that methylation mostly affects the relative stability of  with respect to the two lowest nπ* states and
with respect to the two lowest nπ* states and  , which increases by ∼0.1 eV with respect to 1-Me-Cyt and ∼0.2 eV with respect to Cyt. The lowest absorption band red-shifts by ∼0.15 eV, with respect to 1-Me-Cyt in agreement with the experimental indications.18 To the best of our knowledge vertical excitations computed with accurate post-Hartree−Fock methods have never been reported in the literature for 1,5-diMe-Cyt in the gas phase. In water, CAM-B3LYP indications are consistent with those provided by MS-CASPT2, though the strong mixing between the different dark states makes any comparison not straightforward.18 More data in the gas phase are available for cytosine and in ref. 25 we showed that CAM-B3LYP is in line with MS-CASPT2 results.
, which increases by ∼0.1 eV with respect to 1-Me-Cyt and ∼0.2 eV with respect to Cyt. The lowest absorption band red-shifts by ∼0.15 eV, with respect to 1-Me-Cyt in agreement with the experimental indications.18 To the best of our knowledge vertical excitations computed with accurate post-Hartree−Fock methods have never been reported in the literature for 1,5-diMe-Cyt in the gas phase. In water, CAM-B3LYP indications are consistent with those provided by MS-CASPT2, though the strong mixing between the different dark states makes any comparison not straightforward.18 More data in the gas phase are available for cytosine and in ref. 25 we showed that CAM-B3LYP is in line with MS-CASPT2 results.
| State | CAM-B3LYP | ||||
|---|---|---|---|---|---|
| E aFC | E dmin | Charactera | δ OPA | Transition | |
| a For CAM-B3LYP the character assigned to S2, S5 and S7 is qualitative, since they exhibit more than one contribution see also Fig. S2 in the ESI. | |||||
| S1 | 4.81 | 4.48 |

|
0.10 | H → L |
| S2 | 5.32 | 4.82 |

|
0.00 | H−3 → L |
| H−2 → L | |||||
| S3 | 5.67 | 5.53 | πHRyσ1 | 0.00 | H → L+1 |
| S4 | 5.85 | 5.47 |
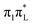
|
0.13 | H−1 → L |
| S5 | 5.87 | 5.02 |

|
0.00 | H−2 → L |
| H−3 → L | |||||
| S6 | 6.08 | 5.92 | πHRyσ2 | 0.01 | H → L+2 |
| S7 | 6.16 | 5.60 |

|
0.00 | H−2 → L+7 |
| H−2 → L | |||||
Starting from the Cs ground-state structures we built on LVC models. In Section S2 of the ESI† we report the LVC parameters for both PBE0 and CAM-B3LYP, the energies of the diabatic minima and mono-dimensional cuts of the LVC diabatic and adiabatic potential energy surfaces (PESs) along the coordinates connecting the GS minimum with the diabatic minima of the first two lowest ππ* and nπ* states. They show that even in simple LVC models, different states form an intricate network of crossings, with many local minima on the adiabatic PESs, providing the first explanation to the complex photoexcited dynamics observed in the experiment. Comparison with TD-DFT scans of the three lowest-energy adiabatic surfaces along these coordinates indicates that LVC model potentials are remarkably accurate. A partial exception is found along the coordinate leading from the GS minimum to the minimum of the nπ* state with a predominant  character, which is dominated by the C
character, which is dominated by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (mode 42). For significant displacements from the GS minimum, the S1 TD-DFT PES, with a
O stretching (mode 42). For significant displacements from the GS minimum, the S1 TD-DFT PES, with a  character, is flatter than the LVC one, suggesting that in
character, is flatter than the LVC one, suggesting that in 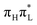 mode 42 has a significantly lower frequency than in the GS. Strong couplings between nπ* states (see Tables S14 and S19 in the ESI†) introduce remarkable differences between the diabatic and adiabatic PESs. They produce local (CAM-B3LYP) or global (PBE0) minima with nπ* character on the S1 lowest adiabatic PES. We also performed optimizations of the lowest adiabatic states in Cs symmetry with both CAM-B3LYP and PBE0 (Tables S11 and S22 of the ESI†). Comparison of the minima optimized with TD-DFT and predicted with the LVC models (Section S2.4 of the ESI†) confirms that
mode 42 has a significantly lower frequency than in the GS. Strong couplings between nπ* states (see Tables S14 and S19 in the ESI†) introduce remarkable differences between the diabatic and adiabatic PESs. They produce local (CAM-B3LYP) or global (PBE0) minima with nπ* character on the S1 lowest adiabatic PES. We also performed optimizations of the lowest adiabatic states in Cs symmetry with both CAM-B3LYP and PBE0 (Tables S11 and S22 of the ESI†). Comparison of the minima optimized with TD-DFT and predicted with the LVC models (Section S2.4 of the ESI†) confirms that  and
and  minima lie on the S1 adiabatic surface. For what concerns
minima lie on the S1 adiabatic surface. For what concerns  , although its optimization failed with PBE0 we proved that, in agreement with LVC predictions, there is a region of the coordinate space where nOπ* corresponds to S1 and is more stable than in the
, although its optimization failed with PBE0 we proved that, in agreement with LVC predictions, there is a region of the coordinate space where nOπ* corresponds to S1 and is more stable than in the  minimum. Differently from PBE0, CAM-B3LYP optimization locates
minimum. Differently from PBE0, CAM-B3LYP optimization locates  on S2, while LVC places it on S1 (but almost isoenergetic to
on S2, while LVC places it on S1 (but almost isoenergetic to  ). As shown in Section S2.3.2 of the ESI,† and further discussed below, this inaccuracy can be corrected by taking into account the different frequency of mode 42 in
). As shown in Section S2.3.2 of the ESI,† and further discussed below, this inaccuracy can be corrected by taking into account the different frequency of mode 42 in  and in GS.
and in GS.
Before concluding this section we notice that, for the sake of completeness, in the following we run QD simulations including the effect of the two Rydberg states. However, as expected, they have a very minor impact on the population transfer between ππ* and nπ* states (see Section S3.3.1 of the ESI†).
3.2 Electronic population dynamics
As shown in Fig. 1 (top), the predictions of the two functionals for the time evolution of the electronic populations after an excitation to are remarkably different. According to CAM-B3LYP (left panels), more than 90% photoexcited population remains on
are remarkably different. According to CAM-B3LYP (left panels), more than 90% photoexcited population remains on  , due to the large energy gap between the
, due to the large energy gap between the 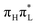 and the other excited states. PBE0 predicts instead a significant population transfer to the two lowest dark states (
and the other excited states. PBE0 predicts instead a significant population transfer to the two lowest dark states ( and, especially,
and, especially,  ). The population of this latter state is twice larger, although it is less stable than
). The population of this latter state is twice larger, although it is less stable than  in the FC region. This is due to the fact that the minimum of
in the FC region. This is due to the fact that the minimum of  is more stable than that of
is more stable than that of  (Table S21 of the ESI†), since the former state has a reorganization energy (EaFC − Edmin) 2.5 times larger than the latter (Table 1).
(Table S21 of the ESI†), since the former state has a reorganization energy (EaFC − Edmin) 2.5 times larger than the latter (Table 1).
As analyzed in more detail in Sections S2.1, S2.2 and S3.3.2 of the ESI,† the different predictions of CAM-B3LYP and PBE0 can be partially rationalized by the different energy gaps of the involved excited states at the GS minimum (Table 1), especially for dynamics started from  . On the other hand, the role of energy gradients and inter-state couplings (connected to the different compositions of the nπ* states according to the two functionals) is also significant.
. On the other hand, the role of energy gradients and inter-state couplings (connected to the different compositions of the nπ* states according to the two functionals) is also significant.
The analysis of the time evolution of the diabatic and adiabatic energies at the average position of the WP (Fig. S24 of ESI†) provides additional insights into the population dynamics. According to CAM-B3LYP,  is always remarkably more stable than the
is always remarkably more stable than the  states, explaining why the population transfer is <10%. For PBE0,
states, explaining why the population transfer is <10%. For PBE0,  and
and  become instead practically degenerate, in line with the much larger population transfer. Moreover, an analysis of the adiabatic states recomputed at the TD-DFT level along the trajectory clarifies that the
become instead practically degenerate, in line with the much larger population transfer. Moreover, an analysis of the adiabatic states recomputed at the TD-DFT level along the trajectory clarifies that the 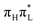 population is transferred to a state with a predominant
population is transferred to a state with a predominant 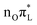 character. Comparison of these energy profiles confirms that the LVC model is quite accurate in general. For an initial excitation to
character. Comparison of these energy profiles confirms that the LVC model is quite accurate in general. For an initial excitation to  with PBE0, in the region of the nOπ* minimum the
with PBE0, in the region of the nOπ* minimum the  LVC state is less stable than that computed by TD-DFT. This is in line with that observed with the static scans discussed in the previous section.
LVC state is less stable than that computed by TD-DFT. This is in line with that observed with the static scans discussed in the previous section.
Considering photoexcitation to  (Fig. 1, bottom), both functionals predict that within 50 fs ≥90% of its population is transferred to the lower-lying states. According to CAM-B3LYP after 250 fs ∼40% of the photoexcited population is on
(Fig. 1, bottom), both functionals predict that within 50 fs ≥90% of its population is transferred to the lower-lying states. According to CAM-B3LYP after 250 fs ∼40% of the photoexcited population is on 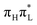 , while another ∼40% is divided between
, while another ∼40% is divided between 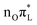 and
and  . According to PBE0, although the population loss of
. According to PBE0, although the population loss of  is similar, most of the photoexcited population (∼70%) is transferred to the dark
is similar, most of the photoexcited population (∼70%) is transferred to the dark  states, whereas the population on
states, whereas the population on  remains ≤0.2.
remains ≤0.2.
In order to test the reliability of our predictions, we also simulated the CAM-B3LYP dynamics by expanding the LVC model at the minima of the  state and the two lowest nπ* states (see Computational details and Section S3.4 of the ESI†). At these geometries the two nπ* states acquire an even more clear nNπ* or nOπ* character. The overall picture is similar to the one just discussed, obtained with the LVC model expanded at the FC point. However, for an excitation to
state and the two lowest nπ* states (see Computational details and Section S3.4 of the ESI†). At these geometries the two nπ* states acquire an even more clear nNπ* or nOπ* character. The overall picture is similar to the one just discussed, obtained with the LVC model expanded at the FC point. However, for an excitation to  , when the LVC model is built at
, when the LVC model is built at  minimum, the population lost from
minimum, the population lost from  increases up to 20%. In summary, what is interesting to stress is that, with all parameterizations,
increases up to 20%. In summary, what is interesting to stress is that, with all parameterizations,  population flows mainly to the
population flows mainly to the  state.
state.
As an additional test, we modified the LVC Hamiltonians reducing the frequency of mode 42 on the  state so as to better fit the TD-DFT adiabatic PES in the vicinity of the
state so as to better fit the TD-DFT adiabatic PES in the vicinity of the  minimum (Section 3.4 of the ESI†). For CAM-B3LYP, QD simulations with these modified Hamiltonians show negligible (excitation to
minimum (Section 3.4 of the ESI†). For CAM-B3LYP, QD simulations with these modified Hamiltonians show negligible (excitation to  ) or moderate (excitation to
) or moderate (excitation to  ) differences. For PBE0 changes are instead more significant, with the long time limit population on
) differences. For PBE0 changes are instead more significant, with the long time limit population on  increasing from ∼0.15 to ∼0.5 (excitation to
increasing from ∼0.15 to ∼0.5 (excitation to  ) or ∼0.6 (excitation to
) or ∼0.6 (excitation to  ). However, this refined model does not change the main qualitative differences between CAM-B3LYP and PBE0 provided by LVC Hamiltonian. Therefore we focus on LVC results for the forthcoming analysis of the coupled vibration/electronic dynamics.
). However, this refined model does not change the main qualitative differences between CAM-B3LYP and PBE0 provided by LVC Hamiltonian. Therefore we focus on LVC results for the forthcoming analysis of the coupled vibration/electronic dynamics.
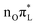 and
and  ,25 whereas for 1,5-diMe-Cyt these two states are not mixed. For an initial excitation to
,25 whereas for 1,5-diMe-Cyt these two states are not mixed. For an initial excitation to  (top panels), methylation at C5 decreases by ∼0.05–0.1 the population transfer from
(top panels), methylation at C5 decreases by ∼0.05–0.1 the population transfer from  to the nπ* states. This effect is relatively larger for CAM-B3LYP, where the population transfer, already small in 1-Me-Cyt, is halved in 1,5-diMe-Cyt.
to the nπ* states. This effect is relatively larger for CAM-B3LYP, where the population transfer, already small in 1-Me-Cyt, is halved in 1,5-diMe-Cyt.
Considering photoexcitation to  , according to CAM-B3LYP, C5-methylation leads to an ∼10% decrease of the long-time limit transfer to
, according to CAM-B3LYP, C5-methylation leads to an ∼10% decrease of the long-time limit transfer to  . At the same time, the population of the
. At the same time, the population of the  and, especially, nOπ* states increase. In particular, the transfer to
and, especially, nOπ* states increase. In particular, the transfer to  , which is almost degenerate with
, which is almost degenerate with  , increases by 10%. According to PBE0, C5-methylation plays a very minor role in dynamics initiated on
, increases by 10%. According to PBE0, C5-methylation plays a very minor role in dynamics initiated on 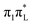 . In fact, the bottom-right panel of Fig. 1 shows that the time evolution of the electronic populations is very similar for 1-Me-Cyt and 1,5-diMe-Cyt. In summary, the most remarkable effect due to C5-methylation is a decrease of the loss of an initial population on
. In fact, the bottom-right panel of Fig. 1 shows that the time evolution of the electronic populations is very similar for 1-Me-Cyt and 1,5-diMe-Cyt. In summary, the most remarkable effect due to C5-methylation is a decrease of the loss of an initial population on  according to CAM-B3LYP. As extensively discussed in Section S3.3.6, this is essentially due to the stabilization of the
according to CAM-B3LYP. As extensively discussed in Section S3.3.6, this is essentially due to the stabilization of the  state.
state.
3.3 Analysis of the nuclear dynamics after an excitation on 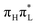
In this section we analyse the motion of the nuclear wave packet (WP) associated with the time evolution of the electronic populations discussed above.
 | ||
| Fig. 2 A′ (top) and A′′ (bottom) normal modes of 1,5-diMe-Cyt more relevant for the dynamics, computed with CAM-B3LYP (PBE0 modes are very similar). | ||
| Bond | CAM-B3LYP | ||||
|---|---|---|---|---|---|
| GS | |||||
| C6–N1 | 1.36 | 1.36 | 1.40 | 1.39 | 1.41 |
| N1–C2 | 1.42 | 1.45 | 1.41 | 1.41 | 1.39 |
| C2–N3 | 1.36 | 1.32 | 1.35 | 1.36 | 1.26 |
| N3–C4 | 1.31 | 1.37 | 1.36 | 1.39 | 1.36 |
| C4–C5 | 1.44 | 1.39 | 1.40 | 1.37 | 1.42 |
| C5–C6 | 1.36 | 1.42 | 1.38 | 1.40 | 1.36 |
| N1–C10 | 1.46 | 1.45 | 1.45 | 1.45 | 1.44 |
| C2–O7 | 1.22 | 1.24 | 1.22 | 1.23 | 1.32 |
| C4–N8 | 1.36 | 1.37 | 1.38 | 1.38 | 1.38 |
| C5–C9 | 1.50 | 1.49 | 1.50 | 1.50 | 1.50 |
| Bond | PBE0 | ||||
|---|---|---|---|---|---|
| GS | |||||
| C6–N1 | 1.35 | 1.37 | 1.40 | 1.41 | 1.39 |
| N1–C2 | 1.42 | 1.43 | 1.39 | 1.35 | 1.40 |
| C2–N3 | 1.36 | 1.32 | 1.34 | 1.27 | 1.37 |
| N3–C4 | 1.32 | 1.38 | 1.37 | 1.38 | 1.37 |
| C4–C5 | 1.44 | 1.39 | 1.38 | 1.38 | 1.38 |
| C5–C6 | 1.36 | 1.42 | 1.39 | 1.40 | 1.42 |
| N1–C10 | 1.45 | 1.45 | 1.45 | 1.45 | 1.44 |
| C2–O7 | 1.22 | 1.25 | 1.25 | 1.29 | 1.23 |
| C4–N8 | 1.36 | 1.37 | 1.37 | 1.37 | 1.38 |
| C5–C9 | 1.50 | 1.49 | 1.50 | 1.50 | 1.49 |
| Angles | CAM-B3LYP | ||||
|---|---|---|---|---|---|
| GS | |||||
| C6–N1–C2 | 121.1 | 120.4 | 122.5 | 123.4 | 114.9 |
| N1–C2–N3 | 117.1 | 121.2 | 110.4 | 117.7 | 126.2 |
| C2–N3–C4 | 120.8 | 118.2 | 131.3 | 117.8 | 120.1 |
| N3–C4–C5 | 124.0 | 123.2 | 116.4 | 126.9 | 119.6 |
| C4–C5–C6 | 114.6 | 118.4 | 117.4 | 115.1 | 118.2 |
| C5–C6–N1 | 122.5 | 118.3 | 122.0 | 119.1 | 121.1 |
| N8–C4–C5 | 119.2 | 122.7 | 126.0 | 124.3 | 124.0 |
| C9–C5–C6 | 123.0 | 119.5 | 122.9 | 122.3 | 121.2 |
| C6–N1–C10 | 122.0 | 121.0 | 121.5 | 120.6 | 123.4 |
| N1–C2–O7 | 118.2 | 113.8 | 120.1 | 119.3 | 114.5 |
| Angles | PBE0 | ||||
|---|---|---|---|---|---|
| GS | |||||
| C6–N1–C2 | 121.2 | 120.1 | 121.5 | 117.6 | 124.0 |
| N1–C2–N3 | 117.1 | 122.2 | 116.8 | 121.9 | 117.9 |
| C2–N3–C4 | 120.8 | 118.0 | 123.3 | 125.1 | 117.3 |
| N3–C4–C5 | 124.1 | 123.1 | 121.3 | 116.3 | 127.9 |
| C4–C5–C6 | 114.3 | 118.4 | 117.0 | 119.2 | 114.7 |
| C5–C6–N1 | 122.4 | 118.2 | 120.1 | 119.9 | 118.4 |
| N8–C4–C5 | 119.1 | 123.0 | 124.6 | 126.8 | 123.5 |
| C9–C5–C6 | 123.0 | 119.7 | 122.2 | 120.9 | 122.2 |
| C6–N1–C10 | 122.0 | 120.7 | 120.9 | 122.7 | 120.4 |
| N1–C2–O7 | 118.1 | 114.0 | 115.3 | 119.7 | 119.6 |
Fig. 3 plots the expectation value of the A′ normal coordinates (it is zero by symmetry for A′′ modes) as a function of time for an initial photoexcitation to  . Both functionals predict large and rather regular oscillations along modes 12 and 39. Mode 12 corresponds to a ring in-plane breathing mode, whereas mode 39 is a collective stretching with a large component on the C5–C6 bond, coupled to CH and NH bendings (see Fig. 2). The strong activation of mode 39 is consistent with the large increase of the C5–C6 bond distance in
. Both functionals predict large and rather regular oscillations along modes 12 and 39. Mode 12 corresponds to a ring in-plane breathing mode, whereas mode 39 is a collective stretching with a large component on the C5–C6 bond, coupled to CH and NH bendings (see Fig. 2). The strong activation of mode 39 is consistent with the large increase of the C5–C6 bond distance in  (see Table 2 and Table S6 in the ESI†) since the LUMO is antibonding with respect to the C5
(see Table 2 and Table S6 in the ESI†) since the LUMO is antibonding with respect to the C5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C6 double bond. PBE0, in addition to modes 12 and 39, predicts a remarkable movement also along mode 42, which corresponds to the C2–O7 stretching. After a large displacement in the first 50 fs, this mode exhibits weak oscillations around a new equilibrium position, corresponding to a longer C–O bond-distance. This shift is due to the population of the nπ* state. The elongation of the C2–O7 bond is another hint that the populated state has a clear nOπ* character, since in fact its minimum exhibits a significantly longer C2–O7 bond distance than S0 (see Table S6 in the ESI†). PBE0 calculations predict a notable displacement also along the low-frequency mode 9 corresponding to a combined in plane bending of the amino and methyl (at N1 position) groups.
C6 double bond. PBE0, in addition to modes 12 and 39, predicts a remarkable movement also along mode 42, which corresponds to the C2–O7 stretching. After a large displacement in the first 50 fs, this mode exhibits weak oscillations around a new equilibrium position, corresponding to a longer C–O bond-distance. This shift is due to the population of the nπ* state. The elongation of the C2–O7 bond is another hint that the populated state has a clear nOπ* character, since in fact its minimum exhibits a significantly longer C2–O7 bond distance than S0 (see Table S6 in the ESI†). PBE0 calculations predict a notable displacement also along the low-frequency mode 9 corresponding to a combined in plane bending of the amino and methyl (at N1 position) groups.
 | ||
Fig. 3 Expectation values of average positions of A′ modes obtained by LVC Hamiltonians parameterized with CAM-B3LYP (top) or PBE0 (bottom) calculations for initial photoexcitation of  . . | ||
More in general, Fig. 3 shows that several other modes (sketched in Fig. S12 of Section S2.1.1 of the ESI†) exhibit significant oscillations with both functionals. A remarkable consequence of this multimode dynamics is that, on the timescale we investigated, the minimum of the 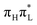 diabatic PES is never really reached (see Fig. S28 in the ESI†). Interestingly, this happens also in CAM-B3LYP simulations, even if the dynamics largely involves only
diabatic PES is never really reached (see Fig. S28 in the ESI†). Interestingly, this happens also in CAM-B3LYP simulations, even if the dynamics largely involves only 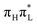 , whose population is always ≥0.9. This result, seemingly puzzling, is simply due to the fact that many modes are displaced and, due to the different frequencies, they reach their equilibrium value at different times.
, whose population is always ≥0.9. This result, seemingly puzzling, is simply due to the fact that many modes are displaced and, due to the different frequencies, they reach their equilibrium value at different times.
The WP can also be characterized looking at its standard deviation σ along the different normal modes, so as to monitor how its width changes in time. As reported in Fig. 4σ depends on time for both A′ and A′′ modes.
 | ||
Fig. 4 Standard deviation of the average position of A′ (solid line) and A′′ normal modes obtained by LVC Hamiltonians parameterized with CAM-B3LYP (top) or PBE0 (bottom) calculations for initial photoexcitation of  . The standard deviation of the low-frequency mode 2 undergoes very large changes (maximum is 1.57 for CAM-B3LYP and 2.87 for PBE0). The full plot is shown in Fig. S27 of the ESI.† . The standard deviation of the low-frequency mode 2 undergoes very large changes (maximum is 1.57 for CAM-B3LYP and 2.87 for PBE0). The full plot is shown in Fig. S27 of the ESI.† | ||
Fig. 4 shows that the largest oscillations of σ are observed for A′′ modes. In our LVC model, these modes change in time only if they couple different states. Therefore, σ helps visualizing the importance of each mode in promoting the coupling among the ππ* (A′) and nπ* (A′′) states. The most relevant A′′ modes are plotted in Fig. 2. Although as expected, oscillations of σ are larger according to PBE0, which predicts a larger population transfer to nπ*, the dynamics of several A′′ modes is strongly perturbed also according to CAM-B3LYP.
All A′′ modes correspond to out-of plane distortions of the molecular structure and have a relatively low frequency. Modes 2, 3, 6 and 11 show large variations of σ for both CAM-B3LYP and PBE0. Mode 2 is a complex out-of-plane deformation which involves the substituents and the ring atoms they are bound to. It is in-phase for the oxygen and the methyl in position 1 and out-of-phase for the amino group and the methyl in position 5 (which also rotates). Mode 3 mainly corresponds to a rotation of the methyl group bound to N1. Finally, mode 6 and mode 11 are out-of-plane deformations of the ring mainly concentrated on N3 and C6, respectively. Mode 11 shares some similarities to the mode promoting ππ*/nπ* transfer in uracil derivatives.39 Additionally, according to CAM-B3LYP mode 8, an out-of-phase movement out-of-plane of N1 and C5 atoms, shows remarkable oscillations of σ. For each mode, these σ values correspond to distortions of the ring dihedrals by a few degrees. For instance, a displacement along mode 2 by the maximum value reached by its σ (1.57 for CAM-B3LYP and 2.87 for PBE0) corresponds to an angle C6N1C2N3 equal to 8.7 degrees for CAM-B3LYP and 16.0 degrees for PBE0.
The only A′ mode exhibiting remarkable changes of σ in time is mode 42, and only for PBE0 parametrization. For mode 42 σ increases steeply and, though showing large oscillations, it never recovers the initial value. The splitting of the WP between  and
and 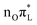 thus affects the behaviour of the CO stretching. The part of the WP remaining on
thus affects the behaviour of the CO stretching. The part of the WP remaining on  tends to oscillate around different values with respect to that transferred to
tends to oscillate around different values with respect to that transferred to 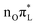 . This feature induces a large broadening of the WP along this mode, as clearly shown by Fig. 5, where the reduced density of the WP along mode 42 is plotted. When σ is maximum, at t = 18 and 38 fs, the WP assumes a bimodal shape with peaks at the initial position, corresponding roughly to a C2–O7 bond length of 1.22 Å (associated with
. This feature induces a large broadening of the WP along this mode, as clearly shown by Fig. 5, where the reduced density of the WP along mode 42 is plotted. When σ is maximum, at t = 18 and 38 fs, the WP assumes a bimodal shape with peaks at the initial position, corresponding roughly to a C2–O7 bond length of 1.22 Å (associated with  ), and at a displaced structure where C2–O7 is ∼1.34 Å (typical of
), and at a displaced structure where C2–O7 is ∼1.34 Å (typical of  ). Even according to CAM-B3LYP, notwithstanding the small population transfer, the WP along mode 42 spreads in time, so much to span at t = 220 fs a large region corresponding to CO distances between ∼1.2 and ∼1.35 Å.
). Even according to CAM-B3LYP, notwithstanding the small population transfer, the WP along mode 42 spreads in time, so much to span at t = 220 fs a large region corresponding to CO distances between ∼1.2 and ∼1.35 Å.
Methylation at C5 clearly affects the vibrational dynamics. The out-of-plane bending of the C5 substituent involves modes at much lower frequency in 1.5-diMe-Cyt (modes 6 and 8 with ω = 235 and 297 cm−1 respectively) than in 1-Me-Cyt (modes 13 and 15 with ω = 726 and 785 cm−1 respectively). Therefore, the time-evolution of σ of the WP along these modes is different and oscillates with a markedly different period (see Fig. S33 in the ESI†). Quite interestingly, these differences do not have a direct impact on the dynamics of the electronic populations. In fact, neglecting these modes has only a marginal effect on the population transfers both for 1-Me-Cyt and 1,5-diMe-Cyt (see Fig. S34 and S35, ESI†).
 , and the largest changes (≥0.1 Å) are observed for N3–C4, C4–C5 and C5–C6 bonds. Interestingly, their oscillations are less regular than those of the normal modes (check, for example, mode 39 in Fig. 3). Bond lengths derive indeed from the combination of several normal modes with different frequencies. This induces a dephasing that hampers the oscillations.
, and the largest changes (≥0.1 Å) are observed for N3–C4, C4–C5 and C5–C6 bonds. Interestingly, their oscillations are less regular than those of the normal modes (check, for example, mode 39 in Fig. 3). Bond lengths derive indeed from the combination of several normal modes with different frequencies. This induces a dephasing that hampers the oscillations.
The population transfer to nπ* states makes the PBE0 picture rather different. C2–O7 bond length increases steeply in the first 50 fs, whereas at later times it only shows damped oscillations around 1.3 Å, close to the equilibrium value of 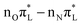 (see Table 2) and the S1 adiabatic minimum with
(see Table 2) and the S1 adiabatic minimum with  character (see Table S6 in the ESI†). With a similar time-scale, after a significant compression in ∼50 fs, a new regime sets on for N1–C2 and C2–N3 in which they weakly oscillate around values remarkably smaller than their initial ones and closer to the equilibrium position of
character (see Table S6 in the ESI†). With a similar time-scale, after a significant compression in ∼50 fs, a new regime sets on for N1–C2 and C2–N3 in which they weakly oscillate around values remarkably smaller than their initial ones and closer to the equilibrium position of 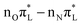 (Table 2).
(Table 2).
Bond angles undergo only small oscillations, apart from the two consecutive C6N1C2 and N1C2N3 angles, which exhibit quite irregular motions, spanning a range of 5–6 degrees. For CAM-B3LYP, the fairly large oscillations of these bond angles occur around a value similar to the initial one. For PBE0, due to the progressive population of nπ*, their average value significantly shifts, by ∼−4° for C6N1C2, and by ∼+3° for N1C2N3. These average values approach those of the  minimum (Table 3). Interestingly, however an analogous shift is not observed for other angles, even if their equilibrium values in GS and in
minimum (Table 3). Interestingly, however an analogous shift is not observed for other angles, even if their equilibrium values in GS and in  show similar differences (e.g. N8C4C5 which varies by ∼7–8 degrees). These degrees of freedom in fact undergo only limited fluctuations, confirming that, at least on the investigated time-scale, the minimum structures of the populated states are not reached.
show similar differences (e.g. N8C4C5 which varies by ∼7–8 degrees). These degrees of freedom in fact undergo only limited fluctuations, confirming that, at least on the investigated time-scale, the minimum structures of the populated states are not reached.
The effect of methylation at position 5 on the dynamics of the bond distances and bond angles is not large (see Section S3.3.5 and Fig. S36–S39 in the ESI†). According to PBE0, for an initial excitation on  the largest difference is seen for the C4–C5 bond, which shows smaller oscillations (∼0.05 Å) in 1,5-diMe-Cyt than in 1-Me-Cyt, and for the ‘flexible’ C6N1C2 angle. For CAM-B3LYP, also in this case, C5 methylation affects a larger number of bond distances (N1–C10 and many inter-ring ones). For example, the oscillations of the bond distances of the two molecules go quickly out-of-phase (see Fig. S37 of the ESI†). Concerning bond angles, beyond C6N1C2, also other angles like C4C5C6 show significant differences. As expected, the most affected angle is the in-plane bending of the C5 substituent i.e. HC5C6 in 1-Me-Cyt and C9C5C6 in 1,5-diMe-Cyt, and the former exhibits larger oscillations (see the ESI†).
the largest difference is seen for the C4–C5 bond, which shows smaller oscillations (∼0.05 Å) in 1,5-diMe-Cyt than in 1-Me-Cyt, and for the ‘flexible’ C6N1C2 angle. For CAM-B3LYP, also in this case, C5 methylation affects a larger number of bond distances (N1–C10 and many inter-ring ones). For example, the oscillations of the bond distances of the two molecules go quickly out-of-phase (see Fig. S37 of the ESI†). Concerning bond angles, beyond C6N1C2, also other angles like C4C5C6 show significant differences. As expected, the most affected angle is the in-plane bending of the C5 substituent i.e. HC5C6 in 1-Me-Cyt and C9C5C6 in 1,5-diMe-Cyt, and the former exhibits larger oscillations (see the ESI†).
3.4 Analysis of the nuclear dynamics after an excitation on 
Excitation to the second bright state  potentially deposits much more energy on the vibrational degrees of freedom so that a more complex nuclear dynamics is expected. Moreover, for the specific case of CAM-B3LYP, large and fast population transfers occur to
potentially deposits much more energy on the vibrational degrees of freedom so that a more complex nuclear dynamics is expected. Moreover, for the specific case of CAM-B3LYP, large and fast population transfers occur to 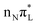 and
and  states, while they are very scarcely populated after an initial excitation to
states, while they are very scarcely populated after an initial excitation to 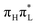 . Their population is significant even at t > 50 fs, when the largest fraction of the excited population is on
. Their population is significant even at t > 50 fs, when the largest fraction of the excited population is on  (Fig. 1). This rich electronic dynamics is mirrored by the nuclear motion. In fact, many modes, more than after exciting
(Fig. 1). This rich electronic dynamics is mirrored by the nuclear motion. In fact, many modes, more than after exciting  , show remarkable oscillations and large σ values (Fig. 8). In particular, the large increase of σ also for several A′ modes indicates that the WP spreads much more in the coordinate space due to the involvement of several different states with different equilibrium positions (see Fig. 2 and Fig. S12 of the ESI† for a plot of additional modes). The behavior of mode 42 (i.e. the CO stretching) is very instructive (Fig. 8). According to CAM-B3LYP, its σ increases steeply right after the excitation, as a consequence of the fact that nπ* states acquire a large transient population (Fig. 1). Afterward, for t > 50 fs, when the largest fraction of the population moves to
, show remarkable oscillations and large σ values (Fig. 8). In particular, the large increase of σ also for several A′ modes indicates that the WP spreads much more in the coordinate space due to the involvement of several different states with different equilibrium positions (see Fig. 2 and Fig. S12 of the ESI† for a plot of additional modes). The behavior of mode 42 (i.e. the CO stretching) is very instructive (Fig. 8). According to CAM-B3LYP, its σ increases steeply right after the excitation, as a consequence of the fact that nπ* states acquire a large transient population (Fig. 1). Afterward, for t > 50 fs, when the largest fraction of the population moves to  , the σ of mode 42 reduces remarkably, but, nonetheless, it remains far larger than in the case of an initial excitation on
, the σ of mode 42 reduces remarkably, but, nonetheless, it remains far larger than in the case of an initial excitation on  , documenting the effects of different diabatic PESs on the WP. This is made even more evident by the inspection of the WP along such a coordinate in Fig. 5. In fact, at t < 50 fs the density is bimodal with a second peak in correspondence with large C2–O7 bond lengths, while at long times (t = 220 fs) a single but very broad peak, centered in correspondence with a C2–O7 distance equal to 1.27 Å, is observed. On the contrary, according to PBE0 there is a progressive population of both the
, documenting the effects of different diabatic PESs on the WP. This is made even more evident by the inspection of the WP along such a coordinate in Fig. 5. In fact, at t < 50 fs the density is bimodal with a second peak in correspondence with large C2–O7 bond lengths, while at long times (t = 220 fs) a single but very broad peak, centered in correspondence with a C2–O7 distance equal to 1.27 Å, is observed. On the contrary, according to PBE0 there is a progressive population of both the  and the two
and the two  states and after the first 20–30 fs the WP remains always remarkably broad (see Fig. 5 and the ESI†).
states and after the first 20–30 fs the WP remains always remarkably broad (see Fig. 5 and the ESI†).
Interestingly, according to both CAM-B3LYP and PBE0 (see Fig. S29 and S30 of the ESI†) the increase of σ along mode 2 is much smaller for an initial excitation to  than to
than to  . This finding indicates that this mode triggers more efficiently the couplings with the nearby
. This finding indicates that this mode triggers more efficiently the couplings with the nearby  states of
states of 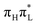 than those of
than those of  .
.
The richer dynamics after an excitation to 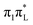 is also mirrored in the dynamics of the bond stretching and bond angles. In particular, despite the larger available energy, the oscillations of the bond distances appear even more damped and less regular. Further details are provided in Section S3.3.4 of the ESI.†
is also mirrored in the dynamics of the bond stretching and bond angles. In particular, despite the larger available energy, the oscillations of the bond distances appear even more damped and less regular. Further details are provided in Section S3.3.4 of the ESI.†
According to PBE0, the time evolution of the electronic populations changes only moderately for an initial excitation to  or
or  . As documented in the ESI,† the nuclear dynamics is similar to that described in the previous section. Nonetheless many relevant features, such as the increase of σ also for A′ modes, are clearly visible also in the PBE0-based QD simulations.
. As documented in the ESI,† the nuclear dynamics is similar to that described in the previous section. Nonetheless many relevant features, such as the increase of σ also for A′ modes, are clearly visible also in the PBE0-based QD simulations.
4 Discussions and conclusions
In this work we investigated the ultrafast dynamics of 1,5-diMe-Cyt as a model for 5-Me-dCyd, and compared them with the results for 1-Me-Cyt, a model for dCyd, focusing in particular on the possible population of dark nπ* states. Though the relevant experimental studies have been performed in solution, making the comparison with our simulation less direct, our QD simulations with CAM-B3LYP are fully consistent with the indication that methylation at position 5 leads to a decrease of the population loss of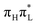 . A substantial
. A substantial  transfer is instead predicted by PBE0 QD simulations, which, though significantly reduced, remains remarkable also when using a refined Hamiltonian, accounting for the decrease of the C
transfer is instead predicted by PBE0 QD simulations, which, though significantly reduced, remains remarkable also when using a refined Hamiltonian, accounting for the decrease of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequency on the
O stretching frequency on the  state. Waiting for a full assessment of the solvent effect, this result suggests that PBE0 underestimates the energy gap between
state. Waiting for a full assessment of the solvent effect, this result suggests that PBE0 underestimates the energy gap between  and nπ* states and/or overestimates the stability of the nOπ* minimum.25
and nπ* states and/or overestimates the stability of the nOπ* minimum.25
For what concerns the possible effect of the excitation wavelength on the 5-Me-Cyd dynamics in polar solvent,15 our gas phase QD simulations do not provide any indication of the presence of an additional nπ* decay channel, active only when exciting  . In this respect, it should be remembered that varying the excitation wave-length also changes the amount of energy deposited on the chromophore. This fact, especially in the presence of an energy barrier towards the conical intersection, as happens for 1,5-diMe-Cyt,18 could also affect the dynamics at longer times, not investigated here.
. In this respect, it should be remembered that varying the excitation wave-length also changes the amount of energy deposited on the chromophore. This fact, especially in the presence of an energy barrier towards the conical intersection, as happens for 1,5-diMe-Cyt,18 could also affect the dynamics at longer times, not investigated here.
Methylation at C5 induces some moderate but notable differences in the vibrational dynamics, especially for bending angles and a few bond distances closely related to the 5 position. As expected, the out-of-plane motion of the C5 substituent is strongly affected and is much slower in 1,5-diMe-Cyt due to the larger mass of the methyl group with respect to the hydrogen. However, this does not have a direct impact on the time-evolution of the electronic populations. Therefore we can conclude that the smaller population transfer from  to nπ* states observed for 1,5-diMe-Cyt with respect to 1-Me-Cyt is essentially due to the stabilization of
to nπ* states observed for 1,5-diMe-Cyt with respect to 1-Me-Cyt is essentially due to the stabilization of  in 1,5-diMe-Cyt.
in 1,5-diMe-Cyt.
As discussed in the preceding paragraph, depending on the functional (CAM-B3LYP) and on the bright state initially excited ( or
or  ), we explored very different population dynamics, ranging from a situation where the WP essentially is on a single diabatic state (CAM-B3LYP/
), we explored very different population dynamics, ranging from a situation where the WP essentially is on a single diabatic state (CAM-B3LYP/ excitation) to cases where 4/5 different diabatic states have a population ≥0.05 after 250 fs (e.g. when exciting
excitation) to cases where 4/5 different diabatic states have a population ≥0.05 after 250 fs (e.g. when exciting 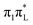 ). We exploited this opportunity to investigate the effect that the internal conversions have on the vibrational dynamics, a topic whose interest goes beyond the studied system. To this aim, we coupled an analysis of the normal modes (the most direct approach for a LVC model) with that of the valence coordinates, i.e. made in term of bond distances and bond angles. This latter reference system resulted to be very useful to more easily grasp the consequences of the electronic dynamics on the nuclear degrees of freedom.
). We exploited this opportunity to investigate the effect that the internal conversions have on the vibrational dynamics, a topic whose interest goes beyond the studied system. To this aim, we coupled an analysis of the normal modes (the most direct approach for a LVC model) with that of the valence coordinates, i.e. made in term of bond distances and bond angles. This latter reference system resulted to be very useful to more easily grasp the consequences of the electronic dynamics on the nuclear degrees of freedom.
For example, the motion of mode 42, essentially the C2–O7 stretching, is markedly different for CAM-B3LYP and PBE0. According to the LVC model parameterized with PBE0 this bond distance elongates remarkably as a consequence of the population transfer to a  state.
state.
Dynamics involves many modes and, while normal modes are characterized by rather regular oscillations, the time-evolution of bond lengths and angles appear quite complicated and their oscillations quickly damped. A trivial consequence of the multimode dynamics is that, in contrast to what a static analysis may suggest, on a timescale of hundreds of femtoseconds, 1,5-diMe-Cyt does not reach the minimum of the  PES, even when no remarkable population transfer occurs as in Fig. S28 in the ESI.† The explanation is simply the rapid dephasing of the modes, each one oscillating with its own frequency.
PES, even when no remarkable population transfer occurs as in Fig. S28 in the ESI.† The explanation is simply the rapid dephasing of the modes, each one oscillating with its own frequency.
It is also interesting to remark that, also in the case where we do not observe a significant population transfer, the motion of the WP on the 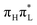 PES appears to be affected by the coupling with the other diabatic states. For example the WP is remarkably spread over the C2–O7 stretching (see Fig. 5, top/left panel). Such interaction, by itself, is also sufficient to cause a spread of the WP along out-of-plane coordinates, populating structures in which the ring exhibits significant distortions from planarity (>10°). Electron dynamics further complicates this picture. When exciting
PES appears to be affected by the coupling with the other diabatic states. For example the WP is remarkably spread over the C2–O7 stretching (see Fig. 5, top/left panel). Such interaction, by itself, is also sufficient to cause a spread of the WP along out-of-plane coordinates, populating structures in which the ring exhibits significant distortions from planarity (>10°). Electron dynamics further complicates this picture. When exciting  (CAM-B3LYP) or
(CAM-B3LYP) or 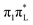 (both functionals) the WP becomes very broad along the C2–O7 bond distance (∼0.3 Å) even assuming a two-peak shape. It is likely that in such a situation interferential quantum effects become important, so that it will be interesting to investigate in the future if semiclassical approaches are able to accurately determine this dynamics, and if they can, how many trajectories are necessary.
(both functionals) the WP becomes very broad along the C2–O7 bond distance (∼0.3 Å) even assuming a two-peak shape. It is likely that in such a situation interferential quantum effects become important, so that it will be interesting to investigate in the future if semiclassical approaches are able to accurately determine this dynamics, and if they can, how many trajectories are necessary.
As a final remark we highlight that a detailed analysis of the vibrational dynamics at a fully-quantum level is not simply a theoretical speculation. In fact, the increasing time resolution of pump–probe and 2D spectroscopies, which have already led to sub-100 fs applications to some nucleobases,40 promises to be able shortly to unveil the signatures of vibrational coherences in nucleobases and their interpretation will need theoretical models and simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No. 765266 (LightDyNAmics).Notes and references
- P. A. Jones, Nat. Rev. Genet., 2012, 13, 484–492 CrossRef CAS.
- R. Lister and J. R. Ecker, Genome Res., 2009, 19, 959–966 CrossRef CAS.
- Z. D. Smith and A. Meissner, Nat. Rev. Genet., 2013, 14, 204–220 CrossRef CAS.
- R. J. Klose and A. P. Bird, Trends Biochem. Sci., 2006, 31, 89 CrossRef CAS.
- S. B. Baylin and P. A. Jones, Nat. Rev. Cancer, 2011, 11, 726–734 CrossRef CAS.
- S.-G. Jin, W. Xiong, X. Wu, L. Yang and G. P. Pfeifer, Genomics, 2015, 106, 322–330 CrossRef CAS.
- M. F. Denissenko, J. X. Chen, M.-S. Tang and G. P. Pfeifer, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 3893 CrossRef CAS.
- S. Tommasi, M. F. Denissenko and G. P. Pfeifer, Cancer Res., 1997, 57, 4727 CAS.
- A. Banyasz, L. Esposito, T. Douki, M. Perron, C. Lepori, R. Improta and D. Markovitsi, J. Phys. Chem. B, 2016, 120, 4232–4242 CrossRef CAS.
- L. Martinez Fernandez, A. Banyasz, L. Esposito, D. Markovitsi and R. Improta, Sig. Transduct. Target. Ther. 2, 2017, 2, 17021 CrossRef.
- R. J. Malone, A. M. Miller and B. Kohler, Photochem. Photobiol., 2003, 77, 158 CrossRef CAS.
- A. Sharonov, T. Gustavsson, V. Carré, E. Renault and D. Markovitsi, Chem. Phys. Lett., 2003, 380, 173 CrossRef CAS.
- L. Esposito, A. Banyasz, T. Douki, M. Perron, D. Markovitsi and R. Improta, J. Am. Chem. Soc., 2014, 136, 10838 CrossRef CAS.
- C. Ma, C. C.-W. Cheng, C. T.-L. Chan, R. C.-T. Chan and W.-M. Kwork, Phys. Chem. Chem. Phys., 2015, 17, 19045 RSC.
- X. Wang, Z. Zhou, Y. Tang, J. Chen, D. Zhong and J. Xu, J. Phys. Chem. B, 2018, 122, 7027–7037 CrossRef CAS.
- M. A. Trachsel, S. Blaser, S. Lobsiger, L. Siffert, H.-M. Frey, L. Blancafort and S. Leutwyler, J. Phys. Chem. Lett., 2020, 11, 3203–3210 CrossRef CAS.
- L. Martínez-Fernández, A. J. Pepino, J. Segarra-Martí, A. Banyasz, M. Garavelli and R. Improta, J. Chem. Theory Comput., 2016, 12, 4430–4439 CrossRef.
- L. Martínez-Fernández, A. J. Pepino, J. Segarra-Martí, J. Jovaišaitė, I. Vaya, A. Nenov, D. Markovitsi, T. Gustavsson, A. Banyasz, M. Garavelli and R. Improta, J. Am. Chem. Soc., 2017, 139, 7780–7791 CrossRef.
- A. Nakayama, S. Yamazaki and T. Taketsugu, J. Phys. Chem. A, 2014, 118, 9429 CrossRef CAS.
- S. Lobsiger, M. Etinski, S. Blaser, H. M. Frey, C. Marian and S. Leutwyler, J. Chem. Phys., 2015, 143, 234301 CrossRef.
- M. A. Trachsel, S. Lobsiger and S. Leutwyler, J. Phys. Chem. B, 2012, 116, 11081 CrossRef CAS.
- K. Röttger, H. J. B. Marroux, H. Böhnke, D. T. J. Morris, A. T. Voice, F. Temps, G. M. Roberts and A. J. Orr-Ewing, Faraday Discuss., 2016, 194, 683–708 RSC.
- A. L. Sobolewski, W. Domcke and C. Hättig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906 CrossRef CAS.
- T. Schultz, E. Samoylova, W. Radloff, I. V. Hertel, A. L. Sobolewski and W. Domcke, Science, 2004, 306, 1765–1768 CrossRef CAS.
- M. Yaghoubi Jouybari, Y. Liu, R. Improta and F. Santoro, J. Chem. Theory Comput., 2020, 16, 5792–5808 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- M. Enzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029 CrossRef.
- Y. Liu, J. Cerezo, N. Lin, X. Zhao, R. Improta and F. Santoro, Theor. Chem. Acc., 2018, 137, 40 Search PubMed.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- O. Vendrell and H.-D. Meyer, J. Chem. Phys., 2011, 134, 044135 CrossRef.
- A. Raab, G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936–946 CrossRef CAS.
- J. Cerezo, Y. Liu, N. Lin, X. Zhao, R. Improta and F. Santoro, J. Chem. Theory Comput., 2018, 14, 820–832 CrossRef CAS.
- Y. Liu, L. Martínez Fernández, J. Cerezo, G. Prampolini, R. Improta and F. Santoro, Chem. Phys., 2018, 515, 452–463 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- G. A. Worth, K. Giri, G. W. Richings, M. H. Beck, A. Jäckle and H.-D. Meyer, The QUANTICS Package, Version 1.1, University of Birmingham, Birmingham, UK, 2015 Search PubMed.
- G. A. Worth, Comput. Phys. Commun., 2020, 248, 107040 CrossRef.
- R. Improta, V. Barone, A. Lami and F. Santoro, J. Phys. Chem. B, 2009, 113, 14491–14503 CrossRef CAS.
- R. Borrego-Varillas, D. C. Teles-Ferreira, A. Nenov, I. Conti, L. Ganzer, C. Manzoni, M. Garavelli, A. Maria de Paula and G. Cerullo, J. Am. Chem. Soc., 2018, 140, 16087–16093 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all optimized structures. Additional tables listing the energies and properties of the excited states at different optimized geometries. Plots of the Kohn–Sham molecular orbitals, NTOs and differences of the electronic densities at the FC point. Expression of the LVC Hamiltonian and tables with the parameters. Convergence test for the ML-MCTDH propagation and effect of Rydberg states on the dynamics. 1D plots of the diabatic and adiabatic (LVC and TD-DFT) PES. Plot of the diabatic and adiabatic energies and of the KS-MOs along the trajectory of the wavepacket average position. Further analysis of the dynamics. Time evolution of electronic populations predicted by LVC expanded at the excited state stationary points and by a LVC with a quadratic correction. See DOI: 10.1039/d0cp04123h |
| This journal is © the Owner Societies 2020 |