The development of a full range analytical interatomic potential†
Abstract
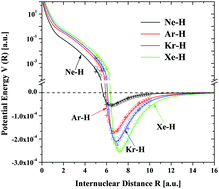
A chronological account is given to the development of a full range interatomic potential. Starting with a simple phenomenological model, the terms in the model are gradually modified, so that they can carry some definite physical meaning. To gain insight, a systematic, order by order interaction potential theory is developed. Conversely, this theory suggests the functional form for the potential model. At present, we have a simple interaction model that is capable of describing the van der Waals potentials of many systems from R = 0 to R → ∞.
- This article is part of the themed collections: 2021 PCCP HOT Articles and Festschrift for Peter Toennies - New Horizons in the Dynamics of Molecules: from Gases to Surfaces


 Please wait while we load your content...
Please wait while we load your content...