 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A probabilistic spin annihilation method for quantum chemical calculations on quantum computers†
Kenji
Sugisaki
 *ab,
Kazuo
Toyota
a,
Kazunobu
Sato
*ab,
Kazuo
Toyota
a,
Kazunobu
Sato
 *a,
Daisuke
Shiomi
a and
Takeji
Takui
*a,
Daisuke
Shiomi
a and
Takeji
Takui
 *ac
*ac
aDepartment of Chemistry and Molecular Materials Science, Graduate School of Science, Osaka City University, 3-3-138 Sugimoto, Sumiyoshi-ku, Osaka 558-8585, Japan. E-mail: sugisaki@sci.osaka-cu.ac.jp; sato@sci.osaka-cu.ac.jp
bJST, PRESTO, 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
cResearch Support Department/University Research Administrator Center, University Administration Division, Osaka City University, 3-3-138 Sugimoto, Sumiyoshi-ku, Osaka 558-8585, Japan. E-mail: takui@sci.osaka-cu.ac.jp
First published on 17th September 2020
Abstract
A probabilistic spin annihilation method based on the quantum phase estimation algorithm is presented for quantum chemical calculations on quantum computers. This approach can eliminate more than one spin component from the spin contaminated wave functions by single operation. Comparison with the spin annihilation operation on classical computers is given.
One of the most anticipated applications of quantum computers is electronic structure simulations of atoms and molecules.1–10 Quantum computers are capable of calculating the full-CI energy in polynomial time against the size of a molecule by utilizing a quantum phase estimation (QPE) algorithm,1 while it requires an exponentially longer time when executed on classical computers. A quantum–classical hybrid algorithm known as a variational quantum eigensolver (VQE)2,3 has also been well studied for near-future applications in noisy intermediate-scale quantum (NISQ) devices.11 Quantum chemical calculations on quantum computers form an interdisciplinary field including chemistry, physics, mathematics, biology and information science. The quantum devices that are currently available are noisy and do not have an enough number of qubits to implement quantum error correction codes and thus it is difficult to perform quantum chemical calculations on quantum computers of a size that is impossible for classical computers. However, recent runtime estimation revealed that the full-CI with more than 50 spatial orbitals can be executed on fault-tolerant quantum computers with ∼2000 logical qubits within a few days.12
From the viewpoint of chemistry, the calculation of correct spin states is a crucial task because molecular properties such as magnetic parameters and reactivities depend on the relevant spin states. In the VQE-based electronic structure calculations, a constrained VQE was proposed to capture the desired spin state by adding a penalty term μ[S2 − S(S + 1)] to a Hamiltonian of the system.13–15 Here, S2 denotes a spin operator and S a spin quantum number. Spin symmetry preserving quantum circuits for wave function preparation16,17 and application of spin projection operators18,19 have been discussed. Simple symmetry verification quantum circuits with ancilla qubit measurement have also been reported and demonstrated for one-body operators like a number operator of electrons and an Sz operator.20–22
For QPE-based quantum chemical calculations, quantum circuits to construct spin symmetry-adapted configuration state functions (CSFs)23,24 and multi-configurational wave functions25 on quantum computers have been proposed; these can be used to prepare initial guess wave functions having larger overlap with the exact ground state than the Hartree–Fock wave function. Development of compact wave function encoding methods by utilising spatial and spin symmetries is also the topic of ongoing interests.26–28 An approach for the calculation of the spin quantum number S of arbitrary wave functions on quantum computers has also appeared recently.29 These approaches enable us to compute the wave functions of desired spin states and to check whether quantum simulations terminate with the desired spin state or not.
Now, the simple and fundamental question arises: can we purify the spin contaminated wave functions obtained from quantum simulations by eliminating unwanted spin components? In the quantum chemical calculations on real quantum computers, hardware errors, arising from qubit decoherence and incomplete quantum gate operations, and mathematical errors, such as those due to a Trotter decomposition, can be the sources of the spin contamination. The hardware errors can be alleviated via various error mitigation techniques30 and overcome if quantum error correction31 is implemented, but the mathematical errors cannot be circumvented even if fault tolerant quantum computations become available. The QPE-based quantum chemical calculation requires the simulation of the time evolution of the wave function exp(−iHt)|Ψ〉 with large t, and the mathematical errors can be prominent. It should be noted that symmetry verification using the Sz operator is not able to eliminate spin contaminants and thus the use of the S2 operator is essential. A general symmetry adaptation approach by utilising Wigner projection operators, which is applicable to spin symmetry, was discussed by Whitfield,32 but here we focus on another approach that is based on QPE. We propose a probabilistic spin annihilation (PSA) method based on the QPE algorithm to eliminate the spin contaminants.
Before discussing the spin annihilations on quantum computers, we briefly review the spin annihilations and spin projections of wave functions on classical computers. In quantum chemical calculations on classical computers, a spin annihilation operator As+1 given in eqn (1) is often applied to spin contaminated wave functions.33–37
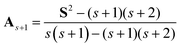 | (1) |
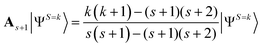 | (2) |
To eliminate more than one spin contaminant, corresponding spin annihilation operators should be applied consecutively. A Löwdin's projection operator Ps in eqn (3) can eliminate all spin components except for the S = s state.39
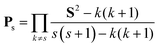 | (3) |
Because both the spin annihilation operator As+1 and the spin projection operator Ps are not unitary, the execution of spin annihilations and spin projections on quantum computers requires at least one non-unitary operation, namely the measurement of the quantum state, and the relevant operation becomes probabilistic. We have achieved this non-unitary operation by means of one-qubit QPE.
QPE is a method to find the eigenvalues and eigenvectors of unitary operators on quantum computers exponentially faster than on their classical counterparts.40 In the QPE-based full-CI calculations the time evolution of the wave function is simulated on quantum computers and the relative phase difference before and after the time evolution is read out by means of inverse quantum Fourier transformation. For the calculations of the spin quantum number S, the time evolution operator of electron spin exp(−iS2t) is used instead of exp(−iHt), where H is a Hamiltonian of the system. In this setting, we can compute the eigenvalue of the S2 operator, S(S + 1), of the wave function being used.29 Note that H and S2 have simultaneous eigenfunctions because H and S2 commute. An additional quantum gate Zη defined in eqn (4) is introduced to efficiently calculate the spin quantum number of odd-electron systems.
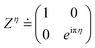 | (4) |
The introduction of the Zη gate corresponds to the use of an (S2 − ηπ1/t) operator instead of the S2 in time evolution. By utilising the Zη gate, the time evolution of the wave function of a particular spin state can be cancelled, which enables us to discriminate the spin-doublet state (S = 1/2) from the spin-quartet (S = 3/2) state in the one-qubit QPE.29
To achieve the PSA on a quantum computer, a quantum circuit depicted in Fig. 1 is constructed. In Fig. 1, |ΨCont〉 and |ΨAnni〉 stand for spin contaminated and spin annihilated wave functions, respectively. This quantum circuit corresponds to the one-qubit QPE for the spin quantum number determination with t = π/2(s + 1) and η = s(s + 1)t/π = s/2. Under this quantum circuit, the wave function of the spin quantum number S = k evolves as in eqn (5) and (6).
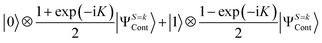 | (5) |
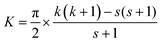 | (6) |
From these equations, the measurement of the top qubit in Fig. 1 always gives the |0〉 state for k = s, and returns the |1〉 state for k = s + 1. Thus, if the measurement outcome is the |0〉 state the S = s + 1 spin components can be projected out. The success probability of PSA is given as [1 + cos(K)]/2.
Importantly, the PSA can scavenge more than one spin component by a single operation. Let us assume the spin singlet (S = 0) wave function contaminated by the spin-triplet (S = 1) and spin-quintet (S = 2) states, as in eqn (7).
| |ΨCont〉 = c0|ΨS=0〉 + c1|ΨS=1〉 + c2|ΨS=2〉 | (7) |
Applying the PSA, the quantum state before the measurement is described as in eqn (8).
| |0〉⊗c0|ΨS=0〉 + |1〉⊗[c1|ΨS=1〉 + c2|ΨS=2〉] | (8) |
Clearly, not only the spin-triplet but also spin-quintet components are removed simultaneously if the measurement gives the |0〉 state. For general spin contaminated wave functions, the quantum state before the measurement can be written as in eqn (9).
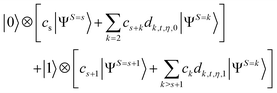 | (9) |
Here, ck denotes the coefficient of the component of the spin quantum number S = k in |ΨCont〉 and dk,t,η,u is a coefficient depending on the spin quantum number k, the evolution time t, the rotation angle η, and the measurement outcome u. Although the spin annihilation on a quantum computer is probabilistic, it can eliminate more than one spin contaminant, in contrast to the spin annihilation using As+1.
To demonstrate the PSA, the numerical simulations of the quantum circuit given in Fig. 1 were carried out by using the python program developed with OpenFermion41 and Cirq42 libraries. In the time evolution of the wave function under the S2 operator, we used a generalised spin coordinate mapping (GSCM) proposed before29 in conjunction with the second-order Trotter decomposition as given in eqn (10) and N = 2. The GSCM was designed to perform spin operations on quantum computers equipped with a smaller number of quantum gates than conventional approaches like Jordan–Wigner transformation (JWT)1,43 and Bravyi–Kitaev transformation (BKT).44 In the GSCM, the occupancy of a molecular orbital is mapped onto two qubits, the same as JWT and BKT. In the GSCM, the first qubit represents whether the molecular orbital is open-shell (|1〉) or not (|0〉), and the second one denotes the occupation number of the β-spin orbital. Thus, the doubly occupied, singly occupied by spin-α electron, singly occupied by spin-β electron, and unoccupied orbitals are represented as |01〉, |10〉, |11〉, and |00〉, respectively. In the GSCM, the number operator for unpaired electrons becomes a one-qubit operation, while it requires a two-qubit operation in JWT. By adopting the GSCM, the number of quantum gates required for the time evolution simulations under the S2 operator is greatly reduced. In addition, we checked Trotter decomposition errors of the time evolution with six electrons in a twelve spin-orbital model with randomly prepared initial states with MS = 0, the findings indicated that GSCM is very robust against the Trotter decomposition, although JWT brings large Trotter decomposition errors (see ESI† for details). These facts mitigate the requirement for the number of quantum gates. To calculate the success probability of the PSA we have carried out 1000 simulations and counted the number to get the |0〉 state in the measurement.
| e−i(h1+⋯ +hm)t ≈ [(e−ih1t/2N…e−ihm−1t/2N) × e−ihmt/N × (e−ihm−1t/2N…e−ih1t/2N)]N | (10) |
We have carried out the PSA of the spin-singlet wave function contaminated by spin-triplet states, by changing the amount of spin contaminants from 0 (pure spin-singlet) to 1 (pure spin-triplet). The starting wave function is given in eqn (11), where 2, u, d, and 0 stand for doubly occupied, singly occupied by spin-α electron, singly occupied by spin-β electron, and unoccupied, respectively.
| |ΨCont〉 = cud|2ud0〉 + cdu|2du0〉 | (11) |
In eqn (11), the |ΨCont〉 is a spin eigenfunction of S = 0 when cud = −cdu. In the case of cud = cdu the |ΨCont〉 is an S = 1 spin eigenfunction. A quantum circuit for the preparation of the |ΨCont〉 state is given in Fig. 2a. By changing θ from −π/2 to π/2 in radian to increase the spin-triplet contaminant, the success probability of PSA decreases from 1 to 0 as illustrated in Fig. 2b (see ESI† for details). If the PSA succeeds, the quantum state after the PSA is given in eqn (12) regardless of the amount of spin contaminations.
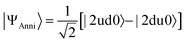 | (12) |
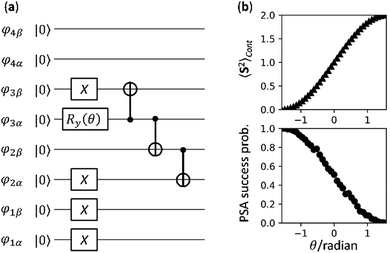 | ||
| Fig. 2 Numerical simulations of the PSA with the spin-singlet wave function contaminated by spin-triplet states. (a) A quantum circuit for the preparation of |ΨCont〉 given in eqn (11). (b) The 〈S2〉 value of the spin contaminated wave function |ΨCont〉 (Top) and the PSA success probability calculated from the numerical quantum circuit simulations (Bottom). | ||
To study the system comprising more than one spin contaminant, numerical simulations of PSA with the spin-contaminated wave functions given in eqn (13) and (14) were executed.
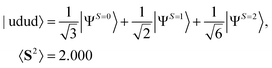 | (13) |
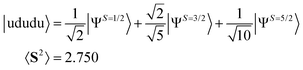 | (14) |
Note that these single determinant wave functions are representatives in which the application of As+1 increases the 〈S2〉 value. The spin annihilated wave functions of eqn (13) and (14) after normalization are given in eqn (15) and (16), respectively.
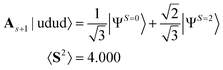 | (15) |
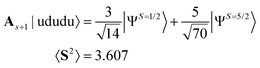 | (16) |
Theoretically PSA can generate the S = 0 spin eigenfunction given in eqn (17) when it is applied to the |udud〉 state. The 〈S2〉 value of |ΨAnni〉 is 0.0045 and the square overlap between the wave function obtained from numerical simulation and that given in eqn (17) is 0.9970. The explicit expansion of |ΨAnni〉 is provided in the ESI.† The Trotter decomposition error is responsible for the deviation from the spin eigenfunction. In fact, by increasing the Trotter slice N in eqn (10), the 〈S2〉 value of |ΨAnni〉 becomes smaller, giving 〈S2〉 < 0.0001 for N = 7 (see ESI†). The success probability of the PSA with the |udud〉 wave function is 0.340 in our numerical simulations, which is very close to the theoretical value 1/3.
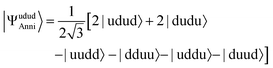 | (17) |
For the |ududu〉 wave function the theoretical success probability of PSA is 0.525 and 〈S2〉 of |ΨAnni〉 is 1.131. In this case, the spin-sextet (S = 5/2) spin component cannot be removed completely by applying the single PSA. Our numerical simulations gave the |0〉 state 511 times out of 1000 trials, and 〈S2〉 after the PSA is 1.132. Applying another PSA with s = 3/2 to |ΨAnni〉 can eliminate the remaining spin-sextet components and give 〈S2〉 = 0.753.
We emphasise that the 〈S2〉 value of |ΨAnni〉 is smaller than that of |ΨCont〉, in contrast with the As+1 operation in eqn (15) and (16). The PSA on a quantum computer is more powerful than the As+1 on a classical computer with respect to the scavenging ability of spin contaminants.
In conclusion, we have developed a PSA method based on one-qubit QPE to remove spin contaminants of wave functions stored on quantum computers. The PSA has the ability to eliminate more than one spin contaminant by the single operation, and the 〈S2〉 value after the PSA is always smaller than that obtained from the conventional spin annihilation operation As+1. Another possible approach to obtain spin annihilated wave functions from the spin contaminated ones is to combine an adiabatic quantum algorithm known as an adiabatic state preparation (ASP)1,5,45,46 with the S2 operator. The study of spin purification using ASP is underway and will be discussed in the forthcoming paper.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the AOARD Scientific Project on “Molecular Spins for Quantum Technologies” (Grant No. FA2386-17-1-4040, 4041), USA, and by KAKENHI Scientific Research B (Grant No. 17H03012) and Scientific Research C (Grant No. 18K03465) from JSPS, Japan, and PRESTO project “Quantum Software” (Grant No. JPMJPR1914) from JST, Japan.Notes and references
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik and E. Solano, Sci. Rep., 2014, 4, 3589 CrossRef.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, Nat. Commun., 2014, 5, 4213 CrossRef CAS.
- B. P. Lanyon, J. D. Whitfield, G. G. Gillett, M. E. Goggin, M. P. Almeida, I. Kassal, J. D. Biamonte, M. Mohseni, B. J. Powell, M. Barbieri, A. Aspuru-Guzik and A. G. White, Nat. Commun., 2010, 2, 106–111 CAS.
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu and D. Lu, Phys. Rev. Lett., 2010, 104, 030502 CrossRef.
- P. J. J. O'Malley, R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik and J. M. Martinis, Phys. Rev. X, 2016, 6, 031007 Search PubMed.
- J. Argüello-Luengo, A. González-Tudela, T. Shi, P. Zoller and J. I. Cirac, Nature, 2019, 574, 215–220 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Vois and A. Aspuru-Guzik, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. Benjamin and X. Yuen, Rev. Mod. Phys., 2020, 92, 015003 CrossRef.
- Y. Li, J. Hu, X.-M. Zhang, Z. Song and M.-H. Yung, Adv. Theory Simul., 2019, 1800182 CrossRef CAS.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555–7560 CrossRef CAS.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, New J. Phys., 2016, 18, 023023 CrossRef.
- I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, J. Chem. Theory Comput., 2019, 15, 249–255 CrossRef CAS.
- I. G. Ryabinkin and S. N. Genin, 2018, arXiv:1812.09812, arXiv, preprint.
- B. T. Gard, L. Zhu, G. S. Barron, N. J. Mayhall, S. E. Economou and E. Barnes, npj Quantum Info., 2020, 6, 10 CrossRef.
- G. S. Barron, B. T. Gard, O. J. Altman, N. J. Mayhall, E. Barnes and S. E. Economou, 2020, arXiv:2003.00171, arXiv, preprint.
- A. F. Izmaylov, J. Phys. Chem. A, 2019, 123, 3429–3433 CrossRef CAS.
- T.-C. Yen, R. A. Lang and A. F. Izmaylov, J. Chem. Phys., 2019, 151, 164111 CrossRef.
- X. Bonet-Monroig, R. Sagastizabal, M. Singh and T. E. O'Brien, Phys. Rev. A, 2018, 98, 062339 CrossRef CAS.
- S. McArdle, X. Yuan and S. Benjamin, Phys. Rev. Lett., 2019, 122, 180501 CrossRef CAS.
- R. Sagastizabal, X. Bonet-Monroig, M. Singh, M. A. Rol, C. C. Bultink, X. Fu, C. H. Price, V. P. Ostroukh, N. Muthusubramanian, A. Bruno, M. Beekman, N. Haider, T. E. O'Brien and L. DiCarlo, Phys. Rev. A, 2019, 100, 010302 CrossRef CAS.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, J. Phys. Chem. A, 2016, 120, 6459–6466 CrossRef CAS.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Chem. Phys. Lett.: X, 2019, 1, 100002 Search PubMed.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, ACS Cent. Sci., 2019, 5, 167–175 CrossRef CAS.
- S. A. Fischer and D. Gunlycke, 2019, arXiv:1907.01493, arXiv, preprint.
- S. Gulania and J. D. Whitfield, 2019, arXiv:1904.10469, arXiv, preprint.
- K. Setia, R. Chen, J. E. Rice, A. Mezzacapo, M. Pistoia and J. Whitfield, J. Chem. Theory Comput. DOI:10.1021/acs.jctc.0c00113.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Phys. Chem. Chem. Phys., 2019, 21, 15356–15361 RSC.
- A. Kandala, K. Temme, A. D. Córcoles, A. Mezzacapo, J. M. Chow and J. M. Gambetta, Nature, 2019, 567, 491–495 CrossRef CAS.
- J. Roffe, Contemp. Phys., 2019, 60, 226–245 CrossRef.
- J. D. Whitfield, J. Chem. Phys., 2013, 139, 021105 CrossRef.
- J. E. Harriman, J. Chem. Phys., 1964, 40, 2827–2839 CrossRef CAS.
- A. Hardisson and J. E. Harriman, J. Chem. Phys., 1967, 46, 3639–3648 CrossRef CAS.
- H. B. Schlegel, J. Chem. Phys., 1986, 84, 4530–4534 CrossRef CAS.
- W. Chen and H. B. Schlegel, J. Chem. Phys., 1994, 101, 5957–5968 CrossRef CAS.
- H. Yuan and D. Cremer, Chem. Phys. Lett., 2000, 324, 389–402 CrossRef CAS.
- B. N. Plakhutin, E. V. Gorelik, N. N. Breslavskaya, M. A. Milov, A. A. Fokeyev, A. V. Novikov, T. E. Prokhorov, N. E. Polygalova, S. P. Dolin and L. I. Trakhtenberg, J. Struct. Chem., 2005, 46, 195–203 CrossRef CAS.
- P. O. Löwdin, Rev. Mod. Phys., 1964, 36, 966–976 CrossRef.
- A. Abrams and S. Lloyd, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. S. Fried, C. Gidney, B. Gimby, P. Gokhale, T. Häner, T. Hardikar, V. Havlíček, O. Higgott, C. Huang, J. Izaac, Z. Jiang, X. Liu, S. McArdle, M. Neeley, T. O’Brien, B. O’Gorman, I. Ozfidan, M. D. Radin, J. Romero, N. P. D. Sawaya, B. Senjean, K. Setia, S. Sim, D. S. Steiger, M. Steudtner, Q. Sun, W. Sun, D. Wang, F. Zhang and R. Babbush, Quantum Sci. Technol., 2020, 5, 034014 CrossRef.
- Cirq. https://github.com/quantumlib/Cirq.
- P. Jordan and E. Wigner, Eur. Phys. J., 1928, 47, 631–651 CAS.
- J. T. Seeley, M. J. Richard and P. J. Love, J. Chem. Phys., 2012, 137, 224109 CrossRef.
- E. Farhi, J. Goldstone, S. Gutmann and M. Sipser, 2000, arXiv:quant-ph/0001106, arXiv, preprint.
- L. Veis and J. Pittner, J. Chem. Phys., 2014, 140, 214111 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Trotter decomposition error in the quantum simulation of time evolutions of the wave function under the S2 operator, preparation of spin-mixed wave functions on quantum computers and Trotter slice number dependence of the probabilistic spin annihilation. See DOI: 10.1039/d0cp03745a |
| This journal is © the Owner Societies 2020 |

