Harnessing deep neural networks to solve inverse problems in quantum dynamics: machine-learned predictions of time-dependent optimal control fields†
Abstract
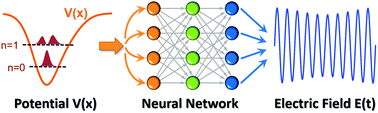
Inverse problems continue to garner immense interest in the physical sciences, particularly in the context of controlling desired phenomena in non-equilibrium systems. In this work, we utilize a series of deep neural networks for predicting time-dependent optimal control fields, E(t), that enable desired electronic transitions in reduced-dimensional quantum dynamical systems. To solve this inverse problem, we investigated two independent machine learning approaches: (1) a feedforward neural network for predicting the frequency and amplitude content of the power spectrum in the frequency domain (i.e., the Fourier transform of E(t)), and (2) a cross-correlation neural network approach for directly predicting E(t) in the time domain. Both of these machine learning methods give complementary approaches for probing the underlying quantum dynamics and also exhibit impressive performance in accurately predicting both the frequency and strength of the optimal control field. We provide detailed architectures and hyperparameters for these deep neural networks as well as performance metrics for each of our machine-learned models. From these results, we show that machine learning, particularly deep neural networks, can be employed as cost-effective statistical approaches for designing electromagnetic fields to enable desired transitions in these quantum dynamical systems.
- This article is part of the themed collection: Emerging AI Approaches in Physical Chemistry


 Please wait while we load your content...
Please wait while we load your content...
