 Open Access Article
Open Access ArticlePhotodissociation dynamics of methyl iodide probed using femtosecond extreme ultraviolet photoelectron spectroscopy†
Emily M.
Warne
 a,
Briony
Downes-Ward
a,
Joanne
Woodhouse
a,
Michael A.
Parkes
a,
Briony
Downes-Ward
a,
Joanne
Woodhouse
a,
Michael A.
Parkes
 b,
Emma
Springate
b,
Emma
Springate
 c,
Philip A. J.
Pearcy
c,
Yu
Zhang
c,
Philip A. J.
Pearcy
c,
Yu
Zhang
 c,
Gabriel
Karras
c,
Adam S.
Wyatt
c,
Gabriel
Karras
c,
Adam S.
Wyatt
 c,
Richard T.
Chapman
c,
Richard T.
Chapman
 c and
Russell S.
Minns
c and
Russell S.
Minns
 *a
*a
aSchool of Chemistry, University of Southampton, Highfield, Southampton SO17 1BJ, UK. E-mail: r.s.minns@soton.ac.uk
bDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
cCentral Laser Facility, STFC Rutherford Appleton Laboratory, Didcot, Oxfordshire OX11 0QX, UK
First published on 26th October 2020
Abstract
Femtosecond pump–probe photoelectron spectroscopy measurements using an extreme ultraviolet probe have been made on the photodissociation dynamics of UV (269 nm) excited CH3I. The UV excitation leads to population of the 3Q0 state which rapidly dissociates. The dissociation is manifested as shifts in the measured photoelectron kinetic energy that map the extending C–I bond. The increased energy available in the XUV probe relative to a UV probe means the dynamics are followed over the chemically important region as far as C–I bond lengths of approximately 4 Å.
1 Introduction
Photoelectron spectroscopy is a highly effective probe of dynamic molecular structure, showing sensitivity to both the electronic and nuclear degrees of freedom.1 The evolution in geometric structure manifests itself in the photoelectron spectrum as changes in the distribution of vibrational states populated in the ion, due to changing Franck–Condon (FC) factors, and, for larger scale motions like those associated with dissociation, as shifts in the measured binding energy.2–5 The geometry information contained within the photoelectron spectrum is, however, indirect, meaning identification of specific structures relies on careful calculation of the geometry dependent photoelectron spectrum, something that is still a challenge to modern theoretical methods. Obtaining sensitivity to large scale geometry changes also often requires high probe energies in order to ionise along a large portion of the reaction coordinate. Recent experiments based on XUV probes generated from high harmonic generation (HHG) and free electron laser sources have demonstrated this capability, producing full maps of the reaction path in a few molecular systems.2,6–9 Experiments using high harmonic radiation have shown the transition between molecular and atomic orbitals in Br2,8 observed large geometry dependent changes in ionisation potential in CS2,2 measured internal conversion and intersystem crossing dynamics in CS2,2 and observed internal conversion and dissociation in NO2.7 Here we present the results of recent femtosecond HHG-based XUV photoelectron spectroscopy experiments on the dissociation dynamics of UV excited methyl iodide.The UV driven dissociation of methyl iodide following excitation into the A-band has been extensively studied by numerous techniques and stands as a benchmark system against which new chemical dynamics methods are often tested.10–12 The dynamics of the system following excitation on the red side of the A-band can be reasonably well explained with reference to the cuts through the potential energy surfaces along the dissociative coordinate, as plotted in Fig. 1.13 Upon absorption of light around 266 nm, population is transferred from the tightly bound ground state predominantly into the strongly dissociative 3Q0 state. The absorption leads to a σ*(C–I) ← n(I) transition, where promotion of a non-bonding electron from the iodine atom into an antibonding orbital associated with the C–I bond14 causes a weakening of this C–I bond. The large gradient along the dissociative C–I coordinate leads to rapid extension of the C–I bond and dissociation of the molecule within approximately 100 fs. Along the dissociative coordinate, the wavepacket passes a crossing between the 3Q0 and 1Q1 states where population transfer can occur, leading to formation of both the ground I(2P3/2) and excited I*(2P1/2) spin–orbit states of atomic iodine, in conjunction with the ground state methyl radical. This relatively simple picture of the dynamics has been shown to be consistent along a reasonable range of energies on the red side of the A-band,10,11,15–22 although recent photoelectron spectroscopy measurements suggest the dynamics on the blue side may not be so straight forward.22 To date there have been surprisingly few measurements of the excited state dynamics of the A-band when compared with measurements of the product state distributions. The dynamics have been probed using Coulomb explosion imaging,10,23,24 XUV transient absorption spectroscopy11,25 and multiphoton ionisation photoelectron spectroscopy.22 The CEI experiments show strong sensitivity to geometry changes at extended bond lengths, but struggle to capture the early time (<100 fs) dynamics due to limited temporal resolution and/or strong field effects in the probe process.10,23,24 The XUV transient absorption experiments, meanwhile, are sensitive to the intermediate transition state region, providing a timeframe for transition through this region, but they do not show structural sensitivity.11 The multiphoton ionisation photoelectron spectroscopy experiments provide timeframes for exiting the Franck–Condon region but the limited ionisation energy means the reaction cannot be followed to extended bond lengths.22 Here we report new XUV photoelectron spectroscopy measurements of the photodissociation dynamics of methyl iodide towards the red side of the A-band, following excitation at 269 nm. The experimental results show energy shifts in the photoelectron spectrum that provide a sensitive measure of the instantaneous geometry at early times, mapping out the C–I bond length during dissociation, which we subsequently compare to a classical 1D model of the dynamics.
 | ||
| Fig. 1 1D slices through the multidimensional potential energy surfaces of methyl iodide along the C–I dissociation pathway. The energies plotted have been taken from Alekseyev et al.13 for the neutral curves and from Marggi-Poullain et al.26 for the ion states, and have been calculated such that they allow for relaxation of the CH3 pyramidal structure during dissociation. The relative position of the ion states has been set by the measured vertical ionisation limits. | ||
2 Experiment
The time resolved photoelectron spectroscopy experiments presented follow the same method as outlined in Smith et al.2 with very small differences. Briefly, a UV pump at 269 nm (4.6 eV) with pulse energies around 3.7 μJ is generated via second harmonic generation of the sum-frequency generated output of an OPA (HE-TOPAS) pumped by an amplified Ti:sapphire system (Red Dragon, KMLabs). This pump pulse predominantly populates the 3Q0 state of the A-band in methyl iodide. The residual ground state and excited state populations are subsequently ionised by a time delayed XUV pulse at a photon energy of 22.6 eV. As in ref. 2, this XUV probe is generated via high harmonic generation, using approximately 450 μJ of 395 nm light produced via second harmonic generation of the fundamental output of the Red Dragon laser. The 7th harmonic of the 395 nm light is isolated using a time preserving monochromator, and is subsequently reflection focused with a toroidal mirror to the centre of the interaction chamber. The CH3I beam is created via an effusive expansion of the room temperature vapour of CH3I through a 200 μm diameter nozzle. The nozzle is located a few centimetres away from the interaction region where the molecular beam and laser beams cross at the entrance to an electron time-of-flight spectrometer (Kaesdorf ETF11). The electron spectrometer has a ΔE/E resolution of approximately 2% in the 13.5–18.0 eV electron kinetic energy range. The pump and probe beams are linearly polarised along the time-of-flight axis, with a pump–probe cross-correlation duration of approximately 60 fs (full width at half maximum), and cross at a small angle of approximately 3°. The maximum overlap between the pump and probe pulses, defined as time zero, is taken from a fit to the sum of the time profiles across the region of the strong initial![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 features in the spectrum observed at binding energies between 4.96–6.14 eV. The time offsets presented later in the manuscript are therefore relative to the time zero obtained here.
2E1/2 features in the spectrum observed at binding energies between 4.96–6.14 eV. The time offsets presented later in the manuscript are therefore relative to the time zero obtained here.
3 Results and discussion
The photoelectron spectra associated with ionisation of the ground and initially excited states of CH3I are plotted in Fig. 2. For both spectra, and throughout this paper, the binding energy is calculated as: BE = hνprobe − eKE. The ground state spectrum is plotted in blue with the intensity scale shown on the right-hand axis. Each feature is labelled with the asymptotic dissociation products as assigned from the calculations of Marggi-Poullain et al.,26 while the lower binding energy features are also identified with C3v symmetry labels to aid comparison to earlier work. Of most importance to the time resolved analysis is the ionisation into the two lowest spin–orbit states of the CH3I+ ion, the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2, which lie at binding energies of 9.54 eV and 10.16 eV respectively. Using Mullikens analogy between the alkyl halides and HI,14 these ion states result from the removal of a non-bonding electron from the ground state electronic configuration of (σ)2(n)4 to form a doublet with configuration (σ)2(n)3. Both ion states adiabatically lead to the production of ground state CH3+ ions and the ground spin–orbit state of neutral I(2P3/2) at extended C–I distances. The broad feature at 12.5 eV is a result of removing one of the C–I bonding electrons from the HOMO−1 level, giving a configuration of (σ)1(n)4. The higher lying ion states accessible with the probe photon correlate with higher energy fragments and are in good agreement with the theoretical predictions of ref. 26. The assignments are based on the vertical ionisation energies obtained from ref. 26 and are labelled with the dissociation limits as used in the reference.
2E1/2, which lie at binding energies of 9.54 eV and 10.16 eV respectively. Using Mullikens analogy between the alkyl halides and HI,14 these ion states result from the removal of a non-bonding electron from the ground state electronic configuration of (σ)2(n)4 to form a doublet with configuration (σ)2(n)3. Both ion states adiabatically lead to the production of ground state CH3+ ions and the ground spin–orbit state of neutral I(2P3/2) at extended C–I distances. The broad feature at 12.5 eV is a result of removing one of the C–I bonding electrons from the HOMO−1 level, giving a configuration of (σ)1(n)4. The higher lying ion states accessible with the probe photon correlate with higher energy fragments and are in good agreement with the theoretical predictions of ref. 26. The assignments are based on the vertical ionisation energies obtained from ref. 26 and are labelled with the dissociation limits as used in the reference.
 | ||
Fig. 2 Photoelectron spectrum measured following ionisation of the ground state (blue plot, 9.5–22 eV) and excited states (red plot, 4–9.5 eV) of CH3I with a 22.6 eV photon generated using high harmonic generation. The pump at 269 nm (4.6 eV) populates the Q-band of the CH3I molecule which is subsequently ionised, with the spectrum plotted in red showing the resulting signal close to time zero (t = 7 fs). States are labeled with the final ion state symmetry where known and with asymptotic products based on the calculations of Marggi-Poullain et al.26 The feature labelled with a 'star' is due to ionisation into the lowest quartet state of the ion, which as far as we are aware has not been measured or calculated previously. Both intensity scales are normalised to the photoelectron signal associated with ionisation of the ground state into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 ion state such that the relative intensity of the excited state features can be compared to the ground state spectrum. 2E1/2 ion state such that the relative intensity of the excited state features can be compared to the ground state spectrum. | ||
UV excitation drives an σ*(C–I) ← n(I) transition and leads to an electronic configuration of (σ)2(n)3(σ*)1. Ionisation of the excited states at a delay of 7 fs (the measured data point closest to time zero) leads to the spectrum plotted in red in Fig. 2, with the intensity scale on the left of the figure. The transient signal is a factor of 2000 times smaller than the ground state signal, due to the limited excited state population and low ionisation cross-section with the XUV probe. The absence of any XUV background and low noise levels mean the excited state signal-to-noise ratio is sufficiently high to allow the dynamics of the excited state to be determined.
The lowest binding energy features in the excited-state photoelectron spectrum result from the removal of the σ* electron, giving the same electronic terms, ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2, for the ion states as obtained from ionisation of the ground state. These two
2E1/2, for the ion states as obtained from ionisation of the ground state. These two ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ion states sit at binding energies of 5.2 eV and 5.7 eV respectively. Features from ionisation into the
ion states sit at binding energies of 5.2 eV and 5.7 eV respectively. Features from ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 ion states are again labelled in Fig. 2 by the symmetry of the final ion states and the asymptotic dissociation limit. As observed in previous UV photoionisation of the excited state, the cross-section into the upper spin–orbit state of the
2E1/2 ion states are again labelled in Fig. 2 by the symmetry of the final ion states and the asymptotic dissociation limit. As observed in previous UV photoionisation of the excited state, the cross-section into the upper spin–orbit state of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state of the CH3I+ cation is higher than that of the lower spin–orbit state.22
state of the CH3I+ cation is higher than that of the lower spin–orbit state.22
The broad feature in the excited state spectrum at a binding energy of 8 eV is reminiscent of the feature in the ground state spectrum at 12.5 eV that corresponds to ionisation to the A-state of the ion, having a similar difference in energy to the lowest ion state. Ionisation from the neutral excited state into the A ion state would, however, be a 2 electron transition, meaning this is strongly forbidden. The origin of the feature at 8 eV is therefore quite different and corresponds to removal of one of the non-bonding electrons localised on the iodine atom. The resulting ion state electronic configuration14 is therefore (σ)2(n)2(σ*)1, which leads to a lowest energy term of quartet character. Based on the electronic configuration, we therefore assign the feature at 8 eV as this quartet state, which to the best of our knowledge has not been observed or calculated previously, and is labelled in Fig. 2 with a *.
The time-dependent photoelectron spectra associated with the excited-state dynamics are plotted in Fig. 3. While our probe energy of 22.6 eV is high enough to ionise from both the ground state of CH3I and the CH3 and I products, the low excitation fractions mean that it is not possible to isolate any features associated with ground-state depletion or product formation. We therefore show the time-dependent spectra only in the region where the spectrum is not dominated by features associated with the residual ground-state population.
 | ||
| Fig. 3 Time dependent photoelectron spectra of CH3I following excitation at 269 nm (4.6 eV). The intensity profile is seen to shift to higher binding energies as a function of delay as the molecule dissociates. The coloured bars on the right mark the binding energy regions of the time profiles shown in Fig. 4. The spectra used to create the colour map are plotted in the ESI† as Fig. S1. | ||
At delays close to time zero, the excited-state spectrum is dominated by three photoelectron bands corresponding to ionisation to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2,
2E3/2, ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 and quartet states, with binding energies of 5.2 eV, 5.7 eV and 8 eV respectively. The peaks associated with ionisation into the
2E1/2 and quartet states, with binding energies of 5.2 eV, 5.7 eV and 8 eV respectively. The peaks associated with ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states shift to higher binding energies as a function of pump–probe delay, leading to a rapid decay in intensity at the initially observed binding energies. The shift of the peaks to higher binding energies forms a continuum starting at the features associated with ionisation from the FC geometry into the
states shift to higher binding energies as a function of pump–probe delay, leading to a rapid decay in intensity at the initially observed binding energies. The shift of the peaks to higher binding energies forms a continuum starting at the features associated with ionisation from the FC geometry into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states and moving towards the ionisation limits associated with the dissociation products as the pump–probe delay increases.
states and moving towards the ionisation limits associated with the dissociation products as the pump–probe delay increases.
To show this shift in binding energy more clearly, we take the measured photoelectron intensity as a function of delay for four different binding energy regions (indicated by the shaded blocks at the side of Fig. 3), and fit the data to a single exponential decay convolved with a Gaussian instrument response function:
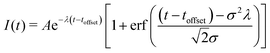 | (1) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ion states at extended C–I bond lengths at later times. This energy region is therefore fitted to the sum of two time separated components, each with the form of eqn (1), and will be described in more detail later in this paper.
ion states at extended C–I bond lengths at later times. This energy region is therefore fitted to the sum of two time separated components, each with the form of eqn (1), and will be described in more detail later in this paper.
The choice of fitting function matches that used in many previous photoelectron spectroscopy experiments and the motivation for its use here is as follows: if one considers the dynamics of a dissociating Gaussian wavepacket moving through the geometries associated with the energy regions presented, one would expect the shape of the signal to be controlled by the wavepacket motion into, and out of, each region measured. The rising and falling edges of the signal would therefore map cumulative distribution functions of the incoming and outgoing wavepacket which may not necessarily have the same widths. If we assume the energy region is sufficiently small that the population does not plateau for an extended period, the overall shape of the signal will remain close to Gaussian, as seen in the experiment and the 1D model described later. If we consider the initial 5–6 eV energy region that defines the FC geometry, we see a rise in the signal related to the laser pulse parameters that define the excitation process, and an extended tail that maps the population leaving the geometries associated with these binding energies. Such a temporal profile can be accurately described using eqn (1). We have checked that the choice of equation does not affect the key values associated with the time offset obtained for each energy region. A second fit using an equation consisting of separate Gaussian cumulative distribution functions for the rising and falling edges of the signal has also been performed. The use of the Gaussian cumulative distribution function also provides good quality fits to the data with consistent values for the comparable temporal offset but suffers from significant cross-talk between many of the parameters used. We therefore chose to present the fits and parameters obtained from eqn (1) as this provides a consistently reliable fit to the data, from an analytically simple equation with the minimum number of free fitting parameters. The values obtained then allow us to discuss the observed changes in temporal profile in a consistent and reliable manner. The values for the time offset provide an accurate measure of the delay in appearance between the regions, while the observation time constants presented measure the time taken to leave the observation window defined by the photoelectron energy range, and no further significance of these is implied.
The energy regions are selected to provide four discrete bands, below the onset of the ground state spectrum, where we can observe the changing intensity profile with time. This allows us to capture the time required to reach the geometries that maximise signal in these regions, which can be compared to the dynamics calculations presented later. The lowest and highest binding energy regions are selected to overlap with the main features in the FC spectrum, while the two intermediate energies are selected to minimise overlap with the FC features while highlighting the shift to later times. The data and fits for the four energy regions considered are plotted in Fig. 4, with the values for the fitted observation time constant and time offset given in Table 1. The time profiles plotted in Fig. 4 have been individually normalised and vertically offset to allow for an easier comparison. This is necessary due to the much higher ionisation cross sections observed at the Franck–Condon (FC) geometry when compared with those at extended bond lengths. For each energy region the data points are plotted along with the corresponding fits, and with red lines indicating the obtained temporal offset, toffset. The error bars on the data points and the toffset lines are calculated using a bootstrapping analysis of the data. They show one standard deviation either side of the bootstrapping mean values. The plots are presented in binding energy order to highlight the shift in toffset to later times as the binding energy increases.
 | ||
Fig. 4 Temporal profiles of the photoelectron signal integrated across four different regions of the spectrum: the lower three profiles correspond to ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and 2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 ion states in the FC geometry (5.0–6.0 eV), and at geometries with intermediate C–I bond lengths (6.6–7.0 eV and 7.0–7.4 eV). At early times the top graph (7.7–8.5 eV) contains signal from ionisation into the quartet state at the FC geometry, while at later times there is also signal due to ionisation into the 2E1/2 ion states in the FC geometry (5.0–6.0 eV), and at geometries with intermediate C–I bond lengths (6.6–7.0 eV and 7.0–7.4 eV). At early times the top graph (7.7–8.5 eV) contains signal from ionisation into the quartet state at the FC geometry, while at later times there is also signal due to ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and 2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 states at the most extended bond lengths measured. In all plots, the solid circles correspond to the measured data points. For the lower three plots, the solid lines show fits to eqn (1). For the 7.7–8.5 eV plot, the data points are fitted to a sum of eqn (1) and a scaled fit to the 5.0–6.0 eV region; this total fit is shown by the dashed line. The dot-dashed line shows the contribution from the quartet feature, while the solid line shows the fit to eqn (1) for the shifting feature in that region. The vertical red lines in each plot show the toffset value obtained from the fit to eqn (1). The error bars indicate ± 1 standard deviation, calculated using bootstrapping analysis. 2E1/2 states at the most extended bond lengths measured. In all plots, the solid circles correspond to the measured data points. For the lower three plots, the solid lines show fits to eqn (1). For the 7.7–8.5 eV plot, the data points are fitted to a sum of eqn (1) and a scaled fit to the 5.0–6.0 eV region; this total fit is shown by the dashed line. The dot-dashed line shows the contribution from the quartet feature, while the solid line shows the fit to eqn (1) for the shifting feature in that region. The vertical red lines in each plot show the toffset value obtained from the fit to eqn (1). The error bars indicate ± 1 standard deviation, calculated using bootstrapping analysis. | ||
| Energy region (eV) | Time offset (fs) | Observation time constant (fs) |
|---|---|---|
| 5.0–6.0 | 0 ± 5 | 23 ± 6 |
| 6.6–7.0 | 12 ± 10 | <20 |
| 7.0–7.4 | 35 ± 10 | <20 |
| 7.7–8.5 | 71 ± 10 | <20 |
The lowest energy region covers the features between 5.0–6.0 eV, corresponding to ionisation of CH3I in its initial FC geometry into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 ion states. The fitted toffset is 0 ± 5 fs, as expected for the initial excited state geometry. The next two higher energy regions plotted cover the range of binding energies between the two early time features associated with ionisation at the FC geometries into the
2E1/2 ion states. The fitted toffset is 0 ± 5 fs, as expected for the initial excited state geometry. The next two higher energy regions plotted cover the range of binding energies between the two early time features associated with ionisation at the FC geometries into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and quartet ion states. The first of these energy regions covers a binding energy of 6.6–7.0 eV, just beyond the bright features associated with ionisation of the FC geometry into the
and quartet ion states. The first of these energy regions covers a binding energy of 6.6–7.0 eV, just beyond the bright features associated with ionisation of the FC geometry into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states, while the second covers higher binding energies between 7.0–7.4 eV, just before the signal starts to overlap with the feature from ionisation at the FC geometry into the quartet ion state. These two energy regions therefore correspond to ionisation of the molecule at extended C–I bond lengths where the wavepacket has left the Franck–Condon region and has started to travel down the dissociative 3Q0 excited state potential shown in Fig. 1 en route to dissociation. In both energy regions, the ionisation propensity is much lower than that associated with the FC geometry, presumably due to weaker vibrational overlap between the neutral and ion states. The fits of the data to eqn (1) give values for toffset of 15 ± 10 fs and 37 ± 10 fs for the 6.6–7.0 eV and 7.0–7.4 eV regions respectively.
states, while the second covers higher binding energies between 7.0–7.4 eV, just before the signal starts to overlap with the feature from ionisation at the FC geometry into the quartet ion state. These two energy regions therefore correspond to ionisation of the molecule at extended C–I bond lengths where the wavepacket has left the Franck–Condon region and has started to travel down the dissociative 3Q0 excited state potential shown in Fig. 1 en route to dissociation. In both energy regions, the ionisation propensity is much lower than that associated with the FC geometry, presumably due to weaker vibrational overlap between the neutral and ion states. The fits of the data to eqn (1) give values for toffset of 15 ± 10 fs and 37 ± 10 fs for the 6.6–7.0 eV and 7.0–7.4 eV regions respectively.
The upper plot shows the temporal profile in the 7.7–8.5 eV region, where the shifting feature associated with ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ion states at geometries with extended C–I bond lengths overlaps in binding energy with the feature from ionisation to the quartet ion state at FC geometries. Here, the data has been fitted to a sum of two exponentially decaying functions convolved with a Gaussian, as given by eqn (1), with different parameters for the two components of the total fit. The first component is an amplitude-scaled copy of the fit in the 5.0–6.0 eV region. This provides a measure of the ionisation from FC geometries and is shown by the dot-dashed line in Fig. 4. The second component, which relates to the shifting feature, is subsequently fitted in the same way as in the other energy regions, with an associated time offset. The resulting total fit is represented by the dashed line, while the contribution of the secondary feature alone is shown by the solid line. The assumption that the quartet state ionisation feature has the same temporal profile as the ionisation to the
ion states at geometries with extended C–I bond lengths overlaps in binding energy with the feature from ionisation to the quartet ion state at FC geometries. Here, the data has been fitted to a sum of two exponentially decaying functions convolved with a Gaussian, as given by eqn (1), with different parameters for the two components of the total fit. The first component is an amplitude-scaled copy of the fit in the 5.0–6.0 eV region. This provides a measure of the ionisation from FC geometries and is shown by the dot-dashed line in Fig. 4. The second component, which relates to the shifting feature, is subsequently fitted in the same way as in the other energy regions, with an associated time offset. The resulting total fit is represented by the dashed line, while the contribution of the secondary feature alone is shown by the solid line. The assumption that the quartet state ionisation feature has the same temporal profile as the ionisation to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 states enables the signal due to the shifting feature in this region to be isolated, despite the domination of the quartet state signal. The fit to the shifting feature shows a continuation of the progression to later times at higher binding energies, with a calculated toffset of 73 ± 10 fs as marked by the red line in Fig. 4.
2E1/2 states enables the signal due to the shifting feature in this region to be isolated, despite the domination of the quartet state signal. The fit to the shifting feature shows a continuation of the progression to later times at higher binding energies, with a calculated toffset of 73 ± 10 fs as marked by the red line in Fig. 4.
The increase in toffset with increasing binding energy provides a measurement of the excited-state wavepacket as it travels down the 3Q0 potential energy surface after excitation, mapping the transition from the bound FC geometry to the dissociation fragments, I, I* and CH3, which have much higher ionisation potentials, as seen in Fig. 1. The fits also include an observation time constant that gives a measure of how long the excited state wavepacket takes to move out of the energy window considered. While we can confidently assign a time constant of 23 ± 6 fs to the region between 5.0–6.0 eV, the constants obtained from the fit for the other regions (16 fs, 10 fs and 9 fs for the 6.6–7.0 V, 7.0–7.4 eV, and 7.7–8.5 eV energy regions respectively) are below our experimental resolution, such that we simply provide an upper bound of 20 fs in Table 1.
As mentioned earlier, the low excited state population means we cannot isolate the dynamic signals out to the final energies associated with the dissociation products, as they strongly overlap with the much stronger ground state signals. However, the time profiles in Fig. 4 map the increase in binding energy due to the lengthening of the C–I bond from its initial 2.2 Å out to almost 4 Å (as calculated from the potentials shown in Fig. 1), which is well beyond the region of the conical intersection and close to the neutral state asymptotic limit, but still within the bound well of the ground ion state potentials. Subsequent changes in the measured ionisation potential are therefore largely driven by the changes in the ion state potential.
To further characterise the dissociative increase in C–I bond length and the accompanying increase in binding energy with time after excitation, we perform classical 1D trajectory calculations on the 3Q0 potential shown in Fig. 1 and calculate approximate binding energies based on the separation between the neutral and ion states involved. The large energy gradient of the 3Q0 state along the C–I bonding coordinate means that extension of the C–I bond dominates the dynamics of the system. Detailed trajectory calculations on full dimensional potential energy surfaces10 show that during this rapid dissociation process, the ICH bond angle, θICH, decreases from that associated with the pyramidal Franck–Condon structure (θICH ∼ 110°), towards the planar CH3 geometry associated with the dissociation product. We therefore perform a classical dynamics simulation of the dissociation processes using the 1D cuts through the potentials of ref. 13 that include the θICH relaxation.
Our simulation starts on the 3Q0 state at an initial C–I bond length of 2.27 Å. This initial bond length is chosen by comparing the binding energy observed upon initial excitation with the calculated binding energy obtained for a range of internuclear separations. The dynamics along the 3Q0 surface are subsequently propagated using the classical velocity Verlet algorithm, with an initial velocity of 0, and with the resultant acceleration calculated from the potential energy surface in ref. 13. As the dissociation dynamics at this energy are dominated by the production of the spin–orbit excited I*(2P1/2) product,27 we only consider the dynamics on the 3Q0 surface and ignore any small contribution that may come from a non-adiabatic transition onto the 1Q1. For each time delay following excitation we therefore have a time dependent C–I bond length for trajectories that dissociate on the 3Q0 potential. To check the validity of the 1D model, we calculate fragment appearance times as defined in ref. 12, and find good agreement between our 1D model calculations (127 fs) with those obtained on both 4D (114 fs) and 9D (108 fs) surfaces as well as from experiment (114 fs).12
To calculate an approximate binding energy for each internuclear separation, we take the energy difference between the dissociative neutral surface upon which the dynamics proceed and the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ion state surfaces these will project on to. The ion state potentials are taken from ref. 26 and account for the relaxation of θICH, as with the neutral surfaces. This angle relaxation reduces the ionisation potential relative to keeping the θICH angle constant; using the relaxed potentials therefore provides a lower limit for the measured binding energy of the two ion states considered. The neutral and ion state potentials therefore allow us to convert the energy ranges measured in the experiment and presented in Fig. 4 to their equivalent bond length ranges. The bond lengths for each region are presented in Table 2, and show that each energy region corresponds to a sub-Angstrom range of bond lengths. If we assume ionisation into the
ion state surfaces these will project on to. The ion state potentials are taken from ref. 26 and account for the relaxation of θICH, as with the neutral surfaces. This angle relaxation reduces the ionisation potential relative to keeping the θICH angle constant; using the relaxed potentials therefore provides a lower limit for the measured binding energy of the two ion states considered. The neutral and ion state potentials therefore allow us to convert the energy ranges measured in the experiment and presented in Fig. 4 to their equivalent bond length ranges. The bond lengths for each region are presented in Table 2, and show that each energy region corresponds to a sub-Angstrom range of bond lengths. If we assume ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1/2 state dominates the spectrum at all C–I bond lengths (as it does at the FC geometry) we can see that following excitation it takes approximately 15 fs for the C–I bond to reach bond lengths between 2.50–2.64 Å, 40 fs to reach 2.64–2.78 Å, and 70 fs to reach 2.91–3.42 Å. The decrease in ionisation cross section across these ranges makes providing more accurate measurements difficult, but the ranges chosen provide approximate values of extending bond length.
1/2 state dominates the spectrum at all C–I bond lengths (as it does at the FC geometry) we can see that following excitation it takes approximately 15 fs for the C–I bond to reach bond lengths between 2.50–2.64 Å, 40 fs to reach 2.64–2.78 Å, and 70 fs to reach 2.91–3.42 Å. The decrease in ionisation cross section across these ranges makes providing more accurate measurements difficult, but the ranges chosen provide approximate values of extending bond length.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3/2 and
3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1/2 ion state. See text for more detail
1/2 ion state. See text for more detail
| Energy region (eV) | Bond length ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3/2 (Å) 3/2 (Å) |
Bond length ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1/2 (Å) 1/2 (Å) |
|---|---|---|
| 5.0–6.0 | 2.24–2.51 | 2.06–2.33 |
| 6.6–7.0 | 2.71–2.85 | 2.50–2.64 |
| 7.0–7.4 | 2.85–3.03 | 2.64–2.78 |
| 7.7–8.5 | 3.20–3.89 | 2.91–3.42 |
Combining the calculated bond lengths from the classical dynamics calculations with the binding energy calculation described allows us to generate a time dependent spectrum. To aid comparison with the experimentally measured equivalent, the calculated time-dependent spectrum is convolved with energy and temporal widths of 0.7 eV and 60 fs (FWHM) respectively, taken from those observed for the initial ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) features in the experiment. The relative intensities of the features from ionisation to the
features in the experiment. The relative intensities of the features from ionisation to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1/2 and
2E1/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E3/2 states are taken from the relative intensities experimentally observed at time zero, and these are maintained throughout the rest of the simulation.
2E3/2 states are taken from the relative intensities experimentally observed at time zero, and these are maintained throughout the rest of the simulation.
The resulting simulated time resolved photoelectron spectrum is shown in Fig. 5b, with the intensity normalised according to the maximum value for each energy slice, since the geometry-dependent ionisation propensity is not known. Superimposed on the colourmap we plot a pair of lines to highlight the underlying details of the simulation. These show the calculated binding energies associated with ionisation to the lowest two ion states, before convolution with the experimental temporal and spectral response functions. Fig. 5a shows the same experimental spectrum as in Fig. 3, this time normalised to the maximum intensity at each energy, and with a cubic spline interpolation in time, to aid comparison with the simulated spectrum. In Fig. 5a, as well as the consistent shift to higher binding energies, the renormalisation can make it appear that the signal associated with ionisation into the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3/2 state around 5.2 eV initially experiences a slight shift to a lower binding energy. Any such shift is, however, below the resolution of our measurements and does not show the same clear and consistent trend as seen at higher binding energies, such that this is not considered significant. This is supported by comparison to earlier multiphoton ionisation photoelectron spectroscopy experiments at the same pump energy which also show no shifts to lower binding energy at this pump wavelength.22
3/2 state around 5.2 eV initially experiences a slight shift to a lower binding energy. Any such shift is, however, below the resolution of our measurements and does not show the same clear and consistent trend as seen at higher binding energies, such that this is not considered significant. This is supported by comparison to earlier multiphoton ionisation photoelectron spectroscopy experiments at the same pump energy which also show no shifts to lower binding energy at this pump wavelength.22
Since we do not have a potential energy surface for the quartet ion state, we are unable to include ionisation to this state in the simulated spectrum. We therefore divide the plots in Fig. 5 into a region below around 7.3 eV where we expect a good match between the experimental and simulated spectra, and a region of higher binding energy where ionisation to the quartet state starts to contribute strongly to the signal, and only the less intense shifting feature is expected to correspond between the spectra.
As with the experimental spectrum, the simulated spectrum shows the shifting binding energy associated with the extending C–I bond length. At early times the agreement is good, with population in the binding energy region between 6.6–7 eV reaching a maximum between 15–25 fs, in good agreement with the experimentally measured profile. As the propagation continues, however, the higher energy bands are populated much more rapidly than seen in the experiment. While the simulations therefore show the same trend as the experiment over the full range, the 1D potentials appear to overestimate the acceleration, meaning higher binding energies are reached much more rapidly. This is perhaps unsurprising, as for a 1D classical model, all of the excitation energy is projected along the dissociation coordinate, meaning the bond length will increase faster than in the full system where energy can go into any of the other degrees of freedom.
To obtain precise values for the associated bond lengths, an accurate route to calculating the full photoelectron spectrum over a range of geometries and electronic states is required. This is a highly challenging problem such that our analysis remains, for the moment, qualitative, limited by the noise on the measurement and our ability to accurately calculate the expected photoelectron energy. Routes to accurate calculations of experimental observables are now key to the future analysis of modern time-resolved spectroscopy experiments.
4 Summary
We have measured the dissociation dynamics of CH3I following UV excitation using an XUV photoelectron spectroscopy probe. The measurements show features in the spectrum that undergo large shifts in binding energy with time, which map the extending C–I bond as the molecule dissociates. The shifts are analysed using a simple 1D classical model that allows us to extract approximate bond lengths. Fully exploiting the capabilities of XUV probe photoelectron spectroscopy to monitor changes in both electronic and geometric structure clearly requires highly accurate routes to calculating the full photoelectron spectrum, and accurate full dimensional potentials upon which to propagate the dynamics. In this sense CH3I remains an extremely challenging system. The complexity of the highly spin–orbit coupled potential energy surfaces, with dynamics and ionisation into multiple non-adibatically coupled states, makes this a real challenge. If we compare the timeframes measured here with those obtained in previous XUV transient absorption spectroscopy measurements of Attar et al.,11 we note that the intermediate signals in their XUV measurements reached a maximum around 40 fs and returned to baseline levels by delays of 90–100 fs. This is strikingly similar to the transient signal we have measured between 7–7.4 eV corresponding to bond lengths between 2.64–2.8 Å. The significance of this region to the transient absorption experiments is difficult to understand, but covers geometries after the traversal of the conical intersection as the neutral dissociative potential begins to level off. For modern chemical dynamics experiments, accurate calculations of observables are now vital for the analysis of photoelectron spectroscopy measurements where the observation of multiple reaction pathways project onto multiple ion states.The data presented also highlights many of the challenges associated with the time resolved photoelectron spectroscopy experiments with lab based XUV sources. Low excitation and ionisation cross sections, and signals that overlap with ground state features, combined with the necessarily small excitation fractions required to avoid multiphoton excitation, mean that further improvements are required to obtain good statistics across the full reaction pathway. This requires the continued development of high flux sources or the use of coincidence techniques that can be used to deconvolve the photoelectron spectrum into its constituent parts. Developments are ongoing at our lab and at many others that can provide high flux at high repetition rates that should allow for measurements to move beyond the relatively simple systems studied here.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. S. M. thanks the Royal Society for a University Research Fellowship (UF100047, UF150655). R. S. M. and J. W. thank the EPSRC for funding (EP/R010609/1). B. D. W. thanks the Central Laser Facility and Chemistry at the University of Southampton for a studentship. E. M. W. thanks Chemistry at the University of Southampton for a studentship. We also acknowledge funding from the EC's Seventh Framework Programme (LASERLAB-EUROPE, grant agreement 228334). Access to Artemis at the Central Laser Facility was provided by the STFC. We thank John Dyke for very useful conversations and Phil Rice for technical assistance.Notes and references
- A. Stolow, Annu. Rev. Phys. Chem., 2003, 54, 89–119 CrossRef CAS.
- A. D. Smith, E. M. Warne, D. Bellshaw, D. A. Horke, M. Tudorovskya, E. Springate, A. J. H. Jones, C. Cacho, R. T. Chapman, A. Kirrander and R. S. Minns, Phys. Rev. Lett., 2018, 120, 183003 CrossRef CAS.
- R. Spesyvtsev, T. Horio, Y.-I. Suzuki and T. Suzuki, J. Chem. Phys., 2015, 142, 074308 CrossRef CAS.
- T. Horio, R. Spesyvtsev and T. Suzuki, Opt. Express, 2013, 21, 22423–22428 CrossRef.
- C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Geßner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464–1468 CrossRef CAS.
- A. Ciavardini, M. Coreno, C. Callegari, C. Spezzani, G. De Ninno, B. Ressel, C. Grazioli, M. de Simone, A. Kivimäki, P. Miotti, F. Frassetto, L. Poletto, C. Puglia, S. Fornarini, M. Pezzella, E. Bodo and S. Piccirillo, J. Phys. Chem. A, 2019, 123, 1295–1302 CrossRef CAS.
- H. J. Wörner, J. B. Bertrand, B. Fabre, J. Higuet, H. Ruf, A. Dubrouil, S. Patchkovskii, M. Spanner, Y. Mairesse, V. Blanchet, E. Mével, E. Constant, P. B. Corkum and D. M. Villeneuve, Science, 2011, 334, 208–212 CrossRef.
- L. Nugent-Glandorf, M. Scheer, D. A. Samuels, A. M. Mulhisen, E. R. Grant, X. Yang, V. M. Bierbaum and S. R. Leone, Phys. Rev. Lett., 2001, 87, 193002 CrossRef CAS.
- R. J. Squibb, M. Sapunar, A. Ponzi, R. Richter, A. Kivimäki, O. Plekan, P. Finetti, N. Sisourat, V. Zhaunerchyk, T. Marchenko, L. Journel, R. Guillemin, R. Cucini, M. Coreno, C. Grazioli, M. Di Fraia, C. Callegari, K. C. Prince, P. Decleva, M. Simon, J. H. D. Eland, N. Došlić, R. Feifel and M. N. Piancastelli, Nat. Commun., 2018, 9, 637 CrossRef.
- M. E. Corrales, J. González-Vázquez, R. de Nalda and L. Bañares, J. Phys. Chem. Lett., 2019, 10, 138–143 CrossRef CAS.
- A. R. Attar, A. Bhattacherjee and S. R. Leone, J. Phys. Chem. Lett., 2015, 6, 5072–5077 CrossRef CAS.
- M. L. Murillo-Sánchez, J. González-Vázquez, M. E. Corrales, R. De Nalda, E. Martínez-Núñez, A. García-Vela and L. Bañares, J. Chem. Phys., 2020, 152, 14304 CrossRef.
- A. B. Alekseyev, H.-P. Liebermann, R. J. Buenker and S. N. Yurchenko, J. Chem. Phys., 2007, 126, 234102 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1940, 8, 382 CrossRef CAS.
- M. E. Corrales, V. Loriot, G. Balerdi, J. González-Vázquez, R. De Nalda, L. Bañares and A. H. Zewail, Phys. Chem. Chem. Phys., 2014, 16, 8812–8818 RSC.
- L. Rubio-Lago, A. García-Vela, A. Arregui, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 174309 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1999, 110, 832–844 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1998, 109, 4758–4767 CrossRef CAS.
- R. De Nalda, J. G. Izquierdo, J. Durá and L. Bañares, J. Chem. Phys., 2007, 126, 021101 CrossRef CAS.
- J. Durá, R. de Nalda, J. Álvarez, J. G. Izquierdo, G. A. Amaral and L. Bañares, ChemPhysChem, 2008, 9, 1245–1249 CrossRef.
- J. Durá, R. de Nalda, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 134311 CrossRef.
- E. M. Warne, B. Downes-Ward, J. Woodhouse, M. A. Parkes, D. Bellshaw, E. Springate, P. Majchrzak, Y. Zhang, G. Karras, A. S. Wyatt, R. T. Chapman, A. Kirrander and R. S. Minns, Phys. Chem. Chem. Phys., 2019, 21, 11142–11149 RSC.
- F. Allum, M. Burt, K. Amini, R. Boll, H. Köckert, P. K. Olshin, S. Bari, C. Bomme, F. Brauße, B. Cunha de Miranda, S. Düsterer, B. Erk, M. Géléoc, R. Geneaux, A. S. Gentleman, G. Goldsztejn, R. Guillemin, D. M. P. Holland, I. Ismail, P. Johnsson, L. Journel, J. Küpper, J. Lahl, J. W. L. Lee, S. Maclot, S. R. Mackenzie, B. Manschwetus, A. S. Mereshchenko, R. Mason, J. Palaudoux, M. N. Piancastelli, F. Penent, D. Rompotis, A. Rouzée, T. Ruchon, A. Rudenko, E. Savelyev, M. Simon, N. Schirmel, H. Stapelfeldt, S. Techert, O. Travnikova, S. Trippel, J. G. Underwood, C. Vallance, J. Wiese, F. Ziaee, M. Brouard, T. Marchenko and D. Rolles, J. Chem. Phys., 2018, 149, 204313 CrossRef.
- K. Amini, E. Savelyev, F. Brauße, N. Berrah, C. Bomme, M. Brouard, M. Burt, L. Christensen, S. Düsterer, B. Erk, H. Höppner, T. Kierspel, F. Krecinic, A. Lauer, J. W. L. Lee, M. Müller, E. Müller, T. Mullins, H. Redlin, N. Schirmel, J. Thøgersen, S. Techert, S. Toleikis, R. Treusch, S. Trippel, A. Ulmer, C. Vallance, J. Wiese, P. Johnsson, J. Küpper, A. Rudenko, A. Rouzée, H. Stapelfeldt, D. Rolles and R. Boll, Struct. Dyn., 2018, 5, 014301 CrossRef.
- L. Drescher, M. C. E. Galbraith, G. Reitsma, J. Dura, N. Zhavoronkov, S. Patchkovskii, M. J. J. Vrakking and J. Mikosch, J. Chem. Phys., 2016, 145, 011101 CrossRef CAS.
- S. Marggi Poullain, D. V. Chicharro, J. González-Vázquez, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2017, 19, 7886–7896 RSC.
- R. de Nalda, J. Durá, A. García-Vela, J. G. Izquierdo, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2008, 128, 244309 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03478a |
| This journal is © the Owner Societies 2020 |

