Open Access Article
Open Access ArticleStructural characterization of supramolecular hollow nanotubes with atomistic simulations and SAXS†
Ilias
Patmanidis
 a,
Alex H.
de Vries
a,
Tsjerk A.
Wassenaar
a,
Wenjun
Wang
b,
Giuseppe
Portale
a,
Alex H.
de Vries
a,
Tsjerk A.
Wassenaar
a,
Wenjun
Wang
b,
Giuseppe
Portale
 c and
Siewert J.
Marrink
c and
Siewert J.
Marrink
 *a
*a
aGroningen Biomolecular Science and Biotechnology Institute and Zernike Institute for Advanced Materials, University of Groningen, Groningen, The Netherlands. E-mail: s.j.marrink@rug.nl; Tel: +31 50 36 34457
bLeiden University Medical Center, Leiden, The Netherlands
cDepartment of Polymer Chemistry, Zernike Institute for Advanced Materials, University of Groningen, Groningen, The Netherlands
First published on 9th September 2020
Abstract
Self-assembled nanostructures arise when building blocks spontaneously organize into ordered aggregates that exhibit different properties compared to the disorganized monomers. Here, we study an amphiphilic cyanine dye (C8S3) that is known to self-assemble into double-walled, hollow, nanotubes with interesting optical properties. The molecular packing of the dyes inside the nanotubes, however, remains elusive. To reveal the structural features of the C8S3 nanotubes, we performed atomistic Molecular Dynamics simulations of preformed bilayers and nanotubes. We find that different packing arrangements lead to stable structures, in which the tails of the C8S3 molecules are interdigitated. Our results are verified by SAXS experiments. Together our data provide a detailed structural characterization of the C8S3 nanotubes. Furthermore, our approach was able to resolve the ambiguity inherent from cryo-TEM measurements in calculating the wall thickness of similar systems. The insights obtained are expected to be generally useful for understanding and designing other supramolecular assemblies.
1 Introduction
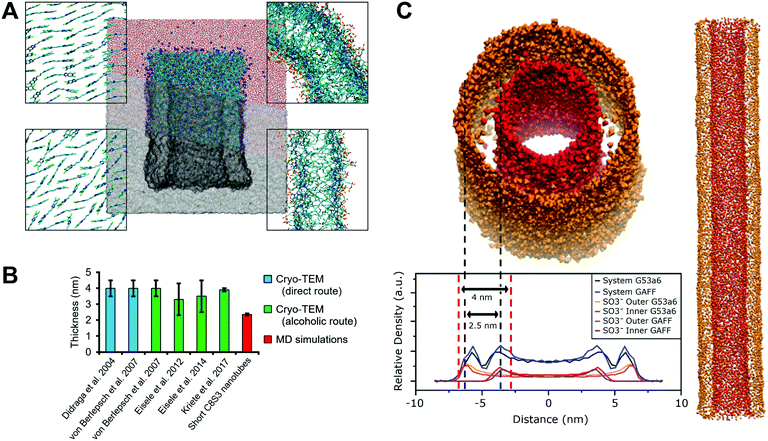
Cyanine dyes are molecules with extraordinary optical and structural properties, including ultrafast emission, sharp absorption and fast electronic transfer.1–3 These properties make cyanine dyes excellent model systems for fundamental research on exciton transfer and energy transport at the molecular level and have caused a surge of interest in these systems and their applications in fields such as photography,4,5 labelling,6,7 nonlinear optics,8etc.Over the past decades, several cyanine dyes that incorporate the chromophore 5,5′,6,6′-tetrachloro-benzimida-carbocyanine and different substituents have been synthesized and studied.9,10 Most of these dyes have the ability to aggregate and form highly ordered supramolecular structures of various shapes and sizes that exhibit different optical properties.11,12 An interesting example is the amphiphilic cyanine dye 3,3′-bis(2-sulfopropyl)-5,5′,6,6′-tetrachloro-1,1′-dioctyl-benzimida-carbocyanine (C8S3). The chemical structure of a single C8S3 monomer can be divided into three parts, the hydrophilic heads, the cyanine dye chromophore (aromatic core) and the hydrophobic tails (Fig. 1A). When solvated in polar solvents, C8S3 monomers spontaneously self-assemble into double-walled tubular aggregates (hollow nanotubes)12 (Fig. 1B).
 | ||
| Fig. 1 C8S3 nanotube organization. (A) Chemical structure of a C8S3 monomer. (B) Graphical representation of a C8S3 nanotube (center). Cryo-TEM image of C8S3 nanotubes (top left). Slice from the top view of a proposed arrangement model (top right), slice from the side (bottom right) and C8S3 monomers arranged in the Herringbone formation (bottom left). Images have been prepared in ChemDraw and VMD.14 | ||
The driving force for the formation of the C8S3 nanotubes is a combination of intermolecular interactions, where entropic and enthalpic contributions are carefully balanced. The hydrophobic effect determines the orientation of the polar groups toward the solvent on the inside and outside of the nanotube and the non-polar groups toward the interior of the nanotube, whereas electrostatics and pi–pi stacking create a network of interactions that regulates the position and arrangement of the aromatic cores with respect to each other. The high polarizability of the conjugated system generates strong van der Waals forces (induced dipole interactions) and dense packing of the C8S3 monomers. Additionally, the organized packing leads to special excitation states of the electrons of the aromatic backbone, called Frenkel excitons,13 which are responsible for the optical properties of the C8S3 nanotube and other cyanine dye aggregates in general.
Despite the various experimental data, mainly from cryo-Transmission Electron Microscopy (cryo-TEM),12,15–18 the resolution of the current techniques is not sufficient to reveal the atomistic structural details of the C8S3 nanotubes. On the other hand, theoretical models for the molecular arrangement of the C8S3 monomers reproduce the transition dipole moments of the experimental spectra, but they lack an explicit atomistic description.19–22
Computer simulations, in particular molecular dynamics (MD) simulations, are an invaluable tool to obtain information not accessible by experimental methods and fill the gaps between theory and experiments.23–25 Previous MD simulations on the C8S3 nanotubes or other members of the cyanine dye family presented good agreement with experimental results.26 However, the simulated structures were either not stable or were simulated for short time scales (∼10 ns). There are several issues that render the tasks of constructing and performing MD simulations of such systems far from trivial. The first group of issues is related to the dimensions of the aggregates and the arrangement of the monomers. Experiments do not always provide enough information at the same resolution as atomistic simulations. Consequently, it is extremely difficult to estimate accurately the number of C8S3 molecules in the inner and outer wall and construct structures that maintain their designed formation, if the initial number of molecules is not optimal. Since experimental evidence for the packing of C8S3 is not yet available, the packing motifs (e.g. Brickwork, Herringbone, Staircase) are extrapolated from the experimental results based on similar molecules or theoretical models.27–29 Furthermore, experimental or theoretical based approaches to construct models provide ideal structures that diminish the presence of disorder and do not necessarily produce either correct or stable structures. The second group of issues is related to the differences between the available force fields in MD simulations that can ultimately produce results that do not converge. Last, the feasible simulated time scales for such large systems are usually inadequate to sample different packing rearrangements and reach the most favourable energy states, especially, if the systems are kinetically trapped in intermediate low energy states.
In this work, we employed MD simulations to shed light on the structural properties of C8S3 nanotubes and on the preferred arrangement of the C8S3 monomers inside the aggregates. To alleviate some of the aforementioned problems, we optimized specific parameters of the standard GROMOS force field by using Quantum Mechanical (QM) methods to obtain a better description for C8S3 monomers and performed simulations of different systems (bilayers and nanotubes) to understand the behavior of these molecules in different arrangements. We also took great care in the way the nanotube systems were prepared to avoid possible initial stresses resulting in nanotube collapses. The timescales of our simulations were extended to 100–500 ns allowing us to distinguish stable conformations from unstable ones. To verify our findings, we conducted Small Angle X-ray Scattering (SAXS) experiments and compared the profiles with simulated SAXS spectra from our C8S3 nanotube simulations. In addition, we were able to match our simulated density profiles to cryo-TEM data, suggesting that the nanotube thickness and the inner wall boundaries, as reported from cryo-TEM, need reinterpretation.
2 Methods
2.1 MD simulations
C8S3 bilayer and nanotube simulations were performed with the GROMACS 5.1.4 simulation package30,31 and the G53a632 force field. Those systems were solvated in rectangular or cubic boxes with explicit SPC water molecules.33 Counter ions (Na+) were introduced to neutralize all systems. Since C8S3 molecules are bought as powder (C8S3− Na+) and they are dissolved with ultrapure water/methanol, no excess of salt was added to stay as close as possible to the experimental setup. The temperature was kept constant at 300 K by using the Canonical Sampling Velocity-Rescaling (CSVR) thermostat with a time constant of 0.1 ps.34 For the pressure coupling, the Berendsen barostat35 was used to maintain the pressure constant at 1 bar with a time constant of 1 ps and compressibility of 4.5 × 10−5 bar−1. Semi-isotropic pressure coupling was used for all bilayer systems to allow the systems to equilibrate separately in the z-dimension, which coincides with the bilayer normal, and in the x–y dimensions (bilayer plane). For the solvated nanotubes, an isotropic pressure bath was used. The cut-off for electrostatic and van der Waals interactions was set to 1.4 nm and the Verlet scheme was used for the short range non-bonded interactions. Long range interactions were calculated with the reaction field method.36 The LINCS algorithm was employed for constraining the bond lengths.37 All systems were minimized for 103 steps by using the steepest descent algorithm and equilibrated in two phases, in the NVT and NPT conditions with a 1 fs time step. The NVT equilibration lasted 100 ps for the bilayer and the short nanotube simulations, and 10 ps for the long nanotubes. The NPT equilibration lasted 100 ps for the bilayer simulations, 1 ns for the short nanotubes, and 5 ns for the long nanotubes. During equilibration, the aromatic cores of the C8S3 molecules were kept in place by using position restraints with 1000 kJ mol−1 force constant. Restraining the aromatic cores allowed the water and side chains of the C8S3 molecules to relax before the start of the production phase. The production phase was performed in the NPT ensemble, and the time step for integration was set to 2 fs. Each bilayer trajectory was 500 ns long and each short nanotube trajectory was 100 ns long, whereas the long nanotube simulations lasted 10 ns.Additional C8S3 bilayer and nanotube simulations were performed with the General Amber Force Field38 (GAFF) to compare the results between G53a6 and GAFF. In GAFF simulations, TIP3P water model39 was used instead of SPC. Apart from the force field comparison, the effect of the temperature and the solvent on the bilayers were tested. Specifically, an extra set of bilayer simulations with the G53a6 force field was performed at 288 K, the temperature at which AFM40 experiments on C8S3 layers were conducted. C8S3 nanotubes can self-assemble through a direct route (pure water) or an alcoholic route (water and methanol solution), and the final aggregates differ in size.16 The effect of methanol was measured by substituting a portion of water with methanol (20% v/v) to resemble the conditions of cryo-TEM experiments.16–18 Parameters for methanol were obtained from the Automated Topology Builder41 (https://atb.uq.edu.au/, ATB molecule ID: 15607). The duration of these simulations was 250 ns, and for the systems at 288 K and those that included methanol the final frames of the initial G53a6 simulations were used as starting coordinates.
2.2 C8S3 parametrization
Molecules of this family of cyanine dyes have not been previously parametrized for the GROMOS force fields and G53a632 force field mainly focuses on small molecules, so we resorted to higher levels of theory (QM methods) to improve the C8S3 parameters. In order to study the properties of the aromatic core and optimize the dihedral angles of the polymethine bridge of the C8S3 molecule, we prepared a simpler cyanine dye, 5,5′,6,6′-tetrachloro-1,1′,3,3′-tetramethylbenzimidacarbocyanine (C1C1), and used it as a reference for the QM calculations (see Fig. S1A of the ESI†). The QM calculations were performed by using the hybrid density functional B3LYP42–45 with the 6-31G* basis set, and Dipole preserving analysis (DPA)46 in the GAMESS-UK package47 was used to determine the partial charges of the molecules. The results for the dihedral profiles are presented in Fig. S1B and Table S1 of the ESI,† and the partial charges are reported in Table S2 of the ESI.†2.3 C8S3 bilayers
Small systems where the monomers were organized in preformed bilayers were constructed to study the arrangement of C8S3 molecules and allow the calculation of structural properties (such as bilayer thickness, molecular arrangement, tail order parameter, etc.) of small slices representative of the C8S3 nanotubes. The box size of these systems was ∼10 × 7 × 10 nm, and each box contained ∼200 C8S3 molecules. The crystal structures of molecules with the same aromatic core27,28 and previous models for the arrangement of the monomers12,29 were used as templates for the preparation of the initial coordinates of each system. Bilayers with three different arrangements were created (Brickwork, Herringbone and Staircase formation). The initial thickness of the bilayers was set to ∼4.0 nm, close to the reported values for the thickness of the C8S3 nanotube in several experimental studies.16,18,22 Our main goal was to verify whether or not the bilayers would maintain their initial thickness and find an optimal thickness value for constructing nanotubes. A detailed list of all the simulated bilayers is presented in Table S3 of the ESI.† Measured structural properties for each simulation separately are included in Tables S4 and S5 of the ESI.† Statistical analyses for different observables as a function of time are presented in Fig. S2 of the ESI.† Furthermore, the similarity with the initial conformation and the overall order of the aromatic rings are shown in Fig. S3 in the ESI.† The last 100 ns of each trajectory were used for the analysis of the bilayers.2.4 C8S3 nanotubes
MD simulations of preformed C8S3 nanotubes were conducted to evaluate the ability of C8S3 molecules to maintain a tubular formation. The initial coordinates were generated by creating 2D lattices from single unit cells and rolling them into cylinders with specific rolling angles (α, eqn (1)) and radii (r, eqn (2)). The rolling angles and radii depend on the unit cell size and the imposed pitch providing discrete values for both parameters. This procedure used was inspired by previous methods to study similar systems.12,29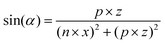 | (1) |
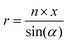 | (2) |
The rolling angle (α) is a function of the imposed pitch, which is proportional to the dimension of the unit cell in the z-axis (p × z), and the number of unit cells in the x-axis (n × x). The z-axis represents the height and the x-axis the width of the lattice. The radius (r) of the folded cylinder is a function of the rolling angle and the width of the lattice.
Short nanotubes (∼1500 C8S3 molecules) with a tube length of ∼15 nm were generated. According to cryo-TEM measurements, the inner and outer radii are ∼3.0 and ∼6.5 nm,19 respectively. Several systems were prepared in which the radius of the inner and outer wall was set in the range of 2.5 to 4.0 and 5.5 to 7.0 nm, respectively, and the rolling angle of the lattice was set in the range of ∼20–30° (see Table S6 of the ESI†). The constructed C8S3 nanotubes were solvated in cubic boxes with water. The size of the periodic boxes was ∼25 × 25 × 25 nm to allow enough space between the periodic images of the nanotube. Finally, simulations of solvated nanotubes with ∼8000 C8S3 molecules, referred as long nanotube with length ∼100 nm were performed. The box size was 18 × 18 × 120 nm and the center of mass motion was removed every 0.1 ps to ensure that the nanotube does not cross the periodic boundary conditions. The last 50 ns were used for the analysis of the short nanotubes. Statistical analyses for nanotube thickness as a function of time are presented in Fig. S4 of the ESI.† Furthermore, to show that the water is well equilibrated during our simulations, we plotted the density of the water molecules at different stages of the system preparation and the end of the production phase, Fig. S5 of the ESI.†
2.5 Order parameter
The ordering of the aromatic cores with respect to the initial formation was measured by defining a second-rank order parameter, P2 (eqn (3)) for the angle theta (θ) between the vector along the last carbons of the polymethine bridge at the initial conformation (average orientation of the molecules) and during the simulation. The same order parameter was used to calculate the angle between the bilayer normal and the vectors defined by each bond of the hydrophobic tails.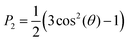 | (3) |
P 2 ranges from −0.5 to 1, where values close to −0.5 indicate that the aromatic core vector and the average direction are perpendicular, whereas values close to 1 indicate that the vectors are parallel. Values close to 0 indicate either a lack of preference (random orientation) or orientation at the magic angle (54°).
2.6 SAXS
SAXS measurements were performed in solution at the MINA laboratory instrument (Groningen, NL). The instrument is built on a Cu rotating anode providing a high flux X-ray beam of wavelength lambda = 1.5413 Ang. The samples were prepared according to the protocol described in Kriete et al.48 In order to cover a wide angular range, two different SAXS patterns were acquired per each sample using two different sample-to-detector (S-to-D) distances, 240 mm and 3100 mm respectively. The SAXS patterns were acquired using two Bruker Vantec detectors. Before performing radial averaging around the direct beam position, the SAXS patterns were corrected for the sample absorption and the background signal was subtracted. The radial averaging was performed using MATLAB to obtain SAXS 1D profiles. The angular scale was calibrated using the known peak position from a AgBe standard sample and the two profiles were merged into a single profile using MATLAB. Data were handled using the OriginLab software and the simulations were performed using the SASfit program.493 Results and discussion
3.1 C8S3 bilayers
In order to probe the most robust packing arrangement, several bilayers were simulated to measure structural features of C8S3 molecules in small systems representative of vertical slices of the double-walled C8S3 nanotube (Fig. 2A). We were mainly interested in the thickness and the packing arrangement of these formations, since they can be compared to the available experimental results from AFM40 for C8S3 and X-ray crystallography27,28 for cyanine dyes of the same family, respectively. The packing arrangements tested were a Brickwork, a Herringbone and a Staircase formation illustrated in Fig. 2B. Additionally, we tested different conditions, such as solvent types, temperature and force field parameters. Initial and final frames of representative simulations are shown in Fig. 2A and B, which contain side views and top views of the simulated systems, respectively.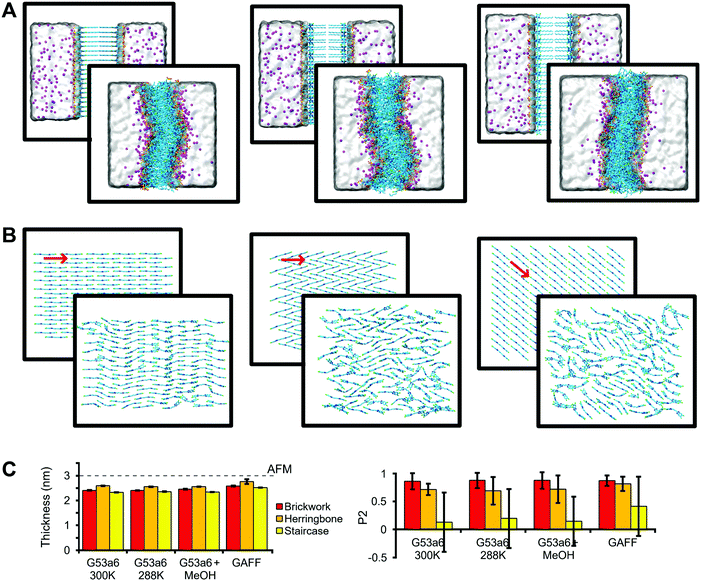 | ||
| Fig. 2 Structural arrangement of C8S3 bilayers. (A) Snapshots of a side view of the systems before and after the MD simulation, starting from Brickwork (left), Herringbone (middle), and Staircase (right) conformation. Water is represented as a transparent surface and Na+ cations as magenta spheres. (B) Top view for each conformation. Solvent and side chains have been removed for clarity. The red arrows indicate the average direction of the core. (C) Comparison between experimental bilayer thickness measured by AFM40 (dashed line) and the thickness calculated with MD simulations (left). Order rank parameter (P2) for the orientation of the polymethine bridge with respect to average direction in the initial structure (right). The error bars correspond to standard deviation. | ||
The initial thickness of each bilayer was set to ∼4.0 nm, but, in all cases, the bilayers collapsed from the separated leaflet formation to an interdigitated one with reduced thickness (Fig. 2A and C). Furthermore, the bilayers became slightly curved in all simulations. Regarding the lateral arrangement, the Brickwork formation proved to be the most robust arrangement, since it remained almost intact throughout the simulations (Fig. 2B). The Herringbone formation was in general disordered, but locally, small regions maintained the initial arrangement, whereas the Staircase formation was completely lost. As a quantitative measure of ordering, we used a second-rank order parameter (P2), which is shown in Fig. 2C and underlines our statement of highest order for the Brickwork formation and lowest order for the Staircase one, which is also evident in Fig. S3 in the ESI.† Details of the P2 calculation are described in the Methods section.
In general, the simulated values for thickness (2.48 ± 0.12 nm, mean value ± standard deviation of the mean values for each system), as measured from the distance between the center of mass of the SO3− groups in the upper and lower leaflets, are smaller than the reported experimental values (3.00 ± 0.15 nm) from AFM40 (Fig. 2C). An explanation for the difference could be that the AFM experiments were performed at 288 K, whereas most MD simulations were conducted at 300 K. Small changes in the temperature can affect the thickness and the organization of the lipid tails in the vicinity of the phase transition. However, if such an effect is present, it was not captured by our simulations performed with the G53a6 force field at 288 K (Fig. 2C).
C8S3 aggregates assemble in either water or water–methanol solutions, but the type of solvent affects their diameter.11,16 In order to test the effect of methanol on the thickness or the order of the monomers, additional simulations in which part of the solvent was replaced by methanol were conducted. We found that methanol does not seem to alter the structural features that we were interested in (Fig. 2C). We conclude that the main effect of methanol is increasing the solubility of the monomers due to its amphiphilic nature, in agreement with the current view in the literature.11
Furthermore, to test the effect of the force field, we performed an additional set of simulations using the generalized Amber force field (GAFF). Though the thickness as well as order parameter increase somewhat with respect to the results obtained with the Gromos force field, the increase is not enough to match the AFM data (Fig. 2C). Importantly, the C8S3 molecular arrangement becomes also interdigitated with the GAFF force field.
Apart from the bilayer thickness and the local order of the aromatic cores, we have measured additional structural features to understand and quantify the organization of the C8S3 monomers when aggregates are formed. Specifically, for all simulated systems, the aliphatic tails are not parallel to the bilayer normal (tail order parameter: 0.17 ± 0.06), suggesting the aliphatic tails are splayed and supporting our statement that the C8S3 molecules are interdigitated. Furthermore, the area per molecule does not change significantly among simulations (area per molecule: 0.86 ± 0.04 nm2), indicating the integrity of the bilayers is not really affected by the different simulation conditions. Finally, C8S3 molecules have diffusion coefficients indicative of very low lateral mobility (7.8 ± 4.0 μm2 s−1). The measurements for each system separately are reported in Table S5 of the ESI.†
Taken together, our bilayer simulations show that the C8S3 molecules interdigitate in the lamellar geometry, resulting in an optimal packing of the hydrophobic tails. The C8S3 bilayer thickness converged to ∼2.5 nm regardless of the MD simulation setup. Both Brickwork and Herringbone arrangements are plausible, with Brickwork being more ordered. According to our measurements, the C8S3 bilayer thickness is smaller than the reported values from AFM.40 However, looking at the raw height histogram in the AFM experiments40 suggests that the thickness of the bilayer is close to 3 nm, albeit slightly smaller. Furthermore, the proposed model for the arrangement of the C8S3 molecules in the bilayer assumes the aliphatic tails are fully extended, which could explain why the C8S3 bilayer thickness reported is a bit higher in AFM.
3.2 C8S3 nanotubes
Next, we built short C8S3 nanotubes, ∼15 nm in length and consisting of ∼1500 C8S3 molecules to systematically test the ability of the constructed models to maintain a tubular formation. We performed four 100 ns simulations, two with the Brickwork and two with the Herringbone formation. For each conformation different tube radii were considered, all of them with an initial double-wall thickness ∼2.5 nm. Initial inner and outer wall radii, as well as rolling angles for each wall are reported in Table S6 of the ESI.† All simulated systems maintained the tubular structure during the simulations. A snapshot from a short C8S3 nanotube at the end of the simulation is shown in Fig. 3A and more snapshots that present the initial and final arrangement of the monomers is shown in Fig. S5 of the ESI.† The Staircase formation was no longer considered as this conformation lost its initial arrangement in the bilayer simulations described above. Furthermore, a short nanotube simulation with the Staircase formation showed that within the first 10 ns, the initial arrangement was not maintained, Fig. S6 of the ESI.† Experiments and theory suggest that a high degree of order is present when such aggregates are formed.12,15–18In line with the bilayer simulations, the C8S3 molecules adopted a stable formation where the aliphatic tails were interdigitated with a nanotube thickness of 2.31–2.39 nm at the end of the simulations. The measured thickness from our MD simulations is similar to the thickness in the bilayer configuration, but it is significantly lower than the reported values in literature, 3.5–4.0 ± 0.5 nm12,15–18 (Fig. 3B). The final dimensions of each nanotube are reported in Table S7 of the ESI.†
To assess whether the short length of the simulated nanotubes somehow resulted in artificial behavior, we also constructed a long C8S3 nanotube (∼100 nm) that was simulated for 10 ns with the G53a6 and the GAFF force field. The nanotubes maintained the tubular formation in both simulations and the final nanotube thickness was ∼2.5 nm, comparable to the short nanotubes (Fig. 3C). The long nanotubes were subsequently used to compute electron density profiles that allow a more direct comparison to the experimental cryo-TEM data. Electron density profiles of such systems can be used to decipher the contribution of the inner and outer wall to the total signal, since the separation of the inner and outer wall density is feasible in the MD simulations (Fig. 3C). Specifically, the areas with the highest SO3− density, that should correspond to the surface of the nanotube, can be used to define the double-wall boundaries. Our results show that when the thickness is calculated by the distance between the SO3− groups of the inner and outer wall, the values are considerably smaller. Based on this interpretation of the electron density profiles, we consider that our definition of the C8S3 nanotube thickness is more realistic.
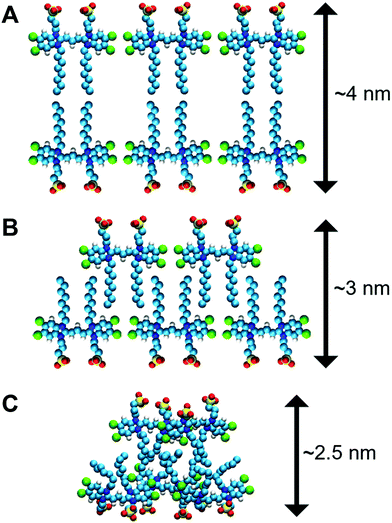
There are additional data that support our idea of interpreting the nanotube thickness and are summarized in Fig. 4. In more detail, if two C8S3 molecules are placed stretched and flat next to each other, the maximum distance between the SO3− groups would be ∼4.0 nm (Fig. 4A). However, this arrangement suggests there are gaps between the aliphatic tails. At room temperature, the area occupied by the aliphatic tails is ∼0.2 nm2 in lipid bilayers,50 and in the C8S3 bilayers the area per molecule is ∼0.86 nm2 (Table S5 of the ESI†). Consequently, in the bilayer formation for every C8S3 molecule approximately four aliphatic tails are required to fill the available space suggesting a strongly interdigitated model (Fig. 4B). The thickness of the C8S3 bilayer in this formation is ∼3 nm, as reported in AFM experiments.40 To reach this thickness, the aliphatic tails would have to be in the gel phase close to room temperature, but the length of the tails does not suggest so. In general, as the length of an aliphatic tail decreases, so does the temperature at which it enters the gel phase. For example, typical phospholipids such as dilauroyl-phosphatidylcholine (DLPC) and dipalmitoyl-phosphatidylcholine (DMPC) lipids have twelve and fourteen carbons in their aliphatic tails, respectively, and their transition temperature to the gel phase is 277 and 297 K. The size of the C8S3 aliphatic tails is only eight carbons suggesting that the transition temperature to the gel phase is significantly lower than 277 K. It is quite unlikely that the molecules are actually stretched to that extent at room temperature. This argument is also supported by the values of the aliphatic tail order parameter during the simulations (Table S5 of the ESI†). To summarize, the most realistic representation for the arrangement of the C8S3 molecules would be when the tails are disordered (melted) and interdigitate to fully occupy the inter-leaflet space (Fig. 4C). The thickness in this formation should be ∼2.5 nm.
3.3 SAXS and MD
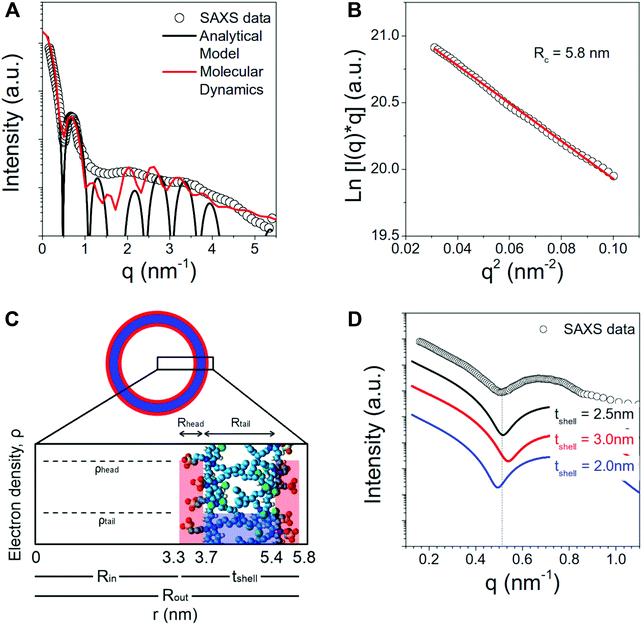
SAXS and MD simulations can be combined in different ways to obtain structural and dynamical information for various systems.51–53 In SAXS experiments, the scattering intensities of the samples after being exposed to X-rays are recorded. The distribution of the intensities provides information on the shape and size of objects inside the sample. In order to interpret the SAXS profiles, structural models can be employed,54 but choosing the correct model and fitting it to the experimental results is not always trivial. Implications arise from the sensitivity of the SAXS measurements to the contrast of the object and its hydration layer with respect to the solvent and from possible conformational fluctuations of the object that are necessarily present in the structural models.55 MD simulations reproduce correctly the hydration layer of the sample and the solvent density, and provide information on the conformational fluctuations of the molecules, thus making the combination of SAXS and MD a powerful for simulating scattering intensities.55–57To validate further our simulation results, we conducted SAXS experiments to characterize the structural features of C8S3 nanotubes in water/methanol solution.48 The obtained SAXS spectra were compared to MD simulated spectra55 from short C8S3 nanotubes with different dimensions that are reported in Table S7 of the ESI.† The experimental spectrum was also compared to a number of simple models for the electron density distribution in tubular assemblies (Fig. 5). Simulated scattering intensities for every short nanotube and the comparison to the experimental profile are presented in Fig. S7 of the ESI.†
The scattering curve of the C8S3 nanotubes shows a decaying trend with the scattering vector q, characterized by several oscillations characteristic for the size of self-assembled objects. The decay of the intensity in the low q region (q < 0.5 nm−1) is typical for long anisotropic objects, in agreement with the long nanotubes observed by cryo-TEM,12,15–18Fig. 5A. In order to first measure the radius of the nanotubes, we have estimated the cross-sectional radius using the Guinier analysis.58 The cross-sectional Guinier plot for the C8S3 nanotubes is plotted in Fig. 5B. The cross-sectional radius of gyration Rc is found to be 5.8 nm.
The region for q < 1 nm−1 can be well described by the scattering intensity from a cylinder with three concentric shells of high–low–high electron density (black curve in Fig. 5A), with parameters R1 = Rin = 3.3 nm, R2 = 3.7 nm, R3 = 5.4 nm and R4 = Rout = 5.8 nm (see Fig. 5C). The discrepancy between the experimentally measured scattering intensity and the model for q > 1 nm−1 can be ascribed to several factors. Size polydispersity, structural disorder and limited instrumental resolution can smear the intensity oscillations. Moreover, this portion of the curve is expected to also contain contributions from the intermolecular distances among the molecules of the nanotube walls that are not considered in the analytical model.
Notably, the low-q region can be used to verify the validity of the structural parameters from MD calculations. Fig. 5D shows the comparison between the experimental data and the simulated curves with different shell thickness but same nanotube outer radius (5.8 nm). It can be seen that the shape and first minimum position of the experimental data can be well reproduced by the model with total shell thickness 2.5 nm.
These SAXS results indicate that the optimal thickness calculated from MD is highly probable. Moreover, the simulated scattering spectra from the MD nanotube structure (red curve in Fig. 5A) is in excellent agreement with the experimentally measured SAXS data.
3.4 Cryo-TEM and SAXS/MD
To date, the most frequently used technique for the structural characterization of the molecular nanotubes has been cryo-TEM. Cryo-TEM has been proven particularly useful working hand in hand with exciton theory/spectral calculations and MD simulations by providing constraints on the characteristic sizes and geometry of such system.19,26,29,48 The distinct double-peak modulation of the cross-sectional profile extracted from cryo-TEM images clearly resolves the nanotubes' structure, comprising the inner and outer concentric tubes. At the same time, the objects remain as close as possible to their native state, thanks to the fast freezing that prevents the emergence of artifacts due to the temperature change. However, it is not straightforward to extract the characteristic sizes (e.g. inner and outer tube diameter) from these profiles, as there is no one-to-one correspondence between the contrast (amplitude) in the cryo-TEM image to the underlying molecular structure. As a consequence, different metrics concerning the nanotubes' characteristic sizes exist in literature.12,19,48,59While the diameter of the outer tube layer is well-defined against the background in the image and, thus, consistently reported as ∼13 nm, the diameter of the inner nanotube layer is subject to more ambiguity, with the reported values ranging from ∼5.0 to ∼6.7 nm. Part of this ambiguity arises from the fact the inner tube is always imaged at the background of the outer tube that encases the inner tube. The variations of the inner tube diameter also lead to variations of the reported wall thickness of C8S3 nanotubes (calculated as the difference between the outer and inner tube radii), ranging from ∼3.5 to ∼4.0 nm depending on the chosen metric. Having an accurate measure of the wall thickness, however, is of particular relevance to assess the (electronic) coupling between the inner and outer tube, which in turn governs the nanotubes' excitonic properties.
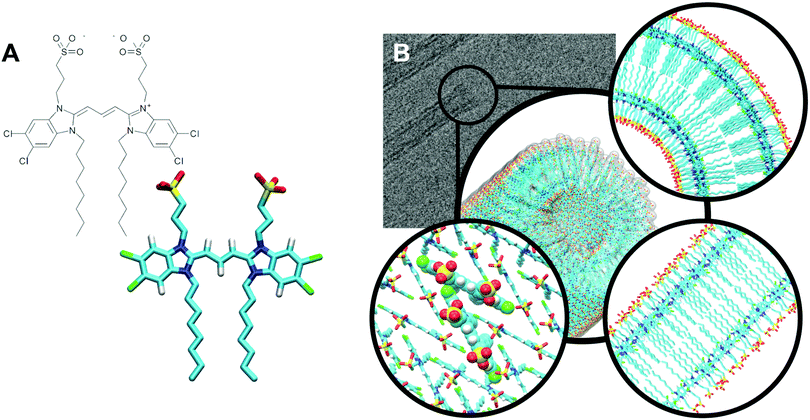
An electron density profile obtained from MD simulations is superimposed with the cross-section of a cryo-TEM image,48Fig. 6. If we assume that the contrast in the TEM image is directly proportional to the electron density (that gives rise to elastic scattering of electrons and phase contrast), matching of the MD and experimental data is very reasonable for the Herringbone 1 model. These results are fully consistent with the SAXS measurements. A more quantitative comparison to cryo-TEM would require simulation of the TEM images based on the molecular structure, which accounts for image formation in a TEM (including defocus, etc.) as well as other imaging-related effects such as the formation of Fresnel fringes.29 Moreover, different molecular entities, e.g. the extended π-electron backbone versus the apolar side-chains, interact differently with the incident electrons giving rise to different phase contrast in the image. Such treatment however, goes beyond the scope of the current paper. The comparison of the electron density profiles from all short nanotube simulations is presented in Fig. S8 of the ESI.† A similar thickness (∼2.4 nm) for C8S3 nanotubes is also suggested by recent results on modelling the inner and outer wall radii in flash-dilution experiments.60
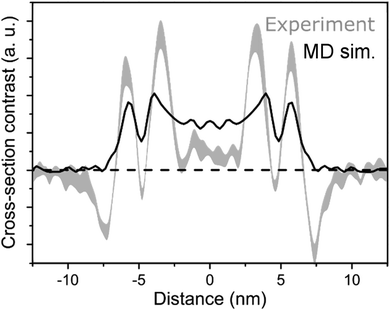 | ||
| Fig. 6 Comparison of MD and cryo-TEM. In black, the projected electron density profile of Herringbone 1 simulation, and in grey, a cryo-TEM cross-section.48 | ||
3.5 Unstable nanotube models
Apart from the successful simulations, attempts have been made to construct stable C8S3 nanotubes by using the previously suggested models,19 but they were fruitless. We speculate that the main problems were the initial arrangement of the monomers based on the phenomenological modelling. Similar problems have been reported by Megow et al.26 Nanotubes that were periodically connected to their own image (thereby modelling an infinitely long tube) were constructed, but these proved unstable in the production phase, losing their tubular structure within a few nanoseconds. Specifically, when the double-wall collapsed, the lack of available water molecules inside the nanotubes increased the pressure inside the aggregate forcing the structure to contract. A snapshot from a deformed periodic nanotube is presented in Fig. S9 of the ESI.†3.6 From preformed nanotubes to self-assembly
Even if our results provide a high-resolution description of the C8S3 nanotube dimensions, there are issues that could not be addressed by our current methodology, such as identifying the native arrangement of the monomers inside the aggregates or witnessing the formation of bundles.17 Intrinsic pitfalls of atomistic MD simulations render such tasks extremely difficult or even beyond the realm of feasibility, at least by using brute force atomistic MD simulations.23 The main issues are the time scales, at which these events occur, and the free energy landscape of the procedures, that is rugged with many local minima in which the systems get trapped. Coarse-grained (CG) approaches are a common solution to alleviate these problems.61–65 The simplified representation of the atomistic coordinates and the smaller number of interactions that need to be calculated in CG simulations offer significant speed-ups and smoothen the free energy landscape, facilitating the formation of self-assembled aggregates.66 Similar approaches could be used to study the early steps of nucleation of the C8S3 aggregates, the preferred arrangement in self-assembled structures and, ultimately, the formation of bundles from merging nanotubes.4 Conclusions
We performed atomistic simulations of C8S3 molecules in different systems. Specifically, based on stable packing arrangements inside small bilayer patches, we were able to construct stable nanotubes of different sizes that maintained their tubular formation, in contrast to previous attempts. Generating the initial structures is not a trivial task and the preparation procedure needs to meet certain requirements in terms of the monomer arrangement and the dimensions of the aggregate. Our approach of constructing such structures guarantees that these criteria are met.Most simulated systems resulted in structures close to the initial formations indicating both Brickwork and Herringbone arrangements to be plausible and with the Brickwork arrangement being more stable. However, the thickness of the final structures was always lower compared to the reported values in literature. Our results suggest that the thickness of the C8S3 nanotubes was overestimated by the way the cryo-TEM profile scans were interpreted. The actual values for the thickness of the double-wall is closer to the size of the C8S3 bilayers as measured by AFM. A lower thickness is also suggested by our SAXS measurements on C8S3 nanotubes. The overestimated thickness and the imbalance of molecules in the inner and outer cylinder could explain why previous attempts to model these systems generated unstable structures. Consequently, extra care should be taken when modelling such systems and properties that rely on their relative position and arrangement.
Our simulations provide high resolution results on the structure of C8S3 nanotubes. Both experimental and theoretical studies would greatly benefit from an explicit atomistic description of the monomer position and arrangement. Our approach of constructing such complex systems and our findings on the dimensions of these aggregates pave the way for simulating more complex processes, such as the self-assembly of the C8S3 nanotubes or the formation of bundles, whose mechanisms are still not fully understood.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank B. Kriete for providing the figures and data from cryo-TEM experiments, as well as the samples for the SAXS measurements. We acknowledge J. Knoester, T. L. C. Jansen, A. S. Bondarenko, M. S. Pshenichnikov and B. Kriete for the discussions on improving the models and their contributions in this work. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.Notes and references
- M. Mohseni, Y. Omar, G. S. Engel and M. B. Plenio, Quantum Effects in Biology, Cambridge University Press, 2014 Search PubMed.
- T. Kobayashi, J-Aggregates, World Scientific, 1996 Search PubMed.
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS.
- A. Mishra, R. K. Behera, P. K. Behera, B. K. Mishra and G. B. Behera, Chem. Rev., 2000, 100, 1973–2012 CrossRef CAS.
- B. I. Shapiro, Russ. Chem. Rev., 2006, 75, 433–456 CrossRef CAS.
- S. R. Mujumdar, R. B. Mujumdar, C. M. Grant and A. S. Waggoner, Bioconjugate Chem., 1996, 7, 356–362 CrossRef CAS.
- A. Waggoner, Curr. Opin. Chem. Biol., 2006, 10, 62–66 CrossRef CAS.
- F. Würthner, R. Wortmann and K. Meerholz, ChemPhysChem, 2002, 3, 17–31 CrossRef.
- A. Pawlik, S. Kirstein, U. De Rossi and S. Daehne, J. Phys. Chem. B, 1997, 101, 5646–5651 CrossRef CAS.
- A. Pawlik, A. Ouart, S. Kirstein, H.-W. Abraham and S. Daehne, Eur. J. Org. Chem., 2003, 3065–3080 CrossRef CAS.
- S. Kirstein and S. Daehne, Int. J. Photoenergy, 2003, 2006, 21 Search PubMed.
- C. Didraga, A. Pugžlys, P. R. Hania, H. von Berlepsch, K. Duppen and J. Knoester, J. Phys. Chem. B, 2004, 108, 14976–14985 CrossRef CAS.
- J. Frenkel, Phys. Rev., 1931, 37, 17–44 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- H. von Berlepsch, C. Böttcher, A. Ouart, C. Burger, S. Dähne and S. Kirstein, J. Phys. Chem. B, 2000, 104, 5255–5262 CrossRef CAS.
- H. von Berlepsch, S. Kirstein, R. Hania, A. Pugžlys and C. Böttcher, J. Phys. Chem. B, 2007, 111, 1701–1711 CrossRef CAS.
- D. M. Eisele, D. H. Arias, X. Fu, E. A. Bloemsma, C. P. Steiner, R. A. Jensen, P. Rebentrost, H. Eisele, A. Tokmakoff, S. Lloyd, K. A. Nelson, D. Nicastro, J. Knoester and M. G. Bawendi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3367–E3375 CrossRef CAS.
- B. Kriete, A. S. Bondarenko, V. R. Jumde, L. E. Franken, A. J. Minnaard, T. L. C. Jansen, J. Knoester and M. S. Pshenichnikov, J. Phys. Chem. Lett., 2017, 8, 2895–2901 CrossRef CAS.
- D. M. Eisele, C. W. Cone, E. A. Bloemsma, S. M. Vlaming, C. G. F. van der Kwaak, R. J. Silbey, M. G. Bawendi, J. Knoester, J. P. Rabe and D. A. Vanden Bout, Nat. Chem., 2012, 4, 655–662 CrossRef CAS.
- S. S. Lampoura, C. Spitz, S. Dähne, J. Knoester and K. Duppen, J. Phys. Chem. B, 2002, 106, 3103–3111 CrossRef CAS.
- C. Didraga, J. A. Klugkist and J. Knoester, J. Phys. Chem. B, 2002, 106, 11474–11486 CrossRef CAS.
- C. Didraga and J. Knoester, J. Lumin., 2004, 110, 239–245 CrossRef CAS.
- P. W. J. M. Frederix, I. Patmanidis and S. J. Marrink, Chem. Soc. Rev., 2018, 47, 3470–3489 RSC.
- J. W. Fredy, A. Méndez-Ardoy, S. Kwangmettatam, D. Bochicchio, B. Matt, M. C. A. Stuart, J. Huskens, N. Katsonis, G. M. Pavan and T. Kudernac, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11850–11855 CrossRef CAS.
- D. Bochicchio, S. Kwangmettatam, T. Kudernac and G. M. Pavan, ACS Nano, 2019, 13, 4322–4334 CrossRef CAS.
- J. Megow, M. I. S. Röhr, M. Schmidtam Busch, T. Renger, R. Mitrić, S. Kirstein, J. P. Rabe and V. May, Phys. Chem. Chem. Phys., 2015, 17, 6741–6747 RSC.
- D. L. Smith and H. R. Luss, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 2793–2806 CrossRef.
- S. Kirstein, H. von Berlepsch, C. Böttcher, C. Burger, A. Ouart, G. Reck and S. Dähne, ChemPhysChem, 2000, 1, 146–150 CrossRef CAS.
- C. Friedl, T. Renger, H. von Berlepsch, K. Ludwig, M. Schmidtam Busch and J. Megow, J. Phys. Chem. C, 2016, 120, 19416–19433 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, Interaction Models for Water in Relation to Protein Hydration, Springer Netherlands, Dordrecht, 1981, pp. 331–342 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- H. J. C. Berendsen, J. P. M. V. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- V. V. Prokhorov, E. I. Mal'tsev, O. M. Perelygina, D. A. Lypenko, S. I. Pozin and A. V. Vannikov, Nanotechnol. Russ., 2011, 6, 286 CrossRef.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- B. T. Thole and P. T. van Duijnen, Theor. Chem. Acc., 1983, 63, 209–221 Search PubMed.
- M. F. Guest, I. J. Bush, H. J. J. V. Dam, P. Sherwood, J. M. H. Thomas, J. H. V. Lenthe, R. W. A. Havenith and J. Kendrick, Mol. Phys., 2005, 103, 719–747 CrossRef CAS.
- B. Kriete, J. Lüttig, T. Kunsel, P. Malý, T. L. C. Jansen, J. Knoester, T. Brixner and M. S. Pshenichnikov, Nat. Commun., 2019, 4615 CrossRef.
- I. Breßler, J. Kohlbrecher and A. F. Thünemann, J. Appl. Crystallogr., 2015, 48, 1587–1598 CrossRef.
- D. Marsh, CRC handbook of lipid bilayers, 2013 Search PubMed.
- J. S. Hub, Curr. Opin. Struct. Biol., 2018, 49, 18–26 CrossRef CAS.
- C. Paissoni, A. Jussupow and C. Camilloni, J. Chem. Theory Comput., 2020, 16, 2825–2834 CrossRef CAS.
- E. R. Draper, B. Dietrich, K. McAulay, C. Brasnett, H. Abdizadeh, I. Patmanidis, S. J. Marrink, H. Su, H. Cui, R. Schweins, A. Seddon and D. J. Adams, Matter, 2020, 2, 764–778 CrossRef.
- D. K. Putnam, E. W. J. Lowe and J. Meiler, Comput. Struct. Biotechnol. J., 2013, 8 Search PubMed.
- P. Chen and J. Hub, Biophys. J., 2014, 107, 435–447 CrossRef CAS.
- S. Park, J. P. Bardhan, B. Roux and L. Makowski, J. Chem. Phys., 2009, 130, 134114 CrossRef.
- C. J. Knight and J. S. Hub, Nucleic Acids Res., 2015, 43, W225–W230 CrossRef CAS.
- A. Guinier and G. Fourmet, Small angle scattering of X-rays, John Wiley and Sons, New York, 1955 Search PubMed.
- H. von Berlepsch, K. Ludwig, S. Kirstein and C. Böttcher, Chem. Phys., 2011, 385, 27–34 CrossRef CAS.
- B. Kriete, C. J. Feenstra and M. S. Pshenichnikov, Phys. Chem. Chem. Phys., 2020, 22, 10179–10188 RSC.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, 1–17 CrossRef.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS.
- P. C. T. Souza and S. J. Marrink, 2020, http://cgmartini.nl.
- H. I. Ingólfsson, C. A. Lopez, J. J. Uusitalo, D. H. de Jong, S. M. Gopal, X. Periole and S. J. Marrink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 225–248 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03282d |
| This journal is © the Owner Societies 2020 |