Nanoscale kinetics of amorphous calcium carbonate precipitation in H₂O and D₂O

Abstract

Calcium carbonate (CaCO₃) is one of the most well-studied and abundant natural materials on Earth. Crystallisation of CaCO₃ is often observed to proceed via an amorphous calcium carbonate (ACC) phase, as a precursor to more stable crystalline polymorphs such as vaterite and calcite. Despite its importance, the kinetics of ACC formation have proved difficult to study, in part due to rapid precipitation at moderate supersaturations, and the instability of ACC with respect to all other polymorphs. However, ACC can be stabilised under confinement conditions, such as those provided by a nanopipette. This paper demonstrates electrochemical mixing of a Ca²⁺ salt (CaCl₂) and a HCO₃⁻ salt (NaHCO₃) in a nanopipette to repeatedly and reversibly precipitate nanoparticles of ACC under confined conditions, as confirmed by scanning transmission electron microscopy (STEM). Measuring the current as a function of applied potential across the end of the nanopipette and time provides millisecond-resolved measurements of the induction time for ACC precipitation. We demonstrate that under conditions of electrochemical mixing, ACC precipitation is extremely fast, and highly pH sensitive with an apparent third order dependence on CO₃²⁻ concentration. Furthermore, the rate is very similar for the equivalent CO₃²⁻ concentrations in D₂O, suggesting that neither ion dehydration nor HCO₃⁻ deprotonation represent significant energetic barriers to the formation of ACC. Finite element method simulations of the electrochemical mixing process enable the supersaturation to be estimated for all conditions and accurately predict the location of precipitation.

---

Introduction

The crystallisation of calcium carbonate (CaCO₃) is an area of great interest,^1,2 especially in biomineralisation,³ where CaCO₃ can exist as a variety of structural forms and morphologies. The formation of particular CaCO₃ polymorphs is crucial to many global biogeochemical processes,⁴ and carbonate mineral formation has been proposed as a safe long-term method for carbon capture and storage.⁵ CaCO₃ is also used in a wide variety of commercial products: it is an extender in paints, pharmaceuticals and adhesives, a filler in cement and plaster, and a mild abrasive in cleaning products. The earliest forming, least stable solid phase of CaCO₃ is amorphous calcium carbonate (ACC), a variably hydrated, poorly ordered metastable precursor to more stable polymorphs such as vaterite, aragonite and calcite.¹ While the ability to study and control the nucleation and growth of ACC may provide insight into how control is achieved in biological systems⁶ and how polymorphism can be controlled in synthetic crystals,⁷ current theories around the nucleation and growth of ACC and its subsequent crystallisation remain controversial, with various intermediates and pathways being suggested.^8,9

Liquid-like forms have been observed in quenched samples recovered from solutions immediately prior to CaCO₃ precipitation,^10,11 leading to suggestions that under certain conditions precipitation may be aided by a liquid–liquid phase separation, in which a supersaturated solution can decompose into a solute-rich phase consisting of ions, ion pairs or clusters and a solute-poor phase.^12–14 Above a certain concentration (marked by the spinodal) the solution becomes unstable with respect to this transformation, leading to the rapid formation of a disordered emulsion-like solution structure.¹⁰ The limit of solution stability has been determined to lie between [Ca²⁺] = 3–4 mM,¹⁵ in agreement with previous reports of a change in the mechanism of CaCO₃ precipitation in this concentration range.¹⁶ There is also experimental evidence for the association of Ca²⁺ and CO₃²⁻ in stable so-called pre-nucleation clusters in both undersaturated and supersaturated solutions.^17–19 The formation of such clusters has been supported by molecular dynamics simulations, although there is ongoing debate in the literature about the existence and role of pre-nucleation clusters in the formation of CaCO₃.^12,13,17,20 Measurement of the water dynamics using THz spectroscopy during precipitation suggests that aggregation of pre-nucleation clusters may be the origin of the liquid–liquid phase separation.²¹ Irrespective of whether ACC forms from a dense liquid phase or directly from the mother solution, desolvation of the constituent ions must occur, with desolvation of the cation conventionally considered to be the rate determining step in crystallisation.²²

Given the apparent significance of the solvent in the precipitation of ACC, it is surprising there are no studies comparing the precipitation rates in H₂O with that in D₂O. In general, the stronger H-bonding in D₂O leads to significant differences in its solvation behaviour when compared to H₂O.^23,24 In the case of ion pairs or clusters, D₂O would be expected to favour aggregation, and has previously been suggested to decrease the dissociation constant of the ion pair Pb(NO₃)⁺,²⁵ as well as favouring the exchange of water for Cl⁻ (i.e. formation of an ion pair) in several transition metal complexes.²⁶ Isotopic exchange also provides an opportunity to examine the role of HCO₃⁻ in the kinetics of ACC precipitation. While not directly included in the solubility product, HCO₃⁻ provides a source of CO₃²⁻ in solution, and appears in clusters simulated under lower pH conditions (though we note the lack of a dynamic equilibrium of the form CO₃²⁻ ⇌ HCO₃⁻ in these simulations).²⁷ The enhanced strength of the D–O bond in DCO₃⁻ stabilises DCO₃⁻ relative to HCO₃⁻, significantly decreasing the acid dissociation constant (pK^D_a − pK^H_a = 0.748)²⁸ and therefore the extent to which it will replace consumed CO₃²⁻ ions.

Electrochemical methods have been used extensively in the study of inorganic precipitation reactions, usually to report on average properties, such ion activities with ion selective electrodes, in bulk solution.^11,17,29 The use of nanopores, however, allows for convenient analysis of precipitation at the nanoscale by using an applied potential to mix solutions inside a confined volume and monitor the resulting changes in the ion current. Previously, the precipitation of weakly soluble phosphate salts of Zn,³⁰ Ca,³¹ Co,³¹ as well as CoCl₂,³² and even organic crystals³³ have been studied. We have used this approach to measure induction times for ACC precipitation in the presence of various scale inhibitors.³⁴ This method has several advantages over other techniques based on bulk conductivity,³⁵ turbidimetry¹⁶ or (high speed) imaging,³⁶ as mixing is well defined, occurs on small time (10⁻³ s) and length (10⁻⁸ m) scales and is readily reversed (either via dissolution or migration of the particle away from the orifice³⁰) to reset the system for the collection of hundreds of repeat measurements. The fast time resolution allows rapid precipitation events to be quantified, enabling measurements at high supersaturations that other techniques are not able to access easily. This allows experimental exploration of solution conditions closer to the limit of solution stability, where molecular dynamics simulations of CaCO₃ solutions are often performed.^12,14,27 Furthermore, since precipitation in confined volumes stabilises ACC against further crystallisation,^37–41 products formed in the nanopore can subsequently be characterised ex situ, e.g. with Raman spectroscopy and electron microscopy, without further work up.

Here, we have measured the induction times and imaged the products formed from the reaction of a CaCl₂ solution with a solution containing a range of CO₃²⁻ concentrations (corresponding to a range of pH values) and compared the results between H₂O and D₂O. These experimental conditions were further investigated through detailed finite element method (FEM) simulations of the mixing process in order to understand the resulting temporal-spatial changes in supersaturation during these measurements.

Experimental

Single-barrelled quartz nanopipettes, with tip diameters between 20–50 nm were used as reaction centres for the precipitation of ACC. For most studies, the nanopipettes were filled with a solution of 100 mM NaHCO₃ titrated to a particular CO₃²⁻ concentration and were placed in a bath of 20 mM CaCl₂ (Fig. 1A). All solutions were made up using either 18.2 MΩ cm water (Purite Select) or D₂O (99.8 atom %D, Sigma Aldrich) and chemicals used were purchased from Sigma Aldrich.

Fig. 1 (A) Schematic of the principles of growth and dissolution of an ACC precipitate within a nanopipette under −0.025 V and +0.2 V bias, respectively. (B) Current–time trace of several precipitation and dissolution cycles – showing the reproducibility of the cycle, with the corresponding voltage–time trace below. The tip is open to ion current flow at positive tip bias and precipitation of ACC occurs, with a distinctive current–time trace, at negative tip bias, with the current tending to zero. (C) A single blocking current transient, showing in detail how the induction time, t_ind, is defined.

Experiments were run with several nanopipettes in parallel, usually three, immersed in the same bath and the current–time response measured simultaneously at each as the applied potential was switched. The two closely similar nanopipettes pulled from each capillary were used to compare H₂O and D₂O (i.e. nanopipette 1 in H₂O was the sister of nanopipette 1 in D₂O). This configuration allowed any effect of small variations in nanopipette geometry from different capillaries to be ruled out in the comparison of H₂O and D₂O solutions (all other conditions being identical), as well as increasing throughput and the total number of measurements. Before being submerged in the bath solution, a positive bias (0.25 V for 7 and 16 mM CO₃²⁻, and 0.2 V for 36 and 48 mM CO₃²⁻) was applied to the Ag/AgCl quasi-reference counter electrodes (QRCEs) in each nanopipette with respect to a similar QRCE in bulk solution to counteract the diffusional mixing of the Ca²⁺ ions from the bath and the CO₃²⁻ ions in the nanopipette that would otherwise occur. To start the induction time measurement, a negative bias (−0.025 V) was applied to the nanopipette electrodes, reversing the ion fluxes (current) and causing Ca²⁺ and CO₃²⁻ ions to accumulate in the tip of the nanopipette (vide infra) and create a localised region of high supersaturation, S (eqn (1)), where a(Ca²⁺), a(CO₃²⁻) and K_sp represent the activity of Ca²⁺, the activity of CO₃²⁻, and the solubility product of ACC, respectively, where K_sp is taken to be 3.8 × 10⁻⁸ M².^17,42

Upon application of the negative tip bias, precipitation occurred, with precipitate filling the end of the nanopipette and blocking the current completely. The distinctive current–time trace provided a well-defined end point for statistical analysis of many such ion current blocking transients. Significantly, the tip bias could be returned to the positive value to remove the blockage and restore the ion current to the ‘open’ value. This ability to restore the initial conditions allowed the process to be repeated multiple times in a single experiment across the 3 nanopipettes.

These precipitation and dissolution events were found to have a high degree of reproducibility (Fig. 1B). By monitoring the variations in current as a function of time, the real-time precipitation of ACC in a small, well-defined region of solution was observed. From the current transients, we define the induction time, t_ind, the time between creating a supersaturated solution and forming an appreciable amount of new phase,⁴³ as being the time taken for the current to decrease to 1% of its maximum value following the voltage step to the negative nanopipette potential. As with any practical measurement, this will necessarily include some element of growth time, however we note that by limiting the growth to a few tens of nanometers an upper limit is placed on the contribution of this time to t_ind which would be difficult to achieve with other techniques.

Through the repeated precipitation and dissolution of these precipitates, followed by an automated analysis using a Matlab script, we determined the mean induction time and its standard deviation for a variety of conditions. Care was also taken to ensure that repetitive precipitation events were truly independent, by checking that the induction time was independent of the repeat number (Fig. S1, ESI†).

To enable comparison of rate measurements between H₂O and D₂O at different CO₃²⁻ activities, without relying on pH/pD measurement and speciation models, the CO₃²⁻ concentration was determined spectroscopically for each solution.⁴⁴ The protocol is discussed in detail in the ESI† (Section S2). Briefly, the CO₃²⁻ and HCO₃⁻ ions show distinctive Raman scattering in both H₂O and D₂O solutions. Concentration analysis was conducted by making a solution of 100 mM NaHCO₃ in each solvent system, and titrating it to a high pH with NaOH (or NaOD) until only a CO₃²⁻ peak (and no HCO₃⁻ peak) was visible in the Raman spectrum. Through serial dilution, an accurate set of peak areas for a range of concentration values was obtained, from which a calibration curve was constructed allowing solutions of specific [CO₃²⁻] to be prepared by titration with Na₂CO₃ while monitoring the area of the CO₃²⁻ peak. Concentrations determined in this way typically had a 95% confidence interval of ±30%.

Nanopipettes were fabricated using quartz capillaries with filaments (outer diameter 1.0 mm, inner diameter 0.5 mm, custom manufactured, Friedrich and Dimmock) using a laser puller (P-2000, Sutter Instruments; parameters of: Line 1: Heat 750, Fill 4, Vel 30, Del 150, Pull 80; Line 2: Heat 650, Fil 3, Vel 40, Del 135, Pull 150) to give a tip opening diameter of approximately 20–50 nm. The electrometer and current–voltage converter used were home built, while the user control of voltage output and data collection was via custom made programs in LabVIEW (2013, National Instruments) through an FPGA card (7852R, National Instruments). Raman spectroscopy was conducted using a Raman microscope (Horiba LabRam HR Evolution) fitted with a charged couple device (CCD) detector and a 488 nm OPSS laser. A 50× (0.5 NA) objective and 600 line mm⁻¹ grating was employed for mapping experiments with 10 × 2 s acquisitions averaged per spectrum, giving a spectral resolution of 1.3 cm⁻¹ and a nominal lateral resolution of 595 nm. A 10 mm path length quartz cuvette in a double pass accessory with an 1800 line mm⁻¹ grating was used for measurements in solution with 4 × 60 s acquisitions averaged per spectrum to give a spectral resolution of 0.34 cm⁻¹. Pulled nanopipettes were characterized regarding their inner radius and overall probe geometry by scanning transmission electron microscopy (STEM) using a Zeiss Gemini 500 SEM.

Results and discussion

Characterisation of the precipitate

The goal of this study was to characterise the effect of pH and solvent on the kinetics of ACC formation. It was therefore necessary to confirm the presence of ACC within the nanopipette after precipitation. Although often unstable with respect to crystallisation into a more stable polymorphs, ACC has been shown to be stabilised when under confinement,³⁹ and such an environment is provided by a nanopipette. After precipitation was induced by the applied negative nanopipette potential, as summarised in the experimental section, nanopipettes were removed from solution and quickly submerged in ethanol to remove solution left on the outside of the nanopipette and to further inhibit transformation of the ACC. The nanopipettes were then dried under vacuum. Blocking experiments were conducted over a range of comparable CO₃²⁻ concentrations, [CO₃²⁻], in both H₂O and D₂O, with precipitates being observed in all cases. STEM images of nanopipettes after precipitation reveal a region of contrast near the tip (Fig. 2A–F, false coloured for clarity). This region was not observed in either as-pulled nanopipettes or nanopipettes which had been filled with NaHCO₃ solution and then dipped in CaCl₂ bath solution without electrochemical mixing (Fig. S4, ESI†), and is therefore attributed to the precipitate. While formation of further precipitates along the nanopipette cannot be ruled out, due to the difficulty in imaging through the increasingly thick quartz walls further from the end, the formation of a precipitate at the very tip of the nanopipette is consistent with this region reaching the highest supersaturation and is supported by FEM modelling of the mixing process, vide infra.

Fig. 2 (A–F) STEM images of nanopipette tips, containing a range of CO₃²⁻ concentrations in the nanopipette (indicated), after electrochemically-triggered precipitation in either H₂O or D₂O solution. Bath solution 20 mM CaCl₂. A colour look up table was used to highlight subtle changes in contrast further into the nanopipette. Light grey arrows point to particles. Dark grey arrows show meniscus region. (G) Map of 1080 cm⁻¹ peak intensity overlaid onto optical microscope image of a nanopipette after precipitation from 48 mM CO₃²⁻ in H₂O. Scale bars: 100 nm (A, B, D–F); 200 nm (C); 5 μm (G).

At lower concentrations (Fig. 2A, B, D and E), precipitates were consistently observed within the first 100 nm of the tip of the nanopipette, and appeared to completely occlude the nanopipette (light grey arrows). The images were comparable between H₂O and D₂O experiments. For the highest concentration (Fig. 2C and F), in addition to the particles observed in the first 100 nm, a darker region with a curved meniscus is observed further into the pipette (dark grey arrows). The presence of such meniscus-like forms are observed at various positions throughout the first 2–3 μm of all nanopipettes imaged used at the highest CO₃²⁻ concentrations and are absent from those used in the lower concentrations (ESI,† Section S3 and Table S1). This will be discussed later in relation to the mass transport simulations. Raman maps of nanopipettes used in experiments at CO₃²⁻ concentrations of 7.7, 16 and 36 mM (in a 20 mM CaCl₂ bath) did not reveal any CO₃²⁻-related signals in the region of the nanopipette, as expected due to the small size and low density of the nanoparticles observed in the STEM images. However, Raman spectra from the nanopipette used in the 49 mM CO₃²⁻ experiment (20 mM CaCl₂ bath) yielded spectra with a single peak at 1080 cm⁻¹,⁴⁵ with no peaks at 711 cm⁻¹ which would have indicated calcite,¹⁶ or at 1043 cm⁻¹ which would have indicated NaHCO₃,⁴⁶ confirming the precipitate is ACC (Fig. S5, ESI†). Mapping over the region of the nanopipette tip showed the 1080 cm⁻¹ signal was present throughout the 35 μm long section studied (Fig. 2G). Thus, at lower concentrations (supersaturations), precipitation is confined to the nanopipette tips, while at the highest concentrations it occurs over a more significant region from the nanopipette end.

Kinetics of ACC formation

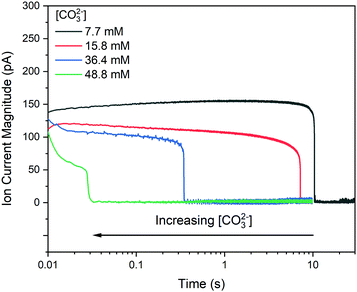
Fig. 3 shows typical current transients for blocking events at each concentration studied, where time zero is the first point at which the sign of the nanopipette voltage was switched from positive to negative. An important aspect of these data is whether the growth of the precipitate is under kinetic or mass transport control. This can be assessed by comparing the total flux of ions through the nanopipette during the precipitation (available from the integrated ion current) with an estimate of the total number of ions required to form the precipitate observed in STEM (ESI,† Section S5). At 7.7 mM CO₃²⁻ the amount of Ca²⁺ transferred within the induction time (t_ind = 21 s) is 6.77 × 10⁻¹⁵ mol, while an upper estimate for the amount of Ca²⁺ in the precipitate is 5.52 × 10⁻¹⁸ mol, suggesting that mass transport should not limit the rate of precipitation. In contrast, the much shorter induction time (t_ind = 18 ms) at 49 mM CO₃²⁻ means the amount of Ca²⁺ transferred is only 8.79 × 10⁻¹⁸ mol, while the precipitate is estimated to require 2.60 × 10⁻¹⁸ mol, suggesting that growth will be under mixed kinetic and mass transport control under these conditions.

Fig. 3 Current transients for typical blocking events at the four CO₃²⁻ concentrations (black line: 7.7 mM, red line: 15.8 mM, blue line: 36.4 mM and green line: 48.8 mM) studied in H₂O. Note the use of current magnitude and logarithmic timescale for clarity.

By pulsing the potential between mixing/blocking and unmixing/unblocking regimes it was possible to record >100 induction times for each pH, across several nanopipettes. The huge influence of CO₃²⁻ concentration on the induction time is confirmed in histograms of the repeat measurements (Fig. 4). As expected, an increase in CO₃²⁻ concentration, which leads to a higher supersaturation upon mixing, results in a decrease in induction time. When −log(t_ind) is plotted against log[CO₃²⁻] directly (Fig. 5A) the data reveal a third-order dependence of induction time on [CO₃²⁻]. A similarly high reaction order of 4 was reported previously for the induction time for vaterite crystals.²⁹ However, it is generally more insightful to study the relationship between the supersaturation, S, and t_ind as this can be compared to theoretical predictions based on various precipitation mechanisms.⁴⁷

Fig. 4 Effect of [CO₃²⁻] and solvent on CaCO₃ induction times. Spectroscopically determined CO₃²⁻ concentrations are shown above induction time histograms obtained in H₂O (top row) and D₂O (bottom row) with frequency shown on the left axis. In each case cumulative probability (shown on the right axis) is determined from the histogram (points) and fitted using eqn (4) (line). Black, red and blue bars, lines and points correspond to data obtained from the three different nanopipettes.

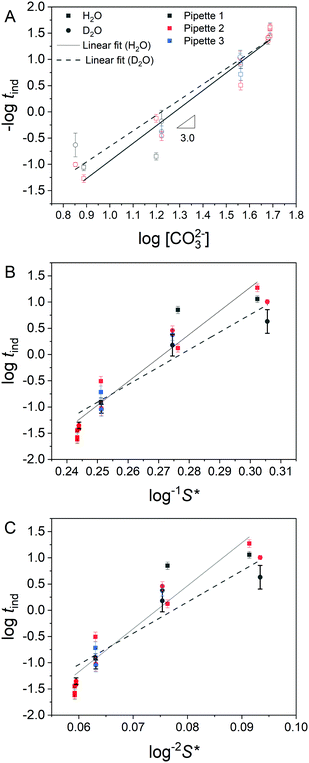Fig. 5 Analysis of observed induction times. (A) Log–log plot of blocking frequency (−log t_ind) as a function of log[CO₃²⁻]. Lines of best fit are shown, where the gradients correspond to the reaction order with respect to [CO₃²⁻] and are ca. 3 in both cases. (B) Relationship between induction time, t_ind, and log⁻¹ S*, where S* is the supersaturation based on perfect mixing of the starting solutions and is linear in the case of mononuclear growth control (eqn (3)). (C) Relationship between t_ind and log⁻² S*. The relationship is linear in the case that nucleation time dominates, or is comparable to, the growth time (eqn (2)). A similar goodness of fit to the lines of best fit is observed in B and C. The legend applied to all panels: squares and solid lines represent measurements in H₂O, circles and dashed lines are from D₂O. Black, red and blue colours indicate data from replicates 1, 2 and 3. Error bars show relative standard deviation.

Where the nucleation time either dominates, or is comparable to the growth time, the relation

log t_ind = B/T³ log² S − A (2)

is expected to hold, where T is temperature and A and B are constants, such that log t_ind is proportional to log⁻² S.⁴⁷ In contrast, were the growth time dominates the induction time, assuming mononuclear growth, the equivalent expression becomes

log t_ind = C/T² log S − D (3)

where C and D are different constants and log t_ind is instead expected to be proportional to log⁻¹ S.⁴⁷ To determine if these two cases could be resolved graphically, log t_ind was plotted as a function of both log⁻¹ S* (Fig. 5B) and log⁻² S* (Fig. 5C), with estimates of maximum supersaturation, S*, based on the perfect mixing of the starting solutions. Straight lines of best fit were determined for both plots, however although measurements were made over a significant pH range, the limited effective range of S* meant that the goodness of fit for both plots was similar, preventing reliable discrimination between the two cases. As a result further analysis to extract e.g. the surface energy of the critical nucleus was not attempted. The mean induction time for transients from each nanopipette run was calculated (Table S2 in ESI†) and used to derive the mean induction time for each solution (Table 1). For the 3 lower concentrations, the mean induction time is slightly lower in D₂O than H₂O, although there is some variation in the data for different nanopipettes. This small difference implies that ion (Ca²⁺ or CO₃²⁻) desolvation does not represent a significant energetic barrier to ACC growth, consistent with atomistic simulations.⁴⁸ Interestingly the D₂O studies also showed less variation than their H₂O counterparts, which is especially evident in the [CO₃²⁻] = 36 mM case. Previously it was suggested that an increase in induction times, observed when CO₃²⁻ salts with smaller counter cations were used, was due to stabilisation of pre-nucleation clusters.⁴⁹ This conclusion contrasts with our observation, if we assume that D₂O would also stabilise ion clusters. The longer induction times at [CO₃²⁻] = 48 mM in D₂O may be indicative of the role of mass transport in precipitation predicted at this concentration, with diffusion coefficients, D, lower in D₂O than H₂O (D(H₂O)/D(D₂O) = 1.23).⁵⁰

Table 1 Mean values of recorded induction time, derived growth time and stationary nucleation rate

H2O				D2O
[CO3^2−] (mM)	t ind(H2O) (s)	t g(H2O) (s)	J·V(H2O) (m^−3 s^−1 m^3)	[CO3^2−] (mM)	t ind(D2O) (s)	t g(D2O) (s)	J·V(D2O) (m^−3 s^−1 m^3)
Values of tind show the mean of the individual nanopipette means ± the standard error of the means. Individual nanopipette data is shown in Table S2, ESI.
7.7	14.8 ± 3.6	9.00	0.199	7.1	8.145 ± 2.31	3.75	0.228
15.8	2.77 ± 2.2	1.29	3.07	16.7	2.60 ± 0.86	1.55	0.717
36.4	0.219 ± 0.08	0.157	16.3	36.3	0.100 ± 0.005	0.066	40.7
48.8	0.031 ± 0.005	0.024	145	47.8	0.052 ± 0.005	0.044	164

---

The data were also analysed based on fitting the cumulative probability distribution derived from each experiment (points, Fig. 4), assuming a classical nucleation model. The probability, P(t), to detect crystals at a time, t, which were nucleated at an earlier time is given by eqn (4), where J is the stationary nucleation rate and t_g is the time taken for a nucleus to grow to an appreciable (detectable) size.⁵¹ This distribution function was fitted to each data set (lines, Fig. 4) and the parameters extracted (Table 1 and Table S2 in ESI†). While some cumulative distributions are well fitted by the model, most are not. Of the distributions that do fit well, they follow the expected Poisson distribution with a tail towards longer times, however this trend is time-dependent (Fig. S1, ESI†), rather than stochastic, leading us to conclude that precipitation in these nanopipettes is not well described by existing models of induction time.

P(t) = 1 − exp[−JV(t − t_g)] (4)

Simulations of the development of supersaturation over time

In order to understand why the precipitate is formed within the first 100 nm of the pipette, the time-dependent evolution of the solution composition inside the nanopipette upon mixing was simulated using FEM calculations (Fig. 6). A full description of the model is given in the ESI† (Section S7) and is summarised here. Briefly, the Poisson–Nernst–Planck equations were used to describe the relationship between the electric field generated between the QRCEs in the nanopipette and bulk solution, and the transport of species by diffusion and migration, with an additional term in the continuity equation to ensure that the various chemical equilibria between species were satisfied. The simulation geometry was constructed based on STEM images of typical nanopipettes, with boundaries representing the bulk in the nanopipette and the bath each located 50 μm from the end of the nanopipette (Fig. S7, ESI†). The equilibria and subsequent calculations of S were based on the species activity, calculated from concentrations and activity coefficients derived from the Davies equation applying the local ionic strength.

Fig. 6 Simulated S at the four initial carbonate concentrations in H₂O and D₂O. (A) The steady state value of S in H₂O at the different CO₃²⁻ concentrations. (B) The maximum value of S at the observed t_ind in H₂O (black squares) and D₂O (red circles).

Simulations reveal that S changes dramatically upon application of the potential step, reaching steady state within 100 ms (Fig. S9A, ESI†). Each concentration investigated gives rise to a different steady state value of S after around 100 ms. At this time, the position of maximum supersaturation is found to be between 250 to 625 nm into the nanopipette, from the end (Fig. 6A and Fig. S9D, ESI†). Comparison with the STEM images in Fig. 2 shows good agreement between these simulations and experimental results – the precipitate forms in the region where there is a significant increase in supersaturation. Although the location of maximum S varies depending on the initial experimental concentration, it remains in the first 600 nm of the nanopipette, where the radius is only 2.5 times larger than at the tip. Similarly, while the half rise time of S varies with concentration (Fig. S9C, ESI†), steady state is reached by 100 ms for all concentrations, which is significantly faster than the induction time for all but the highest concentration blocking experiment. This finding agrees with the experimental assessment, based on the ionic current, that mass transport is only likely to limit growth in the [CO₃²⁻] = 48 mM case. The simulations also show that, within the approximations used (S7, ESI†), D₂O will have only small effect on the mass transport, not modifying the value of supersaturation reached by more than 6% from the H₂O case. This suggests that at 7, 15 and 36 mM CO₃²⁻ the evolution of supersaturation is controlled by the initial concentration itself, such that the value of S is comparable between the H₂O and D₂O cases.

The absolute value of S is significant, however, as at steady state, in all cases, it exceeds the spinodal, estimated to be between 3–4 mM in stoichiometric CaCO₃ solution,¹⁵ corresponding to an ion activity product (IAP) of between 5–8 × 10⁻⁷ M,⁴² or a value of S between 13 and 21. In all cases the system reaches S = 21 in the simulations on a much shorter timescale than t_ind. Given that decomposition of the unstable region will occur within microseconds of the spinodal being reached,⁵⁵ formation of a dense liquid phase by itself cannot explain the decrease in current magnitude (although diffusion coefficients, and hence ion currents, within the dense liquid phase are expected to be up to three orders of magnitude lower than in typical dilute solutions¹²). It is therefore suggested that it is the formation of the solid ACC phase within the dense phase which is responsible for the observed current blockade and observed induction time. It is noted that particles must grow to almost the diameter of the pipette before the current flow is significantly perturbed (Fig. S10, ESI†).

Finally, it is interesting to compare the apparent differences in the STEM images of the pipettes after precipitation from different CO₃²⁻ concentrations (Fig. 2, Section S3 and Table S1, ESI†), with the differences in ion fluxes and distributions obtained from simulation (Fig. 6). As expected, the gradient of S along the centre of the nanopipette is steeper at higher [CO₃²⁻], leading to greater ion fluxes. A higher flux would enable a larger region of solution to exceed the spinodal, leading to larger dense liquid regions. Since the transformation from dense liquid to solid must involve loss of water into the dilute phase at the phase boundary, regions with lower surface area–volume ratios would require longer to complete this transformation. It is tentatively suggested that this may explain the liquid-like appearance of the residues from the [CO₃²⁻] = 48 mM experiments, where the larger volume of dense phase was not able to solidify on the timescale of the experiment. We note a novel aspect of the experimental approach is the ability to monitor such small regions of solution. As methods for preparing nanopipettes of smaller dimensions improve, this technique may be able to probe effects related to confinement, where mass transport properties can change dramatically.^52–54

Conclusions

A system where ACC can be reliably and repeatedly precipitated and dissolved under the confined conditions of a nanopipette has been demonstrated. This system allows high resolution induction time measurements to be made, and the kinetics of individual, readily characterisable precipitates to be studied. It is observed that under the present conditions, relatively small increases in CO₃²⁻ concentration can decrease induction times by orders of magnitude, consistent with the expected change in supersaturation. Consideration of mass transport, and approximation of the observed precipitate volume, suggest that at low CO₃²⁻ concentrations, the process is kinetically controlled, but at the highest concentration ACC growth become limited by mass transport. The similarity of induction times between H₂O and D₂O solutions of equivalent CO₃²⁻ concentration suggests that neither ion desolvation nor HCO₃⁻ deprotonation represent significant energetic barriers for the growth of ACC, as predicted in previous molecular dynamics simulations. Differences in the appearance of precipitates formed at higher CO₃²⁻ concentrations are observed and rationalised using differences in the local ion flux. The system demonstrated in this work provides a useful platform for studying the effect of confinement and electric fields on the nucleation and growth of crystals from solution.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Aaron Finney for useful discussions and acknowledge use of the Spectroscopy Research Technology Platform, University of Warwick. We acknowledge an EPSRC Programme Grant (grant EP/R018820/1) which funds the Crystallisation in the Real World consortium. PDM was further supported by an EPSRC studentship. GNM acknowledges financial support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 790615 (FUNNANO). PRU thanks the Royal Society for a Wolfson Research Merit Award. The research data underpinning this article can be accessed at: http://wrap.warwick.ac.uk/142002.

Notes and references

1. J. W. Morse, R. S. Arvidson and A. Lüttge, Chem. Rev., 2007, 107, 342–381.
2. J. J. De Yoreo, Rev. Mineral. Geochem., 2003, 54, 57–93.
3. L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970.
4. A. Ridgwell and R. Zeebe, Earth Planet. Sci. Lett., 2005, 234, 299–315.
5. E. H. Oelkers, S. R. Gislason and J. Matter, Elements, 2008, 4, 333–337.
6. Y. Politi, R. A. Metzler, M. Abrecht, B. Gilbert, F. H. Wilt, I. Sagi, L. Addadi, S. Weiner and P. U. P. A. Gilbert, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17362–17366.
7. D. Gebauer, P. N. Gunawidjaja, J. Y. P. Ko, Z. Bacsik, B. Aziz, L. Liu, Y. Hu, L. Bergström, C.-W. Tai, T.-K. Sham, M. Edén and N. Hedin, Angew. Chem., Int. Ed., 2010, 49, 8889–8891.
8. A. Van Driessche, New perspectives on mineral nucleation and growth: from solution precursors to solid materials, Springer Berlin Heidelberg, New York, NY, 2016.
9. H. Du and E. Amstad, Angew. Chem., Int. Ed., 2020, 59, 1798–1816.
10. J. Rieger, T. Frechen, G. Cox, W. Heckmann, C. Schmidt and J. Thieme, Faraday Discuss., 2007, 136, 265–277.
11. M. A. Bewernitz, D. Gebauer, J. Long, H. Cölfen and L. B. Gower, Faraday Discuss., 2013, 159, 291–312.
12. P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. D. Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7882–E7890.
13. K. Henzler, E. O. Fetisov, M. Galib, M. D. Baer, B. A. Legg, C. Borca, J. M. Xto, S. Pin, J. L. Fulton, G. K. Schenter, N. Govind, J. I. Siepmann, C. J. Mundy, T. Huthwelker and J. J. D. Yoreo, Sci. Adv., 2018, 4, eaao6283.
14. A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. D. Yoreo, Science, 2013, 341, 885–889.
15. Z. Zou, W. J. E. M. Habraken, L. Bertinetti, Y. Politi, A. Gal, S. Weiner, L. Addadi and P. Fratzl, Adv. Mater. Interfaces, 2017, 4, 1600076.
16. Y.-W. Wang, Y.-Y. Kim, C. J. Stephens, F. C. Meldrum and H. K. Christenson, Cryst. Growth Des., 2012, 12, 1212–1217.
17. D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822.
18. D. Gebauer, P. Raiteri, J. D. Gale and H. Cölfen, Am. J. Sci., 2018, 318, 969–988.
19. D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371.
20. A. Carino, A. Testino, M. R. Andalibi, F. Pilger, P. Bowen and C. Ludwig, Cryst. Growth Des., 2017, 17, 2006–2015.
21. F. Sebastiani, S. L. P. Wolf, B. Born, T. Q. Luong, H. Cölfen, D. Gebauer and M. Havenith, Angew. Chem., Int. Ed., 2017, 56, 490–495.
22. J. A. Koskamp, S. E. Ruiz-Hernandez, D. Di Tommaso, A. M. Elena, N. H. De Leeuw and M. Wolthers, J. Phys. Chem. C, 2019, 123, 26895–26903.
23. V. M. Vdovenko, Y. V. Gurikov and E. K. Legin, At. Energy, 1965, 19, 1393–1397.
24. Y. Chen, H. I. Okur, N. Gomopoulos, C. Macias-Romero, P. S. Cremer, P. B. Petersen, G. Tocci, D. M. Wilkins, C. Liang, M. Ceriotti and S. Roke, Sci. Adv., 2016, 2, e1501891.
25. F. Alkan, T. Small, S. Bai, A. Dominowski and C. Dybowski, J. Struct. Chem., 2016, 57, 369–375.
26. H. Taube, J. Am. Chem. Soc., 1960, 82, 524–526.
27. R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590.
28. M. Paabo and R. G. Bates, J. Phys. Chem., 1969, 73, 3014–3017.
29. A. G. Xyla, E. K. Giannimaras and P. G. Koutsoukos, Colloids Surf., 1991, 53, 241–255.
30. B. Vilozny, P. Actis, R. A. Seger and N. Pourmand, ACS Nano, 2011, 5, 3191–3197.
31. L. Innes, M. R. Powell, I. Vlassiouk, C. Martens and Z. S. Siwy, J. Phys. Chem. C, 2010, 114, 8126–8134.
32. E. T. Acar, P. Hinkle and Z. S. Siwy, J. Phys. Chem. C, 2018, 122, 3648–3654.
33. F. M. Maddar, D. Perry and P. R. Unwin, Cryst. Growth Des., 2017, 17, 6565–6571.
34. D. Perry, A. S. Parker, A. Page and P. R. Unwin, ChemElectroChem, 2016, 3, 2212–2220.
35. O. Söhnel and J. W. Mullin, J. Cryst. Grow., 1978, 44, 377–382.
36. R. Zahorán, Á. Kukovecz, Á. Tóth, D. Horváth and G. Schuszter, Phys. Chem. Chem. Phys., 2019, 21, 11345–11350.
37. E. Loste, R. J. Park, J. Warren and F. C. Meldrum, Adv. Funct. Mater., 2004, 14, 1211–1220.
38. C. J. Stephens, Y.-Y. Kim, S. D. Evans, F. C. Meldrum and H. K. Christenson, J. Am. Chem. Soc., 2011, 133, 5210–5213.
39. C. J. Stephens, S. F. Ladden, F. C. Meldrum and H. K. Christenson, Adv. Funct. Mater., 2010, 20, 2108–2115.
40. L. Li, J. R. Sanchez, F. Kohler, A. Røyne and D. K. Dysthe, Cryst. Growth Des., 2018, 18, 4528–4535.
41. Y. Wang, M. Zeng, F. C. Meldrum and H. K. Christenson, Cryst. Growth Des., 2017, 17, 6787–6792.
42. J. T. Avaro, S. L. P. Wolf, K. Hauser and D. Gebauer, Angew. Chem., Int. Ed., 2020, 59, 6155–6159.
43. D. Kashchiev, Nucleation: basic theory with applications, Butterworth Heinemann, Oxford; Boston, 2000.
44. B. G. Oliver and A. R. Davis, Can. J. Chem., 1973, 51, 698–702.
45. J. Ihli, W. C. Wong, E. H. Noel, Y.-Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169.
46. M. de Veij, P. Vandenabeele, T. De Beer, J. P. Remon and L. Moens, J. Raman Spectrosc., 2009, 40, 297–307.
47. O. Söhnel and J. W. Mullin, J. Colloid Interface Sci., 1988, 123, 43–50.
48. P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634.
49. A. Burgos-Cara, C. Putnis, C. Rodriguez-Navarro and E. Ruiz-Agudo, Minerals, 2017, 7, 126.
50. P.-O. Gendron, F. Avaltroni and K. J. Wilkinson, J. Fluoresc., 2008, 18, 1093.
51. S. Jiang and J. H. ter Horst, Cryst. Growth Des., 2011, 11, 256–261.
52. D. Di Tommaso, M. Prakash, T. Lemaire, M. Lewerenz, N. H. De Leeuw and S. Naili, Crystals, 2017, 7, 57.
53. M. Prakash, T. Lemaire, M. Caruel, M. Lewerenz, N. H. de Leeuw, D. Di Tommaso and S. Naili, Phys. Chem. Miner., 2017, 44, 509–519.
54. M. Tagliazucchi and I. Szleifer, Mater. Today, 2015, 18, 131–142.
55. Assuming the timescale, t, is related to that of ion diffusion (typical diffusion coefficient, D = 10⁻⁵ cm² s⁻¹) across the diameter, d, of the pipette via t = d²/D.

---

Footnotes

† Electronic supplementary information (ESI) available: Histogram and statistics from all experiments, Raman analysis of solutions used, control STEM images, Raman spectrum of precipitate, details of the FEM simulations. See DOI: 10.1039/d0cp03032e

‡ These authors contributed equally to this work.

---