The unique catalytic role of water in aromatic C–H activation at neutral pH: a combined NMR and DFT study of polyphenolic compounds

Abstract

Direct activation of aromatic C–H bonds in polyphenolic compounds in a single step, without the use of late transition metals, is demonstrated with the use of D₂O and common phosphate buffer at neutral pD and near ambient temperatures. Detailed variable temperature and pD ¹H NMR studies were carried out to investigate, for the first time, the Gibbs activation energy (ΔG^‡), the activation enthalpy (ΔH^‡), and activation entropy (TΔS^‡) of H/D exchange reactions of the natural product catechin and the model compounds resorcinol and phloroglucinol. NMR and DFT calculations support a catalytic cycle comprising two water molecules in a keto–enol tautomeric process. The reduction of ΔG^‡ values due to the catalytic role of two molecules of water by a factor of 20–30 kcal mol⁻¹ and the resulting acceleration of the H/D exchange rate by a factor of 10²⁰–10³⁰ should be compared with a minor reduction in ΔG^‡ of 0.4 to 4.5 kcal mol⁻¹ due to the effect of an additional electron donating oxygen group and the deprotonation of OH groups. It can therefore be concluded that although the H/D exchange process can be accelerated by a small amount of an acid or a base to break a C–H bond, water as a catalyst plays the major role. This approach opens a new vistas for the combined use of NMR and DFT studies as tools to understand the molecular basis of the catalytic role of water.

---

Introduction

The growing interest in H/D-exchange reactions at carbon centers^1,2 is due to intensive basic research on C–H bond activation,^3–5 in mechanistic investigations on catalysts and reaction pathways,^6–8 and the increasing demand for isotopically labeled compounds as reference materials in mass spectrometry and for pharmacokinetic and metabolic studies.^9,10 The methods for H/D exchange may be broadly divided into two classes, pH-dependent H/D exchange and metal-catalyzed H/D exchange. Acid-catalyzed methods, through an electrophilic aromatic substitution reaction mechanism, have been utilized with strong deuterated Brønsted acids or alternatively Lewis acids, in combination with a deuterium source.^11–13 Base-catalyzed H/D-exchange reactions can also provide a convenient method for the exchange of acidic hydrogen atoms by means of keto–enol equilibria in a variety of carbonyl compounds.^14–16

A central component of the methodological developments of H/D and H/T exchange was the study of metal-catalyzed activations, thus resulting in exchange reactions under milder conditions in sensitive classes of compounds.^17–21 Since the seminal research studies in the late 1960s on H/D exchange by homogeneous catalysis, many efficient methods have been developed which allow a high degree of deuteration in both aromatic and aliphatic substrates.^22–25 An important technical advantage was the development of heterogeneous catalysis due to the possibility to remove the catalyst by simple filtration at the end of the reaction. However, side reactions such as the formation of products of dehalogenation, hydrogenation, and hydrolysis, as well as epimerization and racemization have been frequently encountered.²⁶

Traditionally most organic catalytic reactions have been conducted in aprotic or non-polar organic solvents. These notions, arising mainly from reactivity and solubility considerations, have been modified with the discovery of the effect of water as a solvent in a variety of organic reactions.²⁷ Water can have a significant catalytic effect because it can act as both a proton donor and a proton acceptor and, thus, mediates intra- and inter-molecular proton transfer reactions. In particular, a great importance has been attributed to the explicit role of one or more water molecules shuttling the proton between various reaction sites. Nevertheless, despite the considerable efforts directed into understanding the physicochemical basis of the rate acceleration in homogeneous and heterogeneous water reactions,^27–35 the nature of the interactions that influence Gibbs activation energy and, thus, reactivity was not fully understood.³⁶

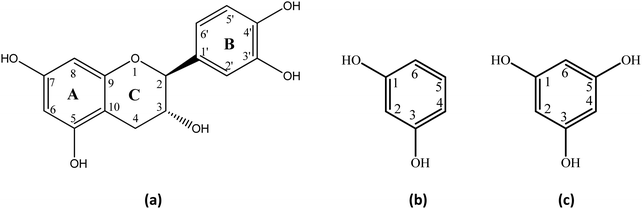
Herein, we describe the investigation of the unique catalytic role of H₂O in aromatic C–H activation of a natural product catechin (a) and the model compounds resorcinol (b) and phloroglucinol (c) (Fig. 1) through keto–enol tautomerization at neutral pH and near ambient temperatures with the use of variable temperature and pD NMR studies and DFT calculations.

Fig. 1 Chemical structures of catechin (a), resorcinol (b), and phloroglucinol (c).

Results and discussion

NMR studies

It has been suggested that the mechanism of H/D exchange reaction of aromatic C–H protons in acid or basic conditions of polyphenolic compounds^37–41 follows a two-step process,⁴¹ as shown in Fig. 2. In the first step, the solvent D⁺ is transferred to the aromatic carbon atom with the formation of an intermediate σ-complex carbocation. In the second step, the hydrogen atom linked to the same carbon is eliminated as H⁺ from the σ-complex. Furthermore, it was found that oxygen substituents on the aromatic ring are expected to stabilize the σ-complex carbocation intermediate⁴² and, thus, to increase the exchange rate.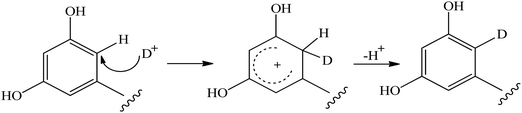

Fig. 2 Suggested mechanism of the H/D exchange process of aromatic C–H protons of flavonoids.⁴¹

Due to the mesomeric effects of electron-donating substitution groups, such as hydroxyl groups, the aromatic rings of flavonoids have certain electronic density at specific sites. For instance, the substitution pattern of ring A can facilitate the electrophilic aromatic substitution reactions involving hydrogen exchange with deuterium at a particular carbon atom. In a basic solution, a path for exchange via a ketone–enolate intermediate has been suggested,^43,44 which also results in the formation of σ-complexes.

The H/D exchange reaction of catechin (a), resorcinol (b), and phloroglucinol (c) (2.5 mM) was investigated using variable temperature and pD 1D ¹H NMR spectroscopy. The NMR experiments were performed with the use of phosphate buffer (25 mM) in order to maintain a constant ionic strength and minimize temperature variation of the pD of solution due to the pK_a values of the compounds investigated^45–47 (Table S1 in ESI†). Fig. 3 illustrates the expanded region of the ¹H NMR spectra of catechin (a) recorded at different time intervals. The assignment of the resonances was confirmed using 2D ¹H–¹³C HSQC and HMBC experiments. The H2′, H5′ and H6′ resonances of ring B, which are well separated from the other aromatic signals, do not show H/D exchange and, thus, were used as an internal integration reference. In contrast, H/D exchange at C(8)–H and C(6)–H of ring A was clearly observed even at pD = 6.92 and 7.93 and at 298 K. The pD values of the solutes in D₂O were estimated using the following relationship:⁴⁸

pD = pH (reading) + 0.4 (1)

The number of spectra to generate a single C(6)–H and C(8)–H H/D kinetic curve was 86 to 30. Fig. 4 and Fig. S1 in ESI† illustrate the decay of the C(6)–H and C(8)–H NMR signals as a function of time at pD values 6.93 and 8.88, respectively. The data were fitted to the relative integrals of the C(8)–H and C(6)–H protons and follow first-order kinetics with reactivity order C(6)–H > C(8)–H. The experimental data demonstrate an increase in the exchange rate at pD = 8.88 as compared with pD = 6.93. The decay of the ¹H NMR signal of phloroglucinol (c) as a function of time at pD values 6.93 and 7.94 is illustrated in Fig. 5. At pD = 8.48 the exchange rate was very fast which did not allow the accurate determination of the thermodynamic parameters of the activation energy (see discussion below). In contrast, in the case of resorcinol (b), the exchange rate was very slow even at pD = 9.91. Fig. 6 illustrates the significant reduction of the integral of the composite signal of the C(4,6)–H protons at δ = 6.45 ppm, compared to that of C(2)–H. The integral of the C(5)–H proton at δ = 7.15 ppm remained constant and clearly shows the presence of a doublet due to ³J coupling of the C(6)–D, C(5)–H, C(4)–H and C(6)–H, C(5)–H, C(4)–D isotopomers (Fig. 6(b)–(d)). The decay of the C(4)–H, C(6)–H and C(2)–H signals as a function of time was, therefore, investigated at elevated temperatures (Fig. S2 in ESI†). The reactivity order was found to be C(4,6)–H > C(2)–H.

Fig. 3 Selected 1D ¹H NMR (400 MHz) spectral range illustrating C(6)–H and C(8)–H H/D exchange of 2.5 mM catechin (a) in D₂O, T = 298 K and 25 mM phosphate buffer at pD = 6.92 (a), pD = 7.93 (b), and pD = 8.88 (c). The spectra were recorded at time intervals of 6.6 min. Total experimental time 8 h, and 48 min for (a–c), respectively.

Fig. 4 C-6 (A) and C-8 (B) H/D exchange kinetic curves of 2.5 mM catechin (a) in D₂O, phosphate buffer solution (25 mM), pD = 6.93 at 298 K and 308 K.

Fig. 5 Composite C(2)–H, C(4)–H and C(6)–H H/D exchange kinetic curves of 2.5 mM phloroglucinol (c) in D₂O, phosphate buffer solution (25 mM): (A) pD = 6.94 at 298 K (a) and 303 K (b), (B) pD = 7.94 at 298 K (a) and 303 K (b), (C) D = 8.94 at 293 K (a) and 298 K (b).

Fig. 6 Selected 1D ¹H NMR (400 MHz) spectral range illustrating the C(2)–H and C(4,6)–H H/D exchange of 2.5 mM resorcinol (b) in D₂O, T = 333 K, and 25 mM phosphate buffer solution, pD = 9.91. The spectra were recorded at time intervals of 0 h (a), 10 h (b), 20 h (c), and 30 h (d).

According to the linear form of the Eyring equation:

where ΔH^‡ is the enthalpy of activation (kcal mol⁻¹), ΔS^‡ is the entropy of activation (kcal mol⁻¹ K ⁻¹), k_B is Boltzmann's constant (0.32984183 × 10⁻²⁶ kcal K⁻¹), T is the absolute temperature in Kelvin (K), k is the rate constant in s⁻¹, R is the ideal gas constant (1.9872036 × 10⁻³ kcal K⁻¹ mol⁻¹), and h is Planck's constant (1.582611 × 10⁻³⁷ kcal s). The values for ΔH^‡ and ΔS^‡ can be determined from kinetic data, obtained from a plot. Eqn (2) is a straight line with a negative slope,, and a y-intercept . The Gibbs energy of activation, ΔG^‡ (kcal mol⁻¹), is given by

ΔG^‡ = ΔH^‡ − TΔS^‡ (3)

The Eyring plots of H/D exchange reactions of catechin (a), resorcinol (b), and phloroglucinol (c) are illustrated in Fig. 7. In all cases very good linear regression correlation coefficients (R² = 0.93–0.99) and standard deviation (±0.30 to ±1.92 kcal mol⁻¹ and ±0.02 to ±5.1 kcal mol⁻¹ for ΔH^‡ and TΔS^‡ values, respectively) were obtained. The effects of pD on ΔH^‡, TΔS^‡ and ΔG^‡ for H/D exchange reactions of catechin (a), resorcinol (b), and phloroglucinol (c) are presented in Table 1. The experimental ΔG^‡ values of catechin (a) and phloroglucinol (c) were found to be in the range of 20.96–19.50 kcal mol⁻¹ at pD values 6.90–8.94. The enthalpy term, ΔH^‡, is the major contributor to the Gibbs energy of activation, ΔG^‡, with the entropic term, TΔS^‡, playing a minor role. The ΔG^‡ values of resorcinol (b) were found to be in the range of 22.7 to 23.9 kcal mol⁻¹ and, thus, are larger than those of catechin (a) and phloroglucinol (c). Surprisingly, the entropic term TΔS^‡ in the case of resorcinol (b) increases significantly and becomes of nearly equal importance to the ΔH^‡ term; however, the statistical error also increased significantly. The Eyring plots do not show any curvature or temperature dependence of the activation energies. This indicates that tunneling phenomena are not of importance for the temperature range and activation energies (19.50 to 23.9 kcal mol⁻¹) investigated. This is contrary to the importance of tunneling phenomena in umbrella-like inversion of pyramidalized amines at low temperatures and with small and narrow activation barriers (<3.5 kcal mol⁻¹).⁴⁹

Fig. 7 Eyring plots of (A) C(6)–H (a) and C(8)–H (b) protons of 2.5 mM catechin (a); (B) C(2)–H (a), and C(4,6)–H (b) protons of 2.5 mM resorcinol (b), and (C) C(2,4,6)–H protons of 2.5 mM phloroglucinol (c) in D₂O, phosphate buffer solution (25 mM) at various pD values.

Table 1 Effects of pD on activation enthalpy (ΔH^‡), activation entropy (ΔS^‡) and Gibbs activation energy (ΔG^‡), for H/D exchange reactions of catechin (a), resorcinol (b), and phloroglucinol (c) at a buffer concentration of 25 mM

Compound	pD	ΔH^‡ (kcal mol^−1)	−TΔS^‡ (kcal mol^−1)	ΔG^‡ (kcal mol^−1)	ΔH^‡ (kcal mol^−1)	−TΔS^‡ (kcal mol^−1)	ΔG^‡ (kcal mol^−1)
Catechin	C(8)–H				C(6)–H
	6.90	17.25 ± 1.31	3.24 ± 0.39	20.50	16.00 ± 1.32	4.42 ± 0.60	20.42
	7.90	18.43 ± 1.63	2.52 ± 0.33	20.96	18.03 ± 1.56	2.90 ± 0.37	20.94
	8.90	20.38 ± 0.65	−0.64 ± 0.02	19.74	20.93 ± 0.66	−1.43 ± 0.06	19.50
Resorcinol	C(2)–H				C(4,6)–H
	8.91	15.14 ± 1.92	8.74 ± 2.94	23.88	13.72 ± 1.79	9.41 ± 3.47	23.13
	9.91	12.91 ± 1.67	10.56 ± 4.81	23.47	11.48 ± 1.64	11.20 ± 5.10	22.68
Phloroglucinol		C(2,4,6)–H
	6.94	17.46 ± 0.30	3.50 ± 0.09	20.96
	7.94	16.05 ± 0.78	3.69 ± 0.26	19.74
	8.94	16.55 ± 1.15	2.86 ± 0.29	19.41

---

Literature pK_a values^45–47 for the molecules investigated in the present work are shown in Table S1 in ESI.† Catechin (a) exists in the uncharged (non-deprotonated) state at pD = 6.9; at pD = 7.9, ∼20% of the molecules exist in the mono-deprotonated form, and at pD = 8.9, nearly 60% of the molecules exist in the mono-deprotonated form. At pD = 7.9, the Gibbs activation enthalpy of catechin (a) is slightly larger. At pD = 8.9, the exchange rate of catechin (a) increases significantly, and the Gibbs activation energy is reduced by 0.76 and 0.92 kcal mol⁻¹ for C-8 and C-6 protons, respectively. This demonstrates that the deprotonation of the OH group can result in the reduction of the ΔG^‡ values. Phloroglucinol (c) at pD = 6.94 exists mainly (>90%) in the uncharged state; at pD = 7.94, 40% of the molecules exist in the mono-deprotonated state which results in the reduction of the ΔG^‡ values by ∼1.2 kcal mol⁻¹. At pD = 8.94, one of the OH groups is 90% and a second one is 40% in the deprotonated states. Despite the subtle changes in the ionization state, the ΔG^‡ value reduces by only ∼1.55 kcal mol⁻¹ which is slightly larger compared with the results obtained for catechin (a). Resorcinol (b) at pD = 8.91 exists essentially in the uncharged state; at pD = 9.91, 70% of the molecules exist in the mono-deprotonated state but the reduction of the ΔG^‡ value for both C-2 proton and the C-4 and C-6 protons is only 0.4 to 0.5 kcal mol⁻¹. This demonstrates that the acceleration of the H/D exchange rate and, thus, the reduction in ΔG^‡ values of catechin (a) and phloroglucinol (c) upon deprotonation of an OH group are not only due to the synergistic effect of the two –OH groups in meta position, but also due to the presence of an additional electron donating oxygen group.

Several experiments were also performed at constant concentration (2.5 mM) of resorcinol and catechin with variable concentration of the phosphate buffer (c = 5 mM, 25 mM and 50 mM at pD = 7.5 and C = 5 mM, 25 mM and 100 mM at pD = 9.6). The maximum reduction of the ΔG^‡ values at high buffer concentration was found to be ≤1.5 kcal mol⁻¹. This demonstrates a minor catalytic effect of the phosphate buffer.

DFT mechanistic studies

Our experimental NMR results that H/D substitution reactions can be performed at neutral pD and at ambient temperatures clearly demonstrate that water can play a major catalytic role. An alternative reaction mechanism, therefore, via a keto–enol tautomerization was investigated with quantum chemical methods in which a water-assisted proton transfer takes place from the phenol OH group to the α-carbon.

The catalytic effect of water molecules in resorcinol (b) was investigated: (i) at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level of theory,⁵⁰ by incorporating also the semi-empirical Grimme's dispersion correction GD3BJ,⁵¹ and (ii) at the M0-62X/6-31+G(d)⁵² and ωB97XD/6-31+G(d)⁵³ level with van der Waals functionals. The following cases were investigated: (i) in vacuum, (ii) in IEF-PCM (water) without explicit water molecules, and (iii) in IEF-PCM (water) in the presence of one, two, and four explicit molecules of water (Table 2 and Tables S3, S4 in ESI†). In all cases the keto–enol species are in thermodynamic equilibrium with overwhelming preference of the phenol-type tautomer.

Table 2 Computed activation enthalpy (ΔH^‡), activation entropy (−TΔS^‡) and Gibbs activation energy (ΔG^‡) for resorcinol, phloroglucinol and catechin for various molecular solvation species

Functional	Complex	Group	ΔH^‡, kcal mol^−1	−TΔS^‡, kcal mol^−1	ΔG^‡, kcal mol^−1
B3LYP/6-31+G(d) (IEF-PCM water)	Resorcinol (in–out conformer)	C(2)–H	61.7	0.3	62.0
		C(4,6)–H	61.0	0.4	61.4
B3LYP/6-31+G(d) (IEF-PCM water)	Resorcinol + 2H2O (in–out conformer)	C(2)–H	24.8	3.7	28.5
		C(4,6)–H	26.0	5.0	31.0
B3LYP-GD3BJ/6-31+G(d) (IEF-PCM water)	Resorcinol + 2H2O (in–out conformer)	C(2)–H	22.1	3.5	25.6
		C(4,6)–H	22.3	3.4	25.7
B3LYP/6-31+G(d) (IEF-PCM water)	Resorcinol + 4H2O (in–out conformer)	C(2)–H	21.4	7.5	28.9
		C(4,6)–H	27.2	2.5	29.7
B3LYP-GD3BJ/6-31+G(d) (IEF-PCM water)	Resorcinol + 4H2O (in–out conformer)	C(2)–H	22.5	4.8	27.3
		C(4,6)–H	26.6	2.0	28.6
B3LYP/6-31+G(d) (IEF-PCM water)	Resorcinol + 4H2O (in–in conformer)	C(2)–H	23.8	2.5	26.3
		C(4,6)–H	—	—	—
B3LYP-GD3BJ/6-31+G(d) (IEF-PCM water)	Resorcinol + 4H2O (in–in conformer)	C(2)–H	22.1	2.1	24.2
		C(4,6)–H	—	—	—
B3LYP/6-31+G(d) (IEF-PCM water)	Phloroglucinol + 2H2O	C(2,4,6)–H	26.8	2.1	28.9
B3LYP-GD3BJ/6-31+G(d) (IEF-PCM water)	Phloroglucinol + 2H2O	C(2,4,6)–H	19.6	3.6	23.2
B3LYP/6-31+G(d) (IEF-PCM water)	Catechin + 2H2O	C(6)–H	23.5	4.3	27.8
		C(8)–H	23.1	2.4	25.5

---

For the ground state of resorcinol (b), three orientations of the two –OH groups in meta position were investigated (Fig. S3 in ESI†). The phenolic OH groups were found to invariably lie in the plane of the aromatic ring. The homodrome configuration⁵⁴ (in–out) of the two –OH groups was found to be of lower energy. The resulting activation energies of this conformer in vacuum were found to be ΔG^‡ (C(2)–H) = 62.5 kcal mol⁻¹ and 50.9 kcal mol⁻¹, and ΔG^‡ (C(4,6)–H) = 61.6 kcal mol⁻¹ and 50.1 kcal mol⁻¹, with optimization of the structures at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level, respectively. These values were significantly reduced in the water continuum model (IEF-PCM) and in the presence of a single explicit water molecule: ΔG^‡ (C(2)–H) = 38.2 kcal mol⁻¹ and 36.0 kcal mol⁻¹ and ΔG^‡ (C(4,6)–H) = 37.6 kcal mol⁻¹ and 35.5 kcal mol⁻¹, with optimization of the structures at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level, respectively (Table S2 in ESI†). In the presence of two explicit water molecules, further significant reduction in ΔG^‡ values was obtained: ΔG^‡ (C(2)–H) = 28.5 kcal mol⁻¹ and 26.2 kcal mol⁻¹ and ΔG^‡ (C(4,6)–H) = 31.0 kcal mol⁻¹ and 28.4 kcal mol⁻¹ with optimization of the structures at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level, respectively (Table 2, Table S3 and Fig. S4 in ESI†).

The use of the empirical Grimme's dispersion correction GD3BJ⁵¹ results in further improvements of the calculated ΔG^‡ values. Thus, at the B3LYP-GD3BJ/6-31+G(d) (IEF-PCM water) level, the computational values ΔG^‡ (C(2)–H) = 25.6 kcal mol⁻¹ and ΔG^‡ (C(4,6)–H) = 25.7 kcal mol⁻¹ (Table 2) are in quantitative agreement with the experimental values ΔG^‡ (C(2)–H) = 23.88 kcal mol⁻¹ and ΔG^‡ (C(4,6)–H) = 23.13 kcal mol⁻¹ (Table 1). Similar results were obtained at the PBE1PBE-GD3BJ/6-31+G(d) (IEF-PCM water) level (Table S3 in ESI†). In contrast, the computational values ΔG^‡ at the M0-62X/6-31+G(d) (IEF-PCM water) and ωB97XD/6-31+G(d) (IEF-PCM water) level with van der Waals functionals were found to deviate from the experimental data (Table S4 in ESI†). The above results clearly demonstrate the advantages of the semi-empirical Grimme's dispersion correction,⁵¹ and the unique catalytic role of two water molecules in reducing the activation energies ΔG^‡. In the transition state, the phenol –OH group and the two water molecules provide one proton for a hydrogen bond to C-2 carbon in a homodrome configuration.⁵⁴ This imposes for the water molecules a rotation so that molecule 1 directs a proton to molecule 2 and molecule 2 to C-2 between the two –OH groups in meta position (Fig. 8).

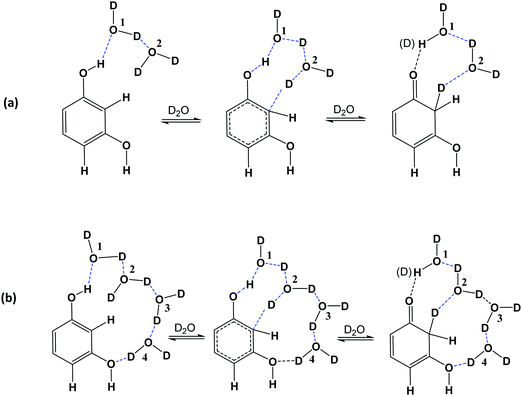Fig. 8 Aromatic C–H activation of resorcinol in the presence of two (a) and four (b) bound molecules of D₂O.

Mehr et al.⁵⁵ investigated deuteration of aromatic rings under very mild conditions through keto-enamine tautomeric equilibrium. It was found that a chain of five water molecules has a significant role in lowering the activation barrier. This particular hydrogen bond framework, which can afford activation barriers as low as 27.3 kcal mol⁻¹, was considered to be indispensable since several calculations using fewer than five molecules of H₂O raised ΔG^‡ values considerably. In order to clarify the above issue, we performed additional computations for resorcinol with four discrete molecules of H₂O at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level. With both functionals, the ΔG^‡ values increased relative to those with two discrete molecules of H₂O. Inclusion of the semi-empirical Grimme's dispersion correction GD3BJ did not improve the results (Table 2 and Table S3 in ESI†). In order to get computational results comparable to those of the experimental data, it was necessary to use the higher energy in–in conformer (Fig. S3 in ESI†, Table 2 and Table S3 in ESI†). From the above it can be concluded that two and not four discrete molecules of H₂O are catalytically important (Fig. 8).

The transition state (TS) structure of resorcinol (b) in the presence of two and four discrete water molecules is shown in Fig. 9. The geometric arrangements are the same either in the gas phase or in aqueous solution. The normal modes, corresponding to the reaction coordinate, for the TS structures with two and four discrete water molecules in aqueous solution associated with the imaginary or negative frequency were found to be ν^‡ = 1001.03i cm⁻¹ and 381.44i cm⁻¹ respectively. By comparing the numerical values of the imaginary frequencies it can be concluded that the imaginary frequency for the transition state structure with two discrete water molecules is greater by a factor of ∼2.62 compared to the one with four water molecules. Examination of the corresponding vibrational modes for Fig. 9(a) shows that the greatest movements involve the hydrogen atoms H2, H5 and H3. This indicates that the geometric distortion of the solvation complex of resorcinol (b) + 2H₂O is relatively large particularly with respect to the normal mode concerning the atom H2 which has the largest magnitude (|v⃑_H2| = 0.929 Å). The geometric distortions in Fig. 9(b) involve the atoms H′2, H′5 and H′3. However, inspection of all normal modes for the two transition states shows that in Fig. 9(b), the two extra water molecules (denoted O′3 and O′4) do not participate in the exchange mechanism. Hence, the first TS involves the optimal number of two water molecules, given also the fact of the greater value of the imaginary frequency. Consequently, the TS involving four water molecules becomes of secondary importance. A rigorous proof of the above transition state (TS) was obtained through an IRC (Intrinsic Reaction Coordinate) calculation,^56–58 as shown in Fig. 10. This type of computation starts from the transition state and examines the reaction path on the potential energy surface (PES) on either side of the TS, leading down to reactants and products. The IRC curve was obtained using the LQA (Local Quadratic Approximation) algorithm,^59,60 where the reaction path is represented as a Taylor series expansion of the arc length truncated to second order.

Fig. 9 The transition state with normal mode vectors of resorcinol (b) in the presence of two (a) and four (b) discrete water molecules.

Fig. 10 IRC path in the gaseous phase from the transition state towards reactants (resorcinol (b) plus two discrete water molecules) and products (keto product).

Similar DFT calculations were carried out for phloroglucinol (c). In the lower energy ground state of phloroglucinol (c), the three –OH groups were found to be in a homodrome configuration and in the plane of the aromatic ring. As in the case of resorcinol (b), activation energies were significantly reduced in the water continuum model (IEF-PCM) and in the presence of two explicit water molecules (Fig. S5 in ESI†). Interestingly at the B3LYP-GD3BJ/6-31+G(d) and PBE1PBE-GD3BJ/6-31+G(d) level, the resulted Gibbs activation energies (Table 2 and Tables S2, S3 in ESI†) were found to be significantly lower than those of resorcinol (b), in excellent agreement with the experimental data (Table 1).

The 2R,3S configuration was used in the DFT calculations of catechin (a).^61,62 The water starting arrangement was to place both water molecules either in the vicinity of the phenol C(7)–OH and C(6)–H groups or in the vicinity of C(9)–OH and C(8)–H groups. After optimization, the water molecules turn out to be hydrogen bonded to each other. The DFT structures of the ground states of catechin (a) with respect to its transition state with two discrete molecules of H₂O are illustrated in Fig. 11. Again, a significant reduction in ΔG^‡ values was obtained with respect to ΔG^‡ values in the absence of discrete molecules of H₂O. The overall excellent agreement of computational and experimental ΔG^‡ values, therefore, demonstrates a unique catalytic effect of H₂O⁶³ of over 23–30 kcal mol⁻¹. Interestingly, the synergistic effect of two OH groups in meta position, the presence of an additional electron donating oxygen group, and the deprotonation of OH groups result only in a moderate reduction of ΔG^‡ values by a factor of 0.4 to 4.5 kcal mol⁻¹.

Fig. 11 DFT structures of the ground states of catechin (a) with respect to its transition state with two discrete molecules of water at the C(6)–H proton with minimization of the structures at the DFT/B3LYP/6-31+G(d) (IEF-PCM Water) (A) and at the DFT/PBE1PBE/6-31+G(d) (IEF-PCM Water) level of theory (B).

The computed values of the different contributions to the total activation entropy, ΔS^‡, are shown in Table S5 (ESI†). The vibration entropy, ΔS_Vib, makes a major contribution to the activation energy with translational entropy, ΔS_Trans, and rotational entropy, ΔS_Rot, playing a negligible role at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level of theory. The significant effect of vibrational entropy is in agreement with the previous analysis of Fig. 9. A natural bond orbital (NBO) analysis of catechin (a), resorcinol (b), and phloroglucinol (c) was carried out to explain the effect of charge transfer and delocalization on the H/D exchange process (Table S6, ESI†). The NBO charges, at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level, indicate a significant variation of the charges of the carbon atoms, involved in the H/D exchange process. Thus, the charge density of C(2), C(4), and C(6) of phloroglucinol (c) (−0.413) shows a significant increase with respect to C(2) (−0.380), and C(4), C(6) (−0.368) of resorcinol (b). The plot of the NBO charge densities of the aromatic carbons involved in H/D exchange vs. the respective computational or experimental Gibbs activation energies for catechin (a), resorcinol (b), and phloroglucinol (c), however, does not show any functional dependence.

Materials

All chemicals were of reagent grade and were purchased commercially.

NMR spectroscopy

¹H NMR spectra were obtained on Bruker AV-500 and AV-400 NMR instruments using 2.5 mM catechin (a), resorcinol (b), and phloroglucinol (c) dissolved in 25 mM phosphate buffer in D₂O solutions at specified pD values.

Computational details

Calculations were performed with the DFT method, with the B3LYP and PBE0 (PBE1PBE) hybrid functional as implemented in the Gaussian 09W Package.⁴⁹ The molecular structures of catechin (a), resorcinol (b), and phloroglucinol (c) without and with one and two discrete water molecules were optimized at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) basis set level in the gas phase, as well as using the IEF-PCM model (Integral Equation Formalism-Polarizable Continuum Model). For resorcinol, further computations were performed at the M0-62X/6-31+G(d) and ωB97XD/6-31+G(d) level with two discrete H₂O molecules and at the B3LYP-GD3BJ/6-31+G(d) and PBE1PBE-GD3BJ/6-31+G(d) level with two and four discrete H₂O molecules. For phloroglucinol, further computations were performed at the B3LYP-GD3BJ/6-31+G(d) and PBE1PBE-GD3BJ/6-31+G(d) level. In order to investigate the transition state, as well as the structure of the products, calculations were carried out at the same level of theory using gas phase and IEF-PCM models without and with one, two, and four discrete water molecules. The computed geometries were verified as minima by frequency calculations at the same level of theory (no imaginary frequencies).

Conclusions

We have reported that aromatic H/D substitution reactions can be performed in water at neutral pH and at near ambient temperatures by the use of water catalysis under unprecedented mild conditions. The experimental ΔG^‡ values of catechin and phloroglucinol were found to be in the range of 21–19.5 kcal mol⁻¹ at pD values of 6.9–8.8. The enthalpic ΔH^‡ term was found to be the major contributor to the ΔG^‡ values with a minor contribution (up to 3.7 kcal mol⁻¹) of the entropic TΔS^‡ term. In contrast, the exchange rates for H/D exchange were significantly slower in resorcinol with ΔG^‡ values in the range of 22.5 to 23.9 kcal mol⁻¹, at pD values 8.9–9.9. This demonstrates that the acceleration of the H/D exchange rate and, thus, reduction in ΔG^‡ values of catechin and phloroglucinol are not only due to the synergistic effect of the two –OH groups in meta position, but also due to the presence of an additional electron donating –OH group. The experimental data were compared with DFT calculations at the B3LYP/6-31+G(d) and PBE1PBE/6-31+G(d) level of theory using the IEF-PCM model. Without explicit molecules of water, ΔG^‡ values were found to be in the range of 62 to 50 kcal mol⁻¹. In contrast, inclusion of two discrete solvation molecules of H₂O results in a significant reduction of ΔG^‡ values which were found to be in the range of 30 to 23 kcal mol⁻¹. The use of the empirical Grimme's dispersion correction GD3BJ⁵¹ results in further improvement of the calculated ΔG^‡ values for resorcinol and phloroglucinol which are in quantitative agreement with the experimental values. This study demonstrates that the activation enthalpy (ΔH^‡), activation entropy (ΔS^‡) and Gibbs activation free energy (ΔG^‡) can be of predictive value for the aromatic C–H activation in polyphenolic compounds, making their physicochemical interpretation an invaluable tool for the understanding of mechanisms and reactivity. This approach is meaningful for several reasons:

(i) the present data necessitate the incorporation of water catalysis (Fig. 8) in undergraduate textbooks in addition to the acid/base catalyzed H/D exchange mechanism (Fig. 2);

(ii) aqueous chemistry predominates in biological processes and, thus, the catalytic role of water may have implications for biocatalytic reactions and artificial biomimetic systems;

(iii) water catalysis by definition is a green chemistry and environmentally friendly method, since it avoids the use of dipolar aprotic solvents;

(iv) water catalysis may require lower reaction temperatures given the high concentration of D₂O as a cheap and environmentally benign deuterium source which can potentially translate into large scale processes.

Author contributions

AF conducted the NMR experiments, AF, MGS and PV conducted the computations, and MGS, MIC, A-t-W and IPG conceived and designed the project, analyzed the data and prepared the manuscript.

Conflicts of interest

There are no conflicts to declare.

References

1. M. Siskin and A. R. Katritzky, Chem. Rev., 2001, 101, 825–835.
2. J. Atzrodt, V. Derdau, T. Fey and J. Zimmermann, Angew. Chem., Int. Ed., 2007, 46, 7744–7765.
3. R. H. Crabtree, J. Organomet. Chem., 2004, 689, 4083–4091.
4. X. Ribas, R. Xifra, T. Parella, A. Poater, M. Solà and A. Llobet, Angew. Chem., Int. Ed., 2006, 45, 2941–2944.
5. D. A. Colby, R. G. Bergman and J. A. Ellman, Chem. Rev., 2011, 110, 624–655.
6. D. M. Marcus, K. A. McLachlan, M. A. Wildman, J. O. Ehresmann, P. W. Kletnieks and J. F. Haw, Angew. Chem., Int. Ed., 2006, 45, 3133–3136.
7. E. M. Simmons and J. F. Hartwig, Angew. Chem., Int. Ed., 2012, 51, 3066–3072.
8. M. Gómez-Gallego and M. A. Sierra, Chem. Rev., 2011, 111, 4857–4963.
9. I. V. Tetko, P. Bruneau, H. W. Mewes, D. C. Rohrer and G. I. Poda, Drug Discovery Today, 2006, 11, 700–707.
10. R. P. Yu, D. Hesk, N. Rivera, I. Pelczer and P. J. Chirik, Nature, 2016, 529, 195–199.
11. P. M. Yavorsky and E. Gorin, J. Am. Chem. Soc., 1962, 84, 1071–1072.
12. P. McGeady and R. A. Croteau, J. Chem. Soc., Chem. Commun., 1993, 9, 774–776.
13. P. S. Kiuru and K. Wähälä, Steroids, 2006, 71, 54–60.
14. P. Ryberg and O. Matsson, J. Org. Chem., 2002, 67, 811–814.
15. C. Berthelette and J. Scheigetz, J. Labelled Compd. Radiopharm., 2004, 47, 891–894.
16. T. Furuta, A. Suzuki, M. Matsuzawa, H. Shibasaki and Y. Kasuya, Steroids, 2003, 68, 693–703.
17. A. Sharma and J. F. Hartwig, Nature, 2015, 517, 600–604.
18. R. Y. Tang, G. Li and J. Q. Yu, Nature, 2014, 507, 215–220.
19. J. C. Lewis, P. S. Coelho and F. H. Arnold, Chem. Soc. Rev., 2011, 40, 2003–2021.
20. S. M. Paradine, J. R. Griffin, J. Zhao, A. L. Petronico, S. M. Miller and M. C. A. White, Nat. Chem., 2015, 7, 987–994.
21. Y. Y. Loh, K. Nagao, A. J. Hoover, D. Hesk, N. R. Rivera, S. L. Colletti, I. W. Davies and D. W. MacMillan, Science, 2017, 358, 1182–1187.
22. J. L. Garnett and R. J. Hodges, J. Am. Chem. Soc., 1967, 89, 4546–4547.
23. R. H. Crabtree, Chem. Rev., 1995, 95, 987–1007.
24. S. S. Stahl, J. A. Labinger and J. E. Bercaw, Angew. Chem., Int. Ed., 1998, 37, 2180–2192.
25. B. A. Arndtsen and R. G. Bergman, Science, 1995, 270, 1970–1973.
26. M. Beller and C. Bolm, Transition metals for organic synthesis, Wiley-VCH, Verlag GmbH, 1998.
27. R. Breslow, Acc. Chem. Res., 1991, 24, 159–164.
28. S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, Angew. Chem., Int. Ed., 2005, 44, 3275–3279.
29. U. M. Lindström, Chem. Rev., 2002, 102, 2751–2772.
30. A. Chanda and V. V. Fokin, Chem. Rev., 2009, 109, 725–748.
31. Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502.
32. T. G. Kim, Y. Kim and D.-J. Jang, J. Phys. Chem. A, 2001, 105, 4328–4332.
33. D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604.
34. S. Otto and J. B. Engberts, Org. Biomol. Chem., 2003, 1, 2809–2820.
35. N. A. Isley, R. T. Linstadt, S. M. Kelly, F. Gallou and B. H. Lipshutz, Org. Lett., 2015, 17, 4734–4737.
36. T. Kitanosono, K. Masuda, P. Xu and S. Kobayashi, Chem. Rev., 2018, 118, 679–746.
37. M. Pohjoispää, E. Leppälä and K. Wähälä, J. Labelled Compd. Radiopharm., 2007, 50, 521–522.
38. S. Rasku and K. Wähälä, Tetrahedron, 2000, 56, 913–916.
39. S. Rasku, K. Wähälä, J. Koskimies and T. Hase, Tetrahedron, 1999, 55, 3445–3454.
40. H. Jiang, H. Fang, L. Jiang, L. Zheng, N. Wang, A. Zheng, F. Deng and M. Liu, Chin. J. Chem., 2010, 28, 2281–2286.
41. M. Jordheim, T. Fossen, J. Songstad and O. M. Andersen, J. Agric. Food Chem., 2007, 55, 8261–8268.
42. M. Lohrie and W. Knoche, J. Am. Chem. Soc., 1993, 115, 919–924.
43. E. S. Hand and R. M. Horowitz, J. Am. Chem. Soc., 1964, 86, 2084–2085.
44. A. J. Kresge and Y. Chiang, J. Am. Chem. Soc., 1961, 83, 2877–2885.
45. J. M. Herrero-Martínez, M. Sanmartin, M. Rosés, E. Bosch and C. Ràfols, Electrophoresis, 2005, 26, 1886–1895.
46. S. E. Blanco, M. C. Almandoz and F. H. Ferretti, Spectrochim. Acta, Part A, 2005, 61, 93–102.
47. D. Wang, K. Hildenbrand, J. Leitich, H. P. Schuchmann and C. von Sonntag, Z. Naturforsch., B: J. Chem. Sci., 1992, 48, 478–482.
48. P. K. Glasoe and F. A. Long, J. Phys. Chem., 1960, 64, 188–190.
49. N. Mandal, A. K. Pal, P. Gain and A. Datta, J. Am. Chem. Soc., 2020, 142, 5331–5337.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, B. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010.
51. S. Grimme, S. Ehrlish and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
52. Y. Zhao and D. G. Truhlar, J. Phys. Chem., 2006, 110, 5121–5129.
53. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
54. A. Michaelides and K. Morgenstern, Nat. Mater., 2007, 6, 597–601.
55. S. H. M. Mehr, K. Fukuyama, S. Bishop, F. Lelj and M. J. MacLachlan, J. Org. Chem., 2015, 80, 5144–5150.
56. F. Jensen, Introduction to Computational Chemistry, Wiley, Chichester, 2nd edn, 2007.
57. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
58. K. Fukui, Int. J. Quantum Chem., 1981, 15, 633–642.
59. M. Page and J. W. McIver Jr, J. Chem. Phys., 1988, 88, 922–935.
60. M. Page, C. Doubleday and J. W. McIver Jr, J. Chem. Phys., 1990, 93, 5634–5642.
61. J. K. Harper, J. A. Doebbler, E. Jacques, D. M. Grant and R. B. Von Dreele, J. Am. Chem. Soc., 2010, 132, 2928–2937.
62. F. R. Fronczek, R. W. Hemingway, G. W. Mcgraw, J. P. Steynberg, C. A. Helfer and W. L. Mattice, Biopolymers, 1993, 33, 275–282.
63. G. Alagona, C. Ghio and P. I. Nagy, Phys. Chem. Chem. Phys., 2010, 12, 10173–10188.

---

Footnote

† Electronic supplementary information (ESI) available: pK_a values, NBO charges, H/D exchange of catechin and resorcinol, isomers of resorcinol, DFT structures of the ground and transition states of resorcinol and phloroglucinol, computed ΔH^‡, TΔS^‡ and ΔG^‡ values. See DOI: 10.1039/d0cp02826f

---