Insights into the photoprotection mechanism of the UV filter homosalate

Abstract

Homosalate (HMS) is a salicylate molecule that is commonly included within commercial sunscreen formulations to provide protection from the adverse effects of ultraviolet (UV) radiation exposure. In the present work, the mechanisms by which HMS provides UV photoprotection are unravelled, using a multi-pronged approach involving a combination of time-resolved ultrafast laser spectroscopy in the gas-phase and in solution, laser-induced fluorescence, steady-state absorption spectroscopy, and computational methods. The unique combination of these techniques allow us to show that the enol tautomer of HMS undergoes ultrafast excited state intramolecular proton transfer (ESIPT) upon photoexcitation in the UVB (290–320 nm) region; once in the keto tautomer, the excess energy is predominantly dissipated non-radiatively. Sharp transitions are observed in the LIF spectrum at close-to-origin excitation energies, which points towards the potential presence of a second conformer that does not undergo ESIPT. These studies demonstrate that, overall, HMS exhibits mostly favourable photophysical characteristics of a UV filter for inclusion in sunscreen formulations.

---

Introduction

Salicylates are defined as salts or esters derived from salicylic acid, several of which have uses within the personal care and pharmaceutical industries.¹ In addition to being included in cosmetics for fragrance and antioxidant properties,^1,2 salicylates are used as chemical (organic) filters in sunscreen blends, for solar protection via absorption of ultraviolet (UV) radiation, specifically UVB radiation (290–320 nm).^3,4 Even though regulated exposure to UV radiation has positive effects on human health, such as facilitating the synthesis of vitamin D, the use of UV filters in sunscreen formulations is necessary to prevent the adverse effects of overexposure, such as an increased risk of skin cancers.^5–12

Despite having a low extinction coefficient compared to other available UV filters,¹³ salicylates are an appealing choice for sunscreen formulators for several reasons. Firstly, the minimal solvatochromic shift that is observed in salicylates upon significant changes in solvent polarity has been demonstrated in at least 13 different solvents.^14,15 This negligible shift in peak absorption implies that a range of excipients may be used in a formulation without changing the protection range of wavelengths afforded by these molecules. Furthermore, salicylates contained within sunscreen formulations can serve as solubilizers for other UV filters such as avobenzone, which to date remains the most widely implemented UVA (320–400 nm) filter in the world.^16–18 In addition, salicylates have a favourable safety record, with few reports of allergenic effects of these compounds.^19,20 However, a consensus is yet to be reached on whether salicylates used in sunscreens are photostable, that is, if they do not degrade upon prolonged UV exposure. Many publications report that they are indeed photostable,^18,21–23 while other reports also exist to the contrary.^24,25

The molecule chosen as the focus of this study is homomenthyl salicylate (herein referred to as homosalate, HMS); its molecular structure and the range of UV protection it provides is shown in Fig. 1. This molecule is approved for use in sunscreen formulations worldwide and can be employed in substantial quantities (e.g. up to 15% w/w in the United States).²⁶ Recent studies in rat models have shown that HMS has low dermal permeability and does not cause any endocrine disruption, both of which are major concerns for many existing UV filters used in sunscreen formulations.^27,28 In addition, HMS has been deemed to have a favourable toxicological profile.²⁹ However, in the MCF-7 cell line, HMS was shown to have cytotoxic and genotoxic characteristics, and extensive studies on the toxicological effects of HMS are recommended.³⁰

Fig. 1 (a) Normalised UV-visible spectra of homosalate (HMS) in acetonitrile (blue line), ethanol (black line) and cyclohexane (red line), with molecular structure of HMS (enol form) inset. The dashed line indicates the presence of an intramolecular hydrogen bond.

In this study, femtosecond (fs,  10⁻¹⁵ s) pump–probe spectroscopy techniques in both the gas-phase and in solution have been used to elucidate the excited state photodynamics of HMS upon absorption of UVB radiation. By using ultrafast spectroscopy, a deeper insight into the specific relaxation mechanism(s) of salicylates upon exposure to solar radiation can be gained, which in turn can be beneficial to determine whether molecules of this type dissipate their incident UV radiation safely, i.e. quickly and without generating any harmful and/or reactive photoproducts.^31,32 Other UV filters with an intramolecular hydrogen bond have previously been investigated with these techniques.^33–35 For example, upon excitation at its UVA absorption maximum, oxybenzone was shown to exhibit excited state intramolecular proton transfer (ESIPT), followed by a molecular rotation which facilitated a fast decay to the ground electronic state on a picosecond timescale, an ideal behaviour for a UV filter.³³ Conversely, menthyl anthranilate (MenA) was shown to undergo hydrogen atom dislocation, rather than transfer, and a significant energetic barrier towards a nearby conical intersection (CI) was found to prevent fast and efficient excited state relaxation.³⁵ Due to its long-lived nature (≫nanoseconds), MenA is not an ideal candidate for inclusion in sunscreen formulations as it is vulnerable to detrimental relaxation pathways.³⁵ Therefore, the effect of the intramolecular hydrogen bond in these salicylates is worthy of further investigation. A review of sunscreen molecules that undergo keto–enol tautomerisation and ESIPT, studied by ultrafast spectroscopy techniques, has been published previously.³⁶

In the present work, a bottom-up approach is employed to investigate the ultrafast molecular dynamics of HMS upon photoexcitation with UVB radiation. The starting point is taken to be HMS in the gas-phase, whereby the influence of external stimuli is eliminated, focusing on establishing the intramolecular photodynamic processes in operation. Complexity is then increased through the addition of a solvent; the added intermolecular interactions act as a stepping stone towards simulating the photoprotection mechanisms of single UV filters within a complex sunscreen formulation. It is crucial that photodynamics of UV filters such as salicylates in these simpler mixtures are well understood before progressing to studies of more realistic blends.³² The ultrafast pump–probe spectroscopy measurements conducted in this work are supported by laser-induced fluorescence measurements and computational calculations, which can assist with the assignment of spectral features to molecular photodynamics. The results of these complementary techniques combine, not only to enrich our understanding of the photoprotection mechanisms within HMS, thus informing on its inclusion in sunscreens and other cosmetic formulations, but also to compile further information for future UV filter design and sunscreen formulation development.

Methods

Ultrafast laser spectroscopy setup

A fundamental laser beam centred at 800 nm with ∼40 fs pulse width, ∼3 mJ per pulse and 1 kHz repetition rate was produced by a commercial femtosecond laser system comprised of a Ti:sapphire oscillator (Spectra-Physics Tsunami) and a regenerative amplifier (Spectra-Physics Spitfire XP). This fundamental beam was subsequently split into three beams of ∼1 mJ per pulse each, two of which were used to pump two separate optical parametric amplifiers (Light Conversion, TOPAS-C), producing the pump beams for the experiments both in the gas-phase and in solution. Experiments in the gas-phase employed a single-wavelength probe, while in solution the probe beam consisted of a white light continuum, as detailed below.

Experiments in vacuum

a. Time-resolved ion yield (TR-IY). The time-resolved ion yield (TR-IY) apparatus used for the present experiments has been previously described in detail;³⁷ specific details relevant to the present work are provided herein.

Homosalate (HMS, provided by Lipotec SAU) was studied as provided and without any further purification. HMS was vaporised via heating to approximately 130 °C and subsequently seeded into helium buffer gas (∼3 bar). The gaseous mixture was then expanded into vacuum (∼10⁻⁷ mbar) via an Even–Lavie pulsed solenoid valve³⁸ to create the sample molecular beam. The pump and probe beams intersected the molecular beam, while the pump–probe time delay (at predefined time intervals Δt) was controlled by a gold retroreflector mounted on a motorised delay stage along the 800 nm fundamental beam path (used to generate the 200 nm probe, see below). The maximum temporal window provided by the delay stage was 1.3 nanoseconds (ns). At the laser-molecular beam intersection point, the pump photoexcited the sample and the probe ionised the excited species.

The pump wavelengths for TR-IY measurements (λ_pump = 305–335 nm) were chosen in order to sample the different absorption regions probed in our laser induced fluorescence measurements (see Results and discussion section below), starting from the S₁(v = 0) origin of HMS (29 833.4 cm⁻¹, ∼335 nm) and evaluating the effect of photoexcitation with higher energies. The 200 nm probe beam used to photoionize any excited species was generated by successive frequency conversion of the remaining ∼1 mJ part of the fundamental 800 nm beam using barium borate (BBO) crystals in the following sequence: type I, type II, type I.

The pump–probe ion signal was monitored with a time-of-flight (TOF) mass spectrometer apparatus, equipped with a detector consisting of two microchannel plates (MCPs) coupled to a metal anode. The output from the MCP was measured by a digital oscilloscope (LeCroy LT372 Waverunner) and gated in ion flight time over the mass channel of the parent (HMS⁺) ion. The parent TOF signal was then monitored as a function of pump–probe time delay (Δt), resulting in the TR-IY transients. For all TR-IY measurements, the polarizations of the pump and probe beams were kept at magic angle (54.7°) with respect to each other in order to minimize any rotational effects.³⁹ Additionally, power dependence studies were conducted to ensure single-photon initiated dynamics under the current experimental conditions, as shown in Section S1.1.1 (S1.1.1), Fig. S1 of the ESI.† ⁴⁰

The quoted time constants were extracted from the TR-IY transients by a non-linear curve fitting algorithm (further discussed in the ESI,† S1.1.2), comprising a sum of exponential decays convoluted with a Gaussian instrument response function (IRF, typically ∼170 fs at relevant powers for this experiment, see S1.1.3, Fig. S2, ESI†). The kinetic model employed in these fits assumes parallel dynamics, i.e. it assumes that all processes start at Δt = 0. The standard errors provided by the kinetic fit have been herein reported as estimated errors associated with quoted time constants.

b. Laser induced fluorescence (LIF) and dispersed fluorescence (DFL). To complement our gas-phase ultrafast laser spectroscopy studies, high frequency resolution laser induced fluorescence (LIF) measurements were carried out using a separate laser system to the one described above; a detailed description of this apparatus has been provided in previous publications^41–43 and therefore only specific details pertaining to the present studies are given here.

Helium was used as the seed gas at a pressure of 3–4 bar, flowing over a sample of HMS maintained at 110 °C to produce sufficient vapour pressure. A pulsed valve (Parker General Valve Series 9) with an orifice of 500 μm operating at 20 Hz was used to supersonically cool the sample as it expanded into vacuum. The sample was interrogated with the doubled output of a Nd:YAG (Quantel Q-smart 450) pumped tunable dye laser (Radiant Dyes Narrowscan). LIF excitation scans were recorded by collecting the emission from the jet-cooled molecules with a set of collection/steering optics, and imaging the emission onto a UV-enhanced photomultiplier tube (PMT). The PMT was protected by long-pass filters to reduce the scattered light from the laser. A sampling gate was placed around the fluorescence decay profile, digitized by an oscilloscope (Tektronix, model 3052B), and integrated. The tunable dye laser (Exciton laser dye: DCM) was scanned in the 29 800–32 800 cm⁻¹ (335.5–305.0 nm) range.

This setup was also employed to obtain gas-phase dispersed fluorescence (DFL) spectra of HMS. These spectra were obtained by fixing the laser wavelength resonant with selected transitions in the excitation spectrum, and imaging the fluorescence onto the entrance slit of a ¾ m monochromator. Since the fluorescence was spread over a large range, red-shifted from the excitation frequency, distinct peaks were not observed in the DFL spectrum. In order to obtain the shape of the broad DFL spectra, the slit width was set at 1 mm and an intensified CCD camera (Andor SOLIS iStar) collected the total dispersed emission signal impinging on the CCD at a fixed grating position. The grating position was tuned point-by-point and the entire spectrum for a given central grating position was integrated. Fluorescence lifetime traces were also recorded by exciting select transitions, and directly recording the time profile of the fluorescence signal from the PMT on the digital oscilloscope. The gas-phase fluorescence lifetimes of HMS were extracted from the resulting transients following the same method as for the TR-IY transients (see above and further details in the ESI,† S1.1.4 and Fig. S3), using, in this case, an instrument response full width at half maximum of 8 ns.

Experiments in solution

a. Transient electronic absorption spectroscopy (TEAS). The ultrafast transient electronic (UV-visible) absorption spectroscopy (TEAS) setup used in the present studies, which uses the aforementioned ultrafast laser spectroscopy setup, has been described previously;⁴⁴ specific details regarding these experiments are provided below.

Three separate solutions of HMS dissolved in cyclohexane (CHX, Fisher Scientific, >99.9%), ethanol (EtOH, VWR Chemicals, >99.9%) and acetonitrile (ACN, Fisher Scientific, >99.8%) were prepared to a concentration of ∼10 mM. To prevent photodegradation of the sample over time, a diaphragm pump (Simdos K2) was used to recirculate the solutions via a flow-through sample cell (Harrick Scientific) between two CaF₂ windows (thickness 1–2 mm, 25 mm diameter). PTFE spacers maintained a sample path length of 100 μm. This path length ensured a sample absorbance of less than 0.5.

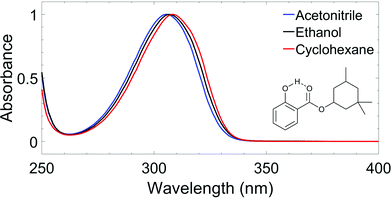
The wavelength of the pump pulses (λ_pump) was chosen to be the peak absorption of HMS in each solvent, shown in Fig. 1: λ_pump = 309 nm in CHX, 307 nm in EtOH and 306 nm in ACN. The fluence of the pump pulses at all wavelengths was ∼0.5 μJ cm⁻². The probe consisted of broadband white light pulses (320–720 nm), generated by focusing a 5 mW portion of the fundamental 800 nm beam onto a CaF₂ crystal (2 mm thick). The pump–probe time delays in our TEAS setup were controlled by a gold retroreflector mounted on a motorised delay stage, similar to that described for the TR-IY setup. In this instance, the delay stage was situated along the portion of the 800 nm fundamental that generates the white light continuum, and facilitated a maximum Δt of 2 ns. The fluence of the probe pulse was changed post-sample by a neutral density filter as required to avoid saturating the detector.

The transient absorption data collected with this setup was quantitatively analysed via global analysis fitting using Glotaran, a graphical user interface for the R package TIMP.^45–47 The fitting was carried out assuming both parallel and sequential kinetic models; more details regarding the fitting procedures and the IRF of our TEAS experiments are given in the ESI,† in Sections S1.2.1 and S1.2.2 (Fig. S4) respectively. Moreover, similar to our experiments in the gas-phase, TEAS power dependence studies were carried out to ensure single-photon initiated dynamics for our experiments in solution (S1.2.3, Fig. S5 and S6, ESI†).

Steady-state spectroscopy

UV-visible spectroscopy measurements were conducted for solutions (∼100 μM) of HMS in each solvent (CHX, EtOH and ACN) using a quartz cuvette of 10 mm path length in a Agilent Cary-60 spectrophotometer. All fluorescence measurements of HMS (emission spectra and lifetimes, see S1.2.4, ESI,† for further details) were acquired using a Horiba Fluorolog-3. Each solution of HMS was prepared in this instance to a concentration of around ∼10 μM to ensure that the absorbance of the solution was under 0.1. More detailed information pertaining to these fluorescence measurements, alongside the UV-visible spectra of all fluorescence samples, can be found in Fig. S7 (ESI†). The quantum yield of HMS was also determined; full experimental details can be found in the ESI,† (S1.2.5).

Computational methods

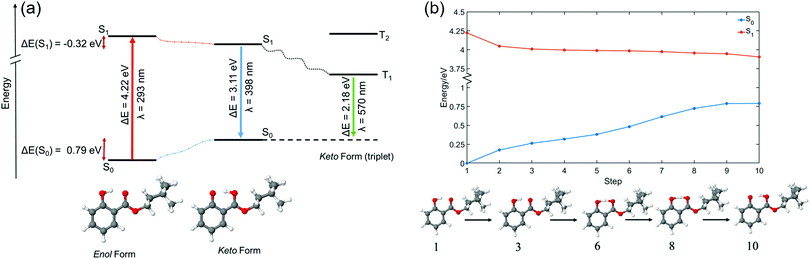
All calculations were conducted in the NWChem software package.⁴⁸ Density functional theory (DFT) geometry optimisation was performed on two conformers of HMS, each of which was suspected to be close to a local geometric energy minimum. This relaxation was conducted with the PBE functional and cc-pVTZ basis set.⁴⁹ The single-point energies of each of these structures were calculated with the functionals PBE and PBE0, both with the cc-pVTZ basis set. These were also calculated with the post Hartree–Fock method MP2 using the cc-pVDZ basis set, in order to compare relative energies in the gas-phase. These results can be found in Table S1 in the ESI.† Of the two previously mentioned structures of HMS, the one of lowest energy—herein referred to as the enol form (conformer 1), see Fig. 2a—was selected as the likely global minimum and carried forward for further testing. These calculations were conducted in vacuum as well as in implicitly modelled EtOH, CHX and ACN using the COSMO solvent model inbuilt in NWChem to generate four structures.^50–52 The higher energy conformer, also an enol with an intramolecular hydrogen bond (H-bond) between the enol OH and ester oxygen, was also retained for further testing (herein referred to as conformer 2). The structures of both conformers are presented in the ESI,† Fig. S8.

Fig. 2 (a) A representation of the different energy levels of HMS (conformer 1) in vacuum in the enol (left) and keto (right) form, as predicted using the PBE0/cc-pVTZ level of theory. In (a), the red arrow represents the absorption of a photon, the blue arrow represents fluorescence, and the green arrow represents phosphorescence. The dotted lines in blue and orange between the S₀ and S₁ states are indicative of the linear interpolation of internal coordinates calculated for HMS in vacuum at the PBE0/cc-pVTZ level of theory, shown in further detail in (b) alongside the predicted structures of HMS at selected steps. These calculations suggest that, when in the ground state, conformer 1 of HMS exists in the enol form, whereas in the first excited singlet state (S₁) HMS converts to the keto state in an energetically barrierless process.

The global minimum enol structure (conformer 1) was then relaxed in the first excited singlet state (S₁, ππ*) in order to predict the structure of the system after photoexcitation in vacuum. This was achieved by first relaxing at the PBE/cc-pVTZ and then the PBE0/cc-pVTZ level of theory. Following this, the species was further relaxed in each of the implicit solvents. These relaxations resulted in the keto form of HMS shown in Fig. 2a, which was again taken forward for further analysis employing the PBE0/cc-pVTZ level of theory as is now described. Using each of the eight structures, enol and keto structures in all three implicit solvents and vacuum, time-dependent DFT was carried out in order to find singlet (S_n) and triplet (T_n) vertical excitations. The energy of the T₁ state was more accurately calculated using a ΔSCF methodology.⁵³ This was achieved by conducting single point energy calculations with state multiplicity set to 3 (triplet state) on each of the previously obtained enol and keto structures; the results were then compared to the S₀ energies for each form, once again in all three solvents as well as in vacuum. Conformer 2 also underwent excited state relaxation along the first excited singlet state (S₁, ππ*), conducted at the PBE0/cc-pVTZ level of theory. In this case, tautomerisation did not occur. In order to calculate comparable energies with the excited-state relaxed geometries, single point energy calculations were conducted on both conformers 1 and 2 (previously optimized with PBE/cc-pVTZ) in vacuum at the PBE0/cc-pVTZ level of theory.

In order to estimate the excited state barrier between the enol and keto forms (conformer 1), a set of linear interpolations of internal coordinates (LIIC) were acquired. Vertical excitations, again at the PBE0/cc-pVTZ level of theory, were calculated in vacuum for each step, and the resulting ground state (S₀), S₁ and S₂ energies were plotted. The results of these calculations along a LIIC are shown in Fig. 2b (for S₀ and S₁; results for S₂ are shown in the ESI,† Fig. S9).

Finally, two further reaction pathways were probed, both of which involving the rotation around the aliphatic bond between the aromatic ring and the large ester unit of HMS. In both cases this bond was fixed in 10 degree increments between 0 and 180 degrees. The first path involved then relaxing all remaining degrees of freedom in the ground state at the PBE/cc-pVTZ level of theory. This allowed for the estimation of the barrier height between the two conformers discussed previously. The second path involved relaxing all other degrees of freedom in the S₁ at the PBE0/cc-pVTZ level of theory. This allowed for the investigation of a potential CI between the ground and excited states.

Results and discussion

Gas-phase experiments

TR-IY HMS parent ion (HMS⁺) transients are presented in Fig. 3 along with the extracted time constants at λ_pump = 305 nm, 320 nm and 335 nm (the latter of which corresponds to photoexcitation centred at the S₁ origin of HMS, see below), with λ_probe = 200 nm. In all cases, the gas-phase photodynamics of HMS following UV photoexcitation are described by two time constants. In what follows, we will firstly focus on discussing the assignment of τ₁ and addressing apparent discrepancies between our time- and frequency-resolved studies, after which the discussion regarding the assignment of τ₂ will become straight-forward.

The first time constant, τ₁, is defined within our IRF (typically ∼170 fs, see Fig. S2, ESI†). We assign τ₁ to ESIPT, involving migration of the proton on the –OH group along the O–H⋯O coordinate towards the neighbouring carbonyl group (thus forming the keto tautomer). We draw confidence that the tautomerisation occurs within 170 fs from previous literature on similar systems such as methyl salicylate where ESIPT occurs within 100 fs;^54–57 we add here that power studies in the gas-phase were carried out to verify single-photon-induced dynamics (presented in S1.1.1 and Fig. S1, ESI†). In fact, our computational studies, the results of which are presented in Fig. 2, predict a barrierless S₁-enol to S₁-keto tautomerisation for conformer 1 of HMS, with the keto tautomer lying 0.32 eV lower in energy than the enol tautomer (see Fig. 2). In addition, the large Stokes shift observed in the DFL spectrum of HMS upon photoexcitation at its S₁(v = 0) origin, as shown in Fig. S3 in the ESI,† suggests a significant geometry change upon excitation to the S₁ state. The experimentally observed Stokes shift in the gas-phase is approximately 0.72 eV, which compares with the theoretically calculated 1.1 eV difference between the S₁–S₀ transitions for the enol and keto tautomers (in vacuum, see Fig. 2a and Tables S2 and S3 in the ESI†). While there is a discrepancy of approximately 0.4 eV between the experimental and theoretical value for this Stokes shift, DFT methods have generally been found to overestimate transition energies.^58,59 Nevertheless, the experimental observation of a large Stokes shift upon photoexcitation to the S₁ state of HMS, in accordance with and in addition to the large computationally predicted Stokes shift, supports the hypothesis that ESIPT would take place in HMS within τ₁.

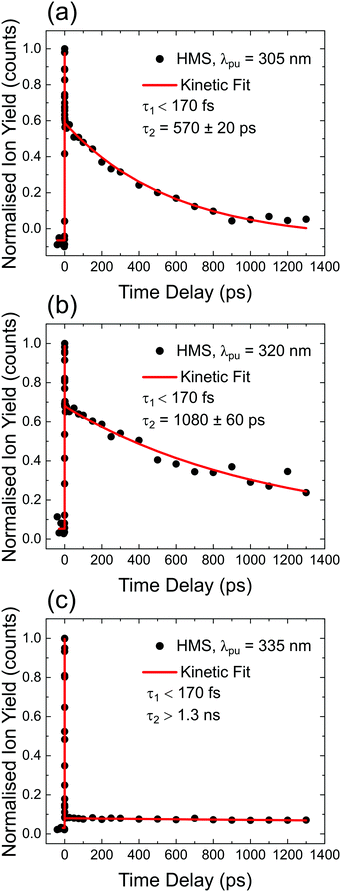Fig. 3 TR-IY magic angle transients for HMS photoexcited at (a) 305 nm, (b) 320 nm and (c) 335 nm, the S₁(v = 0) origin of HMS, with a 200 nm probe. Black circles are experimental points, while the red curves correspond to kinetic fits (discussed in S1.2 in the ESI†), from which the time constants shown inset are extracted. The baseline for all plots is zero within the signal-to-noise ratio of our measurements.

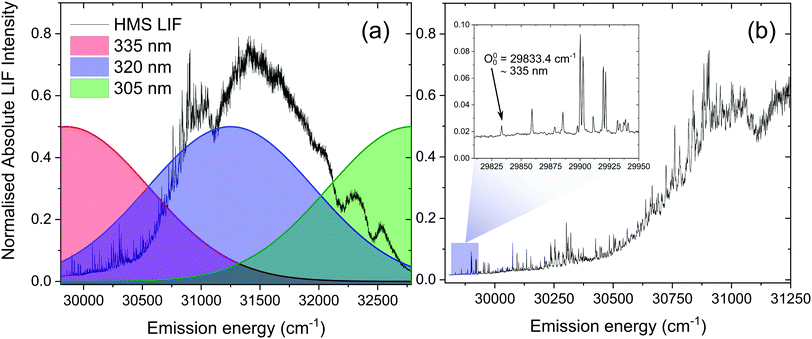
We note, however, that sharp features in the LIF spectrum of HMS, shown in Fig. 4, are retained even at energies >1000 cm⁻¹ above the S₁(v = 0) origin. Excitation energies above 31 000 cm⁻¹ result in a loss of the fine structure, which could point towards vibronic congestion.⁶⁰ The rotational band contours of the LIF origin peak (see ESI,† S2.1.1 and Fig. S10) suggest a significantly longer S₁ origin lifetime than the IRF-limited τ₁ extracted from our TR-IY measurements. We reconcile these contradictory observations by considering previously published work in which the existence of different conformers is suggested for closely related salicylates. For example, Bisht et al. proposed two potential conformers in salicylic acid undergoing different excited state dynamics,⁶¹ while Zhou et al. hypothesised that the slowest dynamics observed in their studies on methyl salicylate could be due to a conformer in which the ESIPT process is hindered.⁶² Moreover, both Zhou et al. and Massaro et al.⁶³ report an energy difference between the two lowest energy conformers of methyl salicylate in the ground state (∼0.1–0.2 eV) that is comparable to the energy difference predicted by our computational studies for conformers 1 and 2 of HMS (0.17 eV, see Fig. S8 in the ESI†). In addition, Zhou et al. have shown that interconversion of the two lowest energy conformers in the ground state has a significant barrier (+0.63 eV with respect to the lowest energy conformer), preventing this interconversion.⁶² The energy of this barrier for HMS was calculated by fixing the dihedral angle that dictates the path of conformer 1 to conformer 2 in 10 degree increments. Following this, all other degrees of freedom were relaxed at the PBE/cc-pVTZ level of theory and the energy of each intermediate state was plotted (Fig. S11, ESI†). This gave rise to the same barrier energy observed by Zhou et al. of +0.63 eV with respect to conformer 1.⁶² Taken together, and given that our calculations show that there is a stable excited state structure of the enol tautomer of conformer 2, we propose that conformer 2 is photoexcited and trapped in its enol structure (i.e. not undergoing ESIPT), which fluoresces, thus accounting for the sharp features observed in our LIF measurements. However, the (apparent) low abundance of this conformer makes it difficult to identify from our TR-IY measurements. We add that further experiments (such as spectral hole-burning) are warranted to confirm the existence (and spectral location) of conformer 1 and 2.

Fig. 4 (a) LIF spectrum of vaporised HMS upon photoexcitation in the 29 806–32 787 cm⁻¹ energy region, with Gaussian curves (FWHM = 500 cm⁻¹) demonstrating the regions photoexcited in the TR-IY measurements with λ_pump = 335 nm (red), 320 nm (blue) and 305 nm (green). (b) The same LIF spectrum in more detail, with the inset showing the peak and energy corresponding to the S₁(v = 0) origin of HMS.

The second time constant, τ₂, clearly decreases with increasing photoexcitation energy, i.e. energy dissipation becomes faster with increasing energy. This behaviour is typical of systems for which there is an energetic barrier to be surmounted in order for a key relaxation pathway to be accessed.^64,65 Presumably, when exciting HMS at the S₁(v = 0) origin (within the 500 cm⁻¹ bandwidth of the pump pulse used in our time-resolved measurements, see Fig. 4) excited state population is unable to access any nearby CIs and therefore fluorescence takes place to the ground state as excited state population samples the shallow S₁ energy potential. Indeed, the LIF measurements presented in Fig. 4 show that there is significant fluorescence from the vibrational levels accessed by λ_pump = 335 nm used in our TR-IY measurements, further supporting our assignment of τ₂ > 1.3 ns (at this pump wavelength) to a long-lived, fluorescent S₁ state. As the pump energy is increased, τ₂ decreases considerably, now being defined within the temporal window of our measurements (1.3 ns). It is plausible that, at these higher pump energies, excited state population would be increasingly more likely to access a nearby CI within the S₁ state through which it would undergo internal conversion (IC) to the S₀ state. Nevertheless, while fluorescence may not be the predominant relaxation pathway at above-origin pump energies (for which IC becomes increasingly competitive), the strong LIF signal at these energies is evidence that it is still an active relaxation pathway for conformer 1.

We add that attempts were made to theoretically examine the CI between the S₀ and S₁ states. Owing to the size of HMS, and therefore the relatively high computational expenditure, it was not possible to perform a CI search using multistate CASPT2 as has been conducted in other studies.⁵⁵ Based on previous studies, the CI could be presupposed to be located along the rotation of the aliphatic bond between the aromatic ring and the large ester unit of HMS.^55,66 As such, this coordinate was evaluated for HMS by fixing the dihedral angle in 10 degree increments between 0 and 180 degrees, relaxing all other degrees of freedom in the first excited state in TDDFT, and observing the relative energies of this and the ground state. We observed that between 40 and 130 degrees, where the internal H-bond is broken, the calculation relaxed to a structure with a negative excitation energy. This is a common error when using TDDFT to study a CI, owing to the inexactness of the ground state and excited state energies.⁶⁷ Whilst this is indicative that a CI likely occurs on this coordinate, exact energies, structures, and energetic barriers are unreliable as TDDFT is significantly less accurate in cases such as this with extensive state mixing.⁶⁸

Gas-phase fluorescence lifetime measurements taken upon photoexcitation at 305–335 nm, an example of which is presented in the ESI,† (S1.1.4), yielded fluorescence lifetimes of 12–20 ns. Attempts to detect gas-phase phosphorescence from HMS were unsuccessful, suggesting that triplet states are unlikely to be involved in the gas-phase photodynamics of HMS on the timescales of the present measurements. Nevertheless, one could envisage that excited state population would migrate to nearby triplet states (the existence of which is confirmed by our computational work) and then undergo reverse intersystem crossing (ISC) back into a singlet state (namely S₀), thus justifying the absence of observable phosphorescence. Moreover, it is also possible that photoreactions would take place from the excited triplet state manifold. The absence of observable phosphorescence does not, therefore, conclusively rule out ISC as a potential relaxation pathway for HMS in the gas-phase.

In summary, our gas-phase and computational results suggest that conformer 1 of HMS (the lowest energy conformer) undergoes ultrafast enol–keto tautomerisation, followed by either fluorescence from the S₁ surface or, in the case of higher photoexcitation energies which allow for a higher lying CI to be accessed, fast repopulation of the S₀ state via IC. Furthermore, we suggest that the sharp peaks in the LIF spectrum of HMS around S₁(v = 0) origin energies – which do not agree with a fast ESIPT process taking place – are due to the presence of a second conformer in the molecular beam. We found no evidence of phosphorescence within the timescales of our experiments and, therefore, propose that any contribution from triplet states to the gas-phase photodynamics of HMS, while possible, would be small.

Transient electronic absorption spectroscopy (TEAS)

To gain further insights into the behaviour of HMS in environments with different polarities and protic natures, ultrafast spectroscopy studies were conducted in solution, in line with a bottom-up approach.

Given the similarities of the UV-visible spectra of HMS in different solvents (as shown in Fig. 1), it could be expected that the excited state dynamics of HMS would not differ dramatically in the different solvent environments. Indeed, all transient absorption spectra (TAS) of HMS, displayed as both false colour heat maps and line-outs at selected pump–probe time delays in Fig. 5, resemble one another and reveal similar dynamics; as such, it seems appropriate that the results should be discussed together.

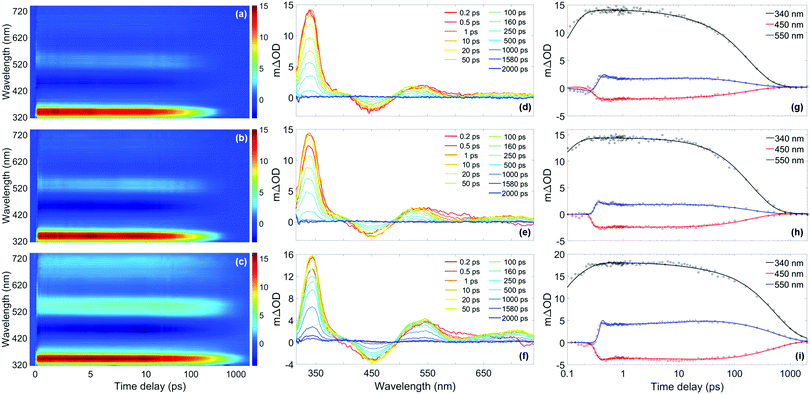Fig. 5 (a)–(c) False colour heat maps showing all transient absorption spectra (TAS) of homosalate (HMS) in acetonitrile (ACN) (λ _pump = 306 nm), ethanol (EtOH) (λ_pump = 307 nm) and cyclohexane (CHX) (λ _pump = 309 nm) respectively. In these plots, the time delay axis is shown as a linear scale until 10 ps and as a logarithmic scale thereafter. (d)–(f) TAS at selected pump–probe time delays for HMS in ACN, EtOH and CHX respectively. These plots are attained by taking vertical slices through the false colour heat maps at the given time delay and are presented on the same mΔOD scale as the corresponding false colour heat map. (g)–(i) Kinetic fits of the transient data at 340 nm (black), 450 nm (red) and 550 nm (blue) for HMS in ACN, EtOH and CHX respectively. The circles denote the raw data at each wavelength and the solid line is the fit attained using the parallel model described in the main text. In each case, the time delay axis is presented on a logarithmic scale. False colour heat maps containing residuals for every datapoint can be found in the ESI† (Fig. S12).

Each solute/solvent combination displays a strong excited state absorption (ESA) in the range 330–360 nm, with evidence of a positive feature, tailing off at ∼400 nm. A separate ESA feature appears between 500–590 nm. There is also a stimulated emission (SE) feature, the negative ΔOD feature between probe wavelengths of 430–500 nm. A quantitative insight into the assignment of these spectral features has been attained by following the global fitting procedure described in the ESI,† (Section S1.2.1). As is the case for the time-resolved gas-phase data, this procedure implements a parallel model, which assumes all processes begin immediately after excitation. The results of this fitting are shown in Table 1, and the quality of this fit at selected wavelengths is evident in Fig. 5, with full residual information given in Fig. S12 (ESI†). A parallel model has been chosen to model our data in solution, in line with fitting to our gas-phase data. Nevertheless, for comparison, the data in solution has also been fitted using a sequential model, yielding similar time constants as presented in the ESI,† (Section S2.2.1 and Table S4). The quality of these fits at selected wavelengths is demonstrated in Fig. S13 (ESI†).

Table 1 Extracted transient electronic absorption spectroscopy (TEAS) time constants for three homosalate solutions, following photoexcitation at their respective absorption maxima, obtained via global fitting techniques using a parallel model.⁴⁵ Whilst the error for τ₁ is given by half the instrument response in each solvent (Fig. S4, ESI), the errors presented for τ₂ to τ₄ are those provided by the fitting software package; the quality of the fits can be gauged from the corresponding kinetic fits (Fig. 5) and residuals (Fig. S12, ESI)

Time constant	Ethanol	Cyclohexane	Acetonitrile
a Outside the temporal window of the instrument (2 ns).
τ 1 (fs)	55 ± 35	105 ± 30	80 ± 40
τ 2 (ps)	10.4 ± 0.4	14.2 ± 0.5	9.4 ± 0.4
τ 3 (ps)	199 ± 2	532 ± 6	180 ± 2
τ 4 (ns)	>2^a	>2^a	>2^a

---

For all sets of TEAS data (in all solvents and at all pump wavelengths), τ₁ is defined within instrument response (Fig. S4, ESI†). Following consideration of our previous observations and discussion regarding our gas-phase results, and given that ESIPT has been observed experimentally on comparable timescales in similar systems in solution (e.g. methyl salicylate), we assign τ₁ in our studies in solution to enol–keto tautomerisation.^69–72 Further evidence for ESIPT in HMS is two-fold. Akin to the dispersed fluorescence observations in gas-phase, there is a large Stokes shift (∼120 nm, see Fig. S14 in the ESI†) upon photoexcitation of HMS at its respective absorption peak in each solvent, which is indicative of a significant structural change upon photoexcitation to the S₁ state. This observation is similar to that previously reported for methyl salicylate and ethylhexyl salicylate.^72,73 Moreover, our computational studies reveal that the S₁-keto tautomer is lower in energy than its S₁-enol counterpart and it is therefore anticipated that ESIPT would remain barrierless for HMS in solution.

The elucidation of the remaining time constants extracted from our TEAS data for HMS is assisted herein by comparison with the previously studied HMS analogue, ethylhexyl salicylate (EHS, also known as octisalate), for which the ester unit connects to an alkane chain rather than the cycloalkane unit of HMS (structure inset in Fig. S15a, ESI†).^73,74 Equivalent TEAS studies on EHS following the same experimental methodology as for HMS have been performed and the results are presented in full in the ESI† (Section S2.2.2: TAS data Fig. S15–S17, time constants Tables S5 and S6, residuals Fig. S12, ESI†). Overall, the photodynamical behaviour of EHS is virtually unaltered from that observed for HMS. As such, we assume that comparisons between the photodynamic behaviours of HMS and EHS are valid. Moreover, EHS also produces an emission peak at 450 nm (as reported by Krishnan and Nordlund)⁷³ that is very similar to the emission of HMS shown in Fig. S14 (ESI†), in terms of both central wavelength and bandwidth, further validating the comparison between these two molecules.

In light of the aforementioned assumption (and returning to discuss τ₂ below), τ₃ and τ₄ for HMS have been assigned. The faster of these time constants, τ₃, is likely due to the decay of the S₁-keto tautomer via fluorescence. The presence of fluorescence is confirmed in the TAS of HMS in all solvents by the appearance of the SE feature centred at 450 nm, which directly corresponds to the peaks observed in the emission spectra (Fig. S14, ESI†). For additional confirmation of the assignment of τ₃, the fluorescence lifetimes of HMS in all three solvents have been determined; these were found to be within our instrument response (<1.2 ns, see S1.2.4, ESI† for further details). More exact fluorescence lifetimes for EHS have been quoted by Krishnan and Nordlund, and range from 150 ps in methanol to 460 ps in toluene.⁷³ Krishnan and Nordlund's results are in good agreement with the values of τ₃ that have been extracted for both HMS and EHS in our studies, as shown in Table 1 and Table S5 (ESI†), respectively. These time constants, alongside the fluorescence lifetimes obtained in the present and previous studies, thus support our assignment of τ₃ in both EHS and HMS to fluorescence, dependent on rate-determining internal conversion (IC) and intersystem crossing (ISC, see below).⁷³

Our assignment of τ₄ > 2 ns to the lifetime of the triplet state following ISC is in the first instance supported by additional TAS of HMS and EHS, with Δt = 3 ns, which are presented in the ESI,† (Fig. S18). The spectral features in these TAS (see ESI,† S2.2.3 for further details) resemble those reported by Sugiyama et al.⁷⁴ as the absorption spectra of the T₁ state, lending credibility to our assignment. The hypothesis that τ₄ is associated with the lifetime of a triplet state is also corroborated by our computational results, which reveal the existence of nearby triplet states in HMS that are accessible in all three solvents (Table S3, ESI†). While a number of decay pathways could be accessible to the triplet states of HMS and EHS, such as phosphorescence or reverse ISC,⁷⁵ we are unable to pinpoint which, if any, dominates in the present measurements. Phosphorescence quantum yields (Φ_P) have been reported to be 4.9% in HMS and 5.4% in EHS in ethanol at 77 K.⁷⁴ However, cryogenic cooling, solvent deoxygenation, heavy atom perturbation or a combination of these approaches have been required to observe phosphorescence in salicylates.^74,76 As such, it is likely that under our experimental conditions, phosphorescence is quenched.

Although both fluorescence and ISC do occur in HMS and EHS as discussed, these are unlikely to be the dominant relaxation pathways for these molecules, given the expected low quantum yields of radiative decay. In EHS, the fluorescence quantum yield (Φ_F), has been reported to be 0.6–1.9% (depending on solvent),⁷³ while for HMS we have determined Φ_F values of 3.5% in ACN, 4.6% in EtOH and 11.6% in CHX (upper limits, see S1.2.5 (ESI†) for further details). As such, the remaining time constant extracted from our TEAS measurements, τ₂, is assigned to vibrational cooling and IC to the S₀-keto species. It is then energetically favourable for the S₀-enol species to be reformed, according to the S₀ energy differences between the keto and enol forms calculated using DFT (between 0.76 and 0.80 eV). Further to this, a full list of excited-state energies can be found in Tables S2 and S3 of the ESI.† Fast, non-radiative relaxation for ground-state recovery is favourable for sunscreen applications,⁷⁷ therefore HMS and EHS mostly satisfy this criterion.

In summary, our studies in solution on HMS (and EHS) reveal an initial ultrafast process which, similarly to the system in the gas-phase, we assign to ESIPT (enol–keto tautomerisation). The S₁ state of the keto tautomer then undergoes radiative and non-radiative decay, with IC (and some component of vibrational cooling) predominantly taking place alongside low yield components of fluorescence and ISC. While it appears from our results that solvent environments have only minor effects on the observed photodynamics of HMS, it is clear that solvation seems to facilitate ISC and thus introduce an additional competing (yet non-dominant) decay pathway for HMS. This is an important consideration for sunscreen design, since the presence of triplet states is undesirable in sunscreen formulations due to the increased probability of harmful side-reactions.

To conclude our discussion, we propose that our work provides further valuable guidance for sunscreen design with regards to the choice between salicylates, such as HMS, and anthranilates, such as MenA. As reported in previous work,³⁵ the potential energy cut along the ESIPT coordinate for methyl anthranilate (MA, a precursor to MenA) is nearly flat, resulting in there being no energetic drive for ESIPT to take place. In HMS, on the other hand, computational work reveals a significant energetic drive for ESIPT (Fig. 2b), with the (apparent) absence of a barrier for this process being allied to a relatively more stable keto tautomer.

The marked differences in the excited state surfaces of HMS when compared to MA are likely associated with the differences in electron affinity of the nitrogen and oxygen atoms, ultimately resulting in different strengths for the intramolecular H-bond, a crucial factor for the ESIPT process. It has been reported that not only systems with strong intramolecular H-bonds readily undergo ESIPT, but also that a weaker intramolecular H-bond may slow down or even preclude the ESIPT process.⁷⁸ In addition, recent work on a range of amino- and hydroxy-type H-bonding molecules^57,79 has shown that molecules containing an OH group tend to undergo ultrafast ESIPT (within 80 fs), whereas molecules containing NH groups undergo ESIPT within a wide range of (typically longer) timescales. As such, in the first instance formulation scientists could be encouraged to look for compounds with strong intramolecular H-bonds, by preferring O–H⋯O compounds over N–H⋯O species, for example; intramolecular H-bond strength seems to influence the molecule's potential energy landscape such as to allow fast internal conversion to take place (via a CI along a rotation reaction coordinate), a closer-to-ideal photophysical behaviour for a sunscreen.

Conclusions

In the present work we have explored the excited state dynamics of the UV filter homosalate (HMS) after photoexcitation in the 305–335 nm wavelength range, both in vacuum and in solution. We found that these dynamics are almost unaltered in solution when compared to the gas-phase and can be broadly described by an initial ultrafast decay, which is in all cases assigned to ESIPT; followed by fast internal conversion to the ground state and lower quantum yields of fluorescence and intersystem crossing. In line with previous observations on analogous molecules (e.g. methyl salicylate), we also report on experimental observations in the gas-phase that point towards the presence of a second, long-lived conformer of HMS which does not undergo ESIPT.

Interestingly, the studies presented here on HMS (and also for EHS in solution) are in stark contrast with the behaviour observed for the comparable UVA filter menthyl anthranilate (MenA).³⁵ In the gas- and solution-phase studies of MenA, it was found that the ESIPT process is incomplete, i.e. H-atom dislocation occurs.³⁵ Furthermore, while there is a nearby S₁/S₀ conical intersection (CI), a large energetic barrier needs to be surmounted in order for it to be accessed. This barrier hinders fast and efficient excited state relaxation in MenA, effectively rendering its photophysical behaviour unfavourable for sunscreen use.

From our observations in the present study, it appears that by substituting the amino group of MenA with the hydroxy group in HMS, a CI becomes accessible and the excited state energy can be dissipated effectively. It is therefore evident that the ESIPT process plays a key role in the photodynamics of both HMS and MenA, ultimately defining their suitability for use as UV filters in sunscreen formulations. As such, a more detailed understanding of the ESIPT process (e.g. substituent position and functional group effects) in this type of molecule is warranted and could be crucial for sunscreen design. For example, investigating the effect of substituent position on the photodynamics of HMS, i.e. placing the hydroxy group in the meta and para positions on the chromophore where ESIPT is no longer possible, constitutes an interesting avenue for future work, both in the gas-phase and in solution.

Overall, and within the limits of our studies, HMS appears to have mostly favourable excited-state relaxation characteristics and, on this basis alone, its inclusion in sunscreen formulations is justified. Nevertheless, favourable photodynamics do not guarantee that the molecule is completely safe when applied to the skin. The proposed triplet states in solution, despite their low quantum yield, could be of concern to formulation scientists, owing to their ability to produce singlet oxygen, a cytotoxin that can also incite allergenic responses.⁸⁰ The effects of potential triplet–triplet state energy transfer of HMS to other UV filters also warrants further investigation.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors would like to thank Juan Cebrián and Laurent Blasco, from Lipotec SAU, for fruitful collaboration and for providing the HMS samples for these experiments. The authors also thank the Warwick Centre for Ultrafast Spectroscopy (WCUS) for the use of the Cary 60 and Fluorolog-3. E. L. H. and M. A. P. T. thank the Engineering and Physical Sciences Research Council (EPSRC) for a PhD studentship through the EPSRC Centre for Doctoral Training in Molecular Analytical Science, grant number EP/L015307/1. Computing facilities were provided by the Scientific Computing Research Technology Platform of the University of Warwick. We acknowledge the use of Athena at HPC Midlands+, which was funded by the EPSRC by Grant EP/P020232/1, in this research, as part of the HPC Midlands+ consortium. K. M. K. also thanks the EPSRC for doctoral funding. P. M. and T. S. Z. gratefully acknowledge support from the Department of Energy Basic Energy Sciences Gas-Phase Chemical Physics program under Grant No. DE-FG02-96ER14656. N. d. N. R. thanks the University of Warwick's Institute of Advanced Study and Institute for Advanced Teaching and Learning for a joint Early Career Fellowship. Finally, V. G. S. thanks the EPSRC for an equipment grant (EP/J007153), the Leverhulme Trust for a research grant (RPG-2016-055) and the Royal Society and Leverhulme Trust for a Royal Society Leverhulme Trust Senior Research Fellowship. This project has also received funding from the European Union’s Horizon 2020 Research and Innovation programme, under the grant agreement no. 828753.

References

1. D. Ekinci, M. Sentürk and Ö. İ. Küfrevioğlu, Expert Opin. Ther. Pat., 2011, 21, 1831–1841.
2. M. T. Baltazar, R. J. Dinis-Oliveira, J. A. Duarte, M. L. Bastos and F. Carvalho, Curr. Med. Chem., 2011, 18, 3252–3264.
3. N. Serpone, D. Dondi and A. Albini, Inorg. Chim. Acta, 2007, 360, 794–802.
4. N. A. Shaath, Photochem. Photobiol. Sci., 2010, 9, 464–469.
5. M. F. Holick, Anticancer Res., 2016, 36, 1345–1356.
6. P. H. Hart, M. Norval, S. N. Byrne and L. E. Rhodes, Annu. Rev. Pathol.: Mech. Dis., 2019, 14, 55–81.
7. Y. Matsumura and H. N. Ananthaswamy, Toxicol. Appl. Pharmacol., 2004, 195, 298–308.
8. F. R. de Gruijl, Eur. J. Cancer, 1999, 35, 2003–2009.
9. L. A. Baker, B. Marchetti, T. N. V. Karsili, V. G. Stavros and M. N. R. Ashfold, Chem. Soc. Rev., 2017, 46, 3770–3791.
10. M. Wlaschek, I. Tantcheva-Poór, L. Naderi, W. Ma, L. A. Schneider, Z. Razi-Wolf, J. Schüller and K. Scharffetter-Kochanek, J. Photochem. Photobiol., B, 2001, 63, 41–51.
11. G. J. Fisher, Z. Wang, S. C. Datta, J. Varani, S. Kang and J. J. Voorhees, N. Engl. J. Med., 1997, 337, 1419–1429.
12. J. D'Orazio, S. Jarrett, A. Amaro-Ortiz and T. Scott, Int. J. Mol. Sci., 2013, 14, 12222–12248.
13. C. Couteau, M. Pommier, E. Paparis and L. J. M. Coiffard, Pharmazie, 2007, 62, 449–452.
14. L. E. Agrapidis-Paloympis, R. A. Nash and N. A. Shaath, J. Soc. Cosmet. Chem., 1987, 38, 209–221.
15. L. Beyere, S. Yarasi and G. R. Loppnow, J. Raman Spectrosc., 2003, 34, 743–750.
16. G. J. Mturi and B. S. Martincigh, J. Photochem. Photobiol., A, 2008, 200, 410–420.
17. A. Benazzouz, L. Moity, C. Pierlot, V. Molinier and J.-M. Aubry, Colloids Surf., A, 2014, 458, 101–109.
18. M. D. Palm and M. N. O'Donoghue, Dermatol. Ther., 2007, 20, 360–376.
19. C. G. Mortz, H. Thormann, A. Goossens and K. E. Andersen, Dermatitis, 2010, 21, 7–10.
20. A. R. Heurung, S. I. Raju and E. M. Warshaw, Dermatitis, 2014, 25, 289–326.
21. C. L. Hexsel and H. W. Lim, in Preventive Dermatology, ed. R. Norman, Springer London, London, 2010, pp. 81–91.
22. N. Lowe, Dermatol. Clin., 2006, 24, 9–17.
23. D. R. Sambandan and D. Ratner, J. Am. Acad. Dermatol., 2011, 64, 748–758.
24. C. Couteau, A. Faure, J. Fortin, E. Paparis and L. J. M. Coiffard, J. Pharm. Biomed. Anal., 2007, 44, 270–273.
25. C. A. Bonda and D. Lott, in Principles and Practice of Photoprotection, ed. S. Q. Wang and H. W. Lim, Springer International Publishing, Cham, 2016, pp. 247–273.
26. S. Q. Wang and H. W. Lim, J. Am. Acad. Dermatol., 2011, 65, 863–869.
27. T. H. Kim, B. S. Shin, K.-B. Kim, S. W. Shin, S. H. Seok, M. K. Kim, E. J. Kim, D. Kim, M. G. Kim, E.-S. Park, J.-Y. Kim and S. D. Yoo, J. Toxicol. Environ. Health, Part A, 2014, 77, 202–213.
28. M. Erol, I. Çok, Ö. B. Gayret, P. Günes, Ö. Yigit, E. Sayman, A. Günes, D. S. Çelik, S. Hamilçikan, S. Altinay and O. Ercan, Toxicol. Ind. Health, 2017, 33, 775–791.
29. J. F. Nash, Dermatol. Clin., 2006, 24, 35–51.
30. S. Yazar and S. K. Ertekin, J. Cosmet., Dermatol. Sci. Appl., 2020, 19, 246–252.
31. L. A. Baker, S. E. Greenough and V. G. Stavros, J. Phys. Chem. Lett., 2016, 7, 4655–4665.
32. E. L. Holt and V. G. Stavros, Int. Rev. Phys. Chem., 2019, 38, 243–285.
33. L. A. Baker, M. D. Horbury, S. E. Greenough, P. M. Coulter, T. N. V. Karsili, G. M. Roberts, A. J. Orr-Ewing, M. N. R. Ashfold and V. G. Stavros, J. Phys. Chem. Lett., 2015, 6, 1363–1368.
34. M. T. Ignasiak, C. Houée-Levin, G. Kciuk, B. Marciniak and T. Pedzinski, ChemPhysChem, 2015, 16, 628–633.
35. N. D. N. Rodrigues, N. C. Cole-Filipiak, M. D. Horbury, M. Staniforth, T. N. V. Karsili, Y. Peperstraete and V. G. Stavros, J. Photochem. Photobiol., A, 2018, 353, 376–384.
36. N. D. N. Rodrigues and V. G. Stavros, Sci. Prog., 2018, 101, 8–31.
37. A. Iqbal, L.-J. Pegg and V. G. Stavros, J. Phys. Chem. A, 2008, 112, 9531–9534.
38. U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071.
39. F. P. M. Baskin, J. Spencer and A. H. Zewail, J. Chem. Phys., 1987, 86, 2483–2499.
40. S. R. Gandhi and R. B. Bernstein, Chem. Phys., 1986, 105, 423–434.
41. N. R. Pillsbury, J. A. Stearns, C. W. Müller, D. F. Plusquellic and T. S. Zwier, J. Chem. Phys., 2008, 129, 114301.
42. C. A. Arrington, C. Ramos, A. D. Robinson and T. S. Zwier, J. Phys. Chem. A, 1998, 102, 3315–3322.
43. F. A. Ensminger, J. Plassard and T. S. Zwier, J. Chem. Phys., 1995, 102, 5246.
44. S. E. Greenough, G. M. Roberts, N. A. Smith, M. D. Horbury, R. G. McKinlay, J. M. Żurek, M. J. Paterson, P. J. Sadler and V. G. Stavros, Phys. Chem. Chem. Phys., 2014, 16, 19141–19155.
45. J. Snellenburg, S. Laptenok, R. Seger, K. Mullen and I. H. M. van Stokkum, J. Stat. Soft., 2012, 49, 1–22.
46. K. M. Mullen and I. H. M. van Stokkum, J. Stat. Soft., 2007, 18, 1–46.
47. I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, 2004, 1657, 82–104.
48. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
50. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
51. D. M. York and M. Karplus, J. Phys. Chem. A, 1999, 103, 11060–11079.
52. P. Winget, D. M. Dolney, D. J. Giesen, C. J. Cramer and D. G. Truhlar, Department of Medicinal Chemistry and Supercomputer Institute, University of Minnesota, Minneapolis, MN, 1999, p. 55455.
53. R. J. Charlton, R. M. Fogarty, S. Bogatko, T. J. Zuehlsdorff, N. D. M. Hine, M. Heeney, A. P. Horsfield and P. D. Haynes, J. Chem. Phys., 2018, 148, 104108.
54. J. L. Herek, S. Pedersen, L. Bañares and A. H. Zewail, J. Chem. Phys., 1992, 97, 9046–9061.
55. J. D. Coe, B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2007, 111, 11302–11310.
56. F. Ling, D. Liu, S. Li, W. Li, B. Zhang and P. Wang, J. Chem. Phys., 2019, 151, 094302.
57. A. Watwiangkham, T. Roongcharoen and N. Kungwan, J. Photochem. Photobiol., A, 2020, 389, 112267.
58. S. Grimme and F. Neese, J. Chem. Phys., 2007, 127, 154116.
59. D. Jacquemin, Y. Zhao, R. Valero, C. Adamo, I. Ciofini and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 1255–1259.
60. J. C. Dean, R. Kusaka, P. S. Walsh, F. Allais and T. S. Zwier, J. Am. Chem. Soc., 2014, 136, 14780–14795.
61. P. B. Bisht, H. Petek and K. Yoshihara, J. Chem. Phys., 1995, 103, 5290–5307.
62. P. Zhou, M. R. Hoffmann, K. Han and G. He, J. Phys. Chem. B, 2014, 119, 2125–2131.
63. R. D. Massaro, Y. Dai and E. Blaisten-Barojas, J. Phys. Chem. A, 2009, 113, 10385–10390.
64. A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 1999, 1, 3065–3072.
65. A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 1999, 300, 533–539.
66. N. D. N. Rodrigues, M. Staniforth and V. G. Stavros, Proc. R. Soc. A, 2016, 472, 1–29.
67. A. Toniolo, M. Ben-Nun and T. Martinez, J. Phys. Chem. A, 2002, 106, 4679–4689.
68. R. O. Jones, Rev. Mod. Phys., 2015, 87, 897.
69. P. Zhou and K. Han, Acc. Chem. Res., 2018, 51, 1681–1690.
70. M. Rini, A. Kummrow, J. Dreyer, E. T. J. Nibbering and T. Elsaesser, Faraday Discuss., 2003, 122, 27–40.
71. S. J. Formosinho and L. G. Arnaut, J. Photochem. Photobiol., A, 1993, 75, 21–48.
72. K.-Y. Law and J. Shoham, J. Phys. Chem., 1994, 98, 3114–3120.
73. R. Krishnan and T. M. Nordlund, J. Fluoresc., 2008, 18, 203–217.
74. K. Sugiyama, T. Tsuchiya, A. Kikuchi and M. Yagi, Photochem. Photobiol. Sci., 2015, 14, 1651–1659.
75. M. Kasha, J. Heldt and D. Gormin, J. Phys. Chem., 1995, 99, 7281–7284.
76. J. Catalán and C. Díaz, J. Phys. Chem. A, 1998, 102, 323–328.
77. L. A. Baker and V. G. Stavros, Sci. Prog., 2016, 99, 282–311.
78. B. M. Uzhinov and M. N. Khimich, Russ. Chem. Rev., 2011, 80, 553–577.
79. N. Kanlayakan, K. Kerdpol, C. Prommin, R. Salaeh, W. Chansen, C. Sattayanon and N. Kungwan, New J. Chem., 2017, 41, 8761–8771.
80. J. M. Allen, C. J. Gossett and S. K. Allen, Chem. Res. Toxicol., 1996, 9, 605–609.

---

Footnotes

† Electronic supplementary information (ESI) available: See DOI: 10.1039/d0cp02610g. The underlying data of this publication can be accessed via the Zenodo Archive at DOI: 10.5281/zenodo.3698070.

‡ These authors contributed equally to this work.

---