 Open Access Article
Open Access ArticleAccurate reproducing kernel-based potential energy surfaces for the triplet ground states of N2O and dynamics for the N + NO ↔ O + N2 and N2 + O → 2N + O reactions†
Debasish
Koner
 a,
Juan Carlos
San Vicente Veliz
a,
Juan Carlos
San Vicente Veliz
 a,
Raymond J.
Bemish
a,
Raymond J.
Bemish
 b and
Markus
Meuwly
b and
Markus
Meuwly
 *a
*a
aDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: m.meuwly@unibas.ch
bAir Force Research Laboratory, Space Vehicles Directorate, Kirtland AFB, New Mexico 87117, USA
First published on 15th July 2020
Abstract
Accurate potential energy surfaces (PESs) have been determined for the 3A′ and 3A′′ states of N2O using electronic structure calculations at the multireference configuration interaction level with Davidson correction (MRCI+Q) and the augmented Dunning-type correlation consistent polarized triple zeta (aug-cc-pVTZ) basis set. More than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MRCI+Q/aug-cc-pVTZ energies are represented using a reproducing kernel Hilbert space (RKHS) scheme. The RKHS PESs successfully describe all reactant channels with high accuracy and all minima and transition states connecting them are determined. Quasiclassical trajectory (QCT) simulations are then used to determine reaction rates for N + NO and O + N2 collisions. Vibrational relaxation N2(ν = 1) → N2(ν = 0) and dissociation of N2 → 2N for O + N2 collisions are also investigated using QCT. The agreement between results obtained from the QCT simulations and from available experiments is favourable for reaction and vibrational relaxation rates, which provides a test for the accuracy of the PESs. The PESs can be used to calculate more detailed state-to-state observables relevant for applications to hypersonic reentry.
000 MRCI+Q/aug-cc-pVTZ energies are represented using a reproducing kernel Hilbert space (RKHS) scheme. The RKHS PESs successfully describe all reactant channels with high accuracy and all minima and transition states connecting them are determined. Quasiclassical trajectory (QCT) simulations are then used to determine reaction rates for N + NO and O + N2 collisions. Vibrational relaxation N2(ν = 1) → N2(ν = 0) and dissociation of N2 → 2N for O + N2 collisions are also investigated using QCT. The agreement between results obtained from the QCT simulations and from available experiments is favourable for reaction and vibrational relaxation rates, which provides a test for the accuracy of the PESs. The PESs can be used to calculate more detailed state-to-state observables relevant for applications to hypersonic reentry.
I. Introduction
The [NNO] reactive collision system is relevant in problems ranging from atmospheric and environmental chemistry to those seen in the hypersonic flight regime.1–3 Two particularly relevant reactions involve the N + NO ↔ O + N2 processes. Both the forward (N + NO → O + N2) and reverse (O + N2 → N + NO) reactions are major processes in modelling the hyperthermal interactions during reentry of space vehicles and thus play a significant role in aerospace engineering. The forward reaction produces molecular nitrogen while the reverse reaction generates nitric oxide via the Zeldovich mechanism.4 The forward reaction also plays an important role in the Martian and Venusian atmospheres.5 The ground state of the N2O molecule is 1A′ and asymptotically connects to the N(1D) + NO(X2Π) and O(1D) + N2(X1Σ+g) channels. For the singlet electronic state of N2O the photodissociation dynamics and reactive collisions have been studied previously using theory and experiment.6–11 On the other hand, the triplet manifold of N2O connects with the N(4S) + NO(X2Π) and O(3P) + N2(X1Σ+g) states, with all the atomic and diatomic fragments in their electronic ground states in both channels. The N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) reaction is highly exothermic, plays an important role in the upper atmosphere in removing N(4S),12 and also helps removing the NO pollutant from the atmosphere which leads to ozone depletion. The 4S state of N and 2Π state of NO lead to 3A′, 3A′′, 5A′ and 5A′′ states in Cs symmetry while the O(3P) + N2(X1Σ+g) channel results in 3A′ and 3A′′ states.13 In the absence of spin orbit coupling both reactions occurs adiabatically on the triplet PESs.For the forward reaction, several experiments have reported rates using different techniques. The low temperature rates for this reaction is measured as (3.2 ± 0.6) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(25 ± 16)/T] cm3 s−1 molecule−1 in a continuous supersonic flow reactor at 48–211 K.14 Another experiment measured the N-atom concentration via line absorption and reported a rate of 3 ± 1 × 10−11 cm3 s−1 at 300 K.15 Conversely, using discharge flow-resonance fluorescence (DF-RF) and flash photolysis-resonance fluorescence and a value of 3.4 ± 0.9 × 10−11 cm3 s−1 molecule−1 was suggested from measurements in the 196–400 K temperature range.16 This rate was recommended for chemical modeling of stratospheric processes,17 while another DF-RF experiment18 reported a rate of (2.2 ± 0.2) × 10−11
exp[(25 ± 16)/T] cm3 s−1 molecule−1 in a continuous supersonic flow reactor at 48–211 K.14 Another experiment measured the N-atom concentration via line absorption and reported a rate of 3 ± 1 × 10−11 cm3 s−1 at 300 K.15 Conversely, using discharge flow-resonance fluorescence (DF-RF) and flash photolysis-resonance fluorescence and a value of 3.4 ± 0.9 × 10−11 cm3 s−1 molecule−1 was suggested from measurements in the 196–400 K temperature range.16 This rate was recommended for chemical modeling of stratospheric processes,17 while another DF-RF experiment18 reported a rate of (2.2 ± 0.2) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(160 ± 50)/T] cm3 s−1 molecule−1 over the range 213–369 K. In two different shock tube studies,19,20 the rate was measured at 1850–3160 K and 1251–3152 K to be 3.32 × 10−11 and 3.7 × 10−11 cm3 s−1 molecule−1, respectively. The recommended value, suggested by Baulch et al.,21 for combustion modelling is 3.5 × 10−11 cm3 s−1 molecule−1 over the temperature range 210–3700 K.21 Most of the experiments mentioned above suggest high rates for the forward reaction at low temperatures which points towards a barrierless process.
exp[(160 ± 50)/T] cm3 s−1 molecule−1 over the range 213–369 K. In two different shock tube studies,19,20 the rate was measured at 1850–3160 K and 1251–3152 K to be 3.32 × 10−11 and 3.7 × 10−11 cm3 s−1 molecule−1, respectively. The recommended value, suggested by Baulch et al.,21 for combustion modelling is 3.5 × 10−11 cm3 s−1 molecule−1 over the temperature range 210–3700 K.21 Most of the experiments mentioned above suggest high rates for the forward reaction at low temperatures which points towards a barrierless process.
For the reverse reaction only few experimental studies have been reported. The rate expression obtained from a shock tube experiment at 2384–3850 K by heating N2/O2/N2O/Kr mixtures22 was given as 1.84 × 1014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−76
exp(−76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250/RT) cm3 s−1 mol−1 (corresponding to 3.055 × 10−10
250/RT) cm3 s−1 mol−1 (corresponding to 3.055 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−38
exp(−38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370/T) cm3 s−1 molecule−1). Another, later, experiment23 determined the rate coefficient from O- and N-concentration measurements in shock heated N2/N2O/Ar mixtures at 2400–4100 K to be 3.0 × 10−10
370/T) cm3 s−1 molecule−1). Another, later, experiment23 determined the rate coefficient from O- and N-concentration measurements in shock heated N2/N2O/Ar mixtures at 2400–4100 K to be 3.0 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−38
exp(−38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300/T) ± 40% cm3 s−1 molecule−1. The rate of NO formation in the burned gas region of high temperature oxypropane flame has been estimated from experiment and using mathematical modelling at 2880 K as 107.93 cm3 s−1 mol−1 (corresponding to 1.413 × 10−16 cm3 s−1 molecule−1).24
300/T) ± 40% cm3 s−1 molecule−1. The rate of NO formation in the burned gas region of high temperature oxypropane flame has been estimated from experiment and using mathematical modelling at 2880 K as 107.93 cm3 s−1 mol−1 (corresponding to 1.413 × 10−16 cm3 s−1 molecule−1).24
Theoretical studies have focused primarily on exploring the electronic structure for the system, constructing potential energy surfaces (PESs) and carrying out dynamical simulations on these PESs. Ab initio PESs have been determined for the 3A′ and 3A′′ states of N2O using complete active space self consistent field (CASSCF)/contracted CI (CCI) calculations.13 For the forward reaction, a small barrier of 0.5 kcal mol−1 was found on the 3A′′ PES whereas a considerably larger barrier of 14.4 kcal mol−1 was found on the 3A′ PES. For the reverse reaction the endoergicity was calculated to be 75 kcal mol−1. An analytical PES for the 3A′′ state of N2O was constructed from CASSCF/CCI energies using a Sorbie–Murrell functional form and quasiclassical trajectory (QCT) calculations were performed for the N + NO collisions at 300 K.25
Although the triplet states of N2O are very important for environmental and atmospheric chemistry and high energy collisions in hypersonic flow, only three PESs26–28 are available in the literature. More recent electronic structure calculations have been performed on both the triplet states of N2O using CASSCF, CASPT2 methods and different basis sets.29 Later the CASPT2/cc-pVTZ, energies from ref. 29 were used along with additional energies at the same level of theory to construct analytical representations for the 3A′ and 3A′′ PESs.26 The root mean square deviations of these fits were 2.28 and 1.8 kcal mol−1 for the 3A′ and 3A′′ PESs, respectively. This work confirms that there is no barrier to form N2 + O when approaching from the N + NO side for the 3A′′ state. The rates for the forward and the reverse reactions were calculated from improved canonical variational transition-state (ICVT) theory on the new PESs and also on the PESs from ref. 25. Quantum wave packet dynamics had been carried out to study the N + NO reaction on both triplet states and rates were calculated for a wide range of temperatures using the J-shifting approximation.30,31 The forward reaction was studied using QCT to obtain the rates up to 5000 K and explore the energy distributions and reaction mechanisms.32 Also, the reverse reaction was studied again via QCT on the CASPT2/cc-pVTZ PESs26 to obtain the vibrational relaxation (VR) rates from ν = 1 to ν′ = 0 states.33
Analytical PESs were also constructed for the two lowest triplet states of N2O based on MRCI/maug-cc-pVTZ calculations and applying the dynamically scaled external correlation method with root-mean-squared errors (RMSE) of 4.44 and 3.71 kcal mol−1 for the 3A′ and 3A′′ PESs, respectively.27 Six states were included in the dynamically weighted state-averaged CASSCF calculations and permutational invariant polynomials were used to represent the many-body part of the PESs. Geometries and energetics of the stationary states were found to differ from the earlier PESs.26 Finally, QCT calculations for the O + N2 collisions at high energies34 have been carried out on the triplet PESs of ref. 27.
More recently, reproducing kernel based PESs for the 3A′ and 3A′′ states were calculated using MRCI+Q/cc-pVTZ energies and rates and product state distributions were calculated up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K.28 However, due to presence of a small barrier on the 3A′′ PES in the N + NO channel the calculated QCT rates were smaller at low temperatures. Recently, a state-to-state cross section model for the forward reaction based on the 3A′ PES has been developed using a neural network which predict the reaction rates and product state distributions accurately.35
000 K.28 However, due to presence of a small barrier on the 3A′′ PES in the N + NO channel the calculated QCT rates were smaller at low temperatures. Recently, a state-to-state cross section model for the forward reaction based on the 3A′ PES has been developed using a neural network which predict the reaction rates and product state distributions accurately.35
Reaction rates obtained from the PESs using fits to the CASPT2/cc-pVTZ data26 are in good agreement with the experiments.26,31,32 However, the vibrational relaxation rates for the reverse reaction are significantly smaller than the experimental results up to 7000 K.33 The PESs in ref. 26 were constructed using a lower level of theory (CASPT2/cc-pVTZ) and it is found that number and geometry of the stationary states differs using higher level (MRCI/maug-cc-pVTZ) of theory and more states in the CASSCF calculations.27 These PESs are meant for exploring the dynamics of the O + N2 collisions at high energies. Since the forward reaction is barrierless and is highly reactive at very low temperatures, a very reliable description of the N + NO channel is required in the asymptotic region, which was absent in ref. 27 PESs. On the other hand the reproducing kernel Hilbert space (RKHS) interpolation procedure can capture the correct long range behavior for different types of interactions.36–39
Another relevant quantity that balances the energy content of hot gas flow is the exchange and relaxation of vibrational energy which can also be determined from QCT simulations.40,41 This property has been found to be sensitive to different regions of the PES than reaction rates39 and provides an additional possibility to validate the quality of the PESs. Rates for vibrational relaxation serve also as input data for more coarse grained simulations, such as direct simulation Monte Carlo (DSMC).42 With N2 and O2 as two major components of air, N2 + O inelastic collisions may significantly affect the energy content and energy redistribution in high temperature air flow. The VR rates are calculated from relaxation time parameter (pτvib) using the Bethe–Teller model.41,43
Here, global PESs have been constructed for the 3A′ and 3A′′ electronic states for the reactive [NNO] system using RKHS interpolation from a large number (>10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) of MRCI+Q/aug-cc-pVTZ energies for each state. The present RKHS PESs are constructed using ∼3 times more ab initio energies than the previous PESs27 and cover a wide range of configurations explored in the QCT simulations. Using a RKHS allows one to impose the correct long range behavior for the dipole-induced dipole interactions (∼1/R6) and also reproduce the topology of the ab initio PESs accurately. Quasiclassical trajectories are then run on these new PESs to determine reaction/dissociation and vibrational relaxation rates which allow validation of the PESs by comparing with experiments.
000) of MRCI+Q/aug-cc-pVTZ energies for each state. The present RKHS PESs are constructed using ∼3 times more ab initio energies than the previous PESs27 and cover a wide range of configurations explored in the QCT simulations. Using a RKHS allows one to impose the correct long range behavior for the dipole-induced dipole interactions (∼1/R6) and also reproduce the topology of the ab initio PESs accurately. Quasiclassical trajectories are then run on these new PESs to determine reaction/dissociation and vibrational relaxation rates which allow validation of the PESs by comparing with experiments.
The present article is organised as follows. The methodological details of constructing the RKHS PESs and QCT dynamics are discussed in Section II followed by presenting the results and discussing them in Section III and finally concluding this work in Section IV.
II. Methods
This section summarizes the methods for calculating the ab initio energies for the diatomic and triatomic systems, construction of the analytical representation of the ab initio PESs using RKHS, quasiclassical trajectory calculations on those PESs and finally calculation of reaction and vibrational relaxation rates.A. Electronic structure calculations
Ab initio energy calculations for the triatomic system were performed on a grid defined in Jacobi coordinates (r,R,θ) where r is the diatomic separation, R is the distance between the center of mass of the diatom and the free atom and θ is the angle between![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) . For the present case, two separate grids were used for channels I (O + N2) and II (N + NO), respectively. The Jacobi coordinates for the two reactive systems are shown in Fig. 1. For R, the grid included 30 and 28 points from 1.4 to 12.0 a0 for the two channels. The diatomic separation r for channels I and II are covered by 20 points from 1.55 to 4.0 a0 and 21 points, from 1.50 to 4.0 a0, respectively. For the angular grid Gauss–Legendre quadrature points were used between 0° to 180°. The quadrature points covered the angular domain more efficiently than the regular grid as in the RKHS scheme, the angular grid is transformed to a new coordinate according to
. For the present case, two separate grids were used for channels I (O + N2) and II (N + NO), respectively. The Jacobi coordinates for the two reactive systems are shown in Fig. 1. For R, the grid included 30 and 28 points from 1.4 to 12.0 a0 for the two channels. The diatomic separation r for channels I and II are covered by 20 points from 1.55 to 4.0 a0 and 21 points, from 1.50 to 4.0 a0, respectively. For the angular grid Gauss–Legendre quadrature points were used between 0° to 180°. The quadrature points covered the angular domain more efficiently than the regular grid as in the RKHS scheme, the angular grid is transformed to a new coordinate according to 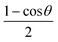 into a grid from 0 to 1 which leads to a denser grid near 0 or 1 and evenly spaced in between. In the present case, 13 quadrature points define the Jacobi angle which are 169.796°, 156.577°, 143.281°, 129.967°, 116.647°, 103.324°, 90.100°, 76.676°, 63.353°, 50.033°, 36.719°, 23.423° and 10.204°.
into a grid from 0 to 1 which leads to a denser grid near 0 or 1 and evenly spaced in between. In the present case, 13 quadrature points define the Jacobi angle which are 169.796°, 156.577°, 143.281°, 129.967°, 116.647°, 103.324°, 90.100°, 76.676°, 63.353°, 50.033°, 36.719°, 23.423° and 10.204°.
The Cs symmetry, which is the highest symmetry for the present system to describe all geometries, was used to perform the electronic structure calculations. The mutlireference configuration interaction with Davidson correction (MRCI+Q)44,45 method and augmented Dunning-type correlation consistent polarized triple zeta (aug-cc-pVTZ)46 basis set were used to calculate the electronic structure for all configurations considered in this work. This level of theory has been found to describe the electronic structures for the C-, N-, O-containing species quite well for the global PES.27,37,39 State-averaged complete active space self-consistent field47–50 calculations were carried out prior to the MRCI calculations in order to obtain a smooth topology of the MRCI PESs. In the State-averaged CASSCF calculations a total of eight states were included (the two lowest states from each spin (singlet and triplet) and spatial (A′ and A′′) symmetry). Including all these eight states in the CASSCF calculations provides consistency in the energies and numerically stabilizes the convergence for configurations with closely-lying states of the same symmetry. The valence orbitals, i.e. the nitrogen and oxygen 2s and 2p orbitals, were ‘active’ whereas the 1s orbitals were ‘closed’. All electronic structure calculations are performed using the Molpro-2019.151 software package.
For each of the electronic states, 4200 and 7644 ab initio electronic structure calculations have been carried out for the N2 + O and N + NO channels, respectively. Here it is worth mentioning that ∼10% of the electronic structure calculations converged to the excited states in the long range interaction regions (i.e., for large values of R and/or r). These energies are excluded from the grid to construct the RKHS. A small number (<0.5%) of ab initio calculations did not converge at all. For both these cases the missing grid points were computed using a 2-dimensional reproducing kernel V(R,r) for a particular value of θ before including them into the final 3D RKHS. Thus, overall, ∼3 times more reference ab initio energies were used to generate the present PESs compared with the previous surfaces for this system.27
B. Reproducing kernel representation of the PES
The reproducing kernel Hilbert space interpolation technique52 has been used to construct the analytical representation of the PESs for both electronic states (3A′ and 3A′′). In the RKHS approach, the approximated value![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (x) of a function f(x) is computed from a set of known values f(xi) as a linear combination of kernel polynomials, where x are variables e.g. set of spatial coordinates. The RKHS procedure is documented in detail in ref. 36 and 52 and has also been used to construct PESs for other triatomic systems.37–39
(x) of a function f(x) is computed from a set of known values f(xi) as a linear combination of kernel polynomials, where x are variables e.g. set of spatial coordinates. The RKHS procedure is documented in detail in ref. 36 and 52 and has also been used to construct PESs for other triatomic systems.37–39
In order to well describe the atom + diatom dissociation channels the total potential V(R,r,θ) energy of N2O is expanded as
| V(R,r,θ) = E(R,r,θ) + V(r) | (1) |
| K(x,x′) = k[2,6](R,R′)k[2,6](r,r′)k[2](z,z′). | (2) |
 (here n = 6) which gives the correct long-range behavior for neutral atom–diatom type interactions. For the angular coordinate a Taylor spline kernel k[2](z,z′) is used where
(here n = 6) which gives the correct long-range behavior for neutral atom–diatom type interactions. For the angular coordinate a Taylor spline kernel k[2](z,z′) is used where 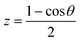 . The definitions of the kernel functions can be found in ref. 36 and 52. The RKHS procedure exactly reproduces the values of the function at the known points for smooth functions. However, often a regularization parameter (here 10−19) is used to numerically stabilize the algorithm.
. The definitions of the kernel functions can be found in ref. 36 and 52. The RKHS procedure exactly reproduces the values of the function at the known points for smooth functions. However, often a regularization parameter (here 10−19) is used to numerically stabilize the algorithm.
The global, reactive 3D PES V(r1,r2,r3) for an electronic state is constructed by summing the individual PESs for each channel
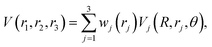 | (3) |
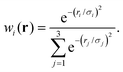 | (4) |
C. Quasiclassical trajectory calculation
The N + NO and O + N2 collisions systems are studied by running QCT on the global RKHS PESs for both 3A′ and 3A′′ states of N2O. The QCT method followed here is well documented in ref. 53–56. In this approach, Hamilton's coupled differential equations of motion are solved using the fourth-order Runge–Kutta method. The integration time step was Δt = 0.05 fs which guaranteed conservation of the total energy and angular momentum up to the sixth and eighth decimal places, respectively. Initial conditions for the trajectory simulations are generated from Monte Carlo sampling. The ro–vibrational states for the reactant and product are computed using the semiclassical theory of bound states. The ro–vibrational states for the product diatom are assigned to the nearest integer using histogram binning (HB) and Gaussian binning (GB) schemes.56–58 Since the results from both binning schemes are similar, only those obtained from HB are discussed unless otherwise mentioned.The probability of an event x (reactive, vibrational relaxation) can be computed as
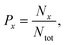 | (5) |
| σx = πbmax2Px | (6) |
The rate for an event x on surface i at a particular temperature T is then obtained as
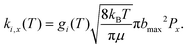 | (7) |
For the N(4S) + NO(X2Π) collision process, the temperature dependent degeneracies for the forward (“f”) reaction and for both triplet states are
 | (8) |
 | (9) |
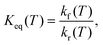 | (10) |
III. Results and discussion
In the following, the topology and accuracy of the PESs, the reaction/dissociation rates and the rates for vibrational relaxation from QCT simulations are presented and discussed.A. Accuracy and topology of the potential energy surfaces
To verify the quality of the RKHS PESs, the correlation between the ab initio and the RKHS energies for both states for the training grid are reported in Fig. S1 upper panel (ESI†). The structures with energy 6.8 eV above the N + N + O asymptote (7908 and 7797 points for the training grid) have R2 values of 0.99995 and 0.99996 and an RMSE of 0.51 and 0.46 kcal mol−1 for the 3A′ and 3A′′ states, respectively. Electronic structure calculations have also been performed at off-grid, randomly generated geometries for both states which serve as additional test data. A correlation diagram for the test grid is shown for 494 and 497 points for the 3A′ and 3A′′ states, respectively, with energies ≤6.8 eV (see Fig. S1 lower panel, ESI†). The correlation coefficients obtained for the test grids are 0.99985 and 0.99988 with RMSE 0.82 and 0.80 kcal mol−1 for the 3A′ and 3A′′ states, slightly larger than for the reference points but still of high quality. The RMSE values for the present PESs are more than three times lower than for previous PESs.26,27The quality of the RKHS PESs developed in this work is further examined by considering 1D cuts along R for different values of θ and constant values of r for the N + NO and O + N2 channels, see Fig. 2. Again, these are off-grid cuts (not part of the training grid) and the agreement between the ab initio and RKHS interpolated energies is excellent for all the cuts.
The topographies of the 3A′ and 3A′′ PESs for the two collision systems N + NO and O + N2 are reported in Fig. 3 as r-relaxed PESs. For this the center of mass of the diatom is placed at the origin and the position of the third free atom is described in 2 dimensions (x, y). The 2D PESs are then computed by determining the minimum energy for a given (x, y) with r ∈ [2.0, 2.5] a0 for N + NO and r ∈ [1.9, 2.4] a0 for O + N2. This was done because a ‘relaxed’ PES better represents all possible stationary states than a conventional 2D PES with a fixed r value.60
Both PESs have significantly different anisotropic topologies depending on the angle at which the reactants approach one another. The topology of the 3A′ PES is highly structured compared with that of the 3A′′ PES for both channels. For both PESs, the global minimum is at the O + N2 asymptote while the N + NO asymptote is higher in energy by 73.1 kcal mol−1. For the N + NO collisions, reactants face barriers along all angular directions on the 3A′ PES. The barrier height ∼9.6 kcal mol−1 (equivalent to 0.4 eV or ∼4800 K) is lowest for ∼135°. On the other hand, the N + NO collisions are barrierless on the 3A′′ PES for ∼135° which will profoundly affect the reactivity at lower temperatures. A potential well is found for the 3A′ PES along for near perpendicular geometries (MIN2, see Fig. 1) which is not present on the 3A′′ PES. For both PESs, the O + N2 approach is characterized by highly repulsive landscapes and a deep potential well with C2v symmetry at high energies on the 3A′ PES along the perpendicular direction (MIN2, see Fig. 1).
The stationary states on the PESs are characterized and presented in Fig. 1 and tabulated in Table 1. The minima and transition states are calculated by using the BFGS and nudged elastic band methods61,62 implemented in the Atomic Simulation Environment (ASE) package.63 The N + NO → N2 + O reaction is barrierless on the 3A′′ PES while the N exchange NA + NBO → NAO + NB reaction has a barrier of 38.03 kcal mol−1 which is ∼4.6 and ∼2.4 kcal mol−1 smaller than for the earlier PESs,26,27 respectively. A very shallow well (∼0.5 kcal mol−1) with a C2v symmetry exists as MIN1 between two TS1 structures.
| R NN | R NO | ∠NON | ΔE1 | ΔE2 | ΔE3 | ΔE4 | |
|---|---|---|---|---|---|---|---|
| 3A′ | |||||||
| TS1 | 2.21 | 2.72 | 27.1 | −7.837 | −180.736 | −187.2 | |
| MIN1 | 2.30 | 2.41 | 26.7 | −7.892 | −181.990 | −188.2 | |
| TS2 | 2.58 | 2.56 | 50.0 | −5.525 | −127.419 | −128.8 | |
| MIN2 | 2.70 | 2.63 | 61.8 | −6.499 | −149.880 | −161.0 | |
| TS3 | 3.86 | 2.56 | 97.5 | −5.061 | −116.703 | −116.8 | |
| MIN3 | 4.38 | 2.46 | 125.9 | −5.381 | −124.080 | −127.6 | −138.66 |
| TS4 | 4.73 | 2.25 | 121.1 | −4.850 | −111.848 | −114.9 | −125.20 |
| TS5 | 3.72 | 2.19 | 47.5 | −5.863 | −135.193 | −141.7 | −144.18 |
| 3A′′ | |||||||
| MIN1 | 3.92 | 2.51 | 102.9 | −4.651 | −107.245 | −110.5 | −113.28 |
| TS1 | 3.97 | 2.36 | 102.0 | −4.629 | −106.746 | −109.4 | −112.08 |
| N + NO | 2.19 | −6.278 | −144.774 | −153.0 | −152.53 | ||
| O + N2 | 2.09 | −9.447 | −217.850 | −227.8 | −228.41 | ||
There are two pathways from N + NO to N2 + O on the 3A′ PES which are similar to ref. 27. The minimum energy path follows N + NO → TS5 → MIN1 → TS1 → N2 + O. TS5 is located 9.58 kcal mol−1 higher than the N + NO asymptote which compares with 10.50 kcal mol−1 and 8.35 kcal mol−1 for the PESs in ref. 27 and 26, respectively. However, MIN1 and TS1 are not present on the 3A′ PES in ref. 26. MIN1 is located at 35.86 kcal mol−1 higher than the O + N2 asymptote and has a depth of 1.25 kcal mol−1 from TS1. The NN bond is shorter than the NO bonds in MIN1. The N exchange path for the NA + NBO → NAO + NB reaction has a barrier of 32.93 kcal mol−1 (TS4) and a potential well with a C2v symmetry of 12.23 kcal mol−1. TS3 has C2v symmetry and it connects MIN3 and MIN2 (C2v geometry and close to an equilateral triangle with angles 61.8°, 59.1° and 59.1°). MIN2 is connected with MIN1 via TS2.
B. Reaction and dissociation rates
Total rate coefficients for the N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) reaction and the N exchange reaction NA(4S) + NBO(X2Π) → NB(4S) + NAO(X2Π) have been calculated from 100 K to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. These rates are based on 50
000 K. These rates are based on 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 quasiclassical trajectories at each temperature. Individual contributions from each state are tabulated in Tables S1 and S2 (ESI†), respectively. Rate coefficients for N2 formation (forward reaction) are plotted between 100 and 5000 K in Fig. 4. In addition to the present computations, those from previous experiments and computations are shown. The rate is high at low temperature (100 K) and gradually decreases with increasing temperature before starting to increase again though the variation is small over the entire range. For the present work, the minimum and maximum rates are 2.595 × 10−11 and 5.095 × 10−11 cm3 s−1 molecule−1 between 100 K and 5000 K, which differ only by a factor of two, consistent with a barrierless reaction in the forward direction. The results from quantum wave packet calculations for the forward reaction (blue squares) are slightly smaller than the present ones for low temperatures and larger by ∼25% at higher temperatures.
000 quasiclassical trajectories at each temperature. Individual contributions from each state are tabulated in Tables S1 and S2 (ESI†), respectively. Rate coefficients for N2 formation (forward reaction) are plotted between 100 and 5000 K in Fig. 4. In addition to the present computations, those from previous experiments and computations are shown. The rate is high at low temperature (100 K) and gradually decreases with increasing temperature before starting to increase again though the variation is small over the entire range. For the present work, the minimum and maximum rates are 2.595 × 10−11 and 5.095 × 10−11 cm3 s−1 molecule−1 between 100 K and 5000 K, which differ only by a factor of two, consistent with a barrierless reaction in the forward direction. The results from quantum wave packet calculations for the forward reaction (blue squares) are slightly smaller than the present ones for low temperatures and larger by ∼25% at higher temperatures.
 | ||
| Fig. 4 Rate coefficients for the N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) for temperatures between 100 and 5000 K. The results calculated in the present work are shown as black open circles connected by solid black line. together with experimental (“E”) and theoretical (“T”) rates from the literature.14,16–20,26,28,31,32 The inset shows an enlarged version of the low temperature region. | ||
As can be seen in Table S1 (ESI†), due to the barrier of 9.58 kcal mol−1 in the entrance channel on the 3A′ PES the contribution is considerably lower at low temperatures than that of the 3A′′ state which is barrierless. Hence, at low temperatures the contribution from the 3A′′ PES dominates. Rates for the forward reaction obtained from ref. 26 using PESs from ref. 25 and 64 (black open squares) and from ref. 28 (cyan open triangle down) are very small at low temperatures and increase monotonically with increasing temperature due to the presence of a small barrier on the 3A′′ PES. In the present work, the results from QCT simulations correctly describe the trends of the experimental results at low temperature. However, the high temperature rate expression obtained from experimental data are temperature independent whereas the QCT rates increase slowly with temperature. On the other hand, the present rates are consistent with those calculated on the many-body expansion representations of the CASPT2/cc-pVTZ calculations (red circles).26,32
Rates for the N exchange reaction NA(4S) + NBO(X2Π) → NB(4S) + NAO(X2Π) are given in Table S2 (ESI†). Due to presence of barriers along the reaction path on both PESs (see Fig. 1), this channel only opens at ∼3000 K (consistent with a barrier height of ∼4800 K, see above) and reactivity increases with increasing temperature. However, the rates for the N exchange reaction are smaller than those for the N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) reaction over the entire temperature range considered.
Rate coefficients for the O(3P) + N2(X1Σ+g) → N(4S) + NO(X2Π) reaction have been calculated from 2800 K to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K by running 5 × 104 to 5 × 105 quasiclassical trajectories for each temperature. The reaction rate increases with increasing temperature (see Fig. 5) and individual contributions from each PES are given in Table S3 (ESI†). This reaction is endothermic and the channel only opens up above ∼3000 K due to the barrier in the entrance channel. Since the rates are small at low temperatures, error margins (1σ) are calculated from bootstrapping by sampling 50
000 K by running 5 × 104 to 5 × 105 quasiclassical trajectories for each temperature. The reaction rate increases with increasing temperature (see Fig. 5) and individual contributions from each PES are given in Table S3 (ESI†). This reaction is endothermic and the channel only opens up above ∼3000 K due to the barrier in the entrance channel. Since the rates are small at low temperatures, error margins (1σ) are calculated from bootstrapping by sampling 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories randomly from 5 × 105 trajectories. This procedure is repeated 100 times, and then average rate coefficients and standard deviations are calculated. The contribution from the 3A′ PES is smaller than that from 3A′′ PES over the entire temperature range. Rates reported from previous experimental and theoretical work are also presented in Fig. 5. Rate expressions obtained by fitting experimental data are given in ref. 23 and 22 which are shown in Fig. 5 along with the recommended values provided by Baulch et al.21 The results obtained in the present work agree well with the experimental data.
000 trajectories randomly from 5 × 105 trajectories. This procedure is repeated 100 times, and then average rate coefficients and standard deviations are calculated. The contribution from the 3A′ PES is smaller than that from 3A′′ PES over the entire temperature range. Rates reported from previous experimental and theoretical work are also presented in Fig. 5. Rate expressions obtained by fitting experimental data are given in ref. 23 and 22 which are shown in Fig. 5 along with the recommended values provided by Baulch et al.21 The results obtained in the present work agree well with the experimental data.
 | ||
| Fig. 5 Rate coefficients for the O(3P) + N2(X1Σ+g) → N(4S) + NO(X2Π) reaction as a function of temperature. The results calculated in the present work are shown as black open circles connected by black line. Experimental and theoretical rates available from the literature are also shown.21–24,26,65 The shaded area shows the confidence limit for the Thielen and Roth66 data. The error margins from bootstrapping (see text) are overlaid on the black open circles. | ||
The equilibrium constants for the N(4S) + NO(X2Π) ↔ O(3P) + N2(X1Σ+g) reaction have been computed using eqn (10) between 3000 and 6000 K and good agreement with the values reported in the JANAF tables67 computed from thermodynamic quantities is found (see Fig. 6). This suggests that the present PESs are accurate enough to describe the forward and the reverse reaction and other electronic states play only a minor role in the dynamics of both reactions.
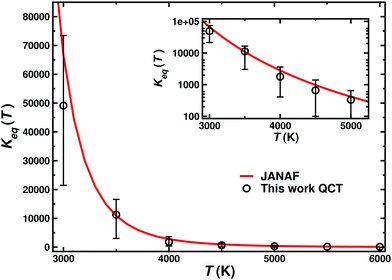 | ||
| Fig. 6 Equilibrium constant Keq(T) for the N(4S) + NO(X2Π) ↔ O(3P) + N2(X1Σ+g) reaction. The main figure reports the results on a linear scale and the inset on a logarithmic scale for Keq including the error bars from Fig. 5. Open circles represent the QCT results and the red line shows the results obtained from JANAF tables.67 | ||
Both N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) and the reverse reaction are among the reactions which play an important role at hyperthermal conditions during the reentry of space vehicles into Earth's atmosphere. Analytical expression for the rates are useful to simulate hypersonic flow during reentry. In this work, the rates are calculated at hyperthermal temperature for both reactions and modified Arrhenius functions (k(T) = ATn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/T)) are fitted to those rates. The parameters (A, n, Ea) are given in Table 2 and the fits are also shown in Fig. 7 along with available rate expressions from literature. For the reverse reaction, except for the fit from ref. 26 all the fits agree well over the entire range.
exp(−Ea/T)) are fitted to those rates. The parameters (A, n, Ea) are given in Table 2 and the fits are also shown in Fig. 7 along with available rate expressions from literature. For the reverse reaction, except for the fit from ref. 26 all the fits agree well over the entire range.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K range are used for the forward reaction while the rates from 3000–20
000 K range are used for the forward reaction while the rates from 3000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K are used for the reverse reaction. Rate coefficients k(T) computed using these parameters have units in cm3 molecule−1 s−1 with [A] = cm3 molecule−1 s−1 and [Ea] = K while n is unitless
000 K are used for the reverse reaction. Rate coefficients k(T) computed using these parameters have units in cm3 molecule−1 s−1 with [A] = cm3 molecule−1 s−1 and [Ea] = K while n is unitless
| Reaction | A | n | E a |
|---|---|---|---|
| Forward | 2.17 × 10−14 | 0.89 | −946.0 |
| Reverse | 2.13 × 10−12 | 0.59 | 38225.4 |
| Dissociation | 4.55 | −2.00 | 129692.6 |
 | ||
Fig. 7 Rate coefficients for the forward N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) (left panel) and the reverse reaction (right panel) at temperatures relevant to hypersonic flight regime, i.e. between 2000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K; for the lower T-region see Fig. 4 and 5. Black open squares represent the QCT rates and the lines represent the Arrhenius fit. Rates calculated from the rate expression reported in literature are also shown as dashed lines.26,33,68 000 K; for the lower T-region see Fig. 4 and 5. Black open squares represent the QCT rates and the lines represent the Arrhenius fit. Rates calculated from the rate expression reported in literature are also shown as dashed lines.26,33,68 | ||
At very high temperatures collisions may lead to dissociation of the diatomic molecules, in particular if they are in highly vibrationally excited states. Here, the dissociation of molecular nitrogen during collisions with an oxygen atom is studied at high temperatures between 8000 K and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The rate coefficients for the N2 + O → 2N + O are shown in Fig. 8 and also given in Table S4 (ESI†). A fit to a modified Arrhenius model is also shown in Fig. 8 along with the rate expression reported in ref. 33 and 68. The parameters for the present fits are given in Table 2 and all fits agree well except at high temperatures for which the fit from ref. 68 gives a higher dissociation rate.
000 K. The rate coefficients for the N2 + O → 2N + O are shown in Fig. 8 and also given in Table S4 (ESI†). A fit to a modified Arrhenius model is also shown in Fig. 8 along with the rate expression reported in ref. 33 and 68. The parameters for the present fits are given in Table 2 and all fits agree well except at high temperatures for which the fit from ref. 68 gives a higher dissociation rate.
 | ||
| Fig. 8 Rate coefficients for N2 dissociation reaction for the O(3P) + N2(X1Σ+g) collisions. Black open squares represent the QCT rates and the lines are the Arrhenius fits. Rates calculated from the rate expression reported in ref. 33 and 68 are also shown as dashed lines. | ||
C. Vibrational relaxation
In three different experiments, pτvib values are reported between 300 K and 4500 K69–71 and rates were calculated from pτvib values and fitted to analytical expressions.72 Here, VR rates are calculated for O + N2(ν = 1, j) → O + N2(ν′ = 0, j′) for temperatures between 300 K and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K and are reported in Fig. 9, along with experimental69–72 and previous theoretical33 results.
000 K and are reported in Fig. 9, along with experimental69–72 and previous theoretical33 results.
 | ||
| Fig. 9 Vibrational relaxation rates for O + N2(ν = 1) → O + N2(ν′ = 0). Green symbols represent the experimentally determined VR rates.69–71 The olive dashed line is the fit to the experimental result.72 Rates obtained in this work from QCT simulations and using HB, GB and a modified HB scheme are given along with the full QCT (magenta solid line) and quasi-reactive QCT (blue solid line) results from ref. 33. The experimental data69–71 was extracted from Fig. 4 in ref. 33 using the software g3data.73 Typical error bars as reported from one of the experiments70 are indicated in yellow for two values. | ||
QCT with histogram binning (QCT-HB) significantly overestimates the VR rates for T > 800 K while the Gaussian binning56–58 (QCT-GB) scheme leads to some improvement. Since only ν = 1 to ν′ = 0 transitions are considered, the way the final state is determined is important and the type of binning scheme used plays a potentially significant role. It is found that for a large number of trajectories vibrational energy exchange was less than one quantum which formally leads to a state with ν′ = 0 but with high energy. Although QCT-GB partly excludes the contributions from such trajectories, the VR rates obtained from QCT-GB are only in fair agreement with experiments. It is found that considering trajectories with ε0,j′ ≤ εv′,j′ ≤ ε0,j′ + 0.075 eV (0.075 eV ≈ 0.3 quanta) to be a VR trajectory gives results consistent with experiment (green line with asterisk in Fig. 9: Modified HB or QCT-MHB). This suggests that a fraction of the trajectories either do not enter the strong coupling region or sample it incompletely which leads to reduced energy exchange (not fully relaxed). VR rates calculated on the PESs from ref. 26 underestimate the experimental values for T < 9000 K. For the comparison with experimental relaxation times it should be mentioned that these are typically carried out on chemically heterogeneous samples, containing species other than N, O, N2 and O2, and that extraction of vibrational relaxation times involves extensive modeling.70
Yet another approach was followed in previous work33 by classifying VR trajectories to be either ‘purely nonreactive’ (PNR) or ‘quasi-reactive’ (QR) and counting the contribution only from QR trajectories. Filtering trajectories following such a “QR procedure” (Esposito1 and Esposito2 in Fig. S2, ESI†) resulted in VR rates closer to the extrapolated VR rates from experiment for T > 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K but did not improve the VR rates at lower temperature.33 For a “QR” trajectory the ratio of any of the two NO distances with N2 (RNO/RN2) became smaller than the ratio for the diatomic equilibrium bond lengths
000 K but did not improve the VR rates at lower temperature.33 For a “QR” trajectory the ratio of any of the two NO distances with N2 (RNO/RN2) became smaller than the ratio for the diatomic equilibrium bond lengths  whereas for a “PNR” trajectory this criterion was never satisfied. For a “QR” trajectory, at least one collision similar to reactive one (O + N2 → N + NO) had occurred during the dynamics and the particles (atom + diatom) further collide to finally produce again the reactant. So overall in a QR trajectory the final outcome was nonreactive. On the other hand, a PNR trajectory was considered to be fully nonreactive.
whereas for a “PNR” trajectory this criterion was never satisfied. For a “QR” trajectory, at least one collision similar to reactive one (O + N2 → N + NO) had occurred during the dynamics and the particles (atom + diatom) further collide to finally produce again the reactant. So overall in a QR trajectory the final outcome was nonreactive. On the other hand, a PNR trajectory was considered to be fully nonreactive.
For direct comparison, the same analysis was also carried out here. Fig. S2 (ESI†) shows that computing the rate for VR by only considering QR trajectories (green line), the results are close to those from ref. 33 (blue line) but do not agree with experiment. Since QR trajectories are similar to reactive trajectories, they sample the strongly interacting region of the PES (lower panel of Fig. S3, ESI†). They also display similar dwell time distributions as reactive trajectories, see Fig. 10. This, together with the result that reaction rates from the two different PESs agree, suggests that the present PES and that from ref. 26 have a similar topography for the short range, strongly interacting region. Conversely, the PNR trajectories sample distinctly different regions in configuration space (see top panel Fig. S3, ESI†) – primarily the long range part of the PES. These are the trajectories that are responsible for the differences in the VR rates between the present and the earlier work33 and is related to differences in the long range part of the PES.
 | ||
| Fig. 10 Dwell/collision time distributions shown for 1000 PNR, QR, and reactive trajectories, respectively. The collision time for a trajectory is defined as the time elapsed between the first and last instances of satisfying the criterion that the sum of three internuclear distances was less than 12 a0. PNR trajectories are dominated by short collision times whereas QR and reactive trajectories have their maximum at ∼65 fs. These three types of trajectories also sample different regions in configuration space, see Fig. S3 (ESI†). | ||
Here, the RKHS representation allows one to correctly capture the long range interactions for neutral–neutral or ion–neutral collision systems as the asymptotic decay can be chosen by employing appropriate kernel functions. The fact that QCT simulations with the PESs from ref. 26 yield reaction rates for the forward and reverse process in good agreement with experiment.26,31–33,68 further suggests that these PESs have certain deficiencies only in the long range part because for reactive processes the short range, strongly interacting region is primarily relevant. As the VR rates from the present analysis agree qualitatively with experiment over the entire temperature range, the present PESs are a good starting point for further improvements on the shape of the PESs.
These findings underline the point that different observables (here reaction and vibrational relaxation rates) can be sensitive to different parts of the PES in the dynamics.39 This is also manifest from Fig. S3 (ESI†): PNR and QR trajectories sample and are sensitive to distinctly different regions of the multidimensional PESs. Reaction and dissociation rates obtained from the earlier PESs26 are comparable with results from the present PESs and agree with experiment but the vibrational relaxation rates are different. Exploiting such sensitivities for other observables, such as relaxation from higher vibrationally excited states (i.e. ν > 1, which was not considered here) will provide the basis for further improvements when compared with experiment.
IV Conclusion
Accurate PESs have been constructed for the lowest lying 3A′ and 3A′′ states for the [NNO] system using more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MRCI+Q/aug-cc-pVTZ energies and RKHS interpolation. Both PESs have smaller RMSE compared with previously reported PESs in the literature. The present PESs accurately describe the important regions that are sampled in reactive and VR processes and their validity is assessed by calculating reaction rates for the N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) and the reverse reaction. The vibrational relaxation rates for the O + N2 collisions are also computed. Good agreement between the experiment and theory for all these observables confirms the high quality of the present PESs and provides useful generalized Arrhenius expressions for reaction rates. These PESs can be used to calculate state-to-state cross sections for more coarse grained simulations such as DSMC.
000 MRCI+Q/aug-cc-pVTZ energies and RKHS interpolation. Both PESs have smaller RMSE compared with previously reported PESs in the literature. The present PESs accurately describe the important regions that are sampled in reactive and VR processes and their validity is assessed by calculating reaction rates for the N(4S) + NO(X2Π) → O(3P) + N2(X1Σ+g) and the reverse reaction. The vibrational relaxation rates for the O + N2 collisions are also computed. Good agreement between the experiment and theory for all these observables confirms the high quality of the present PESs and provides useful generalized Arrhenius expressions for reaction rates. These PESs can be used to calculate state-to-state cross sections for more coarse grained simulations such as DSMC.
QCT simulations over a wide range of temperatures on the present and earlier26 PESs yield reaction rates consistent with experiment but disagree for vibrational relaxation rates at lower temperatures. This suggests that the topographies of the earlier26 and the present PESs are similar in certain aspects but differ in others. One way to probe the sensitivity of different regions of the PES on the observables can be assessed by introducing random noise/perturbation in the PES and recalculating the observables.74 Alternatively, PES morphing-type approaches75 can be considered which will also provide information which parts of the PES need to be further improved. This can follow similar approaches as the one highlighted for vibrational relaxation rates, namely by considering subclasses of trajectories sampling distinct regions of configuration space and determining separate observables (here relaxation rates) for each of the subclass. This is akin to using the fact that in a triatomic complex, such as Ne-HF, stretching and bending vibrations probe complementary regions of the PES.75
Code availability
The code for the RKHS PESs has been made available on github https://github.com/MMunibas/N2O-PESs.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Part of this work was supported by the United State Department of the Air Force which is gratefully acknowledged (to MM). Support by the Swiss National Science Foundation through grants 200021-117810, 200020-188724, and the NCCR MUST (to MM), the sciCORE computer cluster and the University of Basel is also acknowledged.References
- D. F. Strobel, J. Geophys. Res., 1971, 76, 8384–8393 CrossRef CAS.
- G. Brasseur and M. Nicolet, Planet. Space Sci., 1973, 21, 939–961 CrossRef CAS.
- M. Capitelli, R. Celiberto, G. Colonna, G. DAmmando, O. D. Pascale, P. Diomede, F. Esposito, C. Gorse, A. Laricchiuta, S. Longo, L. D. Pietanza and F. Taccogna, Plasma Phys. Controlled Fusion, 2011, 53, 124007 CrossRef.
- Y. Zeldovich, Acta Physicochimica U.S.S.R., 1946, 21, 577–628 CAS.
- D. E. Siskind and D. W. Rusch, J. Geophys. Res.: Space Phys., 1992, 97, 3209–3217 CrossRef.
- G. Black, T. G. Slanger, G. A. St. John and R. A. Young, J. Chem. Phys., 1969, 51, 116–121 CrossRef CAS.
- C. Fell, J. I. Steinfeld and S. Miller, J. Chem. Phys., 1990, 92, 4768–4777 CrossRef CAS.
- R. Schinke, J. Suarez and S. C. Farantos, J. Chem. Phys., 2010, 133, 091103 CrossRef CAS PubMed.
- R. Schinke, Chem. Phys., 2012, 399, 142–145 CrossRef CAS.
- J. Li and A. J. C. Varandas, J. Phys. Chem. A, 2012, 116, 4646–4656 CrossRef CAS PubMed.
- J. Li, P. J. S. B. Caridade and A. J. C. Varandas, J. Phys. Chem. A, 2014, 118, 1277–1286 CrossRef CAS PubMed.
- P. Warneck, Chemistry of the Natural Atmosphere, Academic Press, San Diego, CA, 1988 Search PubMed.
- S. P. Walch and R. L. Jaffe, J. Chem. Phys., 1987, 86, 6946–6956 CrossRef CAS.
- A. Bergeat, K. M. Hickson, N. Daugey, P. Caubet and M. Costes, Phys. Chem. Chem. Phys., 2009, 11, 8149–8155 RSC.
- C. Lin, D. A. Parkes and F. Kaufman, J. Chem. Phys., 1970, 53, 3896–3900 CrossRef CAS.
- J. H. Lee, J. V. Michael, W. A. Payne and L. J. Stief, J. Chem. Phys., 1978, 69, 3069–3076 CrossRef CAS.
- W. B. DeMore, M. J. Molina, R. T. Watson, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard and A. R. Ravishankara, Chemical kinetics and photochemical data for use in stratospheric modeling, Evaluation number 6, Jet Propulsion Lab., California Inst. of Tech., Pasadena, CA, United States, 1983 Search PubMed.
- P. O. Wennberg, J. G. Anderson and D. K. Weisenstein, J. Geophys. Res.: Atmos., 1994, 99, 18839–18846 CrossRef.
- J. V. Michael and K. P. Lim, J. Chem. Phys., 1992, 97, 3228–3234 CrossRef CAS.
- H. J. Mick, H. Matsui and P. Roth, J. Phys. Chem., 1993, 97, 6839–6842 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- J. Monat, R. Hanson and C. Kruger, Symp. (Int.) Combust., 1979, 17, 543–552 CrossRef.
- K. Thielen and P. Roth, Symp. (Int.) Combust., 1985, 20, 685–693 CrossRef.
- J. B. Livesey, A. L. Roberts and A. Williams, Combust. Sci. Technol., 1971, 4, 9–15 CrossRef CAS.
- M. Gilibert, A. Aguilar, M. González, F. Mota and R. Sayós, J. Chem. Phys., 1992, 97, 5542–5553 CrossRef CAS.
- P. Gamallo, M. González and R. Sayós, J. Chem. Phys., 2003, 119, 2545–2556 CrossRef CAS.
- W. Lin, Z. Varga, G. Song, Y. Paukku and D. G. Truhlar, J. Chem. Phys., 2016, 144, 024309 CrossRef PubMed.
- O. Denis-Alpizar, R. J. Bemish and M. Meuwly, Phys. Chem. Chem. Phys., 2017, 19, 2392 RSC.
- P. Gamallo, M. González and R. Sayós, J. Chem. Phys., 2003, 118, 10602–10610 CrossRef CAS.
- P. Gamallo, M. González, R. Sayós and C. Petrongolo, J. Chem. Phys., 2003, 119, 7156–7162 CrossRef CAS.
- P. Gamallo, R. Sayós, M. González, C. Petrongolo and P. Defazio, J. Chem. Phys., 2006, 124, 174303 CrossRef PubMed.
- P. Gamallo, R. Martnez, R. Sayós and M. González, J. Chem. Phys., 2010, 132, 144304 CrossRef PubMed.
- F. Esposito and I. Armenise, J. Phys. Chem. A, 2017, 121, 6211–6219 CrossRef CAS PubMed.
- W. Lin, R. Meana-Pañeda, Z. Varga and D. G. Truhlar, J. Chem. Phys., 2016, 144, 234314 CrossRef PubMed.
- D. Koner, O. T. Unke, K. Boe, R. J. Bemish and M. Meuwly, J. Chem. Phys., 2019, 150, 211101 CrossRef PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Inf. Model., 2017, 57, 1923–1931 CrossRef CAS PubMed.
- D. Koner, R. J. Bemish and M. Meuwly, J. Chem. Phys., 2018, 149, 094305 CrossRef PubMed.
- D. Koner, J. C. San Vicente Veliz, A. van der Avoird and M. Meuwly, Phys. Chem. Chem. Phys., 2019, 21, 24976–24983 RSC.
- J. C. San Vicente Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, Phys. Chem. Chem. Phys., 2020, 22, 3927–3939 RSC.
- E. E. Nikitin and J. Troe, Phys. Chem. Chem. Phys., 2008, 10, 1483–1501 RSC.
- L. L. Northup, Vibrational relaxation of harmonic oscillators including multiple quantum transitions, Iowa State University, 1967 Search PubMed.
- G. A. Bird, Molecular Gas Dynamics and the Direct Simulation of Gas Flows, Clarendon Press, 1994 Search PubMed.
- H. A. Bethe and E. Teller, Deviations from Thermal Equilibrium in Shock Waves, Ballistic Research Labs, 1941, vol. X-117 Search PubMed.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. Werner and W. Meyer, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2019.1, a package of ab initio programs, 2019 Search PubMed.
- T.-S. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584 CrossRef CAS.
- M. Karplus, R. N. Porter and R. D. Sharma, J. Chem. Phys., 1965, 43, 3259–3287 CrossRef CAS.
- D. G. Truhlar and J. T. Muckerman, in Atom – Molecule Collision Theory, ed. R. B. Bernstein, Springer US, 1979, pp. 505–566 Search PubMed.
- N. E. Henriksen and F. Y. Hansen, Theories of Molecular Reaction Dynamics, Oxford, 2011 Search PubMed.
- D. Koner, PhD thesis, Indian Institute of Technology Guwahati, 2016.
- L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 1997, 277, 183–190 CrossRef CAS.
- L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 2004, 397, 106–109 CrossRef CAS.
- J. D. Bender, P. Valentini, I. Nompelis, Y. Paukku, Z. Varga, D. G. Truhlar, T. Schwartzentruber and G. V. Candler, J. Chem. Phys., 2015, 143, 054304 CrossRef PubMed.
- A. Varandas, Chem. Phys. Lett., 1987, 138, 455–461 CrossRef CAS.
- G. Henkelman, B. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- E. L. Kolsbjerg, M. N. Groves and B. Hammer, J. Chem. Phys., 2016, 145, 094107 CrossRef PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- M. Gilibert, A. Aguilar, M. González and R. Sayós, J. Chem. Phys., 1993, 99, 1719–1733 CrossRef CAS.
- D. Bose and G. V. Candler, J. Chem. Phys., 1996, 104, 2825–2833 CrossRef CAS.
- K. Thielen and P. Roth, Symposium (International) on Combustion, 1985, pp. 685–693 Search PubMed.
- J. Malcolm and W. Chase, NIST-JANAF thermochemical tables, American Chemical Society, American Institute of Physics for the National Institute of Standards and Technology, Washington, DC, New York, 4th edn, 1998 Search PubMed.
- H. Luo, M. Kulakhmetov and A. Alexeenko, J. Chem. Phys., 2017, 146, 074303 CrossRef PubMed.
- R. McNeal, M. Whitson and G. Cook, Chem. Phys. Lett., 1972, 16, 507–510 CrossRef CAS.
- D. J. Eckstrom, J. Chem. Phys., 1973, 59, 2787–2795 CrossRef CAS.
- W. D. Breshears and P. F. Bird, J. Chem. Phys., 1968, 48, 4768–4773 CrossRef CAS.
- M. Capitelli, C. M. Ferreira, B. F. Gordiets and A. I. Osipov, Plasma Kinetics in Atmospheric Gases, Springer-Verlag Berlin Heidelberg, 2000 Search PubMed.
- J. Frantz, g3data, http://www.frantz.fi/software/g3data.php/Version, 2000.
- S. Venturi, R. L. Jaffe and M. Panesi, J. Phys. Chem. A, 2020, 124, 5129–5146 CrossRef CAS PubMed.
- M. Meuwly and J. M. Hutson, J. Chem. Phys., 1999, 110, 8338–8347 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02509g |
| This journal is © the Owner Societies 2020 |



