2-Methoxyethanol: harmonic tricks, anharmonic challenges and chirality-sensitive chain aggregation

Abstract

The Raman spectrum of jet-cooled, nearly monoconformational 2-methoxyethanol reveals a strong, aggregation-sensitive resonance in the backbone stretching region and pronounced chirality-dependent dimerisation effects in the OH stretching region. These effects are disentangled by a dual-detection scheme which simultaneously probes the two spectral regions. The performance of mass-scaled harmonic wavenumber predictions and of vibrational perturbation theory in reproducing these spectral features is explored.

---

1 Introduction

Chain molecules support a wide range of fundamental molecular vibrations, from acoustic phonon-like accordion modes to high-frequency stretches of terminal hydrogens. These vibrations probe different anharmonicities of the potential energy hypersurface (PES) and there is a need for simple experimental test systems which allow for the reliable assessment of theoretical treatments addressing this anharmonicity. A complicating factor in the spectroscopy of chain molecules is conformational diversity and its sensitivity to aggregation. Here, we select a molecular system which is conformationally almost uniform, at least when prepared in a supersonic jet expansion. 2-Methoxyethanol HO–CH₂–CH₂–O–CH₃ has three non-trivial torsional angles, HOCC (with the preferred conformations g, g′, t), OCCO (G, G′, T) and CCOC (G, G′, T). This generates up to 27 rotamers, but only two of them, namely gG′T and its mirror image g′GT, are populated significantly at low temperature, supported by intramolecular hydrogen bonding.^1,2 The next diastereomer, gG′G′, is about (5–6) kJ mol⁻¹ higher in energy. Rotamers with a trans OCCO arrangement, which may be trapped behind robust barriers, are even less stable. This conformational uniformity has been observed long ago by microwave spectroscopy³ and some interesting coupled dynamics of the lowest skeletal and torsional modes have been identified.^4,5 The preference for gG′T and its enantiomer is computationally robust due to its internal hydrogen bond optimisation, extending down to the simplest quantum chemical approaches.^6,7 Although the energy gap is expected to shrink somewhat upon aggregation, one can count on a significant gG′T/g′GT preference even in molecular dimers. This situation makes 2-methoxyethanol attractive for benchmark experiments, because it removes complexity and reduces spectral congestion on the monomer side. Nevertheless, there is substantial isomerism in the dimers due to the transient chirality of the dominant monomer⁸ and the availability of multiple acceptor sites for OH hydrogen bonding. The competition between intra- and intermolecular hydrogen bonding^2,9 adds additional subtlety to the situation. The present work explores this isomerism and it investigates the ability of scaled harmonic and perturbational anharmonic treatments of the vibrational dynamics to reproduce the Raman spectra of monomers and dimers of 2-methoxyethanol. We show that anharmonic corrections are robust for the high frequency OH stretching modes but much less uniform for some low frequency backbone and OH torsion vibrations.

Key to the present work is the experimental detection of the vibrations in rotationally cold, isolated molecules by Raman spectroscopy, which provides high sensitivity for low and high frequency chain modes, whereas gas phase infrared spectroscopy is more challenging in the low frequency range.¹⁰ We introduce a dual detection scheme enabling simultaneous recording of both spectral windows on separate detectors, which ensures reliable monomer/dimer/cluster discrimination and assignment.

2 Methods

The presented spectra were obtained in a continuous Raman jet spectroscopy setup, the basics of which are described in detail in ref. 11. Briefly, a powerful, mildly focussed 532 nm laser beam (Spectra Physics Millenia 25 eV) crosses a slit nozzle expansion parallel to its slit at a variable distance in a vacuum chamber. The Raman scattering is collected at a 90° angle, collimated to a diameter of up to 40 mm, led out of the vacuum chamber, and finally collected on a CCD camera in multi-minute exposures after dispersion in a monochromator. Several of these exposures are compared and cosmic ray events are separated from consistent spectral signals by a data-processing procedure. Depolarisation properties of the vibrational signals are investigated by rotating the laser polarisation. Subtraction of the depolarised fraction yields a spectrum which largely consists of narrow Q-branches and also removes rotational contributions from water impurities. The calibration uses atomic Ne transitions.¹²

New to this work is the ability to split the collected scattering signal by a dichroic beamsplitter into separate beams for small and large Stokes shift, which are simultaneously recorded by two separate monochromator/CCD units. Other than for successive recording, the simultaneous detection ensures that both spectra obtained are recorded at exactly the same experimental conditions. In contrast to other sequential¹³ or simultaneous spectroscopy schemes,¹⁴ the same light source and the same light collection is used, making alignment inside the vacuum chamber somewhat easier. An elegant, but somewhat less flexible alternative would be to use the same optical grating but to collect the Raman scattering in different diffraction orders.¹⁵ A detailed description of our approach including a scheme and relevant optical parameters is given in the ESI.† Also new to (part of) this work is the usage of mass flow controllers installed in the gas feed. By replacing the previously used pulsed magnetic valves a stable expansion pressure is ensured. Additionally, the mass flow controllers can be employed in a linked manner that allows for mixing different gases in a defined ratio. Here, this was used to mix substance-enriched helium with pure helium in order to record spectra with varying substance concentration.

On the theoretical side, harmonic vibrational Raman spectra are simulated using Turbomole 7.3 and 7.4¹⁶ on B3LYP/def2-QZVPP level^17–22 with Grimme's dispersion correction, Becke–Johnson damping and three-body-terms D3(BJ,abc).^23,24 For speedup multipole-accelerated resolution of the identity MARI-J²⁵ was used. A detailed description of how Turbomole output is converted to Raman cross sections that are comparable to our experimental setup is given in the ESI.† Calculated spectra are shown as Gauss-convoluted lines (σ = 0.8 cm⁻¹), unless indicated otherwise. Calculated wavenumbers are unscaled unless stated otherwise. Relative energies are obtained with Turbomole by combining electronic energies from single-point calculations on RIJK-CCSD(F12*)(T*)/cc-pVTZ-F12 level^26–29 with zero-point energies from B3LYP/def2-QZVPP.

The procedure to find the lowest energy dimer structures involved automated conformational searches using CREST³⁰ at GFN2-xTB level,^31,32 followed by a reoptimisation of all 475 structures at B97-3c level³³ with Turbomole. The 24 resulting distinct structures in a <11 kJ mol⁻¹ window were reoptimised at MARIJ-B3LYP-D3(BJ,abc)/def2-QZVPP level, leading to 23 distinct final structures in a 10 kJ mol⁻¹ window.

An anharmonic VPT2 analysis is added using the default settings of Gaussian09 Rev. E.01³⁴ and Gaussian16 Rev. A.03³⁵ on B3LYP-D3(BJ)/def2-QZVPP level (see the ESI† for employed keywords). The corresponding harmonic fundamental wavenumbers differ from those obtained by Turbomole by less than 2.5 cm⁻¹ or 0.25% (whichever is smaller), harmonic Raman cross sections differ by ≤20% in part due to a slightly different implementation of the functional, usage of three-body dispersion and MARI-J in Turbomole and numerical details of the quantum chemistry codes. To better understand a prominent and quite unusual coupling between OH torsion and backbone vibrations, mass-tuning of the OH hydrogen is used in the harmonic approximation (Turbomole).

The monomers are classified by the three torsional angles as outlined in the introduction, where lower case letters denote the HOCC torsion angle (360° ≥ g ≥ 240° ≥ t ≥ 120° ≥ g′ ≥ 0°) and upper case letters the corresponding OCCO and CCOC torsions. A consistent exchange of g/G with g′/G′ would have no consequence for the discussion in this work, which only builds on relative chirality. Dimers featuring two reciprocal isolated OH⋯OC hydrogen bonds between the monomers are denoted r and dimers with a cooperative OH⋯OH⋯OC pattern obtained by inserting an OH group into the intramolecular OH⋯O contact of the other are called c. This topological label is preceded by hom (homochiral) or het (heterochiral), depending on whether the two gG′T monomers have the same or opposite handedness. The r pattern allows for C₂ and C_i point group symmetry in the hom and het case, respectively. This symmetry (indicated wherever relevant) is used in the final calculations with one technical exception: C_i symmetry in Turbomole yielded unphysical Raman cross sections and was therefore calculated as C₁.³⁶ Where a second, energetically higher dimer conformation leads to the same label, it is differentiated from the more stable structure by adding one or more primes (′). Such isomerism can arise from the engagement of different lone pairs or enantiotopic faces at the oxygen acceptor and is expected to be prone to efficient relaxation. Racemisation of the monomer and switches between reciprocal (r) and cooperative (c) hydrogen bond topologies are expected to be much less feasible under supersonic jet conditions.³⁷ Therefore, a minimum of four dimer structures (het-r, hom-r, het-c, hom-c) in a nearly statistical ratio is expected, but primed structures should not be ruled out.

3 Results

3.1 Monomer low frequency modes

Fig. 1 provides an overview of the Raman spectra of 2-methoxyethanol expansions under monomer-dominated (lower) and dimer-enriched conditions (upper trace). Larger oligomers can be neglected, as shown later on (Fig. 4). Black arrows mark dimer contributions, which are well separated in the OH stretching region. The absence of extra signals for free OH fundamentals suggests that these dimers do not contain dangling OH-groups and are thus of the cooperative (c) or reciprocal (r) type. Four separate signals demand at least two different conformations, but variations in the signal profiles suggest a larger number. Such dimer fundamentals are much less prominent in the low frequency range and overlap the monomer features. The double detection setup thus ensures that the lower left trace exclusively contains monomer signals, besides some water rotational transitions which are easily identified because they increase with respect to the upper left trace.

Fig. 1 Raman spectra of 2-methoxyethanol expansions in He with very low (lower traces, violet) and larger dimer fraction (higher traces, green, arrows mark aggregation features), using the new double detection setup. Monomer OH stretching intensity at 3635 cm⁻¹ is matched by scaling, the same scaling factor is applied to the low frequency spectrum. Water impurity is marked at 3656 cm⁻¹ with “w” and is also assignable in the low frequency range (see Fig. 3).

Characteristic for Raman spectra of small molecules, some transitions have very weak Q-branches and broad rotational structure (e.g. the lowest fundamental at 92 cm⁻¹) whereas others (e.g. the strongest signal at 361 cm⁻¹) are strongly Q-branch dominated and narrow. This depends on the depolarisation ratio of the vibration (the ratio of parallel to perpendicular Raman scattering relative to the scattering plane in the scattering geometry employed for the standard spectra¹¹), which ranges continuously from 0 (sharp) to ¾ (broad) for such a C₁-symmetric molecule. It is convenient to subtract the depolarised fraction such that all low frequency modes give rise to sharp transitions. This is shown in Fig. 2 for the low frequency range (upper trace), which will be discussed first, in comparison with a harmonic calculation (lower red trace).

Fig. 2 Polarised fraction of Raman spectra of 2-methoxyethanol. Top trace: experimental spectrum, dominated by gG′T. Bottom traces: calculated harmonic Raman spectra with various masses of the OH hydrogen. The signal at 425 cm⁻¹ can be tentatively assigned to a small fraction of gTT.

The spectrum is dominated by a pair of signals in a region where one expects a backbone stretching mode (ν₂₉) and the OH torsion (ν₂₈). These two strong signals frame a weaker signal at 366 cm⁻¹ which is unexpected in the harmonic approximation. Also, the strong signals themselves do not match well with the harmonic prediction (red trace) in position and relative intensity, indicating a congested anharmonic situation. In contrast, the four weak signals below 300 cm⁻¹ are reproduced very well by the harmonic prediction and are straightforwardly assignable to the backbone and methyl torsion modes ν_33–30.

Because some of these low frequency modes have been addressed before from a microwave perspective, they shall be discussed in some detail despite their weakness. Table 1 lists previous experimental estimates of their fundamental and overtone wavenumbers⁵ together with the wavenumbers obtained in this work below 300 cm⁻¹. The agreement is satisfactory, given that the early microwave estimates had to rely on elegant but approximate reduced dimensionality model treatments of the Boltzmann-populated lowest vibrational states and their torsional splittings, without any direct experimental input on the vibrational fundamentals or quantum-chemical support.

Table 1 Estimates of fundamental and combination mode wavenumbers in cm⁻¹ from previous microwave studies,⁵ in comparison to directly observed transitions in this work

Mode	Microwave	This work
ν 33	89 (10)	92
ν 32	152 (10)	137
2ν33	203 (15)
ν 31	221 (20)	217
ν 33 + ν32	242 (20)
3ν33	283 (20)

---

Our assignment also rests on the observation that overtone and combination transitions are usually much weaker than fundamentals in Raman spectroscopy,³⁸ unless there is some intensity stealing from anharmonic mixing.

The low frequency modes also offer a straightforward explanation for the unexpected weak signal at 366 cm⁻¹, because its position corresponds very closely to the sum of ν₃₃ and ν₃₀. It is thus probably a combination mode which evidently borrows intensity from the two strong signals, as it has more Raman activity than its components. The highest wavenumber signal in Fig. 2 agrees perfectly with the harmonic ν₂₇ prediction. The signal at 425 cm⁻¹ can be explained by a small fraction (≈4%) of a second, energetically higher conformer, which is kinetically trapped and becomes visible through its Raman-intense accordion or overall stretching vibration of the heavy-atom backbone. We will argue below based on the double detection that a gTT assignment is somewhat more likely than an assignment to the achiral tTT conformer.

A simple mass (or equivalently force constant) scaling trick remedies the major remaining problem of the harmonic description. The OH torsion ν₂₈ is the most anharmonic mode due to the low periodic potential barrier and small mass of the moving hydrogen atom.³⁹ By artificially increasing its mass from H in the direction of D, the torsional wavenumber is lowered, whereas all other low frequency modes remain largely unaffected, unless they also carry some torsional character. As the simulation (dots) in steps of 0.05 u shows, this is the case for ν₂₉, which as a consequence is lowered as well and transfers some of its Raman intensity to ν₂₈. For a fictitious mass corresponding to 25% deuterium character (≈1.26 u), the agreement between experiment and theory (purple) is particularly close. Further mass increase leads to an avoided crossing between ν₂₈ and ν₂₉ such that the torsion becomes lower in wavenumber than the backbone motion for D, as it should. The simulation in Fig. 2 actually stops at 50% D character (blue), where the intensity ratio is already inverted compared to 0% D (red).

We are not claiming that this mass tuning is a real physical effect, but it efficiently simulates the exceptional diagonal anharmonicity of the OH torsion, which leads to mode mixing and intensity transfer, as observed in experiment. The size of the harmonic mode coupling to ν₂₉ is of the right order of magnitude, as the comparison to the experimental pattern suggests. We note in passing that the anharmonic shift of the OH stretch (Fig. 1) can also be simulated by fractional deuteration of the terminal hydrogen, but one should not expect the same deuteration degree to be successful, as this is a different anharmonic situation. Indeed, a value of 10% D is needed to reproduce the experimental OH stretching wavenumber in the harmonic approximation.

3.2 Monomer VPT2 treatments

A more physical treatment of the anharmonicity in 2-methoxyethanol might be expected from a VPT2 calculation, which accounts for the correct diagonal and off-diagonal contributions to second order. Fig. 3 shows the results of a Gaussian09 (pale red) and a Gaussian16 GVPT2 (pale blue) calculation, using the (different!) standard settings of the respective VPT2 code (freq = anharmonic, see ESI†). Because anharmonic Raman intensities are not available, harmonic intensities (arbitrarily taken from Turbomole) are used instead. One can see that both standard settings fail in reproducing the experimental spectra, even qualitatively. This is not completely unexpected for large amplitude and low frequency modes, but even the very harmonic backbone vibrations are shifted away from experiment quite substantially. The excellent performance of the harmonic calculation, in particular with terminal H mass scaling, is lost. Especially the delicate mixing between the modes ν₂₈ (362 cm⁻¹ from Gaussian09 VPT2, 377 cm⁻¹ in experiment) and ν₂₉ (359 cm⁻¹ from Gaussian09 VPT2, 361 cm⁻¹ in experiment) is not reproduced. We leave it to others to make the right choice of variational anharmonic coupling parameters and cutoffs to match experiment in a more satisfactory way, and also to compare to other implementations of perturbation theory.^40,41 Again, we note in passing that VPT2 with standard settings is much more successful in reproducing the high frequency OH stretching mode. With Gaussian09, one obtains 3621 cm⁻¹, with Gaussian16 3624 cm⁻¹, both rather close to the experimental value of 3635 cm⁻¹.

Fig. 3 Top trace: two experimental Raman spectra of methoxyethanol under monomer-dominated conditions with varying water content. Water signals are marked with a “w”. Middle trace: harmonic Raman simulation for gG′T. Except for the two strongest, coupled modes, the mean absolute deviation of the five low frequency fundamentals from experiment is 1.1%. Bottom trace: anharmonic VPT2 Raman simulation for gG′T constructed from harmonic Raman intensities and anharmonic wavenumbers from Gaussian09 (pale red) or Gaussian16 (pale blue). A connection to the corresponding harmonic fundamental is drawn as a dashed line. The Raman intensities of combination modes are constructed from anharmonic infrared intensity stealing.

Rewardingly, there is one feature which the VPT2 calculation reproduces reasonably well – the intensity stealing of the ν₃₀ + ν₃₃ combination mode which emerges between the two dominant transitions in the experiment. To illustrate this, the Raman intensity of the combination modes is constructed from anharmonic infrared intensities, assuming that the intensity of the dark combination mode is solely due to anharmonic mixing with the bright fundamentals and not due to intrinsic combination band strength. As for Gaussian09, ν₃₃ + ν₃₀ contributes 5.5% to the sum of anharmonic infrared intensities of vibrations ν₂₈, ν₂₉ and (ν₃₃ + ν₃₀). This is transferred to the Raman intensity by drawing the signal at 5.5% of the sum of harmonic Raman intensities of ν₂₈ and ν₂₉, while subtracting 5.5% from each of the fundamental's intensities in order to preserve the total intensity. For Gaussian16, this amounts to 9.4% and another combination mode (ν₃₀ + ν₃₂ with 20.6% intensity stealing) is predicted to be active as well. Because both Gaussian16 combination modes are far away from unexplained experimental signals, the Gaussian09 default parameters provide a superior description. This is also true for some other low frequency signals.

There is thus a clear ranking in the performance of different B3LYP descriptions of the low frequency Raman spectrum of methoxyethanol: by far the best is the OH mass scaled harmonic prediction, followed by the regular harmonic prediction, which misses strong mode mixing between the anharmonic torsion and a bright backbone mode, for the right reason. VPT2 with standard settings in Gaussian09 systematically and expectedly underestimates the fundamental wavenumbers, probably by removing some of the error compensation between electronic deficiencies in the functional and the harmonic approximation. More surprisingly, it does not recover the experimental splitting between the three resonating states near 370 cm⁻¹. Gaussian16 standard settings for VPT2 remove the similarity between theory and experiment to an unexpected extent below 500 cm⁻¹. Variation of the DFT functional or basis set does not improve the picture. Detailed results for PBE0 and B3LYP with def2-TZVPP and def2-QZVPP basis sets calculated with Gaussian09 and Gaussian16 are given in the ESI.†

3.3 Monomer OH stretching range

As already shown in Fig. 1, dimers of 2-methoxyethanol can form during the expansion. By varying the substance concentration in a controlled manner, experimental conditions with varying ratios of monomer, dimers and higher clusters can be created. This is shown in Fig. 4. At the lowest concentration, there are no signals due to dimers or higher oligomers, but only one strong signal at 3635 cm⁻¹ and a much weaker one at 3656 cm⁻¹. For better comparison between theoretical predictions and experiment, harmonic wavenumbers of OH stretching vibrations from B3LYP/def2-QZVPP are scaled by factors that were used in a recent study on the chemically related ethanediol (monomer 0.95907, dimer 0.963).⁴²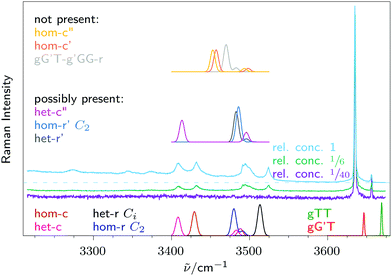

Fig. 4 Three Raman spectra with varying methoxyethanol concentration, with their intensity scaled to the monomer signal at 3635 cm⁻¹. For the blue spectrum a dashed line shows where a horizontal baseline would run. Also included in three simulated traces are calculated Raman spectra for monomers gG′T and gTT, and the energetically lowest 10 dimers, with their frequencies scaled by those obtained from ethanediol (monomer 0.95907, dimer 0.963).⁴² Calculated intensities are not scaled, but dimer signals are drawn at quadrupled width (σ = 3.2 cm⁻¹). Bottom trace: spectra of dimers that can readily be assigned to experimental signals. Middle trace: spectra of dimers that are not necessary to describe the spectrum, but can not be ruled out either. Top trace: spectra of dimers that do not fit the experimental spectrum, therefore they can be excluded.

Now the strong signal at 3635 cm⁻¹ can be readily assigned to gG′T, and the weaker signal at 3656 cm⁻¹ can be assigned to a trace of gTT, which happens to overlap exactly with the symmetric stretching vibration of impurity water. If this signal was to be interpreted purely as gTT it would amount to 8% in the spectrum with lowest concentration, and 4% in the spectra with higher concentration. The latter spectra thus provide an upper limit for the content of this minor conformational isomer. This nicely agrees with the ratio estimated in the low frequency range, where it would be difficult to distinguish between tTT and gTT.

In the OH stretching range, where the predictions for tTT and gTT differ by 22 cm⁻¹, the assignment to gTT is less uncertain. As shown in Table 2 gTT is an energetically high lying conformer, but its presence in the jet expansion can be explained by kinetic trapping. The torsional barriers around both C–O single bonds are sufficiently low to be overcome during the expansion, but the OCCO torsional barrier is too high to be efficiently overcome in a jet expansion.^37,43,44e.g., interconversion between gG′T and its enantiomer is hindered by a barrier in excess of 20 kJ mol⁻¹. Hence the initial population at room temperature is funnelled into a central T and a central G trapping basin by the cooling collisions and only the lowest conformation of each basin survives. Based on harmonic Gibbs energies at 298.15 K including the missing enantiomeric degeneracy for tTT and CCSD(T) electronic energy correction, an initial central T population of 5% may be estimated, in satisfactory agreement with experiment.

Table 2 Relative monomer energies in kJ mol⁻¹ on RIJK-CCSD(F12*)(T*)/cc-pVTZ-F12//MARIJ-B3LYP-D3(BJ,abc)/def2-QZVPP level, without (E_el) and with B3LYP ZPE included (E_ZPE). In parentheses, the results without CCSD(T) correction are given. gG′G and gGG are not stable and are optimised to gG′T and g′GG, respectively

Conformer	E el		E ZPE
gG′T	0	(0)	0	(0)
gG′G′	5.8	(5.5)	6.0	(5.8)
tTT	10.9	(11.0)	9.5	(9.6)
gTT	11.2	(10.8)	10.1	(9.7)
tGT	12.8	(12.2)	11.0	(10.3)
gGT	14.0	(12.8)	12.4	(11.2)
tGG′	13.7	(12.8)	12.7	(11.8)
gGG′	15.6	(14.0)	14.8	(13.1)
gTG′	16.3	(15.6)	15.6	(14.8)
tTG	16.6	(16.3)	15.5	(15.2)
gTG	17.3	(16.6)	16.4	(15.7)
tGG	18.4	(17.4)	17.1	(16.2)
gG′G	—		—
gGG	—		—

---

Based on the predicted relative energies one would expect to observe tTT instead of gTT, because it is slightly more stable, in particular after CCSD(T) correction (Table 2). However, its OH upshift relative to gG′T is predicted at 46 cm⁻¹, which is more than twice the experimental value of 21 cm⁻¹ and in a region where no signal is observed (Fig. 1), whereas gTT is predicted to be upshifted by 24 cm⁻¹ in very good agreement with experiment. Theory thus either fails in predicting the correct energy order or the correct wavenumber splitting, but in either case the deficiency is minor. Microwave spectroscopy, which so far did not detect this minor constituent,^3,45 might provide independent evidence, but for the time being we consider the gTT assignment more likely. It would be interesting, but perhaps also challenging in view of our experimental low frequency findings and the complexity of available relaxation pathways, to refine the gTT/tTT abundance prediction by anharmonic calculations similar to the strategy employed for glycine.⁴⁶ We note that evidence for a central T conformer has been obtained before at room temperature in solution, using Raman and FTIR spectroscopy (see ref. 2 and 47 and work cited therein). The isomer splittings in inert solution are more in line with tTT, but the influence of the solvent prevents a direct comparison to gas phase theory.

3.4 Dimer OH stretching range

Now the four separate dimer signals in Fig. 4 can be discussed in the context of the most stable predicted dimer structures of each type, namely hom(oconfigurational) and het(eroconfigurational) pairings with c(ooperative) or r(eciprocal) hydrogen bond patterns, see the inserts in Fig. 5. Previous solution studies near room temperature were not able to resolve these dimer contributions from each other and from larger aggregates due to thermal broadening.^2,48,49 The signal near 3410 cm⁻¹ can be readily assigned to het-c and the signal at 3430 cm⁻¹ to hom-c. The large downshifts are due to the cooperative and in-phase stretching character of the intermolecular hydrogen bonds. Both het-c and hom-c have a second weak signal at around 3500 cm⁻¹ due to out-of-phase stretching motion, but these are not sufficiently Raman active to fully explain the broad signal in the spectrum. This requires a contribution from non-cooperative dimers.

Fig. 5 Detailed view of the low-frequency range from Fig. 1, with calculated Raman cross sections for the monomer gG′T and the four most stable dimers, with their relative energies given in parentheses in kJ mol⁻¹.

A plausible candidate is hom-r (C₂), for which both OH stretching vibrations are predicted to be in this region with a small vibrational exciton splitting and a stronger Raman intensity of the symmetric combination. The narrow signal at 3520 cm⁻¹ matches better its achiral counterpart het-r (C_i), where only the symmetric component of the excitonic pair is Raman active. Considering solvent and thermal shifts, these two signals fit reasonably well to the broad signal at 3475 cm⁻¹ in CCl₄ solution associated long ago with reciprocal dimers,⁴⁹ but the spectral width in excess of 100 cm⁻¹ covers all four dimers and makes the present study necessary for a discrimination between hydrogen bond topologies and relative chirality. Integration of the three non-overlapping signals and comparison to theoretically predicted cross sections yields approximate relative abundances of het-c, hom-c and het-r (C_i) of 1 : 0.9 : 0.6. The abundances of het-c and hom-c are used to subtract their Raman intensity contribution near 3500 cm⁻¹, providing an estimated Raman intensity of the excitonic hom-r (C₂) doublet. This gives an estimated relative hom-r abundance of 0.7. A purely statistical model of dimerisation, neglecting subtle energy differences in the products (see Table 3) would predict equal abundance of het-c and hom-c and also of het-r (C_i) and hom-r (C₂), which matches experiment (1.0 : 0.9 and 0.6 : 0.7) within experimental and theoretical intensity error. There seems to be a slight (about 3 : 2) statistical preference for unsymmetric (cooperative) aggregation over symmetric (reciprocal) dimerisation.

Table 3 Relative dimer energies in kJ mol⁻¹ on RIJK-CCSD(F12*)(T*)/cc-pVTZ-F12//MARIJ-B3LYP-D3(BJ,abc)/def2-QZVPP level, without (E_el) and with B3LYP ZPE included (E_ZPE). In parentheses, the results without CCSD(T) correction are given. The first four structures are sufficient to explain the main experimental spectral features

Conformer	E el		E ZPE
het-c	0	(0)	0	(0)
hom-r (C2)	2.8	(1.6)	1.4	(0.3)
het-r (Ci)	2.2	(1.9)	1.1	(0.8)
hom-c	2.5	(2.0)	1.5	(0.9)
het-r′	2.9	(2.6)	1.9	(1.6)
hom-r′ (C2)	3.5	(3.0)	2.2	(1.8)
het-c'	4.1	(3.5)	2.9	(2.3)
gG′T-g′GG-r	4.8	(3.5)	4.6	(3.2)
hom-c′	5.8	(5.0)	4.7	(3.9)
hom-c′′	6.0	(5.7)	4.3	(4.1)

---

We note that the energetical driving force from reciprocal to cooperative dimerisation is quite negligible according to our B3LYP calculations (values in parentheses in Table 3), whereas previous B3LYP calculations (without the use of dispersion correction and using smaller basis set)⁴⁸ predicted a cooperative advantage of more than 6 kJ mol⁻¹. After CCSD(T) correction (Table 3), the cooperative advantage increases somewhat, but it is overlaid by a more pronounced stability of het vs. hom complexes, which is not accessible in our experiment due to significant interconversion barriers. There is no experimental evidence for a two-fold symmetry advantage of hom-r over het-r due to its chirality, but even in thermal equilibrium this would be compensated by the rotational symmetry number of hom-r.

While these four dimers are sufficient to explain the experimental spectrum, the presence of further dimers can not be excluded. Such metastable dimers in most of the four gG′T aggregation classes and the most stable one identified with another monomer are also listed in Table 3 together with the most stable one of each class.

Variants of the first three dimers het-c′, het-r′ and hom-r′ (C₂) are predicted to show a very similar Raman spectrum that would fit the experimental spectrum as well. Therefore we do not make any strong claim about their presence or absence. However, some of the energetically less accessible metastable dimers (Fig. 4) are predicted to show OH stretching vibrations at around 3460 cm⁻¹, where no signal is recorded experimentally, which is why major contributions from these dimers can be ruled out.

When the concentration is increased further, new signals arise that are more downshifted than the dimer signals. They result from the formation of trimers and larger oligomers. The seemingly distorted baseline is not an experimental artefact, but instead a true Raman signal due to overlap of very broad, structurally heterogeneous cluster signals, which will not be interpreted in detail. This illustrates how the OH-stretching region can be used as an indicator for the formation of dimers while simultaneously recording a Raman spectrum at the low frequency range.

3.5 Dimer low frequency range

The effects of dimer formation in the low frequency range are less well separated in terms of hydrogen bond topology and relative chirality, but some general trends can be discussed based on Fig. 5. Below 300 cm⁻¹ spectral clutter prevents any detailed analysis, but a trend of increasing dimer signals towards low frequencies can be reproduced. It should be noted that the predicted intensities strongly depend on the assumed vibrational temperature of the low frequency modes and the value implied in the simulation (100 K) is just a rough uniform guess.

At 360 cm⁻¹ a small upshift is predicted for the dimers compared to the monomer, which qualitatively matches an increase of intensity between the two dominant monomer signals. The harmonic agreement is actually better than for the monomer, because the OH torsion is shifted out of the coupling region due to hydrogen bonding. The intense backbone vibration now largely coincides with the low frequency combination mode of the monomer and the latter is no more essential to explain the spectrum. It may or may not persist in the dimers, without major spectral consequences. Therefore, the complex anharmonic coupling pattern which resists a quantitative description for the monomer gives way to a superposition of slightly conformation-dependent, largely harmonic contributions in the dimer. Near 550 cm⁻¹, a small downshift is predicted for the dimers, which corresponds to the growing shoulder in the experimental spectrum but is again hardly resolvable in terms of dimer isomerism.

For the signals at 499 cm⁻¹ and 520 cm⁻¹ no harmonic counterpart is predicted. However, the OH torsional vibrations of the dimers (harmonically predicted at >550 cm⁻¹ and in part even cut off in Fig. 5) are strongly affected by anharmonicity effects on the order of 20%¹⁰ and provide a straightforward explanation for some of these signals. A detailed assignment is not possible without robust anharmonic predictions.

To provide at least a glimpse at this situation, the results of a VPT2 calculation on B3LYP-D3(BJ)/def2-TZVPP using Gaussian16 and C₂/C_i-symmetry for hom/het-r dimers (for which these calculations were feasible) shall be briefly discussed. The predicted anharmonic downshift for the dominant Raman torsional transitions amounts to about 20%. This may be compared to the anharmonic OH stretching wavenumbers, which are about 5% downshifted from their harmonic value in the calculation and underestimate the experimental value by about 2%. The relative magnitude is qualitatively consistent with the harmonic mass scaling needed to bring experiment and theory into agreement for the monomer OH torsion and stretch, respectively. OH torsion is significantly more anharmonic than OH stretching motion in both the monomer and the dimer.

4 Conclusions

In the case of 2-methoxyethanol, dual Raman detection of backbone and hydride stretching vibrations allows for a better discrimination of monomer, dimer and cluster signals in the low frequency range, because the spectral separation is so clear in the OH stretching range. Vice versa, accidental signal overlap in the OH stretching range for a minor conformation can be resolved by monitoring the associated, well-isolated accordion vibration in the low-frequency range.⁵⁰ By ensuring simultaneous recording of both spectral traces for identical expansion conditions, such cross-references are more robust than for alternating probes of the two spectral regions.

In this way, we were able to show that 2-methoxyethanol in the jet expansion is >95% monoconformational. Its two enantiomers form two types of OH⋯O hydrogen-bonded dimers without significant diastereomeric preference except for a slight cooperativity stabilisation in heterochiral pairs. The four dimer species can be unambiguously assigned from their characteristic OH stretching wavenumbers. Cooperative hydrogen bonds are slightly preferred over isolated ones, but dimerisation energy is an unlikely driving force for this subtle preference. It would otherwise prefer cooperative hydrogen bonding and heterochiral pairing according to the theoretical predictions. In this context, the enantiopure (conglomerate) or racemic preference of the crystal form of transiently chiral 2-methoxyethanol would be of interest.

If it were possible to overcome the racemisation and topological isomerisation barriers in future low temperature experiments, 2-methoxyethanol dimers would provide an exquisitely sensitive test for the ability of quantum-chemical methods to describe subtle hydrogen bond energy rankings on the sub-kJ mol⁻¹ scale, because all four dimers are predicted within 1.5 kJ mol⁻¹ and different theoretical approaches disagree in several details. Such relaxation experiments⁴³ are planned using heavier expansion gases and complementary infrared spectroscopy. However, non-cancelling zero-point vibrational energy effects of similar size as chirality and topology factors must be expected due to the strong anisotropy of the underlying OH⋯O hydrogen bonds, such that any experimental energy ranking will be the sum of essential electronic and zero point motion effects.

In combination with ethanediol, 2-methoxyethanol can help to prepare triply hydrogen-bonded mixed dimers which resemble those of ethanediol dimers. The latter show chirality-sensitive metastability with respect to the globally most stable S₄-symmetric quadruply hydrogen-bonded structure⁴² of ethanediol dimer and are of mechanistic interest.

The most interesting benchmarking aspect of 2-methoxyethanol is found in the monomer vibrational spectrum around 400 cm⁻¹. There is a strong mode mixing between the OH torsion and a Raman-intense backbone vibration. This mixing is not present in the harmonic approximation because of the differing diagonal anharmonicities in the two vibrations. Standard vibrational perturbation treatments fail in reproducing the anharmonic resonance, whereas simple harmonic hydrogen mass scaling to mimic the torsional (and OH stretching) anharmonicity provides a formally good match in an otherwise nearly harmonic system. In the dimers, the resonance is efficiently quenched by the upshift of the hydrogen-bonded OH torsions. We hope that this work will trigger further investigations on how to efficiently describe one large amplitude vibration in a bath of nearly harmonic small amplitude vibrations.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 298754033 (SU121/6-1) and 389479699/GRK2455. We thank Enno Meyer for a comprehensive CREST conformer search of the dimers and we thank the institute mechanics and electronics workshops for their support. We acknowledge computer time on the local chemistry cluster – 405832858/INST 186/1294-1 FUGG and the GWDG computer center.

References

1. P. Krueger and H. Mettee, J. Mol. Spectrosc., 1965, 18, 131–140.
2. R. L. Brinkley and R. B. Gupta, Ind. Eng. Chem. Res., 1998, 37, 4823–4827.
3. P. Buckley and M. Brochu, Can. J. Chem., 1972, 50, 1149–1156.
4. W. Caminati, R. Cervellati and Z. Smith, J. Mol. Struct., 1983, 97, 87–92.
5. W. Caminati, R. Meyer and Z. Smith, Chem. Phys., 1986, 110, 67–82.
6. H. Yoshida, K. Takikawa, K. Ohno and H. Matsuura, J. Mol. Struct., 1993, 299, 141–147.
7. H. Yoshida, T. Harada and H. Matsuura, J. Mol. Struct., 1997, 413–414, 217–226.
8. A. Zehnacker and M. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992.
9. P. Asselin, B. Madebène, P. Soulard, R. Georges, M. Goubet, T. R. Huet, O. Pirali and A. Zehnacker-Rentien, J. Chem. Phys., 2016, 145, 224313.
10. F. Kollipost, J. Andersen, D. W. Mahler, J. Heimdal, M. Heger, M. A. Suhm and R. W. Larsen, J. Chem. Phys., 2014, 141, 174314.
11. T. Forsting and M. Suhm, Curry-Jet SETUP, 2019,  DOI:10.6084/M9.FIGSHARE.6395840.V1.
12. A. Kramida and Y. Ralchenko, NIST Atomic Spectra Database, NIST Standard Reference Database 78, 1999.
13. P. Asselin, J. Bruckhuisen, A. Roucou, M. Goubet, M.-A. Martin-Drumel, A. Jabri, Y. Belkhodja, P. Soulard, R. Georges and A. Cuisset, J. Chem. Phys., 2019, 151, 194302.
14. R. S. Barlow, R. W. Dibble and R. P. Lucht, Opt. Lett., 1989, 14, 263.
15. X. Fan, J. Chen and X. Wang, J. Raman Spectrosc., 2019, 50, 563–570.
16. TURBOMOLE V7.4.1 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
17. P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
18. J. C. Slater, Phys. Rev., 1951, 81, 385–390.
19. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
20. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
21. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
24. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
25. M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136–9148.
26. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
27. R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comput. Chem., 2011, 32, 2492–2513.
28. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
29. O. Marchetti and H.-J. Werner, Phys. Chem. Chem. Phys., 2008, 10, 3400.
30. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
31. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
32. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
33. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2013.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016.
36. According to the Turbomole developers, this bug will be fixed in version 7.5, private communication with Uwe Huniar.
37. S. Bocklitz and M. A. Suhm, Z. Phys. Chem., 2015, 229, 1625–1648.
38. D. A. Long, The Raman effect: a unified treatment of the theory of Raman scattering by molecules, Wiley, Chichester New York, 2002.
39. M. Heger, K. E. Otto, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2015, 17, 9899–9909.
40. E. L. Sibert, J. Chem. Phys., 1988, 88, 4378–4390.
41. S. V. Krasnoshchekov, E. V. Isayeva and N. F. Stepanov, J. Phys. Chem. A, 2012, 116, 3691–3709.
42. B. Hartwig, M. Lange, A. Poblotzki, R. Medel, A. Zehnacker and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 1122–1136.
43. R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150.
44. S. Bocklitz and M. A. Suhm, ChemPhysChem, 2017, 18, 3570–3575.
45. S. Shipman, E. Johnson, M. Phillips, E. Riffe and J. Westerfield, Proceedings of the 72nd International Symposium on Molecular Spectroscopy, 2017.
46. V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094.
47. F. P. S. C. Gil, R. Fausto, A. M. Amorim da Costa and J. J. C. Teixeira-Dias, J. Chem. Soc., Faraday Trans., 1994, 90, 689.
48. A. M. Amorim da Costa, A. Duarte and A. Amado, Vib. Spectrosc., 2006, 42, 302–308.
49. L. S. Prabhumirashi and C. I. Jose, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 1545.
50. N. O. B. Lüttschwager and M. A. Suhm, Soft Matter, 2014, 10, 4885–4901.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, auxiliary figures, computational details and results, including an archive of cartesian coordinates. See DOI: 10.1039/d0cp02488k

---