Probing the conformational landscape and thermochemistry of DNA dinucleotide anions via helium nanodroplet infrared action spectroscopy

Abstract

Isolation of biomolecules in vacuum facilitates characterization of the intramolecular interactions that determine three-dimensional structure, but experimental quantification of conformer thermochemistry remains challenging. Infrared spectroscopy of molecules trapped in helium nanodroplets is a promising methodology for the measurement of thermochemical parameters. When molecules are captured in a helium nanodroplet, the rate of cooling to an equilibrium temperature of ca. 0.4 K is generally faster than the rate of isomerization, resulting in “shock-freezing” that kinetically traps molecules in local conformational minima. This unique property enables the study of temperature-dependent conformational equilibria via infrared spectroscopy at 0.4 K, thereby avoiding the deleterious effects of spectral broadening at higher temperatures. Herein, we demonstrate the first application of this approach to ionic species by coupling electrospray ionization mass spectrometry (ESI-MS) with helium nanodroplet infrared action spectroscopy to probe the structure and thermochemistry of deprotonated DNA dinucleotides. Dinucleotide anions were generated by ESI, confined in an ion trap at temperatures between 90 and 350 K, and entrained in traversing helium nanodroplets. The infrared action spectra of the entrained ions show a strong dependence on pre-pickup ion temperature, consistent with the preservation of conformer population upon cooling to 0.4 K. Non-negative matrix factorization was utilized to identify component conformer infrared spectra and determine temperature-dependent conformer populations. Relative enthalpies and entropies of conformers were subsequently obtained from a van’t Hoff analysis. IR spectra and conformer thermochemistry are compared to results from ion mobility spectrometry (IMS) and electronic structure methods. The implementation of ESI-MS as a source of dopant molecules expands the diversity of molecules accessible for thermochemical measurements, enabling the study of larger, non-volatile species.

---

1 Introduction

The complex secondary and tertiary structures adopted by biomolecules rely on a network of intramolecular and solvent–molecule interactions that stabilize the global minimum-energy conformer. For many large biomolecules such as proteins, the progression from disordered chain to folded structure occurs in milliseconds or less, with cooperative folding transitions occurring on a funnel-shaped potential energy surface (PES).¹ These local and global conformational transitions are directed by competing or collaborative non-covalent interactions, including electrostatic attraction or repulsion, cooperative hydrogen bonding, and dispersion interactions. Further experimental and computational studies are required to better analyze and quantify these complex interactions and thereby improve structural analysis and prediction.^2,3

Fundamentally, the conformational PES of biomolecules comprises local energy minima and connecting transition states that form paths leading to the global minimum-energy conformer.^1,4,5 Detailed characterization of the structure of local-minimum conformers and quantification of relative energy can therefore reveal the stabilization provided by specific intramolecular interactions. However, for large biomolecules in the condensed phase, the direct investigation of the conformational landscape is hindered by the myriad of conformational states and local solvent configurations as well as rapid adoption of the stable, fully folded structure.^6,7

To complement direct examination in solution, exemplary biomolecules can be transferred to the gas phase and studied in isolation. These experimental conditions provide more precise control over the preparation and analysis of well-defined species, permitting a comprehensive characterization of the populated conformers.⁸ In addition, the simplified environment of the gas phase facilitates the utilization of electronic structure methods, which can be compared with experimental results to identify the observed conformers and assess the accuracy of various theoretical methods.^9–14

To study electrically neutral biomolecules, samples are typically transferred into vacuum utilizing a supersonic molecular beam that is either seeded with the molecule of interest^15–17 or combined with a laser desorption source.^18–29 The conformational ensemble generated in these sources is then probed using spectroscopic methods such as infrared-ultraviolet (IR-UV) ion dip^22,25 or Fourier transform microwave spectroscopy.^19,26 The majority of experiments on neutral biomolecules in the gas phase have focused on small species, for example di- or tripeptides and nucleobase pairs, although some studies have examined larger peptides^25,28 and peptide aggregates.^30,31 For larger molecules, desorption of intact species becomes increasingly difficult, and incomplete cooling following laser vaporization can lead to substantial spectral congestion.³²

The combination of electrospray ionization and mass spectrometry (ESI-MS) has proven to be the most versatile experimental methodology for the structural interrogation of isolated biomolecular ions. The non-destructive transfer of ions from solution to the gas phase provided by ESI combined with m/z-selective isolation and detection have facilitated the study of an exceptional diversity of species ranging from microsolvated building blocks^33–41 to proteins and polynucleotides.^42–51 Under the appropriate experimental conditions, significant elements of the condensed-phase secondary and tertiary structure can even be preserved upon transfer to vacuum.^46,52–60

To probe the structure of biomolecular ions in vacuum, ESI-MS can be combined with ion mobility spectrometry (IMS), which provides an assessment of an ion's overall shape,^61,62 or infrared (IR) action spectroscopy, which reports on the identity and local environment of individual moieties.^8,24,36,63 IMS-MS has been utilized to elucidate the three-dimensional structure of proteins^46,51,64 and has also been applied to evaluate both static and dynamic conformational ensembles of peptides and nucleotides.^54,65–69 Likewise, IR action spectroscopy of ions at ambient temperature, together with electronic structure methods, has enabled detailed studies of numerous small biomolecular ions, both in isolation^70–74 and as microsolvated complexes.^33,35,75 More recently, cryogenic ion spectroscopy, in which ions are cooled to temperatures as low as 4 K prior to spectroscopic characterization, has emerged as a highly effective approach to probe the conformational landscape of biomolecules in vacuum.^{37,38,76–83} Furthermore, the coupling of IMS and IR action spectroscopy has provided a more comprehensive assessment of the structure of biomolecular ions.^52,84,85

Although the outlined experimental techniques have been successful in identifying low-energy conformers of biomolecules, a quantitative measurement of the conformational thermochemistry (e.g., the relative enthalpy and entropy of conformers) remains challenging. For neutral molecules, direct measurement of isomerization barriers and relative energies has been achieved using stimulated emission pumping spectroscopy in a molecular beam.^86–89 For ionic species, variable-temperature IMS has been employed to determine activation energies and rate constants for conformational transitions of polypeptides and dinucleotides,^90–95 but these methods require large changes in conformation and are not amenable to detecting more subtle structural differences. Additionally, the thermochemistry of microsolvated ion clusters has been measured by temperature-dependent ultraviolet photodissociation spectroscopy⁹⁶ and IR action spectroscopy,⁹⁷ but these approaches are limited by spectral broadening at higher temperatures.

In the last decade, IR spectroscopy of molecules in helium nanodroplets has shown promise as an experimental methodology for the measurement of conformational thermochemistry.^98,99 Molecules captured in helium nanodroplets are cooled to an equilibrium temperature of ca. 0.4 K, and weak interactions with the surrounding helium induce only nominal shifts in band position, making this technique ideal for the acquisition of high-resolution IR spectra.^100–102 Importantly, the rate of cooling following capture is typically faster than the rate of molecular isomerization,^100,101,103 and entrained molecules can be kinetically trapped in local conformational minima. As a result, spectroscopic characterization of a beam of molecule-doped nanodroplets provides a snapshot of the equilibrium conformer population prior to capture. The changes in the infrared spectra with varying pre-capture temperature can be mapped to changes in conformer population, and a van’t Hoff analysis affords a quantitative assessment of relative enthalpies and entropies.^98,99

To date, quantitative thermochemical measurement via helium nanodroplet IR spectroscopy has been applied to small molecules. Skvortsov and Vilesov first investigated conformers of 2-chloroethanol.⁹⁸ Douberly and co-workers further developed this approach to study the conformational thermochemistry of the model dipeptide N-acetylglycine methylamide.⁹⁹ These studies examined electrically neutral species volatilized in a heated cell at temperatures between 300 and 650 K. In the work presented herein, we expand this technique to measure the thermochemistry of biomolecular ions by combining helium nanodroplet IR action spectroscopy with ESI-MS. The integration of a soft ionization method as nanodroplet dopant source significantly broadens the range of species that can be studied using this technique, circumventing the vapor pressure requirements encountered in experiments with neutral dopants. Implementation of a custom-built variable-temperature ion trap enables control of dopant ion temperature prior to capture by helium nanodroplets. This methodology is applied to examine the equilibrium conformer populations of dinucleotide anions, which were previously shown by IMS-MS to exhibit a strong temperature dependence.^65,94,95 Because these systems are too large for the quantitative prediction of IR spectra using electronic structure methods, a non-negative matrix factorization (NMF) algorithm^104–106 is employed to identify the IR spectra of individual conformers from the measured superposition of spectra at each temperature, thereby enabling a quantitative thermochemical analysis.

2 Results and discussion

2.1 IR Spectra with varying pre-pickup ion temperature

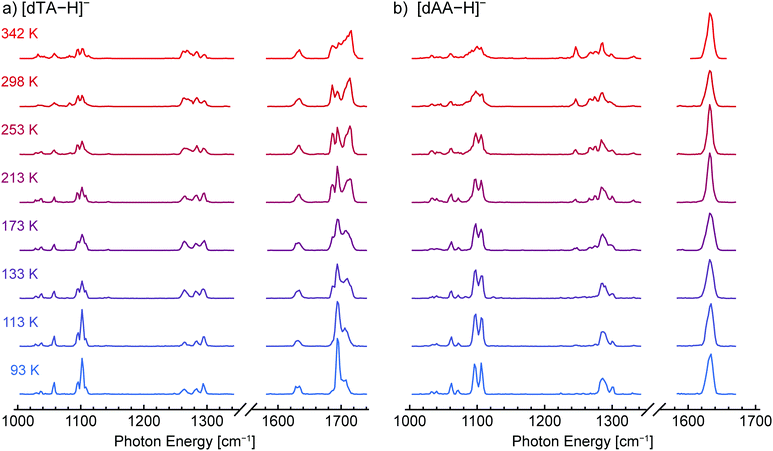
Three DNA dinucleotides anions were examined in this study: [dTA−H]⁻, [dAA−H]⁻, and [dCA−H]⁻, the structures of which are shown in Scheme 1. These species were chosen based upon low activation energies for conformer interconversion reported previously.⁹⁴ Details of the experimental methodology have been detailed in prior publications,^107–110 and a brief overview is provided herein. Gas-phase ions were generated by nanoelectrospray ionization (nESI), transferred to vacuum across an atmospheric pressure interface, isolated using a quadrupole mass filter, and confined in a variable-temperature hexapole ion trap.¹¹¹ At the estimated helium buffer gas pressure of ca. 1 × 10⁻³ mbar, the ions were expected to reach thermal equilibrium with the trap housing within 10 ms.¹¹² Following a pump-out time of 1.5 s for pressure reduction, a pulsed beam of helium nanodroplets was directed through the trap, resulting in ion capture within the nanodroplets. The high kinetic energy of the ion-doped helium nanodroplets enabled them to exit the shallow confining potential of the trap and enter a time-of-flight (TOF) extraction region, where they were irradiated with photons generated by the Fritz Haber Institute free-electron laser (FHI FEL).¹¹³ Sequential absorption of multiple infrared photons resulted in ion release from the helium nanodroplets, and the yield of bare ions detected by TOF MS was monitored as a function of incident photon energy to construct the IR action spectrum.

Scheme 1 Structure of DNA dinucleotide anions examined in this work.

The helium nanodroplet IR action spectra of [dTA−H]⁻ and [dAA−H]⁻ collected at ion trap temperatures between 90 and 350 K are shown in Fig. 1a and b, respectively, and the spectra of [dCA−H]⁻ are shown in Fig. S2 (ESI†). For all three dinucleotide anions, the spectral lines observed between 1080 and 1120 cm⁻¹ are assigned to furanose ring deformation and ribose CO–H stretching modes, and spectral lines between 1240 and 1320 cm⁻¹ are assigned to C–H bending modes and deformation modes of the phosphate moiety.⁶⁹ Weaker spectral lines between 1000 and 1080 cm⁻¹ are attributed to modes comprising CH₂ rocking coupled with furanose ring and phosphate group deformation. Spectral lines corresponding to nucleobase vibrational modes are observed between 1600 and 1740 cm⁻¹, with the RNH₂ scissor and C=O stretching modes of cytosine observed at 1640 and 1668 cm⁻¹, respectively (Fig. S2, ESI†), the RNH₂ scissor mode of adenine observed near 1632 cm⁻¹ (Fig. 1a and b), and the two C=O stretching modes of thymine observed between 1680 and 1720 cm⁻¹ (Fig. 1a).

Fig. 1 Helium nanodroplet infrared action spectra of the DNA dinucleotide anions (a) [dTA−H]⁻ and (b) [dAA−H]⁻ collected with varying ion trap temperature as indicated at left; for both species, the spectra exhibit a strong dependence on ion trap temperature, indicating the kinetic trapping of conformer populations upon cooling to 0.4 K within the helium nanodroplet.

For both [dTA−H]⁻ and [dAA−H]⁻, the acquired spectra show a clear dependence on the ion trap temperature, consistent with kinetic trapping of conformer populations upon cooling to 0.4 K within the helium nanodroplet. In contrast, the IR spectra of [dCA−H]⁻ (Fig. S2, ESI†) show no clear temperature dependence, indicating that the conformer population does not vary with ion trap temperature in the measured range. For [dTA−H]⁻ (Fig. 1a), the most prominent changes in the spectra are observed between 1660 and 1740 cm⁻¹, corresponding to a shift of the thymine C=O stretching modes. A strong temperature dependence is also observed for the C–H bending and phosphate deformation bands between 1240 and 1320 cm⁻¹, and the broadening of the furanose ring deformation bands between 1080 and 1120 cm⁻¹ likewise indicates the population of multiple conformers at elevated trap temperatures.

For [dAA−H]⁻, the bands between 1240 and 1320 cm⁻¹ depend most noticeably on the ion trap temperature, with new lines appearing at 1246, 1267, and 1275 cm⁻¹ as the temperature is increased. Similar to [dTA−H]⁻, the furanose ring deformation bands near 1100 cm⁻¹ become more diffuse at elevated temperatures, reflecting a distribution of oscillator environments arising from multiple conformers. In contrast to the C=O stretching vibrations of thymine in [dTA−H]⁻, the RNH₂ scissor mode of adenine observed at 1632 cm⁻¹ for [dAA−H]⁻ does not exhibit a clear temperature dependence, indicating that the frequency of this mode does not shift strongly in the populated conformers.

2.2 Identification of component spectra by non-negative matrix factorization

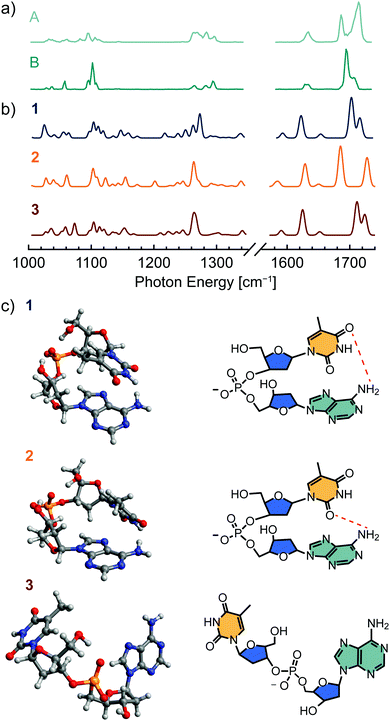
The shifts in band position and intensity in the IR spectra of [dTA−H]⁻ and [dAA−H]⁻ (Fig. 1) reflect the temperature-dependent changes in conformer population, with each measured spectrum comprising a weighted combination of the spectra of individual conformers. To identify these component spectra with minimal user bias, a non-negative matrix factorization (NMF) analysis^104–106 was applied to each data set. As illustrated in Fig. S3 (ESI†), NMF factorizes a data set into basis vectors, which in this case correspond to component spectra, and weighting factors, which here represent the relative abundance of each component. In contrast to other common factorization methods such as principal component analysis, NMF constrains all basis vectors and weighting factors to non-negative values, making it well suited to the analysis of spectroscopic data. Importantly, because the component spectra have an absolute intensity, NMF can also account for conformation-dependent changes in the intensity of spectral lines.

Fig. 2a and Fig. S4a (ESI†) show the component spectra identified by NMF for [dTA−H]⁻ and [dAA−H]⁻, respectively. For both [dTA−H]⁻ and [dAA−H]⁻, a reasonable fit to the experimental data was found by specifying only two component spectra; increasing the number of component spectra led only to redundant band positions for two or more of the identified spectra. Each component spectrum generated by the NMF algorithm is expected to represent the spectrum of a single conformer or family of conformers with similar relative enthalpy and entropy. The lower spectrum in each figure corresponds to an enthalpically favored conformer that is dominant at lower temperatures (B and D, Fig. 2a and Fig. S4a, respectively, ESI†), whereas the upper spectrum corresponds to an entropically favored conformer whose population increases with temperature (A and C, Fig. 2a and Fig. S4a, respectively, ESI†). The NMF spectra for [dTA−H]⁻ (Fig. 2a) are most readily distinguished by the bands in the carbonyl stretching region, which shift from 1695 and 1707 cm⁻¹ in spectrum B to 1686 and 1714 cm⁻¹ in spectrum A. For [dAA−H]⁻, the two NMF spectra (Fig. S4a, ESI†) differ strongly in the region between 1240 and 1320 cm⁻¹, with three bands at 1246, 1267, and 1275 cm⁻¹ present exclusively in the upper spectrum C. These results from NMF are in qualitative agreement with a visual differentiation of infrared bands present at the highest and lowest trap temperatures.

Fig. 2 Non-negative matrix factorization (NMF) of experimental IR spectra of [dTA−H]⁻; component conformer spectra were identified by NMF (a), and the experimental IR spectra (solid lines, b) were fitted as a weighted linear combination of the NMF spectra. The fitted spectra (dashed lines, b) exhibit good agreement with the experimental data.

As introduced in the preceding paragraphs, the NMF algorithm returns not only the spectra of the individual components but also their relative abundance at each temperature. An important question is then the uniqueness of the assignments and in particular the uncertainty in the relative abundance of each component spectrum. To better quantify this uncertainty, the following approach was utilized. At each temperature, combined spectra were generated with the relative amounts of the two component spectra varying from 1% to 99%, and these combined spectra were then fitted to the experimental spectra with only the total intensity as a scaling factor. For each temperature, the goodness of fit was then plotted as a function of the relative amount of the two species, as shown in Fig. S5 and S6 (ESI†). The optimal relative abundance of the two component spectra were obtained at the minima of the goodness of fit curves and are in good agreement with the values obtained directly from the NMF analysis (Tables S1 and S2, ESI†). The uncertainties in the relative abundance were then determined by selecting a threshold above the minimum value of the goodness of fit as detailed in the Methods section. In Fig. 2b and Fig. S4b (ESI†), the best fit spectra (dashed lines) are compared to the experimental spectra (solid lines) for [dTA−H]⁻ and [dAA−H]⁻, respectively. For both data sets, the experimental spectra are well reproduced by the linear combination fit.

2.3 Quantification of conformer thermochemistry

A van’t Hoff analysis was utilized to quantify the thermochemical parameters associated with interconversion between the conformers of the dinucleotide anions. To do so, the equilibrium constant K at each temperature was first calculated from the fitted relative abundance of the NMF component spectra. The natural logarithm of K was then plotted as a function of the inverse temperature 1/T to conform to the van’t Hoff equationwhere R represents the ideal gas constant. The relative enthalpy ΔH and relative entropy ΔS were obtained from the slope and intercept, respectively, of a linear fit to the experimentally derived data. The van’t Hoff plots for [dTA−H]⁻ and [dAA−H]⁻ are shown in Fig. 3a and b, respectively. The increase in the uncertainty of ln(K) measurements with decreasing temperature reflects the nonlinear relationship between the relative conformer population and ln(K) (i.e., as the relative population of a conformer approaches 100%, a small change in population yields a large change in ln(K)). This result can also be visualized in Fig. S5b and S6b (ESI†), which show that the goodness of fit plotted against ln(K) exhibits a shallow minimum for data at low trap temperatures. A linear regression analysis of the van’t Hoff data yielded ΔH and ΔS values of 4.3 ± 2.8 kJ mol⁻¹ and 25 ± 16 J mol⁻¹ K⁻¹, respectively, for [dTA−H]⁻ and values of 5.6 ± 3.2 kJ mol⁻¹ and 26 ± 16 J mol⁻¹ K⁻¹ for [dAA−H]⁻. The similarity of the relative enthalpy and entropy measured for the two dinucleotide anions suggests comparable conformational equilibria in both molecules.

Fig. 3 Quantification of the relative entropy and enthalpy between conformers of [dTA−H]⁻ (a) and [dAA−H]⁻ (b) through a van’t Hoff analysis. Equilibrium constant values K were determined from the weighting factors of the NMF component spectra as detailed in the Methods section. Using the van’t Hoff eqn (1), the linear regression analysis of each data set yields ΔH and ΔS values of 4.3 ± 2.8 kJ mol⁻¹ and 25 ± 16 J mol⁻¹ K⁻¹, respectively, for [dTA-H]⁻ (R² = 0.901) and values of 5.6 ± 3.2 kJ mol⁻¹ and 26 ± 16 J mol⁻¹ K⁻¹ for [dAA-H]⁻ (R² = 0.942).

2.4 Comparison to results from electronic structure methods

To assess the validity of the component spectra identified by NMF and the corresponding thermochemical values, experimental results were compared to spectra and thermochemical parameters calculated by density functional theory (DFT) methods. Candidate structures for each dinucleotide anion were first identified by a force field-based Monte Carlo multiple minimum conformational search and were subsequently optimized with hybrid DFT methods including an empirical dispersion correction. Infrared spectra and thermochemistry were likewise calculated in the harmonic approximation using hybrid DFT methods with empirical dispersion.

The computed structures and IR spectra of the three conformers of [dTA−H]⁻ lowest in free energy are shown in Fig. 4, and additional conformer structures and spectra are shown in Fig. S7 (ESI†). For all investigated dinucleotide anions, the identified low-energy conformers are stabilized by ionic hydrogen bonding between the phosphate moiety and the 5′ and/or 3′ deoxyribose hydroxyl groups. In agreement with previous results from force field-based optimization,⁹⁴ these structures can be grouped into three conformational families: those featuring stacked nucleobases (e.g., structure 1), those with only hydrogen-bonding interactions between nucleobases (e.g., structure 2), and those with an open conformation where the nucleobases are noninteracting (e.g., structure 3). The compact, stacked-nucleobase structures are found to be enthalpically favored, whereas hydrogen-bonded or open structures are entropically favored. The entropic penalty associated with stacked-nucleobase structures can be traced to a blue-shift of the low-frequency vibrational modes that contribute strongly to the calculated entropy.¹²

Fig. 4 Low-energy conformers of [dTA−H]⁻ identified by density functional theory (DFT) methods; the harmonic-approximation IR spectra for each conformer (PBE0-D3/def2-TZVPP, 0.965 scaling factor) are shown in (b), and the spectra derived from NMF analysis of experimental data are shown in (a) for comparison. The corresponding conformer structures are shown in (c) in both a ball-and-stick (left) and structural formula (right) format. Dashed red lines in the structural formula denote hydrogen-bonding interactions.

In addition to nucleobase stacking, the predicted global minimum-energy conformer 1 features a hydrogen bonding interaction between the amine group of adenine and a carbonyl group of thymine. The calculated infrared spectrum of 1 (Fig. 4b) agrees well with the NMF spectrum representing a low-energy conformer (B, Fig. 4a), providing evidence that 1 is the global minimum-energy conformer observed experimentally. In general, predicted bands between 1200 and 1300 cm⁻¹ appear red-shifted with respect to experiment, whereas bands between 1000 and 1200 cm⁻¹ and between 1580 and 1750 cm⁻¹ are not red-shifted with the applied level of theory and scaling factor. The second-most stable structure 2 features a similar backbone conformation to 1 and is distinguished by an exchange of the thymine carbonyl group acting as hydrogen bond acceptor, which yields a hydrogen-bonded rather than stacked-nucleobase conformer. There is qualitative agreement between the predicted IR spectrum of 2 and the NMF spectrum corresponding to a higher-energy conformer (component A, Fig. 4a), although there is a notable discrepancy in the relative intensities of bands in the carbonyl stretching region (1660–1740 cm⁻¹). These differences may arise from the insufficient accuracy of the harmonic approximation or may reflect the contributions of less stable hydrogen-bonded or open conformations such as 3 to the high-energy NMF spectrum.

For the conversion of structure 1 to structure 2, calculation of thermochemical parameters at the PBE0-D3/def2-TZVPP level of theory yields ΔH and ΔS values of 6.9 kJ mol⁻¹ and 16.6 J mol⁻¹ K⁻¹, respectively, in reasonable agreement with the values determined from experiment (Table 1). In contrast, the calculated energies for the transition from structure 1 to structure 3 do not agree well with experiment, with ΔH and ΔS values of 22.4 kJ mol⁻¹ and 61.4 J mol⁻¹ K⁻¹, respectively. Further thermochemical values at multiple levels of theory are listed for six low-energy conformers in Table S3 (ESI†). Taken together, the theoretical results support the experimentally derived thermochemistry and suggest that structures 1 and 2 account for most of the conformer population in the measured temperature range.

Table 1 Experimental and theoretical thermochemistry for interconversion of conformers of [dTA-H]⁻ and [dAA-H]⁻

Conversion	ΔH298^a	ΔS298^b
a Values reported in kJ mol^−1. b Values reported in J mol^−1 K^−1. c Relative energies calculated in the harmonic approximation at the PBE0-D3/def2-TZVPP level of theory.
[dTA-H]^−
1 → 2^c	6.9	16.6
1 → 3^c	22.4	61.4
Experiment	4.3 ± 2.8	25 ± 16
[dAA-H]^−
7 → 9^c	14.5	28.2
7 → 10^c	13.9	23.3
Experiment	5.6 ± 3.2	26 ± 16

---

Shown in Fig. 5 are the computed structures and IR spectra of low-energy conformers of [dAA−H]⁻. Similar to structure 1 of [dTA−H]⁻, the lowest-energy structure 7 exhibits a stacked nucleobase arrangement, which promotes both ionic hydrogen bonding to the phosphate group and inter-nucleobase interactions. The calculated IR spectrum of structure 7 (Fig. 5b) exhibits qualitative agreement with the NMF spectrum corresponding to a low-energy conformer (D, Fig. 5a), with the largest discrepancy in the position and intensity of spectral lines associated with C–H bending and phosphate deformation (1220–1320 cm⁻¹). These differences may arise in part from vibrational anharmonicities that are not accounted for in the calculated IR spectrum. The absence of predicted low-intensity spectral lines in the experimental spectrum may be caused by the nonlinear response of the IR action spectroscopy method employed here, which can lead to a suppression of signal from weak vibrational transitions.^108,114

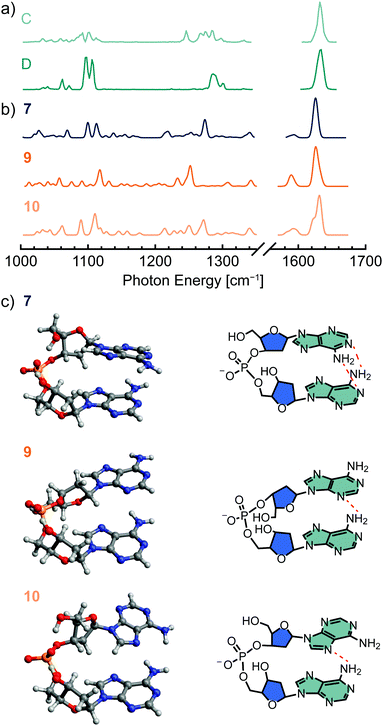Fig. 5 Low-energy conformers of [dAA−H]⁻ identified by density functional theory (DFT) methods; the harmonic-approximation IR spectra for each conformer (PBE0-D3/def2-TZVPP, 0.965 scaling factor) are shown in (b), and the spectra derived from NMF analysis of experimental data are shown in (a) for comparison. The corresponding conformer structures are shown in (c) in both a ball-and-stick (left) and structural formula (right) format. Dashed red lines in the structural formula denote hydrogen-bonding interactions. Structure 8 (Fig. S8, ESI†) differs from structure 7 only by a rotation of the 5′ hydroxyl group about the C4′–C5′ bond.

The second most stable conformer, structure 8 (Fig. S8c, ESI†), is differentiated from structure 7 (Fig. 4c) only by rotation of the 5′ hydroxyl group about the C4′–C5′ bond, and the IR spectra of the two structures are largely comparable (Fig. S8b, ESI†). Therefore, an equilibrium between these two structures is not expected to account for the temperature-dependent changes in the experimental IR spectra. Structures 9 and 10, which exhibit inter-nucleobase hydrogen bonding, were found to yield the best agreement with experimental data, with the computed IR spectra (Fig. 5b) qualitatively reproducing the features of the NMF spectrum representing an entropically favored conformer (C, Fig. 5a) and the computed relative entropies agreeing well with the experimental value (Table 1). However, the predicted relative enthalpies of these conformers are significantly higher than those determined experimentally. Overall, the hydrogen-bonded class of structures were found to have higher relative enthalpies for [dAA−H]⁻ than for [dTA−H]⁻, but the relative enthalpy was found to decrease when utilizing a more augmented basis set (aug-cc-pVTZ vs. def2-TZVPP, Table S4, ESI†).

Low-energy open conformers such as structures 11 and 12 (Fig. S8c, ESI†) were also identified in the conformational search. These structures are enthalpically disfavored but are sufficiently entropically favored to potentially be populated at room temperature. However, although the predicted IR spectra of 11 and 12 (Fig. S8b, ESI†) reproduce some features of the high-temperature NMF spectrum (C, Fig. 5a), including a red-shift of bands in the range of 1220–1320 cm⁻¹ relative to the spectra of lower-energy conformers, the magnitude of the calculated relative enthalpy and entropy values with respect to structure 7 are not consistent with experiment (Table S4, ESI†). Likewise, the relative thermochemistry of the hydrogen-bonded structure 13 (Fig. S8c, ESI†) does not agree well with experiment, in this case because the rigid hydrogen bonding network between the amine groups and a neighboring aromatic nitrogen atom renders the conformer entropically disfavored with respect to structure 7 (Table S4, ESI†). Overall, a conformational equilibrium between the stacked nucleobase structure 7 and the hydrogen-bonded structure 9 or 10 yields the best agreement between experiment and theory. However, the similarity in the computed relative enthalpy of low-energy structures, with most values higher than the experimental results, and the potentially significant error resulting from the calculation of entropy in the harmonic approximation preclude an unambiguous assignment of the conformers observed experimentally.

For [dCA−H]⁻, conformational search indicates that stacked nucleobase conformers are significantly more stable than hydrogen-bonded or open structures (Table S5, ESI†). The predicted global-minimum energy conformer 14 is strongly enthalpically favored over other identified stacked-nucleobase structures (15 and 16), which differ only by rotations of the 5′ hydroxyl group or phosphodiester bond (Fig. S9, ESI†). In addition, the computed relative enthalpy of low-energy open (17, 18) or hydrogen-bonded conformers (19) exceeds 30 kJ mol⁻¹, and the relative entropy is not sufficiently large to favor population of these conformers even at room temperature (Table S5, ESI†). Thus, the results from electronic structure methods are consistent with the experimental results, indicating that only a single conformer or family of structurally similar conformers are populated at all investigated ion trap temperatures.

2.5 Comparison to ion mobility measurements

As noted in the introduction, the DNA dinucleotide anions selected in this work were previously studied by Bowers and co-workers, who reported a temperature-dependent equilibrium between stacked and open structures observed using variable-temperature IMS.^65,94 The barrier heights for conformer interconversion were calculated, and the collision cross section (CCS) values of [dTA−H]⁻ with varying mobility cell temperature were also reported.

To complement these experiments, room-temperature ion mobility measurements were also conducted in this work utilizing a home-built drift-tube instrument.¹¹⁵ As shown in Fig. S10 (ESI†), arrival time distributions (ATDs) were collected with varying drift voltage and were then utilized to calculate the CCS values of each dinucleotide anion. These CCS values are listed in Table 2, where the notation ^DTCCS_He indicates the type of instrument (drift-tube mass spectrometer, DT) and buffer gas (He) used.¹¹⁶

Table 2 Experimental and predicted collision cross section (CCS) values of DNA dinucleotide anions^a

Species	^DTCCSHe	Predicted CCS
a All values reported in square ångströms (Å^2). b Computed as a weighted sum of the calculated CCS values for structures 1 and 2 (Table S3, ESI), with the weighting factors obtained from the NMF conformer population (Table S1, ESI). c Computed as a weighted sum of the calculated CCS values for structures 7 and 10 (Table S4, ESI), with the weighting factors obtained from the NMF conformer population (Table S2, ESI). d Theoretical CCS value of structure 14 (Table S5, ESI).
[dTA−H]^−	140	142 ± 1^b
[dAA−H]^−	145	148 ± 2^c
[dCA−H]^−	130	129.5^d

---

For [dTA-H]⁻, Gidden and Bowers previously reported a CCS value of slightly less than 180 Ų for the compact conformer at 80 K,⁹⁴ in good agreement with the theoretical value of 176.2 Ų computed for structure 1 using the trajectory method (Table S3, ESI†).¹¹⁷ In addition, Gidden and Bowers observed a peak in the 80 K ATD arising from a kinetically trapped conformer with a CCS value of slightly greater than 200 Ų, which was assigned to an open structure. However, the experiments and analysis presented herein did not find evidence for the substantial population of an open conformer. As the experiments of Bowers and co-workers involved kinetic trapping of structures via collisional cooling at high pressure (ca. 5 mbar), they are not necessarily comparable to the IR spectroscopy experiments conducted in this work, in which kinetic trapping was avoided by using a low He buffer gas pressure (ca. 10⁻³ mbar) and thus a slower rate of collisional cooling.

The room-temperature IMS experiments conducted in this work yielded a CCS value of 140 Ų for [dTA−H]⁻, which is approximately 4% smaller than the value of 146 Ų reported previously by Gidden and Bowers.⁹⁴ To compare the experimental CCS value to the results from He nanodroplet IR spectroscopy and DFT calculations, a predicted CCS value was computed as a weighted sum of the calculated CCS values for structures 1 and 2 (Table S3, ESI†), with the weighting factors obtained from the NMF conformer population (Table S1, ESI†). As listed in Table 2, this process gave a predicted CCS value of 142 ± 1 Ų, approximately 1% larger than the experimental value. These results are generally consistent with a conformational equilibrium between structures 1 and 2 and support the thermochemical values obtained by NMF.

IMS analysis of [dAA−H]⁻ yielded a room-temperature CCS value of 145 Ų. A predicted CCS value of 148 ± 2 Ų was calculated as the sum of the theoretical CCS values of structures 7 and 10 (Table S4, ESI†) weighted by the conformer populations from NMF analysis (Table S2, ESI†). The predicted value is more than 2% larger than the measured CCS value, which may indicate that further conformational search is required to find the correct entropically favored structure or that the NMF analysis slightly overpredicts the population of the hydrogen-bonded conformer at room temperature. As with [dTA−H]⁻, the results do not support a substantial population of an extended conformer at room temperature.

Finally, for [dCA−H]⁻, IMS measurements yielded a room-temperature CCS value of 130 Ų, which agrees well with the theoretical CCS value of 129.5 Ų for the low-energy structure 14. Thus, the IMS measurements support the observation from He nanodroplet IR spectroscopy and DFT calculations that only a single conformer or family of structurally similar conformers is populated up to room temperature.

3 Conclusion

We report herein the first combination of ESI-MS and infrared action spectroscopy in helium nanodroplets for the quantitative assessment of molecular thermochemistry through a van’t Hoff analysis. Building upon previous work with neutral molecules,^98,99 we demonstrate that the thermochemical equilibrium of ions held in a variable-temperature ion trap is preserved upon capture and subsequent cooling to 0.4 K in helium nanodroplets. For the dinucleotide anions [dAA−H]⁻ and [dTA−H]⁻, a clear change in the IR spectra with ion trap temperature reveals the shifting of conformer population from enthalpically favored stacked nucleobase structures to entropically favored hydrogen-bonded structures. In contrast, for [dCA−H]⁻, the acquired IR spectra exhibit no dependence on trap temperature, indicating that only a single conformational family is populated in the measured range. For all species measured herein, the results are broadly consistent with results from room-temperature IMS and DFT calculations.

The approach presented herein significantly broadens the diversity of systems whose thermochemical parameters can be measured using the helium nanodroplet capture methodology, permitting analysis of larger, non-volatile molecules that cannot be brought into the gas phase by thermal desorption. The NMF analysis applied here likewise supports the study of larger species, enabling the identification of component IR spectra when affordable electronic structure methods are not sufficiently accurate to provide quantitative prediction. The implementation of IR–IR double resonance measurement schemes^78,101,118 in future experiments will enable the analysis of even more complex systems through the direct experimental identification of component conformer spectra.

4 Methods

4.1 Materials

The dinucleotides dTA, dAA, and dCA were purchased from tebu-bio (Boechout, Belgium) and used without further purification. HPLC-grade water and methanol were purchased from Merck KGaA (Darmstadt, Germany). Stock solutions of dinucleotides were prepared at a concentration of 1 mM in water and were diluted to approximately 25 μM in a 50/50 (v/v) methanol/water solution with 0.1% formic acid for nanoelectrospray ionization (nESI).

4.2 Helium nanodroplet infrared action spectroscopy

The instrumentation utilized for helium nanodroplet infrared action spectroscopy of ions has been described in several previous reports.^107–110 Nanoelectrospray ionization was carried out using pulled glass capillaries fabricated in-house and coated with a Pt/Pd mixture. Ions generated by nESI were transferred to vacuum, mass-selected, and characterized using a modified Q-TOF Ultima mass spectrometer (Waters Corporation, Milford, MA, USA), which was interfaced with custom instrumentation for helium nanodroplet generation, ion capture, and infrared action spectroscopy.

The design of the variable-temperature ion trap utilized in this work was detailed in a prior publication.¹¹¹ A set of hexapole rods operating at a radio frequency (rf) of 1.1 MHz was used to confine the ions radially along the 30 cm length of the trap, and axial confinement was achieved with a static potential of 3–5 V applied to the two endcap electrodes. A temperature-regulated flow of nitrogen through the copper housing of the trap was utilized to adjust trap temperature, which was monitored with two type-K thermocouples mounted to the trap housing and regulated by a Eurotherm 2408 temperature controller (Worthing, United Kingdom). Helium buffer gas was introduced in the trap at an estimated pressure of ca. 1 × 10⁻³ mbar during ion trapping, and the pressure was reduced to ca. 1 × 10⁻⁷ mbar for the transit of helium nanodroplets through the trap.

Helium nanodroplets were generated using an Even-Lavie valve,¹¹⁹ which was operated at 21 K with a backing pressure of ca. 70 bar for the experiments presented herein. Previous measurements under these conditions were found to yield helium nanodroplets containing on average 70 000 He atoms (radius ca. 90 Å) following ion capture.¹⁰⁹ The beam of helium nanodroplets was directed through a beam skimmer and then through the ion trap in the adjacent vacuum chamber, where ion capture occurred. The kinetic energy of the ion-doped helium nanodroplets was sufficiently large to allow escape from the shallow longitudinal potential of the ion trap and transfer to the irradiation region.

In the irradiation region, the beam of ion-doped helium nanodroplets was intersected by coaxially counterpropagating, focused infrared light produced by the Fritz Haber Institute free-electron laser (FHI FEL).¹¹³ The FHI FEL was operated at a macropulse frequency of 10 Hz, with each 10 μs macropulse comprising a series of micropulses ca. 5 ps in length at a repetition rate of 1 GHz. The laser linewidth was approximately 0.5% (full width at half maximum) of the incident photon frequency. Resonant photon absorption by nanodroplet-captured ions was followed by evaporative cooling, yielding a reduction in helium nanodroplet size. The sequential absorption of multiple photons within a macropulse resulted in ion release,^108,120,121 and bare ions were monitored by TOF mass spectrometry (MS). An adaptive IR mirror with variable focal length (A90/70, Kugler GmbH, Salem, Germany) was used to adjust the photon fluence in the irradiation region to yield optimal ion signal. Two designs were utilized in this work for the detection of ions released from helium nanodroplets. In the majority of experiments, the doped nanodroplet beam and infrared radiation were focused between two extraction electrodes, and ions were pulsed directly into a Wiley-McLaren TOF MS.¹⁰⁹ For experiments at 342 K, a new ion detection scheme was implemented in which nanodroplet irradiation occurred within a ring electrode ion guide, and released ions were then pulsed into a high-resolution reflectron TOF MS.¹¹⁰

For each data point in an IR spectrum, ions were first accumulated in the variable-temperature trap for 2.0 s, and the trap pressure was subsequently reduced over 1.5 s. The sequence of nanodroplet generation, ion pickup, IR irradiation, and ion detection was subsequently performed at a rate of 10 Hz for 2.5 s, yielding 25 ion detection events that were averaged in a single mass spectrum. The wavelength of the IR radiation was then incremented by a step of 2 cm⁻¹, and the acquisition cycle was repeated. The integrated ion intensity of the target m/z at each wavelength, with a first-order correction for the laser macropulse energy, was used to construct the IR action spectrum. The spectra presented in this work are the average of three individual IR spectra collected in this manner. Different focal lengths of the adaptive IR mirror were used in the regions of 1000–1350 cm⁻¹ and 1580–1740 cm⁻¹, and the relative intensities were approximated using scans with the same focus in the two ranges.

4.3 Non-negative matrix factorization and spectral fitting

Non-negative matrix factorization (NMF)^104–106 of experimental data sets was performed using a freely available script¹²² implemented in Mathematica 12.0 (Wolfram Research, Oxfordshire, United Kingdom). A linear combination of the two component spectra with variable weighting was then calculated,

L = nA + (1 − n)B (2)

where L is the combined spectrum, n is the weighting factor varying from 0.01 to 0.99 in steps of 0.01, and A and B represent the two NMF component spectra. For each value of n, a scaling factor c was applied to L to minimize the difference to each experimental spectrum, and a χ² goodness-of-fit test was used to assess the optimal value of n,where x_i represents the intensity at a given wavelength in the experimental spectrum, μ_i is the corresponding point in the fit spectrum (i.e., a point in cL), σ_i is the uncertainty associated with each point in the experimental spectrum x_i, and the sum is taken over the N points in each spectrum. The value of σ_i was designated aswhere serves as an approximation of the fluctuations in the signal, and 0.01 × max(x_i) gives an approximation of the baseline uncertainty. For each experimental spectrum, the value of n for which χ² was at a minimum was assigned as the relative conformer population. The uncertainty associated with this population was assigned as the value of n at which χ² reached 1.5 times its minimum value. The uncertainty associated with ln(K) was determined by standard propagation of uncertainty, with the exception of the data for [dAA-H]⁻ at 93 K, where propagation of uncertainty gave an unphysically large error estimate. In this case, the error was assigned directly as the value of ln(K) at which χ² reached 1.5 times its minimum value. Thermochemical values and error estimates were determined from a weighted least squares linear regression analysis of ln(K) vs. 1/T. All analysis was performed using custom scripts in Mathematica 12.0.

4.4 Ion mobility spectrometry-mass spectrometry

Experimental collision cross-sections (CCS) of the dinucleotide anions were obtained on a home-built hybrid drift-tube ion mobility spectrometer-mass spectrometer, described in detail elsewhere.¹¹⁵ Ions were generated by nESI and transferred to and trapped in a radio frequency (rf) entrance funnel. Subsequently, ions were pulsed into a linear drift tube (L = 80.55 cm) filled with ca. 4 mbar helium buffer gas. The ions were guided by a weak electric field (E = 10–15 V cm⁻¹). After exiting the ion mobility cell, ions were selected based on their mass-to-charge ratio (m/z) using a quadrupole mass filter, and their arrival time distribution (ATD) was obtained by recording the time-dependent ion current of the m/z-selected species after release from the ion trap. The ion's drift time was further converted to a rotationally-averaged CCS using the Mason–Schamp equationwhere z is the number of charges on the ion, e the elementary charge, μ the reduced mass, k_B the Boltzmann constant, T the temperature, t_D the drift time, E the electric field, L the drift tube length, N the number density of the buffer gas molecules, and P the buffer gas pressure inside the drift cell (in mbar). ATDs were obtained at drift voltages of 800–1200 V, measured in 50 V-intervals (nine measurements for each dinucleotide anion).

4.5 Conformer search and electronic structure calculations

Initial conformer discovery was carried out using Monte Carlo multiple minimum searches^123,124 with the OPLS3 and AMBER* force fields^125–127 in MacroModel 10.1 as implemented in Maestro 10 (Schrödinger, New York, NY, USA). All identified conformers within 40 kJ mol⁻¹ of the global minimum energy structure were then optimized using DFT methods in the Gaussian 16 software package with default parameter settings.¹²⁸ DFT optimization and thermochemical calculation were first performed at the PBE0-D3/6-311+G(d,p) level of theory,^129–133 and structures with ΔG₂₉₈ values within 15 kJ mol⁻¹ of the lowest-energy structure were further optimized at the PBE0-D3/def2-TZVPP level of theory.^134,135 Finally, the six to seven structures of best match with experiment were also optimized at the PBE0-D3/aug-cc-pVTZ,^136,137 ωB97X-D/def2-TZVPP,¹³⁸ and B3LYP-D3/def2-TZVPP^139,140 levels of theory. Thermochemical parameters were computed in the harmonic approximation without scaling. Conformer collision cross sections in helium drift gas were computed with the trajectory method¹¹⁷ and projection approximation^141–143 as implemented in mobcal.¹⁴⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Prof. Michael T. Bowers for helpful discussions regarding this work and to Petrik Bischoff, Dieter Leese, and Thorsten Nemes in the FHI mechanical workshop for their assistance in designing and implementing the variable-temperature ion trap. D. A. T. acknowledges support from the Alexander von Humboldt Foundation. K. G. thanks the Fonds National de la Recherche (FNR), Luxembourg, for funding the project GlycoCat (13549747). Open Access funding provided by the Max Planck Society.

References

1. K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046.
2. M. Rossi, W. Fang and A. Michaelides, J. Phys. Chem. Lett., 2015, 6, 4233–4238.
3. R. M. Abaskharon and F. Gai, Biophys. J., 2016, 110, 1924–1932.
4. J. D. Bryngelson, J. N. Onuchic, N. D. Socci and P. G. Wolynes, Proteins: Struct., Funct., Genet., 1995, 21, 167–195.
5. A. Sali, E. Shakhnovich and M. Karplus, Nature, 1994, 369, 248–251.
6. W. A. Eaton and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9759–E9760.
7. F. Bergasa-Caceres, E. Haas and H. A. Rabitz, J. Phys. Chem. B, 2019, 123, 4463–4476.
8. A. M. Rijs and J. Oomens, Gas-phase IR spectroscopy and structure of biological molecules, Springer, Switzerland, 2015.
9. F. Schubert, M. Rossi, C. Baldauf, K. Pagel, S. Warnke, G. von Helden, F. Filsinger, P. Kupser, G. Meijer, M. Salwiczek, B. Koksch, M. Scheffler and V. Blum, Phys. Chem. Chem. Phys., 2015, 17, 7373–7385.
10. C. Baldauf and M. Rossi, J. Phys.: Condens. Matter, 2015, 27, 493002.
11. M. Rossi, S. Chutia, M. Scheffler and V. Blum, J. Phys. Chem. A, 2014, 118, 7349–7359.
12. M. Rossi, M. Scheffler and V. Blum, J. Phys. Chem. B, 2013, 117, 5574–5584.
13. T. K. Roy, V. Kopysov, N. S. Nagornova, T. R. Rizzo, O. V. Boyarkin and R. B. Gerber, ChemPhysChem, 2015, 16, 1374–1378.
14. Y. Xie, H. F. Schaefer III, R. Silaghi-Dumitrescu, B. Peng, Q.-S. Li, J. A. Stearns and T. R. Rizzo, Chem. – Eur. J., 2012, 18, 12941–12944.
15. E. G. Robertson and J. P. Simons, Phys. Chem. Chem. Phys., 2001, 3, 1–18.
16. C. J. Chapo, J. B. Paul, R. A. Provencal, K. Roth and R. J. Saykally, J. Am. Chem. Soc., 1998, 120, 12956–12957.
17. R. J. Lavrich, D. F. Plusquellic, R. D. Suenram, G. T. Fraser, A. R. H. Walker and M. J. Tubergen, J. Chem. Phys., 2003, 118, 1253–1265.
18. J. M. Bakker, C. Plützer, I. Hünig, T. Häber, I. Compagnon, G. von Helden, G. Meijer and K. Kleinermanns, ChemPhysChem, 2005, 6, 120–128.
19. J. L. Alonso, C. Pérez, M. Eugenia Sanz, J. C. López and S. Blanco, Phys. Chem. Chem. Phys., 2009, 11, 617–627.
20. E. Gloaguen, B. de Courcy, J. P. Piquemal, J. Pilmé, O. Parisel, R. Pollet, H. S. Biswal, F. Piuzzi, B. Tardivel, M. Broquier and M. Mons, J. Am. Chem. Soc., 2010, 132, 11860–11863.
21. R. J. Plowright, E. Gloaguen and M. Mons, ChemPhysChem, 2011, 12, 1889–1899.
22. E. C. Stanca-Kaposta and J. P. Simons, in Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, 2011 DOI:10.1002/9780470749593.hrs096.
23. C. Cabezas, M. Varela and J. L. Alonso, Angew. Chem., Int. Ed., 2017, 56, 6420–6425.
24. A. M. Rijs and J. Oomens, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer, Cham, Switzerland, 2015, pp. 1–42 DOI:10.1007/128_2014_621.
25. M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612.
26. J. L. Alonso and J. C. López, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer, Cham, Switzerland, 2015, pp. 335–401 DOI:10.1007/128_2014_601.
27. J. M. Bakker, I. Compagnon, G. Meijer, G. von Helden, M. Kabeláč, P. Hobza and M. S. de Vries, Phys. Chem. Chem. Phys., 2004, 6, 2810–2815.
28. A. Abo-Riziq, B. O. Crews, M. P. Callahan, L. Grace and M. S. de Vries, Angew. Chem., Int. Ed., 2006, 45, 5166–5169.
29. J. L. Alonso, I. Peña, J. C. López and V. Vaquero, Angew. Chem., Int. Ed., 2009, 48, 6141–6143.
30. S. Bakels, S. B. A. Porskamp and A. M. Rijs, Angew. Chem., Int. Ed., 2019, 58, 10537–10541.
31. S. Bakels, E. M. Meijer, M. Greuell, S. B. A. Porskamp, G. Rouwhorst, J. Mahé, M.-P. Gaigeot and A. M. Rijs, Faraday Discuss., 2019, 217, 322–341.
32. E. Gloaguen and M. Mons, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer, Cham, Switzerland, 2015, pp. 225–270 DOI:10.1007/128_2014_580.
33. A. Kamariotis, O. V. Boyarkin, S. R. Mercier, R. D. Beck, M. F. Bush, E. R. Williams and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 905–916.
34. D. Liu, T. Wyttenbach and M. T. Bowers, J. Am. Chem. Soc., 2006, 128, 15155–15163.
35. M. F. Bush, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 13544–13553.
36. N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468–494.
37. K. C. Fischer, S. L. Sherman, J. M. Voss, J. Zhou and E. Garand, J. Phys. Chem. A, 2019, 123, 3355–3366.
38. E. Garand, J. Phys. Chem. A, 2018, 122, 6479–6490.
39. J. M. Voss, K. C. Fischer and E. Garand, J. Phys. Chem. Lett., 2018, 9, 2246–2250.
40. T. Wyttenbach and M. T. Bowers, Chem. Phys. Lett., 2009, 480, 1–16.
41. S.-W. Lee, P. Freivogel, T. Schindler and J. L. Beauchamp, J. Am. Chem. Soc., 1998, 120, 11758–11765.
42. D. S. Chorev, L. A. Baker, D. Wu, V. Beilsten-Edmands, S. L. Rouse, T. Zeev-Ben-Mordehai, C. Jiko, F. Samsudin, C. Gerle, S. Khalid, A. G. Stewart, S. J. Matthews, K. Grünewald and C. V. Robinson, Science, 2018, 362, 829–834.
43. B. T. Ruotolo, J. L. P. Benesch, A. M. Sandercock, S.-J. Hyung and C. V. Robinson, Nat. Protoc., 2008, 3, 1139–1152.
44. A. J. R. Heck, Nat. Methods, 2008, 5, 927–933.
45. M. F. Jarrold, Annu. Rev. Phys. Chem., 2000, 51, 179–207.
46. T. Wyttenbach and M. T. Bowers, J. Phys. Chem. B, 2011, 115, 12266–12275.
47. E. S. Baker, N. F. Dupuis and M. T. Bowers, J. Phys. Chem. B, 2009, 113, 1722–1727.
48. N. Khristenko, J. Amato, S. Livet, B. Pagano, A. Randazzo and V. Gabelica, J. Am. Soc. Mass Spectrom., 2019, 30, 1069–1081.
49. M. Porrini, F. Rosu, C. Rabin, L. Darré, H. Gómez, M. Orozco and V. Gabelica, ACS Cent. Sci., 2017, 3(5), 454–461.
50. A. Arcella, J. Dreyer, E. Ippoliti, I. Ivani, G. Portella, V. Gabelica, P. Carloni and M. Orozco, Angew. Chem., Int. Ed., 2015, 127, 477–481.
51. K. B. Shelimov, D. E. Clemmer, R. R. Hudgins and M. F. Jarrold, J. Am. Chem. Soc., 1997, 119, 2240–2248.
52. J. Seo, W. Hoffmann, S. Warnke, M. T. Bowers, K. Pagel and G. von Helden, Angew. Chem., Int. Ed., 2016, 55, 14173–14176.
53. L. Voronina, A. Masson, M. Kamrath, F. Schubert, D. Clemmer, C. Baldauf and T. Rizzo, J. Am. Chem. Soc., 2016, 138, 9224–9233.
54. K. L. Fort, J. A. Silveira, N. A. Pierson, K. A. Servage, D. E. Clemmer and D. H. Russell, J. Phys. Chem. B, 2014, 118, 14336–14344.
55. N. A. Pierson, L. Chen, S. J. Valentine, D. H. Russell and D. E. Clemmer, J. Am. Chem. Soc., 2011, 133, 13810–13813.
56. J. Abi-Ghanem and V. Gabelica, Phys. Chem. Chem. Phys., 2014, 16, 21204–21218.
57. F. Rosu, V. Gabelica, E. De Pauw, R. Antoine, M. Broyer and P. Dugourd, J. Phys. Chem. A, 2012, 116, 5383–5391.
58. R. Ferreira, A. Marchand and V. Gabelica, Methods, 2012, 57, 56–63.
59. F. Rosu, V. Gabelica, L. Joly, G. Gregoire and E. De Pauw, Phys. Chem. Chem. Phys., 2010, 12, 13448–13454.
60. S. Daly, G. Knight, M. A. Halim, A. Kulesza, C. M. Choi, F. Chirot, L. MacAleese, R. Antoine and P. Dugourd, J. Am. Soc. Mass Spectrom., 2017, 28, 38–49.
61. B. C. Bohrer, S. I. Merenbloom, S. L. Koeniger, A. E. Hilderbrand and D. E. Clemmer, Annu. Rev. Anal. Chem., 2008, 1, 293–327.
62. F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281–294.
63. J. Oomens, B. G. Sartakov, G. Meijer and G. von Helden, Int. J. Mass Spectrom., 2006, 254, 1–19.
64. S.-H. Chen and D. H. Russell, J. Am. Soc. Mass Spectrom., 2015, 26, 1433–1443.
65. T. Wyttenbach, N. A. Pierson, D. E. Clemmer and M. T. Bowers, Annu. Rev. Phys. Chem., 2014, 65, 175–196.
66. J. D. Barr, L. Shi, D. H. Russell, D. E. Clemmer and A. E. Holliday, Anal. Chem., 2016, 88, 10933–10939.
67. J. A. Silveira, K. L. Fort, D. Kim, K. A. Servage, N. A. Pierson, D. E. Clemmer and D. H. Russell, J. Am. Chem. Soc., 2013, 135, 19147–19153.
68. C. Bleiholder and M. T. Bowers, Annu. Rev. Anal. Chem., 2017, 10, 365–386.
69. Y. w. Nei, N. Hallowita, J. D. Steill, J. Oomens and M. T. Rodgers, J. Phys. Chem. A, 2013, 117, 1319–1335.
70. J. Oomens, J. D. Steill and B. Redlich, J. Am. Chem. Soc., 2009, 131, 4310–4319.
71. R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2007, 129, 11312–11313.
72. M. F. Bush, J. T. O'Brien, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 1612–1622.
73. M. F. Bush, J. Oomens, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 6463–6471.
74. B. Chiavarino, M. E. Crestoni, S. Fornarini, F. Lanucara, J. Lemaire, P. Maitre and D. Scuderi, Int. J. Mass Spectrom., 2008, 270, 111–117.
75. M. N. Blom, I. Compagnon, N. C. Polfer, G. von Helden, G. Meijer, S. Suhai, B. Paizs and J. Oomens, J. Phys. Chem. A, 2007, 111, 7309–7316.
76. T. R. Rizzo and O. V. Boyarkin, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. M. A. Rijs and J. Oomens, Springer, Cham, Switzerland, 2015, pp. 43–97 DOI:10.1007/128_2014_579.
77. T. R. Rizzo, J. A. Stearns and O. V. Boyarkin, Int. Rev. Phys. Chem., 2009, 28, 481–515.
78. A. B. Wolk, C. M. Leavitt, E. Garand and M. A. Johnson, Acc. Chem. Res., 2014, 47, 202–210.
79. K. C. Fischer, J. M. Voss, J. Zhou and E. Garand, J. Phys. Chem. A, 2018, 122, 8213–8221.
80. N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, Science, 2012, 336, 320–323.
81. N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, J. Am. Chem. Soc., 2010, 132, 4040–4041.
82. N. L. Burke, A. F. DeBlase, J. G. Redwine, J. R. Hopkins, S. A. McLuckey and T. S. Zwier, J. Am. Chem. Soc., 2016, 138, 2849–2857.
83. N. L. Burke, J. G. Redwine, J. C. Dean, S. A. McLuckey and T. S. Zwier, Int. J. Mass Spectrom., 2015, 378, 196–205.
84. M. Z. Kamrath and T. R. Rizzo, Acc. Chem. Res., 2018, 51, 1487–1495.
85. J. Seo, W. Hoffmann, S. Warnke, X. Huang, S. Gewinner, W. Schöllkopf, M. T. Bowers, G. von Helden and K. Pagel, Nat. Chem., 2017, 9, 39–44.
86. J. R. Clarkson, B. C. Dian, L. Moriggi, A. DeFusco, V. McCarthy, K. D. Jordan and T. S. Zwier, J. Chem. Phys., 2005, 122, 214311.
87. J. R. Clarkson, E. Baquero and T. S. Zwier, J. Chem. Phys., 2005, 122, 214312.
88. J. R. Clarkson, E. Baquero, V. A. Shubert, E. M. Myshakin, K. D. Jordan and T. S. Zwier, Science, 2005, 307, 1443–1446.
89. B. C. Dian, J. R. Clarkson and T. S. Zwier, Science, 2004, 303, 1169.
90. B. S. Kinnear, M. R. Hartings and M. F. Jarrold, J. Am. Chem. Soc., 2001, 123, 5660–5667.
91. B. S. Kinnear, M. R. Hartings and M. F. Jarrold, J. Am. Chem. Soc., 2002, 124, 4422–4431.
92. M. R. Hartings, B. S. Kinnear and M. F. Jarrold, J. Am. Chem. Soc., 2003, 125, 3941–3947.
93. A. E. Counterman and D. E. Clemmer, J. Phys. Chem. B, 2003, 107, 2111–2117.
94. J. Gidden and M. T. Bowers, Eur. Phys. J. D, 2002, 20, 409–419.
95. J. Gidden, J. E. Bushnell and M. T. Bowers, J. Am. Chem. Soc., 2001, 123, 5610–5611.
96. H. Ishikawa, I. Kurusu, R. Yagi, R. Kato and Y. Kasahara, J. Phys. Chem. Lett., 2017, 8, 2541–2546.
97. C. T. Wolke, F. S. Menges, N. Tötsch, O. Gorlova, J. A. Fournier, G. H. Weddle, M. A. Johnson, N. Heine, T. K. Esser, H. Knorke, K. R. Asmis, A. B. McCoy, D. J. Arismendi-Arrieta, R. Prosmiti and F. Paesani, J. Phys. Chem. A, 2015, 119, 1859–1866.
98. D. S. Skvortsov and A. F. Vilesov, J. Chem. Phys., 2009, 130, 151101.
99. C. M. Leavitt, K. B. Moore, P. L. Raston, J. Agarwal, G. H. Moody, C. C. Shirley, H. F. Schaefer and G. E. Douberly, J. Phys. Chem. A, 2014, 118, 9692–9700.
100. J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648.
101. M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75.
102. F. Stienkemeier and K. K. Lehmann, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R127–R166.
103. A. Scheidemann, B. Schilling and J. P. Toennies, J. Phys. Chem., 1993, 97, 2128–2138.
104. D. D. Lee and H. S. Seung, Nature, 1999, 401, 788.
105. F. Shahnaz, M. W. Berry, V. P. Pauca and R. J. Plemmons, Inf. Process. Manage., 2006, 42, 373–386.
106. V. P. Pauca, F. Shahnaz, M. W. Berry and R. J. Plemmons, Proceedings of the 2004 SIAM International Conference on Data Mining, Society for Industrial and Applied Mathematics, 2004, pp. 452–456 DOI:10.1137/1.9781611972740.45.
107. A. I. González Flórez, E. Mucha, D.-S. Ahn, S. Gewinner, W. Schöllkopf, K. Pagel and G. von Helden, Angew. Chem., Int. Ed., 2016, 55, 3295–3299.
108. A. I. González Flórez, D.-S. Ahn, S. Gewinner, W. Schöllkopf and G. von Helden, Phys. Chem. Chem. Phys., 2015, 17, 21902–21911.
109. A. I. González Flórez, PhD thesis, Freie Universität Berlin, 2015.
110. E. Mucha, PhD thesis, Radboud University Nijmegen, 2020.
111. D. A. Thomas, E. Mucha, M. Lettow, G. Meijer, M. Rossi and G. von Helden, J. Am. Chem. Soc., 2019, 141, 5815–5823.
112. C. P. Harrilal, A. F. DeBlase, J. L. Fischer, J. T. Lawler, S. A. McLuckey and T. S. Zwier, J. Phys. Chem. A, 2018, 122, 2096–2107.
113. W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. Bluem and A. M. M. Todd, Proc. SPIE, 2015, 9512, 95121L.
114. D. A. Thomas, M. Marianski, E. Mucha, G. Meijer, M. A. Johnson and G. von Helden, Angew. Chem., Int. Ed., 2018, 57, 10615–10619.
115. S. Warnke, J. Seo, J. Boschmans, F. Sobott, J. H. Scrivens, C. Bleiholder, M. T. Bowers, S. Gewinner, W. Schöllkopf, K. Pagel and G. von Helden, J. Am. Chem. Soc., 2015, 137, 4236–4242.
116. V. Gabelica, A. A. Shvartsburg, C. Afonso, P. Barran, J. L. P. Benesch, C. Bleiholder, M. T. Bowers, A. Bilbao, M. F. Bush, J. L. Campbell, I. D. G. Campuzano, T. Causon, B. H. Clowers, C. S. Creaser, E. De Pauw, J. Far, F. Fernandez-Lima, J. C. Fjeldsted, K. Giles, M. Groessl, C. J. Hogan Jr, S. Hann, H. I. Kim, R. T. Kurulugama, J. C. May, J. A. McLean, K. Pagel, K. Richardson, M. E. Ridgeway, F. Rosu, F. Sobott, K. Thalassinos, S. J. Valentine and T. Wyttenbach, Mass Spectrom. Rev., 2019, 38, 291–320.
117. M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086.
118. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273.
119. U. Even, EPJ Tech. Instrum., 2015, 2, 17.
120. X. Zhang, N. B. Brauer, G. Berden, A. M. Rijs and M. Drabbels, J. Chem. Phys., 2012, 136, 044305.
121. S. Smolarek, N. B. Brauer, W. J. Buma and M. Drabbels, J. Am. Chem. Soc., 2010, 132, 14086–14091.
122. A. Antonov, Mathematica for Prediction, https://github.com/antononcube/MathematicaForPrediction, accessed January 13, 2020.
123. G. Chang, W. C. Guida and W. C. Still, J. Am. Chem. Soc., 1989, 111, 4379–4386.
124. M. Saunders, K. N. Houk, Y. D. Wu, W. C. Still, M. Lipton, G. Chang and W. C. Guida, J. Am. Chem. Soc., 1990, 112, 1419–1427.
125. S. J. Weiner, P. A. Kollman, D. T. Nguyen and D. A. Case, J. Comput. Chem., 1986, 7, 230–252.
126. E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296.
127. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666.
128. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
129. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
130. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
131. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
132. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
133. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
134. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
135. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
136. D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371.
137. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
138. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
139. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
140. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
141. G. von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182–8192.
142. E. Mack, J. Am. Chem. Soc., 1925, 47, 2468–2482.
143. T. Wyttenbach, G. von Helden, J. J. Batka, D. Carlat and M. T. Bowers, J. Am. Soc. Mass Spectrom., 1997, 8, 275–282.
144. Martin F. Jarrold Research Group—Software, https://nano.lab.indiana.edu/software/, accessed November 4, 2019, 2019.

---

Footnote

† Electronic supplementary information (ESI) available: Additional IR and mass spectra, IMS ATDs, plots relating to spectral fitting, tabulated thermochemical values, additional structures and spectra from DFT methods, tabulated spectra and structure coordinates. See DOI: 10.1039/d0cp02482a

---