Diagonal Born–Oppenheimer corrections to the ground electronic state potential energy surfaces of ozone: improvement of ab initio vibrational band centers for the 16O3, 17O3 and 18O3 isotopologues†
Received
6th May 2020
, Accepted 31st August 2020
First published on 11th September 2020
Abstract
Mass-dependent diagonal Born–Oppenheimer corrections (DBOCs) to the ab initio electronic ground state potential energy surface for the main 16O3 isotopologue and for homogeneous isotopic substitutions 17O3 and 18O3 of the ozone molecule are reported for the first time. The system being of strongly multiconfigurational character, multireference configuration interaction wave function ansatz with different complete active spaces was used. The reliable DBOC calculations with the targeted accuracy were possible to carry out up to about half of the dissociation threshold D0. The comparison with the experimental band centers shows a significant improvement of the accuracy with respect to the best Born–Oppenheimer (BO) ab initio calculations reducing the total root-mean-squares (calculated–observed) deviations by about a factor of two. For the set of 16O3 vibrations up to five bending and four stretching quanta, the mean (calculated–observed) deviations drop down from 0.7 cm−1 (BO) to about 0.1 cm−1, with the most pronounced improvement seen for bending states and for mixed bending-stretching polyads. In the case of bending band centers directly observed under high spectral resolutions, the errors are reduced by more than an order of magnitude down to 0.02 cm−1 from the observed levels, approaching nearly experimental accuracy. A similar improvement for heavy isotopologues shows that the reported DBOC corrections almost remove the systematic BO errors in vibrational levels below D0/2, though the scatter increases towards higher energies. The possible reasons for this finding, as well as remaining issues are discussed in detail. The reported results provide an encouraging accuracy validation for the multireference methods of the ab initio theory. New sets of ab initio vibrational states can be used for improving effective spectroscopic models for analyses of the observed high-resolution spectra, particularly in the cases of accidental resonances with “dark” states requiring accurate theoretical predictions.
1 Introduction
Accurate potential energy surfaces (PESs) as a function of the nuclear coordinates are prerequisites for reliable theoretical studies of molecular spectroscopy and dynamics. Precise knowledge of vibrational spectra of the ozone molecule is mandatory for spectral analyses because of its importance for atmospheric applications.1–4 Since early ab initio works,5–7 it has been recognized that the ozone molecule possesses quite a complicated electronic structure1,8–11 attracting much attention for the study of both the ground12–14 and excited electronic states.15 On the experimental side, the incentive for in-depth investigations was related to isotopic anomalies in the ozone formation discovered both in the atmosphere and in the laboratory settings.16–21 Over the years this was a motivation for many studies of vibrational energy patterns,12,22–24 infrared spectra of ozone isotopologues (see ref. 24–31, and references therein) and for the dynamics of isotopic exchange reactions.32–38 The non-adiabatic coupling of the electronic states has been discussed in ref. 39 and 40. However, to our knowledge, all available full-dimensional PESs of the ozone molecule1,12–14 have been computed within the framework of the Born–Oppenheimer approximation. The present work aims at the first ab initio calculation of the mass-dependent diagonal Born–Oppenheimer corrections (DBOCs) for the 3-dimensional ozone PES and its use in the calculation of vibrational band centers of the 16O3, 17O3 and 18O3 isotopic species. We show that these contributions permit a significant improvement of vibrational calculations with respect to the most accurate available BO surface.
The paper is structured as follows. The ansatz of DBOC calculations, the wave function model for ozone DBOC and the corresponding computational methodology are described in Section 2. The analytic PES model used for the fit of DBOC electronic energy corrections in terms of nuclear geometries is discussed in Section 3. The subsequent Sections 4 and 5 are devoted to a detailed study of the mass-dependent corrections to vibrational states of the 16O3, 17O3 and 18O3 isotopologues and a comparison to experimental data with the conclusions and discussions in Section 6.
2
Ab initio calculations
2.1 Diagonal Born–Oppenheimer correction
The diagonal Born–Oppenheimer correction (DBOC) is the leading correction term to the Born–Oppenheimer approximation (BOA) first given by Born and Huang:41| |  | (1) |
with Ψ denoting the normalized electronic wave function obtained within the BOA, and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) N being the nuclear kinetic energy operator. The integration in eqn (1) is done over all electronic coordinates represented by r. The DBOC thus takes into account the dependence of the electronic wave function on the nuclear coordinates R, through the calculation of the nuclear kinetic energy contribution. It has the advantage that the adiabatic picture of the BOA is retained so that the notion of a potential energy surface (PES) is still possible. However, the PES becomes dependent on the nuclear mass and will thus be different for, e.g. various isotopologues of the same molecule.
N being the nuclear kinetic energy operator. The integration in eqn (1) is done over all electronic coordinates represented by r. The DBOC thus takes into account the dependence of the electronic wave function on the nuclear coordinates R, through the calculation of the nuclear kinetic energy contribution. It has the advantage that the adiabatic picture of the BOA is retained so that the notion of a potential energy surface (PES) is still possible. However, the PES becomes dependent on the nuclear mass and will thus be different for, e.g. various isotopologues of the same molecule.
The ab initio calculation of ΔEDBOC is possible with analytic derivative techniques. Following the pioneering work of Sellers and Pulay42 and Handy et al.43 who first presented a formula for the evaluation of ΔEDBOC at the Hartree–Fock self-consistent field (HF-SCF) level, several implementations were reported for correlated electronic wave functions.44–52 The work by some of the present authors,51 for the first time, made it possible to calculate ΔEDBOC at various levels of configuration interaction (CI) and coupled cluster (CC) theories via analytic techniques. The implementation of their formulae for the single-reference coupled cluster singles and doubles (CCSD) and configuration interaction singles and doubles (CISD) models, as well as for the Møllet–Plesset perturbation theory are available today in the CFOUR53 program. Using an interface to the MRCC54 program system, calculation of ΔEDBOC is possible not only at any truncation level of single-reference CC and CI theories, but also for various multiconfigurational CI and CC models.55–58 The evaluation of ΔEDBOC requires the explicit calculation of first order wave function response parameters with respect to nuclear coordinates, and it is thus computationally quite demanding.
The DBOC is often regarded as a predominantly one-electron effect, with the contribution of electron correlation being small, even negligible. However, as shown in ref. 51 and 52, this is not at all the case if accurate energy differences are desired, in which the account of electron correlation contribution in DBOC falls easily in the range of the total DBOC effect. Treating DBOC at correlated levels is thus necessary in studies aiming at subchemical (kJ mol−1 or better) accuracy. Fortunately, however, even a relatively low level treatment of dynamic correlation is able to recover a large fraction of the DBOC electron correlation contribution.52 In terms of the basis set size, it is also shown in ref. 51 that the total DBOC can essentially be considered as converged in triple-ζ quality basis sets, but several wavenumbers away from the basis set limit at the double-ζ level. The DBOC corrections have been included in accurate PES calculations for several molecules (see ref. 47, 59–64 and references therein); however, to our knowledge have never been accounted for the ozone molecule.
2.2 Wave function model for ozone DBOC
In the case of ozone, the complexity of the electronic structure makes the use of a multiconfigurational (MC) wave function model necessary, even in points near the equilibrium structure.1,9,10,12 The key step in these calculations is the choice of the reference space, which is in most cases a CAS (complete active space) where the “most important” orbitals (the so called active orbitals) are selected and the “most important” electrons (active electrons) are distributed among them. Technically, CAS is denoted by CAS(m,n), where m is the number of active electrons and n is the number of active orbitals. From the chemical point of view, the model that selects all valence orbitals and electrons as active (often referred to as the full-valence CAS space) is a well-defined, unambiguous, and safe choice even for geometries far from the equilibrium. Unfortunately, this often leads to too large ansätze and therefore some simplification is necessary. In the case of ozone, one intends to use the CAS to generate an expansion space by applying single and double excitations to all determinants of the CAS for the treatment of static and dynamic electron correlation in a single wave function model. This can be done via a multireference CI singles and doubles (MR-CISD) ansatz in the MRCC program. In the case of the DBOC calculation, the implementation is limited to the use of single-reference HF-SCF orbitals, which represent, beyond the limited size of the CAS, one further compromise to be made. Nevertheless, it is reasonable to assume that the electron correlation effects in DBOC can still be well recovered, provided that the CAS is constructed properly.
For ozone, performing the MR-CISD DBOC calculations with a full-valence CAS(18,12) space is not possible, at least not in a reasonably sized basis set. In fact, even a CAS(6,6) space is computationally too demanding if, as discussed in Section 2.1, a triple-ζ quality basis set is to be used.
Such challenges are well known in the field of high-accuracy ab initio thermochemistry,65–74 where sub-kJ mol−1 accuracy is successfully achieved by considering the effect of higher and higher excitations in the electron correlation treatment via energy corrections evaluated in smaller basis sets. This approach, if carried out in the systematic hierarchy of the correlation consistent basis sets of Dunning and co-workers,75–77 was found to work very well not just for contributions to the total energy, but also to structural and spectroscopic parameters.69,74,78 Going along this path with the DBOC surface for ozone, we define the function
| |  | (2) |
which thus accounts for the errors due to the incompleteness of the CAS(4,4) space with respect to the CAS(6,6) one
via a correction term evaluated in the smaller cc-pVDZ basis set. The DBOC surface defined by
eqn (2) is simply referred to as DBOC(6,6) in the subsequent chapters.
2.3 Computational details
DBOC surfaces described by eqn (2), as well as at the simple CAS(4,4)/cc-pVTZ levels were obtained in a set of points corresponding to the sparser grid of the high-accuracy PES from ref. 12. The calculations were performed with the combination of the CFOUR53 and MRCC54 program codes at the MR-CISD level. The CAS(6,6) reference space consisted of the three highest-lying occupied and three lowest-lying unoccupied molecular orbitals of the 2p space (the space of orbitals formed by the 2p atomic orbitals of the oxygen atoms), while in the CAS(4,4) space only the highest- and the lowest-lying two occupied and unoccupied orbitals were included, respectively. Due to the lack of core polarization functions in the cc-pVXZ basis set series, all quantities had to be evaluated with the core electrons excluded from the correlation treatment. All calculations were carried out on the ROMEO 2018 supercomputer facility of the University of Reims Champagne-Ardenne.79
3 Fitting the analytic models to ab initio DBOC values
The summary of calculated ab initio points representing DBOC values at a grid of nuclear geometries for the three symmetric isotopologues of ozone is given in Table 1. Here and below we use the standard convention for abbreviated notations of isotopic species (16O3 = 666, 17O3 = 777, and 18O3 = 888 as specified in the first column), which is generally used in the spectroscopic literature. The upper panel (A) of the table corresponds to the total set of nuclear geometries including those obtained by permutations of r1 and r2 bond distances between the central and terminal oxygen atoms of the ozone molecule. The second column represents the range of the mass-dependent DBOC correction, whereas the range of the Born–Oppenheimer PES values (VBO, ref. 12) corresponding to the grid is given in the fourth column. All energy values for both BO and DBOC are converted to wavenumbers. The number of calculated points is shown in the third column. The last three columns give the extent of the internal bond length (r1, r2) and apex angle (α) coordinates. A graphical overview of the DBOC corrections on the full grid is shown in Fig. 1 for the principal ozone isotopologue 16O3. Differently colored groups of points correspond to two-dimensional cuts of the full PES for fixed values of the apex angle ranging from 100° to 135°.
Table 1 Summary for the calculated DBOC correction at the geometrical grid of ab initio points for the 16O3, 17O3 and 18O3 isotopologues of ozone
| Isotopologue |
ΔEDBOC/cm−1 |
N
points
|
V
BO/cm−1 |
r
1/a.u. |
r
2/a.u. |
∠OOO/deg. |
| (A) Summary of all ab initio points |
| 666 |
−2.152 to 10.157 |
489 |
0–7030.497 |
2.2–3.0 |
2.2–3.0 |
100–135 |
| 777 |
−2.025 to 9.557 |
| 888 |
−1.925 to 9.024 |
|
|
| (B) Summary for the points with VBO ≤ 3000 cm−1 |
| 666 |
−1.597 to 5.422 |
247 |
0–2992.930 |
2.2–2.7 |
2.2–2.7 |
105–130 |
| 777 |
−1.503 to 5.102 |
| 888 |
−1.425 to 4.815 |
|
|
| (C) Summary for the points with 3000 cm−1 < VBO < 4300 cm−1 |
| 666 |
−1.661 to 6.435 |
71 |
3030.595 – 4216.636 |
2.20–2.80 |
2.20–2.80 |
105–130 |
| 777 |
−1.563 to 6.055 |
| 888 |
−1.477 to 5.710 |
 |
| | Fig. 1 Overview of the calculated DBOC geometrical grid points for the 16O3 isotopologue. The ΔEDBOC values are given in the vertical axis in cm−1. Colors refer to distinct values of the OOO apex angle. | |
Several analytical ΔVDBOC(r1,r2,α) models involving polynomial, Gaussian, exponential, inverse hyperbolic functions and their combinations were tested to fit ab initio DBOC values on the full grid of nuclear displacements. At large nuclear displacements from the equilibrium, erratic deviations were obtained for all models. This erratic behavior of the DBOC PES with (ab initio – fit) discrepancies larger than several wavenumbers generally occurred at the energy range above half of the dissociation energy threshold (D0/2), where the experimental value80,81 of D0 is about 8560 cm−1 (as sited in 9) for the 16O3 isotopologue, in terms of the vibrational energy relative to the zero point energy level. Also, for large nuclear displacements corresponding to VBO > D0/2 we have experienced some convergence issues of ab initio DBOC calculations, probably to be attributed to the inappropriateness of single-reference HF-SCF orbitals in these structures.
The most accurate to date ab initio BO PES constructed by Tyuterev et al.12 provided vibrational level calculations with the root mean square deviation of the calculated and observed values (observed–calculated) of about 0.5 cm−1 for low energy vibrations and about 1 cm−1 up to 93% of the dissociation threshold D0. The aim of this work being to improve this accuracy, we focus on the careful investigation of the DBOC corrections at various levels of the theory, at the BO PES range up to 4300 cm−1 that roughly corresponds to D0/2. To this end, our grids of points were chosen significantly denser at the bottom of the potential well near the C2v equilibrium (open geometrical configuration of the ozone molecule). Panels (B) and (C) of Table 1 give the corresponding information for the grids below 3000 cm−1 and between 3000 cm-1 and 4300 cm−1, respectively. In the weighted fit we assigned the largest weights to the points of panel (B), with lower weights for the points presented in panel (C), whereas erratic points beyond D0/2 were excluded from the final fit. Different analytical models gave us quite similar corrections to vibrational levels in this energy range. The final fits were performed with the following analytical form:
| |  | (3) |
where
re and
αe are, respectively, the bond length and angle at the
C2v equilibrium structure, while
a,
b,
c,
C and
dijk are fitted parameters, and
n is the order of the expansion. This functional form accounts for the
C2v symmetry of the PES for the considered isotopic species. The schematic behavior of the PES is described by the Gaussian function of
r1,
r2 and cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α
α, and the finer tuning of the surface is done by means of the symmetrized polynomial part. The asymptotic behavior of the correction is controlled by the “global” Gaussian damping function, which ensures that the correction approaches zero at sufficiently large values of
r and
α, because we do not have reliable
ab initio information at these ranges of geometries. In individual points, DBOC values of the symmetric (666, 777 and 888) isotopologues are related to each other
via a simple scaling factor. Nevertheless, we chose to perform the fit according to
eqn (3) separately for the individual symmetric isotopologues, resulting in different, although very similar parameters of the fitted DBOC correction. The final, isotope-dependent PESs were thus then constructed for each isotopologue separately by adding the fitted DBOC surface to the Born–Oppenheimer BO PES
12 in the form
| | | V(i)(r1,r2,α) = VBO(r1,r2,α) + ΔV(i)DBOC(r1,r2,α) | (4) |
Here (
i) denotes one of the 666, 777, and 888 isotopologues. The fitted models were coded in Python and can be found in the ESI.
† The residuals of the fit are collected in
Fig. 2 for the principal isotopologue and in
Table 2 for all three symmetric isotopologues. The deviations of the fit of the analytical Δ
VDBOC PES (
eqn (3)) to Δ
EDBOC values lie mostly within 0.2 cm
−1 for the configuration energies below 2500 cm
−1, and within the 1 cm
−1 corridor for configurations with energies in the 2500–4300 cm
−1 range, as shown on the lower panel of
Fig. 2.
 |
| | Fig. 2 DBOC values for the geometrical grid points of Fig. 1 (top panel) and fit residuals (bottom panel) for the analytical representation (eqn (3)) plotted for the 666 isotopologue for configurations with potential energy VBO up to 4000 cm−1. | |
Table 2 Summary of the fits of the ab initio DBOC by the model defined by eqn (4)
| Isotopologue |
N
points
|
RMS residual/cm−1 |
Mean residual/cm−1 |
| (A) Total fit summary of the points from (B) and (C) sections |
| 666 |
318 |
0.2892 |
0.1026 |
| 777 |
318 |
0.2740 |
0.0975 |
| 888 |
318 |
0.2606 |
0.0928 |
|
|
| (B) Fit summary for the points with EBO ≤ 3000 cm−1 |
| 666 |
247 |
0.1039 |
0.0021 |
| 777 |
247 |
0.0985 |
0.0020 |
| 888 |
247 |
0.0946 |
0.0019 |
|
|
| (C) Fit summary for the points with 3000 < EBO < 4300 cm−1 |
| 666 |
71 |
0.5795 |
0.4508 |
| 777 |
71 |
0.5492 |
0.4284 |
| 888 |
71 |
0.5217 |
0.4077 |
The behaviour of the DBOC correction with respect to stretching and bending coordinates are, respectively, presented on Fig. 3 and 4. The differences between isotopologues are, as shown by the similarity of the respective curves, very minor. Qualitatively we observe the following properties of the DBOC mass-dependent contributions to the ozone PES. First, they produce somewhat different effects for bond length (stretching) and bond angle (bending) vibrations. The angular dependence of the DBOC correction is quite monotonic, nearly linear in the neighborhood of the BO minimum (Fig. 3). This mainly results in a shift of the equilibrium configuration towards smaller αe values. On the contrary, the adiabatic correction changes the shape of the PES for the stretching degree of freedom r1 (Fig. 4), but in a different manner, depending on the instantaneous value of the other bond length r2. Second, the variation of masses in the case of homogeneous isotopic substitutions 666 → 777 and 666 → 888 produce quite systematic small shifts having nearly the same shape in terms of the coordinate-dependence. It is thus not surprising that DBOC contributions to vibrational levels of 16O3, 17O3, and 18O3, as shown in the next sections, move into the same direction of always being positive.
 |
| | Fig. 3 Fitted DBOC corrections – relative to the equilibrium geometry – along the O–O bond stretching coordinates for the different symmetric isotopologues of ozone. | |
 |
| | Fig. 4 Fitted DBOC corrections – relative to the equilibrium geometry – along the O–O–O bending coordinate for the different symmetric isotopologues of ozone. | |
4
Ab initio vibrational energy levels of 16O3 with DBOC corrections
Global variational methods permit nowadays converging vibrational basis set calculations to the precision of 0.01 or 0.001 cm−1 for small and medium sized molecules,12,24,61–64,82–84 at least in the energy range up to the half of the dissociation threshold. This level of precision is necessary for this study to clearly distinguish the contributions beyond the BOA because the best published ab initio BO ozone calculations12,24,85 were already quite accurate with the average (observed–calculated) discrepancies of 0.5 cm−1 to 1 cm−1. As often recommended, atomic masses were used for calculations of vibrational levels in order to partly account for non-adiabatic contributions.86 Considering non-adiabatic contributions at least in this approximate manner seems to be particularly important if the adiabatic correction via DBOC is also included. This is due to the fact that if the latter shifts the vibrational levels in the positive direction, the usually negative shift by non-adiabatic effects87–89 is, at this level of accuracy, required to avoid the general overestimation of the levels. Here vibrational levels were computed in this range using the same variational technique as described in our previous work,12 the only difference being the inclusion of the mass-dependent DBOC correction to the BO PES according to eqn (4). We consider the effect of vibrational DBOC corrections at two levels of the theory: using complete active spaces CAS(4,4) and CAS(6,6) as described in Section 2. The corresponding results for vibrational levels with the VBO + ΔVDBOC PESs will be denoted as DBOC(4,4) and DBOC(6,6) for the sake of brevity. The vibrational levels of the ozone molecule are usually assigned in terms of normal mode quantum numbers (v1, v2, and v3) where v1 stands for symmetric vibration, v2 for the bending mode and v3 for the anti-symmetric vibration. Due to molecular symmetry and approximate coincidence of harmonic frequencies (ω1 ≈ ω3), they are organized in a series of so called “stretching polyads”.3,22,25 These polyads, denoted as Pb,s, are defined as sets of nearby vibrational states| | | P0,1 = {(100),(001)}, P0,2 = {(200),(101),(002)},…, Pb,1 = {(1b0),(0b1)},…, Pb,s = ∪{(v1bv3)}, | (5) |
where the ∪ symbol stands for a union over v1, and v3 under the condition that v1 + v3 = s, which is the total quantum number of stretching vibrations, and b = v2 is the bending quantum number. The intra-polyad couplings among vibrational modes in ozone are dominated by Darling–Dennison resonances and rotation–vibration couplings by Coriolis resonances.3,25
It is instructive to investigate the DBOC contributions to individual vibrational levels, as well as to the general polyad-by-polyad picture. An improvement of ab initio calculations for vibrational band centers with respect to observations is clearly seen in Tables 3 and 4 where the observed minus calculated discrepancies are collected together with the root-mean-squares (RMS) and mean deviations for various types of polyads. Note that, because of limitations in the construction of accurate DBOC surfaces described in Section 3, all comparisons in this work are given up to energies about VBO = D0/2.
Table 3 Comparison of vibrational levels computed from ab initio potential energy surfaces at various levels of theory with experimental data for the 16O3 ozone isotopologue
| Ta |
O = Obs.b |
(v1v2v3)c |
O-BOd |
O-DBOC(4,4)e |
O-DBOC(6,6)e |
Polyad |
|
Symmetry type of the upper vibrational state.
Observed centers for rovibrational bands (v1v2v3) – (000), collected in (ref. 12, 22, 25, 26 and references therein) up to 4300 cm−1.
(v1v2v3) – normal mode vibrational quantum numbers.
Discrepancies between observed band centers and those calculated using the currently most accurate BO PES of ref. 12.
Discrepancies between observed band centers and those computed with DBOC corrections using CAS(n,n). All values are in cm−1.
|
| Bending states |
| A |
700.93 |
(010) |
0.25 |
0.00 |
−0.02 |
P
1,0
|
| A |
1399.27 |
(020) |
0.51 |
0.02 |
−0.02 |
P
2,0
|
| A |
2094.99 |
(030) |
0.76 |
0.06 |
0.00 |
P
3,0
|
| A |
2787.9 |
(040) |
0.88 |
−0.02 |
−0.10 |
P
4,0
|
| A |
3478. |
(050) |
0.9 |
−0.14 |
−0.24 |
P
5,0
|
|
|
| RMS |
0.71 |
0.07 |
0.12 |
|
| Mean |
0.66 |
−0.02 |
−0.08 |
|
|
|
| Stretching polyads |
| B |
1042.08 |
(001) |
0.53 |
0.34 |
0.09 |
P
0,1
|
| A |
1103.14 |
(100) |
0.01 |
−0.20 |
−0.24 |
P
0,1
|
| A |
2057.89 |
(002) |
1.01 |
0.58 |
0.27 |
P
0,2
|
| B |
2110.78 |
(101) |
0.16 |
−0.27 |
−0.48 |
P
0,2
|
| A |
2201.16 |
(200) |
0.23 |
−0.16 |
−0.23 |
P
0,2
|
| B |
3046.09 |
(003) |
1.21 |
0.58 |
0.30 |
P
0,3
|
| A |
3083.70 |
(102) |
0.10 |
−0.54 |
−0.74 |
P
0,3
|
| B |
3186.41 |
(201) |
0.54 |
−0.07 |
−0.29 |
P
0,3
|
| A |
3289.93 |
(300) |
0.42 |
−0.12 |
−0.18 |
P
0,3
|
| A |
4001.31 |
(004) |
0.78 |
0.01 |
−0.18 |
P
0,4
|
| B |
4021.85 |
(103) |
−0.26 |
−1.05 |
−1.18 |
P
0,4
|
| A |
4141.42 |
(202) |
1.16 |
0.37 |
0.17 |
P
0,4
|
| B |
4250.22 |
(301) |
0.56 |
−0.19 |
−0.36 |
P
0,4
|
| A |
4370.3 |
(400) |
1.0 |
0.40 |
0.36 |
P
0,4
|
|
|
| RMS |
0.70 |
0.44 |
0.45 |
|
| Mean |
0.54 |
−0.02 |
−0.19 |
|
|
|
| Mixed bending-stretching polyads |
| B |
1726.52 |
(011) |
0.82 |
0.42 |
0.15 |
P
1,1
|
| A |
1796.26 |
(110) |
0.21 |
−0.23 |
−0.29 |
P
1,1
|
| B |
2407.94 |
(021) |
1.11 |
0.51 |
0.23 |
P
1,1
|
| A |
2486.58 |
(120) |
0.40 |
−0.24 |
−0.33 |
P
2,1
|
| A |
2726.11 |
(012) |
1.33 |
0.74 |
0.41 |
P
1,2
|
| B |
2785.24 |
(111) |
0.36 |
−0.26 |
−0.49 |
P
1,2
|
| A |
2886.18 |
(210) |
0.37 |
−0.22 |
−0.31 |
P
1,2
|
| B |
3086.22 |
(031) |
1.40 |
0.63 |
0.33 |
P
3,1
|
| A |
3173.93 |
(130) |
0.57 |
−0.25 |
−0.36 |
P
3,1
|
| A |
3390.92 |
(022) |
1.65 |
0.90 |
0.58 |
P
2,2
|
| B |
3455.82 |
(121) |
0.54 |
−0.24 |
−0.48 |
P
2,2
|
| A |
3568.07 |
(220) |
0.51 |
−0.27 |
−0.38 |
P
2,2
|
| B |
3698.29 |
(013) |
1.55 |
0.78 |
0.50 |
P
1,3
|
| A |
3739.43 |
(112) |
0.27 |
−0.51 |
−0.71 |
P
1,3
|
| B |
3849.91 |
(211) |
0.66 |
−0.10 |
−0.33 |
P
1,3
|
| A |
3859. |
(140) |
1.64 |
0.65 |
0.53 |
P
4,1
|
|
|
| RMS |
0.98 |
0.49 |
0.42 |
|
| Mean |
0.84 |
0.14 |
−0.06 |
|
|
|
| Total |
| RMS |
0.84 |
0.43 |
0.41 |
|
| Mean |
0.69 |
0.05 |
−0.12 |
|
Table 4 Observed–calculated statistics for vibrational polyads of 16O3 isotopologue at various levels of ab initio theory
| Polyad |
E
p
|
RMS (observed–calculated) |
Mean (observed–calculated) |
| BOb |
DBOC(4,4) |
DBOC(6,6) |
BOb |
DBOC(4,4) |
DBOC(6,6) |
| All values are in cm−1. Mean value of the vibrational energy of a given polyad, including all the experimentally known levels of Table 3 with the same notations. As computed with the most accurate to date ab initio BO PES.12 |
|
P
1,0
|
700.93 |
0.25 |
0.00 |
0.02 |
0.25 |
0.00 |
−0.02 |
|
P
0,1
|
1072.61 |
0.38 |
0.28 |
0.18 |
0.28 |
0.07 |
−0.08 |
|
P
2,1
|
1399.27 |
0.51 |
0.02 |
0.02 |
0.51 |
0.02 |
−0.02 |
|
P
1,1
|
1761.39 |
0.60 |
0.33 |
0.23 |
0.52 |
0.09 |
−0.07 |
|
P
3,0
|
2094.99 |
0.77 |
0.06 |
0.00 |
0.77 |
0.06 |
0.00 |
|
P
0,2
|
2123.28 |
0.60 |
0.38 |
0.35 |
0.47 |
0.05 |
−0.15 |
|
P
2,1
|
2447.26 |
0.84 |
0.40 |
0.28 |
0.76 |
0.13 |
−0.05 |
|
P
4,0
|
2787.90 |
0.88 |
0.02 |
0.10 |
0.88 |
−0.02 |
−0.10 |
|
P
1,2
|
2799.17 |
0.83 |
0.47 |
0.41 |
0.69 |
0.09 |
−0.13 |
|
P
3,1
|
3130.07 |
1.07 |
0.48 |
0.35 |
0.99 |
0.19 |
−0.02 |
|
P
0,3
|
3151.53 |
0.70 |
0.40 |
0.44 |
0.57 |
−0.04 |
−0.23 |
|
P
2,2
|
3471.60 |
1.05 |
0.56 |
0.49 |
0.91 |
0.13 |
−0.09 |
|
P
5,0
|
3478.00 |
0.91 |
0.14 |
0.24 |
0.91 |
−0.14 |
−0.24 |
|
P
1,3
|
3813.58 |
0.89 |
0.48 |
0.48 |
0.75 |
−0.01 |
−0.21 |
|
P
4,1
|
3859.00 |
1.64 |
0.65 |
0.53 |
1.64 |
0.65 |
0.53 |
|
P
0,4
|
4157.02 |
0.83 |
0.54 |
0.58 |
0.66 |
−0.09 |
−0.24 |
|
P
3,2
|
4184.38 |
0.86 |
0.15 |
0.32 |
0.85 |
−0.07 |
−0.26 |
|
P
2,3
|
4346.73 |
1.86 |
0.97 |
0.71 |
1.86 |
0.97 |
0.71 |
As it is shown in Table 4 and in Fig. 5, the inclusion of DBOC both at the CAS(4,4) and CAS(6,6) levels yields significant improvements with respect to the most accurate available BO calculations,12 with quite similar results for both active spaces.
 |
| | Fig. 5 Mean energy deviations for successive vibrational Pb,s polyads of 16O3 between observations (OBS) and the ab initio calculation (vertical scale) versus the average polyad energies (EP, on the horizontal scale). Blue line: BO approximation,12 green line: BO + DBOC(4,4) and red line: BO + DBOC(6,6). | |
 |
| | Fig. 6 Root-mean-squares (RMS) energy deviations for successive vibrational Pb,s polyads of 16O3 between observations (OBS) and the ab initio calculation (vertical scale) versus the average polyad energies (EP, on the horizontal scale). Blue line: BO approximation,12 green line: BO + DBOC(4,4) and red line: BO + DBOC(6,6). | |
The improvement is particularly pronounced for the bending states as follows from the first part of Table 3 and Fig. 7: the (observed–calculated) errors decrease by an order of magnitude when accounting for the DBOC(4,4) or DBOC(6,6) terms in the PES. For the (010), (020) and (030) bending vibrational states the BO + DBOC(6,6) surface provides nearly experimental accuracy as shown in Fig. 7. Note, that higher very weak bending bands 4ν2 and 5ν2 have not been directly observed. The corresponding vibrational states (040) and (050) were considered in experimental analysis of the spectra as “dark” ones3 and have been evaluated indirectly90 from resonance perturbations of certain rovibrational transitions. The experimental accuracy for these “dark” states roughly corresponds to the number of digits given in the first column of Table 3. Consequently, a part of the (observed–calculated) deviations for (040) and (050) have to be attributed to the experimental uncertainty. The same comments apply to other vibrational states that have been considered as “dark” ones in experimental spectral analyses. This is the case of (400) and (140) in Table 3, for which we give only one decimal digit for the virtually “observed” values. In such cases, the (observed–calculated) deviations can be impacted by experimental uncertainties.
 |
| | Fig. 7 Energy deviations between observations and the ab initio calculation (vertical scale) versus the vibrational energy (Evib) for the bending states of 16O3. Blue line: BO approximation,12 green line: BO + DBOC(4,4), and red line: BO + DBOC(6,6). | |
For a general view on the energy contributions involving stretching bands we plot in Fig. 8 and 9 the mean and RMS (observed–calculated) deviations for the Gs band systems where s = v1 + v3 is a total stretching quantum number. Here the Gs band system gathers all Pb,s polyads with various bending quantum numbers b = v2 using the same cut-off as in Tables 3 and 4:
| |  | (6) |
where the ∪ symbol stands for a union over all
b = v
2 values included in
Tables 3 and 4. The mean vibrational energy of the
Gs groups of levels denoted as
Emean(
Gs) is shown along the horizontal scales of
Fig. 8 and 9, in cm
−1.
 |
| | Fig. 8 Mean energy deviations for Gs groups (eqn (6)) of vibrational levels of 16O3 between observations and ab initio calculations (vertical scale) with the increasing total stretching quantum number s. The average Gs energies are given at the horizontal scale. Blue line: BO approximation,12 green line: BO + DBOC(4,4), and red line: BO + DBOC(6,6). | |
 |
| | Fig. 9 Root-mean-squares (RMS) energy deviations for Gs groups (eqn (6)) of vibrational levels of 16O3 between observations and ab initio calculations (vertical scale) with the increasing total stretching quantum number s. The average Gs energies are given at the horizontal scale. Blue line: BO approximation,12 green line: BO + DBOC(4,4), and red line: BO + DBOC(6,6). | |
In a sense, these plots of Fig. 8 and 9 give hints concerning the errors of the calculation averaged over bending quantum numbers as a function of excitations of the stretching vibrational modes. Again, it is seen that the inclusion of the adiabatic corrections globally improves the set of stretching vibrational levels for the considered energy cut-off. The BO + DBOC(4,4) and BO + DBOC(6,6) show again very similar performance with the average (observed–calculated) discrepancies below 0.5 cm−1.
5
Ab initio vibrational energy levels of 18O3 and 17O3 isotopologues with DBOC corrections
As the next step of this work, let us now examine the mass dependence of the DBOC corrections in vibrational levels for the homogeneous isotopic substitutions 18O3 and 17O3. Experimental spectra of 18O3 have been recorded and analyzed in a series of works (see ref. 26, 91–94, and references therein). There are significantly less observed bands than for the main ozone species, but the general trends in the improvement of the calculations are quite similar. For this reason, we only quote in this case the (observed–calculated) values and statistics at our highest level DBOC calculations using CAS(6,6). The comparisons with the observed band centers are presented in Tables 5 and 6, as well as in Fig. 10–13. As for 16O3, we obtain the most pronounced improvement for the bending states – by more than an order of magnitude – even though the observed series is much shorter, limited here to the ν2 and 2ν2 bands. The inclusion of DBOC corrections also permitted significantly more accurate results for mixed bending-stretching polyads: the RMS (observed–calculated) deviation drops down from 0.93 cm−1 to 0.39 cm−1, while the mean (observed–calculated) deviation is reduced from 0.77 cm−1 to no more than 0.04 cm−1. For pure stretching polyads the improvement is less pronounced, possibly because the errors obtained with the BO PES12 in the v1 band and in the combination series v1 + nv3 were already very small (between 0.02 cm−1 to 0.2 cm−1). This applies for 16O3, 18O3 and 17O3 species as well. However, the general trend in improvement of the total (observed–calculated) statistics is clearly confirmed by the reported comparisons for all three isotopologues.
Table 5 Comparison of vibrational band centers computed from BO and BO + DBOC(6,6) ab initio potential energy surfaces with experimental data for the 18O3 ozone isotopologue
| Ta |
O = Obs.b |
(v1v2v3)c |
O-BOd |
O-DBOC(6,6)e |
Polyad |
|
Symmetry type of the upper vibrational state.
Observed centers for rovibrational bands (v1v2v3) – (000), collected in (ref. 26, 91–94 and references therein) up to 4300 cm−1.
(v1v2v3) – normal mode vibrational quantum numbers.
Discrepancies between observed band centers and those calculated using the currently most accurate BO PES of ref. 12.
Discrepancies between observed band centers and those computed with DBOC corrections using CAS(n,n). All values are in cm−1.
|
| Bending states |
| A |
661.49 |
(010) |
0.21 |
−0.02 |
P
1,0
|
| A |
1320.70 |
(020) |
0.44 |
−0.01 |
P
2,0
|
|
|
| RMS |
0.34 |
0.02 |
|
| Mean |
0.33 |
−0.01 |
|
|
|
| Stretching polyads |
| B |
984.82 |
(001) |
0.48 |
0.10 |
P
0,1
|
| A |
1041.56 |
(100) |
0.02 |
−0.20 |
P
0,1
|
| A |
1946.46 |
(002) |
0.93 |
0.28 |
P
0,2
|
| B |
1995.97 |
(101) |
0.14 |
−0.42 |
P
0,2
|
| A |
2078.37 |
(200) |
0.20 |
−0.20 |
P
0,2
|
| B |
2883.86 |
(003) |
1.14 |
0.34 |
P
0,3
|
| A |
2919.96 |
(102) |
0.11 |
−0.64 |
P
0,3
|
| B |
3012.54 |
(201) |
0.45 |
−0.27 |
P
0,3
|
| B |
3813.41 |
(103) |
0.19 |
−1.02 |
P
0,4
|
| B |
4019.29 |
(301) |
0.48 |
−0.33 |
P
0,4
|
|
|
| RMS |
0.54 |
0.46 |
|
| Mean |
0.38 |
−0.24 |
|
|
|
| Mixed bending-stretching polyads |
| B |
1631.72 |
(011) |
0.73 |
0.15 |
P
1,1
|
| A |
1696.17 |
(110) |
0.18 |
−0.25 |
P
1,1
|
| B |
2275.97 |
(021) |
0.97 |
0.22 |
P
2,1
|
| A |
2348.33 |
(120) |
0.35 |
−0.28 |
P
2,1
|
| A |
2578.99 |
(012) |
1.22 |
0.41 |
P
1,2
|
| B |
2634.24 |
(111) |
0.32 |
−0.41 |
P
1,2
|
| A |
2725.88 |
(210) |
0.33 |
−0.27 |
P
1,2
|
| B |
3269.22 |
(121) |
0.47 |
−0.42 |
P
2,2
|
| B |
3502.23 |
(013) |
1.45 |
0.52 |
P
1,3
|
| B |
4117.32 |
(023) |
1.72 |
0.70 |
P
2,3
|
|
|
| RMS |
0.93 |
0.39 |
|
| Mean |
0.77 |
0.04 |
|
|
|
| Total |
| RMS |
0.73 |
0.41 |
|
| Mean |
0.55 |
−0.09 |
|
Table 6 Observed–calculated statistics for ab initio calculations of vibrational polyads of the 18O3 isotopologue including DBOC corrections
| Polyad |
E
p
|
RMS (observed–calculated) |
Mean (observed–calculated) |
| BOb |
DBOC(6,6) |
BOb |
DBOC(6,6) |
| All values are in cm−1. Mean value of the vibrational energy of a given polyad, including all the experimentally known levels of Table 5 with the same notations. As computed with the most accurate to date ab initio BO PES.12 |
|
P
1,0
|
661.49 |
0.21 |
0.01 |
0.21 |
−0.01 |
|
P
0,1
|
1013.19 |
0.34 |
0.16 |
0.25 |
−0.06 |
|
P
2,0
|
1320.70 |
0.44 |
0.01 |
0.44 |
−0.01 |
|
P
1,1
|
1663.94 |
0.53 |
0.21 |
0.45 |
−0.05 |
|
P
0,2
|
2006.93 |
0.55 |
0.31 |
0.42 |
−0.11 |
|
P
2,1
|
2312.15 |
0.73 |
0.25 |
0.66 |
−0.03 |
|
P
1,2
|
2646.37 |
0.75 |
0.37 |
0.62 |
−0.09 |
|
P
0,3
|
2938.79 |
0.71 |
0.44 |
0.57 |
−0.19 |
|
P
2,2
|
3269.22 |
0.47 |
0.41 |
0.47 |
−0.41 |
|
P
1,3
|
3502.23 |
1.45 |
0.52 |
1.45 |
0.52 |
|
P
0,4
|
3916.35 |
0.36 |
0.76 |
0.14 |
−0.68 |
|
P
2,3
|
4117.32 |
1.72 |
0.70 |
1.72 |
0.70 |
 |
| | Fig. 10 Mean energy deviations for successive vibrational Pb,s polyads of 18O3 between observations and ab initio calculation (vertical scale) versus average polyad energies (EP, on the horizontal scale). Values for both axes are given in cm−1. Blue line: BO approximation,12 and red line: BO + DBOC(6,6). | |
 |
| | Fig. 11 Root-mean-squares (RMS) deviation between observed 18O3 polyads and ab initio calculations (vertical scale) versus mean values EP of vibrational Pb,s polyads (horizontal scale). Values for both axes are given in cm−1. Blue line: BO approximation,12 and red line: BO + DBOC(6,6). | |
 |
| | Fig. 12 Mean energy deviations for Gs groups (eqn (6)) of vibrational levels of 18O3 between observations and the ab initio calculation (vertical scale) with the increasing total stretching quantum number s. The average Gs energies are given on the horizontal scale. Blue line: BO approximation,12 and red line: BO + DBOC(6,6). | |
 |
| | Fig. 13 Root-mean-squares (RMS) energy deviations for Gs groups (eqn (6)) of vibrational levels of 18O3 between observations and ab initio calculations (vertical scale) with the increasing total stretching quantum number s. The average Gs energies are given on the horizontal scale. Blue line: BO approximation,12 and red line: BO + DBOC(6,6). | |
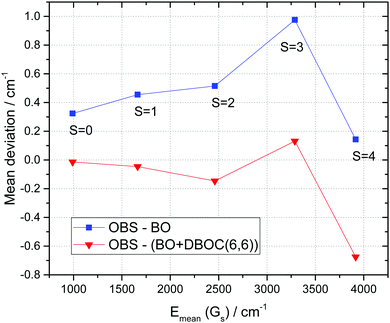
For the rare 17O3 isotopologue only four centers of stretching bands have been deduced from analyses of experimental spectra in ref. 27 and 95. Again, we obtained an improvement for the RMS and mean (observed–calculated) values by accounting for the DBOC corrections as given in Table 7.
Table 7 Comparison of vibrational band centers computed from BO and BO + DBOC(6,6) ab initio potential energy surfaces with experimental data for the 17O3 ozone isotopologue
| Ta |
O = Obs.b |
(v1v2v3)c |
O-BOd |
O-DBOC(6,6)e |
Polyad |
|
Symmetry type of the upper vibrational state.
Observed centers for rovibrational bands (v1v2v3) – (000), from ref. 27 and 95 up to 4300 cm−1.
(v1v2v3) – normal mode vibrational quantum numbers.
Discrepancies between observed band centers and those calculated using the currently most accurate BO PES of ref. 12.
Discrepancies between observed band centers and those computed with DBOC corrections using CAS(n,n). All values are in cm−1.
|
| Bending states |
| B |
1012.16 |
(001) |
0.50 |
0.09 |
P
0,1
|
| A |
1070.95 |
(100) |
0.02 |
−0.22 |
P
0,1
|
| A |
1999.56 |
(002) |
0.83 |
0.14 |
P
0,2
|
| B |
2050.82 |
(101) |
0.16 |
−0.44 |
P
0,2
|
|
|
| RMS |
0.49 |
0.26 |
|
| Mean |
0.38 |
−0.11 |
|
6 Discussion and conclusions
In this work, we computed mass-dependent diagonal Born–Oppenheimer corrections to the ab initio electronic ground state potential energy surface for the main 16O3 isotopologue of the ozone molecule, as well as for homogeneous isotopic substitutions 17O3 and 18O3, which had not been investigated previously. The goal was to improve the accuracy of the PES with respect to the currently best results for vibrational states obtained in the BO approximation,12 which was on average about 0.5 cm−1 for low vibrations and about 1 cm−1 for the entire set of observed bands. The other objective was to investigate the mass-dependence of the PESs in the 16O3, 17O3, and 18O3 isotopic series and the corresponding impact on vibrational states. As the ozone molecule is known to be a strongly multireference system, we used to this end an MR-CISD ansatz in the MRCC program with CAS(4,4) and CAS(6,6) actives spaces. The DBOC contributions to electronic energies were then fitted to an analytical form in terms of nuclear displacements from the equilibrium. Finally, the vibrational band centers were computed using the nuclear motion variational method using the BO + DBOC PESs for the three species and compared to available experimental values. The focus of this work was the energy range of up to about D0/2 – half of the dissociation threshold – for the reasons explained in Sections 2 and 3 and summarized below. The conclusions are the following. The DBOC corrections in all the considered CAS versions produced positive contributions to vibrational energies, which are quite similar for 16O3, 17O3 and 18O3 ranging from 0.3 cm−1 up to 1.1 cm−1 and gradually increasing in absolute values with increasing number of vibrational quanta. The comparison with experimental band centers shows a significant improvement of the accuracy with respect to the best BO calculations. For the low vibrational range the BO calculations of ref. 12 using atomic masses were generally slightly underestimated with positive (observed–calculated) deviations. The DBOC(4,4) and DBOC(6,6) corrections modify this in the right direction, providing a remarkable reduction in the errors of the calculation as is clearly seen in Tables 3 and 4 and on Fig. 7–9. The account of DBOC produces the most pronounced improvement for bending states and for mixed bending-stretching polyads. In the case of (010), (020) and (030) states the errors are reduced by more than one order of magnitude: the (observed–calculated) deviation for BO + DBOC(6,6) is below 0.02 cm−1 (Fig. 7 and Table 3), approaching nearly the experimental accuracy. Similar improvement occurs for the bending states of 18O3 (Table 5). For combination states with three vibrational quanta, the DBOC corrections bring ab initio calculations to the mean errors below 0.2 cm−1 as shown in Tables 3–6 and Fig. 5–13. To our knowledge, this level of ab initio accuracy has not been obtained so far for molecules with such a complex multireference electronic structure as ozone. Note that DBOC(4,4) appears to be competitive with DBOC(6,6) and provides even slightly better results for some polyad series. Possibly, the convergence with respect to the size of the CAS in the considered energy range was approached. Let us remember, however, that full variational electronic energy calculations with the triple-ζ quality basis set were only performed with the the CAS(4,4) space. CAS(6,6) calculations were only possible using an approximate incremental scheme (eqn (2)) using a double-ζ basis set, a novel approach clearly justified by the results. It is curious to note in Fig. 5 and 8 that the mean (observed–calculated) deviations would tend to almost zero values if one takes the average of DBOC(4,4) and DBOC(6,6) – green and red lines in Fig. 5 and 8 – which, although possibly no more than a fortunate coincidence, can be interpreted as a hint that the incremental formulation defined in eqn (2) might be overestimating the effect of the larger CAS to a certain extent.
Anyway, in terms of the mean (observed–calculated) deviations, the improvement is quite striking. In total, they drop down from 0.69 cm−1 (BO) to 0.05 cm−1 (DBOC(4,4)) or to 0.12 cm−1 (DBOC(6,6)) for the considered range including the set of 16O3 vibrations in Table 3 with five bending and four stretching quanta. For 18O3, the mean (observed–calculated) deviations drop down from 0.55 cm−1 (BO) to −0.09 cm−1 (DBOC(6,6)). This means that DBOC corrections almost remove the systematic BO errors in vibrational levels below EBO = D0/2. The remaining (observed–calculated) scattering naturally increases with energy that could be attributed to both BO and to DBOC uncertainties in the analytical models, as well as to individual vibrational modes. However, the DBOC corrections generally reduce the total RMS (observed–calculated) deviations by a factor of two or so: from 0.84 cm−1 to 0.41 cm−1 for 16O3, from 0.73 cm−1 to 0.41 cm−1 for 18O3 and from 0.49 cm−1 to 0.26 cm−1 for 17O3. The present results, including the full sets of calculated vibrational states provided in the ESI† with (observed–calculated) statistics, can be used for improving the effective spectroscopic models for analyses of observations. The Fortran code for the BO PES12 is available in the S&MPO (“Spectroscopy and Molecular Properties of Ozone”) database and information system,26 while the Python code for the DBOC correction surface and calculated vibrational levels are provided in the ESI† of this paper.
Despite significant progress,3,26 some ozone bands below EBO = D0/2 have not yet been fully analyzed. For complicated coupled band systems belonging to overlapping polyads,96ab initio values are often used for constraining parameters, which are missing from direct measurements. Typically, “dark” states are fixed to theoretically predicted values. Their accuracy has thus a considerable impact on spectral perturbations induced by accidental rovibrational Coriolis or Darling–Dennison resonances.3,25,26,85 This is particularly important for rare species like 18O3 and 17O3, where much fewer spectral assignments are yet available. As explained in Sections 2 and 3, reliable DBOC calculations with the targeted accuracy were possible to carry out up to about half of the dissociation threshold – at least using the currently feasible ab initio ansatz with accessible computational facilities. Above this energy corresponding to ≈4300 cm−1, ab initio calculations were not well converged for certain nuclear geometries and/or the fits to analytic models yielded erratic series with outliers much larger than 1 cm−1 despite the use of several trial functions. Although this could potentially happen due to an insufficiently large active space or a too low cardinal number for the atomic basis set, we consider the limitation to the use of single reference Hartree–Fock Self-Consistent-Field orbitals in the DBOC calculations as the major obstacle to achieving higher accuracy. Note that the most accurate to date BO PES,12 which we used in this work, had been constructed using CAS(18,12) with complete active space self-consistent field (CASSCF) orbitals in the X = 5,6 → ∞ extrapolated complete basis set limit. In addition, it accounted for a supplementary correction12 due to a simultaneous optimization of 13 excited electronic states considered by Dawes et al.,10 which had a significant impact on the shape of the PES10,11,14 and the dynamics35,37,38 in the range near the transition state towards the dissociation. Another challenge is to account for non-adiabatic interactions among 27 electronic states corresponding to the same dissociation limit39,97 and for possible effects of the topological phase8 related to conical intersections.40 At a high energy range, the effects of the delocalization of the vibrational state wave functions among three potential wells also have to be accounted for.98 However, the reported results at the present state of the art already provide an encouraging accuracy validation for the multireference methods of the ab initio theory, at least in the range of up to four vibrational quanta. In future works, we plan to address the above issues, as well as to extend DBOC calculations to non-homogeneous isotopic species of ozone.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
This work has been supported by the Russian Science Foundation RNF grant no. 19-12-00171. A. T. acknowledges the support from CNRS for the research stay at Reims University.
References
- R. Siebert, P. Fleurat-Lessard, R. Schinke, M. Bittererová and S. C. Farantos, J. Chem. Phys., 2002, 116, 9749–9767 CrossRef CAS.
-
J.-M. Flaud and J. Orphal, Handbook of High-resolution Spectroscopy, John Wiley & Sons, Ltd, Chichester, UK, 2011 Search PubMed.
- A. Barbe, S. Mikhailenko, E. Starikova, M.-R. De Backer, V. Tyuterev, D. Mondelain, S. Kassi, A. Campargue, C. Janssen, S. Tashkun, R. Kochanov, R. Gamache and J. Orphal, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 172–190 CrossRef CAS.
- L. Costantino, J. Cuesta, E. Emili, A. Coman, G. Foret, G. Dufour, M. Eremenko, Y. Chailleux, M. Beekmann and J.-M. Flaud, Atmos. Meas. Tech., 2017, 10, 1281–1298 CrossRef CAS.
- S. S. Xantheas, G. J. Atchity, S. T. Elbert and K. Ruedenberg, J. Chem. Phys., 1991, 94, 8054–8069 CrossRef CAS.
- A. Banichevich, S. D. Peyerimhoff and F. Grein, Chem. Phys., 1993, 178, 155–188 CrossRef CAS.
- T. Müller, S. S. Xantheas, H. Dachsel, R. J. Harrison, J. Nieplocha, R. Shepard, G. S. Kedziora and H. Lischka, Chem. Phys. Lett., 1998, 293, 72–80 CrossRef.
- P. Garcia-Fernandez, I. B. Bersuker and J. E. Boggs, Phys. Rev. Lett., 2006, 96, 163005 CrossRef.
- F. Holka, P. G. Szalay, T. Müller and V. G. Tyuterev, J. Phys. Chem. A, 2010, 114, 9927–9935 CrossRef CAS.
- R. Dawes, P. Lolur, J. Ma and H. Guo, J. Chem. Phys., 2011, 135, 18–22 CrossRef.
- V. G. Tyuterev, R. Kochanov, A. Campargue, S. Kassi, D. Mondelain, A. Barbe, E. Starikova, M. R. De Backer, P. G. Szalay and S. Tashkun, Phys. Rev. Lett., 2014, 113, 143002 CrossRef.
- V. G. Tyuterev, R. V. Kochanov, S. A. Tashkun, F. Holka and P. G. Szalay, J. Chem. Phys., 2013, 139, 134307 CrossRef.
- M. Ayouz and D. Babikov, J. Chem. Phys., 2013, 138, 164311 CrossRef.
- R. Dawes, P. Lolur, A. Li, B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 201103 CrossRef.
- S. Y. Grebenshchikov, Z.-W. Qu, H. Zhu and R. Schinke, Phys. Chem. Chem. Phys., 2007, 9, 2044 RSC.
- K. Mauersberger, Geophys. Res. Lett., 1981, 8, 935–937 CrossRef CAS.
- M. H. Thiemens and J. E. Heidenreich, Science, 1983, 219, 1073–1075 CrossRef CAS.
- K. Mauersberger, B. Erbacher, D. Krankowsky, J. Günther and R. Nickel, Science, 1999, 283, 370–372 CrossRef CAS.
- H. Hippler, R. Rahn and J. Troe, J. Chem. Phys., 1990, 93, 6560–6569 CrossRef CAS.
- C. Janssen, J. Guenther, D. Krankowsky and K. Mauersberger, Chem. Phys. Lett., 2003, 367, 34–38 CrossRef CAS.
- M. H. Thiemens, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17631–17637 CrossRef CAS.
- V. Tyuterev, S. Tashkun, P. Jensen, A. Barbe and T. Cours, J. Mol. Spectrosc., 1999, 198, 57–76 CrossRef CAS.
- S. Ndengué, R. Dawes, X. G. Wang, T. Carrington, Z. Sun and H. Guo, J. Chem. Phys., 2016, 144, 074302 CrossRef.
- D. Lapierre, A. Alijah, R. Kochanov, V. Kokoouline and V. Tyuterev, Phys. Rev. A, 2016, 94, 042514 CrossRef.
- J. Flaud and R. Bacis, Spectrochim. Acta, Part A, 1998, 54, 3–16 CrossRef.
- Y. L. Babikov, S. N. Mikhailenko, A. Barbe and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2014, 145, 169–196 CrossRef CAS.
- D. Consalvo, A. Perrin, J. Flaud, C. Camypeyret, A. Valentin and C. Chardonnet, J. Mol. Spectrosc., 1994, 168, 92–98 CrossRef CAS.
- E. Starikova, A. Barbe, M.-R. De Backer-Barilly, V. Tyuterev, S. Tashkun, S. Kassi and A. Campargue, Chem. Phys. Lett., 2009, 470, 28–34 CrossRef CAS.
- D. Mondelain, A. Campargue, S. Kassi, A. Barbe, E. Starikova, M.-R. De Backer and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2013, 116, 49–66 CrossRef CAS.
- V. G. Tyuterev, A. Barbe, D. Jacquemart, C. Janssen, S. N. Mikhailenko and E. N. Starikova, J. Chem. Phys., 2019, 150, 184303 CrossRef.
- E. Starikova, A. Barbe and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2019, 232, 87–92 CrossRef CAS.
- R. Schinke, S. Y. Grebenshchikov, M. Ivanov and P. Fleurat-Lessard, Annu. Rev. Phys. Chem., 2006, 57, 625–661 CrossRef CAS.
- C. A. M. Brenninkmeijer, C. Janssen, J. Kaiser, T. Röckmann, T. S. Rhee and S. S. Assonov, Chem. Rev., 2003, 103, 5125–5162 CrossRef CAS.
- A. L. Van Wyngarden, K. A. Mar, J. Quach, A. P. Q. Nguyen, A. A. Wiegel, S.-Y. Lin, G. Lendvay, H. Guo, J. J. Lin, Y. T. Lee and K. A. Boering, J. Chem. Phys., 2014, 141, 064311 CrossRef.
- Z. Sun, D. Yu, W. Xie, J. Hou, R. Dawes and H. Guo, J. Chem. Phys., 2015, 142, 174312 CrossRef.
- T. R. Rao, G. Guillon, S. Mahapatra and P. Honvault, J. Phys. Chem. A, 2015, 119, 11432–11439 CrossRef CAS.
- G. Guillon, P. Honvault, R. Kochanov and V. Tyuterev, J. Phys. Chem. Lett., 2018, 9, 1931–1936 CrossRef CAS.
- C. H. Yuen, D. Lapierre, F. Gatti, V. Kokoouline and V. G. Tyuterev, J. Phys. Chem. A, 2019, 123, 7733–7743 CrossRef CAS.
- M. Tashiro and R. Schinke, J. Chem. Phys., 2003, 119, 10186–10193 CrossRef CAS.
- A. Alijah, D. Lapierre and V. Tyuterev, Mol. Phys., 2018, 8976, 1–11 Search PubMed.
-
M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press, Oxford, 1954 Search PubMed.
- H. Sellers and P. Pulay, Chem. Phys. Lett., 1984, 103, 463–465 CrossRef CAS.
- N. C. Handy, Y. Yamaguchi and H. F. Schaefer, J. Chem. Phys., 1986, 84, 4481–4484 CrossRef CAS.
- R. D. Bardo and M. Wolfsberg, J. Chem. Phys., 1978, 68, 2686–2695 CrossRef CAS.
- R. D. Bardo, L. I. Kleinman, A. W. Raczkowski and M. Wolfsberg, J. Chem. Phys., 1978, 69, 1106–1111 CrossRef CAS.
- J. O. Jensen and D. R. Yarkony, J. Chem. Phys., 1988, 89, 975–982 CrossRef CAS.
- W. Cencek and W. Kutzelnigg, Chem. Phys. Lett., 1997, 266, 383–387 CrossRef CAS.
- E. F. Valeev and C. D. Sherrill, J. Chem. Phys., 2003, 118, 3921–3927 CrossRef CAS.
- S. L. Mielke, D. W. Schwenke and K. A. Peterson, J. Chem. Phys., 2005, 122, 224313 CrossRef.
- M. Przybytek and B. Jeziorski, J. Chem. Phys., 2005, 123, 134315 CrossRef.
- J. Gauss, A. Tajti, M. Kállay, J. F. Stanton and P. G. Szalay, J. Chem. Phys., 2006, 125, 144111 CrossRef.
- A. Tajti, P. G. Szalay and J. Gauss, J. Chem. Phys., 2007, 127, 014102 CrossRef.
-
J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de Search PubMed.
-
M. Kállay, P. R. Nagy, Z. Rolik, D. Mester, G. Samu, J. Csontos, J. Csóka, B. P. Szabó, L. Gyevi-Nagy, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and B. Hégely, MRCC, a quantum chemical program suite CrossRef, See also Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, J. Chem. Phys., 2013, 139, 094105 CrossRef , as well as: http://www.mrcc.hu.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945–2954 CrossRef.
- M. Kállay, P. G. Szalay and P. R. Surján, J. Chem. Phys., 2002, 117, 980–990 CrossRef.
- M. Kállay, J. Gauss and P. G. Szalay, J. Chem. Phys., 2003, 119, 2991–3004 CrossRef.
- M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 6841–6848 CrossRef.
- P. G. Szalay, F. Holka, J. Fremont, M. Rey, K. A. Peterson and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2011, 13, 3654–3659 RSC.
- F. Holka, P. G. Szalay, J. Fremont, M. Rey, K. A. Peterson and V. G. Tyuterev, J. Chem. Phys., 2011, 134, 094306 CrossRef.
- H. Partridge and D. Schwenke, J. Chem. Phys., 1997, 106, 4618–4639 CrossRef CAS.
- X. Huang, D. W. Schwenke and T. J. Lee, J. Chem. Phys., 2008, 129, 214304 CrossRef.
- A. V. Nikitin, M. Rey and V. G. Tyuterev, J. Chem. Phys., 2016, 145, 114309 CrossRef.
- A. Owens, S. N. Yurchenko, A. Yachmenev, J. Tennyson and W. Thiel, J. Chem. Phys., 2016, 145, 104305 CrossRef.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS.
- Y. J. Bomble, J. Vázquez, M. Kállay, C. Michauk, P. G. Szalay, A. G. Császár, J. Gauss and J. F. Stanton, J. Chem. Phys., 2006, 125, 064108 CrossRef.
- M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111 CrossRef.
- J. H. Thorpe, C. A. Lopez, T. L. Nguyen, J. H. Baraban, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2019, 150, 224102 CrossRef.
- M. Heckert, M. Kállay, D. P. Tew, W. Klopper and J. Gauss, J. Chem. Phys., 2006, 125, 044108 CrossRef.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef.
- T. Helgaker, W. Klopper and D. P. Tew, Mol. Phys., 2008, 106, 2107–2143 CrossRef CAS.
- A. Karton, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 292–310 CAS.
- A. Ganyecz, M. Kállay and J. Csontos, J. Chem. Theory Comput., 2017, 13, 4193–4204 CrossRef CAS.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- C. Puzzarini and V. Barone, Phys. Chem. Chem. Phys., 2011, 13, 7189–7197 RSC.
- The ROMEO HPC Center Champagne-Ardenne is an HPC platform hosted by the University of Reims Champagne-Ardenne and supported by the Champagne-Ardenne Region since 2002. See http://romeo.univ-reims.fr.
- B. Ruscic, R. E. Pinzon, M. L. Morton, N. K. Srinivasan, M.-C. Su, J. W. Sutherland and J. V. Michael, J. Phys. Chem. A, 2006, 110, 6592–6601 CrossRef CAS.
-
B. Ruscic, unpublished results obtained from active thermochemical tables (ATcT) based on the Core (Argonne) Thermochemical Network version 1.110, 2010.
- A. G. Császár, E. Mátyus, T. Szidarovszky, L. Lodi, N. F. Zobov, S. V. Shirin, O. L. Polyansky and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 1043–1064 CrossRef.
- O. L. Polyansky, R. I. Ovsyannikov, A. A. Kyuberis, L. Lodi, J. Tennyson and N. F. Zobov, J. Phys. Chem. A, 2013, 117, 9633–9643 CrossRef CAS.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2015, 164, 207–220 CrossRef CAS.
- V. G. Tyuterev, R. V. Kochanov and S. A. Tashkun, J. Chem. Phys., 2017, 146, 064304 CrossRef.
- W. Kutzelnigg, Mol. Phys., 1997, 90, 909–916 CrossRef CAS.
- K. Pachucki and J. Komasa, J. Chem. Phys., 2009, 130, 164113 CrossRef.
- D. W. Schwenke, J. Phys. Chem. A, 2001, 105, 2352–2360 CrossRef CAS.
- X. Huang, D. W. Schwenke, S. A. Tashkun and T. J. Lee, J. Chem. Phys., 2012, 136, 124311 CrossRef.
- A. Barbe, M.-R. De Backer, E. Starikova, S. Tashkun, X. Thomas and V. Tyuterev, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 829–839 CrossRef CAS.
- A. Perrin, A.-M. Vasserot, J.-M. Flaud, C. Camy-Peyret, C. Rinsland, M. Smith and V. Malathy Devi, J. Mol. Spectrosc., 1990, 143, 311–317 CrossRef CAS.
- J.-M. Flaud, C. Camy-Peyret, V. Malathy Devi, C. Rinsland and M. Smith, J. Mol. Spectrosc., 1987, 122, 221–228 CrossRef CAS.
- A. Chichery, A. Barbe, V. Tyuterev and M. Bourgeois, J. Mol. Spectrosc., 2001, 206, 1–13 CrossRef CAS.
- A. Chichery, A. Barbe and V. Tyuterev, J. Mol. Spectrosc., 2001, 206, 14–26 CrossRef CAS.
- A. Barbe and E. Starikova, J. Quant. Spectrosc. Radiat. Transfer, 2019, 232, 116–125 CrossRef CAS.
- S. Mikhailenko and A. Barbe, J. Quant. Spectrosc. Radiat. Transfer, 2020, 244, 106823 CrossRef CAS.
- P. Rosmus, P. Palmieri and R. Schinke, J. Chem. Phys., 2002, 117, 4871–4877 CrossRef CAS.
- V. Kokoouline, D. Lapierre, A. Alijah and V. Tyuterev, Phys. Chem. Chem. Phys., 2020, 22, 15885–15899 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The Python codes for the analytical DBOC representations for each investigated isotopologue and comparisons for the calculated and observed vibrational energies. See DOI: 10.1039/d0cp02457k |
|
| This journal is © the Owner Societies 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Péter G.
Szalay
*a,
Péter G.
Szalay
 a,
Roman
Kochanov
a,
Roman
Kochanov
 bc and
Vladimir G.
Tyuterev
bc and
Vladimir G.
Tyuterev
 *bd
*bd

![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) N being the nuclear kinetic energy operator. The integration in eqn (1) is done over all electronic coordinates represented by r. The DBOC thus takes into account the dependence of the electronic wave function on the nuclear coordinates R, through the calculation of the nuclear kinetic energy contribution. It has the advantage that the adiabatic picture of the BOA is retained so that the notion of a potential energy surface (PES) is still possible. However, the PES becomes dependent on the nuclear mass and will thus be different for, e.g. various isotopologues of the same molecule.
N being the nuclear kinetic energy operator. The integration in eqn (1) is done over all electronic coordinates represented by r. The DBOC thus takes into account the dependence of the electronic wave function on the nuclear coordinates R, through the calculation of the nuclear kinetic energy contribution. It has the advantage that the adiabatic picture of the BOA is retained so that the notion of a potential energy surface (PES) is still possible. However, the PES becomes dependent on the nuclear mass and will thus be different for, e.g. various isotopologues of the same molecule.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, and the finer tuning of the surface is done by means of the symmetrized polynomial part. The asymptotic behavior of the correction is controlled by the “global” Gaussian damping function, which ensures that the correction approaches zero at sufficiently large values of r and α, because we do not have reliable ab initio information at these ranges of geometries. In individual points, DBOC values of the symmetric (666, 777 and 888) isotopologues are related to each other via a simple scaling factor. Nevertheless, we chose to perform the fit according to eqn (3) separately for the individual symmetric isotopologues, resulting in different, although very similar parameters of the fitted DBOC correction. The final, isotope-dependent PESs were thus then constructed for each isotopologue separately by adding the fitted DBOC surface to the Born–Oppenheimer BO PES12 in the form
α, and the finer tuning of the surface is done by means of the symmetrized polynomial part. The asymptotic behavior of the correction is controlled by the “global” Gaussian damping function, which ensures that the correction approaches zero at sufficiently large values of r and α, because we do not have reliable ab initio information at these ranges of geometries. In individual points, DBOC values of the symmetric (666, 777 and 888) isotopologues are related to each other via a simple scaling factor. Nevertheless, we chose to perform the fit according to eqn (3) separately for the individual symmetric isotopologues, resulting in different, although very similar parameters of the fitted DBOC correction. The final, isotope-dependent PESs were thus then constructed for each isotopologue separately by adding the fitted DBOC surface to the Born–Oppenheimer BO PES12 in the form













