AFIR explorations of transition states of extended unsaturated systems: automatic location of ambimodal transition states†
Abstract
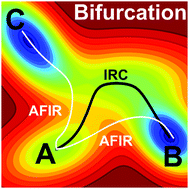
Paths of Diels–Alder reactions between 2-vinylfuran and 3-methoxycarbonylcyclopentadienone were systematically explored by the multicomponent version of the artificial force induced reaction (MC-AFIR) method. In this reaction, the dynamical bifurcation in which a single transition state (TS) relates to two different products has been reported to occur [J. B. Thomas, et al., J. Am. Chem. Soc., 2008, 130, 14544–14555]. In this paper, based on the MC-AFIR method, we propose a procedure to systematically explore so called ambimodal TSs through which the dynamical bifurcation occurs. The present procedure finds candidates of TSs that may cause the dynamical bifurcation from the logs of an automated reaction path search by the MC-AFIR method, without any additional quantum chemical calculations. For this reaction, the MC-AFIR search found 125 unique TSs automatically. Among the 125 TSs, 19 were suggested as candidates, and finally, six including the one reported in the literature were confirmed to cause the dynamical bifurcation. The present procedure would be promising to find TSs involved in the dynamical bifurcation automatically.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...
