Two-dimensional hexagonal chromium chalco-halides with large vertical piezoelectricity, high-temperature ferromagnetism, and high magnetic anisotropy†
Abstract
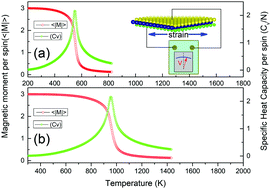
On the basis of density functional theory, we predicted that Janus CrTeI and CrSeBr monolayers possess highly energetic, dynamical, and mechanical stability. Due to noncentral symmetry, the two monolayers exhibit vertical piezoelectricity with large piezoelectric coefficients d31 (1.745 and 1.716 pm V−1 for CrBSe and CrTeI, respectively), which are larger than those of most materials in existence. Both systems are also ferromagnetic (FM) semiconductors, with Curie temperature (TC) higher than 550 K and large in-plane magnetic anisotropy energy. Superexchange interactions are responsible for high-temperature FM order. A semiconductor to half metal transition can be regulated by carrier doping, which can be carried out by gate voltages. Doped systems still retain the same FM order as pristine ones; in particular, hole doping enhances exchange coupling, thereby increasing TC. The combination of piezoelectricity, high TC, and controllable electronic structures and magnetic properties makes magnetic 2D Janus CrSeBr and CrTeI attractive materials for potential applications in nanoelectronics, electromechanics, and spintronics.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...