Spontaneous mirror symmetry breaking: an entropy production survey of the racemate instability and the emergence of stable scalemic stationary states†
Abstract
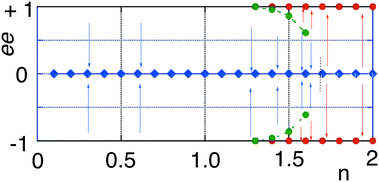
We study the emergence of both stable and unstable non-equilibrium stationary states (NESS), as well as spontaneous mirror symmetry breaking (SMSB) provoked by the destabilization of the racemic thermodynamic branch, for an enantioselective autocatalytic reaction network in an open flow system, and for a continuous range n of autocatalytic orders. The system possesses a range of double bi-stability and also tri-stability depending on the autocatalytic order. We carry out entropy production and entropy flow calculations, from simulations of ordinary differential equations, stoichiometric network analysis (SNA), and consider a stability analysis of the NESS. The simulations provide a correct description of the relationship between energy state functions, the isothermal dissipated heat, entropy production and entropy flow exchange with the surroundings, and the correct solution of the balance of the entropy currents at the NESS. The validity of the General Evolution Criterion (GEC) is in full agreement with all the dynamic simulations.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...