Hexagonal rare-earth manganites and ferrites: a review of improper ferroelectricity, magnetoelectric coupling, and unusual domain walls
Abstract
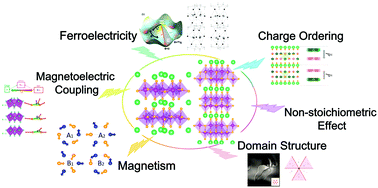
Hexagonal rare-earth manganites and ferrites are well-known improper ferroelectrics with low-temperature antiferromagnetism/weak ferromagnetism. In recent decades, new multi-functional device concepts and applications have provoked the exploration for multiferroics which simultaneously possess ferroelectric and magnetic orders. As a promising platform for multiferroicity, hexagonal manganites and ferrites are attracting great research interest among the fundamental scientific and technological communities. Moreover, the novel type of vortex-like ferroelectric domain walls are locked to the antiphase structural domain walls, providing an extra degree of freedom to tune the magnetoelectric coupling and other properties such as conductance. Here, we summarize the main experimental achievements and up-to-date theoretical understanding of the ferroelectric, magnetic, and magnetoelectric properties, as well as the intriguing domain patterns in hexagonal rare-earth manganites and ferrites. Recent work on non-stoichiometric compounds will also be briefly introduced.
- This article is part of the themed collections: PCCP Perspectives and 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...