Microhydration of protonated biomolecular building blocks: protonated pyrimidine

Abstract

Protonation and hydration of biomolecules govern their structure, conformation, and function. Herein, we explore the microhydration structure in mass-selected protonated pyrimidine–water clusters (H⁺Pym–W_n, n = 1–4) by a combination of infrared photodissociation spectroscopy (IRPD) between 2450 and 3900 cm⁻¹ and density functional theory (DFT) calculations at the dispersion-corrected B3LYP-D3/aug-cc-pVTZ level. We further present the IR spectrum of H⁺Pym–N₂ to evaluate the effect of solvent polarity on the intrinsic molecular parameters of H⁺Pym. Our combined spectroscopic and computational approach unequivocally shows that protonation of Pym occurs at one of the two equivalent basic ring N atoms and that the ligands in H⁺Pym–L (L = N₂ or W) preferentially form linear H-bonds to the resulting acidic NH group. Successive addition of water ligands results in the formation of a H-bonded solvent network which increasingly weakens the NH group. Despite substantial activation of the N–H bond upon microhydration, no intracluster proton transfer occurs up to n = 4 because of the balance of relative proton affinities of Pym and W_n and the involved solvation energies. Comparison to neutral Pym–W_n clusters reveals the drastic effects of protonation on microhydration with respect to both structure and interaction strength.

---

1. Introduction

Nucleobases, the building blocks of the genetic materials RNA and DNA, are derived from two different aromatic N-heterocycles, pyrimidine (Pym, C₄H₄N₂, 1,3-diazine, 1,3-diazabenzene) and purine.^1,2 Pyrimidine bases include uracil, thymine, and cytosine, whereas adenine and guanine belong to purines. The protonated form of these nucleobases plays a key role in physiological media,^3–16 for example in RNA catalysis.¹⁷ The site of protonation as well as the base pairing involving the additional proton leads to structural motifs, which are crucial for the stability of DNA structures.^18–20 For example, the interaction between cytosine and protonated cytosine stabilizes the d(CCCAAT) tetraplex.²¹ Protonated cytosine further participates in Hoogsteen base pairing, which is sensitive to the pH value.²² Such pairing involving a proton is critical because it can alter structure and function of DNA, often resulting in mutagenesis.^23,24

The stability and reactivity of biomolecules in vivo are generally controlled by their (micro-)hydration environment.²⁵ Thus, water (W, H₂O) is considered as an integral part of these bioactive compounds (biological or interfacial water).^26–35 For example, a combined X-ray crystallographic and NMR study on a model dodecamer B-DNA complex shows that the minor groove is more extensively hydrated than the major groove.^36,37 The surface water molecules are strikingly influential for DNA structure and the recognition of proteins and drugs by balancing enthalpic and entropic contributions to the overall free energy.^38–41 Furthermore, water acts as a transport medium in interbase proton transfer reactions.^{26,27,30,42–45}

The molecular picture of the hydration network around small building blocks provides information about their macroscopic function. Mass spectrometry coupled with vibrational spectroscopy and quantum chemical calculations has shown to be a powerful strategic approach for yielding such microscopic insight at the molecular level.^16,46–53 Despite several mass spectrometric studies^54–57 and very limited spectroscopic data on more complex pyrimidine molecules,⁴⁶ the spectroscopic knowledge on the structure of even simple protonated building blocks of nucleobases within their microhydration environment remains elusive.^14,15,58,59 In addition to biochemical topics, the Pym⋯W interaction is also relevant for astrochemical applications related to prebiotic synthesis of DNA/RNA bases. For example, it has been reported that UV irradiation of pyrimidine:H₂O ices leads to the formation of uracil,^60–62 which has been found in carbonaceous chondrites^63–65 and thus provides hints about the enigmatic prebiotic chemistry of the nucleobase⋯water interaction.

Knowledge of protonated pyrimidine–water clusters (H⁺Pym–W_n) offers the opportunity to understand their role in more complex biomolecular architectures as well as the mechanistic chemical route toward uracil. Previous mass spectrometric (ion mobility, thermochemical equilibrium measurements, multiphoton ionization of neutral clusters) and computational studies of H⁺Pym and H⁺Pym–W_n clusters suggest that protonation occurs at one of the two heterocyclic basic N atoms and that the water clusters form an ionic hydrogen-bonded (H-bonded) network attached to the resulting NH group.^66–68 In addition, mass spectrometric experiments suggest that bimolecular dissociative proton transfer according to

H⁺Pym–W_n−1 + W → Pym + W_nH⁺ (1)

becomes exothermic for clusters larger than the critical size n ≥ 4,^66,67 because at this cluster size the proton affinity of W_n clusters (PA = 691, 808, 862, 900, 904, 908 kJ mol⁻¹ for n = 1–6) exceeds that of Pym (PA = 886 kJ mol⁻¹).^69–73 However, all structures calculated so far for [Pym–W₄]H⁺ are of the type H⁺Pym–W₄,^66,67i.e. no intracluster proton transfer (ICPT) from H⁺Pym to W_n occurs in the size range n ≤ 4 due to favourable solvation energies compared to Pym–H⁺W₄ which compensate the difference in proton affinity. In general, no spectroscopic information is available to support these structures and binding motifs in [Pym–W_n]H⁺. Such spectroscopic data provide much more reliable structural information than the bare combination of mass spectrometry and quantum chemistry, which often leads to wrong conclusions, as recently demonstrated for the example of the microhydrated naphthalene cation.^74,75 To this end, we report herein the IR signatures of mass selected [Pym–W_n]H⁺ clusters and interpret them with the aid of reliable density functional theory (DFT) calculations. This approach has recently been applied in our laboratory to a variety of microhydrated protonated aromatic ions and radical cations.^{49–51,53,76–87} A particular question to be addressed is the degree of N–H bond activation and propensity for ICPT to solvent as a function of the degree of hydration, which has been observed for a number of protonated aromatic molecules and cations above a critical hydration size (n ≥ n_c).^{50,85,88–91} Furthermore, the study of H⁺Pym–N₂ elucidates the impact of solvent polarity on the physical properties of H⁺Pym and its solvation pattern. Comparison with neutral Pym–W_n clusters^92,93 reveals the drastic effects of protonation on the microhydration process, with respect to both structure and interaction strength.

2. Experimental and computational methods

IRPD spectra of mass selected H⁺Pym–L_n clusters with L = W (n = 1–4) and L = N₂ (n = 1) are obtained in a tandem quadrupole mass spectrometer coupled to an electron ionization (EI) source and an octopole ion guide.^52,94 In short, the clusters are produced in a pulsed supersonic plasma expansion by electron or chemical ionization and subsequent clustering reactions in the high-pressure region of the expansion. A mixture of N₂ and 5% H₂/He in a 1 : 1 ratio is guided as a carrier gas (8–10 bar) through a sample reservoir containing liquid Pym (Sigma-Aldrich, ≥98%, used without further purification, heated to 60 °C). Distilled water is added to the gas line to produce hydrated clusters. The desired H⁺Pym–L_n parent clusters are mass-selected in the first quadrupole and irradiated in the adjacent octopole with a tunable IR laser pulse (ν_IR, 10 Hz, 2–5 mJ, bandwidth 2 cm⁻¹) of an optical parametric oscillator pumped by a Q-switched Nd:YAG laser. Calibration of ν_IR is achieved by a wavemeter. Resonant vibrational excitation followed by intracluster vibrational redistribution leads to the loss of a single water or N₂ ligand. Loss of Pym is not observed. Resulting H⁺Pym–L_n−1 fragment ions are mass-selected by the second quadrupole and recorded with a Daly detector as a function of ν_IR to derive the IRPD spectrum of the parent cluster. The IRPD yield is linearly normalized for laser intensity variations measured with a pyroelectric detector. The separation of the laser-induced dissociation signal from the signal generated by metastable decay is achieved by triggering the ion source at twice the laser repetition rate and subtracting signals from alternating triggers. The observed peak widths of vibrational transitions are mainly due to unresolved rotational structure, lifetime broadening, sequence hot bands involving inter- and intramolecular modes, and possibly contributions from different structural isomers.

To analyze the IRPD spectra, conceivable H⁺Pym–L_n clusters are characterized at the B3LYP-D3/aug-cc-pVTZ level.⁹⁵ This dispersion-corrected functional accounts well for the electrostatic, induction, and dispersion forces and IR spectra of the investigated clusters.^{49–51,74,77–80,83,86} For instance, there is quantitative agreement between the binding energies computed for W₂ and H⁺Pym–W (D₀ = 1103 and 5854 cm⁻¹) and their experimental values (D₀ = 1105 ± 10 cm⁻¹ and −ΔH⁰ = 5840 ± 350 cm⁻¹)^67,96 indicating that effects of self-interaction errors present in several density functional theory approximations do not play a major role in the evaluation of binding energies using our approach.⁹⁷ For comparison, neutral Pym, W, and Pym–W are also computed to understand the effect of protonation on their molecular properties. All coordinates are allowed to relax during the search for stationary points, and their nature as minima or transition states are verified by harmonic frequency analysis. Harmonic intramolecular vibrational frequencies are subjected to a linear scaling factor of 0.96221, derived from a comparison of computed CH and OH stretch frequencies of neutral Pym and W with their measured values.^98–101 Scaled harmonic IR stick spectra are convoluted with a Gaussian line shape (fwhm = 10 cm⁻¹) for convenient comparison with the experimental spectra. All relative energies (E_e) and equilibrium dissociation energies (D_e) are corrected for harmonic zero-point vibrational energy to derive E₀ and D₀ values. Gibbs free energies (G) are reported for T = 298.15 K. If not stated otherwise, the total intermolecular dissociation energies (D₀) are determined with respect to the molecular H⁺Pym and W monomer fragments. Previous experience with the employed DFT level demonstrates that basis set superposition errors are less than 1%,^49,80 and thus they are not considered further here. Cartesian coordinates of all relevant structures and their energies are available in the ESI.† The atomic charge distribution and second-order perturbation energies (E⁽²⁾) of the donor–acceptor orbital interactions involved in the H-bonds are evaluated using the natural bond orbital (NBO) approach.¹⁰² To further estimate the strength of these H-bonds, noncovalent interaction (NCI) calculations are performed by analyzing the reduced gradient of the electron density, s(ρ) ∼ |grad(ρ)|/ρ^4/3, as a function of electron density ρ oriented by the sign of second eigenvalue λ₂ of the Hessian, ρ* = ρ sign(λ₂).^103,104 The strength of the intermolecular bonds can be estimated by comparing the magnitude of the −ρ* value.

3. Results and discussion

Fig. 1 displays the experimental IRPD spectra of H⁺Pym–L_n recorded between 2450 and 3900 cm⁻¹ in the H⁺Pym–L_n−1 fragment channel. The positions and widths of the bands observed are listed in Table 1, along with the vibrational and isomer assignments based on scaled harmonic frequencies. The spectral range covers the OH (ν_OH), NH (ν_NH), and CH (ν_CH) stretch fundamentals, providing detailed information about the protonation site and the solvation network. Peaks A–C between 3600 and 3800 cm⁻¹ correspond to free OH stretch modes (ν^f_OH), peaks D in the 3200–3500 range are due to H-bonded OH stretch modes (ν^b_OH), bands E near 3200 cm⁻¹ arise from aromatic CH stretch modes (ν_CH), and bands F are associated with free and bound NH stretch fundamentals (ν^f/b_NH). To assign the spectra to structures, we explore possible isomers of H⁺Pym and H⁺Pym–L_n by DFT calculations and compare their predicted IR spectra to the experimental ones.

Fig. 1 IRPD spectra of H⁺Pym–L_n clusters with L = W (n = 1–4) and L = N₂ (n = 1) recorded in the H⁺Pym–L_n−1 fragment channel. The positions, widths, and vibrational and isomer assignments of the transitions observed are listed in Table 1.

Table 1 Positions, widths (fwhm in parentheses), and suggested vibrational and isomer assignments of the transitions observed in the IRPD spectra of H⁺Pym–L_n clusters (Fig. 1) to the most stable isomers obtained at the B3LYP-D3/aug-cc-pVTZ level

	Exp. (cm^−1)	Calc. (cm^−1)	Mode	Isomer
a Ref. 101. b Ref. 118–120. c Ref. 98–100.
W	3756^a	3752 (63, b2)	ν 3	W
	3657^a	3653 (5, a1)	ν 1	W
W2	3746^b	3743 (84, a′′)	ν 3	W2
	3735^b	3724 (86, a′)	ν f	W2
	3654^b	3648 (10, a′)	ν 1	W2
	3601^b	3537 (341, a′)	ν ^bOH	W2
Pym	3074^c	3076 (9, a1)	ν C5H	Pym
	3050^c	3043 (13, a1)	ν C2H	Pym
	3039^c	3032 (18, b2)	ν C4H/C6H(as)	Pym
	3002^c	3029 (14, a1)	ν C4H/C6H(s)	Pym
H^+Pym	3391 ± 3	3396 (159, a′)	ν ^fNH	H^+Pym
		3106 (14, a′)	ν CH	H^+Pym
		3095 (8, a′)	ν CH	H^+Pym
		3079 (10, a′)	ν CH	H^+Pym
		3065 (2, a′)	ν CH	H^+Pym
H^+Pym–N2	F1 3395 (14)	3400 (153)	ν ^fNH	H^+Pym–N2(π)
	F 3313 (41)	3277 (753, a′)	ν ^bNH	H^+Pym–N2(H)
	M 3186 (7)	3219	2βNH	H^+Pym–N2(H)
	E 3127 (45)	3105 (12, a′), 3106 (13)	ν CH	H^+Pym–N2(H), H^+Pym–N2(π)
		3094 (6, a′), 3095 (7)	ν CH	H^+Pym–N2(H), H^+Pym–N2(π)
		3079 (8, a′), 3080 (9)	ν CH	H^+Pym–N2(H), H^+Pym–N2(π)
		3065 (2, a′), 3065 (2)	ν CH	H^+Pym–N2(H), H^+Pym–N2(π)
H^+Pym–W	A 3717 (35)	3722 (147, a′′)	ν 3	H^+Pym–W(H)
	B 3633 (30)	3637 (57, a′)	ν 1	H^+Pym–W(H)
	X 3233 (68)	3220/3247	2βOH/2βNH	H^+Pym–W(H)
	E 3100 (115)	3105 (8, a′)	ν CH	H^+Pym–W(H)
		3093 (6, a′)	ν CH	H^+Pym–W(H)
		3080 (5, a′)	ν CH	H^+Pym–W(H)
		3063 (1, a′)	ν CH	H^+Pym–W(H)
	F 2875 (207)	2933 (1712, a′)	ν ^bNH	H^+Pym–W(H)
H^+Pym–W2	A 3730 (27)	3734 (122)	ν 3	H^+Pym–W2(l1)
	C 3698 (35)	3706 (113)	ν f	H^+Pym–W2(l1)
	B 3645 (24)	3645 (31)	ν 1	H^+Pym–W2(l1)
	D 3340 (75)	3275 (1008)	ν ^bOH	H^+Pym–W2(l1)
	X 3250 (60)	3195, 3261/3272	2βOH/2βNH	H^+Pym–W2(l1)
	F 2605 (broad)	2658 (2701)	ν ^bNH	H^+Pym–W2(l1)
H^+Pym–W3	A 3736 (23)	3739 (224, a′′)	ν 3	H^+Pym–W3(b1)
		3740 (115)	ν 3	H^+Pym–W3(l1)
	C 3709 (30)	3712 (83), 3710 (112)	ν f	H^+Pym–W3(l1)
	B 3647 (16)	3649 (46, a′)	ν 1	H^+Pym–W3(b1)
		3649 (24)	ν 1	H^+Pym–W3(l1)
	D1 3399 (80)	3397 (1300, a′′), 3359 (534, a′)	ν ^bOH	H^+Pym–W3(b1)
		3373 (690)	ν ^bOH	H^+Pym–W3(l1)
	X 3228 (broad)	3180, 3212/3215, 3185	2βOH	H^+Pym–W3(b1), H^+Pym–W3(l1)
	D2 3152 (100)	3068 (1499)	ν ^bOH	H^+Pym–W3(l1)
	E 3105 (broad)	3104 (4, a′), 3105 (5)	ν CH	H^+Pym–W3(b1), H^+Pym–W3(l1)
	F <2450 (broad)	2312 (3640, a′), 2497 (3286)	ν ^bNH	H^+Pym–W3(b1), H^+Pym–W3(l1)
H^+Pym–W4	A 3740 (8)	3715 (82, a′)	ν 3	H^+Pym–W4(r)
		3741 (110), 3739 (114)	ν 3	H^+Pym–W4(b2)
	C 3716 (17)	3715 (94, a′), 3712 (197, a′′)	ν f	H^+Pym–W4(r)
		3698 (89)	ν f	H^+Pym–W4(b2)
	B 3648 (20)	3630 (17, a′)	ν 1	H^+Pym–W4(r)
		3650 (21), 3649 (24)	ν 1	H^+Pym–W4(b2)
	D1 3464 (70)	3529 (439, a′), 3510 (370, a′′)	ν ^bOH	H^+Pym–W4(r)
	D2 3393 (52)	3423 (999), 3380 (380)	ν ^bOH	H^+Pym–W4(b2)
		3348 (1043)	ν ^bOH	H^+Pym–W4(b2)
	D3 3200 (170)	3310 (900, a′), 3304 (718, a′′)	ν ^bOH2βOH	H^+Pym–W4(r)
	X 3200 (170)	3209, 3199	2βOH	H^+Pym–W4(r)
	E 3087 (50)	3103 (3, a′)	ν CH	H^+Pym–W4(r)
		3063 (42)	ν ^bCH	H^+Pym–W4(b2)
	F <2450 (broad)	2274 (3300)	ν ^bNH	H^+Pym–W4(b2)
		2088 (4490, a′)	ν ^bNH	H^+Pym–W4(r)

---

3.1 Pym, H⁺Pym, and W

Pym has a planar equilibrium structure with C_2v symmetry in its ¹A₁ ground electronic state (Fig. 2), as revealed from microwave, IR, and Raman spectroscopy, X-ray crystallography, and quantum chemical calculations.^{98,99,105–109} Our calculated geometric and vibrational parameters compare favourably with experimental values (Table S1 in the ESI†). Furthermore, the measured proton affinity is comparable to the computed one assuming N-protonation (PA = 886 vs. 890 kJ mol⁻¹),⁶⁹ confirming the reliability of the current computational approach.

Fig. 2 Optimized geometries of Pym (along with atomic numbering), H⁺Pym, and the most stable H⁺Pym–N₂ isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies in cm⁻¹ (E₀).

Protonation of Pym reduces its symmetry from C_2v to C_s in its ground electronic state (¹A₁). Protonation can occur either at one of the two equivalent ring N atoms or at the ring C atoms (carbenium ions) (Fig. S1 in the ESI†). C-protonation results in an aliphatic CH₂ group, and the corresponding ν_CH2 modes are calculated below 2850 cm⁻¹ with high IR activity for all isomers (>100 km mol⁻¹, Fig. S2 in the ESI†). All three nonequivalent carbenium isomers are very high in relative energy. Because C-protonation strongly perturbs the aromatic ring, they are less stable than the N-protonated isomer by at least E₀ ≥ 200 kJ mol⁻¹, consistent with previous mass spectrometric and computational findings.^67,68 Thus, we mainly focus herein on the N-protonated isomer denoted H⁺Pym and do not consider carbenium isomers in detail further. The effect of N-protonation is rather large on the ring skeleton (up to Δr_CC/CN < 25 mÅ), while the peripheral C–H bonds are less affected (Δr_CH < 5 mÅ) (Fig. 2 and Table S1 in the ESI†). Nearly half of the positive charge resides on the additional proton (0.45 e), while the remaining partial charge is delocalized over the aromatic ring (mostly on the peripheral hydrogen atoms, Fig. S3 in the ESI†). Protonation increases the average ν_CH frequency with a concomitant decrease in total IR oscillator strength (Δν_CH = 41 cm⁻¹, ΔI_total = −20 km mol⁻¹), and the free NH stretch mode of H⁺Pym calculated at ν^f_NH = 3396 cm⁻¹ is the dominant IR transition in the 3 μm range (I_NH = 159 km mol⁻¹, Fig. 3).

Fig. 3 Comparison of measured IRPD spectrum of H⁺Pym–N₂ with linear IR absorption spectra of Pym, H⁺Pym, and various H⁺Pym–N₂ isomers obtained at the B3LYP-D3/aug-cc-pVTZ level (Table 1).

The O–H bond parameters of neutral W in its ¹A₁ ground state (r_OH = 0.9619 Å, ν_1/3 = 3653/3752 cm⁻¹) are close to the corresponding experimental values (0.9578 Å, 3657/3756 cm⁻¹).^101,110 The minor discrepancy in the ν_OH modes (Δν_OH = −4 cm⁻¹) arises because of the simultaneous consideration of the ν_CH modes of Pym and the ν_OH modes of W when determining the single scaling factor.

3.2 H⁺Pym–N₂

We consider in Fig. 2 all relevant binding motifs for N₂ in H⁺Pym–N₂ with N-protonated Pym. In the most stable H⁺Pym–N₂(H) global minimum (D₀ = 1530 cm⁻¹), N₂ is H-bonded to the acidic NH group (R_NH⋯N2 = 2.061 Å), whereas in the much less stable H⁺Pym–N₂(π) local minimum a π-bonded N₂ ligand is located above the aromatic ring (D₀ = 858 cm⁻¹). In both cases, N₂ is pointing toward the positive charge, because the anisotropy of the charge-quadrupole and charge-induced dipole interactions favour a linear to a T-shaped approach for cation–N₂ clusters.^111,112 The π attachment of N₂ occurs without significant perturbation of the structural and vibrational parameters of the NH group (Δr_NH = −0.4 mÅ, Δν_NH = 4 cm⁻¹, ΔI_NH = −6 km mol⁻¹), and the same is true for the CH groups (Fig. 2, 3 and Table 1). In contrast, the N–H bond in the planar H⁺Pym–N₂(H) isomer is substantially modified by the linearly H-bonded N₂ ligand. The N–H bond elongates with a concomitant decrease in the ν^b_NH frequency and a nearly fivefold increase in IR oscillator strength (Δr_NH = 6.4 mÅ, Δν_NH = −119 cm⁻¹, ΔI_NH = 594 km mol⁻¹). The NBO analysis of the NH⋯N₂ ionic H-bond results in an orbital interaction energy of E⁽²⁾ = 36 kJ mol⁻¹ between the σ* orbital of the N–H bond and the lone pair of N₂, which further supports its relatively high binding energy (Fig. S4 in the ESI†). The NCI calculation also confirms the strong bonding (−ρ* = 0.021 a.u., Fig. S5 in the ESI†). Formation of the NH⋯N₂ H-bond has almost no effect on the ν_CH frequencies, because of the almost unchanged C–H bond lengths (Δν_CH ≤ 1 cm⁻¹, Δr_CH ≤ 0.2 mÅ, Fig. 2 and 3). In addition to the NH-bonded global and doubly degenerate π-bonded local minimum, we also explore the possibility of N₂ binding to the weakly acidic CH groups. All attempts to locate such CH-bonded minima with linear CH⋯N₂ bonds fail. In the case of C2H and C6H, the structures converge to the NH-bonded global minimum. For C4H and C5H, optimization leads to a bifurcated H⁺Pym–N₂(C4/C5) dimer with D₀ = 703 cm⁻¹ (Fig. 2). This isomer is thus less stable than H⁺Pym–N₂(π) but the IR spectra predicted for both local minima are quite similar in the investigated spectral range (Fig. 3). The corresponding C5/C6 structure converges to H⁺Pym–N₂(H). We further consider two N₂-bound isomers of a single C-protonated carbenium isomer, H⁺Pym(C5)–N₂ (Fig. S6 in the ESI†). In these two isomers, N₂ is either H-bonded to one of the aliphatic CH₂ bonds or π-bonded to the aromatic ring (D₀ = 905 and 1016 cm⁻¹). Their intense aliphatic ν_CH2 modes are calculated below 2900 cm⁻¹ (Fig. S7 in the ESI†). Moreover, both isomers are highly unstable compared to H⁺Pym–N₂(H), with respect to both their relative energy (E₀ > 17 500 cm⁻¹) and their intermolecular binding energy.

The IRPD spectrum measured for H⁺Pym–N₂ is compared in Fig. 3 to the linear IR spectra computed for H⁺Pym and its H⁺Pym–N₂ isomers. The IRPD spectrum is dominated by an intense transition F peaking at 3313 cm⁻¹, which is strongly blueshaded indicative of a proton donor stretch vibration. There are much weaker and relatively symmetric bands M, E, and F1 centred at 3186, 3127, and 3395 cm⁻¹. Comparison of the IRPD spectrum with the simulated IR spectra in Fig. 3 suggests an assignment of the strong band F to ν^b_NH of the H-bonded isomer predicted at 3277 cm⁻¹ and the weak peak F1 to ν^f_NH of the π-bonded isomer calculated at 3400 cm⁻¹, in line with both the positions and contours of the bands. Using the ratios of the observed integrated band intensities of bands F and F1 (∼20) and the predicted IR cross sections (∼5), we arrive at a crude estimate of 1 : 4 for the relative abundance of the π and H isomers of H⁺Pym–N₂, consistent with their computed binding energies. Assuming that the two isomers freeze out in their separate wells starting from room temperature and statistical weights of 2 : 1 for π : H, one predicts a population of 8% for the π isomer at thermal equilibrium, which is consistent with the crude experimental estimate. We take the measured ν^f_NH value of H⁺Pym–N₂(π) to derive an accurate estimate for the experimental ν_NH fundamental of bare H⁺Pym as 3391 cm⁻¹ (using the predicted blueshift of +4 cm⁻¹ for π-bonded N₂) and apply this value for evaluating frequency shifts upon H-bonding. The calculations somewhat overestimate the redshift induced by H-bonding with N₂ (−Δν^b_NH = 119 vs. 82 cm⁻¹). The broadish weak band E at 3127 cm⁻¹ is assigned to the four aromatic ν_CH modes predicted in the 3105–3065 cm⁻¹ range for both isomers. Transition M at 3186 cm⁻¹ can not be explained by any fundamental mode. However, the NH bending overtone (2β_NH, strongly coupled to ring CC stretch modes) predicted at 3219 cm⁻¹ for H⁺Pym–N₂(H) can account for this transition (using a scaling factor of 0.98 for the fingerprint range). The 2β_NH overtone may acquire IR activity from the intense ν^b_NH fundamental of H⁺Pym–N₂(H) via anharmonic coupling (Fermi resonance), which increases the splitting between both transitions, as is indicated by the comparison between the observed and computed difference (127 vs. 59 cm⁻¹), because the harmonic treatment does not account for the coupling. Thus, we can fully explain the observed H⁺Pym–N₂ spectrum by the presence of the H-bonded (dominant) and π-bonded (minor) isomers of N-protonated H⁺Pym–N₂. In this scenario, we exclude a substantial population of the CH-bonded isomer, which has a similar predicted IR spectrum as the π isomer, just on the basis of its lower stability and lower statistical weight (1 : 2 for CH to π). On the other hand, we do not observe any transition below 2900 cm⁻¹ indicative of strong transitions expected for aliphatic CH₂ modes of the high-energy N₂-tagged C-protonated isomers of H⁺Pym (Fig. S7 in the ESI†) so that we conclude exclusive N-protonation in H⁺Pym. For this reason, we do not consider carbenium isomers further.

3.3 H⁺Pym–W

In general, the H⁺Pym⋯W interaction is much stronger than the H⁺Pym⋯N₂ interaction because of the additional dominating charge-dipole forces operating in the monohydrate. As a result, the structures optimized for all H⁺Pym–W isomers displayed in Fig. 4 have a cation–dipole orientation with the O atom of W pointing toward the positive charge of N-protonated H⁺Pym. The binding energy of W in the linearly NH-bonded structure (θ_OHN = 179°), H⁺Pym–W(H), is almost twice that of π-bonded H⁺Pym–W(π), D₀ = 5854 vs. 3081 cm⁻¹, consistent with the shorter intermolecular bonds (R_NH⋯O = 1.688 Å, R_O⋯N1/C2 ∼ 2.9–3.0 Å). In the H⁺Pym–W(π) local minimum, the C–H and N–H bond parameters remain mostly unchanged upon monohydration (Δr_CH/NH < 1.3 mÅ), and the corresponding ν_NH/CH frequencies are little affected (e.g., Δν^f_NH = +14 cm⁻¹, Fig. 5). Similar to the N₂ case, W strongly perturbs the NH group in the H⁺Pym–W(H) global minimum through the formation of the linear NH⋯O ionic H-bond, which is reflected in the elongated N–H bond, along with a significant decrease in ν^b_NH and a roughly tenfold enhancement in the IR oscillator strength (Δr_NH = 27 mÅ, Δν^b_NH = −463 cm⁻¹, ΔI_NH = 1553 km mol⁻¹). The high PA of W (691 kJ mol⁻¹)⁶⁹ favours the formation of a strong NH⋯O ionic H-bond by attracting a substantial amount of positive charge (q = 55 me) from H⁺Pym (Fig. S3 in the ESI†). This charge transfer to W induces an elongation of the O–H bonds (Δr_OH = 1.9 mÅ), along with frequency redshifts of −Δν_1/3 = 16/30 cm⁻¹ for the symmetric/antisymmetric OH stretch modes (Fig. 5). In addition, the polarization induced by the nearby positive charge leads to a substantial increase in the IR oscillator strength, which is more pronounced for ν₁ than for ν₃ (factor 11 and 2). The large E⁽²⁾ energy (94 kJ mol⁻¹) and high ρ* value (−0.047 a.u.) obtained from the NBO and NCI analyses further indicate the strength of this NH⋯O ionic H-bond (Fig. S4 and S5 in the ESI†). Monohydration does not significantly affect the C–H bond parameters of H⁺Pym–W(H) (Δν_CH ≤ 2 cm⁻¹, ΔI_CH ≤ 6 km mol⁻¹). In addition to the NH-bonded global and doubly degenerate π-bonded local minimum, we find two local CH-bonded minima with W binding to the CH groups via bifurcated CH⋯O H-bonds (Fig. 4). These C4/C5 and C5/C6 local minima have similarly low binding energies as the π isomer, D₀ = 3027 and 3346 cm⁻¹, and are characterized by intense free NH stretch modes at 3403 and 3402 cm⁻¹ (Fig. 5).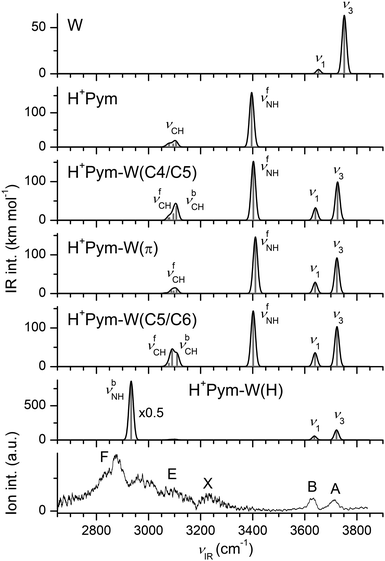

Fig. 4 Stable structures of various H⁺Pym–W_n isomers with n = 1–2 calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G). For comparison, the structures of W and W₂ are also given.

Fig. 5 Comparison of experimental IRPD spectrum of H⁺Pym–W with linear IR spectra of W, H⁺Pym, and various H⁺Pym–W isomers calculated at the B3LYP-D3/aug-cc-pVTZ level (Table 1).

The IRPD spectrum recorded for H⁺Pym–W is compared in Fig. 5 to the IR spectra computed for the all considered H⁺Pym–W dimers and the H⁺Pym and W monomers. At first glance, the IRPD spectrum lacks any signal for a free ν^f_NH band near 3400 cm⁻¹, implying that only the NH-bonded H⁺Pym–W(H) global minimum contributes to the experimental spectrum, consistent with its much larger binding energy. From the integrated band intensities and the achieved signal-to-noise ratio, the abundance of the π-bonded and CH-bonded isomers is estimated to be well below 10%. In general, the overall appearance of the IRPD spectrum agrees well with that predicted for H⁺Pym–W(H). Specifically, the two relatively sharp bands A and B at 3717 and 3633 cm⁻¹ are readily assigned to the free OH stretch modes predicted at ν₃ = 3722 and ν₁ = 3637 cm⁻¹, respectively. The observed redshifts from bare W are consistent with the computed ones (−Δν_1/3 = 24/39 vs. 16/30 cm⁻¹), and also their observed relative intensities are close to the predicted ones. The strong and rather broad band F peaking at 2875 cm⁻¹ is assigned to ν^b_NH of H⁺Pym–W(H) predicted at 2933 cm⁻¹, yielding a reasonable match between experimental and computed redshifts upon monohydration (−Δν^b_NH = 516 vs. 463 cm⁻¹). Feature F is accompanied by satellite bands toward higher frequency. Such a vibrational band pattern is quite typical for strong NH⋯O ionic H-bonds observed previously for a variety of monohydrated aromatic cations.^77,81–84 It arises from (near) resonant anharmonic interaction between the strongly IR active ν_NH fundamental and the essentially dark 2β_NH overtone (and possibly 2β_OH of W) along with weakly IR active overlapping aromatic ν_CH fundamentals. It is difficult to identify the predicted ν_CH modes near 3100 cm⁻¹ experimentally, because they fall within the blue wing of band F. The transition X at 3233 cm⁻¹ is currently attributed to the water bend overtone predicted at 2β_OH = 3220 cm⁻¹ or to 2β_NH = 3248 cm⁻¹ (using a scaling factor of 0.98). In conclusion, the IRPD spectrum is assigned to a single isomer, namely the most stable H-bonded H⁺Pym–W(H) global minimum. This single-photon IRPD spectrum is obtained in the W loss channel, although its computed binding energy is much higher than the IR photon energy (D₀ = 5954 cm⁻¹, ν_IR < 3800 cm⁻¹). Hence, we do not observe IRPD from the ground vibrational state but of ions with substantial internal energy (E_int > 2000–3000 cm⁻¹), explaining the observed larger width of the transitions as compared to the H⁺Pym–N₂ spectrum for which no internal energy is required for IRPD to be observed (D₀ = 1530 cm⁻¹ is actually an upper limit for E_int).

3.4 H⁺Pym–W₂

The IRMPD spectra of H⁺Pym–W_n in Fig. 1 reveal substantial incremental redshifts of band F assigned to ν^b_NH as n increases from 1 to 4, demonstrating that the W ligands successively attach to the NH binding site of H⁺Pym by forming a W_n solvent network. Indeed, in the most stable structure of H⁺Pym–W₂(l1) shown in Fig. 4, a linear H-bonded W₂ dimer is attached to H⁺Pym via a NH⋯O ionic H-bond, with a total binding energy of D₀ = 9945 cm⁻¹. The formation of such a H-bonded solvent network is strongly cooperative because of nonadditive induction forces, so that both the NH⋯O and OH⋯O H-bonds in H⁺Pym–W₂ are much stronger and shorter than in the respective H⁺Pym–W and W₂ dimer subunits (R_NH⋯O = 1.588 vs. 1.688 Å, R_OH⋯O = 1.720 vs. 1.947 Å). This effect is also visible in the binding energies, because the total binding energy of D₀ = 9945 cm⁻¹ is 43% larger than the sum of the two dimer units (D₀ = 6957 cm⁻¹). Similarly, the E⁽²⁾ and −ρ* values for the two H-bonds in the trimer (141 and 74 kJ mol⁻¹, 0.061 and 0.042 a.u.) are larger than those in the dimers (94 and 32 kJ mol⁻¹, 0.047 and 0.026 a.u., Fig. S4 and S5 in the ESI†). The stronger NH⋯O bond in the n = 2 cluster is also rationalized by the higher proton affinity of W₂ as compared to W (808 vs. 691 kJ mol⁻¹),^69,70 leading to a larger charge transfer from H⁺Pym to the solvent (79 vs. 55 me, Fig. S3 in the ESI†). Due to the stronger NH⋯O H-bond in the n = 2 cluster, the N–H bond is more strongly activated by dihydration than by monohydration (Δr_NH = 44 vs. 27 mÅ), leading to a larger redshift in ν^b_NH (−Δν^b_NH = 738 vs. 463 cm⁻¹) and IR enhancement (I_NH = 2701 vs. 1712 km mol⁻¹) as shown in Fig. 6. The O–H bonds of the terminal W in H⁺Pym–W₂ are less elongated than in H⁺Pym–W (Δr_OH = 1.2 vs. 1.9 mÅ), because they are farther away from the positive charge, thus producing smaller redshifts in ν_OH (−Δν_1/3 = 8/18 vs. 16/30 cm⁻¹). The free O–H bond of the proton donor W ligand is much shorter than the bonded one (by 23 mÅ), leading to a much higher frequency for the free OH stretch (ν_f = 3706 cm⁻¹, occurring between ν₁ and ν₃) than the bonded OH stretch (ν^b_OH = 3275 cm⁻¹). The latter one is largely redshifted from that of bare W₂ (ν^b_OH = 3601 cm⁻¹) due to the massive threebody effects induced by the nearby H⁺Pym cation (Fig. 6). Similar to n = 1, the parameters of the C–H bonds including ν_CH are hardly affected for n = 2 upon hydration of the NH group of H⁺Pym (Fig. 4 and Table 1).

Fig. 6 Comparison of experimental IRPD spectrum of H⁺Pym–W₂ with linear IR spectra of W₂ and various H⁺Pym–W₂ isomers calculated at the B3LYP-D3/aug-cc-pVTZ level (Table 1).

We consider in Fig. 4 two further less stable local minima. Like in the l1 global minimum, in the l2 isomer a H-bonded W₂ dimer is attached to the NH group of H⁺Pym. This isomer is further stabilized by a weak CH⋯O contact of the terminal W ligand to the C2H group in ortho position of the NH group. However, to make this contact, the first W ligand has to rotate into the H⁺Pym plane leading to a weaker and longer NH⋯O H-bond. In addition, the W⋯W bond is less linear and weaker due to this additional steric constraint. The weaker OH⋯O and NH⋯O H-bond strengths are also indicated by the NBO and NCI indices (Fig. S4 and S5 in the ESI†). Both of these modifications cost energy so that the l2 isomer is in total ΔE₀ = 199 cm⁻¹ less stable than the global minimum despite its additional CH⋯O H-bond. As a result, the spectral signatures of the l2 isomer are less redshifted ν^b_NH and ν^b_OH transitions than for I1, a weakly appearing ν^b_CH band, and merging of ν_f and ν₃ into a single band (Fig. 6). The third and much less stable H⁺Pym–W₂ isomer denoted H–C5/C6 has two W ligands separately attached to the NH group (linear) and C5H/C6H groups (bifurcated). The H-bonds are slightly weaker than those in the respective H⁺Pym–W dimers, because of the small noncooperative threebody induction forces typical for interior ion solvation. These effects are also visible in the NBO and NCI indices of these H-bonds (Fig. S4 and S5 in the ESI†). As a result, the total binding energy of this isomer, D₀ = 8789 cm⁻¹, is 4.5% smaller than the sum of the two dimer binding energies (D₀ = 9200 cm⁻¹), and thus much smaller than that of the l1 global minimum (by ΔE₀ = 1156 cm⁻¹). The spectral signatures of this isomer are a ν^b_NH band slightly blueshifted from that of H⁺Pym–W(H), a weakly appearing ν^b_CH band, and the lack of any ν^b_OH/ν_f transitions (Fig. 6).

Addition of the second W ligand to H⁺Pym–W leads to several new features occurring in the IRPD spectrum (Fig. 1), such as bands C and D. In addition, band F exhibits a large redshift. Both observations are consistent with the formation of the H⁺Pym–W₂(l1) global minimum shown in Fig. 4. Its predicted IR spectrum is compared in Fig. 6 to the observed IRPD spectrum, along with the spectra computed for the two less stable H⁺Pym–W₂ isomers and bare W₂. At first glance, the IRPD spectrum of H⁺Pym–W₂ shows very good agreement with the spectrum computed for the l1 isomer, suggesting the presence of a single isomer, namely the most stable global minimum. The broad blueshaded band F peaking at 2605 cm⁻¹ is assigned to the ν^b_NH proton donor stretch predicted at 2658 cm⁻¹, implying good agreement between observed and computed redshifts (−ν^b_NH = 786 vs. 738 cm⁻¹). Bands A and B are assigned to ν₃ (3734 cm⁻¹) and ν₁ (3645 cm⁻¹) of the terminal W acceptor ligand. The observed blueshifts with respect to the n = 1 cluster agree well with the prediction (Δν_3/1 = 13/12 vs. 12/8 cm⁻¹). The two new bands C and D at 3698 and 3340 cm⁻¹ are attributed to ν_f and ν^b_OH of the H-bonded W donor ligand computed as 3706 and 3275 cm⁻¹, respectively. Similar to n = 1, the remaining band X at 3250 cm⁻¹ is tentatively attributed to the water bending overtone (2β_OH) or to 2β_NH, which are not included in the harmonic simulations (Table 1). We may exclude a significant population of the two less stable H⁺Pym–W₂ isomers, because their predicted intense ν^b_NH and ν^b_OH bands do not show up as pronounced separate peaks (with sharp P-branch heads and blueshaded shoulders) in the IRPD spectrum. The binding energy of the terminal W ligand in H⁺Pym–W₂(l1) is calculated as 4091 cm⁻¹, implying that single-photon IRPD for W loss should be possible for ions with little vibrational excitation. Thus, the IRPD spectrum of the n = 2 cluster is obtained from ions with lower effective temperature, leading to narrower transitions than for n = 1 (Fig. 1 and Table 1).

3.5 H⁺Pym–W₃

We consider in Fig. 7 four conceivable low-energy isomers of H⁺Pym–W₃, which are derived from the H⁺Pym–W₂(l1/l2) isomers by addition of W to either the bridging or terminal W ligand. This procedure yields two branched and two linear isomers within ΔE₀ = 275 cm⁻¹, with D₀ = 13454 (b1) > 13296 (b2) > 13213 (l1) > 13179 cm⁻¹ (l2), respectively. Based on their small energy difference at T = 0 K, all four may be populated in the supersonic expansion. However, the b1 and l1 isomers are entropically strongly favoured at elevated temperature, because they are more flexible due to the lack of the CH⋯O contact.

Fig. 7 Stable structures of various H⁺Pym–W₃ isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

The H⁺Pym–W₃(b1) global minimum with C_s symmetry has two equivalent terminal W ligands. The increased proton affinity of W₃ (PA = 862 kJ mol⁻¹) improves the binding of the solvent cluster to the acidic NH group of H⁺Pym, which further activates its N–H bond (Δr_NH = 68 mÅ, Δν^b_NH = −1084 cm⁻¹, I_NH = 3640 km mol⁻¹, Fig. 8). The stronger H-bond (R_NH⋯O = 1.500 Å) implies an increasing charge transfer from H⁺Pym to W₃ (111 me), a larger E⁽²⁾ energy (201 kJ mol⁻¹) and a higher ρ* value (−0.077 a.u.) (Fig. S3–S5 in the ESI†). The intermolecular OH⋯O H-bonds within the W₃ network are slightly weaker than in H⁺Pym–W₂ (1.767 vs. 1.720 Å) because of increased charge delocalization in the larger hydrate. As a result, all O–H bonds become slightly shorter (Δr_OH = −6.2 and −0.3 mÅ for bonded and free O–H bonds), resulting in blueshifts of both the bound and the free OH stretch modes (Δν^b_OH = 122/84 cm⁻¹, Δν_1/3 = 4/5 cm⁻¹).

Fig. 8 Comparison of experimental IRPD spectrum of H⁺Pym–W₃ with linear IR spectra of W₃ and various H⁺Pym–W₃ clusters calculated at the B3LYP-D3/aug-cc-pVTZ level (Table 1).

In the H⁺Pym–W₃(l1) local minimum, a linear W₃ chain is attached to the acidic NH group of H⁺Pym. The NH⋯O ionic H-bond is slightly weaker than in H⁺Pym–W₃(b1), as evidenced from longer values for R_NH⋯O (1.545 Å), and smaller E⁽²⁾ (169 kJ mol⁻¹), Δq (96 me), ρ* (−0.069 a.u.), Δr_NH (55 mÅ), Δν^b_NH (−899 cm⁻¹), and I_NH (3286 km mol⁻¹). The two nonequivalent OH⋯O H-bonds (R_OH⋯O = 1.636 and 1.772 Å) give rise to rather different ν^b_OH frequencies of 3068 and 3373 cm⁻¹, while their corresponding ν_f modes are rather similar (3712 and 3710 cm⁻¹). The terminal W ligand is far away from the positive charge, and thus its perturbation from bare W is small (Δr_OH = 0.8 mÅ, Δν_1/3 = −4/−12 cm⁻¹).

The b2 and l2 isomers of H⁺Pym–W₃ are characterized by a weak CH⋯O contact. However, like for the l2 isomer of the n = 2 clusters, this additional H-bond is accompanied by steric strain in the other H-bonds leading as a net effect to only slightly higher relative energies (E₀ = 159 and 275 cm⁻¹) but substantially larger relative free energies at room temperature (G = 653 and 1035 cm⁻¹).

The IRPD spectrum of H⁺Pym–W₃ is compared in Fig. 8 to the IR spectra predicted for the linear and branched isomers, along with the spectrum computed for cyclic W₃. At first glance, it is obvious that the IRPD spectrum mostly arises from the branched H⁺Pym–W₃(b1) global minimum. The bands A and B at 3736 and 3647 cm⁻¹ are attributed to the free ν₃ and ν₁ modes predicted at 3739 and 3649 cm⁻¹. The observed incremental blueshifts from the n = 2 cluster agree well with the prediction (Δν_3/1 = 6/2 vs. 5/4 cm⁻¹). The corresponding symmetric and antisymmetric bound ν^b_OH modes predicted at 3359 and 3397 cm⁻¹ occur as a single blueshaded band D1 peaking at 3399 cm⁻¹. The b2 and l2 isomers can be excluded as major carriers of the experimental spectrum, in line with their high free energies. The spectrum predicted for b2 has two roughly equally intense ν^b_OH modes at 3507 and 3359 cm⁻¹ (with a large splitting of 148 cm⁻¹), and such a pattern is not observed experimentally. A similar argument applies to isomer l2. Band C at 3709 cm⁻¹ cannot be explained by b1 and is thus considered as a unique spectroscopic signature of the l1 local minimum, because it is the only remaining structure with uncoupled free OH stretch oscillators (predicted at 3710 and 3712 cm⁻¹). Its corresponding bound OH stretch modes predicted at 3068 and 3373 cm⁻¹ appear as band D2 centred at 3152 cm⁻¹ and overlap with band D1 at 3399 cm⁻¹, respectively. Similarly, its predicted ν_1/3 bands coincide with those of the b1 isomer resulting in bands A and B. The signal near ∼3100 cm⁻¹ (E) and 3228 cm⁻¹ (X) is attributed to ν_CH and 2β_OH modes of both the linear and branched isomers. At the red end of the experimental spectrum, the signal rises more or less monotonically toward 2450 cm⁻¹ (band F), which is the end of the scanning range of the IR laser. Signal in this spectral range is attributed to the blue wing of the ν^b_NH modes of H⁺Pym–W₃(b1) and H⁺Pym–W₃(l1) predicted at 2312 and 2497 cm⁻¹, respectively. Considering the relative intensities of bands D2 and D1, as well as bands A–C, along with the calculated oscillator strengths, we can clearly conclude a much higher abundance of the b1 global minimum compared to the l1 local minimum, with a crudely estimated population ratio of ∼5 : 1.

3.6 H⁺Pym–W₄

Four low-energy computed minima of H⁺Pym–W₄ are considered in Fig. 9 (structures) and Fig. 10 (IR spectra), all of which are within E₀ < 205 cm⁻¹. In contrast to the n = 1–3 isomers, a new structure with a cyclic H-bonded W₄ ring attached to the NH group of H⁺Pym (C_s) is calculated to be the most stable isomer at T = 0 K, with D₀ = 16675 cm⁻¹. Its additional stability arises from the extra OH⋯O H-bond produced by closing the solvation ring. The enhanced strength of the NH⋯O ionic H-bond in this H⁺Pym–W₄(r) isomer as compared to the most stable n = 3 structure is rationalized by the higher PA of W₄ as compared to W₃ (PA = 862 vs. 900 kJ mol⁻¹). As a result, R_NH⋯O becomes shorter (1.464 vs. 1.500 Å), and the N–H bond gets longer (Δr_NH = 16 mÅ) which lowers ν^b_NH further from 2312 to 2088 cm⁻¹. The enhanced strength of the NH⋯O ionic H-bond is further supported by the increased charge transfer to the solvent cluster (Δq = 129 vs. 111 me) and the larger E⁽²⁾ and ρ* values (E⁽²⁾ = 241 vs. 201 kJ mol⁻¹; −ρ* = 0.086 vs. 0.077 a.u.) documented in Fig. S3–S5 in the ESI.† The characteristic ν^b_OH modes associated with the two single-donor single-acceptor W ligands are calculated at significantly higher frequencies (ν^b_OH = 3529 and 3510 cm⁻¹) than those of the other isomers (ν^b_OH < 3500 cm⁻¹), because their H-bonds to the bridging double-acceptor W ligand are rather weak and long, as also indicated by their NBO and NCI indices. As a result, also the ν₃ and ν₁ frequencies of the latter ligand are slightly higher than those of the other isomers (3715/3630 cm⁻¹).

Fig. 9 Stable structures of various H⁺Pym–W₄ isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

Fig. 10 Comparison of experimental IRPD spectrum of H⁺Pym–W₄ with linear IR spectra of W₄ and various H⁺Pym–W₄ clusters calculated at the B3LYP-D3/aug-cc-pVTZ level (Table 1).

Attaching a further W ligand to the b1 and b2 isomers of the n = 3 clusters leads to the corresponding isomers of n = 4, with a reversed energy order (D₀ = 16 471 and 16 537 cm⁻¹, E₀ = 204 and 138 cm⁻¹). The stability of b2 exhibiting the CH⋯O H-bond is higher than that of b1 (without such a contact) because of the additional cooperative effects induced by the terminal W ligand, leading to a shorter H-bond (R_CH⋯O = 2.386 vs. 2.491 Å) and higher E⁽²⁾ and ρ* values compared to its n = 3 analogue (E⁽²⁾ = 8.6 vs. 5.9 kJ mol⁻¹; −ρ* = 0.011 vs. −0.008 a.u.) (Fig. S4 and S5 in the ESI†). The ν^b_CH mode at 3063 cm⁻¹ becomes slightly more intense (I_CH = 42 km mol⁻¹) by this enhanced interaction, which is however still smaller than the additional OH⋯O interaction in the most stable ring (r) isomer, as reflected from its E⁽²⁾ and ρ* parameters (30 kJ mol⁻¹, −0.025 a.u.). For cooperativity reasons, also the NH⋯O H-bonds are stronger in the b1/b2 isomers of n = 4 as compared to n = 3. Computationally, b2 is the most favoured n = 4 isomer at T = 298 K (G = 0) due to its larger structural flexibility which enhances the entropic contribution.

Unlike the branched isomers, simple linear addition of a W ligand to the linear l1 and l2 isomers of n = 3 converges to the single n = 4 structure at E₀ = 163 cm⁻¹. The resulting linear (l) isomer of n = 4 features a CH⋯O H-bond that renders this isomer more stable than b1. Despite its shorter R_CH⋯O distance (2.213 vs. 2.386 Å), isomer l is slightly less stable than b2, which is rationalized by its partially solvated W ligand adjacent to the H⁺Pym moiety.

For all n = 4 isomers, we fail to optimize Pym–H⁺W₄ structures with the additional proton located at the solvent site, because of barrierless proton transfer leading to formation of the corresponding more stable H⁺Pym–W₄ structures. This result is similar to previous computational efforts^66,67 and at first glance surprising because the proton affinity reported for W₄ is substantially higher than that of Pym (PA = 900 vs. 886 kJ mol⁻¹), in line with the mass spectrometric observation of exothermic bimolecular proton transfer in ion–molecule reaction (1).^66,67 The lack of intracluster proton transfer (ICPT) is rationalized by the difference in solvation energies in Pym–H⁺W₄ and H⁺Pym–W₄, which compensates for the difference in the PA of Pym and W₄. One has also to keep in mind that the minimum geometries of both cyclic W₄ and H⁺W₄ are not conserved during the formation of conceivable Pym–H⁺W₄ and H⁺Pym–W₄ clusters, which also influences the effective PA values of Pym and W₄via solvation and reorganization effects.

The IRPD spectrum of H⁺Pym–W₄ is compared in Fig. 10 to the IR spectra predicted for the cyclic, linear, and branched isomers, along with the spectrum computed for cyclic W₄. Compared to the IRPD spectra recorded for n = 1–3, the signal-to-noise ratio of the n = 4 spectrum is quite low due to the reduced parent ion signal (Fig. 1), making the assignments less certain for the larger hydrate. Three sharp bands A (3740 cm⁻¹), C (3716 cm⁻¹), and B (3648 cm⁻¹) are observed in the free OH stretch range above 3600 cm⁻¹, and assigned to ν₃, ν_f, and ν₁, respectively. These are accompanied by a relatively broad and weakly resolved feature between 3000 and 3500 cm⁻¹ in the bound OH stretch range, which may be divided into transitions D1 (3464 cm⁻¹), D2 (3393 cm⁻¹), D3 (3200 cm⁻¹), and E (3087 cm⁻¹). The bending overtones of the W ligands (2β_OH, band X) may also contribute to some extent to the signal in the spectral range in the vicinity of band D3. Although the quality of the IRPD spectrum is not sufficient to single out the dominating contributing structures, we attempt to tentatively explain the spectrum in terms of the two most stable isomers (which however does not imply the absence of other isomers). Unlike the n = 1–3 clusters, discernible intensity occurs in the spectral range near 3460 cm⁻¹ (D1), which is characteristic of weakly-bonded ν^b_OH modes of single-donor single-acceptor W ligands, and thus a unique signature of the most stable ring isomer, with calculated frequencies of 3529 and 3510 cm⁻¹. The two ν^b_OH modes of the W ligand attached to H⁺Pym (3310 and 3304 cm⁻¹) may explain the broad band D3, while the overlapping ν₃ and ν_f modes of the ring isomer at 3715 and 3712 cm⁻¹ are attributed to band C at 3716 cm⁻¹ and its ν₁ mode (3630 cm⁻¹) to the weak feature B at 3648 cm⁻¹. The free OH stretch bands A–C may also contain ν₃, ν_f, and ν₁ modes of the b2 isomer predicted at 3741/3739, 3697, and 3650/3649 cm⁻¹, respectively. Its three close lying ν^b_OH modes at 3423, 3380, and 3348 cm⁻¹ can be ascribed to band D2 (3393 cm⁻¹). We further assign the unique H-bonded and comparatively intense ν^b_CH mode (3063 cm⁻¹) to the weak band E (3087 cm⁻¹). The assignment of the experimental spectrum could also be extended to the other isomers, and in fact, the presence of all these low-lying isomers (E₀ < 205 cm⁻¹) seems plausible. The smooth evolution of the IRPD spectra of H⁺Pym–W_n with n = 1–4 in Fig. 1 does not provide any experimental evidence for ICPT in this size range, in line with our computational results.

3.7 Effect of solvent environment and cluster growth

The analysis of the IRPD spectra of H⁺Pym–L_n with L = W (n = 1–4) and L = N₂ (n = 1) with the aid of DFT calculations provides detailed insight into the preferred protonation site, the acidity of the NH group, the interaction potential with quadrupolar and dipolar ligands and the evolution of the microhydration network of this fundamental biomolecular building block. Significantly, these IRPD spectra provide the first spectroscopic information about isolated H⁺Pym and its clusters. From the H⁺Pym–L_n spectra it is proven for the first time by spectroscopic means that isolated H⁺Pym indeed protonates at the N atom, as suggested from mass spectrometric and quantum chemical studies,^66–68 as well as condensed phase data.¹¹³ From the H⁺Pym–N₂(π) spectrum, we derive an accurate value for the NH stretch frequency as ν_NH = 3391 ± 3 cm⁻¹. This value may be compared to ν_NH frequencies of related aromatic (heterocyclic) ions, such as protonated imidazole (3470 cm⁻¹),⁸⁴ oxazole (3470 cm⁻¹),⁷⁷ 5-hydroxyindole (3405, 3478, 3503 cm⁻¹ for C3/C4/O-protonation),⁷⁹ and benzonitrile (3555 ± 3 cm⁻¹),⁷⁸ illustrating that the NH group of H⁺Pym has a relatively high acidity leading to low ν_NH. As a result, the NH⋯L ionic H-bonds are relatively strong, and the preferred binding motif for both hydrophobic nonpolar ligands (N₂) and hydrophilic polar ligands (W). Due to the higher PA of W as compared to N₂ (494 vs. 691 kJ mol⁻¹),⁶⁹ the H-bond in H⁺Pym–W(H) is much stronger than in H⁺Pym–N₂(H), as evident from the larger D₀ value (5854 vs. 1530 cm⁻¹), the shorter R_NH⋯L bond (1.688 vs. 2.061 Å), larger values for E⁽²⁾, ρ*, and Δq (94 vs. 36 kJ mol⁻¹, 0.047 vs. 0.021 a.u., 55 vs. 24 me), and the larger perturbation of the NH group (Δr_NH = 27 vs. 6 mÅ), −Δν_NH = 463 vs. 119 cm⁻¹, ΔI_NH = 1553 vs. 594 km mol⁻¹. N-protonation of Pym decreases the acidiy of the C–H bonds, as illustrated by the increase in the ν_CH values. Neutral Pym–Ar/N₂ dimers prefer π-stacking to the aromatic ring because of the dominant dispersion forces between these nonpolar ligands and the aromatic π-electron system of Pym, and the binding energy of Pym–N₂(π) has been estimated as D₀ = 384 ± 33 cm⁻¹ from fluorescence spectroscopy.^114,115 Despite the excess charge, ionization of Pym–N₂(π) induces only a minor increase in bond strength (D₀ = 479 ± 33 cm⁻¹ derived from ΔD₀ = 95 cm⁻¹),¹⁰⁰ because N₂ rotates by 90° upon ionization to optimize the charge-quadrupole and charge-induced dipole forces. On the other hand, our calculations yield D₀ = 858 cm⁻¹ for H⁺Pym–N₂(π), suggesting that protonation changes the preference from π-stacking to H-bonding (D₀ = 1530 cm⁻¹) because of the high acidity of the newly formed NH group, so that H⁺Pym–N₂(π) is much less abundant than H⁺Pym–N₂(H) in our plasma expansion (∼20%). For the polar W ligand, this effect is more dramatic because the energy gap between π-stacking and H-bonding increases from 672 to 2773 cm⁻¹, so that only the H⁺Pym–W(H) global minimum is detected. The strength of the NH⋯O ionic H-bond in H⁺Pym–W may be compared to that in related aromatic clusters with an ionic NH⋯W bond, such as protonated benzonitrile (D₀ = 6924 cm⁻¹),⁵⁰ oxazole (D₀ = 6094 cm⁻¹),⁷⁷ imidazole (D₀ = 5836 cm⁻¹),⁸⁴ and 5-hydroxyindole (D₀ = 5040/3301/4071 cm⁻¹ for C3/O/C4-protonation),⁷⁹ and the radical cations of aminobenzonitrile (D₀ = 6924 cm⁻¹),⁸⁷ pyrrole (D₀ = 5442 cm⁻¹),⁸³ 5-hydroxyindole (D₀ = 4422 cm⁻¹),⁸⁰ acetanilide (D₀ = 4513 cm⁻¹)⁸² and trans/cis-formanilide (D₀ = 4897/4878 cm⁻¹).⁸¹

The evolution of the IRPD spectra of H⁺Pym–W_n with n = 1–4 show drastic effects upon sequential hydration. Significantly, the IRPD spectra provide for the first time an experimental impression for the microhydration structure of this fundamental protonated biomolecule. The spectra are assigned to the single dominating isomers H⁺Pym–W(H), H⁺Pym–W₂(l1), and H⁺Pym–W₃(b1) for n ≤ 3 and predominantly H⁺Pym–W₄(r) for n = 4, in which a H-bonded W_n solvent network is attached to the acidic NH proton. For n = 3, we also identify a less stable linear H⁺Pym–W₃(l) isomer and for n = 4 there may be more contributing isomers. The computed structures agree well with previous predictions.^66,67 Our computed sequential hydration energies decrease as D₀ = 5854 > 4091 > 3509 > 3221 cm⁻¹ for the global minima of n = 1–4, a trend that is well reproduced by the bond enthalpies measured by mass spectrometry for n = 1–3 (−ΔH⁰ = 16.7 ± 1 > 12.7 ± 1 > 11.0 ± 1 kcal mol⁻¹ or 5840 ± 350 > 4440 ± 350 > 3850 ± 350 cm⁻¹).⁶⁷ In general, the proton affinity of W_n increases with cluster size (PA = 691 < 808 < 862 < 900 kJ mol⁻¹ for n = 1–4),^69–72 and thus the strength of the NH⋯W_n H-bond increases with n (R_NH⋯O = 1.688 > 1.588 > 1.500 > 1.464 Å for n = 1–4, D₀ = 5849 < 8842 < 9534 ∼ 9220 kJ mol⁻¹). This drastic cooperative effect is also visible in the increasing charge transfer from H⁺Pym to W_n (Δq = 55 < 79 < 111 < 129 me), and the E⁽²⁾ and −ρ* values of the NH⋯O ionic H-bond (94 < 141 < 201 < 241 kJ mol⁻¹; 0.047 < 0.061 < 0.077 < 0.086 a.u.). The progressive activation of the acidic NH group by sequential microhydration is documented by the elongation of the N–H bond (Δr_NH = 27 < 44 < 68 < 84 mÅ), which goes along with increasing computed ν_NH redshifts (−Δν_NH = 463 < 738 < 1084 < 1308 cm⁻¹) that are consistent with the measured ones for n = 1–3 (516 < 786 < at least 950 cm⁻¹). In general, there is a monotonic trend for the reduction of ν_NH with the proton affinity of the solvent (Fig. 11). While the ν_NH band (F) shifts to the red upon hydration, the bound and free OH stretch frequencies (A–D) tend to increase by hydration, because of increasing delocalization of the positive partial charge on the solvent cluster. For example, band A (ν₃) moves from 3717 to 3740 cm⁻¹, band B (ν₁) from 3633 to 3648 cm⁻¹, band C (ν_f) from 3698 to 3716, and band D(1) from 3340 to 3464 cm⁻¹. These experimental trends are fully in line with the predictions.

Fig. 11 Observed (blue circles) and calculated (red, B3LYP-D3/aug-cc-pVTZ, global minima) ν^b_NH frequencies of the H-bonded H⁺Pym–L dimers (L = N₂, W) and H⁺Pym–W_n clusters (n ≤ 4) as a function of the PA of the ligands.

Up to n = 3, we do not have any evidence for intracluster proton transfer (ICPT) in H⁺Pym–W_n both experimentally and computationally. This may be expected from the PA values of W_1–3 (PA = 691–862 kJ mol⁻¹),^69–72 which are well below that of Pym (886 kJ mol⁻¹). However, from n ≥ 4 onwards, the PA of W_n clusters are larger (PA = 900 kJ mol⁻¹ for W₄) than for Pym so that one may expect ICPT in H⁺Pym–W_n for n larger than a critical size n_c = 4. However, one has to bear in mind that apart from relative PA values also the solvation energies are important for the determination of n_c.^74,90,91,116 Indeed, there is indirect evidence from mass spectrometry that proton transfer from H⁺Pym to W₄ is exotherm in bimolecular reactions, leading to the observation of H⁺W₄ fragment ions, as expected from the PA values.⁶⁷ Multiphoton ionization of neutral Pym–W_m clusters lead to the detection of [Pym–W_n]H⁺ fragment clusters with n < m,⁶⁶ which is explained by ionization of the W_m moiety and subsequent elimination of OH (and further W ligands). Calculations performed in that work⁶⁶ illustrate that the excess proton in [Pym–W_n]H⁺ with n = 1–4 moves from the H⁺W_m solvent to Pym via barrierless ICPT leading to H⁺Pym–W_n structures. These results are consistent with our calculations for [Pym–W₄]H⁺ and suggest that for this cluster size the excess proton should be attached to Pym and not to W₄, in disagreement with the expectation from the bare PA values. One might argue that the experimental PA of W_n clusters is not a well-defined quantity, because the structures of W_n and H⁺W_n are quite different in the bare clusters and also different from the hydration structure within the [Pym–W_n]H⁺ heteroclusters. On the other hand, the mass spectrometric evidence from reaction (1) is consistent with an exothermic reaction for n ≥ 4, indicating that indeed PA(W₄) > PA(Pym).^66,67 Hence, the lack of ICPT in H⁺Pym–W₄ is attributed to the higher solvation energy compared to Pym–H⁺W₄, which overcomes the difference in PA of W₄ and Pym. Thus, the critical size for ICPT in [Pym–W_n]H⁺ must be n_c > 4. For comparison, for related closed-shell protonated aromatic ions, such ICPT has been observed for benzene (n_c = 1, PA = 746 kJ mol⁻¹),^90,91 naphthalene (n_c = 2, PA = 803 kJ mol⁻¹),^86,88 benzonitrile (n_c = 2, PA = 812 kJ mol⁻¹),⁵⁰ benzaldehyde (n_c = 3, PA = 834 kJ mol⁻¹),⁸⁵ and phenol (n_c = 3, PA = 817 kJ mol⁻¹),⁸⁹ but not for aniline up to n = 6 (PA = 883 kJ mol⁻¹).¹¹⁷

It is instructive to compare H⁺Pym–W_n with neutral Pym–W_n to evaluate the drastic effects of protonation on microhydration with respect to both the interaction energy and the structure of the H-bonded solvent network. The geometry and bonding of neutral Pym–W_n clusters have been characterized by microwave (n = 1),⁹² matrix isolation IR (n = 1–2),⁹³ and multiphoton ionization spectroscopy (n = 1–6),⁶⁶ along with quantum chemical calculations (n = 1–2). Pym–W adopts a coplanar structure with a OH⋯N H-bond between the OH donor of W and the basic N atom of Pym as acceptor. This neutral OH⋯N H-bond is much weaker and longer (D₀ = 1790 cm⁻¹, R_OH⋯N = 1.946 Å, Fig. S8 in the ESI†) than the NH⋯O ionic H-bond in H⁺Pym–W(H) between the highly acidic NH proton donor and W, which is stabilized by strong cation–dipole forces (D₀ = 5854 cm⁻¹, R_NH⋯O = 1.688 Å). Furthermore, the structures computed for Pym–W₂ have an H-bonded hydration network incorporating the neighboring CH group as weak proton donor or forming a second H-bond to the highly basic second N atom of Pym as proton acceptor.^66,93 Thus, the additional acidic proton in H⁺Pym strongly increases the interaction with W_n and forms hydration motifs in which the W_n solvent cluster grows away from the aromatic molecule because of the strong anisotropy of the dominant cation–dipole interaction absent the neutral cluster.

4. Concluding remarks

In summary, we combine IRPD spectroscopy of mass-selected H⁺Pym–L_n clusters with L = W (n = 1–4) and L = N₂ (n = 1) in the sensitive CH, NH, and OH stretch range with DFT calculations at the B3LYP-D3/aug-cc-pVTZ level to unravel the solvation structure around this protonated biomolecular building block. Significantly, these spectra provide the first spectroscopic information about isolated H⁺Pym and its clusters with nonpolar and polar ligands. As such, they serve as benchmark for the interaction of protonated nucleobases with a polar hydrophilic protic solvent (W) and a nonpolar hydrophobic aprotic solvent (N₂). The salient results may be summarized as follows. In agreement with previous indirect mass spectrometric data and quantum chemical calculations,^66–68 as well as condensed phase measurements,¹¹³ the analysis of the H⁺Pym–L_n spectra provide the first unambiguous spectroscopic evidence that isolated H⁺Pym has a strong energetic preference (>200 kJ mol⁻¹) for protonation at one of the two equivalent basic N atoms rather than at the C atoms. This is expected because C-protonation strongly perturbs the stability of the aromatic π-electron system. The H⁺Pym–N₂ spectrum is interpreted with the more stable H-bonded H⁺Pym–N₂(H) global minimum and a minor contribution of the less stable stacked H⁺Pym–N₂(π) isomer (∼20%). From the latter spectrum, the ν_NH frequency of bare H⁺Pym is extracted as 3391 ± 3 cm⁻¹. Moreover, the ν_CH frequencies of H⁺Pym are higher than those in neutral Pym, indicating that N-protonation strengthens the aromatic C–H bonds. The H⁺Pym–W spectrum is interpreted with a single H-bonded H⁺Pym–W(H) isomer, and its linear NH⋯W ionic H-bond is much stronger than the NH⋯N₂ H-bond in H⁺Pym–N₂(H) because of the higher PA of the ligand. In the larger H⁺Pym–W_n clusters, a H-bonded W_n cluster is attached to the acidic NH group. Thus, the formation of a H-bonded hydration network (external solvation) supported by large cooperative threebody effects arising from induction forces is strongly preferred to interior ion solvation suffering from small noncooperative threebody effects arising from charge delocalization. For increasing n, the PA of W_n increases, and as a result the NH group is progressively activated upon sequential microhydration. However, no intracluster proton transfer from H⁺Pym to W_n is observed in H⁺Pym–W_n for the size range n ≤ 4, although the PA of W₄ exceeds the one of Pym by 14 kJ mol⁻¹. This result demonstrates that the PA values is not the only criterion for determining the threshold size for ICPT, and differences in solvation energies must be taken into account as well. Thus, the critical size for ICPT in [Pym–W_n]H⁺ must be n_c ≥ 5, and the determination of its exact value remains as a challenging topic of future computational and experimental work. Although the IRPD spectra (at least for n ≤ 3) are well assigned by the most stable static structures at T = 0 K (E₀) as well as T = 289.15 K (G) including at least part of entropic effects at elevated temperatures, it would be interesting to perform molecular dynamics simulations to unravel dynamical effects in more detail. Comparison of the properties of H⁺Pym–W_n with those of neutral Pym–W_n clusters reveals the drastic effects of protonation on microhydration, with respect to both their H-bonded structures and their interaction strength.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by Deutsche Forschungsgemeinschaft (DFG, project DO 729/3-3).

References

1. K. Wei, E. Karen and W. Joanne, Curr. Drug Metab., 2004, 5, 63–84.
2. W. Saegner, Principles of Nucleic Acid Structure, Springer-Verlag New York, 1984.
3. D. Armentano, G. De Munno, L. Di Donna, G. Sindona, G. Giorgi and L. Salvini, J. Am. Soc. Mass Spectrom, 2004, 15, 268–279.
4. S. Y. Han, S. H. Lee, J. Chung and H. B. Oh, J. Chem. Phys., 2007, 127, 245102.
5. D. Leitner, W. Schröder and K. Weisz, J. Am. Chem. Soc., 1998, 120, 7123–7124.
6. S. W. Powell, L. Jiang and I. M. Russu, Biochemistry, 2001, 40, 11065–11072.
7. L. D. Williams and B. R. Shaw, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 1779.
8. C. H. Kang, I. Berger, C. Lockshin, R. Ratliff, R. Moyzis and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 11636.
9. C. Kang, I. Berger, C. Lockshin, R. Ratliff, R. Moyzis and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 3874.
10. D. E. Draper, RNA, 2004, 10, 335–343.
11. U. Nagaswamy, M. Larios-Sanz, J. Hury, S. Collins, Z. Zhang, Q. Zhao and G. E. Fox, Nucleic Acids Res., 2002, 30, 395–397.
12. S. Lemieux and F. Major, Nucleic Acids Res., 2006, 34, 2340–2346.
13. C. Marian, D. Nolting and R. Weinkauf, Phys. Chem. Chem. Phys., 2005, 7, 3306–3316.
14. D. Nolting, C. Marian and R. Weinkauf, Phys. Chem. Chem. Phys., 2004, 6, 2633–2640.
15. D. Nolting, R. Weinkauf, I. V. Hertel and T. Schultz, ChemPhysChem, 2007, 8, 751–755.
16. J.-P. Schermann, Spectroscopy and Modeling of Biomolecular Building Blocks, Elsevier, Amsterdam, 2008.
17. J. L. Wilcox, A. K. Ahluwalia and P. C. Bevilacqua, Acc. Chem. Res., 2011, 44, 1270–1279.
18. J. E. Gee and D. M. Miller, Am. J. Med. Sci., 1992, 304, 366–372.
19. M. D. Frank-Kamenetskii and S. M. Mirkin, Annu. Rev. Biochem., 1995, 64, 65–95.
20. E. N. Nikolova, G. B. Goh, C. L. Brooks and H. M. Al-Hashimi, J. Am. Chem. Soc., 2013, 135, 6766–6769.
21. I. Berger, C. Kang, A. Fredian, R. Ratliff, R. Moyzis and A. Rich, Nat. Struct. Biol., 1995, 2, 416–425.
22. J. L. Asensio, A. N. Lane, J. Dhesi, S. Bergqvist and T. Brown, J. Mol. Biol., 1998, 275, 811–822.
23. S. M. Mirkin, Nature, 2007, 447, 932–940.
24. K. M. Vasquez, L. Narayanan and P. M. Glazer, Science, 2000, 290, 530.
25. P. B. Dervan, Bioorg. Med. Chem., 2001, 9, 2215–2235.
26. D. Zhong, S. K. Pal and A. H. Zewail, Chem. Phys. Lett., 2011, 503, 1–11.
27. P. Ball, Chem. Rev., 2008, 108, 74–108.
28. Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415.
29. M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866.
30. S. K. Pal and A. H. Zewail, Chem. Rev., 2004, 104, 2099–2124.
31. B. Bagchi, Chem. Rev., 2005, 105, 3197–3219.
32. C. Mattos, Trends Biochem. Sci., 2002, 27, 203–208.
33. B. Halle and V. P. Denisov, Biopolymers, 1998, 48, 210–233.
34. B. Schneider, D. Cohen and H. M. Berman, Biopolymers, 1992, 32, 725–750.
35. M. Feig and B. M. Pettitt, Biopolymers, 1998, 48, 199–209.
36. H. R. Drew and R. E. Dickerson, J. Mol. Biol., 1981, 151, 535–556.
37. E. Liepinsh, G. Otting and K. Wüthrich, Nucleic Acids Res., 1992, 20, 6549–6553.
38. B. Nguyen, S. Neidle and W. D. Wilson, Acc. Chem. Res., 2009, 42, 11–21.
39. S. K. Pal, L. Zhao and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8113.
40. T. V. Chalikian, G. E. Plum, A. P. Sarvazyan and K. J. Breslauer, Biochemistry, 1994, 33, 8629–8640.
41. T. V. Chalikian, J. Völker, A. R. Srinivasan, W. K. Olson and K. J. Breslauer, Biopolymers, 1999, 50, 459–471.
42. C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544.
43. M. R. A. Blomberg and P. E. M. Siegbahn, Biochim. Biophys. Acta, Bioenerg., 2006, 1757, 969–980.
44. H. Ishikita and K. Saito, J. R. Soc., Interface, 2014, 11, 20130518.
45. B. Giese and S. Wessely, Chem. Commun., 2001, 2108–2109.
46. A. Filippi, C. Fraschetti, F. Rondino, S. Piccirillo, V. Steinmetz, L. Guidoni and M. Speranza, Int. J. Mass Spectrom., 2013, 354-355, 54–61.
47. P. Hobza and K. M. Dethlefs, Non-Covalent Interactions: Theory and Experiment, Royal Society of Chemistry, Cambridge, UK, 2009.
48. M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612.
49. K. Chatterjee and O. Dopfer, Chem. Sci., 2018, 9, 2301–2318.
50. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 25226–25246.
51. K. Chatterjee, Y. Matsumoto and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3351–3355.
52. O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168.
53. O. Dopfer and M. Fujii, Chem. Rev., 2016, 116, 5432–5463.
54. E. D. Raczyńska, J. F. Gal, P. C. Maria, K. Zientara and M. Szelag, Anal. Bioanal. Chem., 2007, 389, 1365–1380.
55. J. K. Lee, Int. J. Mass Spectrom., 2005, 240, 261–272.
56. R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2007, 129, 569–580.
57. A. Zhachkina, M. Liu, X. Sun, F. S. Amegayibor and J. K. Lee, J. Org. Chem., 2009, 74, 7429–7440.
58. S. Ø. Pedersen, C. S. Byskov, F. Turecek and S. B. Nielsen, J. Phys. Chem. A, 2014, 118, 4256–4265.
59. M. Pitzer, C. Ozga, C. Küstner-Wetekam, P. Reiß, A. Knie, A. Ehresmann, T. Jahnke, A. Giuliani and L. Nahon, J. Phys. Chem. A, 2019, 123, 3551–3557.
60. M. Nuevo, S. N. Milam, S. A. Sandford, J. E. Elsila and J. P. Dworkin, Astrobiology, 2009, 9, 683–695.
61. P. P. Bera, M. Nuevo, S. N. Milam, S. A. Sandford and T. J. Lee, J. Chem. Phys., 2010, 133, 104303.
62. E. Mendoza, G. C. Almeida, D. P. P. Andrade, H. Luna, W. Wolff, M. L. M. Rocco and H. M. Boechat-Roberty, Mon. Not. R. Astron. Soc., 2013, 433, 3440–3452.
63. P. G. Stoks and A. W. Schwartz, Nature, 1979, 282, 709–710.
64. P. G. Stoks and A. W. Schwartz, Geochim. Cosmochim. Acta, 1981, 45, 563–569.
65. M. P. Callahan, K. E. Smith, H. J. Cleaves, J. Ruzicka, J. C. Stern, D. P. Glavin, C. H. House and J. P. Dworkin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13995.
66. B. Zhang, Y. Cai, X. Mu, N. Lou and X. Wang, J. Chem. Phys., 2002, 117, 3701–3710.
67. A. M. Hamid, P. Sharma, M. Samy El-Shall, R. Hilal, S. Elroby, S. G. Aziz and A. O. Alyoubi, J. Chem. Phys., 2013, 139, 084304.
68. V. Q. Nguyen and F. Tureček, J. Am. Chem. Soc., 1997, 119, 2280–2290.
69. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
70. D. J. Goebbert and P. G. Wenthold, Eur. J. Mass Spectrom., 2004, 10, 837–845.
71. A. Courty, M. Mons, J. Le Calvé, F. Piuzzi and I. Dimicoli, J. Phys. Chem. A, 1997, 101, 1445–1450.
72. R. Knochenmuss, O. Cheshnovsky and S. Leutwyler, Chem. Phys. Lett., 1988, 144, 317–323.
73. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Chem. Phys. Lett., 2004, 399, 412–416.
74. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 32262–32271.
75. I. K. Attah, S. P. Platt, M. Meot-Ner, M. S. El-Shall, S. G. Aziz and A. O. Alyoubi, Chem. Phys. Lett., 2014, 613, 45–53.
76. A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., Int. Ed., 2012, 51, 4925–4929.
77. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2019, 123, 7637–7650.
78. K. Chatterjee and O. Dopfer, Astrophys. J., 2018, 865, 114.
79. J. Klyne and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 2706–2718.
80. J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092–3108.
81. J. Klyne, M. Schmies, M. Fujii and O. Dopfer, J. Phys. Chem. B, 2015, 119, 1388–1406.
82. J. Klyne, M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3148–3164.
83. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986.
84. H.-S. Andrei, N. Solcà and O. Dopfer, ChemPhysChem, 2006, 7, 107–110.
85. O. Dopfer, A. Patzer, S. Chakraborty, I. Alata, R. Omidyan, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2014, 140, 124314.
86. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2020, 124, 1134–1151.
87. M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, J. Chem. Phys., 2014, 141, 214301.
88. I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S.-s. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 074307.
89. M. Katada and A. Fujii, J. Phys. Chem. A, 2018, 122, 5822–5831.
90. E. S. Kryachko and M. T. Nguyen, J. Phys. Chem. A, 2001, 105, 153–155.
91. T. C. Cheng, B. Bandyopadhyay, J. D. Mosley and M. A. Duncan, J. Am. Chem. Soc., 2012, 134, 13046–13055.
92. S. Melandri, M. E. Sanz, W. Caminati, P. G. Favero and Z. Kisiel, J. Am. Chem. Soc., 1998, 120, 11504–11509.
93. A. Destexhe, J. Smets, L. Adamowicz and G. Maes, J. Phys. Chem., 1994, 98, 1506–1514.
94. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
95. M. J. Frisch, et al., Gaussian 09, version D.01, Gaussian, Inc., Wallingford, CT, 2009.
96. B. E. Rocher-Casterline, L. C. Ch'ng, A. K. Mollner and H. Reisler, J. Chem. Phys., 2011, 134, 211101.
97. K. Sharkas, K. Wagle, B. Santra, S. Akter, R. R. Zope, T. Baruah, K. A. Jackson, J. P. Perdew and J. E. Peralta, Proc. Natl. Acad. Sci. U. S. A., 2020, 201921258.
98. L. Bokobza-Sebagh and J. Zarembowitch, Spectrochim. Acta, Part A, 1976, 32, 797–805.
99. K. K. Innes, I. G. Ross and W. R. Moomaw, J. Mol. Spectrosc., 1988, 132, 492–544.
100. S. Sato, K. Omiya and K. Kimura, J. Electron Spectrosc. Relat. Phenom., 1998, 97, 121–129.
101. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman Spectra of Polyatomic Molecules, Krieger Publishing Company, Malabar, FL, 1991.
102. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
103. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
104. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
105. L. Fernholt and C. Romming, Acta Chem. Scand., 1978, 32, 271–273.
106. R. C. Lord, A. L. Marston and F. A. Miller, Spectrochim. Acta, 1957, 9, 113–125.
107. Z. N. Heim, B. K. Amberger, B. J. Esselman, J. F. Stanton, R. C. Woods and R. J. McMahon, J. Chem. Phys., 2020, 152, 104303.
108. S. Albert and M. Quack, J. Mol. Spectrosc., 2007, 243, 280–291.
109. F. Milani-Nejad and H. D. Stidham, Spectrochim. Acta, Part A, 1975, 31, 1433–1453.
110. A. G. Császár, G. Czakó, T. Furtenbacher, J. Tennyson, V. Szalay, S. V. Shirin, N. F. Zobov and O. L. Polyansky, J. Chem. Phys., 2005, 122, 214305.
111. D. Roth and O. Dopfer, Phys. Chem. Chem. Phys., 2002, 4, 4855–4865.
112. R. V. Olkhov and O. Dopfer, Chem. Phys. Lett., 1999, 314, 215–222.
113. J. Riand, M. T. Chenon and N. Lumbroso-Bader, J. Am. Chem. Soc., 1977, 99, 6838–6845.
114. H. Abe, Y. Ohyanagi, M. Ichijo, N. Mikami and M. Ito, J. Phys. Chem., 1985, 89, 3512–3521.
115. N. Mikami, Y. Sugahara and M. Ito, J. Phys. Chem., 1986, 90, 2080–2085.
116. D. Bing, T. Hamashima, C.-W. Tsai, A. Fujii and J.-L. Kuo, Chem. Phys., 2013, 421, 1–9.
117. T. M. Chang, J. S. Prell, E. R. Warrick and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 15805–15813.
118. Z. S. Huang and R. E. Miller, J. Chem. Phys., 1989, 91, 6613–6631.
119. F. Huisken, M. Kaloudis and A. Kulcke, J. Chem. Phys., 1996, 104, 17–25.
120. K. Kuyanov-Prozument, M. Y. Choi and A. F. Vilesov, J. Chem. Phys., 2010, 132, 014304.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02110e

---