A kinetic study of the N(2D) + C2H4 reaction at low temperature†
Abstract
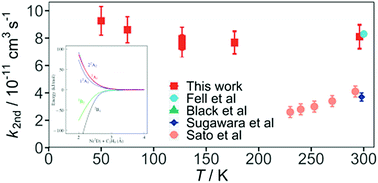
Electronically excited nitrogen atoms N(2D) are important species in the photochemistry of N2 based planetary atmospheres such as Titan. Despite this, few N(2D) reactions have been studied over the appropriate low temperature range. During the present work, rate constants were measured for the N(2D) + ethene (C2H4) reaction using a supersonic flow reactor at temperatures between 50 K and 296 K. Here, a chemical reaction was used to generate N(2D) atoms, which were detected directly by laser induced fluorescence in the vacuum ultraviolet wavelength region. The measured rate constants displayed very little variation as a function of temperature, with substantially larger values than those obtained in previous work. Indeed, considering an average temperature of 170 K for the atmosphere of Titan leads to a rate constant that is almost seven times larger than the currently recommended value. In parallel, electronic structure calculations were performed to provide insight into the reactive process. While earlier theoretical work at a lower level predicted the presence of a barrier for the N(2D) + C2H4 reaction, the present calculations demonstrate that two of the five doublet potential energy surfaces correlating with reagents are likely to be attractive, presenting no barriers for the perpendicular approach of the N atom to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of ethene. The measured rate constants and new product channels taken from recent dynamical investigations of this process are included in a 1D coupled ion-neutral model of Titan's atmosphere. These simulations indicate that the modeled abundances of numerous nitrogen bearing compounds are noticeably affected by these changes.
C bond of ethene. The measured rate constants and new product channels taken from recent dynamical investigations of this process are included in a 1D coupled ion-neutral model of Titan's atmosphere. These simulations indicate that the modeled abundances of numerous nitrogen bearing compounds are noticeably affected by these changes.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...