Open Access Article
Open Access ArticleBalancing dipolar and exchange coupling in biradicals to maximize cross effect dynamic nuclear polarization†
Asif
Equbal
a,
Kan
Tagami
a and
Songi
Han
 *ab
*ab
aDepartment of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106, USA. E-mail: songi@chem.ucsb.edu; Tel: +1 805-832-7461
bDepartment of Chemical Engineering, University of California, Santa Barbara, California 93106, USA
First published on 26th May 2020
Abstract
Dynamic nuclear polarization (DNP) by the cross effect (CE) has become a game changer for solid-state nuclear magnetic resonance (NMR) spectroscopy. The efficiency of CE-DNP depends on the strength of the electron–electron coupling in biradical polarizing agents. Hence, the focus lately has been on designing biradicals with a large net exchange (J) and dipolar (D) coupling. In this study, we reveal that the crucial factor for CE-DNP is not the large sum, J + D, but rather the relative magnitude of J and D, expressed as the J/D ratio. We show that the mechanistic basis of this interference lies in the isotropic vs. the anisotropic nature of the J and D couplings, respectively. This interference can lead to a small (effective) electron–electron coupling for many orientations even when J + D is large, resulting in non-adiabatic rotor-events. We find that when 0 < |J/D| < 1 the CE-DNP efficiency is attenuated for the majority of orientations, with greater attenuation observed at higher magnetic fields and faster magic-angle spinning (MAS) frequency. The interference effect of J and D coupling introduced in this study can explain why many biradicals with high or comparable J + D still show significantly divergent DNP performances. We debut J/D as a consequential criteria for designing efficient biradicals to robustly perform across a large range of B0 fields and MAS frequencies.
1. Introduction
Dynamic nuclear polarization (DNP) is rapidly changing the scope of solid-state nuclear magnetic resonance (NMR) by amplifying its sensitivity by several orders of magnitude. DNP amplified NMR has provided access to structural biology and material characterization, well beyond what was possible with traditional NMR.1–6 Of the various DNP mechanisms in insulating solids, cross effect (CE) DNP has become the most powerful method to enhance the sensitivity of solid-state nuclear magnetic resonance (NMR), especially under magic-angle spinning (MAS). This is because the microwave power requirement for transferring polarization from electron to nucleus is much lower in CE than in solid effect (SE)- another important DNP mechanism. However, in spite of tremendous improvement, the efficiency of CE-DNP is still far below its theoretical maximum. Furthermore, it deteriorates with increasing magnetic field (B0) and/or MAS frequency (νr).7 Concerted efforts are invested into improving the CE-DNP efficiency, especially at the experimentally important regime of high B0 and fast νr for achieving high resolution and high sensitivity for NMR.8–11The CE-DNP is achieved via simultaneous flip–flop–flip of two coupled electron (e) spins and a dipolar coupled nuclear (n) spin with Larmor frequency equal to the frequency difference of the two coupled e spins.12,13 The population difference between the electron spins is transferred to the nuclear spins matching the CE conditions, and this enhanced polarization of the directly coupled, core nuclei is subsequently transferred to bulk nuclei via spin-diffusion.14 In CE DNP, effective coupling of the two CE-inducing electron spins is key to its polarization transfer efficiency. This has led to massive effort in the pursuit of optimizing the chemical linker joining the radical (electron) centers, molecular geometry, solubility, and the associated electron spin relaxation rates of the polarizing agent, typically a biradical.15–18
A common assumption in the literature is that increasing the sum of e–e dipolar (D) and exchange coupling (J), J + D to higher optimum values will increase the CE-DNP enhancement. Augmenting the J value, irrespective of D, has also been presumed to maximize DNP enhancement and minimize the deleterious nuclear depolarization effect under MAS, including in our own studies.19,20 However, this simplified assumption does not consider the relative contribution of D and J. Notably, these two couplings are of different nature with respect to the spatial orientations of molecules in a magnetic field. In this study, we share our discovery that the interference between these two couplings has a huge impact on the CE-DNP enhancement, as well as depolarization, emphasizing that an optimum balance between D and J of the CE-inducing electron spin pair is critical for efficient DNP.
2. Theory
To understand the influence of J coupling on CE-DNP enhancement we use a theoretical framework of MAS-DNP presented by Thurber et al. and Mentink-Vigier et al.12,13,21 These studies used the Landau–Zener (LZ) model to explain the e spin dynamics relevant for CE-DNP under MAS that renders the microwave (μw) induced transitions and the e spin–spin (e–e flip–flop and e–e–n flip–flop–flip) transitions time-dependent. They are also termed rotor-events, as the resonance conditions that lead to these transitions are time-dependent and periodic with respect to sample rotation. According to the LZ model, the adiabatic transition probability (P) at the energy-level crossing of two states is given by:| P(adiabatic) = 1 − exp(−πE12/Ė). | (1) |
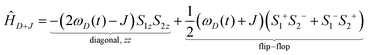 | (2) |
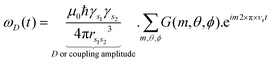 | (3) |
Close examination of the characteristics of ĤD+J in eqn (2) shows that the interference between the dipolar and J couplings can arise from the anisotropic nature of the e–e couplings. In the coupling Hamiltonian, the coefficient ωD(t) is orientation dependent, and is modulated in time between the range of [−D/2, D] due to sample spinning, where D represent the dipolar coupling strength or amplitude. The time-dependent coefficient, ωD(t), depends on the Wigner coefficient: G(m,θ,ϕ)·eim2×π×νrt, where the Fourier index m takes the value of ±1 and ±2, and the angles θ and ϕ define orientation. If D and J are close in magnitude, the effective perturbation (E1) as reflected in the coefficient of the flip–flop term in the coupling Hamiltonian (ωD(t) + J) at the e–e rotor-events can diminish to a small number compared to the rate of crossings Ė for many crystallite orientations; that in turn can make the rotor-event transition diabatic or non-adiabatic in nature. Such rotor-events leads to the equalization of spin polarization or a reduction in the polarization difference between the two electron spins, which eventually results in lower DNP enhancements under μw irradiation conditions, or in larger nuclear depolarization under μw off conditions. This is because the amount of polarization transferred between the nuclear spin and the electron spin in the CE mechanism is proportional to the difference in the polarization difference between the two electron spins relative to the nuclear spin polarization, i.e., ΔPn ∝ ΔPe.22 Therefore, a key strategy to enhancing the CE-DNP efficiency is to maximize the probability of obtaining a large effective coupling at the rotor-events (e–e and e–e–n) for the ensemble of spins.
3. Quantum mechanical simulation results
Experimentally, it is not possible to rationally design a series of radical in which the J and D values are selectively and deliberately varied, while keeping all other spin parameters constant. Therefore, we used advanced quantum mechanical simulations to first find the dependence of CE-DNP enhancement on the sum, J + D and the ratio, J/D of these parameters to clarify basic dependencies and principles. We will next compare our numerical results derived by quantum mechanical simulations with previously published experimental results on eight different polarizing agents (PAs) to test the viability of our discovery.Simulation package
Density matrix simulations in Liouville space have already aided in the understanding of DNP mechanisms, and even in the design of new radical archetypes as PAs.7,19,23,24 Here, we employ the versatile Spin-Evolution package25 to carry out these calculations. Spin-evolution can simulate the spin-dynamics of multi-spin system readily up to 11 spins, mimicking all the essential experimental conditions such as sample-spinning, spin-relaxation, and all key spin interactions including the pseudo-secular coupling interactions. Details on this commercially available package can be found in the original paper by Veshtort et al.,25 in the well maintained online resource (https://spinevolution.com/), as well as in several recent publications from our own group that made extensive use of this simulation package for DNP studies.20,22,26–28 All spin polarization values were calculated with respect to thermal Boltzmann polarization of 1H nuclear spins.Spin-system and parameters
Simulation parameters were primarily modeled on bis-nitroxides that have been the most popular and commercially available polarizing agents for CE-DNP.16–18 Previous computational studies have suggested that tethered bis-nitroxides with nearly perpendicular g-tensor orientations should exhibit maximum probability for CE-DNP.19,23 In our simulations, we modeled a minimal three-spin system, e–e–1H, where the two e spins were chosen to have perpendicular g-tensor orientations and a dipolar coupling of 36 MHz (corresponding to the D coupling value reported for AMUPOL),29 unless mentioned otherwise. DNP enhancement was measured as a function of J. All the other simulation parameters are given in the ESI,† Section-SA. We also modeled the case of a mixed radical displaying a superposition of a broad and narrow EPR lines, as these are the most promising next generation PAs, especially for efficient DNP at higher B0 and faster νr.30–33Influence of J coupling on DNP Enhancement
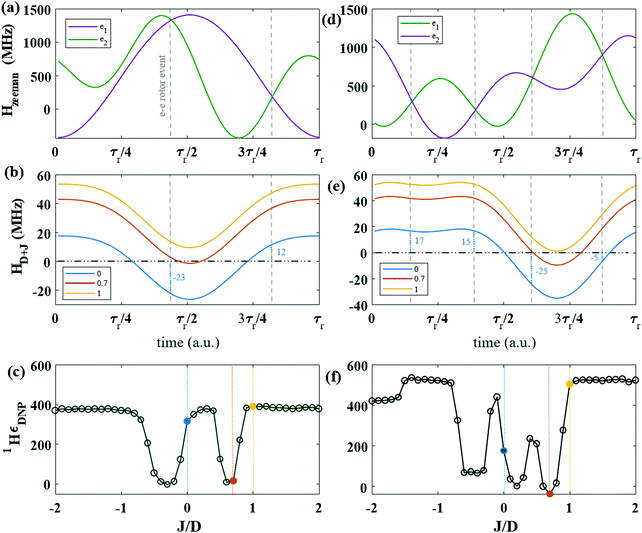
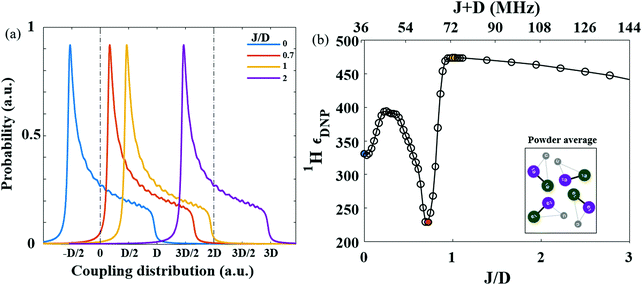
In Section 2, we describe the theory behind the existence of a possible interference between J and D, leading to decreased DNP enhancement. Here, we demonstrate this phenomenon using numerical simulation results. We first scrutinize two (randomly selected) bis-nitroxide radical orientations in an external B0 (with g tensors of the two e spin perpendicular to each other), and subsequently compute the powder-averaged ensemble properties. Fig. 1a and d show the temporal oscillations of the energy levels of the two electron spins participating in CE under MAS during one rotor-period (τr) for two select bis-nitroxide radical orientations with respect to B0. The degeneracy conditions are met when the two electron spins have the same energy, as marked with vertical dashed lines, that also mark the time points for the e–e rotor-events.13 Large e–e coupling at these rotor-events is key to achieving high DNP enhancements. However, large coupling is hard to maintain at rotor events as e–e coupling oscillates in time under MAS. The time-dependence of e–e couplings is illustrated in Fig. 1b for three different relative magnitudes of J over D, namely J/D of 0, 0.7 and 1. In the case where only dipolar coupling is present (i.e. J/D = 0), the ωD(t) values at the two e–e rotor-events during one rotor period are −23 and 12 MHz, respectively (at the intersection of the dashed lines). The effective coupling at these rotor-events can be increased by adding J which is an isotropic coupling, and therefore not oscillated by MAS. However, the value of J should be carefully controlled to ensure that the magnitude of the effective couplings at all e–e rotor events increases, and does not decrease. In the latter case, the addition of exchange interaction J can bring the effective coupling at the rotor event close to zero, and consequently, is detrimental to DNP. This detrimental effect is shown in Fig. 1b: If the added J coupling is close to 23 or −12 MHz, the DNP enhancement will diminish owing to non-adiabatic transitions at either of the two rotor-events. This is reflected in the numerically simulated 1H DNP enhancements as a function of J/D for the selected orientation (Fig. 1c). The two dips at J/D = −0.35 and 0.7 are a result of the interference between the J and D couplings. The analysis holds true in the other select orientation as well (Fig. 1d–f). This orientation gives rise to 4 e–e rotor-events leading to 4 possible deleterious interference conditions that must be avoided in order to obtain consistently high DNP enhancements. Note that different orientations may have different number of e–e rotor events that occur at different time points with respect to the rotor-period. Taken together, any combination of J and D that leads to deleterious interference should be avoided. So far, we have analyzed the effect of J for select orientations to illustrate the interference effect between D and J. However, a real sample will consist of all possible orientations simultaneously and an ensemble analysis is needed.In a powder sample, the spatial distribution of the anisotropic dipolar coupling is represented by a Pake pattern, at any given time point, during the rotor period. The coefficient, ωD, has a range of [−D/2, D], with maximum probability at −D/2 and minimum probability at D. The addition of an isotropic J shifts the coupling distribution (ωD + J), as illustrated in Fig. 2a. In an ideal case, adding J will increase the probability for larger overall (ωD + J) couplings (yielding J/D > 1). However, a non-optimal J can increase the probability for small overall (ωD + J) couplings, as illustrated in Fig. 2a for J/D = 0.7 (red curve). The exact interference pattern between J and D for a powder ensemble is (statistically) dependent on the shape and range of the coupling (ωD + J) distributions at the e–e rotor-events. Hence, a simple analytical prediction of the deleterious regime for J/D cannot be generated from this picture; especially as other factors such as the magnitude of the g-anisotropy, the relative g and D-tensor orientations and the dipolar orientation of the electron-spins influence the exact pattern of interference. We therefore have to find the interference regime numerically for the ensemble.
The interference effect of J on the ensemble was modeled numerically by averaging the DNP enhancement of many orientations. This is shown in Fig. 2b. The DNP enhancement (1H-εDNP) of the e–e–1H three-spin system was calculated as function of the J/D ratio, displayed on the bottom x-axis and the J + D sum, displayed on the top x-axis. The calculation was done at a B0 field of 18.8 T (800 MHz) at optimum μw irradiation conditions. The μw frequency was set at a value corresponding to the 1H Larmor frequency apart from that of the isotropic g value of a nitroxide radical (as in Fig. 1). In the calculations, the J/D and J + D values were modulated by varying J, while the D value was fixed to 36 MHz. It is evident from the shape of the plot shown in Fig. 2b that the 1H-εDNP enhancement does not increase monotonically with increasing J + D. As already observed for select orientations for the bis-nitroxide radical in Fig. 1c and f, a large dip is observed for the powder-averaged DNP enhancement at a range of J/D values. Specifically at J/D = 0.7, and in general under the condition of 0.2 < J/D < 1, the CE-DNP efficiency was dramatically attenuated for bis-nitroxide radicals.
The observed interference between J and D will exist independent of the sign of the J coupling, since the dipolar coupling anisotropy takes both positive and negative values owing to its (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1) orientation dependence (see ESI,† Fig. S7). To present a more complete analysis, we mapped the DNP enhancements for 230 individual bis-nitroxide orientations (relative to B0) for three different J/D values of 0, 0.7 and 1, while keeping all other parameters constant (Fig. 3). The histogram distribution of the enhancements shown in Fig. 3 clearly demonstrates that a J/D of 0.7 leads to strong interference for the majority of bis-nitroxide orientations, and hence reduce the effective coupling (ωD(t) + J) for a large population of orientations. On the other hand, |J/D| > 1 offers optimal DNP enhancements for a large population of bis-nitroxide orientations.
θ − 1) orientation dependence (see ESI,† Fig. S7). To present a more complete analysis, we mapped the DNP enhancements for 230 individual bis-nitroxide orientations (relative to B0) for three different J/D values of 0, 0.7 and 1, while keeping all other parameters constant (Fig. 3). The histogram distribution of the enhancements shown in Fig. 3 clearly demonstrates that a J/D of 0.7 leads to strong interference for the majority of bis-nitroxide orientations, and hence reduce the effective coupling (ωD(t) + J) for a large population of orientations. On the other hand, |J/D| > 1 offers optimal DNP enhancements for a large population of bis-nitroxide orientations.
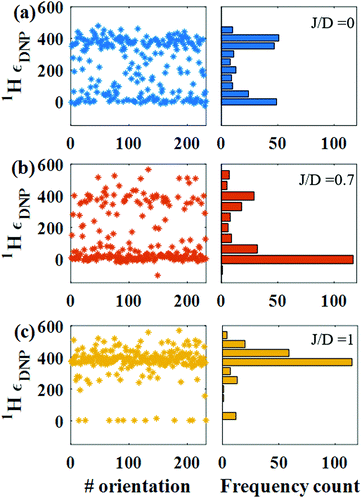 | ||
| Fig. 3 Orientation dependent DNP enhancement. Numerically simulated DNP enhancement of 230 different orientations in a powder and a histogram distribution of their DNP enhancement for three different J/D values, (a) 0, (b) 0.7 and (c) 1. The simulation parameters are the same as in Fig. 2. | ||
Dependence of DNP on magnetic field and MAS frequency
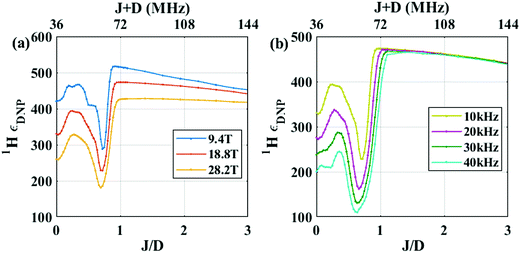
The calculations discussed until now were carried out at a constant external magnetic field (B0) and MAS frequency (νr). We next calculated the DNP enhancement (1H-εDNP) at three different B0 fields of 9.4 T (400 MHz), 18.8 T (800 MHz) and 28.2 T (1.2 GHz) at an optimum μw irradiation frequency. Clearly, the attenuation of 1H-εDNP at J/D = ∼0.7 is observed at all fields, but the interference dip becomes more severe at higher B0 (Fig. 4a). Until now, all enhancement values have been presented with respect to the nuclear Boltzmann polarization under static conditions; and therefore the enhancements do not include depolarization.To investigate the effect on depolarization, we calculated the relative NMR signal intensity under MAS over that under static conditions in the absence of μw irradiation conditions i.e.1H-εdepo = 1H-εspin,no![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μw/1H-εstatic,no
μw/1H-εstatic,no![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μw. We found that the nuclear depolarization showed a similar trend as DNP enhancement with respect to J/D (see ESI,† Fig. S1). Tagami et al. reported that AMUPOl can adopt a distribution of J values in solution, ranging from approximately 12 to 60 MHz depending on the solvent and the sample temperature.20 In another study, Soetbeer et al. had performed multi-frequency EPR29 of AMUPOL in a frozen glassy matrix, and reported the J and D coupling to be ∼30 and ∼36 MHz, respectively.
μw. We found that the nuclear depolarization showed a similar trend as DNP enhancement with respect to J/D (see ESI,† Fig. S1). Tagami et al. reported that AMUPOl can adopt a distribution of J values in solution, ranging from approximately 12 to 60 MHz depending on the solvent and the sample temperature.20 In another study, Soetbeer et al. had performed multi-frequency EPR29 of AMUPOL in a frozen glassy matrix, and reported the J and D coupling to be ∼30 and ∼36 MHz, respectively.
The J/D DNP dependence profile clearly shows that the reported J values for AMUPOL is not optimal to achieve consistently high DNP enhancements, and is especially detrimental at higher B0. Let's take J/D = 0.83 from the Soetbeer et al. study29 as an example. This value lies right on the boundary of the interference dip at 9.4 T, but falls into the interference dip at higher B0, >18.8 T. Therefore, the performance of AMUPOL should deteriorate severely as B0 is increased from 9.4 T to 18.8 T. In fact, a recent study in the literature from Mentink-Vigier et al. reports on dramatically decreasing 1H-εDNP from 43 to 14 fold when going from 9.4 T (& νr = 10 kHz) to 18.8 T (& νr = 8 kHz), respectively,19 corroborating our prediction. According to eqn (1), a smaller perturbation, E1 (or the effective coupling, ωD(t) + J) furthermore attenuates the LZ adiabatic transition probability for e–e–n CE rotor-events. The effect of such interference increases at higher B0 due to an increased rate of the energy crossings, Ė, according to eqn (1), which is owing to an increased g anisotropy with increased B0 for the bis-nitroxide radical. Additionally, increasing the MAS frequency, νr, also increases Ė relative to E1 (eqn (1)), rendering the interference between J and D even more deleterious for CE-DNP. Fig. 4b shows the overlaid 1H-εDNPvs. J/D plots for different MAS frequencies at 18.8 T, with all the other parameters held the same as in Fig. 4a. Clearly, at faster MAS frequency, the interference between J and D becomes more deleterious, causing a larger dip in the interference regime. We will next analyze the MAS frequency dependence of radicals with different J/D values.
The numerical analysis demonstrated that maintaining an optimal balance between J and D (J/D > 1), while ensuring that their sum, J + D, is sufficiently large in magnitude is an effective strategy to maximize the CE-DNP efficiency. However, it is worth noting that, the J coupling should not be too large. This is because a very large J will split the EPR spectral density and reduce the advantageous “self-chirping” effect of MAS that recruits a much larger number of e–e pairs compared to CE-DNP under static conditions.12,34 Also, a large coupling above a threshold value can even abolish the electron polarization differential between the CE-fulfilling electron spins due to homogeneous mixing between the electron spin states fulfilling the CE conditions, which consequently leads to lower DNP effects.33 Using 2D optimization of the coupling and B0 (and νr), we found that J/D in the range of 1.25 to 2.25 correspond to optimum values for a wide range of B0 and νr values. Furthermore, our calculations showed that very large J + D (compared with the nuclear Larmor frequency) leads to attenuation of DNP enhancements. This can be seen by comparing the 1H-εDNPvs. J/D profiles for three different B0: the 1H-εDNP decreases as J/D is increased beyond the optimum value (Fig. 4a). Still, 1H-εDNP remains high as J/D is increased beyond its optimum value for a significant range of J + D. In CE-DNP, the nuclear polarization is strongly correlated with the polarization difference between the two electrons (ΔPe) participating in the CE mechanism, as explained in the theory section. Expectantly, the ΔPe profile as a function of the coupling parameter, J/D, takes a very similar shape as the 1H-εDNP profile. This is shown in ESI,† Fig. S4. This further demonstrates that non-adiabatic transition at the e–e rotor-events is the key reason behind the interference or dip observed in Fig. 3 and 4.
4. Meta-analysis of experimental DNP data
Next, we examine correlations between our numerical analysis, and experimental DNP data. We take this approach because the deliberate and separate tuning of D and J of PAs is beyond the current state of the art of PA synthesis. We analyze published DNP data in the literature of the most widely used biradicals for which J and D values are reported, and mark their J + D and J/D values on our quantum mechanically simulated contour plot of DNP enhancement as a function of J + D and J/D. The aim is not to discuss the superiority of one radical type over another with respect to J and D coupling. In fact, a fair comparison is not possible, given uncertainties and/or unavailability in accurate J value distributions, and given that other electron spin (radical) parameters (e.g. relaxation rates and relative g-tensor orientations) are not held constant for each radical PA compared. In fact, our study by Tagami et al. reported that AMUPOL and TOTAPOL exhibit a wide distribution of J values due to the population of different molecular conformers.20 This distribution depends on the solvent and temperature. Therefore, different conformers would exhibit different interference between D and J, and thus the measured DNP enhancement would depend on sample preparation and cooling methods.35The reported J and D coupling values and DNP enhancements in the literature for these radicals are provided in Table 1. While TOTAPOL has negligible J coupling under typical sample preparation conditions used for DNP experiments20 yielding J/D = 0, TEKPOL has a small J coupling close to the interference region with J/D = 0.16; both conditions lead to a relatively low DNP performance. The J/D value in TEKPOL appears far from optimum, at least for the reported J and D values. However, this is still one of the most commonly used PA in organic solvents and/or for non-aqueous samples, showing a huge scope of development opportunities for PAs in organic solvent. For AMUPOL, the sum J + D ∼ 66 MHz is optimal, but the relative J/D = 0.83 falls within the interference regime at high B0, as discussed earlier, and also shown in Fig. 5a. Optimization of the chemical linker or the functional moieties in the AMUPOL molecule might still offer space for tuning the J/D values into the optimum regime.36,37 Recently, the biradical ASYMPOL-POK19 has been introduced by De Paëpe and coworkers. This radical is reportedly a high performing bis-nitroxide radical at high B0 (18.8 T). Our calculations corroborate this observation with a J + D value of ≥ 196 MHz and a J/D value of ≥2.5 that is large enough to fall outside the interference limit of |J/D| < 1. However, both J + D and J/D values are larger than the required optimum, which may be one of the reasons for its lower performance compared to the theoretical maximum. Overall, the 2D plot (Fig. 5a) shows that the performance of bis-nitroxide radicals exhibit a strong correlation with the e–e coupling parameters, although electron spin relaxation properties remains a major factor that also needs to be carefully considered. Thus, fine tuning the vital parameters, including relative g-tensor, J + D, J/D and electron spin relaxation rate in bis-nitroxides is essential for achieving high CE-DNP enhancements across the relevant experimental regime for MAS DNP (Table 2).
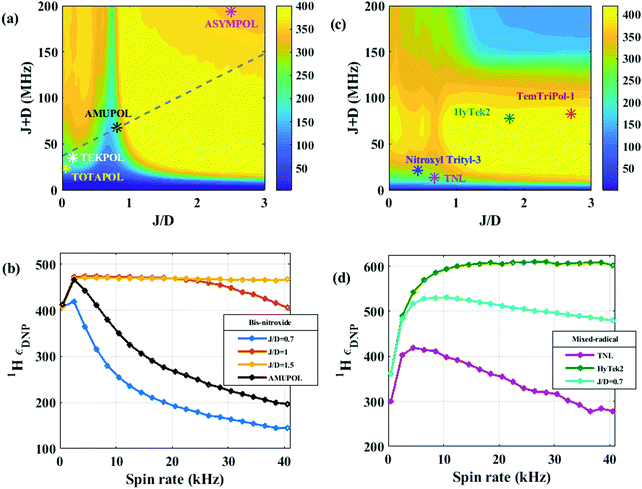 | ||
| Fig. 5 Numerically simulated 2D profile and spin rate dependence. (a) 1H-εDNP for J/D and J + D at 18.8 T B0, using 0.8 MHz μw B1 and at 20 kHz spinning for bis-nitroxide. (b) 1H-εDNPvs. spin rate for bis-nitroxide with different coupling parameters. (c) and (d) are analogous to (a) and (b) respectively for mixed radical systems. All the other spin-parameters are provided in the ESI.† The trace marked with dotted line in (a) essentially maps the plot calculated in Fig. 1a. | ||
| Radical | J + D (MHz) | J/D | [εDNP (B0)] | Ref. |
|---|---|---|---|---|
| a This may have large depolarization, although it is not measured/reported. | ||||
| TemTriPol-1 | (0–200) + 23 = 23–223 | 0–10 | 60 (9.4 T) 51 (18.8 T) | 39 |
| HyTek2 | (30–70) + 28 = 58–98 | 1.07–2.5 | 115 (9.4 T) 140 (18.8 T) | 31 |
| TNT | 172 + 11 = 183 | 15.60 | 7 (18.8 T) | 33 |
| TNL | 5.4 + 8 = 13.4 | 0.67 | 40 (18.8 T)a | 33 |
While bis-nitroxides are currently the most widely used radicals; tethered mixed radicals are gaining in popularity. Significant effort has been made by various research groups in the development of tethered narrow (e.g. Trityl or BDPA) and broad line (e.g. Nitroxide) radicals as mixed-radical or “hybrid-radical” systems. The mixed radicals have shown great potential to maximize the CE-DNP enhancements at high magnetic fields, while simultaneously minimizing the depolarizing effect. Moreover, they require less μw power compared to the bis-nitroxides.32,38–40 Mixed-radicals are fundamentally different from bis-nitroxides for two main reasons: (1) the isotropic g difference of the two electron spins yields a frequency difference close to the 1H Larmor frequency that maximizes the CE probability, and (2) the probability of saturating the narrower EPR line is greater, even at higher B0.38
The contour plots in Fig. 5c map the expected 1H DNP enhancement for a mixed-radical systems with varying J + D and J/D ratio at 18.8 T and 20 kHz νr (contour plots for 1H depolarization with varying J + D and J/D is shown in ESI,† Fig. S3). It should be noted here that given the asymmetry of the g-tensor, the interference pattern is different in these mixed-radical systems compared to bis-nitroxide systems, and moreover is highly dependent on the relative orientations of the interaction D tensor between the narrow and broad-line radicals. Therefore, averaging over relative D-tensor orientations needed to be included in our simulations presented in Fig. 5c. The simulation results showed, again, that the 1H DNP enhancements display a dip for J/D < 1, clearly visible around J/D = 0.7. However, the dips in enhancement are less severe compared to bis-nitroxides. This can be more clearly seen in the horizontal trace in the ESI,† Fig. S2. These dips are also more prominent in the nuclear depolarization profile (ESI,† Fig. S3). In the literature, the mixed radicals have been assumed to exhibit negligible nuclear depolarization effect. However, our analysis shows that this idea only holds when the e–e couplings are optimal. Although the isotropic g-values are separated, the two e spins have partially overlapping anisotropic g tensors. Under the condition of non-optimal J/D, there can be a large nuclear depolarization effect with this radical system due to non-adiabatic e–e rotor events. Overall, to achieve maximum DNP enhancement and minimal depolarization, J/D in the range of 1.25 to 2.25 is optimal. Too large J values split the narrow EPR line of the mixed radical, and hence diminishes the advantage of efficient EPR saturation. Again, finding an balance between J and the magnetic field strength is key. Too small or too large couplings lead to inefficient CE-DNP. This aspect has been discussed and showcased in the literature by Liu and coworkers33 with trityl-nitroxide radicals, TNT and TNL, in which an overly large J of TNT has been shown to be detrimental. In another series of study of nitroxyl-trityl mixed biradical PAs by Bagryanskaya and coworkers, too high or too low J has again been shown to lead to inefficient DNP. Their study of nitroxyl-trityl-140 and Tr–Nf–NO32 found that the experimental enhancements did not strictly scale with J. We performed a 2D optimization of J + D vs. B0 for model mixed radicals, and showed that a J + D of around 1/10 of the 1H Larmor frequency is optimal to achieve 1H-DNP at the optimum J/D (simulated data shown in ESI,† Fig. S5). A large J will split or broaden the narrower EPR line of the mixed radical, and reduce the advantage of the high probability of μw saturation of this narrow line that such a narrow line otherwise holds. This result highlights the crucial point: striking a balance of J and D in mixed radical system is vital for its high performance. A mixed radical that has recently garnered much attention, TemTriPol-1, has been reported to exhibit a wide range of J/D due to molecular flexibility. We therefore place this PA on our simulated map using its reported average coupling parameters, yielding J + D = 83 and J/D = 2.7,39 This places TemTriPol-1 at favorable conditions, which is consistent with its promising performance as a water-soluble PA. Still, its reported performance is far below the theoretical maximum (∼γe/γ1H). This underscores the huge scope left for continued developments in the field of radical design as PAs for DNP.
Effect of MAS frequency on optimal J: HyTek2 and AMUPOL
In the numerically simulated contour plot (Fig. 5c), one can recognize that HyTek2 should be a highly successful radical in this category, as it corresponds to optimal DNP enhancement regime with respect to the coupling parameters. This is in fact corroborated by literature data reported on a high 1H DNP enhancement value of 140 at 18.8 T and under 10 kHz MAS conditions by Wisser et al.31 Furthermore, it was reported that the DNP enhancement of the HyTek2 radical did not attenuate at a faster νr, but rather increase to 185 at νr = 40 kHz compared to ∼130 at νr = 5 kHz. We can attribute this performance to its optimum values for J + D and J/D of 78 and 1.78, respectively. We show simulated results in Fig. 5d that mapped the 1H DNP enhancement as a function of νr at 18.8 T for two conditions: (i) optimal coupling (J + D = 80 MHz and J/D = 2, labeled as HyTek2) and (ii) non-optimal couplings (J + D = 14 MHz and J/D = 0.67 and J + D = 80 MHz (labeled as TNL) and J/D = 0.7). In the optimal range, high enhancements are maintained even under faster νr conditions where Ė is larger, but the number of cross-effect pairs or CE rotor-events per unit time (that is directly proportional to the spin rate) is also higher. The probability of the e–e and e–e–n adiabatic crossing remains significant, as long as the magnitude of the effective e–e couplings (E1) is large compared to the energy-crossing rate (Ė). In fact the trend for HyTek2, when using its reported D and J value, show that the 1H DNP enhancement is predicted to increase by ∼22% when increasing νr from 10 to 40 kHz, which is consistent with the reported observation in the literature.31This holds true even for bis-nitroxide, as illustrated in Fig. 5b. 1H DNP enhancement vs. spin rate is plotted for different J/D parameter, 0.7, 1.0, 1.5 and 0.83 (labelled as AMUPOL). We suggest that it is the non-optimal J/D parameters that leads AMUPOL to yield a large attenuation in the DNP enhancement at faster νr. We assert that an optimum balance between J and D coupling parameters can lead to a better trade-off between the probability of CE per unit time and their adiabaticity. This in turn can maximize the DNP performance at a given condition, as well as maintain it at very high B0, as well as fast νr.
Effect of spin dynamics on the J and D interference
The DNP efficiency depends on a cornucopia of other spin dynamical and structural parameters such as (1) μw power, (2) T1e relaxation, (3) inter-molecular e–e couplings, and (4) relative e spin g-tensor orientations. We next analyzed a select number of these parameters in the context of the present study. The aim is to gain a general understanding of whether the interference effect of J and D is relatively independent of these parameters. To this end, we calculated the J/D profile for bis-nitroxides when the above parameters are varied, fixing all the other parameters as chosen for Fig. 4. Fig. 6a shows 1H-εDNPvs. J/D for three different μw powers. Clearly higher μw power leads to higher enhancement, but the interference between J and D exists independent of the μw power. Similarly, while an optimum T1e is needed to attain optimal EPR saturation, even under effective EPR saturation conditions, the J and D interference effect persists, as shown in Fig. 6b. Next, we analyzed the effect of inter-molecular e–e couplings by extending e1e2n spin system to e1e2e3n. Fig. 6c shows this effect as a function of e1–e3 distance (dipolar coupling). Previous studies have shown that inter-molecular e–e coupling is deleterious to DNP enhancement.41 Our results show that while inter-molecular coupling will decrease the overall DNP enhancement, it will not affect the interference regime. At last, we examined the effect of variation in the relative g-tensor orientation of the two e spins in bis-nitroxide radicals (note that simulations up to here used perpendicular relative g-tensor orientations between the two e spins). Changing the relative g-tensor orientation changes the timing of the e–e rotor events (its position in time, transition probability and frequency). Nevertheless, the interference between J and D remains a robust effect. Although, the exact J/D value where maximum interference is observed may change with the relative g-tensor orientations, in general |J/D| < 1 remains deleterious. Overall, the analysis in Fig. 6 shows that the choice of J/D is probably the most critical parameter to achieve effective CE DNP robustly, especially at high B0 and fast νr.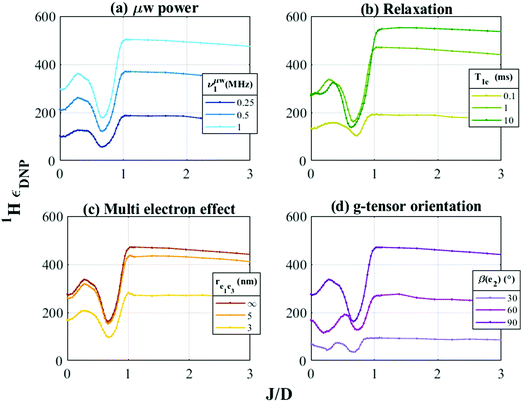 | ||
| Fig. 6 Numerically simulated J/D profiles for bis-nitroxide. 1H-εDNPvs. J/D for varying (a) μw power, (b) T1e relaxation rates, (c) inter-molecular e–e distance (couplings) and (d) relative g-tensor orientation (g-βe2). The simulations were done at 20 kHz spinning, with all the other spin-parameters same as Fig. 4a. In Fig. 6c, the g-tensor of e3 (same as other two e spins) and e1–e3 dipolar coupling were the additional interactions considered in the simulations. | ||
5. Conclusion
In this study we present our discovery of the interference effect of e–e J and D couplings in modulating CE-DNP, and a revised understanding of the role and effects of J and D on the CE-DNP performance. Using quantum mechanical simulations, we demonstrated that non-optimum, |J/D| < 1, can severely impede the CE-DNP enhancement, even if the sum of e–e coupling, J + D, is very large. The interference between J and D is even more pronounced at higher B0 and faster MAS νr regimes. This also explains the reported lower performance seen with many radicals used as PAs at the high B0 (e.g. 18.8 T). The interference between J and D can also aggravate depolarization. Of course, other spin dynamics parameters will also influence the DNP performance, including various electron spin relaxation rates and other EPR spectral properties.27 The best strategy to mitigate the interference between J and D is to synthesize radicals with “Goldilocks” J/D values, numerically found to be between 1.25 < J/D < 2.25. The idea is that a significantly large effective coupling, (ωD(t) + J) must be maintained across the powder orientation distribution, such that e–e and e–e–n rotor events have high adiabaticity. Although higher J/D (>2.5) will not directly interfere with the CE-DNP efficiency, it still can distort the optimal EPR spectral density, which in turn can minimize the constructive self-chirping effect of MAS. Our study also provided a rationale for the high performance observed with TempTriPol-1, ASYMPOL-POK, and in particular with HyTek2. Remarkably, the DNP enhancement when using HyTek2 has been shown to increase with increasing B0, as well as νr, which effect could be replicated with quantum mechanical simulations. However, many of these promising radicals are not yet commercially available, and some are insoluble in aqueous medium or unstable, limiting their current application scope. We believe that our study offers a crucial guideline for the design and synthesis of efficient and ubiquitous radical polarizing agents across a wide range of experimental parameters, B0 and νr for CE-DNP. The synthesis of optimal radicals with optimal chemical-linker, and functional moieties type might be aided by DFT calculations to save time and resources. Also our previous study suggested that sample freezing methods can play an important role in determining the population of molecular conformers with optimal J parameter.20 Even if the design of radicals yielding optimal J and D values is not straightforward, understanding that the most important criteria is not the maximization of J + D, and that the interference between J and D exist, will already avoid investment into deleterious directions. The search for optimum radical is hence still an ongoing endeavor. Lastly, we assert that in the regime of strongly coupled electron spins in concentrated PA, the DNP mechanism in fact may continually transitions from CE to thermal mixing (TM), as observed in the case of Trityl-OX063 where the dominant mechanism crossovered from solid effect to TM at high concentration.42Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Tsatsa Battsengel from UCSB for careful reading of the manuscript. This work was supported by the National Science Foundation Grant No. CHE #1505038 awarded to SH.References
- M. Rosay, L. Tometich, S. Pawsey, R. Bader, R. Schauwecker, M. Blank, P. M. Borchard, S. R. Cauffman, K. L. Felch and R. T. Weber, et al., Solid-state dynamic nuclear polarization at 263 GHz: spectrometer design and experimental results, Phys. Chem. Chem. Phys., 2010, 12, 5850–5860 RSC.
- A. Potapov, W.-M. Yau, R. Ghirlando, K. R. Thurber and R. Tycko, Successive stages of amyloid-β self-assembly characterized by solid-state nuclear magnetic resonance with dynamic nuclear polarization, J. Am. Chem. Soc., 2015, 137, 8294–8307 CrossRef CAS PubMed.
- V. K. Michaelis, B. Corzilius, A. A. Smith and R. G. Griffin, Dynamic nuclear polarization of 17O: direct polarization, J. Phys. Chem. B, 2013, 117, 14894–14906 CrossRef CAS PubMed.
- O. Lafon, A. S. L. Thankamony, T. Kobayashi, D. Carnevale, V. Vitzthum, I. I. Slowing, K. Kandel, H. Vezin, J.-P. Amoureux and G. Bodenhausen, et al., Mesoporous silica nanoparticles loaded with surfactant: low temperature magic angle spinning 13C and 29Si NMR enhanced by dynamic nuclear polarization, J. Phys. Chem. C, 2013, 117, 1375–1382 CrossRef CAS.
- M. Lelli, D. Gajan, A. Lesage, M. A. Caporini, V. Vitzthum, P. Miéville, F. Héroguel, F. Rascón, A. Roussey and C. Thieuleux, et al., Fast characterization of functionalized silica materials by silicon-29 surface-enhanced NMR spectroscopy using dynamic nuclear polarization, J. Am. Chem. Soc., 2011, 133, 2104–2107 CrossRef CAS PubMed.
- A. Rankin, J. Trébosc, F. Pourpoint, J.-P. Amoureux and O. Lafon, Recent developments in MAS DNP-NMR of materials, Solid State Nucl. Magn. Reson., 2019, 101, 116–143 CrossRef CAS PubMed.
- D. Mance, P. Gast, M. Huber, M. Baldus and K. L. Ivanov, The magnetic field dependence of cross-effect dynamic nuclear polarization under magic angle spinning, J. Chem. Phys., 2015, 142, 234201 CrossRef PubMed.
- A. S. L. Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102, 120–195 CrossRef PubMed.
- A. Purea, C. Reiter, A. I. Dimitriadis, E. de Rijk, F. Aussenac, I. Sergeyev, M. Rosay and F. Engelke, Improved waveguide coupling for 1.3 mm MAS DNP probes at 263 GHz, J. Magn. Reson., 2019, 302, 43–49 CrossRef CAS PubMed.
- S. K. Jawla, R. G. Griffin, I. A. Mastovsky, M. A. Shapiro and R. J. Temkin, Second Harmonic 527-GHz Gyrotron for DNP-NMR: Design and Experimental Results, IEEE Trans. Electron Devices, 2019, 67, 328–334 Search PubMed.
- V. K. Michaelis, R. G. Griffin, B. Corzilius and S. Vega, Handbook of High Field Dynamic Nuclear Polarization, John Wiley & Sons, 2019 Search PubMed.
- K. R. Thurber and R. Tycko, Theory for cross effect dynamic nuclear polarization under magic-angle spinning in solid state nuclear magnetic resonance: the importance of level crossings, J. Chem. Phys., 2012, 137, 084508 CrossRef PubMed.
- F. Mentink-Vigier, Ü. Akbey, H. Oschkinat, S. Vega and A. Feintuch, Theoretical aspects of magic angle spinning-dynamic nuclear polarization, J. Magn. Reson., 2015, 258, 102–120 CrossRef CAS PubMed.
- Y. Hovav, A. Feintuch and S. Vega, Theoretical aspects of dynamic nuclear polarization in the solid state-the solid effect, J. Magn. Reson., 2010, 207, 176–189 CrossRef CAS PubMed.
- K.-N. Hu, H.-H. Yu, T. M. Swager and R. G. Griffin, Dynamic nuclear polarization with biradicals, J. Am. Chem. Soc., 2004, 126, 10844–10845 CrossRef CAS PubMed.
- C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, TOTAPOL: a biradical polarizing agent for dynamic nuclear polarization experiments in aqueous media, J. Am. Chem. Soc., 2006, 128, 11385–11390 CrossRef CAS PubMed.
- A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Coperet and A. Lesage, et al., Large molecular weight nitroxide biradicals providing efficient dynamic nuclear polarization at temperatures up to 200 K, J. Am. Chem. Soc., 2013, 135, 12790–12797 CrossRef CAS PubMed.
- C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Highly efficient, water-soluble polarizing agents for dynamic nuclear polarization at high frequency, Angew. Chem., 2013, 125, 11058–11061 CrossRef.
- F. Mentink-Vigier, I. Marin-Montesinos, A. P. Jagtap, T. Halbritter, J. Van Tol, S. Hediger, D. Lee, S. T. Sigurdsson and G. De Paëpee, Computationally assisted design of polarizing agents for dynamic nuclear polarization enhanced NMR: the AsymPol family, J. Am. Chem. Soc., 2018, 140, 11013–11019 CrossRef CAS PubMed.
- K. Tagami, A. Equbal, I. Kaminker, B. Kirtman and S. Han, Biradical rotamer states tune electron J coupling and MAS dynamic nuclear polarization enhancement, Solid State Nucl. Magn. Reson., 2019, 101, 12–20 CrossRef CAS PubMed.
- K. R. Thurber and R. Tycko, Perturbation of nuclear spin polarizations in solid state NMR of nitroxide-doped samples by magic-angle spinning without microwaves, J. Chem. Phys., 2014, 140, 184201 CrossRef PubMed.
- A. Equbal, A. Leavesley, S. K. Jain and S. Han, Cross-Effect Dynamic Nuclear Polarization Explained: Polarization, Depolarization and Oversaturation, J. Phys. Chem. Lett., 2019, 10(3), 548–558 CrossRef PubMed.
- F. A. Perras, A. Sadow and M. Pruski, In silico design of DNP polarizing agents: can current dinitroxides Be improved?, ChemPhysChem, 2017, 18, 2279–2287 CrossRef CAS PubMed.
- F. Mentink-Vigier, S. Paul, D. Lee, A. Feintuch, S. Hediger, S. Vega and G. De Paëpe, Nuclear depolarization and absolute sensitivity in magic-angle spinning cross effect dynamic nuclear polarization, Phys. Chem. Chem. Phys., 2015, 17, 21824–21836 RSC.
- M. Veshtort and R. G. Griffin, SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments, J. Magn. Reson., 2006, 178, 248–282 CrossRef CAS PubMed.
- A. Lund, A. Equbal and S. Han, Tuning nuclear depolarization under MAS by electron T 1e, Phys. Chem. Chem. Phys., 2018, 20, 23976–23987 RSC.
- A. Equbal, Y. Li, A. Leavesley, S. Huang, S. Rajca, A. Rajca and S. Han, Truncated Cross Effect Dynamic Nuclear Polarization: An Overhauser Effect Doppelgänger, J. Phys. Chem. Lett., 2018, 9, 2175–2180 CrossRef CAS PubMed.
- Y. Li, A. Equbal, K. Tagami and S. Han, Electron Spin Density Matching for Cross-Effect Dynamic Nuclear Polarization, Chem. Commun., 2019, 55, 7591–7594 RSC.
- J. Soetbeer, P. Gast, J. J. Walish, Y. Zhao, C. George, C. Yang, T. M. Swager, R. G. Griffin and G. Mathies, Conformation of bis-nitroxide polarizing agents by multifrequency EPR spectroscopy, Phys. Chem. Chem. Phys., 2018, 20, 25506–25517 RSC.
- G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Efficient dynamic nuclear polarization at 800 MHz/527 GHz with trityl-nitroxide biradicals, Angew. Chem., Int. Ed., 2015, 54, 11770–11774 CrossRef CAS PubMed.
- D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea and F. Engelke, et al., BDPA-Nitroxide Biradicals Tailored for Efficient Dynamic Nuclear Polarization Enhanced Solid-State NMR at Magnetic Fields up to 21.1 T, J. Am. Chem. Soc., 2018, 140, 13340–13349 CrossRef CAS PubMed.
- K. Sato, R. Hirao, I. Timofeev, O. Krumkacheva, E. Zaytseva, O. Rogozhnikova, V. M. Tormyshev, D. Trukhin, E. Bagryanskaya and T. Gutmann, et al., Trityl-Aryl-Nitroxide-Based Genuinely g-Engineered Biradicals, As Studied by Dynamic Nuclear Polarization, Multifrequency ESR/ENDOR, Arbitrary Wave Generator Pulse Microwave Waveform Spectroscopy, and Quantum Chemical Calculations, J. Phys. Chem. A, 2019, 123, 7507–7517 CrossRef CAS PubMed.
- W. Zhai, Y. Feng, H. Liu, A. Rockenbauer, D. Mance, S. Li, Y. Song, M. Baldus and Y. Liu, Diastereoisomers of L-proline-linked trityl-nitroxide biradicals: synthesis and effect of chiral configurations on exchange interactions, Chem. Sci., 2018, 9, 4381–4391 RSC.
- A. Equbal, K. Tagami and S. Han, Pulse Shaped Dynamic Nuclear Polarization Under Magic Angle Spinning, J. Phys. Chem. Lett., 2019, 10(24), 7781–7788 CrossRef CAS PubMed.
- A. Leavesley, C. B. Wilson, M. Sherwin and S. Han, Effect of water/glycerol polymorphism on dynamic nuclear polarization, Phys. Chem. Chem. Phys., 2018, 20, 9897–9903 RSC.
- C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Highly efficient, water-soluble polarizing agents for dynamic nuclear polarization at high frequency, Angew. Chem., Int. Ed., 2013, 52, 10858–10861 CrossRef PubMed.
- D. J. Kubicki, G. Casano, M. Schwarzwälder, S. Abel, C. Sauvée, K. Ganesan, M. Yulikov, A. J. Rossini, G. Jeschke and C. Copéret, et al., Rational design of dinitroxide biradicals for efficient cross-effect dynamic nuclear polarization, Chem. Sci., 2016, 7, 550–558 RSC.
- K.-N. Hu, V. S. Bajaj, M. Rosay and R. G. Griffin, High-frequency dynamic nuclear polarization using mixtures of TEMPO and trityl radicals, J. Chem. Phys., 2007, 126, 044512 CrossRef PubMed.
- F. Mentink-Vigier, G. Mathies, Y. Liu, A.-L. Barra, M. A. Caporini, D. Lee, S. Hediger, R. G. Griffin and G. De Paëpe, Efficient cross-effect dynamic nuclear polarization without depolarization in high-resolution MAS NMR, Chem. Sci., 2017, 8, 8150–8163 RSC.
- S. Bothe, J. Nowag, V. Klimavicius, M. Hoffmann, T. I. Troitskaya, E. V. Amosov, V. M. Tormyshev, I. Kirilyuk, A. Taratayko, A. Kuzhelev, A. Kuzhelev, D. Parkhomenko, E. Bagryanskaya, T. Gutmann and G. Buntkowsky, Novel biradicals for direct excitation highfield dynamic nuclear polarization, J. Phys. Chem. C, 2018, 122, 11422–11432 CrossRef CAS.
- F. Mentink-Vigier, S. Vega and G. De Paëpe, Fast and accurate MAS-DNP simulations of large spin ensembles, Phys. Chem. Chem. Phys., 2017, 19, 3506–3522 RSC.
- A. Equbal, Y. Li, T. Tabassum and S. Han, Crossover from a Solid Effect to Thermal Mixing 1H Dynamic Nuclear Polarization with Trityl-OX063, J. Phys. Chem. Lett., 2020, 11(9), 3718–3723 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02051f |
| This journal is © the Owner Societies 2020 |