 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electron scattering cross sections from nitrobenzene in the energy range 0.4–1000 eV: the role of dipole interactions in measurements and calculations†
L.
Álvarez
a,
F.
Costa
a,
A. I.
Lozano
 ab,
J. C.
Oller
ab,
J. C.
Oller
 c,
A.
Muñoz
c,
F.
Blanco
d,
P.
Limão-Vieira
c,
A.
Muñoz
c,
F.
Blanco
d,
P.
Limão-Vieira
 b,
R. D.
White
e,
M. J.
Brunger
fg and
G.
García
b,
R. D.
White
e,
M. J.
Brunger
fg and
G.
García
 *ah
*ah
aInstituto de Fisica Fundamental, CSIC, Serrano 113-Bis, E-28006 Madrid, Spain. E-mail: g.garcia@csic.es
bAtomic and Molecular Collisions Laboratory, CEFITEC, Department of Physics, Universidade NOVA de Lisboa, 2829-516 Caparica, Portugal
cCentro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Avenida Complutense 22, 28040 Madrid, Spain
dDepartamento de Estructura de la Materia Física Térmica y Electrónica e IPARCOS, Universidad Complutense de Madrid, Plaza de Ciencias 1, 28040 Madrid, Spain
eCollege of Science and Engineering, James Cook University, Townsville, Australia
fCollege of Science and Engineering, Flinders University, GPO Box 2100, Adelaide, SA 5001, Australia
gDepartment of Actuarial Science and Applied Statistics, Faculty of Business and Information Science UCSI, Kuala Lumpur 56000, Malaysia
hCentre for Medical Radiation Physics, University of Wollongong, NSW, Australia
First published on 12th June 2020
Abstract
Absolute total electron scattering cross sections (TCS) for nitrobenzene molecules with impact energies from 0.4 to 1000 eV have been measured by means of two different electron-transmission experimental arrangements. For the lower energies (0.4–250 eV) a magnetically confined electron beam system has been used, while for energies above 100 eV a linear beam transmission technique with high angular resolution allowed accurate measurements up to 1000 eV impact energy. In both cases random uncertainties were maintained below 5–8%. Systematic errors arising from the angular and energy resolution limits of each apparatus are analysed in detail and quantified with the help of our theoretical calculations. Differential elastic and integral elastic, excitation and ionisation as well as momentum transfer cross sections have been calculated, for the whole energy range considered here, by using an independent atom model in combination with the screening corrected additivity rule method including interference effects (IAM-SCARI). Due to the significant permanent dipole moment of nitrobenzene, additional differential and integral rotational excitation cross sections have been calculated in the framework of the Born approximation. If we ignore the rotational excitations, our calculated total cross section agrees well with our experimental results for impact energies above 15 eV. Additionally, they overlap at 10 eV with the low energy Schwinger Multichannel method with Pseudo Potentials (SMCPP) calculation available in the literature (L. S. Maioli and M. H. F. Bettega, J. Chem. Phys., 2017, 147, 164305). We find a broad feature in the experimental TCS at around 1.0 eV, which has been related to the formation of the NO2− anion and assigned to the π*(b1) resonance, according to previous mass spectra available in the literature. Other local maxima in the TCSs are found at 4.0 ± 0.2 and 5.0 ± 0.2 eV and are assigned to core excited resonances leading to the formation of the NO2− and O2− anions, respectively. Finally, for energies below 10 eV, differences found between the present measurements, the SMCPP calculation and our previous data for non-polar benzene have revealed the importance of accurately calculating the rotational excitation contribution to the TCS before comparing theoretical and experimental data. This comparison suggests that our dipole-Born calculation for nitrobenzene overestimates the magnitude of the rotational excitation cross sections below 10 eV.
1. Introduction
Early experiments on nitrobenzene derivatives were devoted to analysing their potential use as radiosensitizers.1,2 Their high electron affinity related to the nitro group justified their efficiency to sensitize hypoxic cells to X-ray radiation.2,3 Nitrobenzene-compounds are also important in manufacturing chemical dyes, pharmaceuticals and explosives. Hence an important number of studies were related to the generation of NO2− radicals via electron attachment to nitrobenzene molecules.4–10 In addition, nitrobenzene (C6H5NO2) is a polar molecule with a permanent dipole moment (μ = 4.22 D)11 that is large enough to support dipole-bound states. This property motivated some early low energy electron scattering experiments12–14 from nitrobenzene (NBz), in order to check the validity of the popular rotational excitation approaches which are customarily used in modelling some of the aforementioned applications. Long-range effects in electron scattering by polar molecules calculations and their implications in experiment to theory comparison have been recently reviewed by I. Fabrikant.15 Different theoretical and experimental spectroscopic studies have also been published along the years, in order to characterise its ultraviolet emission spectrum,16,17 electronic structure and spectra,18–22 vibrational spectra,23 electron energy loss measurements,24,25 electron transmission measurements,26 photoabsorption spectra27 and angular resolved photoelectron emission.28,29 All the previous work shed light on the valence electronic structure of this important molecule.In spite of this fundamental and applied interest into the NBz molecule, not many studies measured or calculated its electron scattering cross sections over a wide energy range. In fact, no experimental total electron scattering cross sections (TCS) are currently available for impact energies above 1 eV. However, as we showed in recent papers,30,31 TCS are considered to be crucial reference data to validate electron scattering data sets for modelling purposes, in particular to model radiation damage at the molecular level.32 For this reason, we have recently measured and calculated total electron scattering cross sections for biologically relevant molecules such as pyrimidine,33 pyrazine,34 thiophene,35,36 sevoflurane,37para-benzoquinone,38 pyridine,39 and most recently benzene40 which is considered as a benchmarking molecule for basic carbon ring structures. In this context, nitrobenzene becomes even more relevant since comparison with the case of benzene may help elucidate the role of the NO2 group in electron scattering processes. From the theoretical point of view, electron scattering from NBz molecules has been recently investigated by Maioli and Bettega41 using the Swinger multichannel method with pseudopotentials (SMCPP). They calculated differential and integral elastic as well as momentum transfer cross sections for electron impact energies ranging from 0 to 10 eV.
These latter considerations motivated, at least in part, the present study in which we use two different electron scattering arrangements to determine the TCS for NBz molecules in the combined energy range 0.4–1000 eV, with overall uncertainties to within 7%. For the lower energies [0.4–250 eV] we utilized our new magnetically confined electron scattering apparatus,42 whilst from impact energies from 90 to 1000 eV the linear transmission-beam system described in ref. 40 has been employed. In addition, our independent atom representation with the screening corrected additivity rule including interference effects (IAM-SCARI)43–45 has been applied to calculate the differential and integral elastic scattering cross sections, as well as the momentum transfer and the integral summed excitation and ionisation cross sections, over the whole energy range considered here [0.4–1000 eV]. Note, however, that below 10 eV the present method does not strictly apply,35 so that only qualitative information is able to be provided there. In our calculation, we have accounted for the permanent NBz dipole moment by computing rotational excitation cross sections through an independent procedure based on the Born approximation.35 Present theoretical and experimental data are compared with results from previous studies, leading to the classification of the observed resonances in the TCS and the quantification of common uncertainties connected with describing electron–dipole interactions.
The remaining sections of this paper are structured as follows. In Section 2 we detail the experimental and theoretical methods used in this study, together with an analysis of the corresponding measurement uncertainties and theoretical limitations. Our results are then presented, discussed and compared with the available data in Section 3, including a detailed analysis of the observed resonances and a general discussion on the role of the dipole moment in the scattering process. Finally, some conclusions from this study are summarised in Section 4.
2. Experimental and theoretical methods
2.1 Magnetically confined electron beam (MCEB) system
The experimental apparatus and techniques used for the present low-intermediate (0.4–250 eV) energy measurements have recently been described42 and so will not be detailed again here. Briefly, a linear electron beam is confined by an intense (typically 0.1 Tesla) axial magnetic field which converts any scattering event into a kinetic energy loss in the forward direction, i.e. parallel to the magnetic field (see ref. 42 for full details). The primary electron beam, generated by an emitting filament, is cooled and confined in a magnetic nitrogen gas trap which reduces the initial energy spread of ∼700 meV down to about 100–200 meV. Pulsed voltages applied to the trap electrodes produce a pulsed electron beam with well-defined energy and narrow energy spread to enter the scattering cell (SC). The scattering cell is a 40 mm long gas chamber, defined by two 1.5 mm diameter apertures, through which the pulsed electron beam passes when the NBz pressure inside the chamber is varied from 0 to 2 mTorr (as measured by a MKS-Baratron 627B absolute capacitance manometer). The entire system is externally heated up to about 40–50 °C in order to maintain a constant pressure during the measurements. This temperature is similar to the operating temperature of the MKS-Baratron® capacitance manometer, so that thermal transpiration effects are negligible within the present experimental conditions electrons emerging from the SC are analysed in energy by a retarding potential analyser (RPA) and finally detected by a double microchannel plate (MCP) electron multiplier operating in single counting mode. The total cross section (σT) is determined from the transmitted intensity according to the computerized procedure, based on the Beer–Lambert attenuation law, described in ref. 42, and giving associated statistical uncertainties typically below 4%. Other random uncertainties are related to the temperature measurement (within 1%, according to manufacturer's data) and the numerical fitting procedure (about 1%). By combining these uncertainties, a total uncertainty limit of 5% has been determined for the present TCS measurements. Systematic errors linked to the experimental technique are those connected to the so-called “missing angles”.42,46 Due to the magnetic field confinement, the energy resolution determines the acceptance angle of the detector. As detailed in ref. 42 the magnitude of this systematic error can be evaluated from the theoretical data by integrating the calculated differential elastic cross sections (DCS) over the “missing” experimental angles. This effect is especially important for polar molecules, as is the case here for NBz, since differential rotational excitation cross sections are strongly peaked in the forward direction36 and their contribution to this systematic error could be much higher than that of the elastic channel,36 depending on the experimental angular resolution. Note that the averaged rotational excitation energy at 300 K is below 0.6 meV, and therefore the energy resolution commonly used in scattering experiments is not sufficient to discriminate against this inelastic channel. The significance of this error source in the present experimental results will be discussed further in Section 3. An extensive explanation of the origin and consequences of dipole interactions in polar molecules can be found in ref. 15.2.2 Linear transmission-beam (LTB) apparatus
The experimental arrangement used for intermediate and high energies has also been detailed in a previous article.40 The electron beam is generated by a negatively biased thoriated tungsten hairpin filament, it is focused and then deflected towards the scattering cell (metallic cube defined by two 2 mm diameter apertures which are separated by a 50 mm length). Typical electron currents were 10−9 A with an energy spread of about 600 meV. As described in ref. 40, the total cross sections are directly measured from the attenuation of the electron beam for different gas pressures in the scattering cell. The entire system is differentially pumped by two turbo-pumps reaching a background pressure of about 10−8 Torr. This allows us to maintain an overall pressure in the system below 10−7 Torr during the measurements, while the pressure in the scattering chamber was varied between 1 and 5 mTorr (as again measured with a MKS-Baratron-627B). Statistical uncertainties were maintained below 5%, and by an in quadrature combination of the aforementioned random uncertainties an overall uncertainty limit of about 7–8% has been estimated for these measurements. Concerning the systematic error due to the “missing angles” of the transmitted electron detection procedure, we should note that it is not so much relevant for this experimental configuration. In this case, the average acceptance angle (solid angle subtended by the electron spectrometer aperture as seen from the centre of the scattering cell) is about 1.5 × 10−5 sr and therefore, as discussed in the next section, the contribution of this systematic error is quite negligible in comparison with the other uncertainty sources.2.3 Electron scattering cross section calculation
The independent atom model, in combination with the screening corrected additivity rule and including interference effects (IAM-SCARI procedure),43–45 has been used to determine the differential and integral elastic cross sections as well as the integral inelastic cross sections within the overall energy range considered in this study (0.4–1000 eV). Due to the atomistic nature of this method, only geometrical properties (atom positions and bond-lengths) of the target molecule are taken into consideration and hence a proper description of the scattering below 10 eV (where other molecular features are relevant) cannot be expected. However, we have shown for a wide variety of molecular targets (see ref. 36–40 and references therein) that above this limit both integral elastic and inelastic cross sections agree well, typically to within 10%, with the most accurate experimental results. We thus consider 10% to be a good indication of the total uncertainty associated with the present integral cross section calculations. Within this model inelastic scattering processes are not affected by the interference terms, and they are calculated as a whole from the imaginary part (absorption) of the interaction potential. However, as described in a recent article,47 by alternately using as the threshold energy for the absorption potential either the lowest electronic-state excitation energy or the ionisation energy, we are able to extract the integral summed excitation and the total ionisation cross sections from the calculated overall integral inelastic cross sections. We have recently shown that total ionisation cross sections of some organic molecules,48,49 as derived from this procedure, are in fairly good agreement with the available experimental results.The IAM-SCARI approach is based on a fixed nuclei representation and so no vibrational or rotational excitation is included in the calculation. However, the average rotational excitation energy for NBz is low enough (<0.6 meV at 300 K) to in principle validate the use of the Born approximation. In these conditions, differential and integral rotational excitation cross sections can easily be calculated by considering the molecule as a rigid rotor, with the initial rotational excited state distribution in equilibrium at 300 K, and calculating all the transitions ΔJ = ±1 (J being the rotational quantum number) within the framework of the Born approximation50 but including the correction for the larger angles given by Dickinson (see ref. 50 and references therein).
3. Results and discussion
3.1 Low-intermediate electron impact energy (0.4–250 eV)
Total electron scattering cross sections (in Å2) for nitrobenzene with impact energies ranging from 0.4 to 250 eV, as measured with the experimental configuration described in Section 2.1, are shown in Table 1.| E (eV) | TCS (10−20 m2) | Relative uncertainty (%) | Absolute uncertainty (±10−20 m2) | Δθ (deg.) | ΔE (eV) |
|---|---|---|---|---|---|
| 0.4 | 58.8 | 1.7 | 1.01 | 40.7 | 0.17 |
| 0.5 | 57.1 | 3.0 | 1.71 | 35.0 | 0.18 |
| 0.6 | 55.7 | 2.7 | 1.50 | 33.2 | 0.18 |
| 0.7 | 54.9 | 3.0 | 1.62 | 31.0 | 0.19 |
| 0.8 | 54.2 | 4.9 | 2.66 | 29.2 | 0.19 |
| 1.0 | 63.0 | 2.4 | 1.52 | 24.4 | 0.17 |
| 1.2 | 61.3 | 1.8 | 1.11 | 21.4 | 0.16 |
| 1.4 | 59.1 | 1.0 | 0.62 | 21.6 | 0.19 |
| 1.5 | 59.6 | 1.0 | 0.60 | 21.7 | 0.20 |
| 1.6 | 55.9 | 3.1 | 1.71 | 21.8 | 0.22 |
| 1.8 | 59.3 | 2.6 | 1.54 | 17.9 | 0.17 |
| 2.0 | 60.1 | 1.8 | 1.08 | 18.0 | 0.19 |
| 2.2 | 58.9 | 2.2 | 1.32 | 16.1 | 0.17 |
| 2.4 | 59.3 | 2.1 | 1.27 | 17.6 | 0.22 |
| 2.6 | 60.4 | 1.6 | 0.99 | 15.3 | 0.18 |
| 2.8 | 61.7 | 2.1 | 1.27 | 15.1 | 0.19 |
| 3.0 | 61.4 | 1.6 | 1.01 | 14.2 | 0.18 |
| 3.2 | 61.2 | 1.9 | 1.15 | 12.9 | 0.16 |
| 3.4 | 62.1 | 2.5 | 1.56 | 12.9 | 0.17 |
| 3.6 | 63.8 | 2.4 | 1.54 | 12.9 | 0.18 |
| 3.8 | 64.5 | 3.0 | 1.92 | 12.9 | 0.19 |
| 4.0 | 65.5 | 2.5 | 1.64 | 12.9 | 0.20 |
| 4.2 | 64.9 | 1.3 | 0.83 | 12.6 | 0.20 |
| 4.4 | 64.4 | 2.1 | 1.38 | 12.3 | 0.20 |
| 4.6 | 63.6 | 2.6 | 1.65 | 11.4 | 0.18 |
| 4.8 | 64.9 | 3.0 | 1.93 | 11.2 | 0.18 |
| 5.0 | 65.8 | 2.8 | 1.83 | 11.2 | 0.19 |
| 5.2 | 65.6 | 2.9 | 1.89 | 11.6 | 0.21 |
| 5.4 | 65.3 | 1.5 | 0.97 | 11.6 | 0.22 |
| 5.6 | 65.4 | 2.6 | 1.70 | 11.7 | 0.23 |
| 5.8 | 66.7 | 2.3 | 1.55 | 11.0 | 0.21 |
| 6.0 | 68.9 | 3.2 | 2.18 | 11.0 | 0.22 |
| 6.2 | 71.1 | 2.5 | 1.78 | 11.3 | 0.24 |
| 6.4 | 72.8 | 1.0 | 0.76 | 10.7 | 0.22 |
| 6.6 | 71.6 | 1.3 | 0.92 | 10.8 | 0.23 |
| 6.8 | 73.1 | 3.4 | 2.52 | 9.6 | 0.19 |
| 7.0 | 71.7 | 2.0 | 1.41 | 10.0 | 0.21 |
| 7.3 | 72.9 | 3.8 | 2.79 | 10.2 | 0.23 |
| 7.5 | 71.3 | 4.7 | 3.36 | 9.6 | 0.21 |
| 7.7 | 69.3 | 1.3 | 0.93 | 10.0 | 0.23 |
| 8.0 | 72.1 | 1.6 | 1.13 | 9.1 | 0.2 |
| 8.5 | 71.3 | 3.3 | 2.32 | 9.5 | 0.23 |
| 8.7 | 73.8 | 3.8 | 2.83 | 8.9 | 0.21 |
| 9.0 | 75.5 | 1.6 | 1.18 | 9.0 | 0.22 |
| 9.5 | 73.7 | 1.3 | 0.99 | 8.6 | 0.21 |
| 10.0 | 74.3 | 2.2 | 1.66 | 8.3 | 0.21 |
| 10.5 | 72.7 | 2.3 | 1.69 | 8.7 | 0.24 |
| 11.0 | 71.2 | 1.7 | 1.22 | 7.7 | 0.20 |
| 11.5 | 69.8 | 1.7 | 1.20 | 8.3 | 0.24 |
| 12.0 | 67.8 | 4.5 | 3.06 | 8.0 | 0.23 |
| 12.5 | 68.2 | 2.7 | 1.84 | 7.4 | 0.21 |
| 13.0 | 69.4 | 3.4 | 2.33 | 7.1 | 0.20 |
| 13.5 | 68.7 | 3.3 | 2.24 | 7.0 | 0.20 |
| 14.0 | 66.9 | 2.4 | 1.62 | 6.9 | 0.20 |
| 15.0 | 66.0 | 3.4 | 2.21 | 6.6 | 0.20 |
| 15.5 | 65.4 | 3.3 | 2.13 | 7.0 | 0.23 |
| 16.0 | 64.1 | 3.5 | 2.27 | 6.7 | 0.22 |
| 17.0 | 63.0 | 2.9 | 1.81 | 6.8 | 0.24 |
| 18.0 | 63.9 | 2.7 | 1.72 | 6.6 | 0.24 |
| 19.0 | 65.2 | 3.6 | 2.37 | 5.9 | 0.20 |
| 20.0 | 64.4 | 2.2 | 1.44 | 5.9 | 0.21 |
| 22.0 | 64.0 | 2.5 | 1.61 | 5.9 | 0.23 |
| 25.0 | 63.4 | 3.0 | 1.89 | 5.5 | 0.23 |
| 30.0 | 62.0 | 1.7 | 1.07 | 4.7 | 0.2 |
| 35.0 | 61.0 | 1.2 | 0.74 | 4.7 | 0.24 |
| 40.0 | 59.5 | 3.6 | 2.17 | 4.2 | 0.21 |
| 45.0 | 58.2 | 2.9 | 1.68 | 3.9 | 0.21 |
| 50.0 | 56.6 | 4.5 | 2.55 | 3.8 | 0.22 |
| 60.0 | 54.7 | 2.8 | 1.52 | 3.5 | 0.23 |
| 70.0 | 52.6 | 2.5 | 1.32 | 3.4 | 0.25 |
| 80.0 | 51.1 | 3.1 | 1.57 | 2.9 | 0.21 |
| 90.0 | 48.8 | 3.4 | 1.68 | 2.6 | 0.19 |
| 100 | 46.8 | 2.0 | 0.92 | 2.7 | 0.23 |
| 120 | 44.9 | 2.9 | 1.29 | 2.9 | 0.31 |
| 150 | 40.8 | 3.5 | 1.45 | 2.7 | 0.33 |
| 200 | 35.5 | 2.2 | 0.79 | 2.3 | 0.32 |
| 250 | 29.5 | 2.2 | 0.66 | 2.3 | 0.42 |
We previously noted that the present uncertainty limits have been derived by a root mean square quadratic combination of all the random uncertainty sources described in Section 2.1 (see ref. 42 for a comprehensive analysis of these uncertainty sources). As now shown explicitly in Table 1, these limits range from 1 to 5%, depending on the incident energy. Possible systematic errors are described later with a fuller discussion for them being found in ref. 42. We have also checked that the actual absorption length (L) corresponds to the geometrical length of the scattering chamber, by measuring the well-known electron scattering TCS for molecular nitrogen at selected energies, finding excellent agreement with the benchmark values available in the literature (see ref. 42 for details). The electron intensity count rate was always less than 103 s−1 (i.e. less than a 10−16 A electron current). Under these conditions no dependence of the measured TCS on the electron current was found, so ensuring that possible space charge effects are negligible in this experiment. In order to ensure that multiple scattering processes are absent under our working conditions, attenuation measurements were performed at relatively low NBz gas pressures (from 0 to less than 2 mTorr, depending on the incident energy). The incident energy was calibrated against the well-known resonance energy corresponding to the first peak in the N2 TCS, which is largely due to the ν = 0–1 vibrational excitation of N2.51 As shown in ref. 42, the energy resolution of the incident electron beam (ΔE), derived from the transmitted electron profiles on the RPA, is typically within 100–200 meV. However, by biasing the RPA to the higher energies, to reduce the transmitted intensity by 25% of that for the incident electron intensity, an effective energy resolution better than 100 meV was customarily achieved.42 Additionally, and as explained in ref. 42, due to the axial magnetic field conditions of the present MCEB experiment, the energy resolution and the incident energy (E) are linked to the angular resolution (Δθ°) as follows:
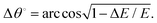 | (1) |
Note that electrons elastically scattered within Δθ° and 180° − Δθ° are, for the MCP detector, indistinguishable from the unscattered electrons, and constitute the main systematic error source of the present measurements.42,46 This effect always tends to lower the measured cross sections from their “true” value, but their magnitude can be estimated by integrating the calculated DCS from 0° to Δθ°and from 180° − Δθ° to 180°. In the case of NBz, due to its permanent dipole moment, rotational excitations also contribute to this effect. In fact, this contribution is a common cause of confusion when comparing experimental with theoretical data and even between experimental results taken with different energy and angular resolutions (for more information about this subject see ref. 15 and references therein). To illustrate this effect, our calculated differential elastic and rotational cross sections, using the procedures described in Section 2.3, are plotted together in Fig. 1. As this figure shows, the angular distribution for rotational excitation is mainly concentrated around the forward direction, being 7 orders of magnitude higher than the elastic cross section at 0°. The acceptance angle of our MCEB apparatus, at 10 eV, is represented in this figure by a dashed line. By integrating the calculated elastic and rotational excitation DCS over the “missing angles”, we have estimated that the contribution of elastic scattering to this effect is only 5.1% of the measured TCS. On the other hand, the contribution of rotational excitation is of the same order of magnitude as the measured TCS value.
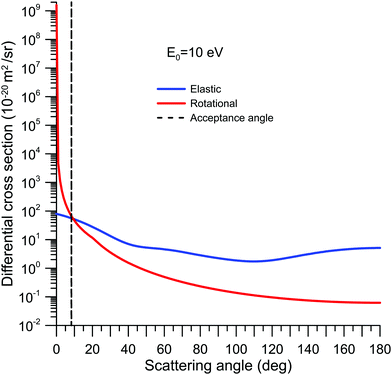 | ||
| Fig. 1 Differential cross sections (10−20 m2 sr−1) for elastic scattering and rotational excitation in NBz at 10 eV incident electron energy. | ||
The results of our IAM-SCARI and Born-dipole calculations (integral elastic, momentum transfer, rotational excitation, summed electronic excitation and ionisation cross sections) for impact energies ranging from 1 to 1000 eV are shown in Table 2. As already mentioned, from previous comparisons with experimental data for other similar molecules,30,36–40 we can establish an overall uncertainty of ∼10% for the IAM-SCARI integral cross sections. The exception to that general claim is for ionisation, for which uncertainties around the ionisation threshold could be of the order of 20–25%.48,49 Below 10 eV our IAM-SCARI method does not in general apply, and so those results are shown in Table 2 just for completeness.
| E (eV) | Elastic | Ionisation | Excitation | Rotational | MTCS |
|---|---|---|---|---|---|
| 1.0 | 116 | 775 | 94.3 | ||
| 1.5 | 96.9 | 540 | 74.9 | ||
| 2.0 | 87.6 | 417 | 67.1 | ||
| 3.0 | 79.8 | 291 | 58.2 | ||
| 4.0 | 75.6 | 224 | 50.5 | ||
| 5.0 | 72.2 | 183 | 44.5 | ||
| 7.0 | 68.9 | 135 | 39.8 | ||
| 10.0 | 66.6 | 0.1 | 97.7 | 38.1 | |
| 15.0 | 61.3 | 0.5 | 3.3 | 67.5 | 30.8 |
| 20.0 | 55.2 | 3.6 | 5.9 | 52.1 | 23.3 |
| 30.0 | 47.6 | 10.4 | 6.0 | 35.8 | 17.2 |
| 40.0 | 42.8 | 13.4 | 5.1 | 27.5 | 12.8 |
| 50.0 | 39.5 | 14.5 | 4.6 | 22.4 | 9.8 |
| 70.0 | 34.4 | 15.1 | 4.1 | 16.4 | 6.6 |
| 100 | 30.0 | 14.6 | 3.7 | 11.8 | 4.5 |
| 150 | 25.0 | 13.1 | 3.3 | 8.1 | 2.8 |
| 200 | 21.8 | 11.8 | 3.1 | 6.2 | 2.0 |
| 300 | 17.7 | 9.7 | 2.7 | 4.3 | 1.1 |
| 400 | 15.0 | 8.3 | 2.4 | 3.2 | 0.8 |
| 500 | 13.1 | 7.3 | 2.2 | 2.6 | 0.6 |
| 700 | 10.5 | 5.9 | 1.8 | 1.9 | 0.3 |
| 1000 | 8.2 | 4.5 | 1.5 | 1.4 | 0.2 |
The present IAM-SCARI integral elastic (IECS), summed electronic excitation (EECS), total ionisation (TICS) and the total (elastic + summed electronic excitation + ionisation) cross sections (TCS) are also plotted in Fig. 2 for impact energies from 10 to 1000 eV. Note that these TCS values do not include the rotational excitation cross section we independently calculated within the Born approximation. As mentioned earlier, this scattering channel is very important for strongly polar molecules, such as nitrobenzene, and its role in cross section measurements and calculations will be discussed in the next subsection. From a first inspection of Fig. 2, we see that there is excellent agreement between the present experimental TCS data and our IAM-SCARI calculation above about 15 eV. However, as already noted, the effect of the elastic scattering into the detection angle and the rotational excitations out of this angle require a deeper analysis before comparing TCS data (as will be discussed later). Below 15 eV, down to 5 eV, the calculated TCS data (not shown) tend to be lower in magnitude than our experimental values reaching discrepancies of about 20% at around 8 eV. This clearly indicates that our IAM-SCARI calculation is underestimating the strength of the electronic excitation cross sections from 5 to 15 eV. The TCSs measured by Lunt et al.12,13 show a completely different behaviour than all the available theoretical and our experimental data. We will discuss in Section 3.3 the possible impact of the dipole moment on these measurements, but the significant discrepancy in the TCSs around 8–10 eV suggests that their absolute values may be affected by some as yet unspecified systematic error.
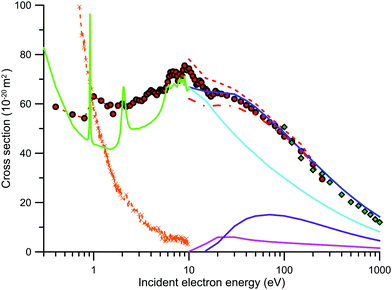 | ||
Fig. 2 Integral and total electron scattering cross sections for nitrobenzene. Present measurements with the MCEB ( ) and LTB ( ) and LTB ( ) experimental systems, respectively, are shown. Experimental data from Lunt et al.12,13 ( ) experimental systems, respectively, are shown. Experimental data from Lunt et al.12,13 ( ) are also given. Present IAM-SCARI calculations: TCS not including rotational excitations ( ) are also given. Present IAM-SCARI calculations: TCS not including rotational excitations ( ), integral elastic ( ), integral elastic ( ), summed electronic excitation ( ), summed electronic excitation ( ) and ionisation ( ) and ionisation ( ) cross sections are further plotted, as are the IECS from Maioli and Bettega41 ( ) cross sections are further plotted, as are the IECS from Maioli and Bettega41 ( ). Corrections to the TCS: experimental results plus the contribution of elastic scattering within the “missing” angles ( ). Corrections to the TCS: experimental results plus the contribution of elastic scattering within the “missing” angles ( ), experimental values plus elastic scattering in the “missing” angles minus the rotational excitation contribution outside the effective detection angle ( ), experimental values plus elastic scattering in the “missing” angles minus the rotational excitation contribution outside the effective detection angle ( ) [see Section 3.3 for details]. ) [see Section 3.3 for details]. | ||
Concerning the IECSs, the SMCPP data from ref. 41 are also plotted in Fig. 2 for comparison. Note we are considering here their SEP41 calculation without their dipole Born correction (see ref. 41 for details). Further note that this Born correction is equivalent to our aforementioned dipole-Born rotational excitation cross section which corresponds to processes not detectable under the present experimental conditions and hence should not be included in this comparison. At 10 eV where both calculations apply the agreement between them is excellent. This in principle might suggest that by combining results from both methods, as far as elastic scattering is concerned, we could accurately cover the whole energy range considered here, from 0.4 to 1000 eV. However, we note that below 4 eV the IECS should be roughly equivalent to the TCS (apart from possible resonance effects, due to temporary electron attachment, that significantly increase the TCS magnitude around the resonant energy). Nevertheless the data calculated in ref. 41 are usually lower than the present experimental values, reaching a maximum discrepancy of about 30% at around 1.5 eV. The origin of this discrepancy is not clear, but we will suggest in the next subsection a possible reason based again on the effect of the dipole interaction and forward angle elastic scattering.
Another important aspect of low energy electron scattering is the possible presence of resonances, due to the temporary electron attachment to either the ground state (shape resonances) or excited states (core-excited or Feshbach resonances), of the NBz molecule. In addition, for highly polar molecules (μ > ∼2D) an electron can be bound by their dipolar electric field leading to a dipole-bound resonance.52 Adams et al.,53 using a photoelectron imaging spectroscopy technique, observed the dipole-bound state of the nitromethane anion with a binding energy ∼12 meV. This feature was distinguished from the vibrational structure of the valence state by the anisotropy induced by the dipole electric field. More recently, accurate photoelectron spectra of benzonitrile have been analysed by Gulania et al.54 with a high-level electronic structure calculation of its anionic states. This investigation reveals the presence of a dipole-bound state, that provides the main mechanism to capture an incoming electron but leads to the formation of valence anions via non-adiabatic relaxation (see ref. 54 and references therein). Interconnections between valence states of anions and dipole-bound states have also been identified in the opposite direction (bifurcation of the excited state wavepacket leading to the formation of a non-valence state) for a common anionic chromophore,55 and the stability of such orbitals in the presence of perturbing molecules has also been studied by the same group.56 Very recently, Anstöter et al.57 showed that the observed emission peaks from the vibrational structure of the nitrobenzene anion can be correlated with an autodetachment mechanism via dipole-bound state formation. In all these cases, dipole-bound states are formed at very low energy, below the lower energy limit of the present experimental study (0.4 eV). Modelli and Venuti7 combined electron transmission spectroscopy (ETS) measurements with ab initio calculations to analyse the electron attachment to nitrobenzene in the energy range 0–6 eV. By comparing the experimental results with the calculation of the vertical electron affinity (0.37 eV) they concluded that the first anion state of nitrobenzene is stable and therefore not observed in ETS. This conclusion is supported by the complementary parent anion detection using mass spectrometry (see ref. 7 for details) showing an intense peak at 0 eV and a much weaker signal at 0.4 eV. In concordance with this result. Maioli and Bettega calculation showed the formation of the anionic bound state (πbound*(b1)) at 0.39 eV using the configuration space of the B1 symmetry. In the energy range considered here, the first resonance found by Modelli and Venuti,7 was placed at 0.55 eV and was associated with the non-interacting ring π*(a2) component of the benzene π*(e2u) lowest unoccupied molecular orbital (LUMO), inductively stabilised by the electron-withdrawing nitro group. They related this resonance with the formation of the parent anion, but probably due to the energy resolution limitations of the present measurements (0.2 eV) we did not observe such narrow feature in the TCS. Note that the SEP calculation of Maioli and Bettega41 placed this resonance at 0.92 eV with an estimated width of 0.013 eV. Pelc et al.10 observed the formation of the parent anion at 0 eV, but we should admit that the energy resolution of the present study (∼±0.2 eV) is not good enough to provide any additional information about this parent anion formation. Our first feature in the measured TCS is observed at around 1.0–1.5 eV. This broad peak is compatible with those observed in the mass spectra of Modelli and Venuti7 (0.7, 1.25 eV), Pelc et al.10 (0.7, 1.4 eV), Compton et al.4 (1.3 eV), Jäger and Henglein6 (1.5 eV) and is connected with the formation of the NO2− anion. It is assigned to the π*(b1) resonance. The SEP calculation41 found this resonance at 2.07 eV, confirming the usual shift to higher energies presented by this calculation with respect to experimental results (see ref. 41 for a comparative discussion between theoretical and experimental resonances in nitrobenzene and their correlation with those of benzene on the basis of their respective molecular orbitals). Between 2.2 and 3.3 eV an increase in the TCS at around 2.8 eV is distinguishable. Although the origin of this feature is not clear, it is worth mentioning that similar structures at those energies were experimentally observed for benzene40 and pyridine39,58 being related to the vibrational excitation of the ground state.39,40 The next feature clearly shown by our TCS is a local maximum at 4.0 ± 0.2 eV, which can be related to those found in ref. 7 and 10 at 3.8 eV. Modelli and Venuti.7 Assigned this peak to a core excited resonance, that according to the mass spectra from ref. 10 may lead to the formation of the NO2− negative fragment. This feature was also observed by Lunt et al.12,13 at around 3.75 eV, and was associated by them with the dissociative electron attachment channel. The resonance at 4.69 eV, found by Modelli and Venuti,7 is assigned to the highest-lying empty π*(b1) state of NBz with a net effect of stabilisation. However, the mass spectra from Pelc et al.10 and Jäger and Henglein6 show a prominent signal at 4.8 and 5 eV, respectively, which are assigned to the formation of the O− anion. The local maximum in the TCS that we observe at 5.0 ± 0.2 eV confirms these observations. Our experimental data show additional broad structures at around 6.8 and 9 eV, which can be attributed to highly excited states just below the threshold ionisation energy (9.9 eV).59
3.2 Intermediate-high electron impact energy (100–1000 eV)
The total electron scattering cross sections measured with the LTB apparatus in the impact energy range 100–1000 eV, as described in Section 2.2, are shown in Table 3 with their respective experimental uncertainty limits.| E (eV) | TCS (10−20 m2) | Relative uncertainty (%) | Absolute uncertainty (±10−20 m2) | Δθ (deg.) | ΔE (eV) |
|---|---|---|---|---|---|
| 100 | 50.6 | 7.0 | 3.5 | 0.16 | 0.5 |
| 120 | 44.3 | 7.0 | 3.1 | 0.16 | 0.5 |
| 150 | 38.0 | 7.0 | 2.7 | 0.16 | 0.5 |
| 200 | 33.2 | 7.0 | 2.3 | 0.16 | 0.5 |
| 250 | 31.7 | 7.0 | 2.2 | 0.16 | 0.5 |
| 300 | 28.2 | 7.0 | 2.0 | 0.16 | 0.5 |
| 400 | 23.2 | 7.0 | 1.6 | 0.16 | 0.5 |
| 500 | 20.2 | 7.0 | 1.4 | 0.16 | 0.5 |
| 600 | 18.7 | 7.0 | 1.3 | 0.16 | 0.5 |
| 700 | 16.4 | 7.0 | 1.1 | 0.16 | 0.5 |
| 800 | 15.1 | 7.0 | 1.1 | 0.16 | 0.5 |
| 900 | 13.2 | 7.5 | 1.0 | 0.16 | 0.5 |
| 1000 | 12.0 | 8.3 | 1.0 | 0.16 | 0.5 |
These results are also plotted in Fig. 2, together with those measured with the MCEB apparatus and the present IAM-SCARI calculation data (not including rotational excitations). As already described, due to the good angular resolution of this apparatus (fixed acceptance angle of 0.16 deg.), the contribution of elastic scattering, as estimated with our calculated elastic DCS, to the “missing” angle effect is less than 1% for the entire energy range (100–1000 eV). Due to the significant dipole moment of NBz, some contribution to this effect from rotational excitation may, however, be expected. By using our calculated rotational excitation DCS, integrated over the acceptance angle of the detector (0–0.16°), we have estimated a contribution to the TCS between 10.7% to 6.2% for energies from 100 to 1000 eV, respectively. As discussed in the previous section this is a systematic error that should be added to the experimental results, when comparing with theoretical calculations including dipole-Born corrections. If a comparison is to be made between different experimental results, the theoretical DCS should then be integrated over their respective angular acceptances in order to obtain comparable data. Under the conditions of the LTB apparatus, the contribution of rotational excitation from the acceptance angle, which should be subtracted from the measured TCS if no rotational excitation is being considered in the comparison to the IAM-SCARI TCS, is less than 1% and therefore negligible, in comparison with the other uncertainty sources.
Finally, we observe that the present LTB measurements are in very good agreement (see Fig. 2), within the combined uncertainty limits, with both the MCEB experimental data and our IAM-SCARI calculations to within the overlapping energy ranges.
3.3 The role of the dipole moment in electron scattering from molecules
In the case of polar molecules, such as nitrobenzene, special attention to the dipole interactions must be paid both from the theoretical and experimental points of view.15 As noted above, electron scattering experiments do not generally have a good enough energy resolution to discriminate against rotational excitations. For this reason, electron transmission measurements tend to give lower TCSs than the “true” values, due to the elastically and rotationally scattered electrons into the detection or acceptance angle (the so called “missing angles”), with the magnitude of this effect dependent on the particular angular resolution in question. In addition, electrons rotationally scattered outside of the “missing angles” affect the measured TCS, as you’d expect in a normal attenuation experiment, so that in those cases where this effect is relevant (e.g. for magnetically confined electron scattering experiments with polar molecules), according to the second alternative proposed in ref. 15, the magnitude of those contributions should be evaluated before comparing theoretical and experimental cross section data, particularly when the theory does not account for the nuclear degrees of freedom (i.e. rotations and vibrations).As discussed in the previous subsection, there is an excellent agreement found between the present TCS measurements and the results of our IAM-SCARI calculation without rotational excitation (i.e. the elastic + summed electronic excitation + ionisation integral cross sections). However, from the above discussion, we must assume that these data are not completely equivalent. Using our calculated elastic DCSs and integrating these values over the “missing” angular ranges, we can calculate the contribution of the elastic scattering to this systematic error.47 Adding this contribution to the measured TCS we therefore obtain the corrected values for elastic scattering into the “missing angles” which are shown in Fig. 2 as the short dashed red line. As may be seen in this figure these “corrected values” are somewhat higher in magnitude than the calculated IAM-SCARI TCS for energies above about 200 eV. The reason for this discrepancy is again linked to the “missing” angles. While for the theoretical TCS we are not considering rotational excitations, the experimental values do include for the effect of rotational excitations scattered outside of the “missing angle” ranges. Although these processes are strongly peaked in the forward direction, their contribution is not negligible below 200 eV. This effect can be estimated by now integrating the dipole-Born rotational excitation DCS over the angular range which is complementary to the experimental acceptance angles (i.e. from Δθ° to 180° − Δθ°). By subtracting that contribution to the former “corrected values” (the short dashed line in Fig. 2), we obtain experimental data corrected for the “missing angle” elastic contribution but now not including rotational excitation. Those data are also plotted in Fig. 2 as a dashed-dot line. Although the latter should be equivalent to the calculated IAM-SCARI TCS without rotations, we can see in Fig. 2 that below 40 eV they tend to be lower than the calculated values. A possible explanation for this discrepancy is that our dipole-Born calculation is overestimating the rotational excitation cross section at the lower energies, which is consistent with the well-known nature and limitations of the first Born approximation.60
Fig. 3 represents a double logarithmic plot of the integral rotational excitation cross section calculated in this study, within the framework of the Born approximation, together with the dipole-Born correction to the IECS calculated in ref. 41 and the low-energy experimental TCS from ref. 12 and 13. The latter includes the elastic scattering processes, but considering the very good energy resolution used in ref. 12 (better than 8 meV) and the relevance of the rotational excitations in the scattering from highly polar molecules, we can expect that they dominate the low energy dependence of the TCS. As may be seen in this figure, all of them can be fitted to straight lines with similar slopes. Both calculations give slopes around −1.0, while that for the experimental data is about −1.3. As mentioned above, the latter includes elastic processes but it gives an indication of the energy dependence we might expect for the rotational excitations which, in the case of such strongly polar molecules as nitrobenzene, are dominant at these low energies. Concerning the absolute values of the rotational integral cross sections, it is clear than the magnitude for those of the present calculation is much higher than that of the others, by a factor 2 when comparing with those from ref. 41. We can hence conclude that even if our Born calculation gives a reasonable energy dependence of the rotational cross sections, it probably overestimates their absolute values.
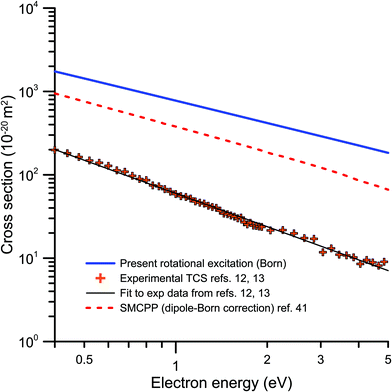 | ||
Fig. 3 Energy dependence of the integral rotational excitation cross sections from 0.4 to 5 eV:  , present dipole-Born calculation; , present dipole-Born calculation;  , dipole-Born correction from ref. 41; , dipole-Born correction from ref. 41;  , experimental TCS from ref. 12 and 13. , experimental TCS from ref. 12 and 13. | ||
3.4 Comparison with benzene
As we discussed in a recent paper devoted to electron scattering from benzene,40 a comparative study with nitrobenzene may contribute to understanding the role of the dipole moment in the scattering process. The geometry of both molecules is shown in Fig. 4. | ||
| Fig. 4 Molecular structure of benzene (a) and nitrobenzene (b), as determined using the Jmol package.61 | ||
The main structural difference is caused by the substitution of one of the H atoms of the benzene ring with the NO2 group, which confers a significant dipole moment to the nitrobenzene molecule. The MCEB experimental TCSs, in the energy range 0.4–300 eV, for both molecules are plotted together in Fig. 5. If we assume that our experimental arrangement is not able to energetically resolve rotational excitations, from pure geometrical considerations the TCSs for both molecules should present a similar structure. As can be seen in this figure, from 10 to 300 eV, the TCSs for both molecules have a similar energy dependence, within the combined uncertainty limits, but in terms of the magnitude those for NBz are around 40% higher, on average, than those for benzene (Bz). This clearly highlights the important role of the molecular polarisability in determining the scattering behaviour.31 From purely empirical considerations, based on the number of electrons (Z) and the molecular polarizability (α), García and Manero62 provided an asymptotic formula for the TCS of some molecules. The number of electrons for NBz and Bz are 64 and 42, respectively, while α is 87.1959 and 70.8359 a.u., respectively. According to this empirical formula,62 the TCS of NBz should be 42.5% higher than that of Bz which is in good agreement with our observation. However, for lower energies (<10 eV) the TCS ratio (NBz/Bz) is much higher than that expected from the empirical considerations, being about a factor 2 larger at around 2.5 eV. The low energies now under consideration are below the electronic excitation threshold, and therefore this difference might be attributed to differing scattering behaviour in the elastic channel. Nonetheless there is no theoretical reason to justify such different behaviour in the IECS for these two molecules, so again we have to consider that rotational excitations in NBz are leading to the deviation from the empirical behaviour of NBz versus Bz. As just discussed, this contribution in NBz can be evaluated by integrating the calculated rotational excitation DCS out of the effective detection angle range. Following the procedure described in the previous section, the TCS-nitrobenzene (no rota.) data, also now plotted in Fig. 5, represents the experimental TCS cross section plus the elastic contribution to the “missing angles” and minus the rotational excitation contribution from out of the acceptance angle range. This correction mainly affects the lower energies, below 20 eV, and gives NBz TCS values which are closer to those of Bz, being even lower than Bz below 4 eV. This comparison again indicates, in concordance with the previous discussion, that our dipole-Born rotational excitation calculation significantly overestimates the magnitude of this contribution.
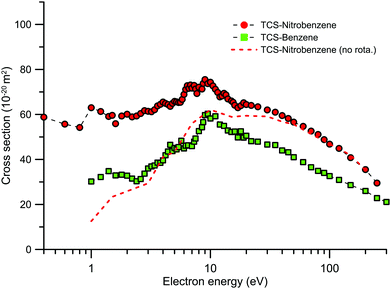 | ||
Fig. 5 Total electron scattering cross sections (10−20 m2) for benzene ( ) and nitrobenzene ( ) and nitrobenzene ( ) as measured with our MCEB apparatus. ) as measured with our MCEB apparatus. | ||
4. Conclusions
We have presented total electron scattering cross sections for nitrobenzene as measured with two different experimental systems, a magnetically confined electron beam arrangement for low-intermediate energies (0.4–250 eV) and a linear transmission-beam apparatus for intermediate-high energies (100–1000 eV), which showed good agreement for the common impact energy range. Random uncertainty limits of these measurements are comprised between 5 and 8%. The systematic error due to elastic and rotational excitation scattering into the acceptance angle of the detector (the “missing” angle effect) has also been carefully analysed for both experimental conditions and numerically quantified with the help of our calculated differential electron scattering cross sections. Due to the significant dipole moment of the nitrobenzene molecule the rotational excitation contribution to this effect is quite considerable for both experimental configurations and therefore needs to be taken into account before any comparison with either theoretical or other experimental data is attempted.Theoretical integral cross sections for elastic and inelastic (summed electronic excitation and ionisation) scattering as well as momentum transfer, as calculated with our IAM-SCARI method, are also presented for the 1–1000 eV impact energy range. Additionally, rotational excitation cross sections were calculated within the dipole-Born approximation. For energies above 10 eV the present theoretical and experimental data show good agreement within the combined uncertainty limits. Below 10 eV, apart from the expected overestimation of the elastic scattering cross section due the failure of the IAM-SCARI approach at such low energies, an underestimation of the summed electronic excitation scattering cross section has also been found. From this evidence, we can conclude that the electronic excitation of nitrobenzene, for impact energies from 4 to 10 eV, is quite significant for this molecule and will require further theoretical investigation. Such a calculation is now feasible with the parallelised version of the SMCPP approach, as evidenced from ref. 63–65. The previous IECS calculation from Maioli and Bettega,41 using the SMCPP method, shows an excellent agreement with the present IAM-SCARI computation at 10 eV, being also compatible with our measured TCS at that energy but tending to be much lower (up to 30%) in magnitude than ours for energies below 4 eV. Although further “ab initio” calculations in this energy range would be desirable to confirm their elastic cross section data below the electronic excitation threshold, we have shown here that for a strong polar molecule such as NBz our low-energy experimental TCS values are affected by the electrons rotationally scattered out of the acceptance angle of the detector, and so that may be the cause (in part) of this up to 30% difference with the SMCPP calculation below 4 eV.
We found a broad feature in the experimental TCS at around 1.0 eV, which has been connected with the formation of the NO2− anion and assigned to the π*(b1) resonance, according to previous mass spectra available in the literature. Other local maxima of the TCSs are found at 4.0 ± 0.2 eV and 5.0 ± 0.2 eV, being assigned to core excited resonances leading to the formation of the NO2− and O2− anions, respectively.
Finally, the present results for nitrobenzene have been compared with those we recently obtained for benzene.40 As a result of this comparison we have confirmed the need for a careful evaluation of the rotational excitation contribution to the experimental TCS measurements before comparing TCS results from different targets. Nonetheless, the TCS comparison between NBz and Bz clearly illustrated the very important role played by the target polarisability in the scattering dynamics. In addition, we have shown that the Born approximation tends to overestimate the rotational excitation cross section for the lower electron impact energies. We can thus conclude that a more sophisticated theoretical electron-molecule scattering analysis, including nuclear motion, is needed to properly quantify the contribution of the rotational excitation to the total cross section.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This study has partially been supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (Project FIS2016-80440) and CSIC (Project LINKA 20085). F. C. acknowledges Radiation Biology and Biophysics Doctoral Training Programme (RaBBiT, PD/00193/2012); UCIBIO (UIDB/04378/2020) and together with P. L. V. the Portuguese National Funding Agency FCT through the Research Grants CEFITEC (UIDB/00068/2020) and PTDC/FIS-AQM/31281/2017. M. J. B. thanks the Australian Research Council for funding through grants DP160102787 and DP180101655. The authors acknowledge Dr N. C. Jones for providing her full experimental TCS data on NBz molecules and Dr L. S. Maioli and Prof. M. H. F. Bettega for providing numerical tables of their SMCPP calculation and taking part in helpful discussions related to this paper. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI). Finally we also acknowledge Dr L. Campbell for his contributions to the final version of this paper.References
- J. A. Raleigh, J. D. Chapman, J. Borsa, W. Kremers and P. Reuvers, Int. J. Radiat. Biol., 1973, 23, 377 CAS.
- J. E. Biaglow and R. E. Durand, Radiat. Res., 1976, 65, 529 CrossRef CAS.
- A. P. Reuvers, J. D. Chapman and J. Borsa, Nature, 1973, 237, 402 CrossRef PubMed.
- R. N. Compton, R. H. Huebner, P. W. Reinhardt and L. G. Christophorou, J. Chem. Phys., 1968, 48, 901 CrossRef CAS.
- L. G. Christophorou, R. N. Compton, G. S. Hurst and P. W. Reinhard, J. Chem. Phys., 1966, 45, 536 CrossRef CAS.
- K. Jäger and A. Z. Henglein, Z. Naturforsch., 1967, 22a, 700 Search PubMed.
- A. Modelli and M. Venuti, Int. J. Mass Spectrom., 2001, 205, 7 CrossRef.
- N. L. Asfandiarov, S. A. Pshenichnyuk, V. G. Lukin, I. A. Pshenichnyuk, A. Modelli and Š. Matejčik, Int. J. Mass Spectrom., 2007, 264, 22 CrossRef CAS.
- O. Kröhl, K. Malsch and P. Swiderek, Phys. Chem. Chem. Phys., 2000, 2, 947 RSC.
- A. Pelc, P. Scheier and T. D. Märk, Vacuum, 2007, 81, 1180 CrossRef CAS.
- NIST Chemistry WebBook, U.S. Department of Commerce, Washington, DC, 2017, https://webbook.nist.gov/chemistry/.
- S. L. Lunt, D. Field, J.-P. Ziesel, N. C. Jones and R. J. Gulley, Int. J. Mass Spectrom., 2001, 205, 197 CrossRef CAS.
- N. C. Jones, private communication.
- D. Field, S. L. Lunt and J. P. Ziesel, Acc. Chem. Res., 2001, 34, 291 CrossRef CAS PubMed.
- I. Fabrikant, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 222005 CrossRef.
- S. Nagakura, M. Kojima and Y. Maruyama, J. Mol. Spectrosc., 1964, 13, 174 CrossRef CAS.
- H. K. Sinha and K. Yates, J. Chem. Phys., 1990, 93, 7085 CrossRef CAS.
- T. E. Peacock, Proc. Phys. Soc., London, 1961, 78, 460 CrossRef CAS.
- O. Matsuoka and Y. I’Haya, Mol. Phys., 1964, 8, 455 CrossRef CAS.
- C. Sieiro and J. Fernández-Alonso, Chem. Phys. Lett., 1973, 18, 557 CrossRef CAS.
- J. W. Rabalais, J. Chem. Phys., 1972, 57, 960 CrossRef CAS.
- F. Zuccarello, S. Millefiori and G. Buemi, Spectrochim. Acta, Part A, 1979, 35, 223 CrossRef.
- J. D. Steill and J. Oomens, Int. J. Mass Spectrom., 2011, 308, 239 CrossRef CAS.
- A. P. Hitchcock, J. Electron Spectrosc. Relat. Phenom., 2000, 112, 9 CrossRef CAS.
- C. C. Turci, S. G. Urquhart and A. P. Hitchcock, Can. J. Chem., 1996, 74, 851 CrossRef CAS.
- D. Mathur and J. B. Hasted, J. Phys. B: At. Mol. Phys., 1976, 9, L31 CrossRef CAS.
- S. Krishnakumar, A. K. Das, P. J. Singh, A. Shastri and B. N. Rajasekhar, J. Quant. Spectrosc. Radiat. Transfer, 2016, 184, 89 CrossRef CAS.
- R. S. Mock and E. P. Grimsrud, J. Am. Chem. Soc., 1989, 111, 2861 CrossRef CAS.
- S. Katsumata, H. Shiromaru, K. Mitani, S. Iwata and K. Kimura, Chem. Phys., 1982, 69, 423 CrossRef CAS.
- A. I. Lozano, K. Krupa, F. Ferreira da Silva, F. Blanco, A. Muñoz, D. B. Jones, M. J. Brunger and G. García, Eur. Phys. J. D, 2017, 71, 226 CrossRef.
- M. J. Brunger, Int. Rev. Phys. Chem., 2017, 36, 333 Search PubMed.
- Radiation Damage in Biomolecular Systems, ed. G. G. Gómez-Tejedor and M. C. Fuss, Springer, London, 2012 Search PubMed.
- M. C. Fuss, A. G. Sanz, F. Blanco, J. C. Oller, P. Limão-Vieira, M. J. Brunger and G. García, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 042702 CrossRef.
- A. G. Sanz, M. C. Fuss, F. Blanco, J. D. Gorfinkiel, D. Almeida, F. Ferreira da Silva, P. Limão-Vieira, M. J. Brunger and G. García, J. Chem. Phys., 2013, 139, 184310 CrossRef CAS PubMed.
- A. Loupas, A. I. Lozano, F. Blanco, J. D. Gorfinkiel and G. García, J. Chem. Phys., 2018, 149, 034304 CrossRef PubMed.
- A. I. Lozano, A. Loupas, F. Blanco, J. D. Gorfinkiel and G. García, J. Chem. Phys., 2018, 149, 134303 CrossRef CAS PubMed.
- A. I. Lozano, A. F. Ferreira da Silva, F. Blanco, P. Limão-Vieira and G. García, Chem. Phys. Lett., 2018, 706, 533 CrossRef CAS.
- A. I. Lozano, J. C. Oller, D. B. Jones, R. F. da Costa, M. T. do, N. Varella, M. H. F. Bettega, F. Ferreira da Silva, P. Limão-Vieira, M. A. P. Lima, R. D. White, M. J. Brunger, F. Blanco, A. Muñoz and G. García, Phys. Chem. Chem. Phys., 2018, 20, 22368 RSC.
- A. I. Lozano, J. Jiménez, F. Blanco and G. García, Phys. Rev. A: At., Mol., Opt. Phys., 2018, 98, 012709 CrossRef CAS.
- F. Costa, L. Álvarez, A. I. Lozano, F. Blanco, J. C. Oller, A. Muñoz, A. Souza Barbosa, M. H. F. Bettega, F. Ferreira da Silva, P. Limão-Vieira, R. D. White, M. J. Brunger and G. García, J. Chem. Phys., 2019, 151, 084310 CrossRef CAS PubMed.
- L. S. Maioli and M. H. F. Bettega, J. Chem. Phys., 2017, 147, 164305 CrossRef PubMed.
- A. I. Lozano, J. C. Oller, K. Krupa, P. Limão-Vieira, F. Blanco, A. Muñoz, R. Colmenares and G. García, Rev. Sci. Instrum., 2018, 89, 063105 CrossRef CAS PubMed.
- F. Blanco and G. García, Phys. Lett. A, 2002, 295, 178 CrossRef CAS.
- F. Blanco and G. García, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 022701 CrossRef.
- F. Blanco, L. Ellis-Gibbings and G. García, Chem. Phys. Lett., 2016, 645, 71 CrossRef CAS.
- M. J. Brunger, S. J. Buckman and K. Ratnavelu, J. Phys. Chem. Ref. Data, 2017, 46, 023102 CrossRef.
- F. Blanco, F. Ferreira da Silva, P. Limão-Vieira and G. García, Plasma Sources Sci. Technol., 2017, 26, 085004 CrossRef.
- W. A. D. Pires, K. L. Nixon, S. Ghosh, R. F. C. Neves, H. V. Duque, R. A. R. Amorim, D. B. Jones, F. Blanco, G. García, M. J. Brunger and M. C. A. Lopes, Int. J. Mass Spectrom., 2017, 422, 32 CrossRef CAS.
- S. Ghosh, K. L. Nixon, W. A. D. Pires, R. A. R. Amorim, R. F. C. Neves, H. V. Duque, M. G. M. da Silva, D. B. Jones, F. Blanco, G. García, M. J. Brunger and M. C. A. Lopes, Int. J. Mass Spectrom., 2018, 430, 44 CrossRef CAS.
- A. G. Sanz, M. C. Fuss, F. Blanco, F. Sebastianelli, F. A. Gianturco and G. García, J. Chem. Phys., 2012, 137, 124103 CrossRef CAS PubMed.
- M. J. Brunger, P. J. O. Teubner, A. M. Weigold and S. J. Buckman, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 1443 CrossRef CAS.
- K. R. Lykke, R. D. Mead and W. C. Lineberger, Phys. Rev. Lett., 1984, 52, 2221 CrossRef CAS.
- C. L. Adams, H. Schneider, K. M. Ervin and J. M. Weber, J. Chem. Phys., 2009, 130, 074307 CrossRef PubMed.
- S. Gulania, T.-C. Jagau, A. Sanov and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 5002 RSC.
- J. N. Bull, C. S. Anstöter and R. R. Verlet, Nat. Commun., 2019, 10, 5820 CrossRef CAS PubMed.
- M. E. Castellani, C. S. Anstöter and R. R. Verlet, Phys. Chem. Chem. Phys., 2019, 21, 24286 RSC.
- C. S. Anstöter, G. Mensa-Bonsu, P. Nag, M. Rancovic, R. Kumar T. P., A. N. Boichenko, A. V. Bochenkova, J. Fedor and R. R. Verlet, Phys. Rev. Lett., 2020, 124, 203401 CrossRef PubMed.
- C. Szmytkowski, S. Stefanowska, N. Tańska, B. Żywicka, E. Ptasińska-Denga and P. Możejko, Mol. Phys., 2019, 2019(117), 395 CrossRef.
- Computational Chemistry Comparison and Benchmark DataBase, https://cccbdb.nist.gov/pollistx.asp.
- H. Tanaka, M. J. Brunger, L. Campbell, H. Kato, M. Hoshino and A. R. P. Rau, Rev. Mod. Phys., 2016, 88, 025004 CrossRef.
- See http://jmol.sourceforge.net/.
- G. García and F. Manero, Chem. Phys. Lett., 1997, 264, 595 CrossRef.
- R. F. da Costa, E. M. Oliveira, M. H. F. Bettega, M. T. do, N. Varella, D. B. Jones, M. J. Brunger, F. Blanco, R. Colmenares, P. Limão-Vieira, G. García and M. A. P. Lima, J. Chem. Phys., 2015, 142, 104304 CrossRef PubMed.
- R. F. da Costa, M. T. do, N. Varella, M. H. F. Bettega, R. F. C. Neves, M. C. A. Lopes, F. Blanco, G. García, D. B. Jones, M. J. Brunger and M. A. P. Lima, J. Chem. Phys., 2016, 144, 124310 CrossRef PubMed.
- R. F. da Costa, J. C. Ruivo, F. Kossoski, M. T. do, N. Varella, M. H. F. Bettega, D. B. Jones, M. J. Brunger and M. A. P. Lima, J. Chem. Phys., 2018, 149, 174308 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02039g |
| This journal is © the Owner Societies 2020 |
