Hydrogen bonds and halogen bonds in complexes of carbones L→C←L as electron donors to HF and ClF, for L = CO, N₂, HNC, PH₃, and SH₂

Abstract

Ab initio MP2/aug’-cc-pVTZ calculations have been carried out to determine the structures and binding energies of the carbone complexes in which the carbone L→C←L acts as an electron pair donor to one and two HF or ClF molecules, for L = CO, N₂, HNC, PH₃, and SH₂. The binding energies increase with respect to the ligand in the order CO < NN < CNH ≪ PH₃ < SH₂, and increase with respect to the acid in the order HF < 2 HF < ClF < 2 ClF. The complexes with the ligands CO, N₂ and PH₃ have C_2v symmetry while those with CNH and SH₂ have C_s symmetry, except for H₂S→C←SH₂:2HF which has C₂ symmetry and a unique structure among all of the carbone complexes. F–H and Cl–F stretching frequencies in the complexes decrease as the F–H and Cl–F distances, respectively, increase. EOM-CCSD spin–spin coupling constants ^2hJ(F–C) increase with decreasing F–C distance. Although the F–H⋯C hydrogen bonds gain some proton-shared character in the most tightly bound complexes, the hydrogen bonds remain traditional hydrogen bonds. ^1xJ(Cl–C) values indicate that the Cl⋯C halogen bonds have chlorine shared character even at the longest distances. ^1xJ(Cl–C) then increases as the Cl–C distance decreases, and reaches a maximum for chlorine-shared halogen bonds. As the Cl–C distance further decreases, the halogen bond becomes a chlorine-transferred halogen bond.

---

Introduction

One of the fundamental tenets of organic and organometallic chemistry is that the carbon atom has a valence of four. However, there exists a set of molecules called carbenes in which carbon has a valence of two. Carbenes are traditionally very reactive species which are usually difficult to isolate,¹ except for the nitrogen heterocyclic carbenes.^2,3 These molecules contain a carbon atom with either two paired electrons in a single orbital giving rise to a singlet electronic configuration, or two unpaired electrons in two different orbitals in a triplet electronic configuration.^4–6 Singlet carbenes are very basic species,^7–10 are found in complexes with metals,¹¹ and can participate in a variety of non-covalent interactions¹² including hydrogen,^13–15 halogen,^16,17 chalcogen,¹⁸ pnicogen^19–21 and tetrel bonds.^22,23

In recent years, Frenking and co-workers have explored the possibility of having carbon(0) compounds called carbones, which are stabilized by two electron pair donor molecules.^24–26 The first carbone, hexaphenylcarbodiphosphorane, was described in 1961.²⁷ The central carbon atom of the carbone molecule has four nonbonded electrons in two orbitals and two electron pairs which form bonds to two ligands, as illustrated in Scheme 1. These carbones are able to act as electron pair donors to two Lewis acids, in contrast to carbenes that can donate only a single pair of electrons.²⁸ Moreover, an extension of the carbones to systems with central atoms other than carbon has been proposed. These systems contain central atoms such as Be, B, N, Mg, Al, Si, P, Ge, Sn, and Pb in low coordination states which are stabilized by electron pair donors.^29–32

Scheme 1 Carbone molecule stabilized by two electron pair donor ligands.

To further investigate carbones, we have carried out a study of five carbones (OC→C←CO, NN→C←NN, HNC→C←CNH, H₃P→C←PH₃, and H₂S→C←SH₂) acting as electron pair donors to one and two Lewis acids HF or ClF. The structures and binding energies of these complexes have been obtained and are analyzed in detail. In addition, we have determined the H–F and Cl–F IR bond stretching frequencies in the complexes, and the EOM-CCSD spin–spin coupling constants ^2hJ(F–C) for coupling across hydrogen bonds, and ^1xJ(C–Cl) for coupling across halogen bonds to further characterize these complexes. It is the purpose of this paper to report the results of this study.

Methods

The structures of the isolated carbone molecules OC→C←CO, NN→C←NN, HNC→C←CNH, H₃P→C←PH₃, and H₂S→C←SH₂, the Lewis acids HF and ClF, and the complexes formed between the carbones and the acids were optimized at second-order Møller–Plesset perturbation theory (MP2)^33–36 with the aug’-cc-pVTZ basis set.³⁷ This basis set was derived from the Dunning aug-cc-pVTZ basis set^38,39 by removing diffuse functions from H atoms.

Complex binding energies (−ΔE) were evaluated as the negative of the reaction energy for the formation of the binary complex from the corresponding isolated, optimized monomers, without the basis set superposition error (BSSE) correction. It is known that the BSSE correction using the Boys and Bernardi counterpoise method⁴⁰ is an overcorrection, since low energy orbitals which are occupied in the complex are unoccupied for the evaluation of the BSSE. In a study of the proton affinities of some neutral and anionic bases using the Dunning basis sets, BSSE uncorrected aug’-cc-pVXZ proton affinities exhibited better convergence properties than BSSE corrected proton affinities, and were in better agreement with experimental values.³⁷ In addition, the removal of diffuse functions from H atoms has a negligible effect on the binding energies of some neutral, positively charged, and negatively charged hydrogen bonded dimers.^41–43

Frequencies were computed to establish that the optimized structures correspond to equilibrium structures on their potential surfaces. These data were also used to examine the effect of complex formation on H–F and Cl–F stretching frequencies. Optimization and frequency calculations were performed using the Gaussian 16 program.⁴⁴

The electron density properties at bond critical points (BCPs) of complexes have been analyzed using the Atoms in Molecules (AIM) methodology^45–48 employing the AIMAll⁴⁹ program. The topological analysis of the electron density produces the molecular graph of each complex. This graph identifies the location of electron density features of interest, including the electron density (ρ) maxima associated with the various nuclei, and saddle points which correspond to bond critical points. The zero gradient line which connects a BCP with two nuclei is the bond path.

Equation of motion coupled cluster singles and doubles (EOM-CCSD) spin–spin coupling constants were evaluated in the CI (configuration interaction)-like approximation^50,51 with all electrons correlated. For these calculations, the Ahlrichs⁵² qzp basis set was placed on ¹³C, ¹⁵N, ¹⁷O, and ¹⁹F, and the qz2p basis on ³¹P, ³³S, ³⁵Cl, and the hydrogen-bonded ¹H atom of FH. The Dunning cc-pVDZ basis set was placed on all other ¹H atoms. All terms that contribute to the total coupling constant, namely, the paramagnetic spin orbit (PSO), diamagnetic spin orbit (DSO), Fermi contact (FC), and spin dipole (SD)⁵³ have been evaluated. Coupling constant calculations were performed using ACES II⁵⁴ on the HPC cluster Oakley at the Ohio Supercomputer Center.

Results and discussion

Overview

Table 1 presents the binding energies of the complexes formed by the carbones and the acids HF and ClF. In Table 1, the carbones are written as L→C←L to emphasize that the ligands CO, N₂, CNH, PH₃, and SH₂ are electron donors to the carbon atom. In the complexes, this central carbon then acts as an electron-pair donor to 1 or 2 HF or ClF molecules. There are three trends that are immediately apparent from the data of Table 1. First, for a fixed acid, the binding energies of the complexes increase with respect to the ligand in the order

CO < N₂ < CNH ≪ PH₃ < SH₂.

Second, the difference between the binding energies of the complexes with HF as the acid and those with ClF depends on the ligand. That difference increases with respect to the ligand in the same order as indicated above. Third, for a fixed carbone molecule, the binding energies increase with respect to the acid in the order

HF < 2HF < ClF < 2ClF.

Table 1 Binding energies (kJ mol⁻¹) of complexes with carbones as electron donors to HF and ClF

Carbone	HF	2HF	ClF	2ClF
OC→C←CO	12.8	20.0	21.9	41.3
N2→C←N2	17.6	29.1	36.1	66.9
HNC→C←CNH	20.0	37.9	41.7	68.8
H3P→C←PH3	62.5	115.6	132.8	243.6
H2S→C←SH2	75.3	134.4	184.0	297.3

---

The binding energies of the complexes with the carbones are functions of the intermolecular distances, as evident from Fig. 1. This figure provides plots of these energies for the five sets of complexes subdivided according to whether there are one or two HF or ClF molecules present, versus the intermolecular F–C hydrogen bond distance, and the Cl–C halogen bond distance. The trendlines are second-degree polynomials with correlation coefficients of 0.990 for complexes with one HF molecule, and 0.958 for those with two HF molecules. For the halogen-bonded complexes with one ClF molecule, the correlation coefficient decreases to 0.906, and then increases to 0.944 when two ClF molecules are present. It is noteworthy that for each set of molecules represented in Fig. 1, there are three carbones with relatively low binding energies, and these have CO, N₂, and HNC as the ligands. In contrast, when PH₃ or SH₂ are the ligands, the binding energies increase dramatically, particularly in the complexes stabilized by halogen bonds.

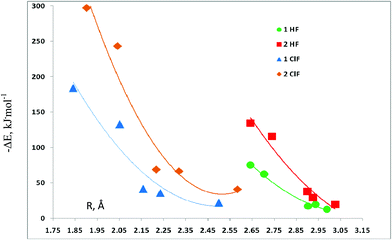Fig. 1 Binding energies versus the F–C distance for complexes stabilized by hydrogen bonds, and versus the Cl–C distance for complexes stabilized by halogen bonds.

It is also noteworthy that one ligand that obviously should have been included in this study is HCN to form the carbone HCN→C←NCH. However, this carbone cannot be described adequately by a single-determinant reference function as indicated by large t2 amplitudes for intruder states which must be taken into account by a multi-reference wavefunction.

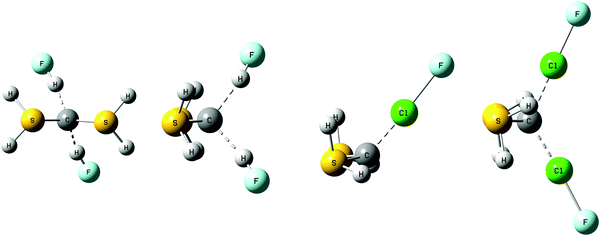
Complexes with OC→C←CO

Table S1 of the ESI† provides the structures, total energies, and molecular graphs of the complexes of OC→C←CO with one and two HF or ClF molecules. Fig. 2 illustrates the structures of complexes with one and two HF molecules. All of these complexes have C_2v symmetry, indicating that the two acid molecules are equivalent in complexes OC→C←CO:2HF and OC→C←CO:2ClF. Table 2 reports binding energies and selected bond distances and bond angles.

Fig. 2 Complexes of OC→C←CO with one and two HF molecules.

Table 2 Complex binding energies (−ΔE, kJ mol⁻¹), C–C and intermolecular F–C and Cl–C distances (R, Å), and C–C–C, H–F–C, and C–Cl–F angles (∠, °) in complexes of OC→C←CO with one and two HF or ClF molecules^a

	−ΔE	R(C–C)	∠C–C–C	R(F–C)	∠H–F–C
a All complexes have C2v symmetry.
OC→C←CO		1.278	168
OC→C←CO:HF	12.8	1.295	142	2.987	0
OC→C←CO:2HF	20.0	1.305	134	3.026	6

---

	−ΔE	R(C–C)	∠C–C–C	R(Cl–C)	∠C–Cl–F
OC→C←CO:ClF	21.9	1.296	143	2.499	180
OC→C←CO:2ClF	41.3	1.303	138	2.584	180

---

The binding energies of the complexes with the carbone OC→C←CO increase in the order HF < 2HF < ClF < 2ClF, and range from 13 to 41 kJ mol⁻¹. The C–C bond length varies from 1.28 Å in the isolated carbone, to 1.30 Å in the complexes with two HF and two ClF molecules, which is a relatively small difference. However, although the change in the C–C bond length is minimal, the C–C–C angle decreases significantly in the complexes with one HF or ClF molecule, and then decreases further when two acid molecules are present. Thus, in the isolated carbone the C–C–C angle is 168°, and it decreases to 142 and 143° in the complexes with one HF and one ClF molecule, respectively. The C–C–C angle further decreases to 134 and 138° when two FH and two ClF molecules, respectively, interact with the carbone. In the hydrogen-bonded complexes with HF, the hydrogen bonds are essentially linear, and based on the F–C distances, the hydrogen bonds are traditional hydrogen bonds. In the halogen-bonded complexes, the C–Cl–F angles are 180°, indicating that electron donation from the carbone C to Cl occurs through the σ-hole on Cl. The C–Cl distances are 2.50 and 2.58 Å in the complexes with one and two ClF molecules, respectively. These distances are shorter than the C–Cl distances in complexes OC:ClY which range from 2.66 to 3.29 Å,⁵⁵ suggesting that the halogen bonds in the carbone complexes have some chlorine-shared character.⁵⁶

Table 3 provides values of the F–H and Cl–F distances for all binary and ternary complexes formed by the carbone and the HF and ClF molecules. From this table it is evident that in the complexes of OC→C←CO with one FH or ClF molecule, the F–H and Cl–F distances increase relative to the isolated HF and ClF molecules. When two HF or ClF molecules are present, the H–F and Cl–F distances still increase relative to the monomers, but are not quite as long as they are in the corresponding binary complexes. This suggests that the hydrogen and halogen bonds individually are not quite as strong in the ternary complexes as they are in the binary, since in the ternary complexes, both bonds form at the same site, namely, the carbone C atom.

Table 3 F–H and Cl–F distances (R, Å) in complexes with carbones

Carbone/acid	R(H–F)^a	2 R(F–H)^a	R(Cl–F)^b	2 R(Cl–F)^b
a Monomer R(H–F) = 0.922 Å. b Monomer R(Cl–F) = 1.638 Å.
OC→C←CO	0.931	0.929	1.672	1.661
NN→C←NN	0.935	0.933	1.714	1.696
HNC→C←CNH	0.936	0.937	1.770	1.742
		0.935		1.676
H3P→C←PH3	0.966	0.962	1.893	1.862
H2S→C←SH2	0.984	0.975	1.972	1.897
				1.867

---

Complexes with NN→C←NN

The structures, total energies, and molecular graphs of the complexes of the carbone NN→C←NN with one and two HF or ClF molecules are reported in Table S2 of the ESI.† All of these complexes have C_2v symmetry, and are structurally similar to the corresponding complexes with OC→C←CO. Table 4 reports the C–N distance and N–C–N angle in the isolated carbone, and these parameters along with the intermolecular F–C and Cl–C distances and the H–F–C and C–Cl–F angles in the complexes of NN→C←NN with one and two HF and ClF molecules. As noted previously, the binding energies of these complexes are greater than the binding energies of the corresponding OC→C←CO complexes, ranging from 18 kJ mol⁻¹ when a single hydrogen bond is present, to 67 kJ mol⁻¹ when two halogen bonds stabilize the complex. The C–N distance is 1.27 Å in the isolated carbone, and increases to 1.31 Å in the complexes with two HF and two ClF molecules, a slightly larger change than found in the corresponding complexes with OC→C←CO. The N–C–N angle is 131° in the isolated carbone, a significantly smaller angle than the C–C–C angle in OC→C←CO. This angle decreases to 122 and 124° in the complexes with one HF and one ClF molecule, and then further decreases to 117 and 118° when two HF and two ClF molecules, respectively, are present. In the hydrogen bonded complexes with one HF, the hydrogen bond is linear, while it deviates from linearity by 8° when there are two hydrogen bonds. These hydrogen bonds are traditional hydrogen bonds. The C–Cl–F angles indicate the presence of linear halogen bonds that arise as the carbone C donates a pair of electrons to ClF through the σ-hole on Cl. The Cl–C distances have decreased relative to the corresponding OC→C←CO complexes, indicating increased chlorine-shared character of the halogen bonds.

Table 4 Complex binding energies (−ΔE, kJ mol⁻¹), C–N and intermolecular F–C and Cl–C distances (R, Å), and selected angles (∠, °) in complexes of NN→C←NN with one and two HF or ClF molecules^a

	−ΔE	R(C–N)	∠N–C–N	R(F–C)	∠H–F–C
a All complexes have C2v symmetry.
NN→C←NN		1.267	131
NN→C←NN:HF	17.6	1.291	122	2.904	0
NN→C←NN:2HF	29.1	1.309	117	2.926	8

---

	−ΔE	R(C–N)	∠N–C–N	R(Cl–C)	∠C–Cl–F
NN→C←NN:ClF	36.1	1.289	124	2.235	180
NN→C←NN:2ClF	66.9	1.311	118	2.319	179

---

Table 3 reports the F–H and Cl–F distances in the complexes of NN→C←NN with one and two HF or HCl molecules. It is apparent that corresponding F–H and Cl–F bonds are longer in the complexes with NN→C←NN than they are when the carbone is OC→C←CO. This observation is consistent with the greater binding energies of the NN→C←NN complexes. Once again, the lengthening of the F–C and Cl–F bonds in the ternary complexes is not as great as it is in the corresponding binary complexes.

Complexes with HNC→C←CNH

Fundamental information including the structures, total energies, and molecular graphs of the complexes of the carbone HNC→C←CNH with one and two HF and ClF molecules can be found in Table S3 of the ESI.† The complexes with HNC→C←CNH have much lower symmetries than the complexes with OC→C←CO and NN→C←NN. The isolated carbone HNC→C←CNH has only C₂ symmetry, the complex with one HF molecule has no symmetry in point group C₁, and the remaining complexes have C_s symmetry. Table 5 presents binding energies and selected distances and angles for these complexes, while Fig. 3 illustrates the structures of HNC→C←CNH:HF, HNC→C←CNH:2HF, and HNC→C←CNH:2ClF.

Table 5 Complex binding energies (−ΔE, kJ mol⁻¹), symmetries, C–C and intermolecular F–C and Cl–C distances (R, Å), and selected angles (∠, °) in complexes of HNC→C←CNH with one and two HF or ClF molecules

Complex	Sym	−ΔE	R(C–C)	∠C–C–C	R(F–C)	∠H–F–C
a For complexes with two nonequivalent HF or ClF molecules, data for the interaction which occurs at the shorter intermolecular distance are given first.
HNC→C←CNH	C 2		1.280	173
HNC→C←CNH:HF	C 1	20.0	1.294	151	2.937	4
HNC→C←CNH:2HF	C s	37.9	1.314	133	2.901^a	2^a
					2.938	9

---

Complex	Sym	−ΔE	R(C–C)	∠C–C–C	R(Cl–C)	∠C–Cl–F
HNC→C←CNH:ClF	C s	41.7	1.316	133	2.158	180
HNC→C←CNH:2ClF	C s	68.8	1.322	132	2.217^a	180^a
					2.550	180

---

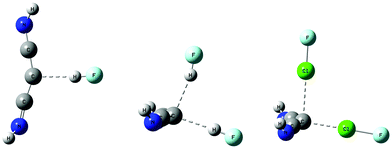Fig. 3 Complexes of HNC→C←CNH with HF and ClF molecules. The complex with one FH has C₁ symmetry, while those with two HF and two ClF have C_s symmetry.

The complex HNC→C←CNH:HF has a binding energy of 20 kJ mol⁻¹ at an F–C hydrogen bond distance of 2.94 Å and has an essentially linear hydrogen bond. The carbone C–C distances in this complex are both 1.29 Å, slightly longer than the monomer distance of 1.28 Å. That this complex has only C₁ symmetry can be seen from the distances from the C atoms of the two HNC ligands to F which are 3.38 and 3.58 Å, the two F–C–C angles which are 109 and 98°, and the different orientations of the N–H bonds of the two HNC ligands, as evident in Fig. 3.

The complex in which two HF molecules interact with the carbone has C_s symmetry. The binding energy of this complex increases to 38 kJ mol⁻¹ as the two intramolecular C–C distances increase to 1.31 Å, and the C–C–C angle decreases to 133°. The two HF molecules are not equivalent, as evident from the intermolecular F–C distances across the hydrogen bonds of 2.90 and 2.94 Å, and the hydrogen bond H–F–C angles of 2 and 9°, respectively. The shorter F–C distance and the H–F–C angle of 2° refer to the FH molecule that interacts with the carbone through the C–C–C σ-electron system, as illustrated in Fig. 3. This hydrogen bond appears to be stronger than the hydrogen bond which forms through the pseudo-π system of the carbone. Based on the F–C distances, both hydrogen bonds would appear to be traditional bonds.

The complexes of HNC→C←CNH with one and two ClF molecules have C_s symmetry and binding energies of 42 and 69 kJ mol⁻¹, respectively. The C–C distance in the complex with one ClF molecule is essentially the same as that distance in the complex with two HF molecules, but when two ClF molecules are present, the C–C distance increases slightly. The C–C–C angles in the complexes with one and two ClF molecules are the same as that angle in the complex with two HF molecules. The Cl–C distance is 2.16 Å in the complex with one ClF molecule, and increases to 2.22 and 2.55 Å in the complex with two ClF molecules. Once again, the stronger halogen bond is associated with the shorter Cl–F distance, and involves electron donation to Cl through the σ-electron system of the carbone. These halogen bonds should be characterized as chlorine shared halogen bonds. The second interaction is better described as a weaker interaction that occurs approximately through the pseudo-π system of HNC→C←CNH. This description is also consistent with the longer Cl–F bond when bond formation occurs through the C–C–C σ-electron system, compared to the shorter Cl–F bond found when the interaction occurs through the pseudo-π-electron system of the carbone, as reported in Table 3.

Complexes with H₃P→C←PH₃

Data for the computed structures, total energies, and molecular graphs of the complexes of H₃P→C←PH₃ with one and two HF or ClF molecules can be found in Table S4 of the ESI.†Table 6 presents the binding energies, symmetries, and selected distances and angles for these complexes. Fig. 4 illustrates the structures of H₃P→C←PH₃:HF, H₃P→C←PH₃:2HF, and H₃P→C←PH₃:ClF.

Table 6 Complex binding energies (−ΔE, kJ mol⁻¹), symmetries, P–C and intermolecular F–C and Cl–C distances (R, Å), and selected angles (∠, °) in complexes of H₃P→C←PH₃ with one and two HF or ClF molecules

Complex	Sym	−ΔE	R(P–C)	∠P–C–P	R(F–C)	∠H–F–C
H3P→C←PH3	C 2v		1.657	120
H3P→C←PH3:HF	C s	62.5	1.661	123	2.703	0
H3P→C←PH3:2HF	C 2v	115.6	1.676	121	2.741	4

---

Complex	Sym	−ΔE	R(P–C)	∠P–C–P	R(Cl–C)	∠C–Cl–F
H3P→C←PH3:ClF	C s	132.8	1.685	125	2.052	180
H3P→C←PH3:2ClF	C 2v	243.6	1.715	129	2.042	179

---

Fig. 4 Structures of H₃P→C←PH₃:HF, H₃P→C←PH₃:2HF, and H₃P→C←PH₃:ClF.

The complex H₃P→C←PH₃:HF has C_s symmetry and a linear hydrogen bond with a binding energy of 62 kJ mol⁻¹ at an F–C distance of 2.70 Å. This binding energy is significantly greater than the binding energies of the complexes that have the first-row ligands CO, NN, and HNC interacting with a single HF molecule, as evident from Table 1. Moreover, H₃P→C←PH₃:HF is more stable than HNC→C←CNH:HF by 42 kJ mol⁻¹ while H₃P→C←PH₃:2ClF is more stable than HNC→C←CNH:2ClF by 175 kJ mol⁻¹. This is a dramatic difference, which most probably reflects the greater electron-donating capability of the second-row ligands, and their larger size which allows for a more diffuse electron distribution. It is also indicative of the nature of the intermolecular bonds in these complexes, which suggests that the hydrogen bonds have some proton-shared character, while the halogen bonds begin to exhibit chlorine-transferred character.

The carbone P–C distance in H₃P→C←PH₃:HF is 1.66 Å, which is similar to the distance in the isolated carbone. The P–C–P angle is 123°, slightly greater than the angle of 120° in H₃P→C←PH₃. The hydrogen bond is linear, with an F–C distance of 2.70 Å. The complex H₃P→C←PH₃:2HF has C_2v symmetry with an increased binding energy of 116 kJ mol⁻¹. Both the P–C and F–C distances are slightly longer in this ternary complex than in the corresponding binary complex, and the hydrogen bonds are slightly nonlinear. The F–H distances in these complexes are noticeably longer than they are in the complexes which have first-row ligands bonded to C, as evident from Table 3. This is consistent with the increased binding energies of H₃P→C←PH₃:HF and H₃P→C←PH₃:2HF, and the changing nature of the hydrogen bonds.

Changes in the energetic and structural parameters describing the halogen bond in the complexes H₃P→C←PH₃:ClF and H₃P→C←PH₃:2ClF compared to HNC→C←CNH:ClF and HNC→C←CNH:2ClF are dramatic. The binding energies of H₃P→C←PH₃:ClF and H₃P→C←PH₃:2ClF increase to 133 and 244 kJ mol⁻¹, the Cl–C distances decrease to 2.05 and 2.04 Å, and the Cl–F distances lengthen to 1.89 and 1.86 Å, respectively. The changes in the Cl–C distances and the Cl–F distances in Table 3 indicate that the nature of the halogen bond itself is changing, as the halogen bond approaches a Cl-transferred halogen bond. In addition, the P–C distances increase from 1.66 in the H₃P→C←PH₃ monomer to 1.69 and 1.72 Å, while the P–C–P angle increases from 120° in the monomer to 125 and 129° in the complexes with one and two ClF molecules, respectively.

Complexes with H₂S→C←SH₂

Data for the final set of complexes in which the carbone is H₂S→C←SH₂ are reported in Table S5 of the ESI.† These include the structures, total energies, and molecular graphs of the complexes of H₂S→C←SH₂ with one and two HF or ClF molecules. Table 7 presents the binding energies, symmetries, and selected distances and angles for these complexes. Fig. 5 illustrates the structures of H₂S→C←SH₂:2HF, H₂S→C←SH₂:ClF, and H₂S→C←SH₂:2ClF.

Table 7 Complex binding energies (−ΔE, kJ mol⁻¹), symmetries, C–S and intermolecular F–C and Cl–C distances (R, Å), and selected angles (∠, °) in complexes of H₂S→C←SH₂ with one and two HF or ClF molecules

Complex	Sym	−ΔE	R(S–C)	∠S–C–S	R(F–C)	∠H–F–C
a For the H2S→C←SH2:2ClF complex with two nonequivalent ClF molecules, data for the interaction with the shorter intermolecular Cl–C distance are given first.
H2S→C←SH2	C 2v		1.280	173
H2S→C←SH2:HF	C 2v	75.3	1.709	104	2.643	0
H2S→C←SH2:2HF	C 2	134.4	1.725	105	2.643	12

---

Complex	Sym	−ΔE	R(S–C)	∠S–C–S	R(Cl–C)	∠C–Cl–F
H2S→C←SH2:ClF	C s	184.0	1.713	109	1.840	177
H2S→C←SH2:2ClF	C s	297.3	1.806	109	1.902^a	176^a
					1.984^a	179^a

---

Fig. 5 Structures of H₂S→C←SH₂:2HF (with two views), H₂S→C←SH₂:ClF, and H₂S→C←SH₂:2ClF.

The binding energies of the complexes with H₂S→C←SH₂ are 75 and 134 kJ mol⁻¹ in the complexes with one and two HF molecules, and 184 and 297 kJ mol⁻¹ with one and two ClF molecules, respectively. The S–C distance increases dramatically upon complex formation, from 1.28 Å in the monomer to 1.71 and 1.73 Å in the complexes with one and two HF molecules, and to 1.71 and 1.81 Å when one and two ClF molecules, respectively, are present. There is also a dramatic decrease in the S–C–S angle, from nearly linear at 173° in the monomer, to between 104 and 109° in the complexes, indicative of a tetrahedral arrangement around the carbone C.

The complexes with one and two HF molecules both have shortened hydrogen bond distances of 2.64 Å, which indicate that these hydrogen bonds have increased proton-shared character. A linear hydrogen bond exists in the H₂S→C←SH₂:HF complex with C_2v symmetry, but a bond that deviates from linearity by 12° is found in H₂S→C←SH₂:2HF, a complex with only C₂ symmetry. This latter complex is unique among all of the carbone complexes, and two views of this complex are illustrated in Fig. 5. The first view is looking along the bisector of the S–C–S angle. This is a most interesting view, since it shows that the two HF molecules are titled with S–C–F angles of 93 and 128°. This is the only complex in which the acid molecules do not lie in a plane containing the bisector of the X–C–X angle, with X the atom of the ligand bonded to the carbone C atom. The second view illustrates the positions of the S–H bonds relative to the carbon atom and the two HF molecules.

The halogen bonded complexes H₂S→C←SH₂:ClF and H₂S→C←SH₂:2ClF have C_s symmetry, and these are also illustrated in Fig. 5. The Cl–C distances have further decreased to 1.84 Å in the complex with one ClF, and 1.90 and 1.98 Å in the complex with two ClF molecules. The decrease in the Cl–C distance is accompanied by an increase in the Cl–F distance to 1.97 Å in the complex with one ClF molecule, and 1.90 and 1.87 Å when two ClF molecules are present. In the complex H₂S→C←SH₂:2ClF, the Cl–F distance is approaching the Cl–C distance, and the nature of the halogen bond has changed. The halogen bonds in these complexes have chlorine-transferred character.

F–H and Cl–F stretching frequencies

Given the changes in the F–H and Cl–F distances in the complexes, it is reasonable to anticipate changes in the corresponding stretching frequencies. The H–F stretching frequencies in isolated FH and the carbone complexes with one and two HF molecules are reported in Table 8. It is apparent that as the H–F distance increases, the F–H stretching frequency decreases, from 4124 cm⁻¹ at an F–H distance of 0.922 Å in the FH monomer, to 2823 cm⁻¹ at an F–H distance of 0.984 Å in the complex H₂S→C←SH₂:HF. The same general pattern is observed for the symmetric and asymmetric F–H stretching frequencies in the complexes with two FH molecules. The symmetric stretching frequency decreases from 3952 to 3022 cm⁻¹, while the asymmetric frequency decreases from 3939 to 2957 in the complexes with ligands CO and SH₂, respectively. A plot of the F–H stretching frequencies versus the F–H distance is shown in Fig. 6. The correlation coefficient of the linear trendline is 0.997.

Table 8 F–H distances [R(F–H), Å] and frequencies [ν(F–H), cm⁻¹] in carbone complexes with one and two HF molecules

	R(F–H)	ν(F–H) 1 FH	ν(F–H) sym 2 HF	ν(F–H) asym 2 HF
a In this complex with two HF molecules with different F–H distances, the frequencies are coupled, but can still be assigned to each one of the two FH molecules.
Isolated HF	0.922	4124
Complexes, L =
CO	0.931	3899
NN	0.935	3804
HNC	0.936	3802
PH3	0.966	3157
SH2	0.984	2823
Complexes L =
CO	0.929		3952	3939
NN	0.933		3853	3834
HNC	0.935		3818^a
	0.937			3761^a
PH3	0.962		3252	3212
SH2	0.975		3022	2957

---

Fig. 6 F–H stretching frequencies versus the F–H distance in carbone complexes with one and two FH molecules.

The Cl–F stretching frequencies in complexes with one and two ClF molecules are reported in Table 9. As observed for the F–H frequencies, the Cl–F frequencies also decrease upon complexation, from 800 cm⁻¹ at a Cl–F distance of 1.638 Å in the ClF monomer, to 388 cm⁻¹ as the Cl–F distance increases to 1.972 Å in the complex H₂S→C←SH₂:ClF. In the complexes with two ClF molecules, the symmetric Cl–F stretching frequency also decreases as the Cl–F distance increases, and ranges from 723 cm⁻¹ at a Cl–F distance of 1.661 Å to 481 cm⁻¹ at a Cl–F distance of 1.867 Å. The asymmetric stretching frequencies range from 719 to 446 cm⁻¹. The change in the stretching frequencies as a function of distance is illustrated in Fig. 7. Once again, there is an excellent correlation between the Cl–F stretching frequencies and the Cl–F distance, as illustrated by the second-order trendline which has a correlation coefficient of 0.967.

Table 9 Cl–F distances [R(Cl–F), Å] and frequencies (ν, cm⁻¹) in carbone complexes with one and two ClF molecules

	R(Cl–F)	ν(Cl–F) 1 ClF	ν(Cl–F) sym 2 ClF	ν(Cl–F) asym 2 ClF
Isolated ClF	1.638	800
OC→C←CO	1.672	693
NN→C←NN	1.714	619
HNC→C←CNH	1.770	517
H3P→C←PH3	1.893	457
H2S→C←SH2	1.972	388
OC→C←CO	1.661		723	719
NN→C←NN	1.696		640	633
HNC→C←CNH	1.676		688
	1.742			553
H3P→C←PH3	1.864		486	480
H2S→C←SH2	1.867		481
	1.897			446

---

Fig. 7 Cl–F stretching frequencies versus the Cl–F distance in carbone complexes with one and two ClF molecules.

Spin–spin coupling constants

Table S6 of the ESI† reports values of the PSO, DSO, FC, and SD terms and the total coupling constants ^2hJ(F–C) and ^1xJ(Cl–C) for complexes of the carbones with one and two HF and ClF molecules, respectively. All of these coupling constants are positive, and are dominated by the FC terms. The PSO terms make non-negligible contributions, which are negative for ^2hJ(F–C) and positive for ^1xJ(Cl–C) except for H₂S→C←SH₂:ClF, in which case ^1xJ(Cl–C) is small and negative. The largest PSO contributions are found for the complexes of H₃P→C←PH₃, which are negative when the acid is HF and positive for ClF. Only total J values are discussed below.

Table 10 presents the coupling constants ^2hJ(F–C) for the carbone complexes. These vary from 13 Hz for OC→C←CO:2HF at an F–C distance of 3.03 Å, to 290 Hz for H₂S→C←SH₂:HF at an F–C distance of 2.64 Å. Complexes with the first-row ligands have their greatest values when the ligand is N₂, but these coupling constants are much smaller than ^2hJ(F–C) for complexes involving the second-row ligands. Fig. 8 presents a plot of ^2hJ(F–C) versus the F–C distance. The trendline is a decaying exponential with a correlation coefficient of 0.910. These coupling constants increase continuously as the F–C distance decreases, indicating that although the hydrogen bonds may gain some proton-shared character, all of the F–H⋯C hydrogen bonds remain traditional hydrogen bonds.

Table 10 Coupling constants ^2hJ(F–C) and ^1xJ(Cl–C) (Hz) for complexes of the carbones L→C←L with one and two HF and ClF molecules

Carbone	^2h J(C–F) 1 HF	^2h J(C–F) 2 HF	^1x J(C–Cl) 1 ClF	^1x J(C–Cl) 2 ClF
a For complexes with two nonequivalent HF or ClF molecules, data for the interaction with the shorter intermolecular distance are given first. b Values of the SD term were estimated from SD terms for the other complexes in this set. See Table S6 of the ESI. c Coupling constant calculations for H2S→C←H2S:2ClF were not feasible.
OC→C←CO	16.8	13.0	29.7	24.3
N2→C←N2	61.8	44.4	66.1	54.7
HNC→C←CNH	17.3	35.5^a	56.5	57.1^a^,^b
		21.5^a		23.7^a^,^b
H3P→C←PH3	136.5	95.2	44.8	53.7
H2S→C←SH2	290.3	164.3	3.5	—^c

---

Fig. 8 ^2h J(F–C) versus the F–C distance and ^1xJ(C–Cl) versus the C–Cl distance for carbone complexes with one and two HF and ClF molecules, respectively.

It is apparent from Fig. 8 that the coupling constants ^1xJ(Cl–C) exhibit a very different distance dependence compared to ^2hJ(F–C). The largest value of ^1xJ(Cl–C) is 66 Hz for the complex N₂→C←N₂:ClF at a C–Cl distance of 2.24 Å, while the smallest value of 4 Hz is found for the complex H₂S→C←SH₂:ClF at a very short C–Cl distance of 1.84 Å. Fig. 8 suggests that none of the Cl⋯C halogen bonds should be characterized as traditional halogen bonds. Rather, even the complexes of the carbone OC→C←CO with one and two ClF molecules, and the weaker halogen bond in the HNC→C←NCH:2ClF complex have some chlorine-shared character. The halogen bonds in the complexes of NN→C←NN and HNC→C←CNH with one and two ClF molecules are chlorine-shared halogen bonds, with Cl–C distances between 2.16 and 2.32 Å, and the largest values of ^1xJ(C–Cl). As the Cl–C distance further decreases to 2.05 and 2.04 Å in the complexes of H₃P→C←PH₃ with one and two ClF molecules, ^1xJ(C–Cl) decreases to 45 and 54 Hz, respectively, as the halogen bonds in this complex gain chlorine-transferred character. ^1xJ(Cl–C) for the halogen bond in the H₂S→C←SH₂:ClF complex has a value of 3.5 Hz at a very short C–Cl distance of 1.84 Å. This halogen bond has significant chlorine-transferred character.

Conclusions

Ab initio MP2/aug’-cc-pVTZ calculations have been carried out to determine the structures and binding energies of the carbone complexes in which the carbone L→C←L acts as an electron pair donor to one and two HF or ClF molecules, for L = CO, N₂, HNC, PH₃, and SH₂. The results of this study support the following statements.

(1) For a fixed Lewis acid, the binding energies increase with respect to the ligand in the order

CO < NN < CNH ≪ PH₃ < SH₂.

For a fixed carbone, the binding energies increase with respect to the Lewis acid in the order

HF < 2 HF < ClF < 2 ClF.

(2) The binding energies of the carbone complexes exhibit a second-order dependence on the F–C distance in hydrogen-bonded complexes with one and two FH molecules, and a second-order dependence on the Cl–C distance in complexes with one and two ClF molecules.

(3) All of the complexes containing OC→C←CO and NN→C←NN with one and two HF or ClF molecules have C_2v symmetry. The complexes of H₃P→C←PH₃ with two acid molecules also have C_2v symmetry, while those with only one acid molecule have C_s symmetry. Complexes with the carbones H₂S→C←SH₂ and HNC→C←CNH have lower symmetries, with HNC→C←CNH:HF having no symmetry in point group C₁, and H₂S→C←SH₂:2HF having C₂ symmetry and a unique structure among all of these complexes.

(4) F–H stretching frequencies in the complexes decrease as the F–H distance increases, and exhibit a linear dependence on that distance. Cl–F stretching frequencies also decrease as the Cl–F distance increases, and exhibit a second-order dependence on that distance.

(5) EOM-CCSD spin–spin coupling constants ^2hJ(F–C) increase with decreasing F–C distance. Although the F–H⋯C hydrogen bond gains some proton-shared character in the most tightly bound complexes, the hydrogen bonds remain traditional hydrogen bonds.

(6) ^1xJ(Cl–C) versus the Cl–C distance exhibits very different behavior. Even the complexes of OC→C←CO with one and two ClF molecules, and the halogen bond at the longer Cl–C distance in HNC→C←CNH:2ClF, exhibit some chlorine-shared character. As the Cl–C distance further decreases in the complexes with NN→C←NN and HNC→C←CNH, the halogen bonds become chlorine-shared halogen bonds, and coupling constants ^1xJ(Cl–C) have their largest values. In the complexes with H₃P→C←PH₃, the Cl–C distance continues to decrease, and ^1xJ(Cl–C) also decreases, indicating that the halogen bonds gain chlorine-transferred character. The complex H₂S→C←SH₂:ClF has the shortest Cl–C distance and ^1xJ(Cl–C) has its smallest value for a chlorine-transferred halogen bond.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades (PGC2018-094644-B-C22) and Comunidad de Madrid (P2018/EMT-4329 AIRTEC-CM). Thanks are also given to the Ohio Supercomputer Center and CTI (CSIC) for their continued computational support.

References

1. M. S. Platz, Kinetics and Spectroscopy of Carbenes and Biradicals, Springer, 1990.
2. A. J. Arduengo, R. L. Harlow and M. Kline, J. Am. Chem. Soc., 1991, 113, 361–363.
3. W. A. Herrmann and C. Köcher, Angew. Chem., Int. Ed. Engl., 1997, 36, 2162–2187.
4. P. H. Mueller, N. G. Rondan, K. N. Houk, J. F. Harrison, D. Hooper, B. H. Willen and J. F. Liebman, J. Am. Chem. Soc., 1981, 103, 5049–5052.
5. K. K. Irikura, W. A. Goddard and J. L. Beauchamp, J. Am. Chem. Soc., 1992, 114, 48–51.
6. I. Alkorta and J. Elguero, Chem. Phys. Lett., 2018, 691, 33–36.
7. A. M. Magill, K. J. Cavell and B. F. Yates, J. Am. Chem. Soc., 2004, 126, 8717–8724.
8. J. R. Keeffe and R. A. M. O’Ferrall, ARKIVOC, 2008, 2008, 183–204.
9. S. T. Belt, C. Bohne, G. Charette, S. E. Sugamori and J. C. Scaiano, J. Am. Chem. Soc., 1993, 115, 2200–2205.
10. M. H. Abraham, J. Elguero and I. Alkorta, Croat. Chem. Acta, 2018, 91, 121–124.
11. G. C. Fortman and S. P. Nolan, Chem. Soc. Rev., 2011, 40, 5151–5169.
12. I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180.
13. I. Alkorta and J. Elguero, J. Phys. Chem., 1996, 100, 19367–19370.
14. J. M. Standard, J. Phys. Chem. A, 2017, 121, 381–393.
15. S. Gehrke and O. Hollóczki, Chem. – Eur. J., 2018, 24, 11594–11604.
16. J. E. Del Bene, I. Alkorta and J. Elguero, Chem. Phys. Lett., 2017, 685, 338–343.
17. H. Lv, H.-Y. Zhuo, Q.-Z. Li, X. Yang, W.-Z. Li and J.-B. Cheng, Mol. Phys., 2014, 112, 3024–3032.
18. Q. Zhao, D. Feng, Y. Sun, J. Hao and Z. Cai, Int. J. Quantum Chem., 2011, 111, 3881–3887.
19. M. D. Esrafili, F. Mohammadian-Sabet and E. Vessally, Mol. Phys., 2016, 114, 2115–2122.
20. J. E. Del Bene, I. Alkorta and J. Elguero, ChemPhysChem, 2017, 18, 1597–1610.
21. H. Lin, L. Meng, X. Li, Y. Zeng and X. Zhang, New J. Chem., 2019, 43, 15596–15604.
22. I. Alkorta, M. M. Montero-Campillo and J. Elguero, Chem. – Eur. J., 2017, 23, 10604–10609.
23. J. E. Del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2017, 121, 4039–4047.
24. W. Petz, C. Kutschera, M. Heitbaum, G. Frenking, R. Tonner and B. Neumüller, Inorg. Chem., 2005, 44, 1263–1274.
25. R. Tonner and G. Frenking, Chem. – Eur. J., 2008, 14, 3260–3272.
26. G. Frenking and R. Tonner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 869–878.
27. F. Ramirez, N. B. Desai, B. Hansen and N. McKelvie, J. Am. Chem. Soc., 1961, 83, 3539–3540.
28. R. Tonner and G. Frenking, Chem. – Eur. J., 2008, 14, 3273–3289.
29. M. Hermann and G. Frenking, Chem. – Eur. J., 2017, 23, 3347–3356.
30. J. L. Dutton and G. Frenking, Angew. Chem., Int. Ed., 2016, 55, 13380–13382.
31. G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, Chem. Soc. Rev., 2014, 43, 5106–5139.
32. L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Coord. Chem. Rev., 2017, 344, 163–204.
33. J. A. Pople, J. S. Binkley and R. Seeger, Int. J. Quantum Chem., Quantum Chem. Symp., 1976, 10, 1–19.
34. R. Krishnan and J. A. Pople, Int. J. Quantum Chem., 1978, 14, 91–100.
35. R. J. Bartlett and D. M. Silver, J. Chem. Phys., 1975, 62, 3258–3268.
36. R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581.
37. J. E. Del Bene, J. Phys. Chem., 1993, 97, 107–110.
38. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
39. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585.
40. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
41. J. E. Del Bene, J. Phys. Chem., 1987, 86, 2110–2113.
42. J. E. Del Bene, J. Comput. Chem., 1987, 810, 810–815.
43. J. E. Del Bene, Int. J. Quantum Chem., Quantum Biol. Symp., 1987, 14, 27–35.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
45. R. F. W. Bader, A Quantum Theory of Molecular Structure and its Applications, Chem. Rev., 1991, 91, 893–928.
46. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Oxford University Press, Oxford, 1990.
47. P. L. A. Popelier, Atoms In Molecules. An Introduction, Prentice Hall, Harlow, England, 2000.
48. C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley-VCH, Weinheim, 2007.
49. T. A. Keith, AIMAll (Version 11.08.23), TK Gristmill Software, Overland Park KS, USA, 2011, http://aim.tkgristmill.com.
50. S. A. Perera, M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1996, 104, 3290–3305.
51. S. A. Perera, H. Sekino and R. J. Bartlett, J. Chem. Phys., 1994, 101, 2186–2196.
52. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
53. S. Kirpekar, H. J. A. Jensen and J. Oddershede, Chem. Phys., 1994, 188, 171–181.
54. ACES II is a program product of the Quantum TheoryProject, University of Florida, J. F. Stanton, J. Gauss, J. D. Watts, M. Nooijen, N. Oliphant, S. A. Perera, P. G. Szalay, W. J. Lauderdale, S. R. Gwaltney, S. Beck, A. Balkova, E. D. Bernholdt, K.-K. Baeck, P. Tozyczko, H. Sekino, C. Huber and R. J. Bartlett, Integral packages included are VMOL (J. Almlof and P. R. Taylor), VPROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. A. Jensen, P. Jorgensen, J. Olsen and P. R. Taylor). Brillouin–Wigner perturbation theory was implement by J. Pittner.
55. J. E. Del Bene, I. Alkorta and J. Elguero, Molecules, 2017, 22, 195.
56. J. E. Del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2010, 114, 12958–12962.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02009e

---