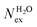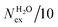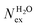Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory based molecular dynamics study of solution composition effects on the solvation shell of metal ions†
Xiangwen
Wang
a,
Dimitrios
Toroz
a,
Seonmyeong
Kim
bc,
Simon L.
Clegg
d,
Gun-Sik
Park
bc and
Devis
Di Tommaso
 *a
*a
aSchool of Biological and Chemical Sciences, Materials Research Institute, Thomas Young Centre, Queen Mary University of London, Mile End Road, E1 4NS, London, UK. E-mail: d.ditommaso@qmul.ac.uk
bCenter for THz-driven Biological Systems, Department of Physics and Astronomy, Seoul National University, Seoul, 08826, Republic of Korea
cAdvanced Institutes of Convergence Technology, Seoul National University, Suwon-Si, Gyeonggi-do 16229, Republic of Korea
dSchool of Environmental Sciences, University of East Anglia, Norwich, NR4 7TJ, UK
First published on 3rd July 2020
Abstract
We present an ab initio molecular dynamics study of the alkali metal ions Li+, Na+, K+ and Cs+, and of the alkaline earth metal ions Mg2+ and Ca2+ in both pure water and electrolyte solutions containing the counterions Cl− and SO42−. Simulations were conducted using different density functional theory methods (PBE, BLYP and revPBE), with and without the inclusion of dispersion interactions (-D3). Analysis of the ion–water structure and interaction strength, water exchange between the first and second hydration shell, and hydrogen bond network and low-frequency reorientation dynamics around the metal ions have been used to characterise the influence of solution composition on the ionic solvation shell. Counterions affect the properties of the hydration shell not only when they are directly coordinated to the metal ion, but also when they are at the second coordination shell. Chloride ions reduce the sodium hydration shell and expand the calcium hydration shell by stabilizing under-coordinated hydrated Na(H2O)5+ complexes and over-coordinated Ca(H2O)72+. The same behaviour is observed in CaSO4(aq), where Ca2+ and SO42− form almost exclusively solvent-shared ion pairs. Water exchange between the first and second hydration shell around Ca2+ in CaSO4(aq) is drastically decelerated compared with the simulations of the hydrated metal ion (single Ca2+, no counterions). Velocity autocorrelation function analysis, used to probe the strength of the local ion–water interaction, shows a smoother decay of Mg2+ in MgCl2(aq), which is a clear indication of a looser inter-hexahedral vibration in the presence of chloride ions located in the second coordination shell of Mg2+. The hydrogen bond statistics and orientational dynamics in the ionic solvation shell show that the influence on the water–water network cannot only be ascribed to the specific cation–water interaction, but also to the subtle interplay between the level of hydration of the ions, and the interactions between ions, especially those of opposite charge. As many reactive processes involving solvated metal ions occur in environments that are far from pure water but rich in ions, this computational study shows how the solution composition can result in significant differences in behaviour and function of the ionic solvation shell.
Introduction
A fundamental understanding of the processes controlling the hydration of ions is of importance to low-temperature geochemistry and biological systems. For example, in aqueous environments the processes of nucleation and growth of ionic crystals such as calcite (CaCO3) or magnesite (MgCO3) are controlled by the dynamics of hydration–dehydration around the cation.1–3 In the hydration model proposed by Frank and Wen to explain deviations of ionic solution behaviour relative to pure water, the insertion of an ion in solution radially aligns water molecules in concentric regions characterised by different levels of interaction between water and ion.4 The water molecules in the innermost region, also known as the first solvation shell (FSS), are tightly bound to the centric ion and exhibit translational and rotational entropy loss compared with pure water.5 Several molecular dynamics (MD) studies of hydrated metal ions (single cation, no counterions) have been conducted to characterize the structure and dynamics of the ionic FSS, with the results confirming what was anticipated by the Frank and Wen hydration model.6–9Ions in aqueous electrolyte solutions are present as free ions only in dilute solutions. Otherwise, cations and anions form contact or solvent-shared ion pairs.10 The structure and dynamics of the ionic solvation shell can, therefore, be significantly affected by the subtle interplay between the level of hydration of the ions, and the interactions between ions, especially those of opposite charge. In more general terms, the composition of the solution, including the balance between ion–solvent and ion–ion interactions, could result in significant differences in behaviour and function of the FSS. Consequently, an accurate characterization of the effect of solution composition on the structure and dynamics of the ionic solvation shell is important to understand and control reactive processes involving ions in solution.
The MD simulation technique has been extensively used to gain insights into the elusive molecular-level processes controlling the properties of aqueous electrolyte solutions.11,12 However, the force field used to describe the ion–water interaction is crucial to obtain an accurate characterization of structure and dynamics in electrolyte solutions.13,14 An important contribution to this field was the development of ab initio MD (AIMD), where forces are derived from the electronic structure,15,16 usually in the framework of density functional theory (DFT),17 which provides the capability of studying non-additivity effects in the dynamics of ions solvation shells. AIMD simulations, using the Car–Parrinello and Born–Oppenheimer schemes, of cations18–23 and anions,24,25 have been mostly conducted on an isolated ion in pure liquid water, with no counterions in solution. Electrolyte solutions, on the other hand, have been subject to only a few AIMD studies, including the characterization of the dissociation of the NaCl in water,26 the cooperative ionic effects are of the Na+ and Cl− on the hydrogen bonding network,27 and the influence of a static electric fields.28
Here, we report an AIMD study of the of the alkali metal ions Li+, Na+, K+ and Cs+, and of the alkaline earth metal ions Mg2+ and Ca2+, in pure water and electrolyte solutions containing the counterions Cl− and SO42−, in order to characterize composition and concentration effects on the structure and dynamics of the ionic solvation shell. We have chosen the above combination of cations and anions because they are commonly found in nature, including in the composition of the sea and groundwater.29 Salt concentrations ranging from 0.9 to 3.8 mol kg−1 were considered to quantify the effect of solution composition on the strength of ion–water interaction and to characterise the structure and low-frequency dynamics of the FSS.
After having introduced details of the simulations, we next report on the effect of the solution composition on the structure and dynamics of the ionic solvation shell. These results are rationalised in terms of the mechanism of water exchange around cations and the strength of ion–water interaction. The distribution of hydrogen bonds and the reorientation dynamics of water molecules, in the bulk solution and the first solvation shell, are finally presented.
Computational details
Ab initio (Born–Oppenheimer) MD simulations were conducted with the electronic structure code CP2K/Quickstep code (4.1).30 CP2K implements DFT based on a hybrid Gaussian plane wave. The Perdew–Burke–Ernzerhof (PBE)31 generalized-gradient approximations for the exchange and correlation terms were used, together with the Grimme's -D3 dispersion correction, to provide a more accurate description of the structure of liquid water.32,33 Simulations were also conducted using the Becke–Lee–Yang–Parr (BLYP) functional34,35 and revised form of the PBE (revPBE),36 with and without the -D3 term. The Goedecker–Teter–Hutter (GTH) pseudopotentials were used to describe the core–valence interactions.37 All atomic species were represented using a double-zeta valence polarized (DZVP) basis set. The plane wave kinetic energy cut off (Ecut) was set to 1000 Ry. The k-sampling was restricted to the Γ point of the Brillouin zone. The tolerance for the wave function optimization was set to 10−6 a.u. that allows for a 1 fs time steps with reasonable energy conservation. AIMD simulations were carried out in the canonical (NVT) ensemble (constant number of particles N, volume V, temperature T) using a Nosé–Hoover chain thermostat to maintain the average temperature at 300 K. Periodic boundary conditions were applied throughout.Simulation protocol
First, we have conducted classical MD simulation of 64 water molecules in the isothermal–isobaric (NPT) ensemble (constant number of particles N, pressure P = 1 atm, temperature T = 300 K) for 1 ns to generate an equilibrated aqueous solution. The last configuration was used to generate solutions of hydrated metal (M) ions (single M, no counterions, by replacing one H2O with one ion (M: Li+, Na+, K+, Mg2+, or Ca2+). Aqueous electrolyte solutions with concentrations ranging from 0.9 to 3.8 mol kg−1 were generated by randomly replacing water molecules with cations, M, and anions, X (Cl− or SO42−) ions, by making sure that the initial configuration did not contain contact ion pairs. Classical MD simulations used the pairwise Lennard-Jones (LJ) potential model developed by Zeron et al.38 (denoted as Madrid-2019 forcefield) for Li+, Na+, K+, Mg2+, Ca2+, Cl−, and SO42− in aqueous solution.38 In Madrid-2019, the water molecules are represented by the TIP4P/2005 model,39 and the monovalent and divalent ions are modelled using charges of 0.85 and 1.7, respectively (in electron units). This potential model allows a very accurate description of the densities of the solutions up to high concentrations.38 The Madrid-2019 has not been developed for Cs+ and to generate equilibrated solutions of CsCl we used the LJ potential model from the Amber database.40 For each system, we conducted 6 ns of classical MD (NPT, T = 300 K and P = 1 atm) to equilibrate the cell volume and the last configuration was used as the starting point of 50 ps of AIMD. Details of the solutions considered in this study (number of ions and water molecules, cell lengths of the NVT simulations, solution concentrations) are reported in Table S1 of ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 For comparison purposes, we have also conducted AIMD simulations of pure liquid water (64 H2O, 1 g cm−3) and of Cl− in 63 H2O molecules. The procedure of first conducting classical MD (NPT) simulations to equilibrate the volume of the simulation box followed by AIMD (NVT) simulations has been routinely adopted to study the properties of hydrated ions.18,20,22,42 We did not attempt to run AIMD in the NPT ensemble, which could determine the “correct” system density at zero pressure, because depending on the DFT method (functional and dispersion correction) equilibrium density of water can change significantly.43 Instead, we chose to fix the system size to match the one obtained using the classical MD simulation of these systems. NPT trajectories must be long enough to assure statistical convergence, and the convergence of pressure for DFT plane wave MD simulations in the NPT ensemble requires a significantly higher basis set cutoff due to grid sensitivity issues when the volume of the simulation cell can fluctuate.44,45
41 For comparison purposes, we have also conducted AIMD simulations of pure liquid water (64 H2O, 1 g cm−3) and of Cl− in 63 H2O molecules. The procedure of first conducting classical MD (NPT) simulations to equilibrate the volume of the simulation box followed by AIMD (NVT) simulations has been routinely adopted to study the properties of hydrated ions.18,20,22,42 We did not attempt to run AIMD in the NPT ensemble, which could determine the “correct” system density at zero pressure, because depending on the DFT method (functional and dispersion correction) equilibrium density of water can change significantly.43 Instead, we chose to fix the system size to match the one obtained using the classical MD simulation of these systems. NPT trajectories must be long enough to assure statistical convergence, and the convergence of pressure for DFT plane wave MD simulations in the NPT ensemble requires a significantly higher basis set cutoff due to grid sensitivity issues when the volume of the simulation cell can fluctuate.44,45
Results and discussion
Solvation structure
| System | b (mol kg−1) | CIP (%) | SSHIP (%) | SSIP (%) |
|---|---|---|---|---|
| LiCl | 1.9 | 85.6 | 14.4 | 0.0 |
| NaCl | 1.9 | 0.0 | 68.9 | 31.1 |
| KCl | 1.9 | 3.3 | 51.4 | 45.3 |
| CsCl | 1.9 | 72.8 | 27.2 | 0.0 |
| MgCl2 | 1.9 | 0.0 | 55.5 | 44.5 |
| CaCl2 | 1.9 | 0.7 | 97.1 | 2.2 |
| MgSO4 | 1.9 | 100.0 | 0.0 | 0.0 |
| CaSO4 | 1.9 | 0.0 | 99.6 | 0.4 |
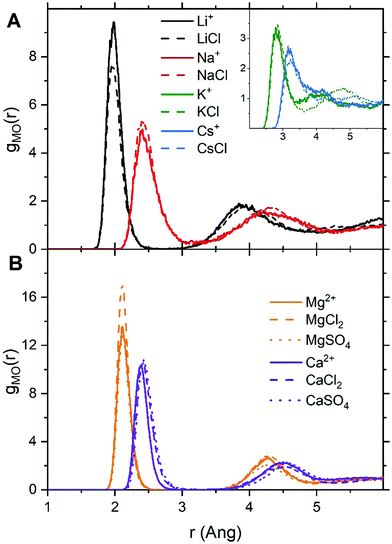
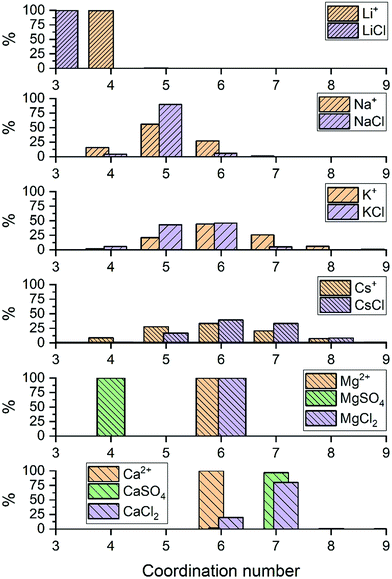
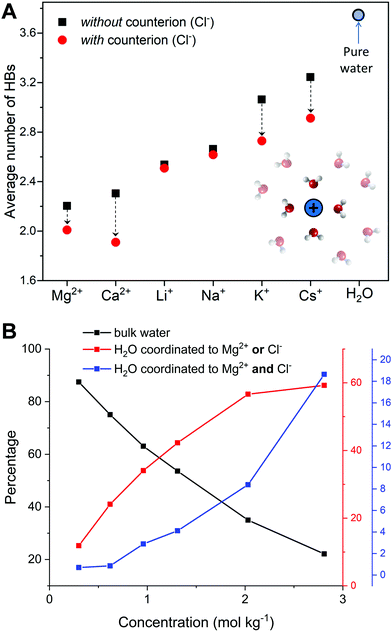
For LiCl(aq), the analysis of the ion–water coordination shell distribution shows that in the presence of Cl−, the number of water molecules coordinated to Li+ reduces from four to three as a result of the formation of Li+⋯Cl− contact ion pairs (Table 1). In 1.9 mol kg−1 NaCl(aq), Na+ and Cl− form solvent-shared or solvent-separated IP+. Despite not being coordinated to Na+, chloride ions induce a significant contraction of the sodium hydration shell: in NaCl(aq) the sodium ions are in the five-coordinated state for 90% of the simulation period, compared to approximately 50% of the simulation period of hydrated Na+ (isolated ion, no counterions). Consequently, counterions such as Cl− can stabilize under-coordinated metal–water complexes even when they are not part of the first coordination shell of Na+. The Cs+ and Cl− ions are, for most of the simulation period, present as CIPs (72%) but due to the high flexibility of caesium first hydration shell, the coordination number distribution is only marginally affected by the presence of chloride ions (Fig. 2). In MgCl2(aq) the hexahydrated [Mg(H2O)6]2+ is the only hydrated complex present in solution, and in MgSO4(aq) only four water molecules are directly coordinated to Mg2+ because the magnesium and sulphate ions form very stable contact ion pairs (Table 1). Static DFT calculations of the free energy of formation (ΔG) of the Mg2+/SO42− and Mg2+/Cl− contact ion pairs confirm the much higher propensity of SO42− to form stable CIPs with Mg2+ compared with Cl−: Mg(H2O)62+ + SO42− → MgSO4(H2O)4 + 2H2O, ΔG = −160 kJ mol−1; Mg(H2O)62+ + Cl− → MgCl(H2O)5+ + H2O, ΔG = −25 kJ mol−1 (wB97XD/aug-cc-pdvz level of theory in the CPCM continuum solvation model). The coordination shell distribution of the calcium ion displays a counterintuitive behaviour, with the coordination number (CN) of Ca2+ increasing from six in pure water to around seven in CaCl2(aq) (Fig. 2). The chloride ions are hardly ever coordinated to the calcium ions, with which they predominantly form SSHIPs (Table 1). Therefore, the chloride ions located in the second coordination shell of Ca2+ stabilize the seven-coordinated Ca(H2O)72+ complex over the six-coordinated Ca(H2O)62+ species. The same behaviour is observed in CaSO4(aq), where Ca2+ and SO42− form almost exclusively SSHIPs (99.6%) and the hepta-hydrated calcium complexes are stabilised by the sulphate ions located in the second hydration shell of metal ion.
The average CN of the first hydration shell of Ca2+ is still a controversial issue for AIMD simulations.51 Several DFT based MD simulations, using the Car–Parrinello and Born–Oppenheimer schemes, of the hydrated calcium ion (single Ca2+, no counterions) reported six water molecules in the first hydration shell of Ca2+,52 which agrees with our result (Fig. 2). However, experimental results from extended X-ray absorption fine structure (EXAFS) measurements in CaCl2 solutions, with concentrations ranging from 0.12 to 6 mol kg−1, resulted in CNs between 6.8 and 8.53,54 As previously discussed, the presence of counterions (Cl− and SO42−), which are normally present in experiments, stabilizes the higher coordination states of Ca2+, yielding a computed CN of Ca2+ in CaCl2(aq) and CaSO4(aq) (6.9) in much better agreement with EXAFS measurements of CaCl2 solutions. Therefore, one simple reason for the disagreement between theory and experiment could be the composition of the solution used to conduct the simulations. Other factors such as the size of the simulation box, the length of the simulation period, and the choice of the density functional method have also been considered by conducting AIMD simulations of hydrated Ca2+ (no counterions) in a box containing 63 and 124 water molecules using the PBE, rev-PBE and BLYP functionals with and without the -D3 dispersion correction (Table 2).
| Method | N H2O/Ca2+ | t sim (ps) | CN | |||
|---|---|---|---|---|---|---|
| % 6 | % 7 | % 8 | Avg. | |||
| PBE | 63 | 50 | 100.0 | 0.0 | 0.0 | 6.0 |
| PBE-D3 | 63 | 50 | 95.1 | 4.9 | 0.0 | 6.0 |
| 100 | 96.6 | 3.4 | 0.0 | 6.0 | ||
| 500 | 98.7 | 1.3 | 0.0 | 6.0 | ||
| 124 | 200 | 47.6 | 51.6 | 0.8 | 6.5 | |
| revPBE | 63 | 50 | 38.2 | 61.7 | 0.1 | 6.6 |
| revPBE-D3 | 63 | 50 | 86.9 | 12.1 | 1.0 | 6.1 |
| BLYP | 63 | 50 | 32.7 | 17.3 | 0.0 | 6.3 |
| BLYP-D3 | 63 | 500 | 15.0 | 80.7 | 4.3 | 6.9 |
The results show that: a simulation period of 50 ps is sufficiently long to get a convergent distribution of the calcium–water coordination shell; Ca2+ in 63 and 124 water molecules yield CNs of 6.0 and 6.5; BLYP-D3 gives a CN of 6.9 and a coordination distribution that is shifted to higher coordination states compared the average CN obtained with PBE-D3 (6.0) and revPBE-D3 (6.1). Both the system size and the DFT method can, therefore, influence the coordination distribution and average coordination size. This analysis suggests that solution composition, system size, and level of theory should all be considered when comparing AIMD simulations and experimental determinations of ionic coordination numbers.
Dynamics of the ionic solvation shell
The frequency of water exchange around cations is generally considered as the rate determining for the reactions involving these ions in aqueous solutions.55–58 We have characterised the dynamics of the first and second hydration shells of the alkali metal ions (Li+, Na+, K+ and Cs+) and alkaline earth metal ions (Mg2+ and Ca2+) in pure liquid water and electrolyte solutions using the “direct” method proposed by Hofer and co-workers.59 This methodology has been previously applied for, among others, the characterization of ligand exchange between coordination shells of hydrated alkaline earth metal ions and their carbonate and bicarbonate complexes,21,22,60 as well as the quantification of the water exchange frequency around calcium sites in calcite–water interface61 and hydroxyapatite nanopores.62 In the “direct” method, the MD trajectories are analysed for water molecule movements and whenever a water molecule crosses the boundary of the cation coordination shell its path is followed; if its new position outside or inside this shell lasts for more than τ* = 0.5 ps then the event is accounted as a real exchange event (Nex). The choice of τ* = 0.5 ps is based on the average lifetime of a hydrogen bond between the solvent molecules, obtained using femtosecond spectroscopy,63 and is the standard value used in the applications of the direct method; setting τ* to 5 ps gives only small differences to the statistics of water exchange (Table S5 of ESI†). From the number of water exchange events, the MRT of the water molecules in the first and second hydration shell of the ion can be computed as MRT = (CN × tsim)/Nex, where CN is the average number of water molecules in the first or second coordination shell and tsim is the duration time of the simulation.41 A recent comparison by Wolthers and co-workers of the direct and survival function methods to characterize the calcium dehydration frequencies from MD trajectories,22 concluded that the direct methods could provide shorter mean residence times than SF, but requires shorter simulation times than SF to obtain statistically meaningful output, and is better suited to analyse shorter trajectories generated by ab initio MD simulations.Table 3 reports the values of Nex in the first and second coordination shell of the metal ions, together with the number of exchange events normalised to 10 ps, Nex/10 ps, which represents a measure of the “lability” of the hydration shell of the metal. For the alkali metal ions, the first shell solvent exchange dynamics increases substantially on going from Li+ (MRT = 11.8 ps) to the other alkali metal ions Na+ (1.1 ps), K+ (0.4 ps) and Cs+ (0.2 ps). The MRT of solvent around H2O and Cl− is approximately 0.5 ps, which is comparable to the values obtained for K+ and Cs+, confirming the lability of these ions. As reported in Table 3, AIMD simulations of hydrated Mg2+ (single ion, no counterions) showed no exchanges around Mg2+, compared with compared to ∼50 of such exchanges (more facile dehydration) in 500 ps around aqueous Ca2+ (61.2 ps). The reactivity of the cations varies, therefore, as follow: Mg2+ ≪ Ca2+ < Li+ ≪ Na+ < K+ ≈ Cs+. We have rationalized this behaviour by conducting classical metadynamics MD simulations to compute the free energy as a function of the metal–water coordination number (CN) for Li+, Na+, Mg2+ and Ca2+, from which thermodynamic information on the accessible coordination states for these cations can be extracted (Fig. S3 in ESI†). Ca2+, Li+ and Na+ have several coordination states corresponding to a minimum on the free energy profile and for Na+ the transition between these states is almost barrierless. On the other hand, the only coordination state accessible at room temperature to Mg2+ is six and the free energy barrier to go from the six to the five coordinate state (32 kJ mol−1) is about three times higher than the free energy barrier of hydrated Ca2+ to interchange between the six and seven coordination environments. As Mg2+ is strongly hydrated, water exchange is drastically retarded in its FSS.
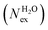 in the first and second coordination shells of the metal ions Li+, Na+, K+, Cs+, Mg2+ and Ca2+, with a duration of more than τ* = 0.5 ps, obtained from the analysis of AIMD (PBE-D3) simulations of hydrated metal ions (single M, no counterions), aqueous electrolyte solution, pure water and hydrated chlorine ion. Values of
in the first and second coordination shells of the metal ions Li+, Na+, K+, Cs+, Mg2+ and Ca2+, with a duration of more than τ* = 0.5 ps, obtained from the analysis of AIMD (PBE-D3) simulations of hydrated metal ions (single M, no counterions), aqueous electrolyte solution, pure water and hydrated chlorine ion. Values of 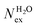 normalized to the number of cations in solution. Mean residence time (MRT) of water molecules in the first hydration shell computed using the relation MRT = (tsim × CN)/Nex, where tsim is the period of simulation (in ps) and CN is the average ion–water coordination number of the first and second coordination shell, which was obtained from the integration of the ion–water radial distribution function up to the first and second minimum, respectively. Concentration (b) in mol kg−1
normalized to the number of cations in solution. Mean residence time (MRT) of water molecules in the first hydration shell computed using the relation MRT = (tsim × CN)/Nex, where tsim is the period of simulation (in ps) and CN is the average ion–water coordination number of the first and second coordination shell, which was obtained from the integration of the ion–water radial distribution function up to the first and second minimum, respectively. Concentration (b) in mol kg−1
| System | b | t sim | First Shell | Second shell | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CN | (ps) | MRT (ps) | CN | (ps) | MRT (ps) | |||||
| Li+ | 0.9 | 50 | 4.0 | 17.0 | 3.4 | 11.8 | 15.3 | 2066 | 413.2 | 0.4 |
| LiCl | 1.9 | 50 | 3.0 | 7.5 | 1.5 | 20.0 | 13.9 | 3760 | 752.0 | 0.2 |
| Na+ | 0.9 | 50 | 5.1 | 233.0 | 46.6 | 1.1 | 20.0 | 1852 | 370.4 | 0.5 |
| NaCl | 0.9 | 50 | 5.1 | 178.0 | 35.6 | 1.4 | 21.4 | 2022 | 404.4 | 0.5 |
| 1.9 | 50 | 5.0 | 195.5 | 39.1 | 1.3 | 20.9 | 3152 | 630.4 | 0.3 | |
| 3.8 | 50 | 4.7 | 186.5 | 37.3 | 1.3 | 19.3 | 7205 | 1441.0 | 0.1 | |
| K+ | 0.9 | 50 | 6.2 | 750.0 | 150.0 | 0.4 | 21.1 | 1675 | 335.0 | 0.6 |
| KCl | 0.9 | 50 | 4.8 | 536.0 | 107.2 | 0.4 | 21.9 | 1852 | 370.4 | 0.6 |
| 1.9 | 50 | 5.5 | 693.5 | 138.7 | 0.4 | 20.4 | 3832 | 766.4 | 0.3 | |
| 3.9 | 50 | 3.9 | 694.0 | 138.8 | 0.3 | 19.5 | 6964 | 1392.8 | 0.1 | |
| Cs+ | 0.9 | 50 | 8.3 | 1299.0 | 259.8 | 0.3 | 21.5 | 1556 | 311.2 | 0.7 |
| CsCl | 1.9 | 50 | 6.3 | 983.0 | 196.6 | 0.3 | 25.0 | 3726 | 745.2 | 0.3 |
| Mg2+ | 0.9 | 40 | 6.0 | — | — | — | 20.0 | 1057 | 264.3 | 0.8 |
| MgCl2 | 1.9 | 50 | 6.0 | — | — | — | 18.9 | 1266 | 253.2 | 0.7 |
| MgSO4 | 1.9 | 50 | 4.5 | — | — | — | 14.8 | 3223 | 644.6 | 0.2 |
| Ca2+ | 0.9 | 500 | 6.0 | 49.0 | 1.0 | 61.2 | 21.0 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
313.9 | 0.7 |
| CaCl2 | 1.9 | 50 | 6.8 | 32.0 | 6.4 | 10.6 | 19.1 | 2429 | 485.8 | 0.4 |
| CaSO4 | 1.9 | 50 | 6.9 | — | — | — | 21.0 | 3121 | 624.2 | 0.3 |
| H2O | — | 50 | 3.9 | 536 | 107.3 | 0.4 | 23.0 | 2316 | 463.3 | 0.5 |
| Cl− | 0.9 | 40 | 6.2 | 502 | 125.5 | 0.5 | 26.4 | 1702 | 425.5 | 0.6 |
As to the dynamics of the second hydration shell, for all ions, the MRTs is less than 1 ps and close to the MRT of solvent around H2O (0.5 ps). This result contrasts with previous values obtained from AIMD simulations of the alkaline earth metal ions Mg2+, Ca2+ and Sr2+, which reported MRTs between 3.3 and 6.8 ps. These simulations, however, used smaller simulation boxes than the one used in this study and did not employ dispersion corrected DFT functionals.21 Regarding the effect of counterions in solution to the dynamics of exchange around the cations, in LiCl(aq) the formation of Li+/Cl− CIPs increases significantly the MRT around Li+ to 20 ps. The other, very labile, alkali ions Na+, K+ and Cs+ are substantially unaffected by the presence of counter-ions in solution and the dynamics of water exchange around Na+, K+ and Cs+ remain very fast. AIMD simulations of MgCl2(aq) and MgSO4(aq) show no exchanges around Mg2+. However, notice the contrasting behaviour of the chloride and sulphate ions on the solvent exchange dynamics around Ca2+. In both solutions the counterion form SSHIPs with Ca2+, but in CaCl2(aq) the MRT is 10.6 ps (faster water dynamics) compared with 61.2 ps (slower water dynamics) in pure liquid water; in CaSO4(aq) there were no accounted water exchange events around the FSS of the calcium ions.
A further comment concerns the effect of the level of theory and system size on the solvent exchange dynamics around Na+, K+, Ca2+ and H2O (Table 4). We conducted calculations using different DFT methods, with and without the -D3 correction, and simulation boxes. While the absolute number of exchanges (Nex) varies significantly, the values of the mean residence time in the solvation shell of Na+ (∼1 ps), K+ (∼0.4 ps) and H2O (∼0.3 ps) is only marginally affected by the density functional and number of water molecules in the simulation box. For Ca2+, no exchanges were accounted with the PBE functional without the -D3 dispersion correction, and the value of MRT varies from 14 ps (revPBE-D3) to (71.7 ± 16.5) ps (PBE-D3) (Table 4). Recent estimates using different interatomic potential models and techniques to characterise the dynamics of water produced give MRT values lying in the range of 60–80 ps, in good agreement with the estimate obtained with the PBE-D3 functional.22 Using the same functional (PBE-D3), the MRT value for Ca2+ reduces to 13.1 ps from 61.2 ps on increasing the system size, which reveals that for Ca2+ the MRT can be sensitive to the system size.
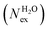 in the first coordination shell of Na+, K+, Ca2+, and H2O with a duration of more than t* = 0.5 ps. The average coordination number (CN) of first shell is given by the integration of the metal–oxygen radial distribution function up to the first minimum. The values of
in the first coordination shell of Na+, K+, Ca2+, and H2O with a duration of more than t* = 0.5 ps. The average coordination number (CN) of first shell is given by the integration of the metal–oxygen radial distribution function up to the first minimum. The values of 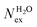 are normalized to the number of metal ions in solution. Mean residence times (MRT) are in ps
are normalized to the number of metal ions in solution. Mean residence times (MRT) are in ps
| N H2O | Method | CN | t sim | MRT | ||
|---|---|---|---|---|---|---|
| a The standard deviations of Nex around Ca2+ have been computed from the variation of overlapping block averages of trajectories lasting 50 ps. b The standard deviations of Nex around H2O have been computed from the averages of the number of exchanges around each water molecule in the simulation box. | ||||||
| Na+ | 63 | PBE-D3 | 5.1 | 50 | 233.0 | 1.1 |
| revPBE-D3 | 5.6 | 50 | 277.0 | 1.0 | ||
| 124 | PBE-D3 | 5.6 | 20 | 86.0 | 1.3 | |
| K+ | 63 | PBE-D3 | 6.2 | 50 | 750.0 | 0.4 |
| revPBE-D3 | 6.1 | 50 | 665.0 | 0.5 | ||
| Ca2+ | 63 | PBE | 6.0 | 50 | 0.0 | — |
| PBE-D3 | 6.0 | 50 | 4.4 ± 1.0a | 71.7 ± 16.5a | ||
| BLYP | 6.3 | 50 | 7.0 | 45.0 | ||
| BLYP-D3 | 6.8 | 50 | 19.6 ± 1.0a | 15.6 ± 2.1a | ||
| revPBE | 6.6 | 50 | 15.0 | 22.0 | ||
| revPBE-D3 | 6.1 | 50 | 22.0 | 13.9 | ||
| Ca2+ | 124 | PBE-D3 | 6.5 | 50 | 26.3 ± 4.3a | 12.7 ± 2.1a |
| H2O | 64 | PBE-D3 | 3.9 | 50 | 536.0 ± 19.3b | 0.4 ± 0.0b |
| revPBE-D3 | 4.1 | 50 | 938.7 ± 12.1b | 0.2 ± 0.0b | ||
| BLYP-D3 | 4.5 | 50 | 822.4 ± 20.6b | 0.3 ± 0.0b | ||
| H2O | 124 | PBE-D3 | 4.2 | 50 | 592.7 ± 42.3b | 0.4 ± 0.0b |
Caging effect in the hydration shell of ions
Towards resolving the origin of the different local ion–water interaction, the velocity-autocorrelation functions (VACFs) of the metal ions (M) were computed.64 VACF is defined as follows: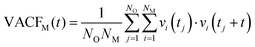 | (1) |
MD studies of amorphous systems have used VACF analysis to probe the strength of interaction of network formers (e.g. Si, Al, P) and network modifiers (e.g. Ca, Na) with the surrounding “cage”.65,66 In particular, the occurrence of a dip to negative values in VACF profiles results from the so-called cage effect for the tagged particle; it takes some time for the particle to escape from the cage formed by its surrounding neighbors.67 The VACF is very sensitive to the local ion hydration environment and changes in the profiles of this time correlation function, such as oscillatory behaviour and position of the first minimum (t0), can be used as descriptors of the strength of ion interaction with the surrounding water molecules and of the rigidity of the interatomic vibration.68 Rigid intra-atomic vibrations lead to a fast-oscillatory trend for the VACFs of Mg2+, Li+ and to a lesser extent Ca2+ (Fig. 3). Conversely, Na+, K+ and Cs+ ions show a much broader first minimum, which is not followed by a marked oscillatory behaviour as their interaction with the surrounding cage is weaker. The VACFs of Na+ (t0 = 0.1 ps), K+ (t0 = 0.16 ps), and Cs+ (t0 = 0.5 ps) in particular, display a smooth decay (Fig. 3A), which suggests a weak caging effect by the solvent; this explains the facile kinetics of dehydration of these cations. The lithium ion shows a much sharper first minimum (t0 = 0.04 ps) followed by a marked oscillatory behavior because of the more rigid interatomic vibration between the smaller Li+ with the surrounding hydration cage. The comparison of the Ca2+ and Mg2+ VACFs (Fig. 3B) shows a very different oscillatory behaviour (t0 = 0.01 ps for Mg2+ and t0 = 0.06 ps for Ca2+), which is indicative of the strengthening of ion-interaction with the surrounding water molecules and increased rigidity of the interatomic vibrations ongoing from Ca2+ to Mg2+. The presence of chloride counterions has no significant effect on the VACF profiles of the alkali metal ions and of the calcium ion. On the other hand, the inset of Fig. 3B shows a smoother decay of the VACF of Mg2+ in MgCl2(aq), which is a clear indication of a looser inter-hexahedral vibration. Therefore, chlorine ions located in the second coordination shell of Mg2+ weaken the Mg(H2O)62+ water ‘cage’ of the ion. This dynamic flexibility further highlights the effect of counterions on the dynamics of water molecules around Mg2+. A final comment concerns the sensitivity of the VACF on the density functional method used in the AIMD simulations. The VACF profiles of hydrated Ca2+ obtained from AIMD simulations using PBE, revPBE, and BLYP, with and without D3 correction, shows some differences (Fig. S5 in ESI†). The PBE method generates the more marked oscillatory behaviour, to which corresponds a more rigid Ca-water coordination environment compared to the other DFT methods, explaining the absence of water exchange events around Ca2+ during the AIMD (PBE) simulation (Table 3).
Hydrogen bond statistics
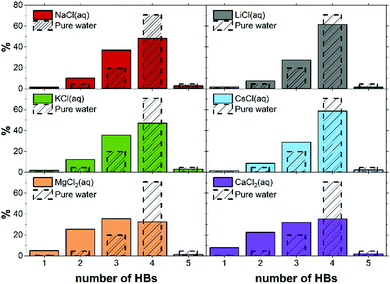
| System | b | Number of HBs (%) in the FSS | Average | |||||
|---|---|---|---|---|---|---|---|---|
| f 0 | f 1 | f 2 | f 3 | f 4 | f 5 | |||
| Li+ | 0.9 | 0.3 | 7. 3 | 31.1 | 60.9 | 0.5 | 0.0 | 2.54 |
| LiCl | 1.9 | 0.3 | 11.1 | 26.8 | 61.0 | 0.8 | 0.0 | 2.51 |
| Na+ | 0.9 | 0.2 | 4.7 | 26.1 | 66.6 | 2.4 | 0.0 | 2.66 |
| NaCl | 0.9 | 0.6 | 1.7 | 26.8 | 62.5 | 2.4 | 0.0 | 2.58 |
| 1.9 | 0.7 | 5.9 | 25.9 | 65.8 | 1.6 | 0.0 | 2.62 | |
| 3.8 | 1.3 | 14.1 | 35.0 | 47.3 | 2.2 | 0.0 | 2.35 | |
| K+ | 0.9 | 0.2 | 1.5 | 13.5 | 61.3 | 23.4 | 0.1 | 3.06 |
| KCl | 0.9 | 0.5 | 4.0 | 27.3 | 57.6 | 10.5 | 0.0 | 2.74 |
| 1.9 | 0.5 | 4.2 | 26.0 | 60.7 | 8.5 | 0.1 | 2.73 | |
| 3.9 | 2.0 | 11.9 | 33.3 | 47.0 | 5.5 | 0.2 | 2.43 | |
| Cs+ | 0.9 | 0.0 | 0.6 | 10.4 | 53.3 | 35.0 | 0.6 | 3.24 |
| CsCl | 1.9 | 0.9 | 4.2 | 20.5 | 52.6 | 21.7 | 0.2 | 2.91 |
| Mg2+ | 0.9 | 0.5 | 12.2 | 53.7 | 33.6 | 0.0 | 0.5 | 2.20 |
| MgCl2 | 1.9 | 0.3 | 14.3 | 69.4 | 15.9 | 0.0 | 0.0 | 2.01 |
| MgSO4 | 1.9 | 6.0 | 32.4 | 41.1 | 20.6 | 0.0 | 0.0 | 1.76 |
| Ca2+ | 0.9 | 0.2 | 8.4 | 52.2 | 39.1 | 0.0 | 0.0 | 2.30 |
| CaCl2 | 1.9 | 1.4 | 26.7 | 51.2 | 20.2 | 0.1 | 0.0 | 1.91 |
| CaSO4 | 1.9 | 3.8 | 25.0 | 41.3 | 29.9 | 0.0 | 0.0 | 1.96 |
| H2O | — | 0.0 | 0.3 | 4.6 | 19.8 | 70.7 | 4.6 | 3.75 |
| Cl− | 0.9 | 0.0 | 0.5 | 5.5 | 25.4 | 65.8 | 2.8 | 3.61 |
Despite the influence to the HB network should be mainly ascribed to the specific Mg2+–water interaction, the HB structure of the first hydration shell is governed by the subtle interplay between the level of hydration of the ions, and the interactions between ions, especially those of opposite charge. In more general terms, the cooperative effect of cations and anions in solution reflects a balance between solute–solvent and solute–solute interactions since relatively minor changes to the chemical characteristics result in dramatic changes to the HB distribution.
Water reorientation dynamics
The rotational dynamics of the water dipole,![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , was computed from the 1st order Legendre polynomial time correlation:74
, was computed from the 1st order Legendre polynomial time correlation:74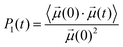 | (2) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (0) and
(0) and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (t) are the unit vectors defining the orientation of
(t) are the unit vectors defining the orientation of ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) at times 0 and t, respectively. The averages were computed using several time origins and overlapping intervals, each of length t = 16 ps (Fig. S6–S9 in ESI†).
at times 0 and t, respectively. The averages were computed using several time origins and overlapping intervals, each of length t = 16 ps (Fig. S6–S9 in ESI†).
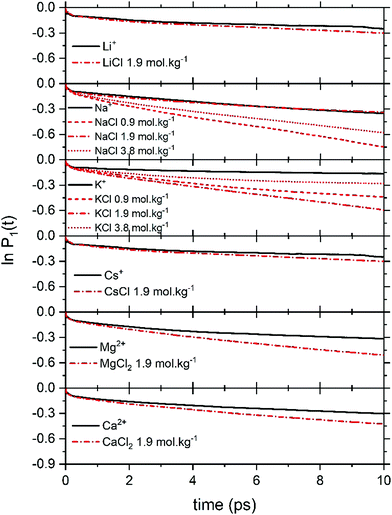
Fig. 6 reports the concentration-dependent time correlation P1(t) profiles of the water molecules, obtained from the AIMD (PBE-D3) simulations of the hydrated cation (single M, no counterions) and of the aqueous electrolyte solutions. The P1(t) function starts at 1 and then decays asymptotically to zero because of the random and isotropic reorientation of the water molecules in solution. The early stages of fast loss of correlation are caused by librational motion, whereas the long term decay is due to reorientational motion and can be fit by a bi-exponential model, exp(−t/τ1) + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2).74 The overall time associated with this process, τreor, is given by the sum of the fitting parameters τ1 and τ2. The value of τreor for pure liquid water (64 H2O), computed at the PBE-D3 level of theory is 5.3 ps, is in good agreement with the experimental value of 4.8 ps.75
exp(−t/τ2).74 The overall time associated with this process, τreor, is given by the sum of the fitting parameters τ1 and τ2. The value of τreor for pure liquid water (64 H2O), computed at the PBE-D3 level of theory is 5.3 ps, is in good agreement with the experimental value of 4.8 ps.75
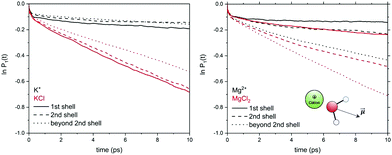
In electrolyte solutions, the presence of solvated ions accelerates the reorientation dynamics of water dipoles (faster P1(t) decay) compared to pure liquid water. However, the P1(t) profiles of NaCl(aq) and KCl(aq) do not consistently decrease with the concentration as they are also influenced by the type of ion pairs present in solution. For NaCl(aq), the fastest reorientation dynamics (fastest P1(t) decay) is observed for the 0.9 mol kg−1 solution, which only contains free Na+ and Cl− ions. On the other hand, the 1.9 and 3.9 mol kg−1 NaCl solutions, which contains contact and solvent-shared pairs, have a water reorientation behaviour similar to that of hydrated Na+ (Fig. 6). The correlation function P1(t) is, therefore, sensitive to solution speciation and can provide insights into the combined effect of cations and anions on the water reorientation dynamics. Chowdhuri and Chandra showed that in the vicinity of ions the diffusion coefficients are reduced and the orientational relaxation times are increased compared with pure water.76 We have computed the reorientation dynamics of the water molecules in the first and second coordination shells of the metal ions, and of the water molecules in the bulk (beyond second coordination shells of all ions in solution). Fig. 7 compares the correlation profiles obtained from the analysis of the AIMD trajectories of the hydrated metal ions K+ and Mg2+ and of 1.9 mol kg−1 aqueous KCl(aq) and MgCl2(aq). For hydrated K+, the reorientation dynamics of water dipoles in the hydration shells is similar to bulk behaviour. The reorientation dynamics of water dipoles is faster in chloride-containing solutions compared to that observed for the hydrated single metal ion: the P1(t) profiles of the water molecules in the first shell of K+ in KCl(aq) are drastically accelerated compared to the behaviour around hydrated K+ (single ion, no counterions). Conversely, the decay of the P1(t) profiles of the water molecules directly coordinated to Mg2+ are drastically slower than in the bulk, but the effect of solution composition (presence of other Mg2+ and Cl− in solution) is not significant. This can be explained by the much stronger ion–water interaction of Mg2+ compared to K+. The correlation function P1(t) is, therefore, sensitive to solution speciation and provide insights into the combined effect of cations and anions on the water reorientation dynamics.
Conclusions
We have conducted DFT based molecular dynamics simulations of the alkali metal ions Li+, Na+, K+, Cs+ and of the alkaline earth metal ions Mg2+ and Ca2+, in pure water and electrolyte solutions containing Cl− and SO42−, with salt concentrations ranging from 0.9 to 3.8 mol kg−1, to determine the effect of solution composition on the structural and dynamic properties of the first solvation shell of metal ions. Based on the results we conclude the following:In aqueous electrolyte solutions, the presence of the Cl− and SO42− counterions does not have a significant effect on the ion–water radial distribution functions of profiles of Li+, Na+, Mg2+ and Ca2+.
The presence of counterions in solution influences the size of the hydration shell not only because of the formation of contact ion pairs, which reduces the coordination sites available around the metal ion, but also when cations and anions form solvent-shared ion pairs. We found, for example, that in CaCl2(aq) and CaSO4(aq), the chlorine and sulphate ions in the second coordination shell of Ca2+ stabilize the seven-coordinated Ca(H2O)72+ complex over the six-coordinated Ca(H2O)62+ species.
Calculation of the velocity autocorrelation function (VACF) of the metal ions has been used to probe the strength of the local ion–water interaction and the rigidity of the interatomic vibration. We found a smoother decay of the VACF of Mg2+ in MgCl2(aq), which is a clear indication of a looser inter-hexahedral vibration. Chlorine ions, located in the second coordination shell of Mg2+ weaken, the Mg(H2O)62+ water ‘cage’ of the ion. This dynamic flexibility further highlights the effect of counterions on the dynamics of water molecules around ions.
Analysis of the hydrogen bond statistics in ionic solvation shell shows how the influence to the water–water network cannot only be ascribed to the specific Mg2+–water interaction, but also to the subtle interplay between the level of hydration of the ions, and the interactions between ions, especially those of opposite charge.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project (FUNMIN) is funded through the ACT programme (Accelerating CCS Technologies, Horizon2020 Project No 294766). Financial contributions made from Department for Business, Energy & Industrial Strategy (BEIS) together with extra funding from NERC and EPSRC research councils, United Kingdom, ADEME (FR), MINECO-AEI (ES). SK and GSP acknowledge financial support from the National Research Foundation of Korea (NRF) through the Korea government (MSIP) under Grant No. 2016R1A3B1908336. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). This research utilized Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT. http://doi.org/10.5281/zenodo.438045.Notes and references
- S. Piana, F. Jones and J. D. Gale, Assisted desolvation as a key kinetic step for crystal growth, J. Am. Chem. Soc., 2006, 128, 13568–13574 CrossRef CAS PubMed.
- O. S. Pokrovsky, S. V. Golubev, J. Schott and A. Castillo, Calcite, dolomite and magnesite dissolution kinetics in aqueous solutions at acid to circumneutral pH, 25 to 150 °C and 1 to 55 atm pCO2: New constraints on CO2 sequestration in sedimentary basins, Chem. Geol., 2009, 260, 317–329 Search PubMed.
- D. Di Tommaso and N. H. De Leeuw, First principles simulations of the structural and dynamical properties of hydrated metal ions Me2+ and solvated metal carbonates (Me = Ca, Mg, and Sr), Cryst. Growth Des., 2010, 10, 4292–4302 CrossRef CAS.
- H. S. Frank and W. Y. Wen, Ion-solvent interaction. Structural aspects of ion-solvent interaction in aqueous solutions: A suggested picture of water structure, Discuss. Faraday Soc., 1957, 24, 133–140 RSC.
- D. Saha and A. Mukherjee, Impact of Ions on Individual Water Entropy, J. Phys. Chem. B, 2016, 120, 7471–7479 CrossRef CAS PubMed.
- L. X. Dang, G. K. Schenter, V. Glezakou and J. L. Fulton, Molecular simulation analysis and X-ray absorption measurement of Ca2 +, K+ and Cl- ions in solution, J. Phys. Chem. B, 2006, 110, 23644–23654 CrossRef CAS PubMed.
- S. Koneshan, J. C. Rasaiah, R. M. Lynden-Bell and S. H. Lee, Solvent Structure, Dynamics, and Ion Mobility in Aqueous Solutions at 25 °C, J. Phys. Chem. B, 1998, 102, 4193–4204 CrossRef CAS.
- B. M. Rode, C. F. Schwenk and A. Tongraar, Structure and dynamics of hydrated ions—new insights through quantum mechanical simulations, J. Mol. Liq., 2004, 110, 105–122 CrossRef CAS.
- H. Ohtaki and T. Radnai, Structure and dynamics of hydrated ions, Chem. Rev., 1993, 93, 1157–1204 CrossRef CAS.
- Y. Marcus and G. Hefter, Ion pairing, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- Y. Marcus, Effect of ions on the structure of water: Structure making and breaking, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- Y. Ding, A. Hassanali and M. Parrinello, Anomalous water diffusion in salt solutions, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3310–3315 CrossRef CAS PubMed.
- C. F. Schwenk, H. H. Loeffler and B. M. Rode, Molecular dynamics simulations of Ca2+ in water: Comparison of a classical simulation including three-body corrections and Born-Oppenheimer ab initio and density functional theory quantum mechanical/molecular mechanics simulations, J. Chem. Phys., 2001, 115, 10808–10813 CrossRef CAS.
- J. A. White, E. Schwegler, G. Galli and F. Gygi, The solvation of Na+ in water: First-principles simulations, J. Chem. Phys., 2000, 113, 4668–4673 CrossRef CAS.
- R. Car and M. Parrinello, Unified approach for molecular dynamics and density-functional theory, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- D. Marx and J. Hutter, Ab initio molecular dynamics: Theory and implementation, John von Neumann Institute for Computing, Julich, 2000, vol. 1 Search PubMed.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. P. Lyubartsev, K. Laasonen and A. Laaksonen, Hydration of Li+ ion. An ab initio molecular dynamics simulation, J. Chem. Phys., 2001, 114, 3120–3126 CrossRef CAS.
- T. T. Duignan, G. K. Schenter, J. L. Fulton, T. Huthwelker, M. Balasubramanian, M. Galib, M. D. Baer, J. Wilhelm, J. Hutter, M. Del Ben, X. S. Zhao and C. J. Mundy, Quantifying the hydration structure of sodium and potassium ions: taking additional steps on Jacob's Ladder, Phys. Chem. Chem. Phys., 2020, 22, 10641–10652 RSC.
- S. Roy and V. S. Bryantsev, Finding Order in the Disordered Hydration Shell of Rapidly Exchanging Water Molecules around the Heaviest Alkali Cs+ and Fr+, J. Phys. Chem. B, 2018, 122, 12067–12076 CrossRef CAS PubMed.
- D. Di Tommaso and N. H. de Leeuw, First principles simulations of the structural and dynamical properties of hydrated metal ions Me2+ and solvated metal carbonates (Me = Ca, Mg, and Sr), Cryst. Growth Des., 2010, 10, 4292–4302 CrossRef CAS.
- J. A. Koskamp, S. E. Ruiz-hernandez, D. Di Tommaso, A. M. Elena, N. H. de Leeuw and M. Wolthers, Reconsidering calcium dehydration as the rate-determining step in calcium mineral growth, J. Phys. Chem. C, 2019, 123, 26895–26903 CrossRef CAS PubMed.
- M. Galib, M. D. Baer, L. B. Skinner, C. J. Mundy, T. Huthwelker, G. K. Schenter, C. J. Benmore, N. Govind and J. L. Fulton, Revisiting the hydration structure of aqueous Na+, J. Chem. Phys., 2017, 146, 84504 CrossRef CAS PubMed.
- B. S. Mallik, A. Semparithi and A. Chandra, A first principles theoretical study of vibrational spectral diffusion and hydrogen bond dynamics in aqueous ionic solutions: D2O in hydration shells of Cl− ions, J. Chem. Phys., 2008, 129, 194512 CrossRef PubMed.
- S. Biswas and B. S. Mallik, Heterogeneous occupancy and vibrational dynamics of spatially patterned water molecules, J. Phys. Chem. B, 2019, 123, 4278–4290 CrossRef CAS PubMed.
- J. Timko, D. Bucher and S. Kuyucak, Dissociation of NaCl in water from ab initio molecular dynamics simulations, J. Chem. Phys., 2010, 132, 114510 CrossRef PubMed.
- A. P. Gaiduk and G. Galli, Local and global effects of dissolved sodium chloride on the structure of water, J. Phys. Chem. Lett., 2017, 8, 1496–1502 CrossRef CAS PubMed.
- G. Cassone, F. Creazzo, P. V. Giaquinta, F. Saija and A. Marco Saitta, Ab initio molecular dynamics study of an aqueous NaCl solution under an electric field, Phys. Chem. Chem. Phys., 2016, 18, 23164–23173 RSC.
- J. D. Hem, Study and interpretation of the chemical characteristics of natural water, U.S Geological Survey Water-Supply, Alevandria, VA, 1985 Search PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, CP2K: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Schmidt, J. VandeVondele, I.-F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, Isobaric−isothermal molecular dynamics simulations utilizing density functional theory: an assessment of the structure and density of water at near-ambient conditions, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed.
- R. Jonchiere, A. P. Seitsonen, G. Ferlat, A. M. Saitta and R. Vuilleumier, Van der Waals effects in ab initio water at ambient and supercritical conditions, J. Chem. Phys., 2011, 135, 154503 CrossRef PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, Comment on “Generalized Gradient Approximation Made Simple”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- I. M. Zeron, J. L. F. Abascal and C. Vega, A force field of Li+, Na+, K+, Mg2+, Ca2+, Cl−, and SO42− in aqueous solution based on the TIP4P/2005 water model and scaled charges for the ions, J. Chem. Phys., 2019, 151, 134504 CrossRef CAS PubMed.
- C. Vega and J. L. F. Abascal, A general purpose model for the condensed phases of water: TIP4P/2005, J. Chem. Phys., 2005, 123, 234–505 CrossRef PubMed.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- B. M. Rode, C. F. Schwenk, T. S. Hofer and B. R. Randolf, Coordination and ligand exchange dynamics of solvated metal ions, Coord. Chem. Rev., 2005, 249, 2993–3006 CrossRef CAS.
- D. J. Harris, J. P. Brodholt and D. M. Sherman, Hydration of Sr2+ in hydrothermal solutions from ab initio molecular dynamics, J. Phys. Chem. B, 2003, 107, 9056–9058 CrossRef CAS.
- S. Biswas, D. Chakraborty and B. S. Mallik, Interstitial voids and resultant density of liquid water: a first-principles molecular dynamics study, ACS Omega, 2018, 3, 2010–2017 CrossRef CAS PubMed.
- M. J. Mcgrath, J. I. Siepmann, I. W. Kuo, J. Mundy, J. Vandevondele, J. Hutter and F. Mohamed, Isobaric–isothermal Monte Carlo simulations from first principles: application to liquid water at ambient conditions, ChemPhysChem, 2005, 6, 1894–1901 CrossRef CAS PubMed.
- M. J. McGrath, J. I. Siepmann, I.-F. W. Kuo and C. J. Mundy, Vapor–liquid equilibria of water from first principles: comparison of density functionals and basis sets, Mol. Phys., 2006, 104, 3619–3626 CrossRef CAS.
- Y. Marcus, Ionic radii in aqueous solutions, Chem. Rev., 1988, 88, 1475–1498 CrossRef CAS.
- V. T. Pham and J. L. Fulton, Contact ion-pair structure in concentrated cesium chloride aqueous solutions: An extended X-ray absorption fine structure study, J. Electron Spectrosc. Relat. Phenom., 2018, 229, 20–25 CrossRef CAS.
- Y. Yonetani, Distinct dissociation kinetics between ion pairs: Solvent-coordinate free-energy landscape analysis, J. Chem. Phys., 2015, 143, 044506 CrossRef PubMed.
- J. Timko, D. Bucher and S. Kuyucak, Dissociation of NaCl in water from ab initio molecular dynamics simulations, J. Chem. Phys., 2010, 132, 114510 CrossRef PubMed.
- M. K. Ghosh, S. Re, M. Feig, Y. Sugita and C. H. Choi, Interionic hydration structures of NaCl in aqueous solution: A combined study of quantum mechanical cluster calculations and QM/EFP-MD simulations, J. Phys. Chem. B, 2013, 117, 289–295 CrossRef CAS PubMed.
- T. Todorova, P. H. Hünenberger and J. Hutter, Car–Parrinello molecular dynamics simulations of CaCl2 aqueous solutions, J. Chem. Theory Comput., 2008, 4, 779–789 CrossRef CAS PubMed.
- I. Bakó, J. Hutter and G. Pálinkás, Car–Parrinello molecular dynamics simulation of the hydrated calcium ion, J. Chem. Phys., 2002, 117, 9838–9843 CrossRef.
- D. Spångberg, K. Hermansson, P. Lindqvist-Reis, F. Jalilehvand, M. Sandström and I. Persson, Model extended X-ray absorption fine structure (EXAFS) spectra from molecular dynamics data for Ca2+ and Al3+ aqueous solutions, J. Phys. Chem. B, 2000, 104, 10467–10472 CrossRef.
- J. L. Fulton, S. M. Heald, Y. S. Badyal and J. M. Simonson, Understanding the effects of concentration on the solvation structure of Ca2+ in aqueous solution. I: The perspective on local structure from EXAFS and XANES, J. Phys. Chem. A, 2003, 107, 4688–4696 CrossRef CAS.
- W. Stumm and J. J. Morgan, Aquatic chemistry: chemical equilibria and rates in natural waters, Wiley, 1996 Search PubMed.
- A. E. Nielsen and J. M. Toft, Electrolyte Crystal Growth Kinetics, J. Cryst. Growth, 1984, 67, 278–288 CrossRef CAS.
- M. Kowacz, C. V. Putnis and A. Putnis, The effect of cation:anion ratio in solution on the mechanism of barite growth at constant supersaturation: Role of the desolvation process on the growth kinetics, Geochim. Cosmochim. Acta, 2007, 71, 5168–5179 CrossRef CAS.
- M. N. Joswiak, M. F. Doherty and B. Peters, Ion dissolution mechanism and kinetics at kink sites on NaCl surfaces, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 656–661 CrossRef CAS PubMed.
- T. S. Hofer, H. T. Tran, C. F. Schwenk and B. M. Rode, Characterization of dynamics and reactivities of solvated ions by ab initio simulations, J. Comput. Chem., 2004, 25, 211–217 CrossRef CAS PubMed.
- D. Di Tommaso, E. Ruiz-Agudo, N. H. de Leeuw, A. Putnis and C. V. Putnis, Modelling the effects of salt solutions on the hydration of calcium ions, Phys. Chem. Chem. Phys., 2014, 16, 7772–7785 RSC.
- M. Wolthers, D. Di Tommaso, Z. Du and N. H. de Leeuw, Variations in calcite growth kinetics with surface topography: Molecular dynamics simulations and process-based growth kinetics modelling, CrystEngComm, 2013, 15, 5506–5514 RSC.
- D. Di Tommaso, M. Prakash, T. Lemaire, M. Lewerenz, N. H. de Leeuw and S. Naili, Molecular dynamics simulations of hydroxyapatite nanopores in contact with electrolyte solutions: The effect of nanoconfinement and solvated ions on the surface reactivity and the structural, dynamical, and vibrational properties of water, Crystals, 2017, 7, 57 CrossRef CAS.
- M. F. Kropman, PhD thesis, Ion solvation in water: femtosecond spectroscopy of hydrogen-bond dynamics, Van’t Hoff Institute for Molecular Sciences, 2004 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1987 Search PubMed.
- P. Demontis, G. B. Suffritti and A. Tilocca, Molecular dynamics simulation of an activated transfer reaction in zeolites, J. Chem. Phys., 1999, 111, 5529–5543 CrossRef CAS.
- A. Tilocca, Structure and dynamics of bioactive phosphosilicate glasses and melts from ab initio molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–13 CrossRef.
- J.-P. Boon and Y. Yip, Molecular Hydrodynamics, McGraw-Hill, New York, 1980 Search PubMed.
- X. Zhang, P. Alvarez-Lloret, G. Chass and D. Di Tommaso, Interatomic potentials of Mg ions in aqueous solutions: structure and dehydration kinetics, Eur. J. Mineral., 2019, 31, 275–287 CrossRef CAS.
- A. Chandra, Effects of ion atmosphere on hydrogen-bond dynamics in aqueous electrolyte solutions, Phys. Rev. Lett., 2000, 85, 768–771 CrossRef CAS PubMed.
- A. Luzar and D. Chandler, Effect of environment on hydrogen bond dynamics in liquid water, Phys. Rev. Lett., 1996, 76, 928–931 CrossRef CAS PubMed.
- A. Rastogi, A. K. Ghosh and S. J. Suresh, in Thermodynamics - Physical Chemistry of Aqueous Systems, ed. J. C. Moreno-Piraján, InTech, 2011, pp. 351–364 Search PubMed.
- E. Guàrdia, D. Laria and J. Martí, Hydrogen Bond Structure and Dynamics in Aqueous Electrolytes at Ambient and Supercritical Conditions, J. Phys. Chem. B, 2006, 110, 6332–6338 CrossRef PubMed.
- D. Di Tommaso, E. Ruiz-Agudo, N. H. de Leeuw, A. Putnis, C. V. Putnis, M. Xu and S. Garde, Modelling the effects of salt solutions on the hydration of calcium ions, Phys. Chem. Chem. Phys., 2014, 16, 7772 RSC.
- G. Stirnemann, E. Wernersson, P. Jungwirth and D. Laage, Mechanisms of acceleration and retardation of water dynamics by ions, J. Am. Chem. Soc., 2013, 135, 11824–11831 CrossRef CAS PubMed.
- M. S. Sansom, I. D. Kerr, J. Breed and R. Sankararamakrishnan, Water in channel-like cavities: structure and dynamics, Biophys. J., 1996, 70, 693–702 CrossRef CAS PubMed.
- S. Chowdhuri and A. Chandra, Dynamics of halide ion-water hydrogen bonds in aqueous solutions: Dependence on ion size and temperature, J. Phys. Chem. B, 2006, 110, 9674–9680 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of simulated systems, additional analysis of MD simulations (ion pairing, dynamics of the hydration shell, velocity autocorrelation function, hydrogen bond statistics, protocol for the calculation of time correlation functions). See DOI: 10.1039/d0cp01957g |
| This journal is © the Owner Societies 2020 |