The missing NH stretch fundamental in S1 methyl anthranilate: IR-UV double resonance experiments and local mode theory†
Abstract
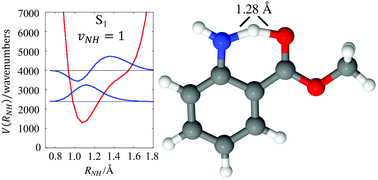
The infrared spectra of jet-cooled methyl anthranilate (MA) and the MA–H2O complex are reported in both S0 and S1 states, recorded using fluorescence-dip infrared (FDIR) spectroscopy under jet-cooled conditions. Using a combination of local mode CH stretch modeling and scaled harmonic vibrational character, a near-complete assignment of the infrared spectra is possible over the 1400–3700 cm−1 region. While the NH stretch fundamentals are easily observed in the S0 spectrum, in the S1 state, the hydrogen bonded NH stretch shift is not readily apparent. Scaled harmonic calculations predict this fundamental at just below 2900 cm−1 with an intensity around 400 km mol−1. However, the experimental spectrum shows no evidence of this transition. A local mode theory is developed in which the NH stretch vibration is treated adiabatically. Minimizing the energy of the corresponding stretch state with one quantum of excitation leads to a dislocation of the H atom where there is equal sharing between N and O atoms. The sharing occurs as a result of significant molecular arrangement due to strong coupling of this NH stretch to other internal degrees of freedom and in particular to the contiguous HNC bend. A two-dimensional model of the coupling between the NH stretch and this bend highlights important nonlinear effects that are not captured by low order vibrational perturbation theory. In particular, the model predicts a dramatic dilution of the NH stretch oscillator strength over many transitions spread over more than 1000 cm−1, making it difficult to observe experimentally.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...
