A model for the effect of ion pairing on an outer sphere electron transfer
Abstract
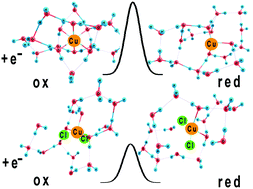
Ion pairing can strongly affect the rates of electron transfer reactions. To explain this effect, we propose a model Hamiltonian that describes the interactions between the pairing ion and the reactant, solvent and inner sphere reorganization, and bond breaking. Explicit expressions for the energies of the initial and final states, and for the energy of activation are derived in the weak adiabatic limit. The model is applied to the reduction of Cu(II) in the presence of chloride ions. For this purpose, the pertinent system parameters are obtained from density functional theory. Our model explains why the chloride ion enhances the rate of the first electron transfer in copper deposition.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...