 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The simulation of NMR data of flexible molecules: sagittamide A as an example for MD simulations with orientational constraints†
Ulrich
Sternberg
 *ab,
Pavleta
Tzvetkova
*ab,
Pavleta
Tzvetkova
 c and
Claudia
Muhle-Goll
c
c and
Claudia
Muhle-Goll
c
aResearch Partner of Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany. E-mail: ulrich.sternberg@partner.kit.edu
bCOSMOS-Software, Jena, Germany
cInstitute of Biological Interfaces 4, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany
First published on 8th July 2020
Abstract
The recently developed MDOC (Molecular Dynamics with Orientational Constraints) simulation is applied for the first time to a fully flexible molecule. MDOC simulations aim to single out the naturally existing configuration of molecules and to elucidate conformer populations. The performance of the method was first demonstrated on a well-studied test case, the five-membered ring lactone (α-methylene-γ-butyrolactone). In the case of sagittamide A, one-bond 1H–13C residual dipolar couplings (RDC) are used as orientational constraints that reorient the molecule or parts of it. In addition, NOE distances and 3J scalar couplings are used as constraints. Five possible configurations of sagittamide A (labelled a to e) are considered. One experimental RDC value per flexible unit was available and this was not sufficient to single out one valid configuration. The problem could be solved by including NOE distances as well as 3J couplings as complementary constraints into the MDOC simulations. In accordance with former investigations, we confirmed the configuration a for the natural product. A detailed analysis of conformers of the central chain of 6 chiral carbon atoms could be given by inspecting the MDOC trajectory. The relative abundance of these conformers is crucial in fulfilling all three sets of constraints.
Introduction
To study molecules that form several rotamers in solutions, molecular dynamics (MD) simulation is the method of choice. However, if one intends to simulate NMR data used in structure determination, traditional all-atom MD simulations cannot bridge the gap of several orders of magnitude between the MD time-scale (up to μs) and that of the equilibria governing NMR (up to ms). It will be shown that this time-scale problem can be solved by restrained MD simulation methods that are guided by NMR parameters. However, there is a distinct difference between NMR parameters like NOE distances or 3J couplings, which are scalars, and NMR interaction tensors: scalar quantities do not change under coordinate transformations but tensors are transformed by proper transformation matrices. To compare calculated interaction tensors such as chemical shift tensors, quadrupolar and dipolar coupling tensors with NMR measurements, they have to be transformed from their local molecular coordinate systems to the common laboratory frame or coordinate system of the external magnetic field. The NMR interaction tensors depend, therefore, on molecular orientations with respect to the outer magnetic field, and are averaged by fast molecular motions in a specific way; if a molecule rotates fast about a fixed axis, all off diagonal elements of the interaction tensors will vanish. The basic idea of MDOC (Molecular Dynamics with tensorial Orientational Constraints) is to use NMR interaction tensors as constraints to force molecular rotations. In NMR experiments of uniaxial oriented media, such as stretched gels or bio-membranes, the fixed axis or vector of orientation (director1) is mostly oriented parallel to the outer magnetic field and the interaction tensors of rapid moving molecules become diagonal in this orientation. Dipolar interactions measured in oriented media2 are called residual dipolar couplings (RDCs) and are used in MDOC to introduce orientational tensorial constraints. In most traditional structure investigations,3 order parameters or more general order tensors are introduced to account for the motional and ensemble averaging of the dipolar interaction. In MDOC, order tensors are avoided and the average is performed by rotating the molecules or parts of them using RDC-derived tensors as constraints. Scalar NMR parameters can be added as constraints to adjust distances and angles if only sparse tensor data are available. NOE distances4 and 3J couplings5 put more realistic weights on conformers that are generated during MDOC simulations.For rigid molecular systems, it is convenient to describe the time and ensemble average observed in NMR experiments by introducing an extra entity, the alignment, or order tensor. This tensor describes the downscaling of tensorial interactions by motions and distributions of orientations. The exploration of the RDC is hampered by the fact that the preferred average orientation of the molecules is not known a priori and there is no straightforward way to extract the alignment tensor from the experimental data. For a given rigid molecule, the five independent elements of the alignment tensor can be derived from a system of linear equations with the experimental RDC as the solution vector (see e.g. Losonsczi et al.6). For molecular systems with several possible conformers, this method is not practicable.
So far, MDOC was applied to membrane-bound molecules with relatively rigid backbones (Sternberg et al.7,8) and to helical peptides (Sternberg et al.9). These first investigations used mainly deuterium quadrupolar splitting tensors as orientational constraints. An MDOC investigation using 1H–13C RDC as constraints was performed by Tzvetkova et al.10 who applied the method to small molecules with a rigid backbone or moderate flexibility. Di Pietro et al.11 performed similar investigations but additionally used 13C–13C RDC to study the conformers and chirality of cellobiose. A simulation on a flexible macrolide system by Farès et al.12 combined RDC data with NOE distances and 3J couplings as constraints in MDOC. Here, the authors determined a high number of NMR data, including even prochiral hydrogen atoms; thus, MDOC has already proven its suitability for partially flexible molecules.
In this paper, the MDOC investigation of two molecules is presented: the five-membered ring lactone (α-methylene-γ-butyrolactone) and sagittamide A, which is produced by sea organisms called tunicates. The well-studied lactone provided the necessary initial tuning for the application of the MDOC simulations to molecules with several rotamers. The first investigation of the relative configuration and the conformers of the lactone using RDC was performed by Thiele et al.13 and the MDOC simulations confirmed their outcome. The MDOC simulations on sagittamide A are the first calculations on a fully flexible molecule with a long chain linker. The chiral part consists of eight stereocenters, and six of them are located in a per-acetylated 1,2,3,4,5,6-hexahydroxyhexane unit. The high mobility caused by the single bonds connecting the carbons gives rise to a multitude of rotamers at ambient temperature. Since the measurements of Schuetz et al.14 provided only 8 13C–1H RDC values, it seems impossible to single out the correct configuration from RDC alone since we had to cope with several conformers with individual orientations and exchange equilibria. In this paper, it is shown that in the case of sparse RDC data, the incorporation of additional constraints like NOE distances and 3J couplings into MDOC simulations can provide definitive conclusions on chirality and conformer equilibria.
Methods
Calculation of pseudo-forces in MDOC simulations
To perform MDOC simulation, pseudo-energy terms were added to the energy expression of the COSMOS-NMR force field15EFF. The pseudo-energies contain expressions depending on the differences between the calculated and experimental dipolar tensors or other NMR parameters such as NOE distances and 3J couplings. | (1) |
 | (2) |
 | (3) |
The second term in eqn (2) represents the orientational pseudo-forces containing the derivatives of all tensor elements of the calculated dipolar tensor Dcalc. These orientational pseudo-forces are evaluated as Cartesian derivatives of the transformation matrices that transform the bond dipolar tensors into the laboratory system:
 | (4) |
Calculation of the dipolar coupling tensors
For the dipolar coupling of two magnetic nuclei, A–B, the interaction tensor DAB (A and B denote the coupling atoms) will be diagonal and axial within the coordinate system connecting the two nuclei and we can easily assign one principal value of DAB to the axis parallel to the connection line and the other two values perpendicular to it: | (5) |
NMR measurements of uniaxially oriented media with the director of the oriented sample oriented parallel to the magnetic field of the spectrometer the dipolar tensor within this laboratory frame will have the same form as eqn (5), but DAB has to be replaced by the RDC value. Since the rotational diffusion around the director is isotropic, the time-averaged tensor becomes diagonal and rotationally symmetric. This must be true for every measured site and, therefore, it is of great value to use the whole tensors as constraints and not only the RDC value. The off-diagonal zeros of the RDC tensor indicate rotations and if used as constraints, molecular rotations are driven by differences to the calculated tensors.
The tensor components of DAB in the molecular frame can be transformed by proper rotation matrices to yield DL in the common laboratory frame according to
 | (6) |
 | (7) |
In the case of bond dipolar couplings tensor Di, it can be assumed that the tensors do not change with time (bond vibrations are neglected) and we have to perform time averaging only over the products of the transformation matrix elements Tαα′Tββ′. In the NMR experiments used in this paper, the director is oriented into the z-direction of the laboratory system and the observed dipolar splittings can then be directly calculated from the zz-component of the time-averaged dipolar tensor:
 | (8) |
 | (9) |
 | (10) |
The introduction of the time average with exponential memory according to eqn (9) effectively introduces a new timescale for rotational reorientations and fluctuations. This new characteristic time τ can be regarded as the lifetime of a molecular orientation. Using eqn (9), we have only to wait for a time period in the order of the memory time τ until a difference between constraint and time mean value builds up and the orientational pseudo-forces are flipping the system into another state. Therefore, τ is now the timescale of our accelerated MDOC simulation. This mode of time averaging, eqn (9) and (10), is also used for all types of properties where running mean values are needed to define pseudo-forces in constraint MDOC simulations, especially for NOE distances and 3J couplings.
The magnitude of the pseudo-forces is governed by the differences between experimental values and mean values calculated according to eqn (9) or (10) but the direction of the orientational pseudo-forces is calculated from derivatives of the actual transformation matrices (see eqn (4)). In this way, any mismatch in the orientation triggers an immediate response proportional to the mismatch. In the first timespan of MDOC simulation, no mean values developed and the resulting strong pseudo-forces could distort the molecule. Therefore, we switched on the pseudo-forces in exponential fashion using a pre-factor 1 − e−t/ρ with ϱ the time constant for the rise of the pseudo-forces. This value was set in our simulation to the same value as the memory time τ (see eqn (9) or (10)).
Calculation of NOE distances
In the calculation of NOE distances during an MD simulation, one has to take into account motional effects influencing the mean values. This can be performed by so-called r−6 averaging (see Vögeli18). For the case where the internal distance between the nuclei i and j changes slower than the overall tumbling of the molecule, we obtain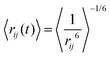 | (11) |
 | (12) |
Calculation of 3J couplings
To determine torsion angles around carbon–carbon single bonds, Karplus19 developed an equation describing the dependence of 3JHH couplings from the torsion angle ϕ, introducing three empirical parameters P1, P2 and P3. To account for the dependence of the 3JHH couplings on influences of substituents in the surroundings of the bond being studied, Haasnoot et al.20 introduced correction terms into the Karplus equation and this approach is called the Altona equation: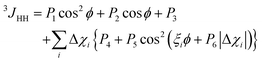 | (13) |
It was shown by Palermo et al.21 that a similar expression to eqn (13) can also be derived for 3JCH couplings and this expression contains an extra electronegativity term with the parameters P4′, P5′ and P6′. The total number of 9 empirical parameters was determined in the case of Palermo et al.21 by quantum chemical calculations of molecular models. These augmented Karplus expressions allow the predictions of 3JHH and 3JCH couplings with an error below 1 Hz and both dependences were implemented in the COSMOS-NMR force field. Additionally, we introduced Cartesian coordinate derivatives of the 3J couplings as prerequisites for the calculation of pseudo-forces in the MDOC simulations. The functional form of the pseudo-forces of the 3J couplings with the pre-factor f(ΔJ) is given in eqn (2).
Data evaluation
All possible configurations of the molecule under study were calculated in MDOC simulations with the same experimental data and MDOC conditions. To measure which of the configurations best fulfills the constraints, we used the quality criterion introduced by Intelmann et al.22 The quality Q = n/χ2 is calculated from the χ2 value: | (14) |
Results and discussion
MDOC simulations of the five-membered ring lactone
The lactone molecule (α-methylene-γ-butyrolactone) serves as a simple model since it has one flexible five-membered ring and a rotating CH3 group at ambient temperature. Thiele et al.13 studied this example and constructed conformer models of the ring with RS (C2-R and C3-S) and SS configuration. The geometries of the models were optimized on the DFT and MP2 level of theory and the resulting dipolar couplings were investigated using alignment tensors. The relative configuration was determined to be C2-R and C3-S (see left panel of Fig. 1). | ||
| Fig. 1 (a) RS (C2-R and C3-S) configuration in two conformations of the 5-membered ring (upper and lower panel – denoted as trans-1a and trans-2b in ref. 26 and 2trans1 and 2trans2 in ref. 24). (b) SS (C2-S and C3-S) configuration in two conformations of the 5-membered ring (upper and lower panel – denoted as cis-1a and cis-2a in ref. 26). | ||
In a subsequent investigation by Thiele et al.23 it was demonstrated that in addition to the relative configuration, the population of the two ring conformers (upper and lower panels of Fig. 1) can also be determined. The possibility of measuring highly precise NOE distances provided the necessary data for the study of the ring conformers. Kolmer et al.24 used newly determined NOE distances to re-investigate the population of the conformers of the lactone.
We used the lactone example taking the NMR data as published by Thiele et al.,13 and the NOE distances as given by Kolmer et al.,24 as constraints for the MDOC simulations of the RS and the SS forms. For the evaluation of the quality of the MDOC result, we used the errors as given in the supplements of the paper,24 with one exception: the errors of the NOE distances were estimated according to the rules as given by Butts et al.25 Distances lower than 2.8 Å can be determined with an error 0.05 Å and longer distances up to 4.5 Å with an error of 0.11 Å.
The MDOC method is nearly independent of the conformer at the start and this feature was demonstrated by using both configurations with different conformers as the initial geometry (see Fig. 1). The final results should only depend on the configuration, providing the simulation is sufficiently long. In the course of the MDOC simulation, all possible conformers are generated and their populations depend on the constraints. Since all internal and total molecular rotations are driven by orientational pseudo-forces, these orientational constraints are necessary to generate the conformers and even CH3-groups will rotate if proper CH one-bond RDCs are present. NOE distances to the protons of CH3 groups can be used in a general way since their fast rotation simulates experimental mean distances.
For the lactone structures as shown in Fig. 1a and b, 80 ns MDOC simulations at 300 K were performed (for the details of the simulations see Tables S1 and S2 in the ESI†). In a preliminary simulation, only the 8 RDC constraints with experimentally-determined signs of the couplings were used as constraints and the other 8 RDC without experimental signs were predicted. For the latter values, an RMS deviation of 0.67 Hz was obtained and the signs as predicted by Thiele et al.13 were confirmed (see Table S4 in the ESI†).
The results of the final MDOC simulations of the five-membered lactone structures are demonstrated in Fig. 2 and as expected, the two simulations with two different conformers (Fig. 1a) developed into highly similar trajectories with almost identical final results. A clear difference can be observed between the two configurations 1 and 2 (see Fig. 1a and b). The quality values for the one bond RDC differ strongly with respect to the configurations. This confirms the results of Thiele et al.,13 that the relative configuration is (C2-R, C3-S) or 2trans.
 | ||
| Fig. 2 Quality statistics of the four MDOC simulations of the five-membered ring lactone (see eqn (14)). The values were calculated as mean values over 2000 data snapshots of time-dependent values obtained with the exponential memory function. | ||
The quality criteria n/χ2 > 1 for the valid configuration indicate that most calculated values are within the error bounds of the constraints (see also Tables S4–S6 in ESI†) but for the NOE distances, an n/χ2 of only 0.5 could be reached. This was caused by the calculated distances of H2 to the CH3 protons deviating by 0.1 Å from the constraints (the error was estimated to 0.05 Å). A critical outlier is also the difference between the experimental and calculated H2 H3 distances of 0.186 Å.
As can be seen in Fig. 3, the five-membered ring is mostly in the conformation with a (C3–C2–O1–C5) torsion angle of −40°. This conformation, as shown in Fig. 3, leads to a trans-conformation of the hydrogen atoms H2 and H3. During the MDOC, it jumps into the other ring conformation with torsion angles (C3–C2–O1–C5) around 40°, which leads to a contribution of this conformation of 33%. Based on the RDC analysis using only one alignment tensor (MCST method), Thiele et al.23 determined a population of (60 ± 20%) for the 2trans1 conformer. The improved analysis with two alignment tensors (MCMT method) led to a population of 65 ± 7%. Using selected NOE distances, a population of 71% for 2trans1 was determined.24 From the sampling, the dihedrals of the geometry snapshots generated within the MDOC trajectory a population of 67% for 2trans1 was reached. This value is in perfect agreement with previous studies using different methods.
MDOC simulations of sagittamide A
In the previous subsection, it was demonstrated on a simple example that MDOC simulations can be applied for the simultaneous determination of the configuration and conformation of flexible fragments in organic molecules. Sagittamide A is much more challenging since this molecule has a long flexible chain linker with a number of chiral centres. NMR data of sagittamide A are available for the central part of the molecule denoted C4 to C10, containing 6 CH–O–C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups linked by C–Cσ bonds (see Fig. 4). Schuetz et al.14 determined for every group one 1H–13C RDC coupling and two values were obtained for the H(a,b)–C4 group. This means for the MDOC simulations that there is only one RDC coupling per flexible unit (except for C4). These data are not sufficient for a complete configurational and conformational study. Using the NMR data, Schuetz et al.14 singled out 5 possible configurations (a–e) for the acetylated units (see Fig. 4). A multitude of conformers are possible and the RDC values alone are not sufficient to assign one configuration.
O groups linked by C–Cσ bonds (see Fig. 4). Schuetz et al.14 determined for every group one 1H–13C RDC coupling and two values were obtained for the H(a,b)–C4 group. This means for the MDOC simulations that there is only one RDC coupling per flexible unit (except for C4). These data are not sufficient for a complete configurational and conformational study. Using the NMR data, Schuetz et al.14 singled out 5 possible configurations (a–e) for the acetylated units (see Fig. 4). A multitude of conformers are possible and the RDC values alone are not sufficient to assign one configuration.
 | ||
| Fig. 4 The upper panel shows the molecular model of sagittamide A in configuration a with the numbering of the carbon atoms, where NMR data are taken into account. The hydrogen atoms for which 1H–13C dipolar couplings are measured14 are shown in red. The lower 5 panels display the investigated part of the molecule in configurations a to e. Only C4 to C11 are displayed and the position of the acetyl group is shown in dark blue. The view of the projections is oriented with the C4–C5 bond (and additionally the C6–C7, C8–C9 and C10–C11 bonds) pointing backwards. | ||
In addition to the RDC values, the authors14 provided 6 3JCH and 7 3JHH couplings and 7 precise NOE distances of the central part of the molecule (see ESI†). At least two of the 3J couplings have intermediate averaged values, suggesting torsional equilibria for the involved bonds (C5–C6 and C6–C7). It will be demonstrated that the MDOC trajectories display equilibria of all conformers including their orientation and this is only possible if MDOC simulations reach the NMR average. All further conclusions on conformer equilibria can only be derived for the central part of the molecule were constraints are given.
The weight factors for the MDOC pseudo-forces were estimated in short preliminary simulations. It turned out that 3J constraints and distance constraints are both necessary since the orientational constraints are by far not sufficient to predict the orientations and conformational equilibria of this molecule. If one set of constraints was left out, most distances and 3J-couplings were far off the error limits. It is not possible to discriminate between the 5 configurations a–e using the RDC values alone. The criterion must be that all NMR data are reasonably represented. This is not the case for the 3J-couplings nor the NOE distances if the data are not used as constraints. Simulations that used the simpler Karplus equation instead of the Altona20 or Palermo21 refined versions failed to discriminate the 5 configurations.
To exclude possible dependences of the results on the simulation time, one should use the final duration of the MDOC simulation much larger than 5τ = 1.0 ns; therefore, we chose 80 ns as the final duration. As can be seen from the trajectories of the calculated properties (see e.g.Fig. 5) for MDOC simulations, this simulation time is sufficient to give stable values for all simulated properties. All 5 configurations of sagittamide A run parallel on the HPC cluster of KIT and lasted 57 h and 25 min (total duration).
 | ||
| Fig. 5 The 80 ns trajectory of the dipolar coupling frequency of the 13C–1H coupling of the C4–H4a bond of sagittamide A. Large values at the beginning of the trajectories are cut off. The dipolar frequencies are scaled down by the order parameter of the alignment medium (Sam = 0.004). Red line: Experimental value, green line: lower limit and yellow line: upper limit. Panel A: Mean value with exponential memory time (see eqn (9) and (10)) calculated at every step of the simulation. Panel B: Running arithmetic mean value (blue) of the data of panel A. | ||
In panel A of Fig. 5, the typical trajectory of the zz-component of the dipolar tensor of the C4–H4a bond is displayed. The upper panel A displays a trajectory of the mean value with exponential memory as calculated using eqn (9). The memory time constant was τ = 200 ps and the actual coupling values were scaled down using an order parameter of the alignment medium of Sam = 0.004. In most of the simulation time we observed fluctuations in the calculated dipolar coupling of the order of magnitude of the experimental error. In the ideal case the value should fluctuate around the measured mean value (shown in red). In the lower panel B, the running arithmetic mean value of the data of panel A is displayed. After about 10 ns, we reached a stable mean value in a range within the experimental error bounds. This means that in this case, after 10 ns, the molecule had sampled all global reorientations and nearly all conformational rotations were performed. Though these reorientations are clearly visible in panel A, throughout the simulation time there is hardly any detectable contribution to the final mean value. This behavior should be observed in a successful MDOC simulation and should be tested for all sites including 3J-couplings and NOE-distances.
Fig. 6 displays the quality criteria of the 5 configurations of sagittamide A calculated from 2000 coordinate snapshots of the 80 ns trajectories. The values in Fig. 6 were obtained by calculating the n/χ2 values from averages over 2000 MDOC snapshots (for example, see the final value of trajectory B in Fig. 5).
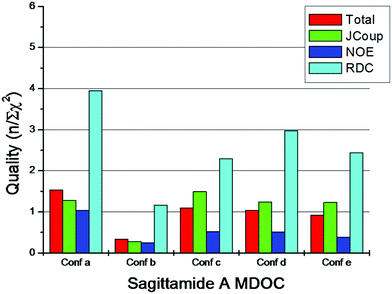 | ||
| Fig. 6 Comparison of the quality Q (see eqn (13)) of the calculated data of an MDOC simulation with respect to the NMR experiment for the configurations a–e of sagittamide A. | ||
A quality of n/χ2 > 1.0 indicates that the calculated values are mostly within the experimental error bounds (see eqn (14)). As per the definition, χ2 has no dimension; the sum in eqn (14) can be extended over different types of parameters, giving a total χ2 and quality. Only configuration a fulfills the quality criterion for all three types of parameters and gives the highest total quality. For the quality criterion, the estimation of the experimental error should be performed with care. For the RDC values, all errors were set to 0.5 Hz. As can be seen from Fig. 6, all 5 simulations fulfilled the quality criterion for the RDC and we could not distinguish the configurations using the RDC alone; as discussed before, this is a consequence of the ambiguities in dipolar tensors. NOE distances had no ambiguities and their errors were estimated to 0.2 Å (except distance H8–H6 with the error of 0.4 Å, see ESI†). Only configuration a could fulfill the NOE quality criterion and this result emphasizes the need for precise NOE distances for flexible systems.
The 3J couplings are ambiguous and one would obtain the same value for the coupling constant for two torsion angles, but the gauche- and trans-states can clearly be discriminated. To estimate the error, we have to take into account the experimental error and the uncertainty of the prediction using the Altona equation. For 3JHH couplings, the experimental error was estimated to be 0.6 Hz, and 1 Hz for the 3JCH couplings (see Schuetz et al.14). Haasnoot et al.20 obtained an RMS deviation of 0.65 Hz for the prediction of 3JHH couplings and Palermo et al.21 got a similar value of 0.662 Hz for the RMS deviation for DFT calculated coupling constants. Taking these errors together, the 3J couplings seem to be slightly weaker constraints than NOE distances; however, since these couplings depend directly on the torsion angles, the pseudo-forces derived from 3J couplings have a big influence on the population of rotamers.
Analysis of the backbone dynamics of sagittamide A
The analysis of the dynamics in the long free chain is a crucial part of the elucidation of the configuration and conformation of the studied molecules. The best way to analyze the dihedral rotations that occur in the course of a MDOC trajectory is to look at the carbon atoms C4 to C10 and the 4 torsion angles in between (rotations about the bonds between C5–C6, C6–C7, C7–C8 and C8–C9). In the course of MDOC simulation for configuration a, the system performs numerous jumps around the bonds between C5 to C10 with a frequency in the order of magnitude of the memory time constant τ (see eqn (6)). Since for the rest of the molecule no orientational constraints are given, the torsions around other bonds could not be investigated.To analyze these trajectories, we counted the occurrence of angles for the whole trajectory and the relative ratios for the 4 torsion angles are given in Fig. 7. There was an obvious trend detectable in the data, namely, growing trans contributions when going from C5–C6 to C9–C10.
 | ||
| Fig. 7 Torsion angle distributions from C4 to C10 obtained from the MDOC simulation of sagittamide A in configuration a. For the atom labels, see Fig. 4. | ||
On analyzing the data, we can also ask whether some torsion states are coupled or independent. In Table 1 we give the relative populations of torsion states that add up to 77.7%. The trend that can be seen in Fig. 7 is also documented in Table 1: in 69% of all torsion states, the first two bonds after the aliphatic chain starting with C10 are in the trans orientation and in 94%, the first bond {C7–C8–C9–C10} is oriented trans (the complete analysis is given in the ESI,† Table S10).
| Probability/% | Torsion angle combination |
|---|---|
| 22.0 | {trans, trans, trans, gauche} |
| 18.0 | {trans, trans, gauche, trans} |
| 14.6 | {trans, trans, trans, trans} |
| 14.4 | {trans, trans, gauche, gauche} |
| 8.7 | {trans, gauche, trans, gauche} |
In the MDOC simulations performed in this investigation, 3JHH and 3JCH are used as constraints and the calculated values gave a maximum deviation from the experiment of about 2 Hz only in the cases of the couplings C8–H10 and H9–H10 (see ESI†). Constraints like NOE distances and 3J couplings are necessary in nearly all the cases to gain information on the secondary structure of molecules.
From the analysis of couplings 3JH5–H6 = 4.8 Hz and 3JH6–H7 = 7.1 Hz, Schuetz et al.14 concluded that these values were caused by conformational averaging around the C5–C6 and the C6–C7 bond, respectively. The C7–C8 bond was assumed to be fixed. Taking this data together with the H5 to H8 NOE distance of 2.5 ± 0.2 Å, Schütz et al.14 estimated the population of H5–C5–C6–H6 and the H6–C6–C7–H7 rotamers, and this population was the prerequisite of the PALES27 RDC analyses,14 which indicated that the configuration a was the most probable. Finally, Seike et al.28 confirmed the configuration a for the natural product of sagittamide A by total synthesis in combination with the analysis of the 3JHH couplings.
Conclusions
It was demonstrated that orientational constraints in MDOC simulations generate a multitude of conformers of flexible molecules. In the case of sparse RDC data, pseudo-forces from scalar constraints as NOE distances or 3J couplings are necessary to adjust the population of these conformers. The time mean values of the RDC of these conformers fulfilled the measured RDC values within the error bounds. These conformers did not have to be inferred from other NMR data but are a direct result of the action of orientational pseudo-forces that reorient the whole molecule or parts of it. For the conformer population of the five-membered ring lactone, the MDOC simulations are in agreement with the results of Kolmer et al.24 In contrast to the former investigations, no refined structures were necessary and alignment tensors were completely avoided.In the case of sagittamide A, we faced a bigger challenge since this molecule can form a multitude of rotamers in solution. Nevertheless, the application of the MDOC simulations indicated that configuration a fulfills the RDC constraints at best, but only when all constraints are taken together did a clear decision for configuration a emerge. This result is in accordance with the previous studies by Schütz et al.14 and Seike et al.28 The advantage of MDOC comes from the possibility of blending several NMR data into a coherent picture of the structure and dynamics of the molecular system.
The most encouraging feature of MDOC simulations is the possibility to derive the occurrence of conformers from NMR measurements and to analyze their relative content. It should be mentioned that MDOC simulations are not dependent on the quality of the initial coordinates. The method opens up future prospects for tackling such questions as, for instance, the reaction of target molecules with flexible protein or nucleic acid receptors.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Burkhard Luy (KIT Karlsruhe) for promoting this work and for many inspiring discussions. We also thank Anne Schuetz for providing additional NOE data on sagittamide A. This work was performed thanks to the support of Karlsruhe Institute of Technology (KIT) and its computational resource bwUniCluster funded by the Ministry of Science, Research and Arts and the universities of the State of Baden-Württemberg, Germany.References
- F. Separovitch, R. Pax and B. Cornell, NMR order parameter analysis of a peptide plane aligned in a lyotropic liquid crystal, Mol. Phys., 1993, 78, 357–369 CrossRef.
- E. Brunner, Residual Dipolar Couplings in Protein NMR, Concepts Magn. Reson., 2001, 13, 238–259 CrossRef CAS.
- R. S. Lipsitz and N. Tjandra, Residual Dipolar Couplings in NMR Structure Analysis, Annu. Rev. Biomol. Struct., 2004, 33, 387–413 CrossRef CAS.
- A. E. Torda and W. F. van Gunsteren, The refinement of NMR structures by molecular dynamics simulation, Comput. Phys. Commun., 1991, 62, 289–296 CrossRef.
- P. L. R. Markwick, S. A. Showalter, G. Bouvignies, R. Brüschweiler and M. Blackledge, Structural dynamics of protein backbone φ angles: extended molecular dynamics simulations versus experimental 3J scalar couplings, J. Biomol. NMR, 2009, 45, 17–21 CrossRef CAS PubMed.
- J. A. Losonsczi, M. Andrec, M. W. F. Fischer and J. H. Prestegard, Order Matrix Analysis of Residual Dipolar Couplings Using Singular Value Decomposition, J. Magn. Reson., 1999, 138, 334–342 CrossRef PubMed.
- U. Sternberg, R. Witter and A. S. Ulrich, All-atom molecular dynamics simulations using orientational constraints, J. Biomol. NMR, 2007, 38, 23–39 CrossRef CAS PubMed.
- U. Sternberg and R. Witter, Molecular dynamics simulations on PGLa using NMR orientational constraints, J. Biomol. NMR, 2015, 63, 265–274 CrossRef CAS PubMed.
- U. Sternberg, M. Klipfel, S. L. Grage, R. Witter and A. S. Ulrich, Calculation of Fluorine Chemical Shift Tensors for the Interpretation of Oriented 19F-NMR Spectra of Gramicidin A in Membranes, Phys. Chem. Chem. Phys., 2009, 11, 7048–7060 RSC.
- P. Tzvetkova, U. Sternberg, T. Gloge, A. Navarro-Vázquez and B. Luy, Configuration Determination by Residual Dipolar Couplings: Accessing the Full Conformational Space by Molecular Dynamics with Tensorial Constraints, Chem. Sci., 2019, 10, 8774–8791, 10.1039/c9sc01084j.
- M. E. Di Pietro, U. Sternberg and B. Luy, Molecular Dynamics with Orientational Tensorial Constraints: A New Approach to Probe the Torsional Angle Distributions of Small Rotationally Flexible Molecules, J. Phys. Chem. B, 2019, 123(40), 8480–8491 CrossRef PubMed.
- C. Farès, J. B. Lingnau, C. Wirtz and U. Sternberg, Conformational Investigations in Flexible Molecules using Orientational NMR Constraints in Combination with 3J-Couplings and NOE Distances, Molecules, 2019, 24, 4417, DOI:10.3390/molecules24234417.
- C. M. Thiele, A. Marx, R. Berger, J. Fischer, M. Biel and A. Giannis, Determination of the Relative Configuration of a Five-Membered Lactone from Residual Dipolar Couplings, Angew. Chem. Int. Ed., 2006, 45, 4455–4460 CrossRef CAS PubMed.
- A. Schuetz, J. Junker, A. Leonov, O. F. Lange, T. F. Molinski and C. Griesinger, Stereochemistry of sagittamide A from Residual Dipolar Coupling Enhanced NMR, J. Am. Chem. Soc., 2007, 129, 15114–15115 CrossRef CAS PubMed.
- M. Möllhoff and U. Sternberg, Molecular mechanics with fluctuating atomic charges – a new force field with a semi-empirical charge calculation, J. Mol. Model., 2001, 7, 90–102 CrossRef.
- R. Witter, W. Prieß and U. Sternberg, Chemical Shift Driven Geometry Optimization, J. Comput. Chem., 2001, 23, 298–305 CrossRef PubMed.
- M. P. Marsan, I. Muller, C. Ramos, F. Rodriguez, E. J. Dufourc, J. Czaplicki and A. Milon, Cholesterol orientation and dynamics in dimyristoylphosphatidylcholine bilayers: a solid state deuterium NMR analysis, Biophys. J., 1999, 76, 351–359 CrossRef CAS PubMed.
- B. Vögeli, The nuclear Overhauser effect from a quantitative perspective, Prog. Nucl. Magn. Reson. Spectrosc., 2014, 78, 1–46 CrossRef PubMed.
- M. Karplus, Contact Electron-Spin Coupling of Nuclear Magnetic Moments, J. Chem. Phys., 1959, 30, 11–15 CrossRef CAS.
- C. A. G. Haasnoot, F. A. A. M. de Leew and C. Altona, The Relationship between Proton-Proton NMR Coupling Constants and Substituent Electronegativities, Tetrahedron, 1980, 36, 2783–2792 CrossRef CAS.
- G. Palermo, R. Riccio and G. Bifulco, Effect of Electronegative Substituents and Angular Dependence on the Heteronuclear Spin–Spin Coupling Constant 3JC–H: An Empirical Prediction Equation Derived by Density Functional Theory Calculations, J. Org. Chem., 2010, 75, 1982–1991 CrossRef CAS PubMed.
- D. Intelmann, G. Kummerlöwe, G. Haseleu, N. Desmer, K. Schulze, R. Fröhlich, O. Frank, B. Luy and T. Hofmann, Chemistry, 2009, 15, 13047–13058 CrossRef CAS PubMed.
- C. M. Thiele, V. Schmidts, B. Böttcher, I. Louzao, R. Berger, A. Maliniak and B. Stevensson, On the Treatment of Conformational Flexibility when Using Residual Dipolar Couplings for Structure Determination, Angew. Chem., Int. Ed., 2009, 48, 6708–6712 CrossRef CAS PubMed.
- A. Kolmer, L. J. Edwards, I. Kuprov and C. M. Thiele, Conformational analysis of small organic molecules using NOE and RDC data: A discussion of strychnine and α-methylene-γ-butyrolactone, J. Magn. Reson., 2015, 261, 101–109 CrossRef CAS PubMed.
- C. P. Butts, C. R. Jones, E. C. Towers, J. L. Flynn, L. Appleby and N. J. Barron, Interproton distance determinations by NOE – surprising accuracy and precision in a rigid organic molecule, Org. Biomol. Chem., 2011, 9, 177–184 RSC.
- C. M. Thiele, A. Marx, R. Berger, J. Fischer, M. Biel and A. Giannis, Determination of the Relative Configuration of a Five-Membered Lactone from Residual Dipolar Couplings, Angew. Chem. Int. Ed., 2006, 45, 4455–4460 CrossRef CAS PubMed.
- M. Zweckstetter and A. Bax, Prediction of Sterically Induced Alignment in a Dilute Liquid Crystalline Phase:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aid to Protein Structure Determination by NMR, J. Am. Chem. Soc., 2000, 122, 3791–3792 CrossRef CAS.
Aid to Protein Structure Determination by NMR, J. Am. Chem. Soc., 2000, 122, 3791–3792 CrossRef CAS. - H. Seike, I. Ghosh and Y. Kishi, Stereochemistry of sagittamide A: Prediction and Confirmation, Org. Lett., 2006, 8, 3865–3868 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01905d |
| This journal is © the Owner Societies 2020 |

