Open Access Article
Open Access ArticleEvolution of the structure and dynamics of bovine serum albumin induced by thermal denaturation
Olga
Matsarskaia
 *a,
Lena
Bühl
ab,
Christian
Beck
*a,
Lena
Bühl
ab,
Christian
Beck
 ab,
Marco
Grimaldo
a,
Ralf
Schweins
ab,
Marco
Grimaldo
a,
Ralf
Schweins
 a,
Fajun
Zhang
a,
Fajun
Zhang
 b,
Tilo
Seydel
b,
Tilo
Seydel
 a,
Frank
Schreiber
a,
Frank
Schreiber
 b and
Felix
Roosen-Runge
b and
Felix
Roosen-Runge
 *cd
*cd
aInstitut Laue-Langevin, 71 Avenue des Martyrs, 38042 Grenoble, France. E-mail: matsarskaia@ill.eu; Tel: +33 (0)4 57 42 82 56
bInstitut für Angewandte Physik, Auf der Morgenstelle 10, 72076 Tübingen, Germany
cDepartment of Biomedical Sciences and Biofilms-Research Center for Biointerfaces (BRCB), Faculty of Health and Society, Malmö University, Sweden. E-mail: felix.roosen-runge@mau.se; Tel: +46 (0)40 66 57 96 9
dDivision of Physical Chemistry, Lund University, Naturvetarvägen 14, 22100 Lund, Sweden
First published on 22nd July 2020
Abstract
Protein denaturation in concentrated solutions consists of the unfolding of the native protein structure, and subsequent cross-linking into clusters or gel networks. While the kinetic evolution of structure has been studied for some cases, the underlying microscopic dynamics of proteins has so far been neglected. However, protein dynamics is essential to understand the specific nature of assembly processes, such as diffusion-limited growth, or vitrification of dense liquids. Here, we present a study on thermal denaturation of concentrated solutions of bovine serum albumin (BSA) in D2O with and without NaCl. Using small-angle scattering, we provide information on structure before, during and after denaturation. Using quasi-elastic neutron scattering, we monitor in real-time the microscopic dynamics and dynamical confinement throughout the entire denaturation process covering protein unfolding and cross-linking. After denaturation, the protein dynamics is slowed down in salty solutions compared to those in pure water, while the stability and dynamics of the native solution appears unaffected by salt. The approach presented here opens opportunities to link microscopic dynamics to emerging structural properties, with implications for assembly processes in soft and biological matter.
1 Introduction
The functionality of soft matter and biological systems is often determined by their structure. A case in point are proteins, the biological functions of which depend on a combination of both structural features and dynamics. As the result of an elaborate and intriguing folding process in living cells, protein structure is determined by a subtle interplay of hydration-driven and electrostatic interactions and is known to be highly dependent on external parameters such as pH, ionic strength, solvent composition, pressure and temperature as well as the concentration of the proteins themselves (crowding) and genetic mutations.1,2 In fact, extreme conditions induced by (combinations of) these parameters can lead to drastic changes in protein structure including denaturation, unfolding and aggregation. In a medical context, the latter processes have been linked to several serious human pathologies, such as Alzheimer's disease,3 inflammation-related conditions4 or eye cataract.5 Interestingly, certain extremophilic organisms such as some types of bacteria, are able to survive and even thrive under drastic conditions such as high pressure in the deep sea,6 high ionic strength7,8 or strongly elevated temperatures in hot springs.9 In addition to aspects such as the presence of osmolytes preventing unfolding,10 the abilities of such microorganisms to resist these extremes can be traced back to specific adaptations of some types of proteins11–15 which evolved to prevent unfolding and a concurrent loss of functionality.While protein denaturation and unfolding are mostly undesirable in the context of living cells and elaborate mechanisms have evolved in order to avoid these processes, controlled denaturation of proteins is an important step in the food industry where it allows for the formation of protein particles. The latter can play crucial roles in the structuring of food products.16
Given their high complexity and ubiquitous presence in nature and everyday life, studying the effects of thermal denaturing on proteins can thus provide valuable information on protein folding as well as on the relation between their structure and function. This study intends to elucidate both the structure and dynamics during protein denaturation by investigating the thermal denaturation of aqueous solutions of bovine serum albumin (BSA) with varying ionic strengths. i.e. without added salt and with 150 mM NaCl. The reason for choosing NaCl for our studies is its relevance in the physiological context. Amongst its other functions such as maintaining the membrane potential and transducing signals,1 NaCl mediates the ionic strength in blood,17,18 of which serum albumins are also an essential constituent, thus motivating their investigations in the presence of NaCl.
Before elaborating on the details of the present study, we will provide a short summary of a selection of previous studies concerned with the thermal denaturation of BSA, in particular in the presence of additives such as salt.
The denaturation temperature of BSA under various conditions has been subject to several studies. Using differential scanning calorimetry (DSC), Giancola et al.19 determined the denaturation temperature of 20 mg ml−1 BSA in 10 mM phosphate buffer and with 150 mM NaCl to be 337 K (64 °C) at pH = 7. Another DSC study by Yamasaki and Yano20 reports an onset of denaturation of 2% BSA solutions with an ionic strength of 0.1 M NaCl at 51.9 °C and the temperature of denaturation itself at 64.3 °C. In addition, a FTIR study by Murayama and Tomida21 determined that in a solution of 20 mg ml−1 BSA in D2O with 100 mM NaCl, irreversible changes occur after 76 °C. For a BSA solution of 500 mg ml−1 in D2O, Hennig et al.22 report a denaturation process taking place in the temperature range between 60 and 81 °C. These studies show that the exact denaturation temperature determined depends on the experimental conditions and methods. In this paper, we provide the denaturation temperature values determined from our quasielastic neutron scattering data in Table 1.
Using differential scanning calorimetry (DSC) and Fourier-transform infrared spectroscopy (FTIR), Boye et al.23 performed a detailed investigation of the effect of pH, sugars, reducing and denaturation agents, detergents and NaCl on the temperature-induced gelation of BSA. In the presence of all additives studied and at pH values between 3 and 9, the authors found a decrease of the α-helix content and an increase in β-sheets and random coils. In addition, they report an enhanced stability of BSA with respect to denaturing in the presence of 0.5 M NaCl, reflected in an increased denaturation temperature compared to BSA samples without added NaCl. These results are corroborated by a calorimetric study by Giancola et al.19 and by rheological studies of heat-induced gelation of BSA by Tobitani and Ross-Murphy.24,25 These authors report a strong sensitivity of the gelation time of low-concentration BSA solutions to the presence of NaCl. Moreover, an increase of the gelation temperature with decreasing BSA concentration was observed. The structure formed by thermally denatured BSA solutions was studied by Lefebvre et al.26via rheology and small-angle neutron scattering. Their results revealed the presence of compact 3D clusters with a smooth surface. On the level of the individual BSA molecules constituting these clusters, a 20% increase of their Stokes radii was found upon denaturation.26
At high NaCl concentrations (2 M), Boye et al. observed more pronounced aggregation upon heating.23 A detailed DSC study on the interplay of denaturation, aggregation and gelation was performed by Barone et al.,27 comparing the behaviors of BSA and its human analog, human serum albumin (HSA). Both proteins showed maxima in their denaturation temperatures at a pH of 5.5, the absolute values of the denaturation enthalpy being lower for HSA. At low pH, denaturation and aggregation coincided.27 Furthermore, Vetri et al.28 performed fluorescence studies on the aggregation behavior of BSA and HSA. In spite of the strong similarities of these two proteins, their studies revealed different pathways towards aggregation for these two proteins. Moreover, their results underlined the significance of tertiary structure changes in BSA aggregation. As a general finding obtained using fluorescence, FTIR and light scattering, Militello et al.29,30 demonstrated the important role of the pH-mediated net protein charge in the aggregation behavior – higher net charges lead to formation of small, β-sheet-type aggregates, whereas lower net charges imply the formation of more polydisperse aggregates.29 Circular dichroism and fluorescence investigations by Bhattacharya et al.31 showed that, at low pH and high temperatures, molten-globule-like BSA oligomers assembled into amyloid-like fibrils. It is important to note that pH changes can per se induce conformational changes in BSA.32 This can be counteracted by additives, as has been shown in a recent study combining small-angle X-ray scattering, spectroscopy, UV and fluorescence by Del Giudice et al.,33 demonstrating that the binding of palmitic acid can stabilize the native form of HSA even at pH values which would typically induce unfolding. The co-binding of ibuprofen and propofol was furthermore shown to prevent HSA unfolding in the presence of urea.34
Different studies using quasi-elastic neutron scattering report on the dynamics of denatured BSA.35 Using neutron time-of-flight spectroscopy, strongly heterogeneous slow dynamics was found in BSA after chemical denaturation by guanidinium hydrochloride.36 In the same system of BSA with guanidinium hydrochloride, Ameseder et al. observed a high internal friction consistent with predictions from polymer theory.37 Grimaldo et al.38 proposed a picture of hierarchical dynamics in the thermally denatured state of BSA, where global translational diffusion is arrested, while localized internal dynamics becomes enhanced. Interestingly, while global dynamics was irreversibly arrested, the localized dynamics returned to its native state.38 Finally, Hennig et al. presented a showcase of following the process of thermal denaturation of BSA in solution, observing a dynamical slowing down upon thermal denaturation, as expected intuitively.22
Given the complex denaturation behavior tuned by different environmental parameters, we limit our study to a more simple basic question, namely, how the variation of the ionic strength as a sole parameter affects the denaturation process. Focusing on this question, we report on a comprehensive characterization of both static and dynamic aspects of thermal denaturation of BSA by a combination of small-angle, elastic and inelastic neutron scattering methods. We explore crowded BSA solutions with concentrations from 150 to 500 mg ml−1 in the presence and absence of NaCl. First, we use small-angle neutron scattering (SANS) to characterize time-averaged static features including protein interactions in the native solution, and the characteristic length and fractal dimensions of our systems. Second, information on diffusive dynamics of BSA in the process of thermal denaturation is obtained by recording quasi-elastic neutron scattering (QENS) by means of neutron backscattering (NBS). QENS is a sensitive tool to monitor changes in neutron energy during the scattering process in the sample, and thereby provides information on the underlying dynamics on pico- to nanosecond time scales. Here, we focus on so-called elastic and inelastic fixed window scans (EFWS/IFWS). From this technique, we obtain information on the temperature-dependent apparent mean-squared displacement, 〈u2〉, of BSA, reflecting the dynamical confinement, as well as a direct measure of diffusivity. Our approach thus provides us with a framework for a detailed and comprehensive characterization of both static and dynamic aspects of protein denaturation as a function of protein concentration, temperature and ionic strength.
This paper is organized as follows. In Section 2, we describe the sample preparation and the principles of the experimental methods (small-angle neutron scattering, quasi-elastic neutron backscattering) employed in this study. In Section 3, we discuss the results obtained before providing conclusions on the work presented here in Section 4.
2 Materials and methods
2.1 Sample preparation
BSA, D2O (99.99% atom purity) and NaCl were purchased from Sigma Aldrich (now Merck KgaA, Darmstadt, Germany). Prior to sample preparation, BSA powder was dried over silica beads in order to reduce incoherent scattering due to potential contamination by water (H2O) absorbed from the surrounding air. D2O was degassed under vacuum to minimize shifts in pD and potential pD-related protein structural changes.SANS and QENS samples containing the desired BSA and NaCl concentrations were prepared by mixing the required amounts of protein in powder form and concentrated NaCl stock solutions. The respective neutron scattering experiments were then performed as described in Sections 2.2 and 2.3.
2.2 Small-angle neutron scattering (SANS)
Solution small-angle neutron scattering (SANS) probes the shape, the spatial distribution and the interactions between solute particles by detecting the radiation scattered by the sample as a function of momentum transfer q. The differential scattering cross-section of a SANS experiment can be expressed as39,40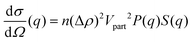 | (1) |
For cross-linked network structures, we use the relation I(q) ∼ q−D in the low-q region, where the fractal dimension D of the system provides additional structural information on the system in question.44–46
The SANS experiments described here were performed on the small-angle scattering instrument D11 (ILL, Grenoble, France).47 Approximately 750 μl of sample solution were filled into square quartz cells (Hellma, Müllheim, Germany) with a path length of 2 mm and the cells were placed on a temperature-controlled sample holder. In order to obtain insights into the structural properties of the protein solution during denaturation, we collected scattering profiles at defined temperatures reaching from room temperature to above the denaturation temperature. Furthermore, we collected a final scattering profile for the denatured sample after cooling it back to room temperature.
Every sample was measured at sample-to-detector distances of 1.5 and 8 m to maximize the range of accessible length scales providing structural information. The incoming neutron wavelength, λ, was 6 Å with a full width-half maximum (FWHM) wavelength spread of 9%. A q range from 0.0064 to 0.4247 Å−1 was covered. Scattered neutrons were detected via a 3He gas detector (CERCA) with a pixel size of 3.75 × 3.75 mm2 and a total pixel number of 256 × 256. Data were calibrated to an absolute scale using water (H2O) scattering intensity, dΣ/dΩ = 0.983 cm−1 as a secondary calibration standard. Raw data were saved in the Nexus (.nxs) format.48 Prior to further analysis, all scattering profiles obtained were corrected for both transmission and background scattering.
2.3 Elastic and inelastic fixed window scans (E/IFWS) of quasi-elastic neutron scattering (QENS)
Quasi-Elastic Neutron Scattering (QENS) encompasses several scattering techniques that allow to measure both the momentum and energy change of neutrons that is induced by the scattering event in the sample. As the central experimental quantity, the dynamic scattering factor S(q,ω) is obtained, where q is the structure vector related to the momentum change, and ħω is the energy change of the neutron in the sample.35Importantly, choosing deuterated solvents, the incoherent neutron scattering from the hydrogen of the protein molecules in the sample dominates the signal, and solvent contributions can be modeled consistently. As hydrogen is rather uniformly distributed in proteins, this experimental protocol provides a unique tool to investigate the averaged dynamics of proteins on (sub)nanosecond time and Ångstrom length scales. On these length and time scales, translational self-diffusion and rotational diffusion are convoluted with internal dynamics.35
In the present study, neutron backscattering (NBS) at the spectrometer IN16B (ILL, Grenoble) was used to measure the QENS signal with a high energy resolution Δ(ħω) ≈ 0.8 μeV FWHM while accessing momentum transfers in the range q ≈ 0.2–2 Å−1. The samples (1.2 ml each) were kept in indium-sealed double-walled cylindrical aluminum cans with a gap of Δr = 0.15 mm holding the liquid sample solutions. The temperature was controlled using a standard Orange cryofurnace.
In the conventional mode, NBS allows to record full QENS spectra S(q,ω) from a sample within an energy range of typically −30 μeV ≤ ħω ≤ +30 μeV, requiring at least 2–4 hours of acquisition time per spectrum. Typically, these data are then fitted with model functions, and provide information, e.g., on hierarchical protein dynamics at few selected temperatures during denaturation.38
So-called fixed window scans (FWS) measure the intensity for only a fixed energy transfer ω0, i.e. either elastic (EFWS, ω0 = 0) or inelastic (IFWS, ω0 ≠ 0) scattering.49 Importantly, this approach allows to focus on the rather high scattering intensity at small energy transfers, which reduces the counting time per point to below one minute. The dramatically reduced counting time per point for E/IFWS compared to full spectra enables both parameter scans, and time-resolved monitoring of temporal dynamical evolution. While this study mixes these approaches by real-time monitoring the dynamical evolution driven by a temperature scan, EFWS and IFWS are particularly promising for future studies focusing, e.g., purely on the evolution of dynamics during assembly and nucleation.50,51
The conventional analysis of EFWS is based on the Gaussian approximation valid in the limit of low q and yielding an apparent mean squared displacement 〈u2〉,52 which characterizes the dynamical confinement of motions within the resolution time of the instrument (for IN16B: ∼10 ns). Different extensions have been suggested53–55 to introduce effects of dynamical heterogeneity, and allow data fitting beyond the immediate low q limit, mainly targeted at hydrated protein powders. We employ the polynomial approach22
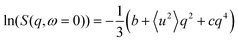 | (2) |
A standard analysis of IFWS has not yet been established. Potential approaches include semi-quantitative analysis based on the pure IFWS intensity49 and the generalized mean-squared displacement.51 Here, we use a new approach exploiting the ratio between the intensity of IFWS and EFWS,
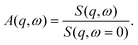 | (3) |
For the ratio analysis, we subtracted the empty can and solvent signal using EFWS and IFWS scans of pure D2O. We stress that for the ratio analysis, residual coherent contributions would only have an effect, if collective and self-dynamics were strongly different, which is unlikely as no correlation peaks are observed at the small length scales corresponding to the q range from 0.2–2 Å−1.
In this study, we combine EFWS and IFWS at ω = 1.3 μeV (cf.eqn (3)) during heating and cooling ramps in concentrated protein solutions, i.e. we monitor the dynamical evolution in real time while continuously changing temperature as a control parameter. We used counting times of 25 and 40 s for EFWS and IFWS, respectively, alternating between the energy offsets for the full duration of the experiment. The heating and cooling ramp rates were set to 0.21 K min−1 (295 K → 370 K), 0.325 K min−1 (295 K → 325 K), and 1 K min−1 (325 K → 295 K), respectively. We remark that the cooling ramp of 150 mg ml−1 BSA with 150 mM NaCl had a programming error, which resulted in an overshooting temperature, and faster cooling back.
For the interpretation of the data obtained, we focus on relative changes in the diffusivity of samples as a function of different conditions, i.e., protein and salt concentration, and use the combination of EFWS and IFWS as a novel indicator for time-resolved changes of dynamical evolution during a temperature scan.
3 Results and discussion
3.1 SANS: structural changes upon thermal denaturation
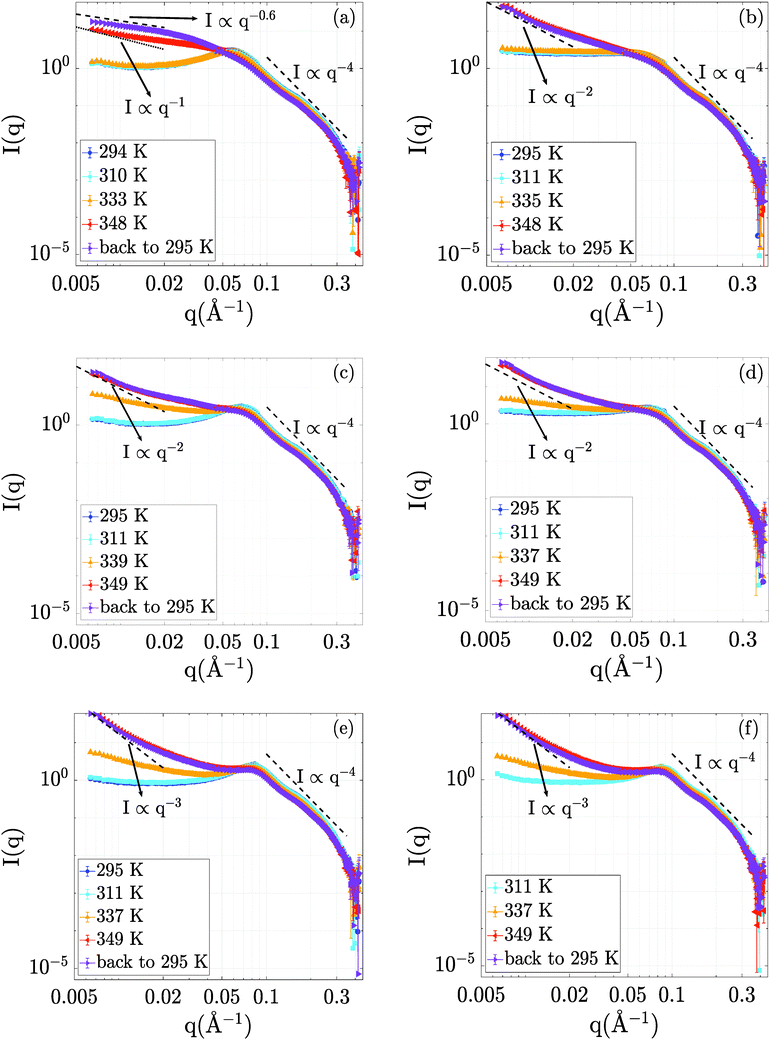
The evolution of the structural properties of the BSA–NaCl samples upon denaturation was probed by SANS. The temperature-dependent SANS data are presented in Fig. 2.Starting from the data at room temperature (295 K), we obtain a picture of protein interactions tuned by ionic strength and concentration, consistent with earlier findings.56 The electrostatic repulsion leads to a correlation peak in the structure factor S(q), such as the clearly visible peak at qcorr = 0.06 Å−1 for BSA at 150 mg ml−1 without NaCl (Fig. 2a). This correlation peak can be related to a correlation length of 2π/qcorr = 10.5 nm in the solution. At higher BSA concentrations (250 and 500 mg ml−1, cf.Fig. 2c and e) the correlation length shifts to 9 and 7.4 nm, respectively, pointing towards a pronounced crowding effect due to the increased protein concentration. The addition of NaCl flattens the correlation peak of the 150 mg ml−1 sample (see Fig. 2b). This effect is due to a NaCl-mediated charge screening and, thus, a decrease in electrostatic repulsion between BSA molecules. In the samples containing 250 mg ml−1 and 500 mg ml−1 BSA, the effect of NaCl on the correlation peak is less pronounced (Fig. 2d and f). We attribute this finding to the fact that at these high concentrations, the distances between BSA molecules are small, and caging effects on the structure are expected.57 Thus, the introduction of charge screening via NaCl leads to a less pronounced variation of protein–protein distances than in the case of the 150 mg ml−1 sample.
Increasing the temperature to 311 K has little or no effect on the scattering profiles, outlining no significant structural effects in this temperature range. At 335 K, all scattering profiles show an upturn in the low-q region. While the low-q upturn signifies emerging attraction and aggregation in the system, the correlation peak at around 0.06 Å−1 is still visible. The latter feature suggests that the protein structure remains in rather compact domains with steric and electrostatic repulsion, but experiences additional attraction due to partial unfolding, as seen in the increase of I(q → 0). Interestingly, no significant changes in I(q) are observed for 150 mg ml−1 at 335 K, which might be due to the larger inter-protein distance rendering a possible short-ranged attraction less efficient.
The curves obtained upon further temperature increase to T = 348 K and also after cooling back to 295 K retain a pronounced low-q upturn as a clear signature of cross-linking and network formation. As a general trend with increasing protein concentration, we observe a steepening of the low-q upturn.
Interestingly, despite the strong attraction due to unfolding, a weaker correlation peak remains present for 500 mg ml−1 and 250 mg ml−1 even at high temperatures and upon cooling down, while the peak becomes insignificant for 150 mg ml−1 at high temperatures and upon cooling. In addition, no strong effect of NaCl on the structures formed is observed at the higher protein concentrations (250 and 500 mg ml−1), while a significant structural difference exists for the aggregated network structures formed at 150 mg ml−1, as is evident for the clearly different slope at low q.
A possible structural interpretation is that, while the protein molecules remain in globular domains within an interconnected network formed upon denaturation, heat-induced partial unfolding induces a strong intermolecular attraction between the protein molecules located in these globular domains. This attraction is reflected in an overall aggregation behavior. Thus, we tentatively explain the different responses to NaCl observed for low and high BSA concentrations as follows: at high BSA concentrations, the crowding effects are strong, meaning that the globular domains present even in the denatured network induce some weak order due to steric repulsion. On the contrary, the aggregated network structures formed at lower protein concentration experience less steric effects. They are therefore more open and disordered, and can thus respond more sensitively to effects of NaCl-induced charge screening.
Notably, the sample containing 150 mg ml−1 BSA without NaCl still changes significantly upon cooling down. This effect is no longer visible in the sample containing 150 mg ml−1 BSA and 150 mM NaCl as well as in all other samples with higher BSA concentrations. We tentatively attribute this observation to a potential aging or slow kinetic effect of the denatured state. As an alternative explanation, we note that this post-denaturation effect could also be traced back to an equilibration process of re-compaction of local domains in the protein upon cooling, as suggested based on dynamical data.38
In order to quantify the effects of temperature on the samples, we compare the low q regions up to q = 0.02 Å−1 with power law curves (I(q) ∝ q−D).44–46 The values of D are indicated in the respective plots in Fig. 2. We remark that the exponent is usually interpreted as a fractal dimension for these kinds of network-forming systems.44–46 In this interpretation, we observe a transition from more open structures with D ≈ 2 corresponding to random-chain-like configurations at lower protein concentrations to steeper signatures for 500 mg ml−1, which signify more compact objects. We remark that the 150 mg ml−1 BSA solution without NaCl cannot be interpreted as a fractal object, but rather appears to be an elongated aggregated object with loose and disordered internal structure. We stress that all samples decay consistent with the Porod scaling of q−4 at larger q (cf.Fig. 2), which evidences overall compact structures of the protein building blocks even in the aggregated networks.
3.2 QENS: dynamical evolution during denaturation
Having investigated the static properties of the samples via SANS, we employed QENS measurements in order to assess the changes in BSA dynamics throughout the process of thermal denaturation. While protein denaturation has been studied in detail using spectroscopic and calorimetric techniques, the understanding of dynamics inside a denatured protein network is very limited. In particular, it is unclear to which extent intramolecular motions are hindered by cross-linked and neighboring protein chains already on small time and length scales, or simply slowed down due to increased hydrodynamic friction in the local neighborhood of the protein molecules. This information would be essential to quantitatively describe macroscopic properties of protein networks such as their rheology, in the spirit of hierarchical models of protein dynamics.We focus our discussion on four systems – lower-concentration samples containing 150 mg ml−1 BSA with and without 150 mM NaCl and high-concentration samples containing 500 mg ml−1 BSA with and without 150 mM NaCl.
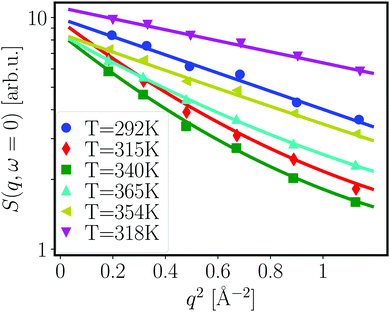
From the fits shown in Fig. 1 we obtain the mean-squared displacement values 〈u2〉(T) for the samples containing 150 and 500 mg ml−1 BSA in the absence and presence of 150 mM NaCl, respectively. This heuristic definition provides an approach to compare different data sets without detailed knowledge of the different contributions to the elastic signal measured.
The systems studied show similar trends of 〈u2〉 with T. With increasing T, 〈u2〉 increases linearly until T ≈ 330 K, reflecting an increase in global protein motion due to the higher thermal energy of the system. At T > 330 K, a decrease of the 〈u2〉 values is observed until T ≈ 365 K. The intuitive interpretation backed up by the SANS data is that proteins partially unfold in this temperature regime, and subsequently form a network-like structure in which protein mobility is strongly decreased. Cooling the system back to 295 K does not restore the initial mobility as is seen in the low 〈u2〉 values in all cases, thus pointing towards an irreversible BSA denaturation at high T.
Comparing the values of 〈u2〉 of both systems, it is well visible that the overall values are lower in the system containing 500 mg ml−1 BSA than in the one with 150 mg ml−1. This observation is expected given that a higher degree of crowding in the high-concentration sample implies a stronger sterical hindrance especially of translational diffusion of the BSA molecules.57–59 This is consistent with the SANS data shown in the previous section where the crowding is reflected in smaller overall inter-particle distances as derived from the respective correlation peaks.
Only small effects of NaCl on the overall temperature-dependent behavior of 〈u2〉 are observed before denaturation (Fig. 3 top). However, once denaturation has taken place, NaCl causes a smaller 〈u2〉 both at high temperatures and during cooling. Stronger differences between the samples with and without NaCl are visible at high temperatures during heating (Fig. 3) (a) as well as during the cooling process in the case of the lower BSA concentration (150 mg ml−1). This observation reflects the SANS results discussed in the previous section – the higher the protein concentration, the less pronounced the effect of charge screening by NaCl, which is consistent with a previous finding that strong steric interactions render electrostatics less effective in BSA solutions.56 We note that, in the presence of NaCl, the 〈u2〉 observed upon cooling have similar values at both 150 and 500 mg ml−1 BSA, indicating that the effect of NaCl might play a more important role than the protein concentration once denaturation has taken place.
 | ||
| Fig. 3 Dynamical information from fixed window scans for 150 mg ml−1 BSA (left column) and 500 mg ml−1 BSA (right column). The arrows in plots (a) and (b) indicate the respective heating (right-pointing arrow) and cooling (left-pointing arrow) ramps performed during the experiments. Apart from the flat heating signature of BSA 150 mg ml−1 without NaCl, all heating profiles are fitted with a two-state function with a smeared step function (eqn (6)). (a) and (b) Apparent mean-squared displacement 〈u2〉 from EFWS. (c)–(f) Apparent intensity ratio A(q,ω = 1.3 μeV) between IFWS and EFWS for two q values. Data sets in (a) (BSA 150 mg ml−1 without NaCl) and (e) are binned by two data points for better visibility. All results show a decrease of dynamics upon the denaturation transition. Samples with NaCl show comparable dynamics before denaturation, and slower dynamics after denaturation. In general, results on dynamical confinement 〈u2〉 from EFWS and dynamics from the ratio A(q,ω) of IFWS and EFWS show comparable trends, suggesting that the changes in 〈u2〉 in these liquid samples are mainly driven by varying dynamics, and not by an evolution of the confinement. | ||
From a theoretical perspective, the apparent mean-squared displacement 〈u2〉 is given by the real time-dependent mean-squared displacement 〈Δr2〉(t) averaged over the time resolution of the neutron spectrometer ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t)51,53,60
(t)51,53,60
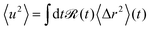 | (4) |
In order to directly obtain information on the underlying dynamics, we therefore used the intensity ratio A(q,1.3 μeV) between IFWS and EFWS as shown in Fig. 3(c–f) for two q values. A larger ratio implies a broader S(q,ω), and thus faster dynamics. Overall, we obtain behavior qualitatively similar to that of 〈u2〉: the ratio increases with temperature until denaturation sets in. After forming a network of denatured proteins, and cooling back, the values of the intensity ratio remain significantly smaller than those observed during heating, indicating, as expected, slower overall dynamics in the crosslinked network than in the native solution state.
For 500 mg ml−1 BSA, the effect of salt on the intensity ratio is almost negligible, while salt seems to induce slower dynamics after denaturation in 150 mg ml−1 BSA. This behavior might be linked to the more open structures formed for 150 mg ml−1 compared to the more compact network structures for 500 mg ml−1 (cf.Fig. 2). Thus, electrostatic repulsion between protein molecules might lead to more motional freedom and hence faster local dynamics for 150 mg ml−1 compared to 500 mg ml−1.
The good agreement between 〈u2〉 and A(q,1.3 μeV) indicates that dynamics are the dominating factor in 〈u2〉 for these samples. This observation is reasonable, as translational diffusion and local fluctuations in the assembled networks are not expected to show strong confinement effects on nanosecond time scales, and might thus dominate the signatures. In this context, the weaker effect of NaCl on dynamics than on dynamical confinement for 500 mg ml−1 BSA could indicate a stronger confinement effect in dense protein networks, which is expected intuitively.
We used a generic two-state function to quantify the overall characteristics of all heating profiles22 (solid lines in Fig. 3):
| f(T) = (a1 + b1T)[1 − Θ(T)] + (a2 + b2T)Θ(T) | (5) |
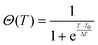 | (6) |
BSA solutions with 150 mg ml−1 without salt (Fig. 3(a)) represent an exception in the fitting, as limited statistics imply that a constant profile is sufficient to represent the data. This flat profile is attributed to the comparably fast dynamics, which implies that the elastic scattering intensities have decreased to close to background levels on the q range used for fitting.
The cooling profiles were fitted with a polynomial
| f(T) = (c + dT + eT2) | (7) |
| Profile | Heating ramp | Cooling ramp | T d [K] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a 1 | b 1 [10−3] | a 2 | b 2 [10−3] | T 0 [K] | ΔT [K] | c | d [10−3] | e [10−6] | ||
| a These fit parameters were fixed due to insufficient statistics. b T d was calculated via T0 − 2.5ΔT (see text for details). | ||||||||||
| BSA 500 mg ml−1 NaCl 0 M | ||||||||||
| 〈u2〉 | −53.7 ± 40.7 | 156 ± 111 | −36.5 ± 7.2 | 135 ± 24 | 343.1 ± 3.2 | 5.49 ± 1.80 | 75.7 ± 42.0 | −494 ± 253 | 820 ± 380 | 329.4 ± 3.7 |
| A(q1,ω1) | −2.16 ± 1.04 | 6.27 ± 2.81 | −0.96 ± 0.07 | 3.91 ± 0.24 | 349.3 ± 2.2 | 6.82 ± 0.77 | 1.10 ± 0.22 | −7.27 ± 1.33 | 12.8 ± 2.0 | 332.3 ± 2.5 |
| A(q2,ω1) | −1.94 ± 0.45 | 5.94 ± 1.23 | −2.05 ± 0.14 | 8.17 ± 0.45 | 340.2 ± 0.6 | 5.49 ± 0.45 | 2.20 ± 0.26 | −14.6 ± 1.62 | 25.3 ± 2.5 | 326.5 ± 0.9 |
| BSA 500 mg ml−1 NaCl 0.15 M | ||||||||||
| 〈u2〉 | −62.7 ± 53.8 | 180 ± 146 | −31.5 ± 6.8 | 121 ± 23 | 345.6 ± 3.5 | 5.66 ± 1.69 | 31.3 ± 35.7 | −210 ± 217 | 363 ± 328 | 331.5 ± 3.9 |
| A(q1,ω1) | −1.03 ± 0.67 | 317 ± 180 | −0.95 ± 0.06 | 3.86 ± 0.18 | 348.3 ± 1.4 | 5.69 ± 0.57 | 1.02 ± 0.17 | −6.48 ± 1.04 | 11.1 ± 1.6 | 334.1 ± 1.7 |
| A(q2,ω1) | −0.91 ± 0.37 | 296 ± 102 | −1.66 ± 0.12 | 6.93 ± 0.40 | 341.1 ± 0.5 | 5.13 ± 0.40 | 1.94 ± 0.18 | −12.7 ± 1.1 | 21.6 ± 1.7 | 328.3 ± 0.8 |
| BSA 150 mg ml−1 NaCl 0 M | ||||||||||
| 〈u2〉 | 9.02 ± 0.15 | 0.00a | 0.00a | 0.00a | −∞a | 1.00a | 18.7 ± 53.7 | −160 ± 313 | 348 ± 451 | 0.00a |
| A(q1,ω1) | −0.07 ± 1.85 | 1.18 ± 5.09 | −1.54 ± 0.25 | 6.68 ± 0.84 | 342.1 ± 2.5 | 4.41 ± 1.55 | 3.47 ± 2.51 | −23.5 ± 15.8 | 40.7 ± 24.8 | 331.1 ± 3.5 |
| A(q2,ω1) | 0.50 ± 0.06 | 0.00a | 0.65 ± 0.02 | 0.00a | 342.8 ± 9.2 | 7.72 ± 7.65 | 5.00 ± 3.86 | −35.0 ± 24.5 | 62.6 ± 38.8 | 325.9 ± 12.2 |
| BSA 150 mg ml−1 NaCl 0.15 M | ||||||||||
| 〈u2〉 | −20.6 ± 95.6 | 667 ± 26 | −1.34 ± 6.76 | 27.7 ± 21.8 | 349.7 ± 7.6 | 4.35 ± 3.27 | 34.3 ± 42.1 | −227 ± 254 | 392 ± 381 | 338.8 ± 8.3 |
| A(q1,ω1) | 0.25 ± 1.08 | −26 ± 294 | −1.14 ± 0.20 | 5.32 ± 0.67 | 345.2 ± 1.4 | 5.02 ± 0.91 | 1.07 ± 0.39 | −6.96 ± 2.39 | 12.2 ± 3.6 | 332.7 ± 2.0 |
| A(q2,ω1) | 0.22 ± 0.01 | 0.00a | 0.62 ± 0.01 | 0.00a | 349.3 ± 0.9 | 5.50 ± 0.91 | 1.76 ± 0.43 | −11.7 ± 2.7 | 20.4 ± 4.1 | 335.6 ± 1.7 |
As a first observation, the denaturation temperature Td is comparably constant within error bars in all samples for both 〈u2〉 and the ratios A(q,ω = 1.3 μeV), except for BSA 150 mg ml−1 without NaCl. When comparing the values for Td with and without NaCl, an overall weak trend for lower Td without salt may be present, suggesting a weak stabilizing effect of salt. This is consistent with results by Yamasaki and Yano20 who reported a NaCl-mediated stabilization of BSA against denaturation at neutral and alkaline pH values. In the present study, the salt effect on the dynamic behavior is, again, most pronounced for BSA solutions with 150 mg ml−1, which might indicate that an interplay of electrostatics and crowding plays a role for protein stability. The central temperature T0 shows more fluctuations than Td. This is reasonable, since Td is a purely thermodynamically determined quantity, while T0 is additionally affected by kinetic contributions.
The observed dynamical signature of thermal denaturation contributes to a consistent picture from multiple techniques. First, starting around 330 K, both DSC23 and our dynamical results show first signatures of denaturation, which might be related to a first conformational transition also observed via peak shifts in FTIR, which was attributed to an increased crevice between protein domains.21 At higher temperatures above 345 K, the secondary structure is affected, as is visible by FTIR and CD spectroscopy, involving irreversible melting of α helices,21,23 which in our dynamical signatures leads to a stronger cross-linking. We remark that our SANS data together with earlier data from QENS38 suggest that compact domains persist, but with a potentially altered secondary structure.
In powder samples, 〈u2〉 is often used to define an effective force constant k = d〈u2〉/dT. While this approach would also be tempting for the cooling ramps, the clear polynomial signature implies that the dynamics are not governed by a universal force constant, but rather by an apparent force constant changing with temperature. This observation might be due to the fact that, upon cooling, the local levels of dynamics return to their initial values in the native structure,38 which suggests a local compaction of the protein structure. This compaction, in line with the overall fractal-like structure, could be a reason for a changing force constant. A second reason is that the polynomial signature is obtained for both 〈u2〉 and the ratios A(q,ω). This suggests that the signature observed might be caused by the dynamical response within a network, and not by the confinement, which is the reasoning behind the effective force constant.
3.3 Remarks on the methodology
On a practical note, we stress that differences in the absolute MSD values 〈u2〉 determined by EFWS depend on the q range measured in the experiments. In addition, contrary to full QENS spectra, the values for 〈u2〉 critically depend on a precise calibration. Finally, the extraction via the Gaussian approximation or also the heuristic polynomial approximation in eqn (2) is valid only for sufficiently small q, which turns out to be less problematic for powder samples than for proteins in solution. In this context, the use of the combined analysis of IFWS and EFWS is a way to obtain an independent set of information which can be successfully used to check and validate the overall interpretation. We remark that the ratio even seems to be statistically more robust than 〈u2〉 for less concentrated samples with comparably fast diffusion, as seen for the case of the BSA solution with 150 mg ml−1 and without NaCl.The combined analysis of the elastic and inelastic fixed window data allows to access additional information on the evolution of (sub)nanosecond dynamics in the sample with a very good kinetic resolution on the order of a few minutes, contrary to full QENS spectra which require several hours. This option is very relevant to study the time-dependence of denaturation, and can be applied to other topics such as assembly and crystallization.52 In particular, the combination with conventional analysis of the EFWS allows to distinguish between effects of geometrical confinement and dynamics on nanosecond motions characterized by 〈u2〉. While we observed a dominance of dynamics for liquid samples, it is interesting to explore to which extent 〈u2〉, e.g. in powder samples, is governed by dynamics or confinement. Our analysis approach opens opportunities to study dynamical landscapes in more microscopic detail.
4 Conclusions
In this study, we applied SANS and QENS to study static and dynamic aspects of thermal BSA denaturation and the way it is influenced by the addition of NaCl. Using SANS, we show that at high BSA concentrations, the screening effect of NaCl is less efficient than at low concentrations and we attribute this observation to strong steric interactions. Upon denaturation, we observe a power-law-like upturn at low q that indicates the formation of a fractal network, which persists also after cooling back to room temperature.Using fixed window scans (FWS) of QENS, we characterize the evolution of dynamical confinement and dynamics during temperature ramps through the denaturation transition. All signatures indicate that a significant fraction of mobility is lost upon denaturation. Comparing the dynamical signal from ratios of inelastic and elastic FWS with the dynamical confinement obtained from the apparent mean-squared displacement, we suggest that the observed signatures of denaturation on nanosecond time scales are dominated by temperature-induced changes of the dynamics, whereas changes of the confinement only contribute weak effects. Thus, crosslinking does not seem to induce confinement of the motions observed on nanosecond time scales. This is a relevant finding for future quantitative modeling of, e.g., rheological properties of protein networks. Our framework combining different scattering methods presents a promising tool for a detailed study of structural and dynamical evolution during assembly processes, opening opportunities for fundamental understanding of processes in e.g. food and life sciences.
Data accessibility
The SANS and QENS data are permanently curated by the ILL and accessible via the DOIs 10.5291/ILL-DATA.9-13-637,61 10.5291/ILL-DATA.8-04-752,62 10.5291/ILL-DATA.9-13-67263 and 10.5291/ILL-DATA.8-04-759.64Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the ILL for beamtime allocation on beamlines D11 and IN16B. Financial support by the DFG (DFG 316738961) and the ANR (ANR-16-CE92-0009, ImmunoglobulinCrowding) as well as by the BMBF is gratefully acknowledged. C. B. acknowledges a PhD studentship cofunded by the ILL and University of Tübingen. O. M. acknowledges a PhD fellowship by the Studienstiftung des deutschen Volkes. L. B. acknowledges an ILL studentship to fund the research for her Diploma thesis carried out in the ILL spectroscopy group. F. R.-R. acknowledges funding from the Royal Physiographic Society of Lund. The authors thank the ILL-ESRF Partnership for Soft and Condensed Matter (PSCM, Grenoble) for sharing lab resources.References
- A. L. Lehninger, D. L. Nelson and M. M. Cox, Lehninger Principles of Biochemistry, W. H. Freeman, New York, 2005 Search PubMed.
- S. Timr, D. Madern and F. Sterpone, in Computational Approaches for Understanding Dynamical Systems: Protein Folding and Assembly, ed. B. Strodel and B. Barz, Progress in Molecular Biology and Translational Science, Academic Press, 2020, vol. 170, pp. 239–272 Search PubMed.
- J. Gunton, A. Shiryayev and D. Pagan, Protein Condensation: Kinetic Pathways to Crystallization and Disease, Cambridge University Press, 2007 Search PubMed.
- E. L. Opie, J. Exp. Med., 1962, 115, 597–608 CrossRef CAS PubMed.
- G. B. Benedek, Invest. Ophthalmol. Visual Sci., 1997, 38, 1911–1921 CAS.
- C. Kato and D. H. Bartlett, Extremophiles, 1997, 1, 111–116 CrossRef CAS PubMed.
- D. J. Kushner, Adv. Appl. Microbiol., 1968, 10, 73–99 CAS.
- A. Ventosa, J. J. Nieto and A. Oren, Microbiol. Mol. Biol. Rev., 1998, 62, 504–544 CrossRef CAS.
- P. Kanokratana, S. Chanapan, K. Pootanakit and L. Eurwilaichitr, J. Basic Microbiol., 2004, 44, 430–444 CrossRef PubMed.
- J. Smiatek, J. Phys. Chem. B, 2014, 118, 771–782 CrossRef CAS PubMed.
- J. K. Lanyi, Bacteriol. Rev., 1974, 38, 272–290 CrossRef CAS.
- R. Jaenicke, Eur. J. Biochem., 1991, 202, 715–728 CrossRef CAS PubMed.
- R. Jaenicke and G. Böhm, Curr. Opin. Struct. Biol., 1998, 8, 738–748 CrossRef CAS.
- D. Madern, C. Ebel and G. Zaccai, Extremophiles, 2000, 4, 91–98 CrossRef CAS.
- R. Sterner and W. Liebl, Crit. Rev. Biochem. Mol. Biol., 2001, 36, 39–106 CrossRef CAS PubMed.
- A. E. I. Coskun, D. Sağlam, P. Venema, E. van der Linden and E. Scholten, Food Hydrocolloids, 2015, 45, 291–300 CrossRef.
- S. Scheingraber, M. Rehm, C. Sehmisch and U. Finsterer, Anesthesiology, 1999, 90, 1265–1270 CrossRef CAS PubMed.
- D. S. Prough and A. Bidani, Anesthesiology, 1999, 90, 1247–1249 CrossRef CAS PubMed.
- C. Giancola, C. De Sena, D. Fessas, G. Graziano and G. Barone, Int. J. Biol. Macromol., 1997, 20, 193–204 CrossRef CAS PubMed.
- M. Yamasaki, H. Yano and K. Aoki, Int. J. Biol. Macromol., 1990, 12, 263–268 CrossRef CAS PubMed.
- K. Murayama and M. Tomida, Biochemistry, 2004, 43, 11526–11532 CrossRef CAS PubMed.
- M. Hennig, F. Roosen-Runge, F. Zhang, S. Zorn, M. W. A. Skoda, R. M. J. Jacobs, T. Seydel and F. Schreiber, Soft Matter, 2012, 8, 1628–1633 RSC.
- J. I. Boye, I. Alli and A. A. Ismail, J. Agric. Food Chem., 1996, 44, 996–1004 CrossRef CAS.
- A. Tobitani and S. B. Ross-Murphy, Macromolecules, 1997, 30, 4845–4854 CrossRef CAS.
- A. Tobitani and S. B. Ross-Murphy, Macromolecules, 1997, 30, 4855–4862 CrossRef CAS.
- J. Lefebvre, D. Renard and A. C. Sanchez-Gimeno, Rheol. Acta, 1998, 37, 345–357 CrossRef CAS.
- G. Barone, C. Giancola and A. Verdoliva, Thermochim. Acta, 1992, 199, 197–205 CrossRef CAS.
- V. Vetri, F. Librizzi, M. Leone and V. Militello, Eur. Biophys. J., 2007, 36, 717–725 CrossRef CAS PubMed.
- V. Militello, V. Vetri and M. Leone, Biophys. Chem., 2003, 105, 133–141 CrossRef CAS.
- V. Militello, C. Casarino, A. Emanuele, A. Giostra, F. Pullara and M. Leone, Biophys. Chem., 2004, 107, 175–187 CrossRef CAS PubMed.
- M. Bhattacharya, N. Jain and S. Mukhopadhyay, J. Phys. Chem. B, 2011, 115, 4195–4205 CrossRef CAS PubMed.
- M. Sogami and J. F. Foster, Biochemistry, 1968, 7, 2172–2182 CrossRef CAS PubMed.
- A. Del Giudice, C. Dicko, L. Galantini and N. V. Pavel, J. Phys. Chem. B, 2017, 121, 4388–4399 CrossRef CAS PubMed.
- A. Del Giudice, C. Leggio, N. Balasco, L. Galantini and N. V. Pavel, J. Phys. Chem. B, 2014, 118, 10043–10051 CrossRef CAS PubMed.
- M. Grimaldo, F. Roosen-Runge, F. Zhang, F. Schreiber and T. Seydel, Q. Rev. Biophys., 2019, 52, 1–63 CrossRef.
- F. Ameseder, A. Radulescu, M. Khaneft, W. Lohstroh and A. M. Stadler, Phys. Chem. Chem. Phys., 2018, 20, 5128–5139 RSC.
- F. Ameseder, A. Radulescu, O. Holderer, P. Falus, D. Richter and A. M. Stadler, J. Phys. Chem. Lett., 2018, 9, 2469–2473 CrossRef CAS PubMed.
- M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. Zhang, N. Jalarvo, M. Zamponi, F. Schreiber and T. Seydel, Phys. Chem. Chem. Phys., 2015, 17, 4645–4655 RSC.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS.
- P. Lindner and T. Zemb, Neutrons, X-rays, and Light: Scattering Methods Applied to Soft Condensed Matter, Elsevier, North-Holland, 2002 Search PubMed.
- P. Debye, Ann. Phys., 1915, 351, 809–823 CrossRef.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, Amsterdam, 2006 Search PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-ray and Neutron Scattering, Plenum Press, New York, 1987 Search PubMed.
- A. Guinier and G. Fournet, Small-angle scattering of X-rays, Wiley, New York, 1955, vol. 14 Search PubMed.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- E. Mircea Anitas, Nanomaterials, 2019, 9, 648 CrossRef CAS.
- K. Lieutenant, P. Lindner and R. Gähler, J. Appl. Crystallogr., 2007, 40, 1056–1063 CrossRef CAS.
- M. Könnecke, F. A. Akeroyd, H. J. Bernstein, A. S. Brewster, S. I. Campbell, B. Clausen, S. Cottrell, J. U. Hoffmann, P. R. Jemian and D. Männicke, et al. , J. Appl. Crystallogr., 2015, 48, 301–305 CrossRef PubMed.
- B. Frick, J. Combet and L. van Eijck, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 669, 7–13 CrossRef CAS.
- C. Beck, M. Grimaldo, F. Roosen-Runge, R. Maier, O. Matsarskaia, M. Braun, B. Sohmen, O. Czakkel, R. Schweins, F. Zhang, T. Seydel and F. Schreiber, Cryst. Growth Des., 2019, 19, 7036–7045 CrossRef CAS.
- F. Roosen-Runge and T. Seydel, EPJ Web Conf., 2015, 83, 02015 CrossRef.
- G. Zaccai, Science, 2000, 288, 1604–1607 CrossRef CAS PubMed.
- R. Zorn, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 603, 439–445 CrossRef CAS.
- J. Peters and G. R. Kneller, J. Chem. Phys., 2013, 139, 135102 Search PubMed.
- D. Zeller, M. T. F. Telling, M. Zamponi, V. García Sakai and J. Peters, J. Chem. Phys., 2018, 149, 234908 CrossRef CAS PubMed.
- F. Roosen-Runge, M. Hennig, T. Seydel, F. Zhang, M. W. Skoda, S. Zorn, R. M. Jacobs, M. Maccarini, P. Fouquet and F. Schreiber, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 68–75 CrossRef CAS PubMed.
- M. Grimaldo, F. Roosen-Runge, F. Zhang, T. Seydel and F. Schreiber, J. Phys. Chem. B, 2014, 118, 7203–7209 CrossRef CAS PubMed.
- F. Roosen-Runge, M. Hennig, F. Zhang, R. M. J. Jacobs, M. Sztucki, H. Schober, T. Seydel and F. Schreiber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11815–11820 CrossRef CAS PubMed.
- M. Grimaldo, H. Lopez, C. Beck, F. Roosen-Runge, M. Moulin, J. M. Devos, V. Laux, M. Härtlein, S. Da Vela, R. Schweins, A. Mariani, F. Zhang, J.-L. Barrat, M. Oettel, V. T. Forsyth, T. Seydel and F. Schreiber, J. Phys. Chem. Lett., 2019, 10, 1709–1715 CrossRef CAS PubMed.
- S. Magazu, F. Migliardo and A. Benedetto, J. Phys. Chem. B, 2010, 114, 9268–9274 CrossRef CAS PubMed.
- Institut Laue-Langevin DOI:10.5291/ILL-DATA.9-13-637.
- Institut Laue-Langevin DOI:10.5291/ILL-DATA.8-04-752.
- Institut Laue-Langevin DOI:10.5291/ILL-DATA.9-13-672.
- Institut Laue-Langevin DOI:10.5291/ILL-DATA.8-04-759.
| This journal is © the Owner Societies 2020 |