Chloride ions as integral parts of hydrogen bonded networks in aqueous salt solutions: the appearance of solvent separated anion pairs

Abstract

Hydrogen bonding to chloride ions has been frequently discussed over the past 5 decades. Still, the possible role of such secondary intermolecular bonding interactions in hydrogen bonded networks has not been investigated in any detail. Here we consider computer models of concentrated aqueous LiCl solutions and compute the usual hydrogen bond network characteristics, such as distributions of cluster sizes and of cyclic entities, both for models that take and do not take chloride ions into account. During the analysis of hydrogen bonded rings, a significant amount of ‘solvent separated anion pairs’ have been detected at high LiCl concentrations. It is demonstrated that taking halide anions into account as organic constituents of the hydrogen bonded network does make the interpretation of structural details significantly more meaningful than when considering water molecules only. Finally, we compare simulated structures generated by ‘good’ and ‘bad’ potential sets on the basis of the tools developed here, and show that this novel concept is, indeed, also helpful for distinguishing between reasonable and meaningless structural models.

---

Introduction

The term ‘hydrogen bonding’ (H-bonding) is traditionally connected to water and ice, where oxygen atoms form bonds with hydrogen atoms of neighboring water molecules by enhancing the electronic density between O and (nonbonded) H by the lone electron pairs of the O atoms.^1–3 The same mechanism works for many other compounds with hydroxyl (–OH) groups: examples are alcohols, organic acids, sugars, proteins, DNA, etc. However, hydrogen bonding is also responsible for the very strong links between the molecules of hydrogen fluoride, HF;^4,5 that is, hydrogen bonds (HBs) may be formed not only by oxygen, but also, by halogen atoms/halide ions (and even by nitrogen, cf. liquid ammonia, NH₃).⁶

The phenomenon of hydrogen bonding with halogen atoms/halide ions is, indeed, well documented in the literature; for instance, the crystal structure of hydrogen chloride hydrates was investigated using diffraction methods half a century ago.^7,8 A fairly large number of hydrogen bond distances to halide ions in crystals were reported a couple of decades ago.⁹ More recently, related investigations were published in ref. 10 and 11. Hydrogen bonding in chloride–water clusters has been considered by Xantheas,¹² and the dynamics of HBs have been studied, via molecular dynamics (MD) simulations, in aqueous solutions of halide ions.¹³

However, quite surprisingly, to the best of our knowledge, halide ions have never been considered as integral parts of the network of hydrogen bonds in aqueous solutions of, e.g., alkali halide salts. Indeed, most of the (faintly) related discussions in earlier papers have been about how ions actually break/disrupt the hydrogen bonding network of water molecules in these solutions (see, e.g., ref. 14–16). The traditional ‘structure making/structure breaking’ roles of ions¹⁷ also concern the issue of whether the presence of ions enhances or deteriorates the HB network of water molecules. What happens when hydrogen bonds between halide anions and water molecules are both treated as network formers has not yet been investigated.

There is a notable, qualitative difference between the ways chloride ions and O atoms of water molecules act as (electron) donors, while forming hydrogen bonds. Water molecules provide extra electron density by the lone electron pairs of their oxygen atoms, i.e., via localised electrons. The extra electron (providing the 1− negative charge) of the chloride ions, on the other hand, is distributed evenly over the ‘surface’ of the ion. This difference is the main reason why water oxygens can donate electrons to two (at most three) neighbouring H-atoms, whereas chloride ions can form 6(−7) hydrogen bonds^18,19 (without specific orientations). In other words, the number of H-bonds formed by chloride ions is limited by steric effects only. A brief demonstration, utilizing quantum mechanical calculations, of the notion that the Cl⋯H–O connection has the attributes of a standard H-bond can be found in the ESI.†

Here, we make use of some of the standard hydrogen bonding related analysis tools^20,21 applied recently to water–methanol,²² water–ethanol²³ and water–isopropanol²⁴ liquid mixtures. The main goal was to learn whether the ‘water molecules only’ (WO) (‘pure’) or the ‘chloride-included’ (CI) (‘mixed’) approach provides the more appropriate description of the hydrogen bonded network in concentrated aqueous LiCl solutions. For this reason, each descriptor of the H-bond network was determined both for the ‘WO’ and ‘CI’ situations. In what follows, a systematic comparison between WO and CI characteristics is provided.

Computational section

As all details of the computer simulations are identical to those that have already been published in detail,¹⁸ only a short summary is provided here (a more complete account can be found in the ESI†).

Classical molecular dynamics (MD) simulations, at 300 K in the NVT ensemble, were performed by the GROMACS software package (version 5.1.1).²⁵ The calculations were performed at a constant volume and temperature (NVT ensemble), at T = 300 K. Cubic simulation boxes were used with periodic boundary conditions. Four different concentrations of aqueous LiCl solutions (from 3.74 mol kg⁻¹ to 19.55 mol kg⁻¹) and pure water were investigated. Simulation boxes contained about 10 000 atoms. Box lengths were calculated according to the experimental densities. The numbers of ions and water molecules, densities, and box sizes are collected in Table 1.

Table 1 Aqueous LiCl solutions investigated: number of ions and water molecules, densities and simulation box sizes. Experimental densities are taken from ref. 26

Molality [mol kg^−1]	0	3.74	8.30	11.37	19.55
N LiCl	0	200	500	700	1000
N water	3333	2968	3345	3416	2840
Density [g cm^−3]	0.9965	1.076	1.1510	1.1950	1.2862
Number density [Å^−3]	0.0999	0.09735	0.0939	0.0919	0.0871
Box length [nm]	4.6425	4.5721	4.8982	5.0232	4.94102

---

Potential parameters applied in this study were chosen from the collection in ref. 19, where 29 force field models were compared according to their appropriateness for describing the structure of highly concentrated aqueous LiCl solutions. In the rest of this work, results obtained by using (one of) the best model(s), JC-S, a model of Joung and Cheatham, III,²⁷ are presented. For comparison, data from a ‘bad’ model, RM, a force field set of Reif and Hünenberger²⁸ are also shown. Several other models have also been tested: their potential parameters and results obtained are presented in the ESI,† along with a demonstration of the ‘goodness-of-fits’ with respect to the measured structure factors.²⁶

During the simulations water molecules were kept rigid by the SETTLE algorithm.²⁹ Coulomb interactions were treated by the smoothed particle-mesh Ewald (SPME) method,^30,31 using a 10 Å cutoff in direct space. The van der Waals interactions were also truncated at 10 Å, with added long-range corrections to energy and pressure.³²

Initial particle configurations were obtained by placing ions and water molecules randomly into the simulation boxes. Energy minimization was carried out using the steepest descent method. After that the leap-frog algorithm was applied for integrating Newton's equations of motion, using a time step of 2 fs. The temperature was kept constant by the Berendsen thermostat³³ with τ_T = 0.1 coupling. After a 4 ns equilibration period, particle configurations were collected at every 80 ps between 4 and 12 ns. The 101 configurations thus obtained were used for hydrogen bond analyses.

Hydrogen bonds (HBs) can be identified by several methods. The results presented here have been obtained by applying geometric considerations.³⁴ All calculations were repeated using the energetic definition of HBs:³⁴ findings of which are shown in the ESI.† According to the geometric definition, two water molecules are identified as H-bonded if the intermolecular distance between an oxygen and a hydrogen atom is less than 2.5 Å, and the O⋯O–H angle is smaller than 30 degrees. A chloride ion is considered to be H-bonded to a water molecule if the H⋯Cl⁻ distance is less than 2.8 Å and the Cl⁻⋯O–H angle is smaller than 30 degrees. According to the energetic definition, in addition to the criteria on the above O⋯H (Cl⁻⋯H) distance, the interaction energy between H-bonded molecules (molecule and ion) should be less than −3.0 kcal mol⁻¹.

Determination of H-bonded molecules and calculations concerning the H-bonded network were performed by an in-house programme, based on the HBTOPOLOGY code.²⁰

Before moving on to displaying and interpreting our present results, a short note is perhaps appropriate here concerning the possibility of applying not classical, but quantum computer simulations (‘ab initio molecular dynamics, AIMD’). Unfortunately, to the best of our knowledge, no relevant AIMD calculations have been performed for highly concentrated aqueous LiCl solutions. What is available for this electrolyte is a simulation with 64 water molecules and two ion pairs,³⁵ which means a concentration of about 3 molar % – whereas the lowest concentration in the present study is about twice that. Also, no direct comparison with measured structural data in the reciprocal space can be found in the corresponding AIMD papers and therefore, it is not possible to establish the relevance of the structural information derived from these high level simulation studies. Although this statement is valid for the thorough AIMD study of Gaiduk et al.¹⁶ on a (rather dilute) aqueous solution of NaCl, there is an issue in this AIMD work, which is relevant from the point of view of the present investigation. Gaiduk et al. discuss the effect of ions on the hydrogen bonded network of water molecules, and they seem to have had difficulty interpreting the role of chloride ions in this respect. What we show in the following is that such a difficulty transforms into a sensible explanation when chloride ions are considered not as modifiers, but as organic constituents of the network of H-bonds in such solutions.

Results and discussion

We wished to facilitate comparability with the literature by taking exactly the same salt concentrations as in previous, related works from our laboratory,^15,18,19,26 namely 3.74 m (mol kg⁻¹; corresponding to 6.3 molar%), 8.3 m (13 molar%), 11.37 m (17 molar%) and 19.55 m (26 molar%). In fact, the calculations providing the atomic assemblies (‘particle configurations’) were identical to those reported recently by one of us.¹⁸ Note that these concentration values are rather high, the highest one representing an ion/water ratio of about 50 : 75. The reason why such systems have been selected is the expectation that the role of the ions in enhancing/disrupting the hydrogen bonded network would be most apparent under such circumstances.

Simulation details, as well as a brief description of the geometric definition of hydrogen bonds used throughout are provided in the ‘Computational section’ (see above, and in the ESI†). Most importantly, H-bonded Cl⁻⋯H maximum distances are somewhat longer than those of O⋯H ones, as they are defined by the first minima of the Cl⁻–H and O–H partial radial distribution functions (see, e.g., ref. 15, 18 and 19). The potential model called ‘JC-S’ from ref. 19 is used below just to demonstrate the features of the ‘mixed’ H-bond network concept.

Cluster size distributions

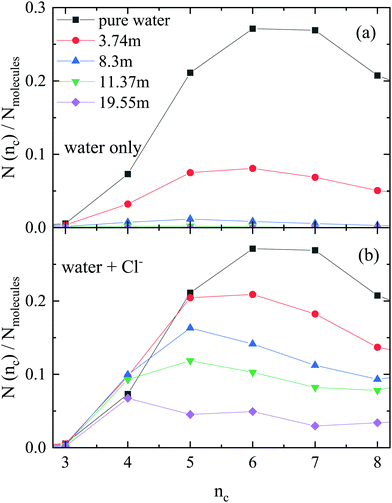
In order to characterize the extent of the H-bonded network, cluster size distributions (as defined in, e.g.ref. 20 and 21) were determined first; these are shown in Fig. 1. Robust hydrogen bonded networks, like those in most alcohol–water mixtures, percolate,^21,23,24i.e. the largest H-bonded cluster is comparable in its size with the system size. From Fig. 1 it is obvious that when chloride ions are not considered as ‘network formers’ then this criterion is fulfilled only for pure water and, to some extent, for the least concentrated LiCl solution. In the more concentrated solutions one can find only isolated water clusters, up to sizes of about 180 (11.37 m) or even only about 20 (19.55 m) molecules. That is, the H-bonded networks of water molecules are really small in comparison with the system size and also, such a picture would suggest a kind of ‘microphase separation’, debated quite hotly in the cases of alcohol–water mixtures.^36,37 On the other hand, when chloride ions are taken into account as parts of the network then cluster sizes are equal (within a few percent) to the cumulative number of water molecules and chloride ions.

Fig. 1 Cluster size distributions calculated for the same atomic configurations. (a) ‘WO’, water molecules only (no Cl⁻ ions in the H-bonded network). (b) ‘CI’, water molecules AND chloride ions (the vertical lines show the number of (a) water molecules and (b) Cl⁻ ions plus water molecules in the system). Note that when chloride ions are included, even the most concentrated systems percolate – which makes sense in a homogeneous solution.

Hydrogen bonded rings

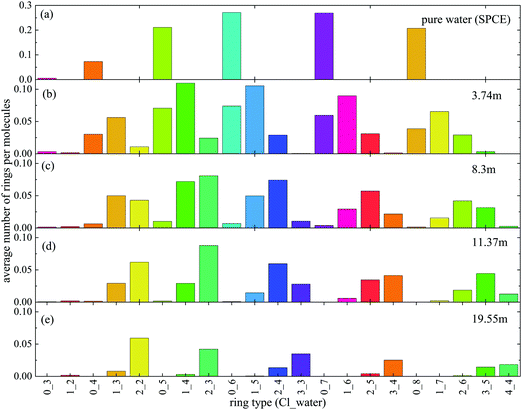
Next, the occurrence of H-bonded cyclic entities was scrutinized (Fig. 2). The number of purely water rings decreases dramatically with increasing ionic concentration, with hardly any cycles present above 8.3 m. On the other hand, there is a fair amount of ‘mixed’ cycles even at the highest ionic concentration when the anions are also counted (even though the number of H-bonded cycles decreases here also, when salt concentration is growing). Interestingly, the size of the rings also decreases with increasing concentration, so much so, that the most frequent ring size in the 19.55 m LiCl solution contains only 4 members.

Fig. 2 Size distributions of cyclic entities, as calculated for the same particle configurations, but (a) ‘WO’, without chloride ions, and (b) ‘CI’, with chloride ions in the H-bonded network. Note the trend: the number of rings decreases, and the rings become smaller, as salt concentration increases.

It is also instructive to investigate the ratio of water molecules and chloride ions in the ‘mixed’ cycles (Fig. 3). Contrary to what was observed in methanol–water liquid mixtures,²² the participation of ions in the H-bonded rings follows roughly the overall concentration of (an)ions in the solutions. Again, it is the most concentrated solution that exhibits the most spectacular feature: the most frequent cycle is the one that consists of two water molecules and two chloride ions (see Fig. 4 for representative parts of the particle configurations).

Fig. 3 Distribution of different types of rings (rings contain Cl⁻ ions and water molecules), normalized by the number of molecules (water + Cl⁻ ions), at different concentrations obtained from the JC-S model. Note that the scale of part (a) is different to that of the others.

Fig. 4 Snapshots of configurations obtained with a JC-S forcefield at concentrations of (a) m = 3.74 and (b) m = 19.55 mol kg⁻¹. Red, gray, purple and green balls represent oxygen, hydrogen, lithium and chlorine atoms, respectively. Some frequent ring types are highlighted, in part (a): (blue) 6-membered ring with 1 Cl⁻ ion and 5 water molecules, (magenta) 5-membered ring with 5 water molecules and (yellow) 6-membered ring containing 6 water molecules; in part (b) (blue) 4-membered rings with 2 Cl⁻ ion and 2 water molecules, (magenta) 5-membered ring with 2 Cl⁻ ions and 3 water molecules and (yellow) 6-membered ring containing 3 Cl⁻ ions and 3 water molecules.

The expectation is that no two chloride ions would be connected directly (it would not even be any kind of a ‘hydrogen bond’). Indeed, closer inspection reveals (cf.Fig. 4, part (b)) that a frequently occurring constellation is where there is one water molecule between two chloride ions: these motifs can be considered as ‘solvent separated anion pairs’. Even though the presence of such particle arrangements is not entirely unexpected (at least once the ‘mixed’ water/anion H-bonded network concept has been introduced), to the best of our knowledge, this is the first occasion when this phenomenon is detected in simulation models, and pictured in a very straightforward manner.

Two quick tests have been performed concerning these solvent separated anion pairs: (1) it has been verified that in a given solution, the H-bonding energy (calculated according to ref. 21, 23 and 24) of a Cl⁻⋯H–O hydrogen bond does not depend on whether this H-bond is a single one, or part of a solvent separated anion pair; (2) the lifetime (calculated according to ref. 24) of solvent separated anion pairs in a given solution is actually about two times that of a single (and also, solitary) Cl⁻⋯H–O bond. More details can be found in the ESI.†

So far, it has been shown that there are marked differences between the concepts of considering the ‘pure’ hydrogen bonded network of water molecules only, and that of a ‘mixed’ network that includes chloride ions, too. We believe that the latter provides a more appropriate characterization of a homogeneous liquid – and since no sign of any small angle scattering could be spotted on either the neutron or the X-ray data²⁶ we argue that however concentrated the solutions in question are, even the 19.55 m LiCl solution is homogeneous.

Utilization of the concept

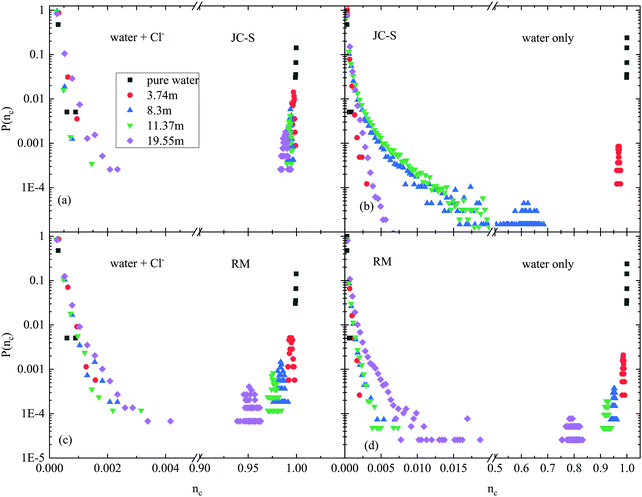
Next, we further demonstrate the usefulness of the ‘mixed’ concept by comparing ‘good’ and ‘bad’ potential models for aqueous LiCl solutions (cf.ref. 19). As a ‘good’ force field, the JC-S combination from ref. 19 was taken, that consists of the SPC/E water model³⁸ and the ionic parameters from ref. 27. The ‘bad’ example, called RM in ref. 19, contains SPC/E water molecules combined with ions as represented in ref. 28. The difference between the two force field combinations is that while the JC-S one reproduces experimental neutron and X-ray diffraction data very well, the RM combination fails to do so. Further details concerning potential parameters are provided in the ‘Computational section’.

Fig. 5 shows cluster size distributions for the JC-S and RM models, using both the ‘pure water’ and ‘mixed’ definitions of the H-bonded network. (Note that the presentation is more condensed here than it was in Fig. 1: on the ‘x’ axis, cluster size values are shown as normalized to the system size.) The difference between the two potential combinations is striking: while pure water H-bonded clusters are larger, mixed water-anion ones are smaller in the case of the ‘bad’ RM model. These observations are consistent with the notion that mixing of ions and water is far from perfect when the RM combination of force fields is applied, leading to a kind of (micro-)phase segregation, between water-rich and ion-rich regions. Please remember: the RM model cannot reproduce diffraction data appropriately, i.e. the behavior detected in Fig. 5 for this model cannot be related to the characteristics of the real system.

Fig. 5 Cluster size distributions calculated for the atomic configurations obtained from (a and b) JC-S and (c and d) RM models. (a and c) Water molecules and chloride ions. (b and d) Water molecules only (no Cl⁻ ions in the H-bonded network). (The x-axes are normalized with the number of (a and c) Cl⁻ ions plus water molecules, and (b and d) water molecules in the configurations.) Note that for the RM model, which was found to be one of the worst when comparing simulated and experimental total structural factors, cluster sizes with Cl⁻ ions (part (c)) appear to be smaller than the percolation limit, whereas pure water clusters (part (d)) are large even at high salt concentrations. This indicates non-perfect mixing (i.e.,‘microphase-segregation’ between water and salt), which is against the observation that all solutions considered are homogeneous.

When the composition of cyclic entities formed in the JC-S and RM structural models is compared (see Fig. 6), an analogous conclusion can be drawn: while in the ‘good’ JC-S structure H-bonded rings contain a number of Cl⁻ ions, which is in accordance with the overall concentration of ions, cycles in the ‘bad’ RM structure tend to contain far less anions than could be expected from the ionic concentration in the solutions. In the RM model, the overwhelming majority of rings are water-dominated even at the highest ionic concentration. This, again, is an indication that the RM combination of water and ion force fields does not lead to homogeneous structures.

Fig. 6 Distribution of different types of rings (rings contain Cl⁻ ions and water molecules), normalized by the number of molecules (water + Cl⁻ ions), at different concentrations, obtained from (b–e) JC-S and (g–j) RM models. The ring size distribution in pure water (a and f) is also shown for reference. Note the difference between the number of pure water rings (dominating in the ‘bad’ RM model, part (g–j)). Again, this shows the (inappropriate, if good solutions are present) tendency against mixing Cl⁻ ions and water molecules in the ‘bad’ model.

Conclusions

In summary, it has been demonstrated that the concept of a ‘mixed’ water-anion hydrogen bonded network provides a sensible characterization of highly concentrated chloride salt solutions. Percolating HB networks, with the participation of chloride ions, could be identified even in the most highly concentrated solution. The ‘mixed’ anion-water network can account for the homogeneity of such systems, contrary to what the ‘pure’ water network suggests. The concept may well appear to be helpful for interpreting earlier findings concerning hydrogen bonding networks of aqueous halide salt solutions (cf., e.g., ref. 14–16).

Concerning hydrogen bonded cyclic entities, the novel concept reveals that the participation of chloride anions in rings is proportional to the ionic concentration. Cycles containing 2 water molecules and 2 chloride ions have been found to be the dominant motifs at the highest salt concentration.

This approach has brought about the observation of ‘solvent separated anion pairs’ that are the dominant motifs in cyclic hydrogen bonded entities at high LiCl concentrations (see Fig. 3 and 4).

The characterization of, and the distinction between, ‘good’ and ‘bad’ potential models of aqueous LiCl solutions becomes very natural via the ‘mixed’ network concept: good models facilitate mixing of ions and water molecules at the atomic scale, whereas inappropriate force fields tend to result in separation of the solvent and solute (micro-)phases (cf.Fig. 5 and 6).

Further explorations are needed (and underway) to establish whether the ‘mixed’ water + halide ion hydrogen bonded network is a useful concept in general for discussing properties of highly concentrated aqueous solutions of (at least) alkali-halides. As a possible next step, we will first look at a situation where the counter-ion is the largest of the alkali cations, namely the case in CsCl solutions (for which experimental data are available from our group³⁹).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the National Research, Development and Innovation Office (NKFIH) of Hungary for financial support through Grants No. 124885 and KH130425.

References

1. G. Pimentel and A. McClellan, The Hydrogen Bond, Franklin Classics, 2018.
2. G. A. Jeffrey, An introduction to hydrogen bonding, Oxford University Press, New York, US, 1997.
3. Hydrogen_bond, https://en.wikipedia.org/wiki/Hydrogen_bond, accessed 17 December 2019.
4. P. A. Kollman and L. C. Allen, J. Am. Chem. Soc., 1970, 92, 753–759.
5. M. E. Cournoyer and W. L. Jorgensen, Mol. Phys., 1984, 51, 119–132.
6. D. D. Nelson, G. T. Fraser and W. Klemperer, Science, 1987, 238, 1670–1674.
7. J.-O. Lundgren and I. Olovsson, Acta Crystallogr., 1967, 23, 966–971.
8. J.-O. Lundgren and I. Olovsson, Acta Crystallogr., 1967, 23, 971–976.
9. T. Steiner, Acta Crystallogr., 1998, B54, 456–463.
10. M. V. Vener, I. Y. Chernyshov, A. A. Rykounov and A. Filarowski, Mol. Phys., 2018, 116, 251–262.
11. D. Braga, F. Grepioni and O. Shemchuk, CrystEngComm, 2018, 20, 2212–2220.
12. S. S. Xantheas, J. Phys. Chem., 1996, 100, 9703–9713.
13. S. Chowdhuri and A. Chandra, J. Phys. Chem. B, 2006, 110, 9674–9680.
14. A. K. Soper and K. Weckström, Biophys. Chem., 2006, 124, 180–191.
15. I. Harsányi and L. Pusztai, J. Chem. Phys., 2012, 137, 204503.
16. A. P. Gaiduk and G. Galli, J. Phys. Chem. Lett., 2017, 8, 1496–1502.
17. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370.
18. I. Pethes, J. Mol. Liq., 2017, 242, 845–858.
19. I. Pethes, J. Mol. Liq., 2018, 264, 179–197.
20. V. Chihaia, S. Adams and W. F. Kuhs, Chem. Phys., 2005, 317, 208–225.
21. I. Bakó, T. Megyes, S. Bálint, T. Grósz and V. Chihaia, Phys. Chem. Chem. Phys., 2008, 10, 5004.
22. I. Bakó, L. Pusztai and L. Temleitner, Sci. Rep., 2017, 7, 1073.
23. S. Pothoczki, L. Pusztai and I. Bakó, J. Phys. Chem. B, 2018, 122, 6790–6800.
24. S. Pothoczki, L. Pusztai and I. Bakó, J. Phys. Chem. B, 2019, 123, 7599–7610.
25. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
26. I. Harsányi, L. Temleitner, B. Beuneu and L. Pusztai, J. Mol. Liq., 2012, 165, 94–100.
27. I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041.
28. M. M. Reif and P. H. Hünenberger, J. Chem. Phys., 2011, 134, 144104.
29. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
30. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
31. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
32. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1987.
33. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
34. R. Kumar, J. R. Schmidt and J. L. Skinner, J. Chem. Phys., 2007, 126, 204107.
35. G. Cassone, F. Creazzo, P. V. Giaquinta, J. Sponer and F. Saija, Phys. Chem. Chem. Phys., 2017, 19, 20420–20429.
36. S. Dixit, J. Crain, W. C. K. Poon, J. L. Finney and A. K. Soper, Nature, 2002, 416, 829–832.
37. A. Perera, L. Zoranić, F. Sokolić and R. Mazighi, J. Mol. Liq., 2011, 159, 52–59.
38. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
39. V. Mile, L. Pusztai, H. Dominguez and O. Pizio, J. Phys. Chem. B, 2009, 113, 10760–10769.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01806f

---