Orientational ordering in heteroepitaxial water ice on metal surfaces
Abstract
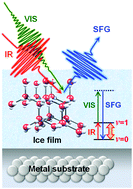
Heteroepitaxial growth of crystalline ice thin films of water on metal substrates under ultrahigh vacuum provides an excellent opportunity to investigate the interior and surface structures of crystalline ice that are closely related to their physicochemical properties. Here we present the spectroscopic studies of the orientational ordering and the surface relaxation of crystalline ice films grown on two representative metal surfaces: Pt(111) and Rh(111). A versatile tool for exploring these structures is sum frequency generation (SFG) vibrational spectroscopy; homodyne detection of SFG signals serves as a good measure of orientational ordering in the interior of crystalline ice films while heterodyne detection enables us to determine the direction of water molecules at the interface with metal substrates, in the interior of crystalline ice films, and at their surfaces. Water molecules on the wetting layer of Pt(111) are preferentially oriented in H-down configuration, and the configuration is passed along into the interior of crystalline ice films. In contrast, water molecules on Rh(111) are adsorbed in a mixture of H-down and H-up configurations, leading to orientationally disordered crystalline ice films. The inter-layer distance at the top of the surface is modulated alternately in accordance with the orientation of molecules hydrogen bonded to the bilayer underneath. Therefore, the molecular orientation also plays an important role in their surface relaxation.
- This article is part of the themed collections: PCCP Emerging Investigators, PCCP Perspectives and 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...