Hydrogen adsorption on In₂O₃(111) and In₂O₃(110)

Abstract

In₂O₃-Based catalysts have been measured to have a high activity for CO₂ hydrogenation to H₃COH. Here, we use density functional theory calculations with and without Hubbard-U corrections in combination with ab initio thermodynamics to investigate the dissociative adsorption of H₂ over In₂O₃(111) and In₂O₃(110). H₂ is found to dissociate heterolytically with a moderate barrier on both facets. Diffusion of hydrogen leads to the preferred homolytic adsorption configuration. Vacancy formation by water formation is thermodynamically preferred at high hydrogen coverages. Both surfaces are found to be hydroxylated at typical reaction conditions with the highest coverage predicted for In₂O₃(110). O 1s core level shifts are calculated for different coverages. The hydroxylated surfaces show two distinct shifts corresponding to different types of OH-groups. The presence of surface oxygen vacancies is not visible in the O 1s signatures. The results show that hydroxylation of the surfaces results in changes of the oxidation state of In-ions, which suggests that the redox properties on In₂O₃ are important for catalytic reduction of CO₂ to added value chemicals.

---

1 Introduction

The search for alternative energy solutions that reduce carbon emissions and facilitate the depart from fossil-fuels has accelerated during the last decades.^1–7 Catalytic conversion of CO₂ to methanol (H₃COH) is one proposed path for synthesis of a fuel with high energy density and simultaneous reduction of greenhouse emissions.^8–12 Conversion of CO₂ to methanol could ideally, if renewable energy sources are used during conversion, allow for a closed carbon-loop with a net-zero carbon emission production of a valuable fuel or stock chemical.^9–12

In₂O₃ has recently attracted significant attention as a viable catalyst for conversion of CO₂ to H₃COH.^13–21 In₂O₃ supported on ZrO₂ has been reported to be highly active and selective under industrially relevant synthesis conditions (T = 573 K, P = 50 Bar, H₂/CO₂= 4 : 1).¹³ Very recently, improved catalytic activity for this reaction was reported for Pd dispersed on In₂O₃.¹⁶ The increase in activity in ref. 16 was attributed to facile H₂ dissociation as compared to the case without Pd.

The degree of surface hydroxylation on In₂O₃(111) upon H₂ adsorption was investigated in ref. 14 Based on density functional theory (DFT) calculations, hydroxylation of the surface was suggested to be thermodynamically unfavorable at T = 573 K, P_H2= 0.96 Bar and Δμ_H2O = −2.0 eV, whereas creation of vacancies through water formation was calculated to be preferred.¹⁴ The relative thermodynamic stability of hydrogen adsorption was in ref. 14 investigated at a high hydrogen coverage with all oxygen atoms protonated together and H-atoms also on the In-sites.

Dissociation of H₂ on In₂O₃(111) has been investigated both experimentally and theoretically.^14–16 The apparent activation energy for H₂ dissociation was in ref. 14 measured to be 0.9 eV. The barrier for dissociation was calculated to be ∼0.85 eV on the pristine surface.^14–16 The presence of oxygen vacancies has been calculated to slightly reduce the barrier for dissociation.^14,16

In a recent study using DFT-calculations,²¹ it was suggested that activation of H₂ on pristine In₂O₃(110) is facile, with a barrier of only 0.3 eV. Moreover, it was proposed that the surface is heavily hydroxylated under typical reaction conditions (T = 573 K, P_H2 = 10–50 Bar). The calculations also indicated that oxygen vacancies are relevant only at high hydrogen coverages and that hydroxylation induces a change in oxidation-state of undercoordinated In-ions. Facile H₂ uptake on In₂O₃ has been measured at 300 K together with substantial surface reduction and reordering at higher temperatures.²² A change in oxidation state of the In-ions during CO₂ reduction to H₃COH has been measured using X-ray spectroscopy.²⁰

The different results reported for In₂O₃(110) and In₂O₃(111) may suggest that H₂ activation and surface hydroxylation depend on the surface orientation. However, the different coverages and thermodynamic conditions considered in the two studies^14,21 might influence the results. Thus, an investigation that accounts for different coverages is needed. Additionally, the DFT results on In₂O₃ surface properties reported so far in the literature^14–16,21 have been performed with the general-gradient approximation (GGA). The incomplete cancellation of the electron self-interaction in GGA is known to underestimate oxide band-gaps and give a spurious over-delocalization. Hubbard corrected (DFT+U) calculations are generally believed to describe better the electronic structure of metal-oxides, including In₂O₃.²³

Herein, density functional theory (DFT) with and without Hubbard-U corrections and ab initio thermodynamics are used to investigate the dissociative adsorption of H₂ on In₂O₃(111) and In₂O₃(110). The results suggest that surface hydroxylation is thermodynamically favorable under typical methanol synthesis reaction conditions, regardless of surface orientation. Hydroxylation is found to induces changes in the oxidation states of the In-cations. The O 1s core level shifts are evaluated to obtain spectroscopic signatures of different adsorbates. Comparison with experimental data suggests the presence of different OH-groups. The qualitative results are found not to depend on the inclusion of the Hubbard-U correction.

2 Computational details

Density Functional Theory (DFT) calculations are performed using the Vienna ab initio simulation package.^24–27 The Kohn–Sham orbitals are expanded with a plane wave basis, truncated at a kinetic energy of 500 eV. Projector augmented wave potentials (PAW) are used to describe the interaction between the valence electrons and the core.^28,29 Hydrogen, oxygen and indium are described with one, six and thirteen valence electrons, respectively. Thus, the valence of indium includes the 4d¹⁰ states. Integration over the Brillouin zone is approximated with finite sampling using the Monkhorst–Pack scheme.³⁰ A 3 × 3 × 3 and 3 × 3 × 1 k-point grid is used for the bulk and surface calculations, respectively. The exchange–correlation energy is calculated with the Perdew, Burke, Ernzerhof (PBE) formulation.³¹ Given the semi-local nature of the approximation, electronic self-interaction might cause artificial delocalization of the electronic states. To localize the In 4d electrons, the effect of a Hubbard correction is investigated.³² The value of the Hubbard correction U_eff (7 eV) is adopted from ref.23 where it was determined by calculations of the lattice constant and the position of the In 4d states. The performance of the chosen U-value is studied by comparative calculations using a functional including exact exchange.^33,34 The energies for oxygen vacancy formation and hydrogen adsorption are found to be in good agreement using the chosen U-value (see ESI†).

Convergence in energy is assumed when a criteria of 10⁻⁶ eV is reached for the electronic optimization. Structural optimization is performed with the use of the conjugate gradient method and convergence is assumed when forces are smaller than 0.01 eV Å⁻¹. Activation energies for H₂ dissociative adsorption and O_v formation are calculated with use of the climbing-image nudge elastic band (CI-NEB)³⁵ technique. Seven to ten images are used along the reaction coordinate to describe the minimum energy path. Vibrational frequency analysis is used to confirm the transition states. A force criteria of 0.05 eV Å⁻¹ is used for the transition states.

Both In₂O₃(111) and In₂O₃(110) are modelled with (1 × 1) surface cells. The surface slabs are described with five [(111)] and four [(110)] layers. The bottom two layers of the slab models are fixed to their bulk positions during the geometry optimizations. Barriers are calculated for a three layer system for (111) to reduce computational cost. The slabs are separated by at least 15 Å of vacuum. The bond length of H₂ in gas phase are calculated to be 0.75 Å, which is in good agreement with the experimental value of 0.74 Å.

To investigate the relative stability of surface hydroxylation and presence of oxygen vacancies at methanol synthesis conditions (573 K, 10–50 Bar, H₂/H₂O:10–50/1), we calculate the surface free energy (Δγ(T,p)) as a function of H₂ chemical potential (μ_H2(T,p)) using ab initio thermodynamics.^36,37 The surface free energy is computed according to:

where A is the area of the surface cell. E_H2/surf and E_prist are the zero-point corrected energies of the complete system and the pristine surface, respectively. N_Ov is the number of oxygen vacancies and N_H2 is the number of adsorbed hydrogen molecules. μ_H2(T,p) and μ_H2O(T,p) refer to the chemical potential of hydrogen and water, respectively. The term in parentheses accounts for the entropic gain of producing water in the gas-phase by creating an oxygen vacancy at the surface. The chemical potential of H₂ is calculated as:where E_H2 is the zero-point corrected energy of the H₂ molecule in gas phase. μ_H2′ is the reference chemical potential of H₂. This term accounts for the entropic contributions of H₂ in the gas phase and is taken from thermodynamic tables.³⁸ The last term accounts for the change in entropy with respect to the standard state. The chemical potential for H₂O is calculated similarly. The average hydrogen binding energy is calculated through:

Thus, a negative value indicates exothermic adsorption.

The O 1s core-level shifts (CLS) are calculated in reference to an O atom in the bulk of the slab:

E_CLS = E* − E_bulk* (4)

E* is the energy of the system of interest with a core hole and E_bulk* is the system with a core hole in the bulk of the slab. In this way, the calculated CLS includes final-state effects.³⁹ The core hole is created in this approach by removal of one 1s electron in the PAW potential. A net jellium background is added to maintain the number of electrons and charge neutrality of the super-cell. The use of a jellium background is needed when treating systems with a band-gap.⁴⁰

Charge analysis of the structures of interest is performed via Bader charges as implemented with the code developed by Henkelman and co-workers.⁴¹

3 Results and discussion

3.1 In₂O₃ bulk

The (110) and (111) surfaces have been constructed from the bixbyite (space group 206) bulk structure, which has 80 atoms in the unit cell. The bixbyite structure is composed of two types of six-fold coordinated In-ions, with oxygen being four-fold coordinated. Density functional theory calculation with the general-gradient approximation are know to spuriously delocalize electronic states on metal–oxides. Bulk structure was optimized both with PBE and PBE+U. We find the equilibrium lattice constant calculated with PBE [PBE+U] functional to be 10.299 [10.030] Å. The experimental value is 10.121 Å. The corresponding values for the band gap are 0.94 (PBE) and 1.77 eV (PBE+U), which are in agreement with previous reports using a similar approach.²³ The experimental band gap is 3.2 eV.⁴²

The effect of the Hubbard correction on the bulk electronic structure is visible in a Density of States (DOS) analysis, Fig. 1. With the PBE functional (top panel), the DOS is divided into three regions. The valence band spreads over approximately 5 eV and is mainly composed of O 2p states, with hybridization with some In 5s and In 5p. The second region, composed of mainly In 4d states with some hybridization with O 2s and O 2p states, is situated at an energy of approximately 11 eV below the Fermi energy and spans ∼2 eV. The third region, which is dominated by O 2s states is located at an energy of circa 17 eV below the Fermi energy. Applying the Hubbard-U correction (bottom panel) shifts the In 4d states in the second region to lower energies by approximately 2 eV and increases the spread of this region by ∼1 eV. In this way, the Hubbard-U correction places the 4d-states close to the experimental position.⁴³ Moreover, a higher degree of hybridization between the In 4d and O 2s states is observed in both the second and third region. The valence band, which is dominated by O 2p and In states, is only weakly affected by the Hubbard correction. The effect of the Hubbard-U correction on the electronic structure is consistent with previous reports.²³

Fig. 1 Density of states for bulk In₂O₃ using PBE and PBE+U.

3.2 In₂O₃(111) and In₂O₃(110)

Stoichiometric In₂O₃(111) and In₂O₃(110) surfaces were cleaved from the bulk structure at the theoretical equilibrium lattice constant. We calculate the surface free energy with PBE [PBE+U] to be 0.78 [1.04] and 1.05 [1.36] J m⁻² for (111) and (110), respectively. These results are in quantitative agreement with previous reports using a similar methodology.⁴⁴

The surface structures for In₂O₃(111) and In₂O₃(110) are shown in Fig. 2 and 3, respectively. The In₂O₃(111) surface is composed of stoichiometric layers, where each layer constitutes an O–In–O trilayer. In₂O₃(111) exhibits three slightly different geometric terminations, however, they are all energetically equivalent. The trilayer consist of an In-layer with 16 atoms sandwiched between two oxygen layers with 12 atoms in each. The In-atoms in the topmost layer can be grouped into six semi-equivalent types, labeled In_a–In_f in Fig. 2, while the oxygen can be grouped into four types, labeled O_a–O_d. In_b and In_d are six-fold coordinated to oxygen, whereas the rest have a five-fold coordination. The six-fold coordinated In-ions are present in one region of the (1 × 1) surface cell, giving rise to a heterogeneous surface. The oxygen atoms in the topmost layer are three-fold coordinated to indium, whereas the rest are fourfold coordinated. The bonds at the surface are expanded with respect to the bulk values. The tri-layer at the surface is on average expanded by about 0.06 Å.

Fig. 2 Structural model of In₂O₃(111). Top panel shows the oxygen and indium sites, labeled O_a–O_d and In_a–In_f. A ball and stick model is used to show the topmost layer, whereas the rest are presented by lines. The surface cell is shown by black lines. The bottom panel shows a side view of the slab, using the ball and sticks representation. Atomic color code: Indium (brown), oxygen (red).

Fig. 3 Structural model of In₂O₃(110). Top panel shows the oxygen and indium sites, labeled O₁–O₆ and In₁–In₄. A ball and stick model is used to show the topmost layer, whereas the rest are presented as lines. The (1 × 1) surface cell is indicated with black lines. The bottom figure shows a side view using the ball and stick representation. Atomic color code as in Fig. 2.

In similarity with In₂O₃(111), In₂O₃(110) consists of stoichiometric layers. The surface is composed of a repeating chain of four In-ions, In₁–In₄ in Fig. 3, and six oxygen, O₁–O₆. All atoms are non-equivalent in the repeating chain. There are 12 oxygen and 8 In-ions in each layer of the surface cell. In₁ and In₂ are four-fold coordinated to oxygen, whereas the rest are five-fold coordinated. All oxygen atoms in the topmost layer are three-fold coordinated to indium atoms. The relaxation for the In₂O₃(110) surface is more complex than for the In₂O₃(111) case. The topmost layer contracts on average by 0.14 Å, with respect to the bulk-constrained layer, whereas the second layer expands by ∼0.06 Å. The (110) orientation has two slightly different geometric terminations, which are energetically equivalent. In one case the O₃ and O₄ are on the same side of the In–O chain (as in Fig. 3), whereas they are on opposite sides in the other case.

The oxygen vacancy formation energy for the non-equivalent oxygen types is calculated for the two surfaces with PBE and PBE+U (see Table 1). We find that the energy to create an oxygen vacancy is systematically higher with PBE+U by about 1 eV. This shows that the In–O bond is stronger when the Hubbard correction is applied, which is consistent with the higher surface energy calculated with PBE+U. The higher stability of the (111) facet is manifested by higher vacancy formation energies as compared to (110).

Table 1 Oxygen vacancy formation energies calculated for non-equivalent oxygen sites in (110) and (111) with and without Hubbard correction. The oxygen vacancy of formation is calculated with respect to thermal desorption of O₂ into the gas-phase

	(110) (U = 0 eV)	(110) (U = 7 eV)		(111) (U = 0 eV)	(111) (U = 7 eV)
O1	1.97	2.84	Oa	2.81	3.81
O2	2.20	3.06	Ob	1.88	2.86
O3	2.47	3.20	Oc	2.65	3.61
O4	2.29	3.04	Od	2.15	3.15
O5	1.83	2.80	—	—	—
O6	1.74	2.69	—	—	—

---

3.3 Surface hydroxylation

The relative stability of In₂O₃(111) and In₂O₃(110) as a function of hydrogen chemical potential (μ_H2) is investigated with the use of ab initio thermodynamics. For In₂O₃(111), nine different situations are considered (See Fig. 4), namely the pristine surface, five hydrogen coverages, one oxygen vacancy in the pristine surface, and two hydrogen coverages in the presence of a vacancy. The coverage is defined as the percentage of oxygen atoms in the topmost layer being occupied with hydrogen. Hence, 16% coverage corresponds to dissociating one H₂ molecule homolytically.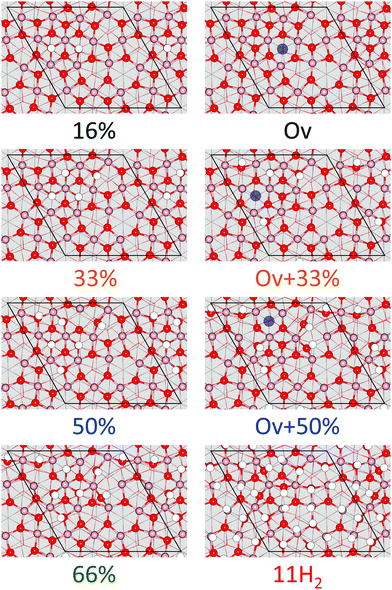

Fig. 4 Structural models of In₂O₃(111) with and without oxygen vacancies for different hydrogen (white) coverages. Atomic color code as in Fig. 2. Position of oxygen vacancy is highlighted as a purple circle in the relevant structures.

The number of possible hydrogen configurations are high at low coverages. To reduce the computational cost, we explored different situations at 16% coverage using a three layer system and only the PBE functional. For In₂O₃(111), we find that adsorption on the O_b–O_b pair to be preferred, with an adsorption energy of −2.70 eV. This is followed by the O_b–O_d and O_b–O_c, with adsorption energies of −2.30 and −1.98 eV, respectively. The adsorption energy at O_d–O_a, O_d–O_c, O_a–O_a and O_a–O_c are calculated to be −1.78, −1.68, −1.46 and −1.38 eV, respectively. A similar trend is found for heterolytic adsorption, where average adsorption energy on In_e–O_b site is −0.63 eV, followed by In_e–O_d (−0.32 eV), In_c–O_c (−0.23 eV) and In_f–O_a (−0.26 eV). The trends in adsorption energies show that the Ob and Od are more reactive to hydrogen adsorption than are Oc and Oa. The exothermicity in the adsorption is found to be inversely correlated to the oxygen vacancy formation energy (See Table 1). It should noted that the most reactive adsorption sites, O_b and O_d, are bonded to the sixfold coordinated In-ions, see Fig. 2.

Based on the experience for the 16%-case, we explored four-five different configurations for the higher hydrogen coverages. It was found that hydrogen preferably adsorbs close to the six-fold coordinated In-atoms. The results demonstrates the heterogeneity of the surface with two regions having different chemical properties. This has been noted previously in connection to water adsorption for In₂O₃(100)⁴⁴ and In₂O₃(111).⁴⁵ The difference in reactivity of the oxygen atoms has been correlated with the proximity of their O 2p states with respect to the valence band maximum.⁴⁵

The OH-groups that are formed upon hydrogen adsorption are at higher coverages (≥50%) displaced from the original oxygen position occupying bridge sites between two In-ions. This is an effect of the increased oxygen ionic radii upon the change in formal charge by hydroxylation. The displacement by hydrogenation has been reported previously for In₂O₃(110).²¹

The average hydrogen adsorption energy is −2.59, −1.69, −1.10, −1.22, −0.75, −0.87 and −0.25 eV for 16%, 33%, 33% + O_v, 50%, 50% + O_v, 66% and 100% covered, respectively. It should be noted that the adsorption of hydrogen takes place on different oxygen sites as the coverage is increased. For 16% coverage, the stable configuration is hydrogen adsorbed on O_b sites. In case of 33% coverage, all O_b sites are occupied together with one O_d site. Finally, all O_b and all O_d sites are occupied at 50% coverage. Once the O_b and O_d are occupied, increased stability of adsorption can only be achieved at high hydrogen pressures (Δμ_H2 > 0). This is the case of the 66% covered surface, where the preferred site for adsorption is a O_a–O_c pair (see in Fig. 4).

On In₂O₃(110), seven cases of hydrogen coverage are considered of which one case is investigated with an oxygen vacancy. The corresponding surface structures are shown in Fig. 5. The average hydrogen adsorption energy is −2.24, −1.65, −1.34, −1.44, −1.41, −1.24 and −1.14 eV for 16%, 50%, 66%, 83%, 83% + O_v, 92% and 100% coverage, respectively. The average binding energies on (110) surface are less affected by increasing hydrogen coverage than on the (111) surface. This is rationalized by the higher reactivity of the (110) surface.

Fig. 5 Structural models of In₂O₃(110) with and without oxygen vacancies for different hydrogen (white) coverages. Atomic color code as in Fig. 2. Position of oxygen vacancy is highlighted as a purple circle in the relevant structures.

The stability of the hydrogen covered surfaces as a function of hydrogen chemical potential at methanol synthesis conditions (573 K, H₂/H₂O:10–50/1) is shown in Fig. 6. The surface free energy is calculated with respect to the pristine surface, indicated as a dashed line at zero energy. The chemical potential corresponding to H₂ partial pressure of 10–50 bar is highlighted in the figures as a purple fringe. Partial pressure of water, relevant for the O_v reduced surfaces, is set to 1 bar. The phase diagram in Fig. 6 (a) shows that the (111) surface is predicted within PBE to be hydroxylated (33% covered) at relevant conditions. The hydroxylation of the surface as a function of hydrogen chemical potential proceeds from a pristine surface, to a 16% at a chemical potential of −2.32 eV, to 33% at −0.52 eV until reducing to O_v + 33% at −0.18 eV. The relevant hydrogen chemical potential at methanol synthesis conditions covers the span from −0.33 to −0.25 eV (10–50 bar), suggesting a hydrogen coverage close to 33% at reaction conditions. Note that the mean coverage does not take the heterogeneity of the surface into account. In fact, at 50% coverage, all oxygen sites close to the six-fold coordinate In atoms are hydrogen covered.

Fig. 6 Surface stability of In₂O₃(111) and In₂O₃(110) as a function of hydrogen chemical potential (μ_H2) and Hubbard parameter at a temperature of 573 K. The results are calculated with respect to the pristine surface at zero energy. Experimental conditions, P_H2 = 10–50 bar, are indicated by a purple fringe. Water chemical potential is set at a pressure of P_H2O = 1 bar. Labels are color-coded in accordance to Fig. 4.

The O_v + 33% covered surface is found to be close in stability to the hydroxylated surface. If a lower partial pressure of water (0.1 Bar) is considered, this surface becomes isoenergetic with the only hydroxylated surface at a chemical potential of −0.30 eV. This results suggest that oxygen vacancies may exist when the surface is hydrogen covered. We find that vacancies on the pristine surface are thermodynamically unfavorable.

The phase diagram for In₂O₃(110) (PBE) is shown in Fig. 6(b). The (110) surface is predicted to be slightly reduced and heavily hydroxylated (83% + O_v) at all relevant reaction conditions. Surface hydroxylation as a function of hydrogen chemical potential proceeds from the pristine surface, to a 16% at −1.98 eV, to 50% at −1.08 eV, to the mildly reduced 83% + O_v at −0.87 eV, well before methanol synthesis conditions are reached. The stability of oxygen vacancies is clearly promoted by a high hydrogen coverage unlike the In₂O₃(111) surface.

The phase diagrams for (111) and (110) calculated with the Hubbard correction are shown in Fig. 6(c) and (d), respectively. (The adsorption energies are reported in the ESI.†) The relative stabilities of all hydrogen coverages are shifted by ∼0.9 eV with respect to the PBE results. The trends are, however, not affected by the choice of functional. On the (111) surface, we find that hydroxylation at 16% is favorable at reaction conditions. The hydroxylated surface becomes thermodynamically favorable over the pristine surface at a hydrogen chemical potential of −1.37 eV and remains the preferred phase up to zero chemical potential. The presence of oxygen vacancies are destabilized when the Hubbard-U correction is applied. From the phase diagram of the (110) surface, Fig. 6(d), we observe a similar behaviour as on the (111) surface. The favorable surface coverage is the 50% covered case. The hydroxylation proceeds similarly as with PBE, however, with transitions occurring at higher chemical potentials and reaching a lower overall hydrogen coverage. Hydroxylation proceeds from the pristine surface, to a 16% at −1.25 eV, to 50% at −0.33 eV, to 83% at −0.11 eV. As for the (111) surface, the creation of an oxygen vacancy at the surface becomes unfavorable with the Hubbard-U correction. The destabilization of the surface upon oxygen vacancy formation is consistent with the increased Ov formation energy (Table 1).

A Bader charge analysis is performed on In₂O₃(111) within PBE. The Bader charge for an In-ion in the In₂O₃ bulk is 11.17 electrons, which should be compared to the number of valence electrons being 13. The formal oxidation state is +3, which gives that the Bader analysis yields 0.61 electrons per formal charge. The charge on the pristine surface is 11.23, which is close to the bulk value. The oxidation state of the In-ions changes marginally in the presence of an oxygen vacancy, Fig. 7(a). Changes are instead calculated when the surface is hydroxylated. The charge on two In-ions change to 12.12 and 12.06 electrons in the case of 33% + O_v. Fig. 7(b). This change corresponds to a formal change in oxidation state to +1. The results suggest that the vacancies alone do not reduce the In-ions, but allow for undercoordination that facilitates a change of the charge upon hydroxylation.

Fig. 7 Bader charge analysis of relevant In₂O₃(111) structures. Charge localization is shown in dark blue. The charge on the pale blue atoms is about ± 0.1 e. Hydrogen atoms are shown in white. A vacancy is indicated by a red circle.

On the 50% covered structure, Fig. 7(c), charge of a single In_e changes from 11.24 to 12.16 electrons, whereas the rest of the atoms change within 0.1 electrons. Similarly, on the 66% structure, Fig. 7(d), we find a greater degree of surface reduction. At this coverage the charge of two In_e and a In_f changes upon hydroxylation in the same way as the 50% covered structure. The change in oxidation state is structurally observable in the change of In–O and In–In distance and leads to the creation of adsorbed OH groups in bridge position between neighboring In-ions.

A bond valence sum analysis^46,47 of the charged In_e at 50% shows a change from 2.79 in the pristine surface to 0.96 upon hydroxylation. The charge and BVS analysis suggest a change in oxidation state from +3 to close to +1 for the reduced In-ions, in agreement with previous reports on change of oxidation state upon hydroxylation on In₂O₃(110).²¹ The results are in agreement with the change of oxidation state of In-ions during reaction.²⁰ A charge analysis was also performed with Hubbard correction, with similar results.

3.4 H₂O formation by H₂ adsorption

A reaction mechanism for dissociative adsorption of H₂ is examined on the pristine (111), Fig. 8 (a), and (110), Fig. 8(b). Two possible routes are considered after H₂ heterolytic dissociation, (i) Hydroxylation of the surface to make OH* + OH* and (ii) water formation by oxygen vacancy creation (O_v + H₂O*), where H₂O is adsorbed on the surface. On (111), we find that the first step of the reaction, heterolytic dissociative adsorption, has a barrier of 0.48 eV. This step is exothermic by 0.58 eV with respect to H₂(g). From here, InH + OH, the reaction path splits into homolytic adsorption or H₂O formation. For path (i) we find that forming two OH-groups is exothermic by 1.62 eV with respect to the InH + OH state. The process has a barrier of 0.78 eV. For path (ii) we find that the creation of an oxygen vacancy is exothermic by 0.50 eV with respect to the heterolytic adsorption and has a barrier of 0.73 eV. The barriers of both path (i) and (ii) on In₂O₃(111) is associated with the diffusion of hydrogen over the In-ion. The two transition states are geometrically similar. The effect of an oxygen vacancy was also investigated for the H₂ dissociative adsorption. We find that the vacancy has an almost negligible effect on the activation energy, as it reduces the barrier by 0.1 eV.

Fig. 8 Relative energy landscapes for H₂ dissociative adsorption and H₂O formation on In₂O₃(111) and In₂O₃(110).

The barrier for H₂ dissociation in the pristine surface is slightly lower than reported previously.¹⁶ This can be attributed to different paths for dissociation, which in ref. 16 was chosen to be homolytic. Our result for dissociation over the vacancy is similar to the one reported in ref. 16. The barrier for H₂ dissociation on the pristine surface is in quantitative agreement with a previous investigation following heterolytic dissociative adsorption.⁴⁸ This is also the case for the formation of adsorbed water on the surface. However, we find a slightly lower energy barrier for the formation of two OH groups at the surface.⁴⁸

Heterolytic dissociation into InH + OH is on the (110) surface exothermic by 1.18 eV with respect to the initial state, having a barrier of only 0.31 eV. For path (i), we find that the formation of OH* + OH* is exothermic by 0.88 eV with respect to the initial InH + OH configuration. The formation of two OH-groups is associated with a barrier of 1.02 eV. The higher barrier as compared to (111) is due to a stronger hydride bond on (110). For Path (ii), we find that the formation of water and an O_v at the surface is endothermic by 0.08 eV with respect to the heterolytically dissociated hydrogen, with an energy barrier of 0.62 eV. The lower energy barrier for water formation can be explained by structural arguments as a shorter elongation of the In–H bond at the transition state is required in the formation of the H₂O than for the two OH-groups.

Similarly to In₂O₃(111), the heights of the barriers on the (110) appear to be related to the energy penalty for hydrogen diffusion over the In-ion. Our results are in quantitative agreement with a previous report.⁴⁸ We note that the calculated activation energies are moderate for the experimental conditions (573 K, 10–50 Bar) and that there is no thermodynamic driving force to form oxygen vacancies on any of the investigated surfaces.

It is experimentally known that H₂ may reduce In₂O₃ surfaces.^13,20,22 Our results show that a reduction of the surface requires a certain coverage of hydrogen. The phase diagram in Fig. 6, shows that structures with vacancies are competitive at a coverage of 0.33 and 0.83% for In₂O₃(111) and In₂O₃(110), respectively.

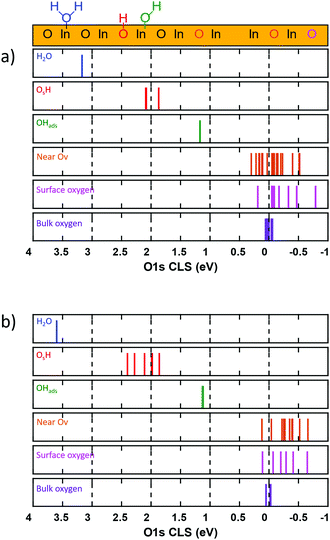
3.5 Hydrogen induced O 1s core-level shifts

The chemical properties and degree of surface hydroxylation of In₂O₃ have been investigated previously using O 1s X-ray photoelectron spectroscopy.^13,49,50 The measured O 1s spectrum has been deconvoluted into three main features,¹³ namely lattice oxygen (530.3 eV), signatures of oxygen vacancies (531.7 eV) and surface OH-groups (532.5 eV). Here we evaluate the O 1s core level shift for different oxygen species with respect to oxygen atoms in the bulk of In₂O₃, see Fig. 9.

Fig. 9 Calculated O 1s core-level shifts for In₂O₃(111) and In₂O₃(110). Top panel: O 1s CLS of In₂O₃(111), OH species are investigated at 16% hydrogen coverage. Bottom panel: O 1s CLS of In₂O₃(110), OH species are investigated at 16% hydrogen coverage.

For In₂O₃(111), Fig. 9(a), we find a slight energetic spread (0.1 eV) of the calculated O 1s CLS on the bulk oxygen. As bulk In₂O₃ in the bixbyite 206 phase has only one unique oxygen atom, the spread is caused by the finite thickness of the slab and can be viewed as the uncertainty of the computations arising from the structure. We find a significant spread in the O 1s CLS for the surface atoms, ranging from 0.18 to −0.73 eV, with respect to the bulk average. The semi-equivalent oxygen atoms have the same O 1s CLS, showing that these oxygen sites are chemically equivalent. For the topmost oxygen layer, we calculate the O 1s CLS for O_a, O_b, O_c and O_d to be −0.08, −0.73, −0.05 and −0.43 eV, respectively. It should be noted that the O-atoms bonded to the six-fold coordinated In-ions (O_b) have a clear shift of the O 1s binding energy to lower energies. The oxygen atoms in the bottom of the In₂O₃(111) topmost trilayer, can be grouped into four groups of semi-equivalent oxygen (see supporting information). The calculated O 1s CLS for these groups are −0.28, −0.14, −0.04 and 0.18 eV, respectively. The results for the bulk and surface oxygen suggest that measurements of the O 1s spectrum of the pristine surface should have a broad feature close to the value for oxygen in the bulk.

To investigate the effect of an oxygen vacancy on the O 1s CLS on neighbouring surface oxygen, we created and oxygen vacancy in the O_b site and calculated the CLS on the remaining oxygen atoms in the topmost layer. We find that the presence of oxygen vacancies does not change significantly the O 1s binding energies for the remaining oxygen atoms. The calculated O 1s CLS for the oxygen atoms close to the O_b oxygen vacancy spans energies from 0.29 to −0.49 eV. We do not find any general trend of the small shifts induced by the vacancy and the chemical equivalency for the different types of O-sites is virtually maintained (see ESI†). The largest effect of the O_v on the surface oxygen is calculated for the O_b and O_d sites. The average calculated O 1s CLS for these sites are −0.48 and −0.25 eV, respectively. The energy span for surface oxygen near an O_v is roughly within the same energy spread as surface oxygen on the pristine, making these sites indistinguishable oxygen sites originating from a pristine surface.

We also investigated the effect of hydrogen adsorption on the O 1s CLS of the formed species. We find that adsorbed hydrogen gives rise to two distinct OH features. OH_ads, which refers to an OH group adsorbed on an In-ion, obtained from H₂O dissociation, has a CLS of 1.27 eV. O_sH, which refers to OH groups with oxygen in a lattice position, has an O 1s CLS of 1.96–2.11 eV. The difference in O–In bonds for the two OH species rationalizes the difference in binding energy. For reference, we calculated the O 1s CLS for adsorbed molecular H₂O, which was found to be 3.30 eV.

For In₂O₃(110), Fig. 9(b), the results are similar to the (111) surface. A seven layered surface was used to calculate accurate O 1s CLS. We find that the bulk oxygen O 1s CLS spans also in this case has a span of 0.1 eV. The surface oxygen, calculated on the pristine surface, show a spread in the calculated CLS, ranging from 0.06 to −0.59 eV. The calculated O 1s CLS for O₁, O₂, O₃, O₄, O₅ and O₆ is −0.26, −0.18, 0.06, −0.11, −0.35 and −0.59 eV, respectively. The results suggest, similarly to the (111) surface, that the measured O 1s spectra should have a broadening around the binding energy for lattice oxygen. The effect of oxygen vacancies on neighbouring O-sites is investigated by removing an O₃ site from the topmost layer of the surface. We find that the O_v induce a minor shift to lower binding energies for neighboring oxygen. The calculated O 1s CLS near an O_v for O-sites in the same chain [and contiguous chain] for O₁, O₂, O₃, O₄, O₅ and O₆ are calculated to be, −0.39 [−0.25], −0.47 [−0.22], O_v [0.05], −0.40 [−0.10], −0.38 [−0.22] and −0.64 [−0.48] eV, respectively.

Similarly to the (111), the O 1s shift for oxygen near an O_v is within the same energy spread as surface oxygen on the pristine, suggesting that the effect of O_v on neighbouring O-sites would be difficult to detect. Also for this surface, we investigated the effect of hydrogen adsorption on the surface oxygen. The results are qualitatively the same as for In₂O₃(111). Two OH features are clearly distinguished. For OH_ads, we calculated the O 1s CLS to be 1.21–1.27 eV, with respect to the bulk reference, whereas the O 1s CLS for O_sH is calculated to be 1.82–2.39 eV. The shift for molecular water on the (110) is calculated to be 3.64 eV.

The results suggest that the experimentally assigned¹³ peak at 531.7 eV could be assigned to adsorbed OH groups on In-ions. Moreover, the peak assigned at 532.5 eV is probably caused to the presence of OH groups in the oxygen lattice position. The CLS were also calculated with Hubbard U-correction, and are in qualitative agreement to the ones without the U-correction (see ESI†).

4 Conclusions

We have used density functional theory calculations to investigate hydrogen adsorption on In₂O₃(111) and In₂O₃(110). The degree of surface hydroxylation has been investigated and O 1s core level shifts calculated for representative structures. The calculations have been performed with PBE as well as PBE augmented with a Hubbard-U correction to the In 4d states.

Dissociative hydrogen adsorption is found to be facile, occurring via a heterolytic dissociation mechanism. Thermodynamic analysis suggests that surface hydroxylation is favorable under experimentally relevant conditions. Moreover, presence of oxygen vacancies is predicted to become thermodynamic relevant upon hydroxylation. Surface hydroxylation is, moreover, found to induce a change of oxidation state, from +3 to close to +1, on surface In-ions on both surfaces.

Calculations of O 1s core level shifts suggest the existence of two distinct types of OH groups on the In₂O₃ catalyst. Furthermore, we do not find any clear spectroscopic signature originating from oxygen vacancies. The calculated CLS are in good agreement with previous XPS measurements.

The Hubbard correction is found to accurately describe bulk characteristics with respect to experimental observations of the In 4d states. We find that the oxygen vacancy formation energies to be higher when the Hubbard-U term is used. Similarly, the adsorption strength of hydrogen is lowered with the Hubbard-U correction. However, the trends in surface stability upon hydroxylation as well as the calculated O 1s CLS, and change of oxidation state upon hydroxylation, are in qualitative agreement with the PBE results. Comparisons with reference calculations including exact exchange, suggest that calculations with a Hubbard-U correction provide a better description of the surface electronic properties than standard PBE calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Knut and Alice Wallenberg Foundation through the project “Atomistic design of catalysts” (No: KAW 2015.0058) is gratefully acknowledged. Additional support has been obtained from Swedish Research Council and Swedish Energy Agency. The calculations have been performed at C3SE (Göteborg), Uppmax (Uppsala) and PDC (Stockholm) through a SNIC grant.

Notes and references

1. M. Dresselhaus and I. Thomas, Nature, 2001, 414, 332–337.
2. M. D. Porosoff, B. Yan and J. G. Chen, Energy Environ. Sci., 2016, 9, 62–73.
3. W. Li, H. Wang, X. Jiang, J. Zhu, Z. Liu, X. Guo and C. Song, RSC Adv., 2018, 8, 7651–7669.
4. T. Reichenbach, K. Mondal, M. Jaeger, T. Vent-Schmidt, D. Himmel, V. Dybbert, A. Bruix, I. Krossing, M. Walter and M. Moseler, J. Catal., 2018, 360, 168–174.
5. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
6. M. Hus, D. Kopac and B. Likozar, ACS Catal., 2019, 9, 105–116.
7. S. Kattel, P. Liu and J. G. Chen, J. Am. Chem. Soc., 2017, 139, 9739–9754.
8. J. Artz, T. E. Mueller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504.
9. A. Goeppert, M. Czaun, J.-P. Jones, G. K. S. Prakash and G. A. Olah, Chem. Soc. Rev., 2014, 43, 7995–8048.
10. G. A. Olah, G. K. S. Prakash and A. Goeppert, J. Am. Chem. Soc., 2011, 133, 12881–12898.
11. G. A. Olah, A. Goeppert and G. K. S. Prakash, J. Org. Chem., 2009, 74, 487–498.
12. G. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639.
13. O. Martin, A. J. Martin, C. Mondelli, S. Mitchell, T. F. Segawa, R. Hauert, C. Drouilly, D. Curulla-Ferre and J. Perez-Ramirez, Angew. Chem., Int. Ed., 2016, 55, 6261–6265.
14. D. Albani, M. Capdevila-Cortada, G. Vile, S. Mitchell, O. Martin, N. Lopez and J. Perez-Ramirez, Angew. Chem., Int. Ed., 2017, 56, 10755–10760.
15. M. S. Frei, M. Capdevila-Cortada, R. Garcia-Muelas, C. Mondelli, N. Lopez, J. A. Stewart, D. C. Ferre and J. Perez-Ramirez, J. Catal., 2018, 361, 313–321.
16. M. S. Frei, C. Mondelli, R. Garcia-Muelas, K. S. Kley, B. Puertolas, N. Lopez, O. V. Safonova, J. A. Stewart, D. C. Ferre and J. Perez-Ramirez, Nat. Commun., 2019, 10, 3377.
17. J. Ye, C. Liu and Q. Ge, J. Phys. Chem. C, 2012, 116, 7817–7825.
18. J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306.
19. C.-Y. Chou and R. F. Lobo, Appl. Catal., A, 2019, 583, 117144.
20. A. Tsoukalou, P. M. Abdala, D. Stoian, X. Huang, M.-G. Willinger, A. Fedorov and C. R. Mueller, J. Am. Chem. Soc., 2019, 141, 13497–13505.
21. A. Posada-Borbón and H. Grönbeck, Phys. Chem. Chem. Phys., 2019, 21, 21698–21708.
22. T. Bielz, H. Lorenz, W. Jochum, R. Kaindl, F. Klauser, B. Kloetzer and S. Penner, J. Phys. Chem. C, 2010, 114, 9022–9029.
23. P. Erhart, A. Klein, R. G. Egdell and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153205.
24. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
33. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
34. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
35. G. Henkelman, B. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904.
36. K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 035406.
37. Q. Sun, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 205424.
38. P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook, NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, http://webbook.nist.gov, 2005, Online; Accessed 3-December-2018.
39. E. Pehlke and M. Scheffler, Phys. Rev. Lett., 1993, 71, 2338.
40. M. V. den Bossche, N. M. Martin, J. Gustafson, C. Hakanoglu, J. Weaver, E. Lundgren and H. Grönbeck, J. Chem. Phys., 2014, 141, 034706.
41. G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360.
42. A. Walsh, J. L. F. Da Silva, S.-H. Wei, C. Koerber, A. Klein, L. F. J. Piper, A. DeMasi, K. E. Smith, G. Panaccione, P. Torelli, D. J. Payne, A. Bourlange and R. G. Egdell, Phys. Rev. Lett., 2008, 100, 1674021.
43. A. Klein, Appl. Phys. Lett., 2000, 77, 2009–2011.
44. P. Agoston and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045311.
45. M. Wagner, P. Lackner, S. Seiler, A. Brunsch, R. Bliem, S. Gerhold, Z. Wang, J. Osieck, K. Schulte, L. A. Boatner, M. Schmid, B. Meyer and U. Diebold, ACS Nano, 2017, 11(11), 11531–11541.
46. I. D. Brown, Chem. Rev., 2009, 109, 6858–6919.
47. J. A. Enterkin, A. E. Becerra-Toledo, K. R. Poeppelmeier and L. D. Marks, Surf. Sci., 2012, 606, 344–355.
48. B. Qin and S. Li, Phys. Chem. Chem. Phys., 2020, 22, 3390–3399.
49. L. B. Hoch, T. E. Wood, P. G. O'Brien, K. Liao, L. M. Reyes, C. A. Mims and G. A. Ozin, Adv. Sci., 2014, 1, 1400013.
50. T. Yan, L. Wang, Y. Liang, M. Makaremi, T. E. Wood, Y. Dai, B. Huang, A. A. Jelle, Y. Dong and G. A. Ozin, Nat. Commun., 2019, 10, 2521.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01749c

---