Critical evaluation of anharmonicity and configurational averaging in QM/MM modelling of equilibrium isotope effects

Abstract

Anharmonic effects upon vibrational frequencies and isotopic partition function ratios are modelled computationally by means of quantum mechanics/molecular mechanics (QM/MM) methods for two systems. First, the methyl cation in explicit water is considered using a B3LYP/6-31+G(d)/TIP3P method in order to check the previous prediction of an inverse equilibrium isotope effect (EIE) K_H3/K_D3 for transfer from vacuum to water at 298 K. A full QM/MM treatment including Lennard-Jones interactions predicts significantly inverse contributions from both internal (0.843 ± 0.001) and external (0.894 ± 0.001) modes of the solute. This treatment yields a much larger harmonic EIE (0.753 ± 0.002, averaged over 928 independent solvent configurations) than is obtained either by projecting out the translational and rotational contributions (0.853) or by treating the solvent by a point-charge representation (0.9360 ± 0.0006, harmonic; 0.9366 ± 0.0006, anharmonic). The contribution of anharmonicity to the EIE affects the value only in the 3rd significant figure. Second, anharmonicity is investigated by means of QM/MM potential-energy scans along 12 normal modes for internal and external vibrations of methyl cation in water and for three modes (one stretching and two bending) for the H_α atom at the carbenium-ion centre in cyclopentyl, cyclohexyl, tetrahydrofuranyl and tetrahydropyranyl cations in explicit water and cyclohexane solvents, as obtained by means of atomic Hessian analysis.

---

Introduction

Equilibrium isotope effects (EIEs) are ubiquitous in chemistry, biology, geology and the environmental sciences, determining fractionation of isotopologues between different chemical environments and providing valuable information about, for example, ambient temperatures in paleoclimatology or the authenticity and origin of wines and spirits.¹ In physical and mechanistic organic chemistry, EIEs may seem less glamorous than kinetic isotope effects (KIEs) but they are important for at least two reasons. First, an observed KIE for a multistep process is the product of EIEs for preceding steps and the KIE for the rate-determining step. Second, the EIE for a reaction is often used to interpret the KIE for the same reaction in terms of the position of the transition state along the reaction coordinate from reactants to products.

A well-known consequence of CH bond anharmonicity is that the average carbon-deuterium bond is shorter than the average carbon-protium bond, because the greater reduced mass of the oscillator involving the heavier isotope causes the zero-point vibrational energy level to be lower.² This leads to a slightly different vibrationally averaged electron distribution within the anharmonic potential energy well which can cause isotopic differences in electrostatic interactions. Some time ago, an anomalous trend in the values of secondary deuterium EIEs K_H/K_β-D6 calculated for gas-phase heterolyses of a range of 2-propyl substrates with different leaving groups X:

(CH₃)₂CHX + (CD₃)₂CH⁺ ⇌ (CD₃)₂CHX + (CH₃)₂CH⁺

was interpreted³ by a computational model employing standard rigid-rotor harmonic-oscillator approximations.² Anharmonic frequencies were not required. However, for the following reason, it was pointed out⁴ that it was an oversimplification to have asserted that the calculated EIE did not require an explanation based on anharmonicity: a change in the harmonic force constant for a vibration may be understood as arising from the effect of a perturbation (in this case due to changing the X group) acting upon the anharmonic potential and altering both the position of the energy minimum and the curvature at the minimum.⁵ The same point was recently reiterated⁶ in response to an assertion that there is no contribution of an inductive effect to secondary deuterium isotope effects upon acidity,⁷ and it sparked a controversy.^8,9

(CH₃⁺)₁ + (CD₃⁺)_ε ⇌ (CH₃⁺)₁ + (CD₃)_ε

More recently we investigated the sensitivity of the EIE K_H3/K_D3 for transfer of methyl cation from vacuum (subscript 1) to a dielectric continuum of varying relative permittivity (subscript ε). The trend towards inverse EIEs (<1) for transfer to a highly polar medium (e.g. ε = 80) predicted by B3LYP/aug-cc-VDZP calculations with the polarizable continuum model (PCM), using a molecule-shaped cavity, was confirmed by the average EIE determined from quantum mechanics/molecular mechanics (QM/MM) simulations employing the AM1 semi-empirical Hamiltonian and the TIP3P potential for a box of ∼2000 explicit water molecules.¹⁰ Subsequently we evaluated anharmonic corrections to vibrational frequencies and isotopic partition function ratios (IPFRs) for methyl-cation isotopologues in vacuum and in implicit water.¹¹ Comparing two methods (B3LYP and MP2) and three basis sets (6-31+G(d), cc-aug-PVDZ, cc-aug-PVQZ), calculated anharmonic frequencies were better than unscaled harmonic frequencies, but scaled harmonic frequencies were better still for less cost. Moreover, whereas both the scaled and unscaled harmonic frequencies provided reasonable estimates of the EIEs for methyl-cation transfer from vacuum to PCM ‘water’, the anharmonic PCM calculations gave erratic results.

Very recently we calculated the harmonic EIE K_H/K_D for transfer of two oxacarbenium cations (tetrahydrofuranyl, THF and tetrahydropyranyl, THP) and their carbocyclic congeners (cyclopentyl, CP and cyclohexyl, CH) from water to cyclohexane by means of QM/MM modelling with explicit solvent.¹² Atomic Hessian analysis, whereby the full Hessian was reduced to the elements belonging to a single atom at the site of isotopic substitution, revealed a remarkable result: the influence of the solvent environment on the EIEs was essentially captured completely by only a 3 × 3 block of the Hessian, although these values needed to reflect correctly the influence of the whole environment.

We wish to establish robust computational protocols for calculating both EIEs and KIEs for reactions in condensed media by means of QM/MM methods. As part of this larger project, we need to know whether the harmonic approximation is adequately fit for purpose. Furthermore, we need to know how many explicit solvent configurations must be considered in order to obtain reliable average isotope effects. This paper reports computational modelling of anharmonic effects upon vibrational frequencies and IPFRs for two systems. First, we consider the methyl cation in explicit water using a DFT/MM method, in order not only to check our previous prediction of an inverse K_H3/K_D3 for transfer from vacuum to water, but also affordably to generate many configurations to assess errors in averaging. Second, we present an analysis of anharmonicity in all 12 normal modes of methyl cation in explicit water and in C_αH stretching and bending modes for the carbenium-ion centre in cyclopentyl (CP), cyclohexyl (CH), tetrahydrofuranyl (THF) and tetrahydropyranyl (THP) cations in explicit water and cyclohexane solvents.

It is worth noting at the outset that the methyl cation does not exist as a discrete intermediate in aqueous solution as there is a negligible barrier to nucleophilic addition of a water molecule to form protonated methanol. It is a well-known fact in organic chemistry that methyl substrates undergo nucleophilic substitution only by the concerted S_N2 and never by the stepwise S_N1 mechanism which would involve methyl cation as an intermediate. The computational simulation reported here is possible only because the water is treated by a classical potential which prevents the electronic reorganisation required for covalent bond formation. To the best of our knowledge, there have been no published experimental reports of microsolvated CH₃⁺ in gaseous water clusters, let alone in bulk solution (although rare-gas microsolvated clusters CH₃⁺·Rg_n, where Rg = He, Ne, Ar, have been reported),¹³ so it is not possible to make any comparison between our predicted results and experiments. Similarly, the secondary carbocations CP, CH, THF and THP are likely to have very short lifetimes in water; our computational simulations for the methoxymethyl cation in water have estimated its lifetime as about 1 ps,¹⁴ which would be too short to allow for experimental determination of EIEs.

Computational methods

Outline of methodology

In view of the relative complexity of the methods described in detail below, and the subtlety of the differences between “QM relaxation and anharmonic frequencies” and “QM/MM relaxation and harmonic frequencies” it is useful to illustrate the plan of the calculations schematically (Fig. 1).

Fig. 1 Outline plan of methodology for QM and QM/MM computations on methyl cation in water.

Initial set-up

The fDynamo^15,16 library was used for all molecular dynamics (MD) and QM/MM work, in combination with the Gaussian 16 program¹⁷ for DFT calculations.¹⁸ B3LYP/6-31+G(d) optimized coordinates for methyl cation were inserted into the centre of a pre-equilibrated cubic box of side length of 31.40 Å containing 1034 TIP3P¹⁹ water molecules. Two solvent molecules whose oxygen atom were within 2.8 Å of the carbon atom were deleted; this radius corresponds to the first peak in the radial distribution function of water. Although a polarisable MM force field might, in principle, be better than a non-polarisable one, none is implemented in fDynamo and so TIP3P was employed, as in many previous instances; the lack of polarizability may be mitigated to some extent by ensemble averaging over many configurations of the MM environment.

Classical MD

A 100 ps MD simulation was performed to equilibrate flexible solvent around a frozen solute. For the methyl cation, electrostatic potential (ESP) derived atomic charges were obtained from the DFT optimisation, and Lennard-Jones parameters for C_sp² and H as in benzene. The MD employed the Langevin-Verlet algorithm with a 1 fs time-step within the NVT ensemble and periodic boundary conditions at 298 K. A 1 ns production MD trajectory was propagated with the same settings, and the coordinates of 1000 solvated configurations were extracted at 1 ps intervals.

QM/MM relaxation and QM anharmonic frequencies

Subsequently, for each snapshot the MM water molecules were frozen and a B3LYP/6-31+G(d) Broyden–Fletcher–Goldfarb–Shanno (BFGS) relaxation for all 12 degrees of freedom of the methyl cation within its solvent cage was performed. At each iteration of the fDynamo BFGS optimization algorithm, a single-point Gaussian 16 gradient evaluation was performed within the field of the point-charges of the MM atoms, and the resulting ESP charges and gradients for the QM atoms were combined with the charges and Lennard-Jones non-bonded potentials of the solvent atoms in fDynamo to determine the next geometry for the QM solute within its MM environment. Although it might have been adequate to have employed the BFGS optimizer within Gaussian 16, within the point-charge representation of its frozen MM solvent environment (see below), it was convenient instead to use the QM/MM interface between fDynamo and Gaussian to ensure the inclusion of solute–solvent Lennard-Jones interactions at this stage. Anharmonic B3LYP/6-31+G(d) frequency calculations were performed for the 6 internal modes of both CH₃⁺ and CD₃⁺ for each converged structure (r.m.s. gradient < 0.5 kJ mol⁻¹ Å⁻¹) within the point-charge environment of the frozen solvent configuration by means of a program relax_anharmonic (ESI†); Gaussian keywords “charge” and “freq = anharmonic” were used. Note that anharmonic frequencies for the 6 external degrees of freedom of the methyl cation could not be computed within Gaussian 16 unless a much larger QM region had been employed, which would have unnecessarily included an anharmonic treatment of solvent vibrations. Gaussian anharmonic frequencies use Barone's second-order perturbative treatment which uses a finite difference method in the directions of the normal modes to obtain all the third and a subset of the fourth derivatives.^20,21

Partition functions from Gaussian 16

The partition functions for translation (t), rotation (r) and vibration (v) together with zero-point energies (z) were extracted directly from the Gaussian 16 outputs for both harmonic and anharmonic frequencies and used to evaluate average QM IPFRs 〈f〉 according towhere n is the number of converged structures; a script Qanh was written for this purpose (ESI†).

Block averaging

The IPFRs from the converged structures were considered as varying along the duration of the original MD trajectory. If there were a significant degree of autocorrelation, these values would not be independent of each other, and the true error would be underestimated. In order to obtain a better estimate of the standard error (SE) in the mean value of the IPFR, the method of block averaging was employed.²² The total number of converged structures was divided into N_b blocks each of length L_b. The average IPFR was calculated for each block yielding N_b values for 〈f〉_i, with i = 1,…, N_b. The block length was gradually increased, and the set of block averages was recalculated for each length, and for each value of L_b the standard deviation σ_L among the block averages was used to calculate a running estimate of the overall block standard error (BSE):

BSE(f, L_b) = σ_L/N_b^1/2 (3)

when L_b is small (and N_b is large), consecutive blocks may be significantly correlated. But when this block length is substantially greater than the correlation time in the IPFR values, then BSE should cease to vary with L_b and should give a reliable estimate of the true SE, provided that N_b is not too small.

QM/MM harmonic frequencies

The same previously converged structures were then each subjected to a further round of BFGS energy minimisation in the fDynamo/Gaussian combination; the only difference was a small change in the values of the outer and inner non-bonded cut-off distances. Subsequent Hessian calculations used the full hybrid B3LYP/6-31+G(d)/TIP3P potential and yielded 12 harmonic frequencies for the methyl cation within the frozen solvent configuration of each converged structure. Together with the atomic masses and Cartesian coordinates, these were used to obtain molecular partition functions q as products of vibrational factors (including zero-point energy) from which IPFRs were obtained by means of eqn (1) as implemented in the UJISO program from the SULISO suite of utilities.²³

The product over all the modes can be factorized into sub-products over internal and external modes.

The use of a cubic box might introduce some anisotropy into these solute relaxations and Hessian determinations. However, this long-range anisotropy is unlikely to influence significantly the isotopic sensitivity of solute frequencies which are affected mainly by short-range anisotropies within the first and second coordination spheres of the surrounding explicit water.

Equilibrium isotope effects

The average value of the EIE for transfer of methyl cation from vacuum to water is obtained as the quotient of the vacuum IPFR and the average aqueous IPFR.

〈EIE〉 = f_vacuum/〈f_water〉 (6)

QM/MM normal modes for other carbocations

The same procedure as above was used for QM/MM simulations of THF, THP, CP and CH cations in water. For cyclohexane solution, a cubic box of side length of 45.13 Å containing 512 molecules was constructed by means of the Packmol program.²⁴ fDynamo was used with OPLS-AA parameters^25,26 (standard atom types for saturated C and H) to perform initial L-BFGS-B energy minimization (1000 steps) followed by 100 ps of MD at 298 K to equilibrate the solvent box. AM1 optimized coordinates for each cation were inserted into the centre of the solvent box, and all solvent molecules possessing a non-hydrogen atom within a specified distance of any non-hydrogen atom of the cation were deleted. Energy minimization (1000 steps, as above) of flexible solvent, treated by OPLS-AA force field, around frozen cation solute, treated by AM1 Hamiltonian,²⁷ was followed by 100 ps MD simulation (as above). For the final structure of each simulation, the cation geometry was relaxed with the MM solvent molecules being frozen, and the Hessian matrix of Cartesian force constants was determined, resulting in 3N non-zero vibrational frequencies for an N-atomic solute.

QM/MM potential-energy scans along normal modes

The 12 eigenvectors obtained by diagonalization of the mass-weighted B3LYP/6-31+G(d)/TIP3P Hessian for methyl cation in explicit water were transformed from Cartesians to local symmetry coordinates by means of a modified version (ESI†) of our CAMVIB program.²³ Vibrational assignment was performed by inspection of internal- and external-coordinate components of the normal modes, together with visualisation of finite displacements along these modes. A single-point full QM/MM energy evaluation was made for incremental displacements of 0.02 Å along the vibrational trajectory (±0.4 Å from the equilibrium position) for each mode. Only the four atoms of the QM methyl cation were moved, within a rigid solvent environment. A single solvated configuration chosen from the final 10% of the MD trajectory, for a structure whose ³H₃ IPFR was almost the same as the overall mean value.

Atomic Hessian analysis and normal-mode scans

The Hessians for the THF, THP, CP and CH cations have dimensions of 36 × 36, 45 × 45, 42 × 42 and 51 × 51, respectively. Deletion of all rows and columns, except for those belonging to the H_α atom at the site of isotopic substitution, gave a 3 × 3 matrix in each case which, when mass-weighted and diagonalized in the usual way, yielded three non-zero eigenvalues and three corresponding eigenvectors. Inspection of these normal modes enabled their assignment as “stretching” along the C_α–H_α axis and “bending” in and out of the plane of the carbenium center at C_α. For each cation in each solvent, a rigid QM/MM potential-energy scan was performed (as above) for incremental displacements of 0.02 Å along the vibrational trajectory (±0.4 Å from the equilibrium position) for the three vibrational modes of the H_α atom.

Results and discussion

QM anharmonic frequencies and isotope effects

Relaxation of snapshot structures. 930 converged structures were obtained for the B3LYP/6-31+G(d) methyl cation embedded within “frozen” configurations of 1032 TIP3P water molecules, each being a “snapshot” extracted at 1 ps intervals from a 1 ns MD trajectory for flexible water surrounding a fixed-geometry methyl cation. Each unconverged structure displayed either a highly non-planar or a dissociated geometry. The mean value of the total QM/MM energy for the methyl cation in its aqueous environment, over all the converged structures, was −104 107 kJ mol⁻¹ with a SE of about 0.001%; there is no trend in the total energy with time (Fig. S1; (tables and figures labelled with “S” are in the ESI†)).

QM evaluation of harmonic and anharmonic frequencies and IPFRs

B3LYP/6-31+G(d) calculated harmonic and anharmonic fundamental frequencies for methyl cation within the point-charge representation of its frozen MM solvent environment were obtained for all converged structures. Some of the CH-stretching frequencies for individual structures are presented in Table S1, ESI.† The mean symmetric-stretch frequency, averaged over all the structures, is 3112 ± 13 cm⁻¹ (harmonic) and 3000 ± 13 cm⁻¹ (anharmonic), and the individual values are linearly correlated: ω_anh = 0.955ω_harm + 26 (r² = 0.997). The formal degeneracy of the asymmetric CH stretching frequencies is split by the instantaneous asymmetry of the aqueous environment. The average magnitude of this splitting (15 cm⁻¹) is the same as the standard deviation about the mean frequency for each individual mode. The harmonic and anharmonic frequencies, taken together for this quasi-degenerate pair of modes, are linearly correlated: ω_anh = 1.063ω_harm − 353 (r² = 0.998), as shown in Fig. 2.

Fig. 2 Correlation of B3LYP/6-31+G(d) anharmonic ω_anh and harmonic ω_harm fundamental frequencies (as wavenumbers/cm⁻¹) for relaxed methyl cation within the point-charge representation of its frozen MM solvent environment for all converged structures. Blue dots: symmetric CH-stretch frequencies. Black and red dots: respectively, higher- and lower-valued frequencies for quasi-degenerate asymmetric CH-stretches.

The Gaussian output for anharmonic frequency calculations does not assign frequencies to specific vibrational modes, but simply presents them in descending order of magnitude. Although the symmetric and quasi-degenerate asymmetric CH-stretching frequencies are clearly distinguishable and occur in the same order, this is not so for the three bending modes (in-plane scissoring and rocking, and out-of-plane wagging), which unfortunately are not in the same order for all structures. The scatter plot for the bending modes displays overlapping bands that cannot easily be deconvoluted into individual correlations (Fig. S2, ESI†).

Some of the partition functions for individual structures are presented in Table S2, ESI.† The mean value of the IPFR for the 6 external degrees of freedom of the methyl cation, i.e. translation and rotation (f_ext = f_trans × f_rot), was 3.718, with a SE of <±3 × 10⁻⁵% (Table 1 and Table S2, ESI†). The mean value of the IPFR (f_vib) for excitation (relative to the zero-point vibrational energy level) of the 6 internal degrees of freedom was very small for both harmonic and anharmonic frequencies: respectively 1.015 and 1.016, also with SE of about ±0.001%. As expected, the dominant factor was zero-point energy, which gave mean IPFR values (f_zpe) of 6782 and 5462 for harmonic and anharmonic frequencies, respectively, with SEs of <± 0.1% (Table S2, ESI†). The larger value for the harmonic treatment arises directly from the higher values of the harmonic frequencies as compared with the anharmonic frequencies. The product of f_vib and f_zpe is f_int, and the product of this with f_ext yields the total IPFR (Table 1).

Table 1 IPFRs (²H₃, 298.15 K) for B3LYP/6-31+G(d) methyl cation in TIP3P water, averaged over 930 solvent configurations, and in vacuum, together with the EIE for transfer from vacuum to water

	f ext	Harmonic		Anharmonic
		f int	f total	f int	f total
Mean	3.718124	6886	25 603	5552	20 642
SD	0.000026	131	487	110	409
SE	0.000001	4	16	4	13
BSE			22		18
Vacuum	3.718162	6352	23 966	5183	19 272
EIE	1.000010	0.9360	0.9360	0.9336	0.9336
SE			0.0006		0.0006

---

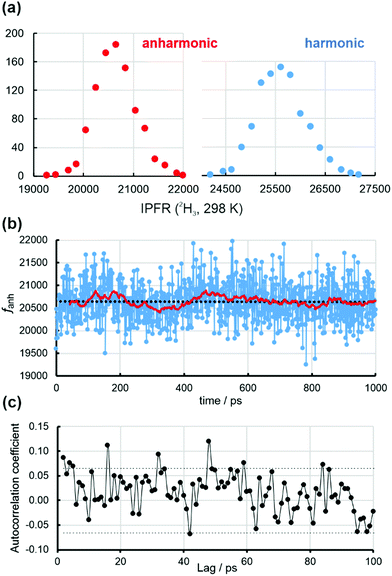
Fig. 3(a) shows distributions of anharmonic and harmonic (²H₃, 298 K) IPFRs for B3LYP/6-31+G(d) methyl cation embedded in point-charge representations of 1032 water molecules in solvent configurations extracted at 1 ps intervals from a 1 ns classical MD trajectory. The 930 structures gave a range of IPFR values that were divided into bins of width 200; this procedure yielded 15 and 16 bins for the anharmonic and harmonic distributions, respectively. The abscissa is the mean value of the IPFR within each bin. Both distributions are essentially normal, suggesting that the structures for which they are evaluated are independent. The IPFR values determined from the anharmonic and harmonic frequencies are linearly correlated (Fig. S5, ESI†):

(f_total)_anh = 0.838(f_total)_har − 217 (r² = 0.997) (7)

Fig. 3 (a) Distributions of anharmonic and harmonic (²H₃, 298 K) isotopic partition function ratios for B3LYP/6-31+G(d) methyl cation embedded in point-charge representations of 1032 water molecules in solvent configurations extracted at 1 ps intervals from a 1 ns classical MD trajectory. A bin width of 200 was used in each case, and the abscissa is the mean value of the IPFR within each bin. (b) Anharmonic isotopic partition function ratio (f_anh) for 930 converged structures of methyl cation within “frozen” solvent configurations along the trajectory. The black dotted line is a linear regression which shows a negligible trend across the whole series. The red solid line is the moving average for the preceding 40 values. (c) Plot of the autocorrelation function of the anharmonic IPFR for varying values of the lag. The dotted lines are the upper and lower bounds of the 95% confidence limit.

Fig. 3(b) displays the ordered series of anharmonic IPFRs, along with a linear regression (black dotted) line through all 930 values. There is a negligible trend, equivalent to <0.1% across the whole series, but with a correlation coefficient of <0.0002. The solid red line traces a simple moving average: each point is the mean of the preceding 40 values. This indicates that there are slight upward and downward trends over shorter time periods within the first half of the trajectory. Fig. 3(c) is the correlogram for the anharmonic IPFRs which suggests that there is almost no significant memory between values for structures separated by even very small time-lags. There is a complete lack of any correlation between the harmonic IPFRs and the total energies of the structures (Fig. S6, ESI†).

The block-averaging technique (Table 1, Tables S4, S5 and Fig. S8, S9, ESI†) indicates that a reliable estimate of the BSE in the mean values of f_total is about ±18 (anharmonic) and ±22 (harmonic) (these values are in Table 1), slightly greater than the SEs obtained by straight averaging over 930 values (Table 1). These values correspond to N_b (number of blocks) = 58, L_b (blocksize) = 16 (Tables S4 and S5, ESI†) and, if this were taken as the number of independent (average) IPFR values, would imply a correlation time of about 17 ps. Note that the slow Debye relaxation time of water at 298 K is about 8 ps, corresponding to collective molecular motions involving structural reorganisation of the hydrogen-bonding network.^28,29

QM evaluation of harmonic and anharmonic EIEs

The quotient (f_total)_vacuum/〈(f_total)_water〉 is the average value of the EIE K(CH₃)/K(CD₃) for transfer of methyl cation from vacuum to water (Table 1). An inverse value is predicted by both the harmonic (0.9360) and anharmonic (0.9366) treatments of the vibrational frequencies, in qualitative agreement with the result of the previous AM1/TIP3P study which considered a much smaller number of configurations.¹⁰ The SE in the EIE, as estimated from the BSE in the mean value of 〈(f_total)_water〉, is ±0.0008 (i.e. <±0.1%). Note that the harmonic and anharmonic EIEs differ by three times the magnitude of the probable error and may therefore be considered as distinctly different values. However, it may be argued that the effort involved in computing anharmonic frequencies is unjustified; we have suggested previously that use of a uniform scaling factor for harmonic frequencies is a more efficient means by which to make an approximate correction for anharmonicity.¹¹

The reason for the inverse EIE is that the three bonds in the methyl cation are each stiffer in water than in vacuum: the B3LYP/6-31+G(d) CH stretching force constant, averaged over three bonds in the first 122 solvated configurations in the point-charge representation of water, is 5.78 aJ Å⁻², as compared with 5.62 aJ Å⁻² in vacuum (Table S3, ESI†). This confirms the qualitative correctness of the result predicted by the PCM method with a molecule-shaped (UFF) cavity within the continuum treatment of water, in contrast to the result of using PCM with a spherical (UA0) cavity.¹⁰

Fig. 4(a) shows the variation in the EIE (²H₃, 298 K) for transfer of B3LYP/6-31+G(d) methyl cation from vacuum into water. Owing to the inverse relationship between this EIE and the aqueous IPFR, and the fact that the IPFR in vacuum is a constant value, the trend in the EIE across the whole series of structures is negligible, as noted above for the IPFR, and the simple moving average (solid red line, average for the values of the preceding 40 ps) mirrors that in Fig. 3(b). It is illuminating to observe the range of individual EIEs, from <0.88 to >1.00, and the extent of fluctuation with changing solvent configuration. A practical question is this: how many individual EIE (or IPFR) values are required in order to obtain a reliable mean value for the EIE? The lower panel, Fig. 4(b), shows the cumulative average EIE evaluated from the first of the 930 converged structures through to the last. Obviously, the initial part of this plot is dominated by a relatively small number of configurations, and the standard error is large, but it is perhaps surprising to note the oscillatory nature of the cumulative average for structures obtained from the first half of the original MD trajectory. Nonetheless, the mean EIE for the 465 structures from the first half of the trajectory (0.9338) is almost the same as that for the second half (0.9342).

Fig. 4 (a) Anharmonic equilibrium isotope effects (²H₃, 298 K) for transfer of B3LYP/6-31+G(d) methyl cation from vacuum into point-charge representations of 1032 water molecules in solvent configurations extracted at 1 ps intervals from a 1 ns classical MD trajectory. The red solid line is the moving average for the values of the preceding 40 ps. (b) Cumulative average of anharmonic EIE for 930 converged structures of methyl cation within “frozen” solvent configurations along the trajectory. The grey lines are the upper and lower bounds of the standard error in the mean.

In order to ascertain an efficient protocol for adequate sampling of solvent configurations and averaging of IPFRs and EIEs, series of structures were considered at 8 ps intervals along the MD trajectory. Eight series were investigated, each with a different offset from structure 0 (Table 2). Because not every structure had converged (see above), the total number of structures in each series varied between 114 and 118 (instead of 125). Therefore, in order to ensure comparability, only the last 100 and the last 10 structures in each series were included in the averages. The final row of Table 2 shows mean values taken at 1ps intervals (i.e. all structures) within the same overall ranges (810 and 85 structures, respectively) as for the 8 ps intervals. Inspection of the results presented in Table 2 indicates that the mean EIE is the same value (0.934) to within ±0.003 regardless of what offset is arbitrarily chosen, provided that the larger sample size of 100 is used. If only 10 structures are selected, there is more variation, with means in the range 0.935 ± 0.010, for the different offsets. Unsurprisingly, it may be concluded that larger samples give better statistics: a more accurate mean value with a smaller standard error. A rough rule can be proposed: provided that the structures are independent, a sample size of 10 yields a mean with an error of ±0.01 (i.e. 2 significant figures), a sample of 100 gives an error of ±0.001 (3 s.f.), and one of ∼1000 is good to ±0.0001 (4 s.f.).

Table 2 Average anharmonic EIEs (²H₃, 298.15 K) for transfer of B3LYP/6-31+G(d) methyl cation from vacuum to water. The first 8 rows relate to structures at 8 ps intervals along the MD trajectory, starting with an offset from structure 0; for each offset the last 100 and the last 10 converged structures were considered. The final row shows the average over all converged structures (i.e. 1 ps interval) within the ranges spanned by the previous rows (i.e. the last 810 and 85 structures, respectively)

Interval/ps	Offset/ps	Last 100	Last 10
8	0	0.9315 ± 0.0017	0.9334 ± 0.0043
	1	0.9328 ± 0.0017	0.9407 ± 0.0059
	2	0.9352 ± 0.0017	0.9337 ± 0.0054
	3	0.9363 ± 0.0019	0.9434 ± 0.0064
	4	0.9329 ± 0.0019	0.9328 ± 0.0067
	5	0.9338 ± 0.0018	0.9261 ± 0.0063
	6	0.9323 ± 0.0020	0.9298 ± 0.0054
	7	0.9369 ± 0.0018	0.9421 ± 0.0045

---

Interval/ps	Offset/ps	Last 810	Last 85
1	0	0.9341 ± 0.0006	0.9351 ± 0.0019

---

The above discussion has been based upon the anharmonic IPFR results, but the same conclusions also derive from the harmonic IPFRs for methyl cation within a “frozen” environment of water molecules represented by their TIP3P point charges. Note that, in this context, there are 6 harmonic frequencies for internal vibrational modes of methyl cation together with 6 external degrees of freedom (translation and rotation) treated within the ideal gas/rigid rotor approximations. This treatment of the isotope-effect calculation can be described as “molecular”: it considers the isotopic sensitivity of the methyl cation within its aqueous environment but vibrationally uncoupled from it.

QM/MM relaxation and harmonic frequencies

It is important to recognise that the Hessian determined in a fully QM/MM treatment of methyl cation in explicit water yields 12 real harmonic frequencies for each structure, corresponding to both internal and external modes. Of the 930 structures that converged within configurations of water molecules represented by point charges only, a further two failed to converge when Lennard-Jones interactions were also included within the TIP3P description of water; 928 structures were carried forward to the next stage of analysis. Since anharmonic frequencies could not be evaluated with the full QM/MM potential, this treatment was purely harmonic. In contrast to the molecular treatment discussed above, this treatment may be described as “supramolecular”: it considers the isotopic sensitivity of the methyl cation within its aqueous environment and vibrationally coupled to it.

B3LYP/6-31+G(d)/TIP3P calculated harmonic fundamental frequencies for methyl cation within its frozen solvent environment were obtained for all converged structures. Some of the CH-stretching and bending frequencies for individual structures are presented in Table S7, ESI.† As for the QM + point charges results discussed above, the formal degeneracy of the asymmetric CH stretching and in-plane bending frequencies is split by the instantaneous asymmetry of the aqueous environment for the full QM/MM system; in fact, it is difficult to distinguish the out-of-plane from the in-plane bending modes due to differing degrees of coupling between these coordinates. It is more instructive to consider average force constants for stretching and bending coordinates, along with average frequencies for stretching modes and for bending modes grouped together (Table 3). Projecting out the external modes from the 12 × 12 full QM/MM Hessian, yielding 6 (projected) internal modes, has very little effect upon either the average frequencies or the average force constants. However, comparison of the full QM/MM results with those from the QM + point charges method shows that inclusion of Lennard-Jones non-bonded interactions between solute and solvent raises the frequencies and the force constants. There are even more significant increases as compared to B3LYP/6-31+G(d) frequencies and force constants for the methyl cation in vacuum.

Table 3 Average B3LYP/6-31+G(d) harmonic frequencies (as wavenumbers) and force constants for methyl cation in water and vacuum

Method	Frequency/cm^−1			Force constant
	No. of freqs.	CH stretch	Bending	CH str./aJ Å^−2	IP bend./aJ rad^−2	OP bend./aJ rad^−2
QM/MM	12	3260 ± 95	1447 ± 18	5.827 ± 0.006	0.4438 ± 0.0005	0.3990 ± 0.0010
	6 (projected)	3258 ± 94	1451 ± 15	5.827 ± 0.006	0.4437 ± 0.0004	0.3990 ± 0.0010
QM	6	3244 ± 95	1413 ± 15	5.776 ± 0.006	0.4269 ± 0.0004	0.3687 ± 0.0008
vacuum	6	3200	1425	5.620	0.434	0.384

---

Some of the partition functions for individual structures are presented in Table S8 (ESI†). Note that, since these are results from QM/MM relaxation and harmonic frequencies (cf.Fig. 1), the vibrational excitation factor (f_vib) and the zero-point vibrational energy factor ( ) are both functions of frequencies for 12 modes. The mean value of f_vib is small (2.255 ± 0.005). In contrast, f_zpe is large, with a mean value of 14 284 ± 67. The product of these factors yields the total IPFR (31 922 ± 80) averaged over 928 solvent configurations. An alternative factorisation is into contributions from 6 internal and 6 external modes (eqn (5)), each being a product f_vib × f_zpe (Table S8, ESI†). The mean value of the external factor (f_ext), for the vibrational modes corresponding to overall translation and rotation of the methyl cation within its solvent cage, is small (4.158 ± 0.005), whereas that for the internal factor (f_int), due to stretching and bending of the methyl cation itself, is large (7668 ± 11).

QM/MM harmonic EIEs

Table 4 shows that both the 6 internal and 6 external frequencies of the methyl cation contribute inversely to the overall EIE for transfer from vacuum to water. Projecting out the translational and rotational contributions from the Hessian yields 6 frequencies for pure internal vibrational modes, the values of which differ from those without projection owing to decoupling. Thus, the external modes contribute nothing to the EIE (i.e. a factor of unity) after projection and the internal modes yield a slightly less inverse factor (0.853 vs. 0.843). Two points are noteworthy. (1) The EIE arising from harmonic frequencies for the internal modes alone is significantly more inverse (0.853 vs. 0.936) for the full QM/MM description (including Lennard-Jones interactions) of methyl cation in explicit water than for the QM treatment of the cation embedded in a field of point charges representing only the classical Coulombic interactions with the surrounding solvent. There is a significant solvatochromic effect. (2) Furthermore, the influence of the non-bonded interactions is also to stiffen the librational degrees of freedom of the cation within its aqueous cage relative to free translational and rotational motions within an ideal gas at 1 atm pressure. The overall average B3LYP/6-31+G(d)/TIP3P EIE has a very different value (0.753 ± 0.002) from the previous AM1/TIP3P estimate (0.853 ± 0.003) which also considered all 12 degrees of freedom of the methyl cation as harmonic vibrations.¹⁰

Table 4 Average B3LYP/6-31+G(d) EIE (²H₃, 298.15 K) for transfer of methyl cation from vacuum to water, evaluated from harmonic frequencies

Method	No. of frequencies	External	Internal	Overall
QM/MM	12	0.8942 ± 0.0011	0.8429 ± 0.0013	0.7528 ± 0.0019
	6 (projected)	1.0000 ± 0.0000	0.8531 ± 0.0010	0.8531 ± 0.0010
QM	6	1.0000 ± 0.0000	0.9360 ± 0.0008	0.9360 ± 0.0008

---

It is instructive to relate IPFR values to Gibbs energies by means of ΔG = −RT ln(f): substituting a heavier isotope into a molecule always stabilizes it (ΔG < 0) since vibrational frequencies are lowered and f is always > 1. Table 5 shows the magnitudes of the Gibbs energy changes for ²H₃ substitution into the methyl cation at 298 K as determined for vacuum and for explicit water described both with and without Lennard-Jones interactions. The change in Gibbs energy that results from isotopic substitution is larger for the internal modes than for the external modes by a factor of 6 or 7, and it is slightly more favourable for the supramolecular treatment (QM/MM with the full TIP3P potential) than for the molecular treatment (QM with surrounding point charges). The energy differences responsible for the EIEs are very small in magnitude (<0.6 kJ mol⁻¹).

Table 5 Average B3LYP/6-31+G(d) IPFRs f (²H₃, 298.15 K) for methyl cation and Gibbs energy differences (ΔG/kJ mol⁻¹) for transfer from vacuum to water

	Internal modes		External modes
	〈f〉	〈ΔG〉	〈f〉	〈ΔG〉
QM vacuum	6445		3.718
QM (point charges)	6782 ± 4	−21.870 ± 0.001	3.718 ± 3 × 10^−5	−3.255 ± 6 × 10^−7
QM/MM (full TIP3P)	7668 ± 11	−22.170 ± 0.004	4.158 ± 0.005	−3.532 ± 0.003

---

Anharmonicity in C_αH stretching and bending modes

B3LYP/6-31+G(d)/TIP3P rigid potential-energy scans for displacements along each of the 12 normal modes for methyl cation in explicit water are shown in Fig. 5, where “CH sym” and “CH asym” refer to the totally symmetric and a′ and a′′ components of asymmetric bond stretching, “OP wag” to out-of-plane wagging, and “IP scis” and “IP rock” to in-plane scissoring and rocking, respectively. T_x, T_y and T_z denote translation in the directions of the locally defined axes x, y and z, and R_x, R_y and R_z denote rotation about these axes. The solid and open black circles, and solid blue circles, denote the computed energy relative to the equilibrium geometry; the red and blue dots delineate quadratic and quartic fits, respectively. The range of displacements considered is much larger than any of the mean square amplitudes of vibration calculated for harmonic frequencies at 298 K, namely 0.02 Å for CH stretching and increasing to 0.09 Å for the external modes of lowest frequency for the chosen structure. It is important to recognize that the scans presented are for a single instantaneous solvent configuration, and therefore do not include any effects of averaging over many configurations.

Fig. 5 B3LYP/6-31+G(d)/TIP3P rigid potential-energy scans for displacements along normal modes for methyl cation in explicit water. Solid black, open black, and solid blue circles: energy relative to the equilibrium geometry; blue dotted line: quartic fit; red dotted line: quadratic fit.

In each case a quartic potential gives an essentially perfect fit to the calculated energies. The quality of the harmonic approximation is very good for all three internal bending modes and is much better for the a′ asymmetric stretch than for the other CH stretching modes. Quadratic fits over a reduced range of displacements (±0.2 Å) from the equilibrium geometry are excellent for modes, internal and external, with r² better than 0.987 in all cases.

AM1/OPLS rigid potential-energy scans for displacements along each of the three normal modes from atomic Hessian analysis for only the H_α at the carbenium ion centre of the CH, THP, CP and THF cations in explicit water and cyclohexane are shown in Fig. S11, ESI,† where OP, IP and STR refer to out-of-plane bending, in-plane bending and stretching, respectively. As found for the methyl cation, in each case a quartic potential gives an essentially perfect fit to the calculated energies, whereas the goodness of fit for the quadratic potentials varies between 0.98 and 1.00. The quality of the harmonic approximation deteriorates if larger displacements are considered, but over the range of ±0.2 Å from the equilibrium geometry it is excellent for the bending modes and good for the stretching mode. For each cation in each solvent, the largest degree of anharmonicity is seen for the stretching mode.

In a previous study it was shown that the ²H_α EIE for transfer of THP cation from water to a series of media with lower polarity (as modelled by the polarised continuum method, PCM) was reproduced entirely by the influence of the medium on the three harmonic vibrational frequencies of H_α obtained from the atomic Hessian analysis. There was a near-perfect linear correlation between the EIE values resulting from the full and atomic Hessians over the range of relative permittivity 2 ≤ ε ≤ 80: all the variation was captured by the influence of the dielectric upon the isotopically substituted atom alone.¹² The QM/MM rigid potential-energy scans along the three H_α normal modes of the CH, THP, CP and THF cations indicate that the harmonic approximation is very good for small displacements from equilibrium, just as it was previously shown to be for the symmetric CH stretch mode of the methyl cation.¹¹

Conclusions

(1) A small inverse average value is predicted for the EIE, K(CH₃)/K(CD₃), for transfer of methyl cation from vacuum to water by B3LYP/6-31+G(d) calculations of both harmonic and anharmonic frequencies for the cation embedded within a point-charge representation of a frozen configuration of 1032 surrounding TIP3P water molecules. The harmonic (0.9360 ± 0.0008) and anharmonic (0.9366 ± 0.0008) average values are distinctly different, but arguably the additional effort involved in computing anharmonic frequencies is unjustified; if it is desired to make an approximate correction for anharmonicity then use of a uniform scaling factor for harmonic frequencies is a more efficient means.

(2) Averaging over a smaller number of solvent configurations reduces the number of significant figures to which the value of an EIE may be reliably stated. Provided that the structures are independent, sample sizes of 10, 100 and 1000 yield mean values with standard errors of about ±0.01 (2 s.f.), ±0.001 (3 s.f.), and ±0.0001 (4 s.f.), respectively, for both harmonic and anharmonic treatments.

(3) EIEs evaluated by consideration of only the internal, vibrational degrees of freedom underestimate the magnitude of the isotope effect for two reasons. First, the solvatochromic influence of the solvent environment on the harmonic frequencies for the internal modes is neglected. Second, and more significantly, treating the six external degrees of freedom of the solute as free translational and rotational motions in an ideal gas neglects the isotopic sensitivity of these motions when treated as vibrations within the solvent cage. The contributions of the external and internal vibrations of methyl cation to the average B3LYP/6-31+G(d) EIE (²H₃, 298.15 K) for transfer from vacuum to water are, respectively, 0.8942 ± 0.0011 and 0.8429 ± 0.0013. The overall EIE (0.7528 ± 0.0019) differs significantly from the values predicted by consideration of (a) only the internal modes within a full QM/MM description (0.8531 ± 0.0010) and (b) only the internal modes in a QM treatment of the solute embedded within a point-charge representation of the solvent (0.9360 ± 0.0008).

(4) QM/MM potential-energy profiles for displacements along each of the 12 normal modes for methyl cation in water and for each of the three normal modes for the isotopically substituted H_α atom in each of the four cations (CH, THP, CP and THF), in water and in cyclohexane, indicate that the harmonic approximation is very good for small displacements from equilibrium.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

IHW thanks Dr James Grant for technical support with software installation on an 8-core Intel i7-4790 processor at the University of Bath. MR thanks the Spanish Ministerio de Economía y Competitividad for a ‘Ramón y Cajal’ contract (RYC-2014-16592) and Universitat Jaume I for UJI-B2016-28 and UJI-B2019-43 projects.

References

1. M. Wolfsberg, W. A. Van Hook, P. Paneth and L. P. N. Rebelo, Isotope Effects in the Chemical, Geological, and Bio Sciences, Springer, Dordrecht, 2010.
2. L. Melander and W. H. Saunders, Reaction Rates of Isotopic Molecules, Wiley-Interscience, New York, 1980.
3. I. H. Williams, J. Chem. Soc., Chem. Commun., 1985, 510–511.
4. E. A. Halevi, personal communication to IHW, August 1985.
5. E. A. Halevi, Prog. Phys. Org. Chem., 1963, 1, 109–221.
6. E. A. Halevi, New J. Chem., 2014, 38, 3840–3852.
7. C. L. Perrin and A. Flach, Angew. Chem., Int. Ed., 2011, 50, 7674–7676.
8. C. L. Perrin, New J. Chem., 2015, 39, 1517–1521.
9. E. A. Halevi, New J. Chem., 2015, 39, 1522–1524.
10. P. B. Wilson, P. J. Weaver, I. R. Greig and I. H. Williams, J. Phys. Chem. B, 2015, 119, 802–809.
11. P. B. Wilson and I. H. Williams, Mol. Phys., 2015, 113, 1704–1711.
12. K. Świderek, A. J. Porter, C. M. Upfold and I. H. Williams, J. Am. Chem. Soc., 2020, 142, 1556–1563.
13. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
14. J. J. Ruiz-Pernía, I. Tuñón and I. H. Williams, J. Phys. Chem. B, 2010, 114, 5769–5774.
15. M. J. Field, A Practical Introduction to the Simulation of Molecular Systems, Cambridge University Press, Cambridge, 1999.
16. M. J. Field, M. Albe, C. Bret, F. Proust-de Martin and A. Thomas, J. Comput. Chem., 2000, 21, 1088–1100.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
18. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
19. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
20. V. Barone, J. Chem. Phys., 2004, 120, 3059–3065.
21. V. Barone, J. Chem. Phys., 2005, 122, 014108.
22. A. Grossfield and D. M. Zuckerman, Annu. Rep. Comput. Chem., 2009, 5, 23–48.
23. I. H. Williams and P. B. Wilson, SoftwareX, 2017, 6, 1–6.
24. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
25. W. L. Jorgensen and J. Tiradorives, J. Am. Chem. Soc., 1988, 110, 1657–1666.
26. J. Pranata, S. G. Wierschke and W. L. Jorgensen, J. Am. Chem. Soc., 1991, 113, 2810–2819.
27. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909.
28. D. Laage and J. T. Hynes, Science, 2006, 311, 832–835.
29. A. Beneduci, J. Mol. Liq., 2008, 138, 55–60.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01744b

---