Excitation/detection energy controlled anisotropy dynamics in asymmetrically cyano substituted tri-podal molecules

Abstract

In the present work, the photophysical properties of two series of asymmetrical tri-podal molecules are studied, in order to determine the dependence of energy localization/delocalization phenomena on excitation and detection wavelength, by means of steady state, femtosecond time-resolved fluorescence and anisotropy spectroscopy. The molecules bear triphenylamine as an electron donating core and an acetylenic or olefinic π-conjugated bridge. At the periphery, they are substituted by no, one, two or three –CN groups used as electron acceptors. Thus, the compounds with only one or two –CN groups are asymmetrically substituted. As a comparison, the photophysics of their dipolar and quadrupolar analogues is also presented. The steady state absorption spectra of the asymmetrical tri-podal compounds exhibit a broadening and a low energy shoulder due to the splitting of the excited states. The fluorescence spectra are more red-shifted in the tri-podal molecules with a single –CN group, providing the first evidence of its mostly dipolar nature. Time-resolved anisotropy measurements by using different excitation and detection wavelengths provide clear evidence that the asymmetrical tri-podal molecules with one or two –CN groups behave like octupolar molecules upon high-energy excitation (the initial anisotropy is found 0.1–0.15), while upon low-energy excitation they reveal a behavior expected for linear dipolar or V-shaped quadrupolar molecules (the initial anisotropy is very close to 0.4 and 0.17, respectively). The symmetrical tri-podal compounds with no or three cyano groups, exhibit an anisotropy depolarization time of 2.5 ps attributed to energy hopping. The amplitude of this energy hopping component is wavelength dependent and increases as the excitation is shifted towards the long wavelength edge.

---

1 Introduction

Multibranched conjugated molecules are nowadays attractive materials for various optoelectronic applications such as organic light emitting diodes, solar energy conversion systems, sensors etc. due to their high energy harvesting ability, enhanced non-linear optical properties and high fluorescence quantum yield.^1–15 A thorough investigation of their fundamental photophysical properties is of outmost importance and provides the necessary theoretical framework for designing novel light harvesting antennae materials with envisaged properties. A variety of interesting phenomena takes place upon excitation of these molecules with ultrashort laser pulses. Among others, excitation energy transfer (EET) between the conjugated branches and/or from the periphery to the core or vice versa takes place in the fs to ps timescale.^16–22 EET depends on the strength of the coupling among the branches and can be coherent (under strong coupling) or incoherent (under weak coupling). In the former case, energy is homogeneously distributed within ∼30 fs and then it localizes on one branch,^23,24 while in the latter case, hopping among the branches occurs on the 1–10 ps timescale.^{17,19,25–29}

Energy localization/delocalization in multibranched systems strongly depends on the nature of the core. In molecules with a benzene or truxene core, the coupling of the branches is weak and energy is transferred among the branches via a hopping mechanism.^{17,21,25,26,30,31} When, a nitrogen atom is used as the central donor, the coupling is strong and EET is coherent.^{19,22–24,32–35} On the other hand, the type of substituents at the periphery also affects the photophysics of these molecules. In the great majority of the previously published studies, the edge substituents, such as cyano, pyridine, benzothiazole etc. play the role of electron accepting groups^{20,22–24,33,36–45} and the overall structure is of the type D–(π–A)₃, while the opposite geometry of the type A–(π–D)₃^17,21,30,46 is more scarce. It is common in both cases, that identical peripheral substituents are utilized, rendering the branches alike and the multibranched systems are symmetrical. However, in most cases in solutions and especially in polar solvents, the symmetry is reduced and energy is localized on a single branch.^{17,19,22,33,37,40,50,51} In this case, the multibranched systems behave like linear dipolar ones, regarding fluorescence properties and solvatochromism.

It is very interesting that very few articles have been published so far, studying multribranched octupolar systems with different branches or substituents at the periphery.^26,40,47,48 The interactions among the chromophores in such systems depend on the difference between the energies of the excited states of the non-interacting chromophores. According to the Frenkel exciton model,^16,22,33,49 in symmetrical octupolar molecules of the C₃-symmetry, the dipoles of the three chromophores interact, producing a set of three states. Two of them are degenerate and lie below the energy of the non-interacting monomers, while the third state lies higher. Excitation to the third state has a vanishing oscillator strength. However, this constraint is lifted in many real systems. On the other hand, according to Ceymann et al. in multibranched systems with different branches, three states with distinct energies are formed with non-vanishing oscillator strengths, i.e. all of them can be populated by linear absorption.⁴⁷

In order to shed more light on the photophysics of multibranched compounds with different conjugated branches, we study herein the photophysical properties and localization/delocalization phenomena by means of steady state and fs fluorescence spectroscopy, of two series of tripodal molecules with a triphenylamine central core, acetylenic or olefinic π-bridge and none, one, two or three –CN electron acceptor groups at the periphery. The asymmetrically substituted compounds are examined and compared to their linear and quadrupolar counterparts. Our results reveal the interactions among the different branches and show that the monosubstituted molecules behave like octupolar or dipolar ones, depending on the excitation energy.

2 Experimental

2.1 Materials

Molecules 1a–d, 2a–d, 1L-CN, 1Q-CN, 2L-CN and 2Q-CN have been prepared according to procedures already described in our earlier studies.^44,45 The synthesis of molecules 1L and 2L has been carried out via cross-coupling reactions as shown in the ESI.† Compounds 1a–d and 2a–d (Fig. 1) have a star-shaped structure bearing a triphenylamine electron donating core and an olefinic or acetylenic π-conjugated bridge. At the periphery, they are either symmetrically or asymmetrically substituted by none, one, two or three –CN acceptors. Specifically, compounds 1a/2a and 1d/2d are symmetrical without and with three –CN groups, while 1b, 1c and 2b, 2c are asymmetrical bearing one or two –CN groups at the periphery. All compounds have shown moderate to exceptional 2-photon absorption (2PA) properties, with 2PA cross sections increasing upon addition of –CN groups, reaching 1500 GM for 2d.⁴⁵ In order to compare the optical properties of the asymmetrical compounds with their linear and pseudo-quadrupolar counterparts, we have also examined the structural analogues 1L and 2L, 1L-CN and 1Q-CN, and 2L-CN and 2Q-CN (Fig. 1). All the herein reported experiments have been conducted in toluene (TOL), while acetone (ACT) has been also used in some cases for comparison.

Fig. 1 Structures of the herein studied molecules 1a–1d and 2a–2d together with their reference materials. 1L and 2L are reference compounds for 1a and 2a, respectively. 1L-CN and 2L-CN are reference compounds for 1b and 2b. 1Q-CN and 2Q-CN are reference materials for 1c and 2c, respectively.

2.2 Methods

The absorption and fluorescence spectra of the samples were measured using a Jasco V-650 UV-Vis and a Horiba Fluoromax spectrophotometer, respectively. The concentration of the TOL solutions was 5 μM. A femtosecond time-resolved fluorescence method employing the upconversion technique was used for the study of the excited state and the anisotropy dynamics.^28,29 The samples were excited at various wavelengths (380, 400 and 430 nm) produced by the second harmonic generation of a Ti:Sapphire mode-locked femtosecond laser (730–870 nm, 80 fs pulse duration, 80 MHz repetition frequency). The samples were put in 1 mm path-length rotating cells and their optical density was below 0.1 at the excitation wavelengths. The instrument's response function (IRF) was ∼250 fs. Magic angle dynamics has been fitted by means of an exponential function convoluted with the excitation pulse which is considered Gaussian.⁵² For determining the anisotropy dynamics, the polarization plane of the excitation beam was varied by using a Berek compensator. The fluorescence anisotropy dynamics was then calculated by the equation:where I_par(t) and I_per(t) are the detected fluorescence intensities with polarization plane parallel or perpendicular to that of the excitation beam. The parameters of the anisotropy dynamics have been determined by fitting the anisotropy itself via exponential decays, while also the difference factor D(t) = I_par(t) − I_per(t) (difference fit) has been fitted.^25,53 Besides, a combined fit in the experimentally derived I_par(t) and I_per(t) dynamics using the equations I_par(t) = (1 + 2r(t))I_magic(t) and I_per(t) = (1 − r(t))I_magic(t) has been performed convoluted with the excitation pulse.⁵⁴ The latter methods are generally used in the case of anisotropy lifetimes similar to the IRF since the anisotropy decay is not amenable to reconvolution. In our case, all methods gave similar results because all anisotropy lifetimes were found longer than 1 ps. Finally, the anisotropy dynamics on the 100 ps timescale were examined by the Time Correlated Single Photon Counting method.²⁸

3 Results and discussion

3.1 Steady state spectroscopy

Fig. 2 shows the absorption and fluorescence spectra of the tri-podal compounds 1a, 1d and 2a, 2d together with those of their linear model analogues 1L, 1L-CN and 2L, 2L-CN in TOL. It is obvious that the absorption and fluorescence spectra of the branched compounds are red-shifted compared to the linear ones, pointing to a delocalization of energy caused by exciton coupling.⁵⁰ By comparing the fluorescence spectra of 1avs.2a and 1dvs.2d, it is obvious that the spectra of the compounds in series 1 are narrower than those of the compounds in series 2. This is due to the planarization of the excited state prior to emission, in series 1, leading to emission which originates from the lower energy geometry relaxed state.²⁶

Fig. 2 Steady state absorption and fluorescence spectra of the tri-podal compounds 1a (a), 1d (b) and 2a (c), 2d (d) in TOL together with their corresponding linear analogues.

The absorption spectra of 1a–d and 2a–d are shown in Fig. 3 and the photophysical parameters are summarized in Table 1. 1a exhibits an absorption spectrum with a peak at 369 nm. In 1b, having one –CN substituted branch, the absorption peak does not change, however, the spectrum becomes broader, while a shoulder emerges close to 400 nm. The broadening of the spectrum is clear evidence for the splitting of the excited states providing three states with different energies. However, specific absorption peaks to be ascribed to these states are not observed here. Two peaks are only evident in the spectrum as mentioned, with the third highest energy state being absent. The latter is one photon allowed, opposite to the case of 1a, but cannot be observed, most likely due to its lower oscillator strength with respect to the other two states according to the excitonic model introduced by Ceymann et al.⁴⁷ Besides, as expected, the shoulder at 400 nm is at lower energy than the main absorption peak of the lowest energy non-interacting chromophore (1L-CN), which has an absorption peak at 380 nm (Fig. 2). In 1c, with two –CN groups, the higher peak at 369 nm red-shifts and merges with the peak at 400 nm, owing to the weaker coupling between the two –CN substituted branches with the unsubstituted one. In addition, the contribution of the low energy peak at 400 nm becomes more prominent.

Fig. 3 Steady state absorption (a), (b) and fluorescence (c), (d) spectra of 1a–d and 2a–d in TOL.

Table 1 Photophysical parameters of the herein studied compounds in TOL

Compound	λ abs (nm)	λ fluor (nm)
1a	369	401
1b	371	437
1c	378	432
1d	390	427
2a	392	436
2b	400	482
2c	408	472
2d	416	467

---

The above discussed experimentally derived spectra are in agreement with the calculated ones in which the asymmetrical molecules with one or two –CN groups, exhibit absorption bands featuring two transitions (HOMO–LUMO and HOMO–LUMO+1), with the longer wavelength one having a larger oscillator strength.⁴⁵ On the other hand, in the case of the symmetrical molecules 1a/2a and 1d/2d, the energies of the LUMO and the LUMO+1 are proved to be degenerate.⁴⁵

The fluorescence spectra of 1a–d are typical for similar chromophores in apolar solvents such as TOL, i.e. they exhibit a relatively narrow peak, while a vibronic shoulder is also slightly observed (Fig. 3). The peak of the fluorescence spectrum for 1a is found at 401 nm (Table 1). For 1b, the peak is shifted to 437 nm, while for 1c and 1d, the spectra are slightly blue shifted to 432 and 427 nm, respectively. The largest red-shift observed in 1b can be correlated with a larger excited state dipole moment, pointing to an excitation that resides in the –CN substituted branch. This is in agreement with the molecular frontier orbitals shown before.⁴⁵ The monosubstituted derivative 1b showed a HOMO that is centered on the electron donating core, while the LUMO lies over the –CN substituted branch. The positions of the HOMO and LUMO confirm its ICT character. Finally, it is noted that the fluorescence spectra of the monosubstituted asymmetrical chromophore, 1b, showed no differences upon exciting at the main peak or at the shoulder, proving that the fluorescence originates from the lower energy spectroscopic unit (Fig. S1, ESI†). Besides, the fluorescence excitation spectra taken upon detection at two different wavelengths are similar to the absorption spectra (Fig. S1 and S2, ESI†).

The absorption and fluorescence spectra of the compounds in series 2, exhibit a red-shift compared to series 1 (Table 1), pointing to a more extended conjugation with the olefinic bridge. This is due to the fact that the acetylenic π-bridge (C≡C), in series 1, has a low rotational barrier (0.025 eV), resulting in various conformations with large dihedral angles and an ICT state lying higher than in the olefinic π-bridge (C=C).^16,26,41,55 On the other hand, the behavior of the compounds in series 2 and 1 is similar. Thus, the absorption spectra show a weak shoulder at lower energies compared to the main peak, when one –CN is incorporated, while the main peak is gradually red-shifted from 2b to 2c to 2d. Also, as in the case of 1b, 2b exhibits a more red-shifted fluorescence spectrum compared to the other compounds within this series.

Fig. S3 (ESI†) shows a comparison between the absorption and fluorescence spectra of 1b, 1c and 2b, 2c with those of their reference molecules 1L-CN, 1Q-CN and 2L-CN, 2Q-CN. While compounds 1b, 2b with one –CN group show, as discussed before, a peak and a shoulder, the absorption spectrum of the reference compounds 1L-CN and 2L-CN exhibit, as expected, a typical broad and unstructured spectrum. By comparing the compounds with two –CN groups, the absorption spectra of 1Q-CN and 2Q-CN are red-shifted compared to those of 1c and 2c. Besides, for compounds 1Q-CN and 2Q-CN, a shoulder is observed at high energies which is due to the splitting of the excited state, predicted for quadrupolar molecules.^{20,22,32,33,47,49} The fluorescence spectra show no striking differences for the compounds in series 1. However, in series 2, the fluorescence spectra of the tri-podal asymmetrical compounds are red-shifted compared to those of the linear compounds.

3.2 Fluorescence dynamics

In order to shed more light on the photophysics of the compounds 1a–d and 2a–d, the excited state dynamics were studied, within the first 50 ps, in TOL and are shown in Fig. 4 and 5. The dynamics were detected at two emission wavelengths, to observe possible fast relaxation phenomena, while in addition, for the –CN substituted compounds, two excitation wavelengths were also used. Specifically, for compounds in series 1 the excitation wavelengths of 380 and 400 nm have been used, while the corresponding values for the series 2 are 400 and 430 nm. Excitation at 400 nm for series 1, mainly excites at the red-shifted shoulder of the –CN substituted molecules. This is clearly observed in Fig. S4 (ESI†) which shows the absorption spectra of 1a and 1b as well as a spectrum calculated by a subtraction between them. The latter spectrum shows a peak at 400 nm, i.e. exactly at the excitation wavelength. The same subtraction between the absorption spectra for compounds 2a and 2b, yields a subtracted spectrum with a peak at 430 nm which is the long excitation wavelength for series 2 (Fig. S4, ESI†). In order to obtain a more quantitative analysis, the absorption spectra (above 320 nm) of 1a and 2a have been fitted with a lognormal function, which has been found to describe the band shapes of steady state absorption and fluorescence spectra remarkably well⁵⁶ (see Fig. S5 for the fitting results and details on the fitting procedure, ESI†). To fit properly the absorption spectra of 1b and 2b (above 320 nm), we used the sum of two lognormal functions, one for every state observed in the spectra. From the decomposed spectra the population of the high energy excitonic state vs. the population of the low energy excitonic state that is excited, can be calculated, depending on the excitation wavelength. When exciting 1b at 380 nm, 88% of the total population belongs to the high energy excitonic state and 12% to the lower one. Moving the excitation to the red and particularly at 400 nm, 9% of the high energy excitonic state participates in the measurements vs. 91% of the lower. The corresponding values for 2b when exciting at 400 (430) nm are 94% (7%) and 6% (93%) for the high and low energy excitonic state, respectively. However, we should also keep in mind the spectral width of the fs laser pulses as it is shown in Fig. S5 (ESI†). From the above discussion, it is concluded that the two excitation wavelengths selected for 1b and 2b excite to a great extent either the population of the high or the low energy excitonic state. Yet, the same cannot be stated for compounds 1c and 2c, where the excitonic states are strongly mixed owing to the weaker coupling of the two –CN substituted branches with the unsubstituted one.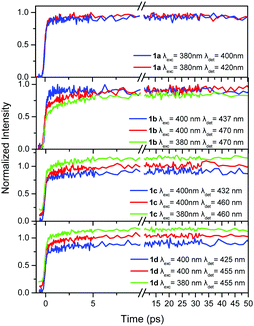

Fig. 4 Fluorescence dynamics within the first 50 ps for the compounds in series 1 in TOL at different excitation/detection wavelengths. An offset is given in some decays for clarity.

Fig. 5 Fluorescence dynamics within the first 50 ps for the compounds in series 2 in TOL at different excitation/detection wavelengths. An offset is given in some decays for clarity.

TOL is an apolar solvent in which significant excited state relaxation phenomena are not expected. This is obvious in our time-resolved results where the dynamics within the first tens of ps for series 1, are similar upon detection at the blue and red part of the spectrum, without rapidly decaying components (Fig. 4). The only differences are observed for 1b, where the dynamics at the short wavelength (437 nm) is slightly faster than that at the long one (470 nm).

In order to determine whether intramolecular EET is operative, the dynamics were detected upon two different excitation wavelengths. This is especially important for compounds having one or two –CN groups, where EET from the higher energy unsubstituted branches to the lower energy ones, having a –CN group, could be expected. More specifically, for the compounds in series 1, the excitation wavelengths 380 and 400 nm were used and the dynamics were detected at the red-part of the spectrum. As shown in Fig. 4, the dynamics were identical upon the two different excitation wavelengths, meaning that through space EET between the branches is not operative. Since the lower energy part of the chromophore, with the –CN group, is responsible for the emission, as revealed by the steady state fluorescence spectra, it is concluded that the excitation is spread towards the lower energy branch via a coherent through-bond mechanism.

By observing the dynamics for the compounds in series 2 (Fig. 5), it is seen that it is faster at the shorter detection wavelength and slower at the longer one, revealing a weak transient spectral relaxation possibly due to the more polar nature of the compounds having an olefinic bridge (series 2) in the excited state, rendering them more sensitive to solvent–solute interactions, compared to the ones having an acetylenic one (series 1).¹⁶ The more obvious spectral relaxation among the compounds in series 2, is observed for 2b, pointing to its increased excited state polarity resembling the behavior of a linear dipolar molecule. Global analysis at the two observation wavelengths gave time constants of 3.8, 3.0 and 4.2 ps for 2b, 2c and 2d respectively, which can be considered as solvation times.⁵⁷ Regarding possible EET phenomena, again two excitation wavelengths were used i.e. 400 and 430 nm, exciting at the high and low energy excitonic states of the chromophores, respectively. By exciting at 430 nm, the lower energy excitonic state, which is responsible for the fluorescence, is directly excited (Fig. S4 and S5, ESI†). As in series 1, the dynamics upon 400 and 430 nm excitation are identical indicating that EET towards the branches having the –CN group is not operative.

3.3 Anisotropy dynamics

Next, the anisotropy dynamics of the compounds in the two series were examined. The anisotropy, when detected in the few tens of ps timescale, is a valuable tool for determining (i) the angle between the absorption and emission dipole moments (via the value of the initial anisotropy r₀), as well as (ii) the possible energy transfer/delocalization phenomena.^{17,19,25–27,31,34,35,53,58–66} The latter phenomena are highly dependent on the initial excited state, that is populated, or the amount of excess energy that is provided to the system, especially in compounds with multiple chromophores.

The anisotropy can also provide evidence of the nature of the chromophoric unit i.e. an r₀ value of 0.4 is a fingerprint for a dipolar linear chromophore, while a value of 0.1 stands for an octupolar chromophore with a C₃ symmetry.³⁵ Besides, the part of the anisotropy decay that is due to EET phenomena is also dependent on the polarity of the solvent used.^19,29 In polar solvents, the dipolar chromophoric units (branches) form solvent relaxed low energy ICT states, rendering the energy hopping less favorable. For this reason, an apolar solvent is used here in order to exclude solvation effects in our results and only a few measurements have been performed in the polar solvent ACT, for comparison.

Before performing fs anisotropy measurements, the overall anisotropy decay due to rotational diffusion has been studied by ns fluorescence measurements. The corresponding results for all molecules in TOL are presented in Table S1 (ESI†). The rotational times range roughly between 190–300 ps. The behavior for the two series is similar. The rotational times increase by adding –CN groups from molecules a to c, while a reduction is observed for molecules d.

The anisotropy dynamics for 1a is shown in Fig. S6 (ESI†) for two detection wavelengths and excitation at 380 nm. The anisotropy initially decays from an r₀ value of 0.2 via a 2.5–3.0 ps component to approximately 0.1 which is the limiting anisotropy for a compound of a C₃ symmetry, in which energy is homogeneously distributed among the three branches.^67,68 This ps decay component can be adequately ascribed to a depolarization effect that originates from energy hopping among the branches.^25,31,34,35 Although fitting procedures using reconvolution analysis have been performed, an ultrafast anisotropy decay has not been found. After 20 ps, the anisotropy decays slowly due to overall molecular rotation with a lifetime of 190 ps (Table S1, ESI†). The anisotropy of 1L is also shown for comparison in Fig. S6 (ESI†), exhibiting an r₀ of 0.35 and a slow decay due to rotational diffusion.

The corresponding results for molecule 2a, are shown in Fig. S7 (ESI†) for excitation at 400 nm and detection at 436 and 460 nm (and for reference compound 2L for excitation/detection at 380/420 nm). The anisotropy decays for 2a are similar for both wavelengths with an initial decay of 3.0–3.5 ps. The main difference appears in the r₀, which is larger/smaller for the high/low energy detection (436/460 nm). Taking into account that in such systems, coherent EET can take place faster than our IRF, then the r₀ is a measure of the strength of the coherent EET, i.e. in the case of smaller r₀, the coherent EET is more intense. When the system is probed at low energy, coherent EET is dominant as the r₀ is small. This is explained because energy is distributed towards all possible low energy states and geometries down the potential energy hill, leading to a randomization of the dipole orientation. On the other hand, when the system is probed at high energy, this randomization is not complete since only an amount of possible geometries is reached.

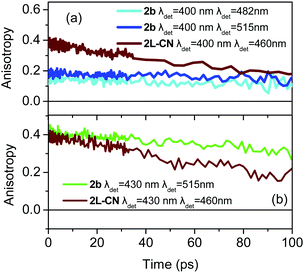
The most interesting anisotropy dynamics is observed for 1b and is presented in Fig. 6 for different excitation/detection wavelengths. As it is obvious, there are important differences in the r₀ value, for the different wavelengths. Upon excitation close to the main absorption peak, i.e. at 380 nm, the anisotropy dynamics is typical for a tri-podal compound, meaning that r₀ is low (∼0.15), pointing to a very fast coherent EET that takes place faster than our IRF and reduces r₀. However, r₀ dramatically changes as the excitation wavelength shifts to 400 nm which lies on the absorption region of the lower energy excitonic state reaching values of 0.27 and 0.36 for detection wavelengths of 437 and 470 nm, respectively. In particular, for detection at 470 nm, r₀ is very close to the theoretically predicted value for linear compounds, meaning that the symmetry is reduced. For comparison, the anisotropy dynamics for 1L-CN, which is the linear reference molecule of 1b, was also measured and is again shown in Fig. 6. The anisotropy dynamics of 1L-CN shows the same r₀ as that of 1b for low energy excitation/detection, while the anisotropy of 1b exhibits a longer correlation time due to the larger volume of 1b compared to 1L-CN. Upon detection at the peak of the fluorescence spectrum (437 nm), the reduced r₀ of 1b, compared to that at 470 nm, indicates that the emission originates not only from the lower energy excitonic state, but also from the other states as well. The final r₀ is therefore due to the contribution of all three emitting units.

Fig. 6 Anisotropy dynamics of compound 1b upon excitation at (a) 380 nm and (b) 400 nm and detection at 437 nm and 470 nm as indicated in the figure. The anisotropy dynamics of the reference linear molecule 1L-CN is also shown.

Based on the anisotropy data discussed above, the tripodal asymmetrically substituted compound 1b can be considered as a linear dipolar molecule, i.e. energy is absorbed and subsequently emitted by a single excitonic state, when excited at the low energy edge of the absorption spectrum and the detection is at the red-edge of the fluorescence. In this case, only one relaxation pathway is operative, i.e. emission from the lowest energy excitonic state, which is also the absorbing state, and thus the initial anisotropy is close to 0.4. The above is also confirmed by the position of the LUMO for 1b, which lies only on the –CN substituted branch. On the other hand, 1b behaves as an octupolar molecule when the excitation lies at the higher energy edge of the absorption spectrum, i.e. when the molecule receives an excess amount of energy. This leads the system to a case where the excitation spreads coherently among branches and emission is depolarized even at zero time.

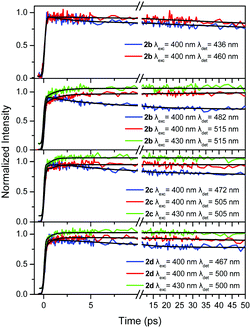
The corresponding results for 2b are shown in Fig. 7 for excitation at 400 and 430 nm. As in the previous case, upon excitation at the higher energy part of the spectrum, the anisotropy resembles the one expected for octupolar molecules, i.e. it has a small r₀ value (Fig. 7a). However, when the excitation is shifted towards lower energies (Fig. 7b), r₀ increases to 0.4 revealing that 2b can also behave as a dipolar molecule.

Fig. 7 Anisotropy dynamics of compound 2b upon excitation at (a) 400 nm and (b) 430 nm and detection at 482 nm and 515 nm as indicated in the figure. The anisotropy dynamics of the reference linear molecule 2L-CN is also shown.

Next, the time-resolved anisotropy of 1c was studied, together with its reference molecule 1Q-CN (Fig. S8, ESI†). Again r₀ is sensitive to the excitation and detection wavelengths. The anisotropy of 1c resembles the one expected for a tri-podal compound when excited at the main absorption peak, i.e. 380 nm. It has a small r₀ of ∼0.15 indicating that the energy is spread almost equally over the three chromophores. Besides, a slight decay on the 1.5 ps timescale is also observed further reducing the anisotropy to ∼0.1 (Fig. S8c, ESI†), before rotational diffusion takes place. This ps component can be ascribed to incoherent energy transfer among adjacent branches. However, for excitation at 400 nm, i.e. at the red edge, r₀ increases (∼0.25, Fig. S8b, ESI†), while again a 4 ps decay component is seen leading to an anisotropy of 0.17 (Fig. S8d, ESI†). The behavior of the reference molecule 1Q-CN is different. It exhibits a high r₀ value of 0.4 without any depolarization mechanism on the ps timescale.

From the above, it is revealed that 1c behaves clearly as an octupolar molecule upon excitation at 380 nm. On the other hand, upon increasing the excitation wavelength to 400 nm, its behavior changes, while the existence of the 4 ps decay component shows that interactions between the branches still exist although on a longer timescale. However, the anisotropy reduces to ∼0.17 (instead of 0.1) which is the theoretical anisotropy for a two-branched system with an angle of 120° between the branches.^17,20 Therefore, 1c for low energy excitation behaves like a pseudo-quadrupolar V-shaped molecule.

Qualitatively similar findings are also observed for 2c (Fig. S9, ESI†). r₀ is small upon excitation at 400 nm, being ∼0.17, resembling a V-shaped molecule. When the excitation is shifted to 430 nm, r₀ increases to ∼0.23 revealing an intermediate behavior among a quadrupolar and a dipolar molecule.

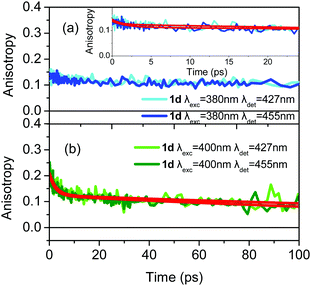
In the case of symmetrically substituted tri-podal molecules, like 1d, the anisotropy dynamics, in general, can reveal ultrafast coherent EET (fs timescale), and incoherent energy hopping (ps timescale), while both mechanisms can also be observed simultaneously. In the case of 1d, for all excitation/detection wavelengths the dynamics of the coherent EET pathway is not observed. On the other hand, the incoherent hopping is observed but its strength depends on the excitation wavelength. When the excitation is at 380 nm, r₀ is close to 0.13 and the incoherent depolarization is barely observed (Fig. 8a). The small r₀ value and almost absent incoherent path means that coherent energy distribution is active on an ultrafast timescale and its dynamics is not observed because it takes place faster than our system's resolution. Therefore, it is concluded that exciting the molecule with excess energy brings the system to an excited state which is capable of initiating the coherent ultrafast EET pathway and r₀ becomes small.²⁵ The coherent path leads to an almost homogeneous distribution of energy. On the other hand, when the excitation energy is lower (at 400 nm), i.e. when initially the low energy excitonic state is excited, then the coherent path is less energetically allowed, as shown by the increased r₀ value of 0.2 (Fig. 8b). Furthermore, it is very interesting that the excitation does not remain localized on a single branch, as this would lead to an anisotropy with a flat temporal profile on the ps timescale, without any decay. In contrast, a hopping process among branches takes place on the 2.5–3.0 ps time regime leading to a decrease of the anisotropy (Fig. 8b and Fig. S10, ESI†). It is concluded, therefore, that the type of EET is dependent on the excitation energy. Coherent EET is dominant in the energy distribution process for high excitation energies, while at lower ones, the hopping process is also operative.

Fig. 8 Anisotropy dynamics of compound 1d upon excitation at (a) 380 nm and (b) 400 nm and detection at 427 nm and 455 nm as indicated in the figure. The inset in (a) shows on a short timescale the anisotropy of 1d upon excitation at 380 nm together with the fitting function.

The anisotropy decay of 2d has a similar behavior, although less pronounced (Fig. 9). The anisotropy has an r₀ of 0.15 for excitation at 400 nm without any incoherent ps depolarization component meaning that coherent EET is mainly responsible for energy redistribution. However, r₀ increases slightly for excitation at 430 nm. Besides, a weak 9 ps decay due to a hopping process is also observed.

Fig. 9 Anisotropy dynamics of compound 2d upon excitation at 400 nm and 430 nm and detection at 467 nm and 500 nm as indicated in the figure.

Finally, in order to investigate the effect of the solvent polarity on the photodynamics and especially on the anisotropy, compounds 1b and 1d have been studied in the polar solvent ACT. The absorption and fluorescence spectra of the compounds are shown in Fig. S11 (ESI†). Although the absorption spectra have minor differences with those in TOL, the fluorescence spectra in ACT experience a significant red-shift due to its positive solvatochromism. As in the case of TOL, the dynamics of both compounds have been studied upon excitation at 380 and 400 nm and detection at two wavelengths corresponding to the peak and low-energy edge of the fluorescence spectra. For 1b, the fluorescence dynamics are shown in Fig. S12 (ESI†), while the anisotropy dynamics in Fig. S13 (ESI†). The fluorescence dynamics exhibit a fast decay at short wavelengths and a slow increase at longer ones, leading to a transient red-shift of the fluorescence spectrum, which is typical in polar solvents. Global analysis gave a time constant of 2.3 ps for this relaxation mechanism, i.e. faster than in TOL. The anisotropy dynamics also present some differences compared to TOL. As shown in Fig. S13 (ESI†), upon 380 nm, the initial anisotropy is higher than in the case of TOL (0.25 vs. 0.15) pointing to a more significant energy localization on the CN-substituted branch. The above means that although in the apolar solvent, TOL, 1b retained some of its octupolar symmetry leading to an initial anisotropy close to 0.1, in the polar solvent, ACT, solvent assisted symmetry breaking is favored, leading to a higher initial anisotropy. This is aided by solvation since the interaction of the CN-substituted branch with solvent molecules is stronger (stronger solvation field) in polar environments leading to more efficient solvation.^69,70 On the other hand, in the apolar medium, the solvent interaction with each branch is weak and therefore energy is almost similarly distributed among the three equally solvated branches.

The effect of the solvent polarity on the anisotropy dynamics has been also studied for 1d and the results are shown in Fig. S14 (ESI†). It is noted that in the case of 1d in TOL, the incoherent hopping mechanism was only observed upon excitation at 400 nm, while in the case of 380 nm excitation, the ultrafast coherent mechanism dominates, reducing the initial anisotropy. Changing the solvent from TOL to ACT, does not cause any differences in the anisotropy upon 380 nm excitation. The most obvious difference is found for 400 nm excitation where the depolarization due to the incoherent EET path is barely observed on the 1–10 ps timescale (Fig. S14b and c, ESI†). This is due to the solvation effect and the participation of the lower energy, solvated excited state of the branches in the EET. Thus, the EET becomes less efficient due to a decrease of the spectral overlap of the emission spectrum of the donor (solvated state) with the absorption spectrum of the acceptor.

4 Conclusions

Tri-podal molecules are attractive systems due to their very rich photophysics as well as due to their potential applications in optoelectronics. They exhibit enhanced energy harvesting ability, fluorescence quantum yields and exceptional non-linear optical properties. The great majority of the studied tri-podal compounds are of the D–(π–A)₃ type, i.e. they are symmetrically substituted at the periphery. Herein, we studied a series of asymmetrically substituted tri-podal molecules, having a triphenylamine electron donating core, olefinic or acetylenic π-conjugated bridge and various numbers of –CN acceptors at the edges. Steady state spectroscopy initially revealed the mostly polar feature of the mono-substituted tri-podal molecules. Next, time-resolved fluorescence anisotropy dynamics with fs resolution has been reported, revealing the possible energy localization/delocalization phenomena based on different excitation/detection energies. Very interestingly, it is observed that the monosubstituted systems behave as octupolar ones for high excitation/detection energies, while their behavior resembles that of dipolar compounds when the excitation/detection energy becomes lower. Similarly, the asymmetrical systems with two –CN groups behave either as octupolar-like or pseudoquadrupolar-like ones depending on the excitation/detection energy.

Conflicts of interest

There are no conflicts to declare.

References

1. L. Chen, P. Li, H. Tong, Z. Xie, L. Wang, X. Jing and F. Wang, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 2854–2862.
2. Y. Yang, Y. Zhou, Q. He, C. He, C. Yang, F. Bai and Y. Li, J. Phys. Chem. B, 2009, 113, 7745–7752.
3. L. Bonardi, H. Kanaan, F. Camerel, P. Jolinat, P. Retailleau and R. Ziessel, Adv. Funct. Mater., 2008, 18, 401–413.
4. P. Pander, R. Motyka, P. Zassowski, M. K. Etherington, D. Varsano, T. J. da Silva, M. J. Caldas, P. Data and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 23934–23942.
5. J. Jin, Y. Tao, H. Jiang, R. Chen, G. Xie, Q. Xue, C. Tao, L. Jin, C. Zheng and W. Huang, Adv. Sci., 2018, 5, 1800292.
6. Y. Wang, W. Liu, Z. Qu, H. Tan, Y. Liu, G. Xie and W. Zhu, Dyes Pigm., 2017, 143, 173–182.
7. L. Chen, C. Zhang, G. Lin, H. Nie, W. Luo, Z. Zhuang, S. Ding, R. Hu, S. J. Su, F. Huang, A. Qin, Z. Zhao and B. Z. Tang, J. Mater. Chem. C, 2016, 4, 2775–2783.
8. S. K. Pathak, R. K. Gupta, S. Nath, D. S. Shankar Rao, S. K. Prasad and A. S. Achalkumar, J. Mater. Chem. C, 2015, 3, 2940–2952.
9. X. Zhang, Y. Zeng, T. Yu, J. Chen, G. Yang and Y. Li, J. Phys. Chem. Lett., 2014, 5, 2340–2350.
10. Q. He, M. Shahid, J. Panidi, A. V. Marsh, W. Huang, M. Daboczi, J. S. Kim, Z. Fei, T. D. Anthopoulos and M. Heeney, J. Mater. Chem. C, 2019, 7, 6622–6629.
11. W. Wu, G. Zhang, X. Xu, S. Wang, Y. Li and Q. Peng, Adv. Funct. Mater., 2018, 28, 1707493.
12. Z. Luo, W. Xiong, T. Liu, W. Cheng, K. Wu, Y. Sun and C. Yang, Org. Electron., 2017, 41, 166–172.
13. S. Körsten and G. J. Mohr, Chem. – Eur. J., 2011, 17, 969–975.
14. A. M. Haughey, B. Guilhabert, A. L. Kanibolotsky, P. J. Skabara, G. A. Burley, M. D. Dawson and N. Laurand, Sens. Actuators, B, 2013, 185, 132–139.
15. Y. Xu, X. Wu, Y. Chen, H. Hang, H. Tong and L. Wang, RSC Adv., 2016, 6, 31915–31918.
16. L. Yan, X. Chen, Q. He, Y. Wang, X. Wang, Q. Guo, F. Bai and A. Xia, J. Phys. Chem. A, 2012, 116, 8693–8705.
17. C. Liu, K. C. Tang, H. Zhang, H. A. Pan, J. Hua, B. Li and P. T. Chou, J. Phys. Chem. A, 2012, 116, 12339–12348.
18. C. Ramanan, C. H. Kim, T. J. Marks and M. R. Wasielewski, J. Phys. Chem. C, 2014, 118, 16941–16950.
19. F. Zieschang, A. Schmiedel, M. Holzapfel, K. Ansorg, B. Engels and C. Lambert, J. Phys. Chem. C, 2013, 117, 19816–19831.
20. Y. Li, G. He, X. Wang, Q. Guo, Y. Niu and A. Xia, ChemPhysChem, 2016, 17, 406–411.
21. J. Hu, Y. Li, H. Zhu, S. Qiu, G. He, X. Zhu and A. Xia, ChemPhysChem, 2015, 16, 2357–2365.
22. Y. Li, M. Zhou, Y. Niu, Q. Guo and A. Xia, J. Chem. Phys., 2015, 143, 034309-1–034309-12.
23. O. Varnavski, X. Yan, O. Mongin, M. Blanchard-Desce and T. Goodson III, J. Phys. Chem. C, 2007, 111, 149–162.
24. Y. Wang, G. S. He, P. N. Prasad and T. Goodson III, J. Am. Chem. Soc., 2005, 127, 10128–10129.
25. N. A. Montgomery, G. J. Hedley, A. Ruseckas, J. C. Denis, S. Schumacher, A. L. Kanibolotsky, P. J. Skabara, I. Galbraith, G. A. Turnbull and I. D. W. Samuel, Phys. Chem. Chem. Phys., 2012, 14, 9176–9184.
26. G. He, C. Yu, Y. Li, J. Hu, Z. Liu, D. Zhang, Q. Guo and A. Xia, Chem. – Asian J., 2016, 11, 2741–2748.
27. H. S. Cho, H. Rhee, J. K. Song, C. K. Min, M. Takase, N. Aratani, S. Cho, A. Osuka, T. Joo and D. Kim, J. Am. Chem. Soc., 2003, 125, 5849–5860.
28. F. Kournoutas, K. Seintis, N. Karakostas, J. Tydlitát, S. Achelle, G. Pistolis, F. Bureš and M. Fakis, J. Phys. Chem. A, 2019, 123, 417–428.
29. K. Seintis, D. Agathangelou, D. Cvejn, N. Almonasy, F. Bureš, V. Giannetas and M. Fakis, Phys. Chem. Chem. Phys., 2017, 19, 16485–16497.
30. Y. Wang, S. Yin, J. Liu, L. Yao, G. Wang, D. Liu, B. Jing, L. Cheng, H. Zhong, X. Shi, Q. Fang and S. Qian, RSC Adv., 2014, 4, 10960–10967.
31. Y. Wang, M. I. Ranasinghe and T. Goodson, J. Am. Chem. Soc., 2003, 125, 9562–9563.
32. N. S. Makarov, S. Mukhopadhyay, K. Yesudas, J. L. Brédas, J. W. Perry, A. Pron, M. Kivala and K. Müllen, J. Phys. Chem. A, 2012, 116, 3781–3793.
33. C. Katan, F. Terenziani, O. Morgin, M. H. V. Werts, L. Porrès, T. Pons, J. Mertz, S. Tretiak and M. Blanchard-Desce, J. Phys. Chem. A, 2005, 109, 3024–3037.
34. O. Varnavski, I. D. W. Samuel, L. O. Pålsson, R. Beavington, P. L. Burn and T. Goodson III, J. Chem. Phys., 2002, 116, 8893.
35. O. Varnavski, J. C. Ostrowski, L. Sukhomlinova, R. J. Twieg, G. C. Bazan and T. Goodson III, J. Am. Chem. Soc., 2002, 124, 1736–1743.
36. C. Sissa, A. Painelli, M. Blanchard-Desce and F. Terenziani, J. Phys. Chem. B, 2011, 115, 7009–7020.
37. M. Jia, X. Ma, L. Yan, H. Wang, Q. Guo, X. Wang, Y. Wang, X. Zhan and A. Xia, J. Phys. Chem. A, 2010, 114(27), 7345–7352.
38. A. Kuang, H. Song, Y. Guo, Q. Guo and A. Xia, Chin. J. Chem. Phys., 2019, 32, 59.
39. C. Sissa, V. Parthasarathy, D. Drouin-Kucma, M. H. V. Werts, M. Blanchard-Desce and F. Terenziani, Phys. Chem. Chem. Phys., 2010, 12, 11715–11727.
40. S. Easwaramoorthi, P. Thamaraiselvi, K. Duraimurugan, A. Jesin Beneto, A. Siva and B. Unni Nair, Chem. Commun., 2014, 50, 6902–6905.
41. A. Bhaskar, G. Ramakrishna, Z. Lu, R. Twieg, J. M. Hales, D. J. Hagan, E. Van Stryland and T. Goodson, J. Am. Chem. Soc., 2006, 128, 11840–11849.
42. Y. N. Luponosov, J. Min, A. N. Solodukhin, A. V. Bakirov, P. V. Dmitryakov, M. A. Shcherbina, S. M. Peregudova, G. V. Cherkaev, S. N. Chvalun, C. J. Brabec and S. A. Ponomarenko, J. Mater. Chem. C, 2016, 4, 7061–7076.
43. P. Hrobarik, V. Hrobarikova, I. Sigmundova, P. Zahradnik, M. Fakis, I. Polyzos and P. Persephonis, J. Org. Chem., 2011, 76, 8726–8736.
44. D. Cvejn, E. Michail, I. Polyzos, N. Almonasy, O. Pytela, M. Klikar, T. Mikysek, V. Giannetas, M. Fakis and F. Bureš, J. Mater. Chem. C, 2015, 3, 7345–7355.
45. M. Klikar, K. Seintis, I. Polyzos, O. Pytela, T. Mikysek, N. Almonasy, M. Fakis and F. Bures, ChemPhotoChem, 2018, 2, 465–474.
46. B. Li, R. Tong, R. Zhu, F. Meng, H. Tian and S. Qian, J. Phys. Chem. B, 2005, 109, 10705–10710.
47. H. Ceymann, M. Balkenhohl, A. Schmiedel, M. Holzapfel and C. Lambert, Phys. Chem. Chem. Phys., 2016, 18, 2646–2657.
48. C. Lambert, W. Gaschler, E. Schmälzlin, K. Meerholz and C. Bräuchle, J. Chem. Soc., Perkin Trans. 2, 1999, 577–588.
49. A. S. Davydov, Theory of Molecular Excitons, Plenum Press, New York, 1971.
50. F. Terenziani, C. Le Droumaguet, C. Katan, O. Mongin and M. Blanchard-Desce, ChemPhysChem, 2007, 8, 723–734.
51. F. Terenziani, A. Painelli, C. Katan, M. Charlot and M. Blanchard-Desce, J. Am. Chem. Soc., 2006, 128, 15742–15755.
52. M. Fakis, E. Stathatos, G. Tsigaridas, V. Giannetas and P. Persephonis, J. Phys. Chem. C, 2011, 115, 13429–13437.
53. A. Kaloudi-Chantzea, E. Martinou, K. Seintis, N. Karakostas, P. Giastas, F. Pitterl, H. Oberacher, M. Fakis and G. Pistolis, Chem. Commun., 2016, 52, 3388–3391.
54. I. Soutar, L. Swanson, R. L. Christensen, R. C. Drake and D. Phillips, Macromolecules, 1996, 29, 4931–4936.
55. M. I. Sluch, A. Godt, U. H. Bunz and M. A. Berg, J. Am. Chem. Soc., 2001, 123, 6447–6448.
56. C. M. Metzler, A. E. Cahill, S. Petty, D. E. Metzler and L. Láng, Appl. Spectrosc., 1985, 39, 333–339.
57. L. Reynolds, J. A. Gardecki, S. J. V. Frankland, M. L. Horng and M. Maroncelli, J. Phys. Chem., 1996, 100, 10337–10354.
58. M. Fakis, J. S. Beckwith, K. Seintis, E. Martinou, C. Nançoz, N. Karakostas, I. Petsalakis, G. Pistolis and E. Vauthey, Phys. Chem. Chem. Phys., 2018, 20, 837–849.
59. E. Martinou, K. Seintis, N. Karakostas, A. Bletsou, N. Thomaidis, M. Fakis and G. Pistolis, J. Phys. Chem. C, 2017, 121, 5341–5355.
60. G. J. Hedley, A. Ruseckas, A. C. Benniston, A. Harriman and I. D. W. Samuel, J. Phys. Chem. A, 2015, 119, 12665–12671.
61. J. Q. Gong, P. Parkinson, D. V. Kondratuk, G. Gil-Ramírez, H. L. Anderson and L. M. Herz, J. Phys. Chem. C, 2015, 119, 6414–6420.
62. C. Ramanan, C. Hoon Kim, T. J. Marks and M. R. Wasielewski, J. Phys. Chem. C, 2014, 118, 16941–16950.
63. F. Schlosser, J. Sung, P. Kim, D. Kim and F. Würthner, Chem. Sci., 2012, 3, 2778–2785.
64. C. Menelaou, J. Schiphorst, A. M. Kendhale, P. Parkinson, M. G. Debije, A. P. H. J. Schenning and L. M. Herz, J. Phys. Chem. Lett., 2015, 6, 1170–1176.
65. J. E. A. Webb, K. Chen, S. K. K. Prasad, J. P. Wojciechowski, A. Falber, P. Thordarson and J. M. Hodgkiss, Phys. Chem. Chem. Phys., 2016, 18, 1712–1719.
66. H. Langhals, A. J. Esterbauer, A. Walter, E. Riedle and I. Pugliesi, J. Am. Chem. Soc., 2010, 132, 16777–16782.
67. G. Weber, Biochem. J., 1952, 51, 145–155.
68. J. R. Lacowicz, Principles of Fluorescence Spectroscopy, Springer, 2006.
69. B. Dereka, A. Rosspeintner, Z. Li, R. Liska and E. Vauthey, J. Am. Chem. Soc., 2016, 138, 4643–4649.
70. B. Dereka, A. Rosspeintner, M. Krzeszewski, D. T. Gryko and E. Vauthey, Angew. Chem., Int. Ed., 2016, 55, 15624–15628.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01726d

‡ Present address: Department of Physical Chemistry, University of Geneva, 30 Quai Ernest-Ansermet, CH-1211, Geneva, Switzerland.

---