The reconstruction of the symmetry between sublattices: a strategy to improve the transport properties of edge-defective graphene nanoribbon transistors†
Abstract
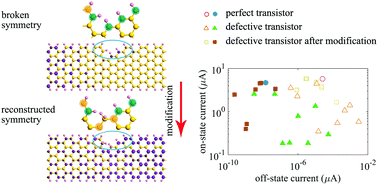
A numerical study that combines device simulation and first-principle calculations is performed, aiming to alleviate the performance degradation of graphene nanoribbon field-effect devices with edge defects. We believe that investigating the symmetry between the sublattices of graphene is a novel approach to understand this key problem. The results show that the edge defects that break the symmetry between the sublattices of graphene cause more severe degradation of the device performance because they induce highly localized electronic states, which dramatically affect the transport of carriers. We propose a strategy to alleviate the localization of electronic states by rebuilding the symmetry between the sublattices. This strategy can be realized by introducing foreign radicals to modify the defective edge. A stability analysis is performed to find the most stable modified structures. The final effect of our strategy on the corresponding devices demonstrates that it can effectively address specific edge defects and remarkably improve the ON-state current and subthreshold swing.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...