Open Access Article
Open Access ArticleUnderstanding ionic mesophase stabilization by hydration: a solid-state NMR study†
Debashis
Majhi
 a,
Jing
Dai
a,
Jing
Dai
 a,
Andrei V.
Komolkin
a,
Andrei V.
Komolkin
 b and
Sergey V.
Dvinskikh
b and
Sergey V.
Dvinskikh
 *ac
*ac
aDepartment of Chemistry, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden. E-mail: sergeid@kth.se
bFaculty of Physics, Saint Petersburg State University, Saint Petersburg 199034, Russia
cLaboratory of Biomolecular NMR, Saint Petersburg State University, Saint Petersburg 199034, Russia
First published on 1st June 2020
Abstract
The correlation between the water contribution to hydrogen bonding within ionic sublayer, mesophase order parameter, and ion translational self-diffusion in the layered ionic liquid crystalline phase is investigated. Changes in hydrogen bonding, conformational and translational dynamics, and orientational order upon hydration were followed by solid-state NMR combined with density functional theory (DFT) analysis. We observed that the smectic mesophase of monohydrated imidazolium-based ionic liquids, which was stabilized in a wider temperature range compared to that of anhydrous materials, counterintuitively exhibited a lower orientational order of organic cations. Thus the role of anisotropic alignment of cations and contribution of dispersion forces in the mesophase stability decreased upon hydration. The local dynamics of cations is controlled by the alignment of the bulky methyl-imidazolium ring, experiencing strong electrostatic and H-bond interactions in the ionic sublayer. Anisotropy of translational diffusion increased in the hydrated samples, thus supporting the layer-stabilizing effect of water. The effect of decreasing molecular order is outweighed by the contribution of water hydrogen bonding to the overall interaction energy within the ionic sublayer.
Introduction
Ionic liquids (ILs) that self-assemble into stable liquid-crystalline phases upon cooling from the isotropic state are referred to as ionic liquid crystals (ILCs). ILCs represent a new class of nonmolecular materials with significant potential in science and technology.1,2 A unique combination of high ionic conductivity in ILCs and anisotropy of their physicochemical properties is exploited in the development of functional materials for low-dimensional transport of electrons, ions, and molecules in electrochemical energy conversion and storage technologies.3 ILCs have been applied as aligning reaction media and nanostructured templates in the synthesis of ordered mesoporous materials.4,5 Similar to conventional isotropic ionic liquids, ILCs possess other important properties such as high electrochemical stability, air and moisture stability, vanishing vapour pressure, nonflammability. There has been a growing body of research aiming at the design of ILCs with an increasingly wider temperature range of the mesophase.1,2,6–15 The thermodynamic properties of ionic mesophases depending on composition have been thoroughly studied by systematic variation in the structure and properties of the constituting ions. For example, in heterocyclic imidazolium-based ILCs, the trend of increasing mesophase temperature range in the anion order BF4 < I < Br < Cl has been related to changes in charge delocalization properties and the hydrogen-bonding capabilities of the anions.1,7,16–18 Amphiphilic ILCs composed of bulky imidazolium cores linked to long alkyl chains of n ≥ 12 and compact inorganic or organic anions exhibit interdigitated smectic A bilayer phases. Charge delocalization in the imidazolium core reduces ionic interaction and thus promotes low transition temperatures.Experimental and computational studies of orientational order in ILCs have shown that the ionic smectic phases exhibit significantly lower molecular orientational order as compared to that in non-ionic liquid crystals.19–24 This suggested that dispersion forces, responsible for anisotropic alignment of neutral mesogenic molecules, are less important for the mesophase stability in ionic smectics. Strong electrostatic interactions in ionic samples contribute to stabilization of layered structures by a segregation of polar and apolar domains. Hydrogen bonding between cations and anions can further contribute to mesophase stabilization.25–33 Evidences of hydrogen bonding in ionic liquids have been obtained from crystal structure investigations in solid phase34–36 and by spectroscopic studies in the isotropic liquid state.25,28,37 Also in ionic mesophase, it has been generally recognized that mesophase stabilization is determined by a suitable balance between hydrogen bonding, electrostatic interactions, and dispersion forces.1 However, understanding the explicit roles and relative contributions of these interactions in determining the properties of ILCs is still a challenging task.
Hydrogen (H)-bonding interaction is particularly crucial for the behaviour of imidazolium-based ILCs with halogen counterions. The H-bond between two ionic species has been referred to as a doubly ionic H-bond to differentiate it from the well-established ionic H bond.31 In ILs containing water, a range of more traditional H-bonds is also present. Water-ionic liquid interactions have been comprehensively studied for non-mesogenic ILs.32,38–47 Mixing with water dramatically changes properties of ILs in a variety of applications. Water not only forms H-bonds with the anion and cation but also alters the cation–anion interactions.32,44,45 MD simulations have indicated that cation–anion coordination decreases in the presence of water compared to that in the neat ILs.46 At high water content hydrogen-bonding network can be disrupted.32 In water-rich systems, aggregation behaviour of ions plays an important role. Due to amphiphilic molecular structure, ionic liquids can exhibit lyotropic mesomorphism in water and other solvents.47–49 The hydrogen bonding between anions and water affects the phase behaviour of hydrated ILCs.1,34,50,51 It has been shown that some nonmesogenic anhydrous ILs exhibit a smectic phase in monohydrate form,51 thus confirming the essential role of water in mesophase formation. The controlled sample hydration provides a strategy for stabilization of the liquid-crystalline phase in a wider temperature range.
Because ILCs exhibit rather low values of the orientational order S, it was intuitively expected that a larger orientational order in the mesophase should correlate positively with higher thermodynamic stability. This logically comes from a physical picture of thermally agitated, highly dynamic molecules with a subtle preferential alignment along a common director. There has been supporting experimental evidence for such a correlation between the mesophase order parameter and stability range from our recent study of imidazolium-based ILCs with varying anions.23 A number of studies have reported on mesophase stabilization by sample hydration.34,35,50,51 However, orientational order and role of dispersion forces has not been addressed. It is worth emphasizing that with more available dynamic H-bond centres in hydrated materials, locally favoured H-bonds would have shorter lifetimes and contribute to molecular dynamics. Moreover, because the anions start to form H-bonds with the water molecules, the hydrogen bonding between cations and anions is weakened. Thus, changes in the H-bonding network not only modify the thermodynamic and structural properties of ILCs but also likely affect their molecular-level dynamics. It has been suggested that hydration modifies cation conformation and imidazolium ring alignment with respect to the layer normal,2,35 however, no experimental evidence supporting this scenario has been reported. To the best of our knowledge, there has been no study on the change in ion dynamics at a molecular level upon hydration. Such a study is crucial to elucidating the coupling between molecular ordering and the hydrogen-bonding contributions to mesophase stabilization.
In the present work, we investigate the hydration effect on ion dynamics in ILCs. Using advanced solid-state NMR methods in combination with density functional theory (DFT) calculations, local and molecular orientational order parameters and cation conformations in mesophases of anhydrous and hydrated imidazolium-based ILCs were determined. Translational dynamics within and across anisotropic aggregates was investigated by the pulse-field gradient NMR technique. We provide experimental evidence that, contrary to our intuition and discussions in the literature,1,2,35 increasing mesophase stability under hydration is accompanied by decreasing molecular order with essentially unmodified cation conformation. Based on the obtained experimental results, we discuss the relationships between the molecular dynamics, hydrogen bonding, and macroscopic mesophase stability.
Experimental section
Ionic mesogenic materials C12mimCl and C12mimBr (1-dodecyl-3-methylimidazolium chloride and bromide, respectively) were purchased from ABCR GmbH, Karlsruhe. Water content in the samples was controlled by recording 1H NMR spectra in isotropic phase. As received C12mimCl sample exhibited negligible water content <0.4 mol%. Anhydrous C12mimBr sample was prepared by equilibrating for a week in a desiccator with P2O5 powder (air relative humidity RH < 0.5%). Monohydrated samples were prepared by equilibrating for about 12 h in a desiccator with RH ≈ 85%, stabilized by a saturated KCl solution. The water contents and phase transition temperatures in the samples used for NMR measurements are indicated in Table S1 in ESI.† The hydrated samples exhibited significantly wider smectic phase ranges.NMR measurements in the smectic phase were performed in static samples aligned in the magnetic field of the NMR spectrometer with the phase director distributed in the plane perpendicular to the magnetic field vector (Fig. 1a), unless stated otherwise. Experiments were performed using the Bruker 500 Avance III spectrometer at Larmor frequencies of 500.1, 125.7, 76.7, and 50.7 MHz for 1H, 13C, 2H, and 15N, respectively. Dipolar 1H–13C spectra were recorded using proton detected/encoded local field (PDLF) NMR spectroscopy (see Section S2 in ESI†) and amplitude-and-phase modulated cross-polarization (APM-CP) spectroscopy in static and magic-angle-spinning (MAS) samples (Section S3), respectively.52–5513C–13C dipolar couplings at natural isotopic abundance were measured by a 2D dipolar double-quantum filtering experiment (Section S4, ESI†).22,5615N–13C dipolar couplings were obtained by a recently developed approach for the 15N–13C dipolar spectroscopy at natural isotopic abundance (Section S5, ESI†).57,58 Natural abundance deuterium (NAD) NMR spectra were recorded in the presence of the proton heteronuclear decoupling (Section S6, ESI†). The diffusion measurements using pulsed field gradient (PFG) 1H NMR were performed with a Bruker microimaging probe MIC5 with 3-directional orthogonal magnetic field gradients of maximum strength 2.8 T m−1. PFG NMR technique combined with spin-decoupling was used.59,60
 | ||
| Fig. 1 (a) Illustration of ionic smectic A layers aligned in the magnetic field B0. (b) 2D 13C–1H PDLF spectrum of C12mimBr·H2O sample in the smectic A phase at 107 °C. (c) Dipolar coupling constants dCH calculated from PDLF spectrum of Fig. 1b. Cation structure and atomic numbering are shown at the top. | ||
The stability of the hydration level during the spectroscopic and diffusion measurements was confirmed by inspecting the 1H NMR water signal intensity in the isotropic phase prior and after completing the experiments. Water peak was observed in the range 3–4 ppm and was well separated from other signals in the spectra (see Fig. S8 in ESI†).
DFT computational analysis of C12mim cation was performed using Gaussian-16 program.61 Several conformers were examined distinguished by trans or gauche conformation of the first segments of the alkyl chain. Reported crystal structures were used to set up input geometries.34–36 Optimization was performed for isolated ions (in vacuo) with B3LYP/6-311++G** theory level. The structure with all-trans chain conformation exhibited lowest energy. Only most probable low-energy conformers (approximately with ΔE < 10 kJ mol−1) were considered.
Results
Dipolar couplings
The proton NMR spectra in mesophase were strongly broadened by homonuclear proton couplings (Fig. S1a in ESI†). In contrast, carbon-13 proton-decoupled spectra were well resolved (Fig. 1b and Fig. S1b in ESI†). Carbon–proton dipolar splittings for each in-equivalent carbon were measured in a two-dimensional (2D) proton detected/encoded local field (PDLF) experiment (Fig. S2a, ESI†).53 A representative 2D plot of the dipolar splittings (vertical axis) correlated to 13C anisotropic chemical shifts (horizontal axis) in the sample C12mimBr·H2O is shown in Fig. 1b. Dipolar cross sections are displayed in ESI† Fig. S2b.It may be recalled that in the PDLF technique, the spectral splitting Δν in the dipolar dimension results from the contribution of the direct dipolar coupling dCH and indirect spin coupling JCH:
| Δν = k(2dCH + JCH) | (1) |
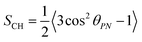 | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γC are gyromagnetic ratios).
γC are gyromagnetic ratios).
Only absolute values of the splittings Δν (eqn (1)) can be obtained from the symmetric doublets in the PDLF spectra. Based on molecular geometry and the director alignment, the coupling constants dCH for the carbons in the alkyl chain were expected to be negative. This was confirmed by comparing the dCH values, calculated from eqn (1), to the corresponding quadrupolar splittings ΔνQ = −(3/4)χQSCH (cf. to eqn (3)), measured in a natural-abundance deuterium (NAD) NMR spectra (representative NAD spectrum is shown in ESI† in Fig. S6). For the aliphatic sites, with a well-defined quadrupolar coupling constant χQ = 168 kHz, these two parameters are simply related as ΔνQ/dCH ≈ 11.7.64 For the chain carbons in the C12mim cation, this condition could be satisfied only by assuming negative signs of dCH in eqn (1).
The same approach to dCH sign determination is, however, not reliable for the imidazolium sites where the quadrupolar coupling constant χQ can vary in a wide range.37 Hence, we designed a different method to determine the signs of the dipolar coupling in the imidazolium ring. Dipolar spectra of the C–H pairs in the imidazolium moiety were recorded under the magic angle spinning (MAS) condition applying the amplitude- and phase-modulated cross-polarization (APM-CP) dipolar recoupling scheme (Fig. S3a and b, ESI†).54 Splittings in the APM-CP spectra are given as  (where
(where  is the scaling factor of the APM-CP sequence54). Thus, comparing the spectral splittings obtained by the PDLF and APM-CP techniques (the comparison is shown in Fig. S3c, ESI†), the magnitudes and signs of the dCH constants for the imidazolium C–H pairs were unambiguously determined.
is the scaling factor of the APM-CP sequence54). Thus, comparing the spectral splittings obtained by the PDLF and APM-CP techniques (the comparison is shown in Fig. S3c, ESI†), the magnitudes and signs of the dCH constants for the imidazolium C–H pairs were unambiguously determined.
Dipolar couplings dCH were obtained in anhydrous and monohydrated samples C12mimCl and C12mimBr depending on mesophase temperature. The dipolar coupling constants dCH, calculated from the 2D PDLF spectrum in Fig. 1b, are shown in Fig. 1c.
Bond order parameter profiles of the alkyl chain
Experimental SCH order parameter profiles for the alkyl chains in hydrated ILC samples in the smectic A phase are displayed in Fig. 2. The SCH values are negative, in agreement with the average directions of the C–H bond perpendicular to the long molecular axis. The conformational mobility of the flexible chains with a gradually increasing population of gauche conformers toward the chain terminal led to a decrease in SCH values along the chain. The slight drop of the SCH value for the first carbon was due to the contribution of lower-probability conformers with a particular alignment of the imidazolium ring, as discussed in the next section.In previous experimental and molecular dynamics (MD) studies of the smectic A phases of these and analogous ILCs, it has been suggested that the chain segments in the vicinity of the imidazolium group are predominantly in trans conformations and that the chain backbone is roughly aligned along the director.21,22 As we show below, such a structure is consistent with the experimental dipolar couplings for the imidazolium ring.
In the C12mimCl·H2O sample, the alkyl chains exhibited consistently higher magnitudes of the bond-order parameters (Fig. 2) in comparison with those in C12mimBr·H2O, if taken at comparable relative temperatures ΔT = TC − T with respect to the clearing temperature TC (temperature of smectic-to-isotropic phase transition). This suggests that the orientational-order parameter S is higher in the chloride salt. A similar trend was previously reported for anhydrous analogs.23
Alignment of imidazolium ring
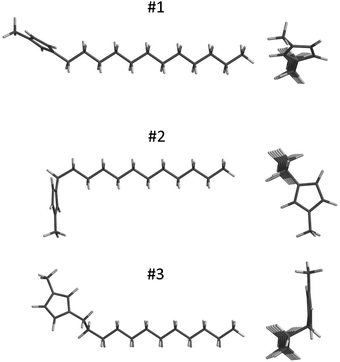
Fig. 3 shows the signs and magnitudes of the C–H bond-order parameters for the imidazolium ring obtained in the smectic A phase of anhydrous and monohydrate C12mimCl and C12mimBr salts. In the following, we interpret these data using structural parameters derived from DFT-optimized molecular geometry. We examined low-energy cation structures with different alignments of the imidazolium moiety with respect to the alkyl chain and long molecular axis. Input geometries were set up based on reported crystal structures.34–36 In the analysis of the bond order parameters, we neglected a possible contribution of the biaxiality term Sxx − Syy of the ordering matrix, tentatively assuming that Szz ≫ Sxx − Syy.64 It turned out that the accuracy of this approximation was sufficient to correctly predict signs and relative magnitudes of the bond-order parameters, both in the imidazolium ring and the alkyl chain.With emphasis on low-energy conformers (ΔE < 10 kJ mol−1, or probability above 5%), three different alignments of the imidazolium ring with respect to the layer normal (along the average direction of the long axis of the cation in the smectic A phase) were identified. The lowest energy was obtained for the most-stretched all-trans chain conformation, structure #1 displayed in Fig. 4. The angular factors P2 = (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2θ − 1)/2 for C–H bond directions, calculated with respect to the alkyl chain long axis, were in reasonable qualitative agreement with the experimental data as concerning the signs and relative values of the SCH parameters (Table 1). Two conformers, distinguished by the 180° flip of the ring plane about the N(1)–C1 bond and exhibiting virtually equal equilibrium energies, displayed similar P2 values (for atom numbering, refer to Fig. 1).
cos2θ − 1)/2 for C–H bond directions, calculated with respect to the alkyl chain long axis, were in reasonable qualitative agreement with the experimental data as concerning the signs and relative values of the SCH parameters (Table 1). Two conformers, distinguished by the 180° flip of the ring plane about the N(1)–C1 bond and exhibiting virtually equal equilibrium energies, displayed similar P2 values (for atom numbering, refer to Fig. 1).
| Conformation | Energya (Hartree) | ΔE,b kJ mol−1 | 〈P2〉 | |||
|---|---|---|---|---|---|---|
| C(2)–H(2) | C(4)–H(4) | C(5)–H(5) | C1–H1 | |||
| a For each conformer, two structures distinguished by the 180° flip of the ring plane about the N1–C1 bond, were optimized and average values are presented in the table. b Energy increase with respect to structure #1. | ||||||
| #1 | −737.883650 | — | −0.472 | 0.129 | −0.220 | −0.498 |
| #2 | −737.883498 | 0.4 | −0.379 | −0.408 | −0.444 | −0.023 |
| #3 | −737.882612 | 3.0 | 0.357 | 0.993 | −0.467 | −0.101 |
Geometry optimization was also done for other low-energy conformers obtained by ±120° rotation around the C1–C2 bond in the chain. The equilibrium energy for this L-shaped structure #2, shown in Fig. 4, was only slightly higher compared to structure #1 (Table 1). However, the ring plane alignment, nearly perpendicular to the long molecular axis, resulted in approximately equal SCH values for the three carbons in the ring, in disagreement with the experimental values. In particular, the L-shaped structure led to large and negative coupling constant for the C(4)–H(4) spin pair, in contrast to a relatively small and positive experimental value. Moreover, the predicted C1–H1 coupling in the chain was much smaller compared to the experimental value.
Conformer #3, with the ring plane parallel to the chain backbone plane, was also analysed (Fig. 4). This was obtained by optimizing the structure with the C2–C3 bond set to gauche conformation. Such a molecular shape, however, has significantly higher equilibrium energy (Table 1). Because it also resulted in order parameters that were inconsistent with the experimental data, its contribution was neglected.
Thus, only the extended molecular structure #1 exhibited bond order parameters consistent with the experimental values. This conclusion was generally valid for investigated C12mimX salts with different anions X = BF4, I, Cl, and Br (Fig. S7 in ESI†). A small contribution of the gauche conformer #2, up to ≈10%, improved agreement of the simulated order parameters with the experimental values for the imidazolium carbons. Additionally, it explains a slight drop of the C–H bond order observed for the first carbon, C1, in the order-parameter profile of the alkyl chain in Fig. 2.
Independent support for the dominant conformation #1 was obtained from longer-range couplings over two chemical bonds. To confirm the trans conformation at the beginning of the chain, we examined the couplings between the atoms C–C or N–C separated by two chemical bonds in the structural motif N(1)–C1–C2–C3–C4–C5. Coupled spin pairs 13C–13C and 15N–13C, occurring at extremely low natural abundance levels of 0.012% and 0.004%, respectively, were selectively detected, whereas a much stronger signal of uncoupled spins was suppressed. 13C–13C couplings were measured by a 2D dipolar double-quantum filtering experiment, described in ESI,† Fig. S4a and b. The 15N–13C couplings were obtained by a recently developed approach for 15N–13C dipolar spectroscopy, explained in Fig. S5a and b (ESI†).57,58
For structure #1, the vector N(1)–C2 is along the chain backbone. Because it is nearly collinear with the Cn–Cn+2 vectors of the chain, similar values of the order parameters SN(1)–C2 ≈ SC1–C3 ≈ SC2–C4 ≈ SC3–C5 were expected in this case. In contrast, for the other two conformations, the N(1)–C2 vector is tilted nearly at the magic angle to the chain axis, and thus it should have led to a vanishing SN(1)–C1 order parameter (for conformation #3, both SN(1)–C1 and SC1–C3 are small). Comparable values of the experimentally determined order parameters for the spin pairs shown in Fig. 5 provided strong evidence for the dominant head group alignment according to structure #1. Comparison to the corresponding C–H bond-order parameters revealed excellent consistency between the two data sets. In Fig. 5, the expected difference by a factor of −0.5 for the vectors along and perpendicular to the molecular axis is indeed observed. These results provide validation for the conformational structure of the cation in the mesophase.
Order parameters of organic cations
Although local bond-order parameters characterize molecular conformation at an atomic level, the S parameter provides a basis to compare various ILCs in a general way. To estimate molecular orientational order parameter S for the organic cation C12mim, we considered a model of the alkyl chain with dominant trans conformation of the groups in the vicinity of the imidazolium core and with the symmetry axis of this part parallel to the long molecular axis.21,22 Neighbouring molecules force the alkyl chains to adopt conformations with the average long molecular axis as near as possible collinear with the layer normal. In keeping with the model, we assumed that the alignment of the imidazolium core depends on the conformation of the first chain segments but not on the conformation of the rest of the chain. This model was adequate to consistently interpret experimental data for the C–H bonds for the alkyl chain for C12mim and C14mim cations with a wide range of anions.22,23 As discussed above, the model correctly predicted the signs and relative magnitudes of the C–H couplings in the imidazolium head. It was also supported by an MD computational analysis in analogous ILCs.21 Thus, the order parameter S was estimated from the relationshipSCH = 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θPM)〉S ≈ −0.5 S θPM)〉S ≈ −0.5 S | (4) |
Translational dynamics
Molecular/ionic translational dynamics (self-diffusion) in smectic liquid crystals, albeit anisotropic, is relatively fast, in spite of high macroscopic viscosity. Typically, diffusion coefficients D in the meso- and isotropic phases are of comparable magnitudes.59 The diffusion coefficient in the isotropic phase is routinely measured by spin-echo-based pulsed-field-gradient (PFG) NMR technique.66 Diffusion in a liquid-crystalline state cannot be measured by conventional PFG NMR methods due to the short lifetimes (<100 μs) of the spin coherences. Fast decay of spin coherences results from strong dipole spin interactions present in anisotropic phases. Hence, PFG NMR techniques combined with spin-decoupling specifically designed for diffusion studies of anisotropic fluids have been used.59,60 To measure the two principal diffusion components in our samples, along and normal to the phase director, the field gradients in orthogonal directions were applied in separate experiments. The sample director was distributed in the plane perpendicular to the external static magnetic field direction. In the experiment with the gradient applied along the magnetic field (z-axis), the diffusion coefficient D⊥ within the layers (that is, perpendicular to the phase director) was calculated directly from spin echo attenuation using the Stejskal–Tanner relation:66 | (5) |
When the gradient is applied in a perpendicular direction (x or y), composite diffusion decay results because of a “2D powder” distribution of the director in the xy-plane.
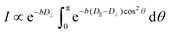 | (6) |
The diffusion coefficient along the director, D‖, was obtained via numerical fit of experimental decays to the integral eqn (6).
Diffusion in the smectic phase was found to be much faster within the layers compared to the diffusion across the layers in both neat and hydrated salts (Fig. 7). The translational mobility in the monohydrate material was faster by nearly one order of magnitude. Activation energy for the translation within the layers decreased significantly upon hydration, from 47 kJ mol−1 to 31 kJ mol−1. Remarkably, diffusion anisotropy in the smectic phase, η = D⊥/D‖, increased in the hydrated samples, contrary to the reorientational anisotropy given by the order parameter S discussed above. Hence, upon hydration, the translational mobility within the layers (D⊥) accelerated to a larger extent compared to that across the layers (D‖). Increasing diffusional anisotropy, with more hindered displacement between the layers, stabilized the smectic structure.
 | ||
| Fig. 7 Cation diffusion coefficients, Diso (○), D‖ (■), and D⊥ (●) in the isotropic and smectic A phases of C12mimBr (left) and C12mimBr·H2O (right) ILs. Lines are visual guides. | ||
Discussion
Orientational order decreases upon hydration
In the context of previous studies, which showed that an increased mesophase stability range is accompanied by increased orientational order of organic cations,23 the unexpected finding of the present work is that the opposite trend is displayed upon hydration. In the following, a molecular-level explanation for this counterintuitive behaviour is suggested.Anisotropic molecular mobility in ionic mesophases is generally characterized by a low orientational order S compared to that in neutral liquid crystals. Molecular theories of a neutral smectic phase predict order parameters above 0.6,67–69 which is in agreement with experimental observations.70,71 Such a high molecular order is essential for mesophase stability because the mutual alignment of neutral molecules is driven by weak van der Waals interactions. In contrast, in ILCs, because of the presence of much stronger electrostatic interactions inducing the segregation of polar and apolar domains, a stable layer structure can form with a low orientational order. Strong hydrogen bonding between cations and halogen anions in imidazolium-based ILCs further contributes to the phase stabilization. The increased stability range of the smectic phase upon hydration has been attributed to the involvement of water molecules in H-bonding interactions within ionic sublayers.2,34 The anion forms hydrogen bonds mainly with imidazolium protons and with water protons. Computational studies have also indicated that, at increasing concentrations, the water molecules can form hydrogen bonds directly with imidazolium ring protons, mainly at position C(2) and to a lesser extent at positions C(4) and C(5).72
Hydration has a twofold effect on the cation dynamics. On one hand, because anions participate in H-bonds with water molecules, the hydrogen bonding between cations and anions is weakened. To prove this, we compared the chemical shifts of imidazolium protons in anhydrous and monohydrate samples. A higher 1H chemical shift is indicative of stronger hydrogen bonding.28,73 The proton chemical shift in the imidazolium ring was found to decrease in the hydrated samples as compared to that in their anhydrous counterparts (Fig. S8 in ESI†). The decreased cation–anion interaction led to increased dynamics of the cation. The mechanism is analogous to the case where a cation is replaced by one with a lower ability for the hydrogen bonding. Indeed, in our previous study of imidazolium-based ILCs with different anions, increased cation dynamics was found in the anion sequence Cl−–Br−–I−–BF4−, exhibiting a decreasing hydrogen-bonding ability.23 The same trend we also observed in the present study of the hydrated materials. Note that other properties of anions, such as ionic volume and charge delocalization, may influence the orientation order and phase stability. The combined effect was decreasing molecular order for bulkier anions.
On the other hand, because of a higher density of H-bond centres, a continuous H-bond network is formed, which coordinates anion–water, anion–cation, and cation–water interactions. This facilitates the mesophase stabilization via supporting the smectic layer structure in spite of a higher dynamic disorder. In other words, enhanced by water, a stronger H-bonding network within an ionic sublayer supports the formation of a thermodynamically stable smectic phase of less-ordered molecules. Further support for this conclusion was obtained from the translational diffusion data.
Hydrogen bond network stabilizes the conformation of cations
C–H dipolar coupling in the imidazolium moiety is a sensitive probe of the ring plane alignment with respect to the phase director. DFT analysis revealed several low-equilibrium-energy conformers with different orientations of the imidazolium core with respect to the molecular axis (Fig. 4). The core alignment is essentially determined by the conformation of the alkyl chain segments near the ring. It has been suggested in the literature that modification of the hydrogen-bonding network, either by changing anions or adding water, leads to changes in molecular conformation.2,35,74 Restricting the conformational dynamics, in general, contributes to higher molecular order and thus to mesophase stability. However, our results do not support this scenario in hydrated mesophases. No evidence of significant changes in the molecular conformation upon mesophase hydration was found, at least in the vicinity of charged moieties of the long-chain organic cations. In fact, order parameters were lower in the hydrated phase, whereas cations adopted essentially the same conformation as that found in anhydrous counterparts.Combined analysis of the experimental C–H, C–C, and C–N dipolar couplings proved predominantly trans conformation for the chain part in the vicinity of the head group. The SCH bond order parameters in the imidazolium head were consistent with the most extended molecular conformation and did not change significantly upon hydration. Diffraction studies of analogous monohydrated salts in solid phase have shown that, although both linear and bent cation conformations (molecules #1 and #2 in Fig. 4, respectively) were present in crystal structures, only for the former case has an infinite OH–halogen hydrogen-bonded network, also involving H bonds to imidazolium atoms, been found.35 This suggested that also in mesophase the linear geometry is favourable for H-bond network formation and thus explained conformation stabilization despite increasing reorientational dynamics (lower orientational order) in monohydrated samples.
Higher diffusional anisotropy correlates with increasing H-bond interactions
The translational dynamics within the layers was faster compared to that across the layers, D⊥ > D‖, and it accelerated upon hydration following increasing reorientational dynamics (Fig. 7). However, the hydrated sample exhibited larger diffusion anisotropy, η = D⊥/D‖. This held also for diffusion in a chlorine salt, reported in our previous work.75 Increasing diffusional anisotropy stabilized the smectic layers of less orientationally ordered cations. In hydrated materials, the H-bond network, localized in ionic sublayers, is denser but it has a more dynamic nature. Cation diffusion within the layers proceeds with less disruption of the hydrogen bonding and is characterized by much low activation energy, in contrast to cation displacement across the layers. Hence, a denser H-bond network in the presence of water molecules leads to increased diffusion anisotropy. Note that the water itself exhibits significant anisotropy of the translational diffusion (Fig. S9 in ESI†). Also, anion diffusion is highly anisotropic, as has been demonstrated in an analogous ILC with BF4 counterions.60,75Conclusions
We studied the orientational order and translational dynamics in monohydrated mesogenic ionic liquids, where water molecules contributed to the mesophase stabilization by the formation of a hydrogen-bonding network in the ionic sublayers. Our findings shed light on the mechanism of layered structure stabilization by hydration from the perspective of molecular-level dynamics. We showed, for the first time, that the increasing mesophase stability upon hydration was accompanied by decreasing cation orientational order. Hence, anisotropic alignment of the long-chain cations became less important for the layer formation. The contribution of water hydrogen bonding to the overall interaction energy shifted the delicate balance between different intermolecular forces responsible for mesophase stabilization.In anhydrous materials, hydrogen bonding between anions and the imidazolium head leads to a restriction of cation mobility. The order parameter increases and the mesophase stability range is extended. The sample hydration, investigated in the current study, resulted in further mesophase stabilization by extending the H-bond network, but counterintuitively the molecular order decreased. However, the cation conformation and imidazolium ring alignment to the layer normal is not significantly affected by the decreasing order. Thus, the hydration effect was twofold. Because of more abundant and dynamic H-bond centres, the imidazolium moiety gained more freedom, which also affected the chain dynamics. The cation order parameter decreased. However, a stronger H-bond network counteracted the increasing molecular disorder by contributing to polar/apolar domain segregation, and the smectic layer structure was stabilized. This mechanism is also supported by translational diffusion data demonstrating higher diffusional anisotropy in the hydrated phase.
Here, we have revealed the correlation in the ionic mesophase between hydrogen bonding modified by hydration, the orientational order parameter, and ion translational dynamics. Increased overall interaction energy in ionic sublayer resulted in a more dynamic phase with significantly extended temperature stability range. The observed effects on the thermodynamics and ionic mobility of ILCs are important for understanding ILC properties and are of particular interest for improving design strategies and expanding the application range of mesogenic ionic liquids.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swedish Research Council VR (project no. 2017-04278) and by the Russian Foundation for Basic Research (project no. 17-03-00057).References
- K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Chem. Rev., 2016, 116, 4643–4807 CrossRef CAS PubMed.
- A. A. Fernandez and P. H. J. Kouwer, Int. J. Mol. Sci., 2016, 17, 731 CrossRef PubMed.
- T. Kato, M. Yoshio, T. Ichikawa, B. Soberats, H. Ohno and M. Funahashi, Nat. Rev. Mater., 2017, 2, 17001 CrossRef.
- C. K. Lee, H. W. Huang and I. J. B. Lin, Chem. Commun., 2000, 1911–1912 RSC.
- A. Taubert, Angew. Chem., Int. Ed., 2004, 43, 5380–5382 CrossRef CAS PubMed.
- L. Douce, J. M. Suisse, D. Guillon and A. Taubert, Liq. Cryst., 2011, 38, 1653–1661 CrossRef CAS.
- M. Wang, X. Pan, S. F. Xiao, C. N. Zhang, W. X. Li and S. Y. Dai, J. Mater. Chem., 2012, 22, 2299–2305 RSC.
- Y. V. Nelyubina, A. S. Shaplov, E. I. Lozinskaya, M. I. Buzin and Y. S. Vygodskii, J. Am. Chem. Soc., 2016, 138, 10076–10079 CrossRef CAS PubMed.
- P. Judeinstein, S. Huet and P. Lesot, RSC Adv., 2013, 3, 16604–16611 RSC.
- K. Stappert, G. Lipinski, G. Kopiec, E. T. Spielberg and A. V. Mudring, Cryst. Growth Des., 2015, 15, 5388–5396 CrossRef CAS.
- M. Yang, K. Stappert and A. V. Mudring, J. Mater. Chem. C, 2014, 2, 458–473 RSC.
- X. J. Wang, F. W. Heinemann, M. Yang, B. U. Melcher, M. Fekete, A. V. Mudring, P. Wasserscheid and K. Meyer, Chem. Commun., 2009, 7405–7407 RSC.
- X. J. Wang, M. Sternberg, F. T. U. Kohler, B. U. Melcher, P. Wasserscheid and K. Meyer, RSC Adv., 2014, 4, 12476–12481 RSC.
- M. Yang, B. Mallick and A. V. Mudring, Cryst. Growth Des., 2014, 14, 1561–1571 CrossRef CAS.
- K. Goossens, L. Rakers, T. J. Shin, R. Honeker, C. W. Bielawski and F. Glorius, Crystals, 2019, 9, 34 CrossRef.
- A. E. Bradley, C. Hardacre, J. D. Holbrey, S. Johnston, S. E. J. McMath and M. Nieuwenhuyzen, Chem. Mater., 2002, 14, 629–635 CrossRef CAS.
- J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133–2139 RSC.
- C. M. Gordon, J. D. Holbrey, A. R. Kennedy and K. R. Seddon, J. Mater. Chem., 1998, 8, 2627–2636 RSC.
- G. C. Ganzenmuller and G. N. Patey, Phys. Rev. Lett., 2010, 105, 137801 CrossRef CAS PubMed.
- G. Saielli, Soft Matter, 2012, 8, 10279–10287 RSC.
- G. Saielli, J. Phys. Chem. B, 2016, 120, 2569–2577 CrossRef CAS PubMed.
- J. Dai, B. B. Kharkov and S. V. Dvinskikh, Crystals, 2019, 9, 18 CrossRef.
- J. Dai, D. Majhi, B. B. Kharkov and S. V. Dvinskikh, Crystals, 2019, 9, 495 CrossRef.
- M. J. Quevillon and J. K. Whitmer, Materials, 2018, 11, 64 CrossRef PubMed.
- A. G. Avent, P. A. Chaloner, M. P. Day, K. R. Seddon and T. Welton, J. Chem. Soc., Dalton Trans., 1994, 3405–3413 RSC.
- K. Dong, S. J. Zhang, D. X. Wang and X. Q. Yao, J. Phys. Chem. A, 2006, 110, 9775–9782 CrossRef CAS PubMed.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef CAS PubMed.
- T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem. – Eur. J., 2010, 16, 9018–9033 CrossRef CAS PubMed.
- A. Wulf, K. Fumino and R. Ludwig, Angew. Chem., Int. Ed., 2010, 49, 449–453 CrossRef CAS PubMed.
- V. Balevicius, Z. Gdaniec, L. Dziaugys, F. Kuliesius and A. Marsalka, Acta Chim. Slov., 2011, 58, 458–464 CAS.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- K. Dong, S. J. Zhang and J. J. Wang, Chem. Commun., 2016, 52, 6744–6764 RSC.
- A. E. Khudozhitkov, J. Neumann, T. Niemann, D. Zaitsau, P. Stange, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 17863–17871 CrossRef CAS.
- A. Getsis and A. V. Mudring, Cryst. Res. Technol., 2008, 43, 1187–1196 CrossRef CAS.
- A. Downard, M. J. Earle, C. Hardacre, S. E. J. McMath, M. Nieuwenhuyzen and S. J. Teat, Chem. Mater., 2004, 16, 43–48 CrossRef CAS.
- A. Getsis and A. V. Mudring, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, O2945–O2946 CrossRef CAS.
- A. Wulf, K. Fumino, D. Michalik and R. Ludwig, ChemPhysChem, 2007, 8, 2265–2269 CrossRef CAS PubMed.
- W. Shi, K. Damodaran, H. B. Nulwala and D. R. Luebke, Phys. Chem. Chem. Phys., 2012, 14, 15897–15908 RSC.
- B. L. Bhargava, Y. Yasaka and M. L. Klein, Chem. Commun., 2011, 47, 6228–6241 RSC.
- E. A. Crespo, N. Schaeffer, J. A. P. Coutinho and G. Perez-Sanchez, J. Colloid Interface Sci., 2020, 574, 324–336 CrossRef CAS PubMed.
- M. D. Fayer, Chem. Phys. Lett., 2014, 616, 259–274 CrossRef.
- T. Koishi, J. Phys. Chem. B, 2018, 122, 12342–12350 CrossRef CAS PubMed.
- Y. Nikawa, K. Fujita and H. Ohno, Phys. Chem. Chem. Phys., 2017, 19, 8148–8151 RSC.
- S. Konar, A. Sharma, S. Banerjee, P. K. Ghorai and R. Biswas, Chem. Phys., 2019, 524, 31–39 CrossRef CAS.
- D. Bankmann and R. Giernoth, Progr. Nucl. Magn. Reson. Spectrosc., 2007, 51, 63–90 CrossRef CAS.
- R. Macchieraldo, L. Esser, R. Elfgen, P. Voepel, S. Zahn, B. M. Smarsly and B. Kirchner, ACS Omega, 2018, 3, 8567–8582 CrossRef CAS PubMed.
- T. Inoue, B. Dong and L. Q. Zheng, J. Colloid Interface Sci., 2007, 307, 578–581 CrossRef CAS PubMed.
- C. Fairhurst, S. Fuller, J. Gray, M. C. Holmes and G. J. T. Tiddy, in Handbook of Liquid Crystals, ed. D. Demus, J. W. Goodby, G. W. Gray, H.-W. Spiess and V. Vill, Wiley-VCH, Weinheim, 1998, vol. 3, pp. 341–392 Search PubMed.
- M. A. Firestone, J. A. Dzielawa, P. Zapol, L. A. Curtiss, S. Seifert and M. L. Dietz, Langmuir, 2002, 18, 7258–7260 CrossRef CAS.
- L. N. Puntus, K. J. Schenk and J. C. G. Bunzli, Eur. J. Inorg. Chem., 2005, 4739–4744 CrossRef CAS.
- H. Chen, D. C. Kwait, Z. S. Gonen, B. T. Weslowski, D. J. Abdallah and R. G. Weiss, Chem. Mater., 2002, 14, 4063–4072 CrossRef CAS.
- S. V. Dvinskikh, H. Zimmermann, A. Maliniak and D. Sandström, J. Magn. Reson., 2003, 163, 46–55 CrossRef CAS PubMed.
- B. B. Kharkov, V. I. Chizhik and S. V. Dvinskikh, J. Magn. Reson., 2012, 223, 73–79 CrossRef CAS PubMed.
- S. V. Dvinskikh, V. Castro and D. Sandström, Phys. Chem. Chem. Phys., 2005, 7, 3255–3257 RSC.
- S. V. Dvinskikh and V. I. Chizhik, J. Exp. Theor. Phys., 2006, 102, 91–101 CrossRef CAS.
- D. Sandström and M. H. Levitt, J. Am. Chem. Soc., 1996, 118, 6966–6974 CrossRef.
- M. Cifelli, V. Domenici, V. I. Chizhik and S. V. Dvinskikh, Appl. Magn. Reson., 2018, 49, 553–562 CrossRef CAS PubMed.
- L. Jackalin, B. B. Kharkov, A. V. Komolkin and S. V. Dvinskikh, Phys. Chem. Chem. Phys., 2018, 20, 22187–22196 RSC.
- S. V. Dvinskikh and I. Furó, Russ. Chem. Rev., 2006, 75, 497–506 CrossRef CAS.
- M. Cifelli, V. Domenici, B. B. Kharkov and S. V. Dvinskikh, Mol. Cryst. Liq. Cryst., 2015, 614, 30–38 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- E. Breitmaier and W. Voelter, Carbon-13 NMR Spectroscopy. High-Resolution Methods and Applications in Organic Chemistry and Biochemistry, VCH, Weinheim, 1990 Search PubMed.
- B. M. Fung, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 41, 171–186 CrossRef CAS.
- J. W. Emsley, P. Lesot, G. De Luca, A. Lesage, D. Merlet and G. Pileio, Liq. Cryst., 2008, 35, 443–464 CrossRef CAS.
- S. V. Dvinskikh, in Modern Methods in Solid-State NMR: A practitioners’ Guide, ed. P. Hodgkinson, Royal Society of Chemistry, Abingdon, 2018 Search PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- W. L. McMillan, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 1238–1246 CrossRef.
- K. K. Kobayashi, Mol. Cryst. Liq. Cryst., 1971, 12, 137–148 CrossRef.
- G. Pajak and M. A. Osipov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012507 CrossRef CAS PubMed.
- J. W. Doane, R. S. Parker, D. Cvikl, D. L. Johnson and D. L. Fishel, Phys. Rev. Lett., 1972, 28, 1694–1696 CrossRef CAS.
- M. Constant and D. Decoster, J. Chem. Phys., 1982, 76, 1708–1711 CrossRef CAS.
- Q. G. Zhang, N. N. Wang and Z. W. Yu, J. Phys. Chem. B, 2010, 114, 4747–4754 CrossRef CAS PubMed.
- A. D. Headley and N. M. Jackson, J. Phys. Org. Chem., 2002, 15, 52–55 CrossRef CAS.
- M. E. Di Pietro, T. Margola, G. Celebre, G. De Luca and G. Saielli, Soft Matter, 2019, 15, 4486–4497 RSC.
- S. V. Dvinskikh, Liq. Cryst., 2019 DOI:10.1080/02678292.2019.1647569.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01511c |
| This journal is © the Owner Societies 2020 |