 Open Access Article
Open Access ArticlePhotophysical properties of the triangular [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) COH)]3 complex and its dimer†
COH)]3 complex and its dimer†
Jonas
Greiner
 a,
Rashid R.
Valiev
a,
Rashid R.
Valiev
 bc and
Dage
Sundholm
bc and
Dage
Sundholm
 *d
*d
aInstitut für Physikalische Chemie, Johannes Gutenberg-Universität Mainz, Duesbergweg 10-14, D-55128 Mainz, Germany. E-mail: jgreiner@students.uni-mainz.de
bInstitute for Atmospheric and Earth System Research, Faculty of Science, FIN-00014 University of Helsinki, Finland. E-mail: valievrashid@gmail.com
cTomsk State University, Lenin Avenue 36, Tomsk 634050, Russia
dDepartment of Chemistry, Faculty of Science, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014 University of Helsinki, Finland. E-mail: Dage.Sundholm@helsinki.fi
First published on 17th April 2020
Abstract
Rate constants for radiative and non-radiative transitions of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex and its dimer were calculated within the Herzberg–Teller approximation based on quantum mechanical principles. A high triplet quantum yield was estimated for the monomer. Internal conversion (IC) was found to be the major competing process to the intersystem crossing (ISC) from the lowest excited singlet state (S1) to the lowest triplet state (T1). ISC and IC from the spin-mixed
COH)]3 complex and its dimer were calculated within the Herzberg–Teller approximation based on quantum mechanical principles. A high triplet quantum yield was estimated for the monomer. Internal conversion (IC) was found to be the major competing process to the intersystem crossing (ISC) from the lowest excited singlet state (S1) to the lowest triplet state (T1). ISC and IC from the spin-mixed ![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 state also dominate the triplet relaxation process resulting in a negligible phosphorescence quantum yield for the monomer. The IC and ISC rate constants of the dimer are considerably smaller due to much lower Franck–Condon factors. For the dimer a triplet quantum yield of 0.71 was estimated using the extended multi-configuration quasi-degenerate second-order perturbation theory (XMCQDPT2) method to calculate the transition energies. Fluorescence is the major competing process to the ISC relaxation of the S1 state of the dimer. The ISC and IC processes are insignificant for the relaxation of the T1 state, resulting in unity phosphorescence quantum yield. The high triplet and phosphorescence quantum yields of the [Au(HN
1 state also dominate the triplet relaxation process resulting in a negligible phosphorescence quantum yield for the monomer. The IC and ISC rate constants of the dimer are considerably smaller due to much lower Franck–Condon factors. For the dimer a triplet quantum yield of 0.71 was estimated using the extended multi-configuration quasi-degenerate second-order perturbation theory (XMCQDPT2) method to calculate the transition energies. Fluorescence is the major competing process to the ISC relaxation of the S1 state of the dimer. The ISC and IC processes are insignificant for the relaxation of the T1 state, resulting in unity phosphorescence quantum yield. The high triplet and phosphorescence quantum yields of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer make it and its higher oligomers potential candidates as dopants for phosphorescent organic light emitting diodes and as down-converters in solid-state lighting systems.
COH)]3 dimer make it and its higher oligomers potential candidates as dopants for phosphorescent organic light emitting diodes and as down-converters in solid-state lighting systems.
1 Introduction
The incorporation of gold atoms into organic molecules to form organogold compounds has lead to many interesting structures that have been studied experimentally and theoretically for their optical properties and their ability to form metallophilic bonds.1–17 Many organogold complexes exhibit high intensity and short phosphorescence lifetime at room temperature.6,7,9,18 Therefore, compounds such as the trinuclear gold(I) carbeniate complexes [Au(RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COR′)]3 studied in this work are of considerable interest due to their optoelectronic properties. Gold(I) complexes are often able to form intermolecular bonds energetically comparable to hydrogen bonds that are based on strong aurophilic interactions.11,19–21 These interactions influence the solid state structures and are strong enough to affect the properties of the molecules in solution.22–25 Due to these interactions [Au(RN
COR′)]3 studied in this work are of considerable interest due to their optoelectronic properties. Gold(I) complexes are often able to form intermolecular bonds energetically comparable to hydrogen bonds that are based on strong aurophilic interactions.11,19–21 These interactions influence the solid state structures and are strong enough to affect the properties of the molecules in solution.22–25 Due to these interactions [Au(RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COR′)]3 complexes can assemble into dimers, trimers and oligomers and form extended chains in the solid state.18,26–30
COR′)]3 complexes can assemble into dimers, trimers and oligomers and form extended chains in the solid state.18,26–30
The [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 compound studied in this work has to our knowledge not been synthesized. Therefore there are no comparable experimental properties available. However, [Au(HN
COH)]3 compound studied in this work has to our knowledge not been synthesized. Therefore there are no comparable experimental properties available. However, [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 can be treated as a model system for the [Au(RN
COH)]3 can be treated as a model system for the [Au(RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COR′)]3 group of compounds. The prominent example for this structure is [Au(MeN
COR′)]3 group of compounds. The prominent example for this structure is [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3, first synthesized by Minghetti et al.31 There has been much experimental and computational investigation into this compound, especially concerning its solvoluminescent properties.18,26–29,32–37 After irradiating the hexagonal crystals of this compound with near-UV light and adding a drop of solvent a bright yellow flash can be observed.26,32 This solvoluminescence has been explained by the excitation of [Au(MeN
COMe)]3, first synthesized by Minghetti et al.31 There has been much experimental and computational investigation into this compound, especially concerning its solvoluminescent properties.18,26–29,32–37 After irradiating the hexagonal crystals of this compound with near-UV light and adding a drop of solvent a bright yellow flash can be observed.26,32 This solvoluminescence has been explained by the excitation of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 in the solid state resulting in luminescence emission from dimers in the solution.37 Better solvents for this compound lead to higher luminescence intensity.33 In its solid state [Au(MeN
COMe)]3 in the solid state resulting in luminescence emission from dimers in the solution.37 Better solvents for this compound lead to higher luminescence intensity.33 In its solid state [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 exhibits white light emission in the visible region (400 nm to 700 nm) which has been explained through the combination of two bands: a blue band that results from the solid state band gap and leads to a contraction of the intermolecular Au–Au-distances upon excitation and an orange-red band that arises from trapped excitons within the disordered stacks of the structure.18 Crystallized needles of [Au(MeN
COMe)]3 exhibits white light emission in the visible region (400 nm to 700 nm) which has been explained through the combination of two bands: a blue band that results from the solid state band gap and leads to a contraction of the intermolecular Au–Au-distances upon excitation and an orange-red band that arises from trapped excitons within the disordered stacks of the structure.18 Crystallized needles of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 have also been used as a molecular nanowire to fabricate p-type semiconductors in an organic field transistor.18
COMe)]3 have also been used as a molecular nanowire to fabricate p-type semiconductors in an organic field transistor.18
[Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 could be of interest for diode lighting applications due to its broad white light emission. The white color produced by one phosphor is not susceptible to visual discoloration effects over the diodes lifespan, which is problematic when mixing the colors of multiple fluorophors or phosphors with different lifetimes.18 Therefore, this phosphor could be used as a down-converter in conjunction with regular light emitting diodes (LEDs) or organic light emitting diodes (OLEDs).38,39 Due to their high phosphorescence intensity in the solid state, gold(I) carbeniate complexes are also possible candidates as dopants in phosphorescent organic light emitting diodes (PhOLEDs).38,40 These potential applications validate an investigation into the energies, kinetics and lifetimes of the electronic states of these systems. Efficient PhOLED applications require short phosphorescence lifetimes and large intersystem crossing (ISC) rates to ensure that both triplet and singlet excitons generated through charge injection are utilized effectively for visible light emission. This would yield near 100% quantum efficiency that could potentially reduce the power consumption by 75% compared to high quantum yield fluorescent OLEDs.38,40 The ability to transform singlet excitons into triplet excitons through ISC is even more important for down-conversion phosphor applications as this method solely produces singlet excited states.39
COMe)]3 could be of interest for diode lighting applications due to its broad white light emission. The white color produced by one phosphor is not susceptible to visual discoloration effects over the diodes lifespan, which is problematic when mixing the colors of multiple fluorophors or phosphors with different lifetimes.18 Therefore, this phosphor could be used as a down-converter in conjunction with regular light emitting diodes (LEDs) or organic light emitting diodes (OLEDs).38,39 Due to their high phosphorescence intensity in the solid state, gold(I) carbeniate complexes are also possible candidates as dopants in phosphorescent organic light emitting diodes (PhOLEDs).38,40 These potential applications validate an investigation into the energies, kinetics and lifetimes of the electronic states of these systems. Efficient PhOLED applications require short phosphorescence lifetimes and large intersystem crossing (ISC) rates to ensure that both triplet and singlet excitons generated through charge injection are utilized effectively for visible light emission. This would yield near 100% quantum efficiency that could potentially reduce the power consumption by 75% compared to high quantum yield fluorescent OLEDs.38,40 The ability to transform singlet excitons into triplet excitons through ISC is even more important for down-conversion phosphor applications as this method solely produces singlet excited states.39
The phosphorescence quantum yield is obtained as41,42
 | (1) |
 | (2) |
The fluorescence rate from state S1 can be approximated from oscillator strengths using the Strickler–Berg equation.45 Spin–orbit coupling has to be considered for transition processes between states of different multiplicity such as ISC and phosphorescence. Instead of using the exact two-component or the Breit-Pauli-Hamiltonian the spin–orbit coupling can be approximated as an effective one-electron operator (ĤSO). This operator can be treated as a perturbation if the spin–orbit coupling is small compared to the transition energy of the involved states, which was found to be true for all systems treated in this work. The lifetime and phosphorescence rate of the triplet state can be calculated from the transition strengths.46 The non-radiative transition rate constants are calculated using a method developed by Valiev et al.,43,44 where the expression for the rate constant of internal conversion is
 | (3) |
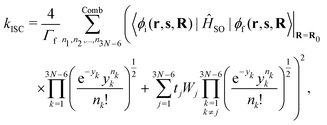 | (4) |
 | (5) |
 | (6) |
 and the electronic wave functions are needed for calculation of kIC between S1 and S0. Matrix elements of the spin–orbit coupling operator and the electronic wave functions are needed for calculation of kISC between S1 and T1 and between T1 and S0.
and the electronic wave functions are needed for calculation of kIC between S1 and S0. Matrix elements of the spin–orbit coupling operator and the electronic wave functions are needed for calculation of kISC between S1 and T1 and between T1 and S0.
Spin–orbit coupling between the triplet state T1 and the singlet states of the system leads to a spin-mixed ![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 state. IC from
1 state. IC from ![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 to S0 is possible and is another process that competes with the phosphorescence and ISC transition from T1.47,48
1 to S0 is possible and is another process that competes with the phosphorescence and ISC transition from T1.47,48
2 Computational methods
Density functional theory (DFT) optimizations of the ground and excited state molecular structures and calculations of the vibrational frequencies were carried out with Turbomole49–52 using the Karlsruhe triple-zeta basis set augmented with a double set of polarization functions (def2-TZVPP),53,54 the B3-LYP functional55–57 and the m5 integration grid.58 No symmetry constraints were imposed. The 60 inner electrons of the gold atoms were replaced by an effective core-potential (ECP) to consider scalar relativistic effects and to reduce computational costs.59 Dispersion corrections have to be taken into account to describe gold–gold interactions accurately. The D3-BJ dispersion correction was used in all DFT calculations.60 The optimized ground state molecular structures are shown in Fig. 1. The singlet excited state geometries were optimized using the time-dependent DFT (TD-DFT) method using the B3-LYP functional.55–57,61–64 The molecular structures of the lowest triplet state were calculated using unrestricted ground state DFT with a triplet occupation.51 | ||
| Fig. 1 Molecular ground state structures of the studied molecules. H in white, C in grey, N in blue, O in red and Au in yellow. The graphics were created using Avogadro.65,66 | ||
The ground state vibrational frequencies were calculated from the analytic second derivative of the energy using the AOFORCE module.67,68 The second derivatives of the excited states of the molecules were calculated numerically from the analytical gradients using the NUMFORCE module.
The excitation energies and oscillator strengths were calculated using the molecular structures optimized at the DFT and TD-DFT levels. We employed TD-DFT calculations61,62,64 and second-order approximate coupled-cluster theory (CC2) calculations using the resolution-of-the-identity approximation69,70 implemented in the Turbomole program49,50,52 as well as calculations at the extended multi-configuration quasi-degenerate second-order perturbation theory (XMCQDPT2) level71 implemented in the Firefly program.72 This procedure was chosen because the involved states may exhibit multireference character and because accurate excitation energies are needed for the calculation of rate constants. Active spaces consisting of 12 electrons in 12 molecular orbitals and 8 electrons in 9 molecular orbitals were chosen in the multireference calculations of the monomer and the dimer, respectively.
The non-adiabatic coupling matrix elements73 were calculated with Turbomole at the TD-DFT level using the S1 geometry.49,50,52 The spin–orbit coupling (SOC) matrix elements74 were computed with GAMESS-US75,76 at the complete active space self-consistent field (CAS-SCF) level using the full Breit-Pauli spin–orbit operator. The molecular structures of the S1 and T1 states were used in the SOC calculations.
The fluorescence rates (kr) were obtained from the oscillator strengths using the Strickler–Berg equation.45 The phosphorescence rates (kphos) were calculated using perturbation theory (PT) with Turbomole49,50,52 at the SOC-PT-CC2 level46 using the TD-DFT geometries. The IC and ISC rate constants (kIC and kISC) were calculated within the Herzberg–Teller approximation77 using the methodology developed by Valiev et al.43,44 The IC rate constant from the ![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 state to the S0 ground state was calculated from the state mixing coefficients and the excitation energies using the formula by Artyukhov et al.47,48
1 state to the S0 ground state was calculated from the state mixing coefficients and the excitation energies using the formula by Artyukhov et al.47,48
3 Results and discussion
3.1 Monomer
The ground state of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex is a planar molecule belonging to the C3h point group. The lowest excited singlet and triplet states break the planar symmetry of the ground state by moving an OH group and a NH group out of the plane. Two enantiomers are possible due to the chiral nature of the molecular structure of the excited states. The optimized ground and excited state structures of the [Au(HN
COH)]3 complex is a planar molecule belonging to the C3h point group. The lowest excited singlet and triplet states break the planar symmetry of the ground state by moving an OH group and a NH group out of the plane. Two enantiomers are possible due to the chiral nature of the molecular structure of the excited states. The optimized ground and excited state structures of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex are shown in Fig. 2. The vertical excitation energies calculated for the molecular structure of the excited states of the monomer at the TD-DFT, CC2 and XMCQDPT2 levels are reported in Table 1.
COH)]3 complex are shown in Fig. 2. The vertical excitation energies calculated for the molecular structure of the excited states of the monomer at the TD-DFT, CC2 and XMCQDPT2 levels are reported in Table 1.
 | ||
Fig. 2 The molecular structures of the lowest electronic states of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex. H in white, C in grey, N in blue, O in red and Au in yellow. The graphics were created using Avogadro.65,66 COH)]3 complex. H in white, C in grey, N in blue, O in red and Au in yellow. The graphics were created using Avogadro.65,66 | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex at the respective equilibrium geometries of the excited state calculated at the TD-DFT, CC2 and XMCQDPT2 levels
COH)]3 complex at the respective equilibrium geometries of the excited state calculated at the TD-DFT, CC2 and XMCQDPT2 levels
| Structure | Transition | TD-DFT | CC2 | XMCQDPT2 |
|---|---|---|---|---|
| S0 | S0 → S1 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741 (4.803) 741 (4.803) |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224 (5.359) 224 (5.359) |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 (5.220) 100 (5.220) |
| S1 | S1 → S0 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 (2.008) 197 (2.008) |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 973 (1.980) 973 (1.980) |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 (2.100) 939 (2.100) |
| T1 | T1 → S0 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 (1.405) 333 (1.405) |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 (1.543) 448 (1.543) |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503 (1.798) 503 (1.798) |
The de-excitation energies for the S1 → S0 transition calculated at the three levels of theory agree within 0.12 eV, whereas the calculated values for the transition energy from the lowest triplet state (T1) to S0 calculated at the B3-LYP level is 0.4 eV smaller than the XMCQDPT2 value. The phosphorescence energy of the T1 state calculated at the CC2 level is 0.25 eV smaller than obtained in the XMCQDPT2 calculation. The differences between the singlet and triplet excitation energies calculated at the B3-LYP, CC2, and XMCQDPT2 levels using the S1 geometry are 0.247, 0.122, and 0.186 eV, respectively. B3-LYP has a tendency to underestimate excitation energies of triplet states,78 whereas a comprehensive benchmark study showed that CC2 triplet energies are in good agreement with reference data.79 It is not elucidated whether the excitation energies calculated at the CC2 or the XMCQDPT2 level are more accurate, since XMCQDPT2 excitation energies have never been properly benchmarked. However, the employed multi-state XMCQDPT2 approach is expected to treat the excited states in a more balanced manner than low-order single-reference methods implying that the energy difference between the S1 and T1 states is most likely more accurate at the XMCQDPT2 level than obtained in the CC2 calculations.
A very large Stokes shift of more than 2.7 eV was obtained using all three methods, which can be attributed to the differences in the equilibrium structures of the ground state and the excited states. The molecular structures of the singlet and triplet excited states as well as their excitation energies are similar, which means that little vibrational relaxation is necessary for the ISC process from S1 to T1. The [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 molecule absorbs light in the UV region and emits between 400 nm and 450 nm in chloroform solution.18,26,32 The fact that the calculated de-excitation energies are much smaller than the experimental emission energies suggests that the monomer is not the emitting species in solution.
COMe)]3 molecule absorbs light in the UV region and emits between 400 nm and 450 nm in chloroform solution.18,26,32 The fact that the calculated de-excitation energies are much smaller than the experimental emission energies suggests that the monomer is not the emitting species in solution.
Photophysical properties have also been calculated at the different levels of theory. The calculated oscillator strengths, spin–orbit coupling matrix elements and phosphorescence lifetimes at their respective level of theory are presented in Table 2. The radiative and non-radiative rate constants were calculated using both CC2 and XMCQDPT2 transition energies. The phosphorescence lifetime was only calculated at the CC2 level. The obtained results are presented in Table 3.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex calculated at the given levels of theory
COH)]3 complex calculated at the given levels of theory
| f(S1 → S0) | 〈S1|ĤSO|T1〉 | 〈T1|ĤSO|S0〉 | τ | |
|---|---|---|---|---|
| CC2 | XMCQDPT2 | CAS-SCF | CAS-SCF | CC2 |
| 0.003 | 0.003 | 4 cm−1 | 28 cm−1 | 0.13 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex calculated at the CC2 and XMCQDPT2 levels of theory
COH)]3 complex calculated at the CC2 and XMCQDPT2 levels of theory
| Level | k r | k IC | k ISC | k phos |
|---|---|---|---|---|
| S1 → S0 | ||||
| CC2 | 5 × 105 s−1 | 2 × 1010 s−1 | ||
| XMCQDPT2 | 5 × 105 s−1 | 7 × 109 s−1 | ||
| S1 → T1 | ||||
| CC2 | 3 × 1010 s−1 | |||
| XMCQDPT2 | 2 × 1010 s−1 | |||
| T1 → S0 | ||||
| CC2 | 2 × 103 s−1 | 1 × 104 s−1 | 8 s−1 | |
| XMCQDPT2 | 2 × 103 s−1 | 8 × 103 s−1 | — | |
The strong spin–orbit coupling between S1 and T1 and the large Franck–Condon factors of the S1 → T1 transition are responsible for the fast ISC rate, which leads to large triplet quantum yields. The Franck–Condon factors are large, because high-energy vibrational modes have significant vibronic coupling due to small differences in the molecular structures of the two excited states. The small energy gap between S1 and T1 also leads to large Franck–Condon factors, because only low excitations of the vibrational modes are needed to fulfill the energy conservation condition of the transition.
The IC from S1 to S0 is the main competing process to ISC, even though the energy difference between S1 and S0 is much larger than between S1 and T1. Large Franck–Condon factors were obtained for the S1 → S0 transition due to a strong non-adiabatic coupling, which results in a large rate constant for the IC process.
Fluorescence from S1 is insignificant because the oscillator strength between S1 and S0 is very small. A slow phosphorescence rate was obtained for the monomer, which leads to a long phosphorescence lifetime of 0.13. Strong spin–orbit and vibronic coupling between T1 and S0 cause the ISC and IC processes from the spin-mixed ![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 state to dominate the triplet relaxation process resulting in a negligible phosphorescence quantum yield.
1 state to dominate the triplet relaxation process resulting in a negligible phosphorescence quantum yield.
The results calculated at the CC2 and XMCQDPT2 levels are quite similar. The very small differences in the IC and ISC rate constants obtained at the two levels stem from the similar energy differences reported in Table 1. The XMCQDPT2 calculations yield larger energy gaps as well as smaller kISC and kIC rate constants. A larger number of combined vibrational transitions is therefore necessary to fulfill the energy conservation condition, which leads to smaller Franck–Condon factors and slower IC and ISC rates. The larger kISC/kIC ratio obtained in the XMCQDPT2 calculations leads to a slightly larger triplet quantum yield. The calculated triplet and phosphorescence quantum yields are reported in Table 4. The rate constants calculated at the XMCQDPT2 level are summarized in the Jablonski diagram in Fig. 3.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 complex calculated at the CC2 and XMCQDPT2 levels
COH)]3 complex calculated at the CC2 and XMCQDPT2 levels
| Level | ϕ T | ϕ phos |
|---|---|---|
| CC2 | 0.60 | 0.0007 |
| XMCQDPT2 | 0.74 | 0.0007 |
The monomer is not suitable for optoelectronic applications because non-radiative transitions dominate the relaxation of the singlet and triplet excited states. Comparison of excitation energies and prior research also suggest that the monomer is neither the emitting species in the solution nor in the solid state.
3.2 Dimer
In the ground state, two planar monomers form a stacked slided dimer. The intermolecular Au–Au distances are reduced upon excitation and the parallelism of the monomers is broken. The OH and NH groups move out of the monomer planes. The structural differences between the equilibrium structures of the singlet and triplet excited states of the dimer are larger than for the monomer. The optimized ground and excited state structures of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer shown in Fig. 4 were obtained by using the staggered structure as initial structure. Excitation energies for different molecular structures of the dimer calculated at the TD-DFT, CC2 and XMCQDPT2 levels are reported in Table 5.
COH)]3 dimer shown in Fig. 4 were obtained by using the staggered structure as initial structure. Excitation energies for different molecular structures of the dimer calculated at the TD-DFT, CC2 and XMCQDPT2 levels are reported in Table 5.
 | ||
Fig. 4 The molecular structures of the lowest electronic states of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer. H in white, C in grey, N in blue, O in red and Au in yellow. The graphics were created using Avogadro.65,66 COH)]3 dimer. H in white, C in grey, N in blue, O in red and Au in yellow. The graphics were created using Avogadro.65,66 | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer at the respective equilibrium geometries of the excited state calculated at the TD-DFT, CC2 and XMCQDPT2 levels
COH)]3 dimer at the respective equilibrium geometries of the excited state calculated at the TD-DFT, CC2 and XMCQDPT2 levels
| Structure | Transition | TD-DFT | CC2 | XMCQDPT2 |
|---|---|---|---|---|
The peak maximum of the solvoluminescence emission band between 510 and 620 nm is at 552 nm, which corresponds to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 or 2.25 eV.26 100 cm−1 or 2.25 eV.26 |
||||
| S0 | S0 → S1 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089 (3.979) 089 (3.979) |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 (4.491) 225 (4.491) |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 (3.986) 150 (3.986) |
| S1 | S1 → S0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 (2.973) 981 (2.973) |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 (3.399) 414 (3.399) |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 (3.215) 931 (3.215) |
| T1 | T1 → S0 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 (1.637) 202 (1.637) |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 (1.828) 745 (1.828) |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 507 (2.047) 507 (2.047) |
The Stokes shift of the S1 state of about 1 eV between absorption and fluorescence is much smaller than for the monomer. The de-excitation energies of the S1 and T1 states as well as the difference between them are larger than in the case of the monomer. A large amount of vibrational relaxation is therefore necessary for the ISC process from S1 to T1 due to the large difference between the singlet and triplet de-excitation energies. The difference between the singlet and triplet excitation energies calculated using the S1 geometry is small. At the B3-LYP, CC2, and XMCQDPT2 levels they are only 0.102, 0.090, and 0.038 eV, respectively. Thus, structural relaxation leads to the large energy difference between S1 and T1. The large structural differences between S0 and T1 result in a very large Stokes shift of more than 2.3 eV between absorption and phosphorescence, which is also observed experimentally for [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3. Experimentally, [Au(MeN
COMe)]3. Experimentally, [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 absorbs at 230 nm and 300 nm, while the emission occurs between 400 nm and 450 nm.18,26,32 The same emission can also be assigned to the molecule-like orange-red component of the solid-state emission, which has been explained by the de-excitation of dimer subunits in the solid state that also exhibits a large Stokes shift.18 The calculated excitation energy of the [Au(HN
COMe)]3 absorbs at 230 nm and 300 nm, while the emission occurs between 400 nm and 450 nm.18,26,32 The same emission can also be assigned to the molecule-like orange-red component of the solid-state emission, which has been explained by the de-excitation of dimer subunits in the solid state that also exhibits a large Stokes shift.18 The calculated excitation energy of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer fits well into the experimental absorption energy range of [Au(MeN
COH)]3 dimer fits well into the experimental absorption energy range of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3. The triplet emission energy is too small compared to the one measured for [Au(MeN
COMe)]3. The triplet emission energy is too small compared to the one measured for [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3. Calculations have shown that the higher emission energies can be reproduced when studying [Au(MeN
COMe)]3. Calculations have shown that the higher emission energies can be reproduced when studying [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 instead of the [Au(HN
COMe)]3 instead of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 model compound.37 A direct comparison of the calculated dimer emission energies and the experimental emission spectrum may be difficult due to complexities of aggregate emission.80
COH)]3 model compound.37 A direct comparison of the calculated dimer emission energies and the experimental emission spectrum may be difficult due to complexities of aggregate emission.80
Photophysical properties of the dimer have been calculated at different levels of theory. The calculated oscillator strengths, spin–orbit coupling matrix elements, and phosphorescence lifetimes at their respective level of theory are listed in Table 6. The rate constants of the radiative and non-radiative transitions were calculated using CC2 and XMCQDPT2 transition energies. The phosphorescence lifetime was calculated only at the CC2 level. The obtained rate constants are summarized in Table 7.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer calculated at the given levels of theory
COH)]3 dimer calculated at the given levels of theory
| f(S1→S0) | 〈S1|ĤSO|T1〉 | 〈T1|ĤSO|S0〉 | τ | |
|---|---|---|---|---|
| CC2 | XMCQDPT2 | CAS-SCF | CAS-SCF | CC2 |
| 0.02 | 0.04 | 0.27 cm−1 | 1.6 cm−1 | 0.19 s |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer calculated at the CC2 and XMCQDPT2 levels of theory
COH)]3 dimer calculated at the CC2 and XMCQDPT2 levels of theory
| Level | k r | k IC | k ISC | k phos |
|---|---|---|---|---|
| S1 → S0 | ||||
| CC2 | 1 × 107 s−1 | 5 × 10−4 s−1 | ||
| XMCQDPT2 | 2 × 107 s−1 | 1 × 10−1 s−1 | ||
| S1 → T1 | ||||
| CC2 | 5 × 106 s−1 | |||
| XMCQDPT2 | 5 × 107 s−1 | |||
| T1 → S0 | ||||
| CC2 | 0 s−1 | 0 s−1 | 5 s−1 | |
| XMCQDPT2 | 0 s−1 | 0 s−1 | — | |
The oscillator strength of the de-excitation from S1 to S0 is an order of magnitude larger than for the monomer leading to a higher fluorescence rate, which makes fluorescence the main competing process to the ISC from S1 to T1. The spin–orbit couplings between the ground state, the lowest excited singlet state and the lowest triplet state of the dimer are much smaller than for the monomer. Therefore, the ISC and the phosphorescence processes of the dimer are slower than for the monomer. The ISC process from S1 to T1 is still much faster than the IC process and slightly faster than the fluorescence due to the small transition energy for the S1 structure. The significant differences between the excited state structures leads to strong vibronic coupling of the vibrational modes, which results in a high yield of the triplet state at the XMCQDPT2 level. The IC rate from S1 is slow due to the small Franck–Condon factors and the large energy of the S1 → S0 transition. The small Franck–Condon factors can be explained by the strong intermolecular aurophilic interactions that lead to dimer formation. The out-of-plane vibrational modes are sterically hindered in the dimer preventing vibrational relaxation through these modes. The constraints on the vibrational modes also affect the IC and ISC processes of the T1 state. The IC and ISC rates are therefore insignificant for the T1 → S0 transition leading to unity phosphorescence quantum yield. An increased quantum yield has been attributed to small Franck–Condon factors in the past.81
For the dimer, there are significant differences between the rate constants calculated using the CC2 and XMCQDPT2 transition energies. The IC and ISC rate constants from S1 are larger at the XMCQDPT2 level, because the de-excitation energy of the S1 state is smaller than obtained in the CC2 calculations. The XMCQDPT2 triplet quantum yield is therefore much higher than obtained at the CC2 level. The fluorescence rate from the S1 state is also faster at the XMCQDPT2 level, because the oscillator strength is twice as large as the value calculated with CC2. The calculated triplet and phosphorescence quantum yields are reported in Table 8. The rate constants calculated at the XMCQDPT2 level are summarized in the Jablonski diagram in Fig. 5.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer calculated at the CC2 and XMCQDPT2 levels
COH)]3 dimer calculated at the CC2 and XMCQDPT2 levels
| Level | ϕ T | ϕ phos |
|---|---|---|
| CC2 | 0.33 | 1.00 |
| XMCQDPT2 | 0.71 | 1.00 |
The dimer displays long lifetime phosphorescence with unity quantum yield and may therefore be the species responsible for the solvoluminescent properties of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3. Thus, when dissolving [Au(MeN
COMe)]3. Thus, when dissolving [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 crystals, the excited state transfers from the solid state to the dimer in solution leading to a long-lived phosphorescent emission that is visible by the naked eye.26,32,37 The fact that the intensity increases in good solvents of [Au(MeN
COMe)]3 crystals, the excited state transfers from the solid state to the dimer in solution leading to a long-lived phosphorescent emission that is visible by the naked eye.26,32,37 The fact that the intensity increases in good solvents of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 further supports this notion.33 There is a large difference between the triplet quantum yields calculated using the two methods. The high phosphorescence quantum yield of the [Au(MeN
COMe)]3 further supports this notion.33 There is a large difference between the triplet quantum yields calculated using the two methods. The high phosphorescence quantum yield of the [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 dimer could validate further investigations of the [Au(RN
COMe)]3 dimer could validate further investigations of the [Au(RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COR′)]3 group of compounds as potential candidates for down-conversion phosphors and as dopants for PhOLEDs. The relaxation of the excited states of the dimer is dominated by the radiative channels. Depending on the employed method, 30% to 70% of the generated singlet states lead to fluorescence on the violet side of the visible spectrum, while the rest of the excited state relaxation happens through phosphorescence on the orange-red side of the spectrum. Triplet and singlet excited states are obtained in a ratio of 3 to 1, when they are created through charge injection. Therefore, a high triplet quantum yield is not as important as the unity phosphorescence quantum yield for PhOLED applications. In the solid state of [Au(MeN
COR′)]3 group of compounds as potential candidates for down-conversion phosphors and as dopants for PhOLEDs. The relaxation of the excited states of the dimer is dominated by the radiative channels. Depending on the employed method, 30% to 70% of the generated singlet states lead to fluorescence on the violet side of the visible spectrum, while the rest of the excited state relaxation happens through phosphorescence on the orange-red side of the spectrum. Triplet and singlet excited states are obtained in a ratio of 3 to 1, when they are created through charge injection. Therefore, a high triplet quantum yield is not as important as the unity phosphorescence quantum yield for PhOLED applications. In the solid state of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3, the orange-yellow phosphorescence band resulting from dimer subunits within the solid state structure and the blue band resulting from the solid state band gap combine leading to white light emission.18 The high efficiency of the dimeric emission could qualify this compound for the use in solid-state lighting systems.
COMe)]3, the orange-yellow phosphorescence band resulting from dimer subunits within the solid state structure and the blue band resulting from the solid state band gap combine leading to white light emission.18 The high efficiency of the dimeric emission could qualify this compound for the use in solid-state lighting systems.
4 Conclusion
Rate constants for internal conversion (IC) and intersystem crossing (ISC) have been calculated within the Herzberg–Teller approximation using ab initio methods. The relaxation pathway of the lowest excited singlet state is obtained by comparing calculated rate constants of the IC and ISC processes to the calculated rate constants for the fluorescence and phosphorescence emission. The calculations also show how energy differences and Franck–Condon factors affect the relaxation pathway of the lowest singlet state.The calculation of radiative and non-radiative transition rates of the [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 monomer showed that this compound is not suitable for optoelectronic applications, because non-radiative transitions are the dominating decay channels of the lowest excited states. The calculated emission energies are also very low compared to the experimental luminescence energies of [Au(MeN
COH)]3 monomer showed that this compound is not suitable for optoelectronic applications, because non-radiative transitions are the dominating decay channels of the lowest excited states. The calculated emission energies are also very low compared to the experimental luminescence energies of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3. The higher experimental de-excitation energies can be explained by dimer formation due to intermolecular aurophilic interactions. Another indication that the dimer might be the emissive species is the experimentally observed large Stokes shift that is also obtained in the phosphorescence calculation for the dimer of the model system but not for the monomer. The [Au(HN
COMe)]3. The higher experimental de-excitation energies can be explained by dimer formation due to intermolecular aurophilic interactions. Another indication that the dimer might be the emissive species is the experimentally observed large Stokes shift that is also obtained in the phosphorescence calculation for the dimer of the model system but not for the monomer. The [Au(HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH)]3 dimer has a high triplet and phosphorescence quantum yield at a wavelength of about 600 nm. The long phosphorescence lifetime can explain the yellow solvoluminescence of [Au(MeN
COH)]3 dimer has a high triplet and phosphorescence quantum yield at a wavelength of about 600 nm. The long phosphorescence lifetime can explain the yellow solvoluminescence of [Au(MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COMe)]3 that has been observed in good solvents after irradiation of the crystals with UV light. The photophysical properties of the model system dimer make the [Au(RN
COMe)]3 that has been observed in good solvents after irradiation of the crystals with UV light. The photophysical properties of the model system dimer make the [Au(RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COR′)]3 dimer and its oligomers potential candidates as dopants for PhOLEDs and as down-conversion phosphors in solid state lighting applications.
COR′)]3 dimer and its oligomers potential candidates as dopants for PhOLEDs and as down-conversion phosphors in solid state lighting applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Academy of Finland through projects 314821 and 325369, the Swedish Cultural Foundation in Finland, and Magnus Ehrnrooth Foundation. J. G. thanks the ERASMUS+ SMP program for financial support. The CSC – the Finnish IT Center for Science and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) are acknowledged for computer time.References
- H. Schmidbaur, Gold Bull., 1990, 23, 11–21 CrossRef CAS
.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456 CrossRef PubMed
.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412 RSC
.
- F. Scherbaum, A. Grohmann, B. Huber, C. Krüger and H. Schmidbaur, Angew. Chem., Int. Ed. Engl., 1988, 27, 1544–1546 CrossRef
.
- H. H. Murray, R. G. Raptis and J. P. Fackler, Inorg. Chem., 1988, 27, 26–33 CrossRef CAS
.
- C. King, J. C. Wang, M. N. I. Khan and J. P. Fackler, Inorg. Chem., 1989, 28, 2145–2149 CrossRef CAS
.
- V. W.-W. Yam and K. K.-W. Lo, Chem. Soc. Rev., 1999, 28, 323–334 RSC
.
- E. J. Fernández, M. C. Gimeno, A. Laguna, J. M. L. de Luzuriaga, M. Monge, P. Pyykkö and D. Sundholm, J. Am. Chem. Soc., 2000, 122, 7287–7293 CrossRef
.
- Q.-M. Wang, Y.-A. Lee, O. Crespo, J. Deaton, C. Tang, H. J. Gysling, M. C. Gimeno, C. Larraz, M. D. Villacampa, A. Laguna and R. Eisenberg, J. Am. Chem. Soc., 2004, 126, 9488–9489 CrossRef CAS PubMed
.
- K. M.-C. Wong, X. Zhu, L.-L. Hung, N. Zhu, V. W.-W. Yam and H.-S. Kwok, Chem. Commun., 2005, 2906 RSC
.
- F. Mendizabal, D. Reyes and C. Olea-Azar, Int. J. Quantum Chem., 2005, 106, 906–912 CrossRef
.
- A. Kishimura, T. Yamashita and T. Aida, J. Am. Chem. Soc., 2005, 127, 179–183 CrossRef CAS PubMed
.
- C. Yang, M. Messerschmidt, P. Coppens and M. A. Omary, Inorg. Chem., 2006, 45, 6592–6594 CrossRef CAS PubMed
.
- S. M. Tekarli, T. R. Cundari and M. A. Omary, J. Am. Chem. Soc., 2008, 130, 1669–1675 CrossRef CAS PubMed
.
- M. Rodríguez-Castillo, M. Monge, J. M. L. de Luzuriaga, M. E. Olmos, A. Laguna and F. Mendizabal, Comput. Theor. Chem., 2011, 965, 163–167 CrossRef
.
- D. Burgos, C. Olea-Azar and F. Mendizabal, J. Mol. Model., 2011, 18, 2021–2029 CrossRef PubMed
.
- F. Mendizabal and R. Salazar, J. Mol. Model., 2012, 19, 1973–1979 CrossRef PubMed
.
- R. N. McDougald, B. Chilukuri, H. Jia, M. R. Perez, H. Rabaâ, X. Wang, V. N. Nesterov, T. R. Cundari, B. E. Gnade and M. A. Omary, Inorg. Chem., 2014, 53, 7485–7499 CrossRef CAS PubMed
.
- Y. Jiang, S. Alvarez and R. Hoffmann, Inorg. Chem., 1985, 24, 749–757 CrossRef CAS
.
- P. Pyykkö and Y. Zhao, Angew. Chem., Int. Ed. Engl., 1991, 30, 604–605 CrossRef
.
- P. Pyykkö and F. Mendizabal, Inorg. Chem., 1998, 37, 3018–3025 CrossRef
.
- H. Schmidbaur, W. Graf and G. Müller, Angew. Chem., Int. Ed. Engl., 1988, 27, 417–419 CrossRef
.
- A. L. Balch, E. Y. Fung and M. M. Olmstead, J. Am. Chem. Soc., 1990, 112, 5181–5186 CrossRef CAS
.
- D. E. Harwell, M. D. Mortimer, C. B. Knobler, F. A. L. Anet and M. F. Hawthorne, J. Am. Chem. Soc., 1996, 118, 2679–2685 CrossRef CAS
.
- J. Zank, A. Schier and H. Schmidbaur, J. Chem. Soc., Dalton Trans., 1998, 323–324 RSC
.
- J. C. Vickery, M. M. Olmstead, E. Y. Fung and A. L. Balch, Angew. Chem., Int. Ed. Engl., 1997, 36, 1179–1181 CrossRef CAS
.
- R. L. White-Morris, M. M. Olmstead, F. Jiang, D. S. Tinti and A. L. Balch, J. Am. Chem. Soc., 2002, 124, 2327–2336 CrossRef CAS PubMed
.
- R. L. White-Morris, M. M. Olmstead, S. Attar and A. L. Balch, Inorg. Chem., 2005, 44, 5021–5029 CrossRef CAS PubMed
.
- F. Mendizabal, B. Aguilera and C. Olea-Azar, Chem. Phys. Lett., 2007, 447, 345–351 CrossRef CAS
.
- L. Zhu, V. Coropceanu, Y. Yi, B. Chilukuri, T. R. Cundari and J.-L. Brédas, J. Phys. Chem. Lett., 2013, 4, 2186–2189 CrossRef CAS
.
- G. Minghetti and F. Bonati, Inorg. Chem., 1974, 13, 1600–1602 CrossRef CAS
.
- E. Y. Fung, M. M. Olmstead, J. C. Vickery and A. L. Balch, Coord. Chem. Rev., 1998, 171, 151–159 CrossRef CAS
.
- M. M. Olmstead, F. Jiang, S. Attar and A. L. Balch, J. Am. Chem. Soc., 2001, 123, 3260–3267 CrossRef CAS PubMed
.
- K. Winkler, M. Wysocka-Żołopa, K. Rećko, L. Dobrzyński, J. C. Vickery and A. L. Balch, Inorg. Chem., 2009, 48, 1551–1558 CrossRef CAS PubMed
.
- F. Mendizabal, Int. J. Quantum Chem., 2009, 1279–1286 Search PubMed
.
- A. Muñoz-Castro, D. M.-L. Carey and R. Arratia-Pérez, Chem. Phys. Lett., 2009, 474, 290–293 CrossRef
.
- H. Rabaâ, M. A. Omary, S. Taubert and D. Sundholm, Inorg. Chem., 2017, 57, 718–730 CrossRef PubMed
.
- Y. Sun, N. C. Giebink, H. Kanno, B. Ma, M. E. Thompson and S. R. Forrest, Nature, 2006, 440, 908–912 CrossRef CAS PubMed
.
- J. McKittrick and L. E. Shea-Rohwer, J. Am. Ceram. Soc., 2014, 97, 1327–1352 CrossRef CAS
.
- M. A. Baldo, M. E. Thompson and S. R. Forrest, Nature, 2000, 403, 750–753 CrossRef CAS PubMed
.
- D. Escudero, Chem. Sci., 2016, 7, 1262–1267 RSC
.
- X. Zhang, D. Jacquemin, Q. Peng, Z. Shuai and D. Escudero, J. Phys. Chem. C, 2018, 122, 6340–6347 CrossRef CAS
.
- R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133 RSC
.
- R. R. Valiev, V. N. Cherepanov, R. T. Nasibullin, D. Sundholm and T. Kurten, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500 RSC
.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS
.
- B. Helmich-Paris, C. Hättig and C. van Wüllen, J. Chem. Theory Comput., 2016, 12, 1892–1904 CrossRef CAS PubMed
.
- V. Y. Artyukhov, O. K. Bazyl and G. V. Maier, J. Appl. Spectrosc., 2006, 73, 841–845 CrossRef CAS
.
- R. R. Valiev, V. N. Cherepanov, V. Y. Artyukhov and D. Sundholm, Phys. Chem. Chem. Phys., 2012, 14, 11508 RSC
.
- TURBOMOLE V7.4 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS
.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS
.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 91–100 Search PubMed
.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed
.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed
.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS
.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS
.
-
D. Rappoport and F. Furche, in Theoretical and Computational Chemistry, ed. M. Olivucci, Elsevier Science, 2005, ch. III, vol. 16 Search PubMed
.
- Avogadro: an open-source molecular builder and visualization tool. Version 1.2.0. http://avogadro.cc/.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminform., 2012, 4, 17 CrossRef CAS PubMed
.
- P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518 CrossRef CAS
.
- P. Deglmann and F. Furche, J. Chem. Phys., 2002, 117, 9535–9538 CrossRef CAS
.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154 CrossRef
.
- C. Hättig and K. Hald, Phys. Chem. Chem. Phys., 2002, 4, 2111–2118 RSC
.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed
.
- Alex A. Granovsky, Firefly version 8, http://classic.chem.msu.su/gran/firefly/index.html.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed
.
- D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592 Search PubMed
.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS
.
-
M. S. Gordon and M. W. Schmidt, Theory and Applications of Computational Chemistry, Elsevier, 2005, pp. 1167–1189 Search PubMed
.
- G. Herzberg and E. Teller, Z. Phys. Chem., 1933, 21B, 410–446 Search PubMed
.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103 CrossRef PubMed
.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed
.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed
.
- W. Cai, A. Zhao, K. Ren, R. He, M. Li and W. Shen, J. Phys. Chem. C, 2019, 123, 17968–17975 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: The Cartesian ground and excited state coordinates of the optimized molecular structures are available free of charge. See DOI: 10.1039/d0cp01406k |
| This journal is © the Owner Societies 2020 |


